Numerical Modeling of Anisotropic Particle Diffusion through a Cylindrical Channel
Abstract
:1. Introduction
2. Results and Discussion
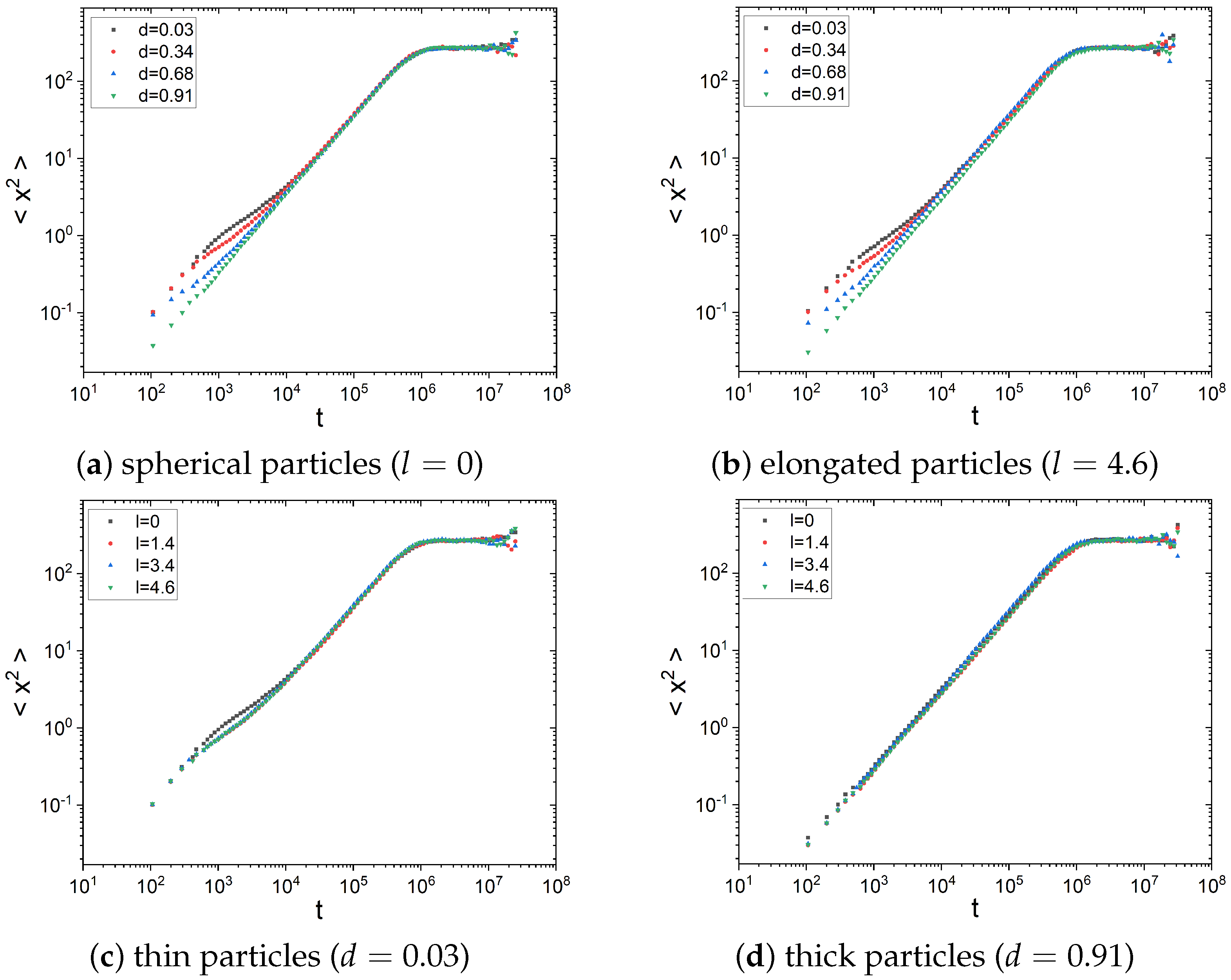
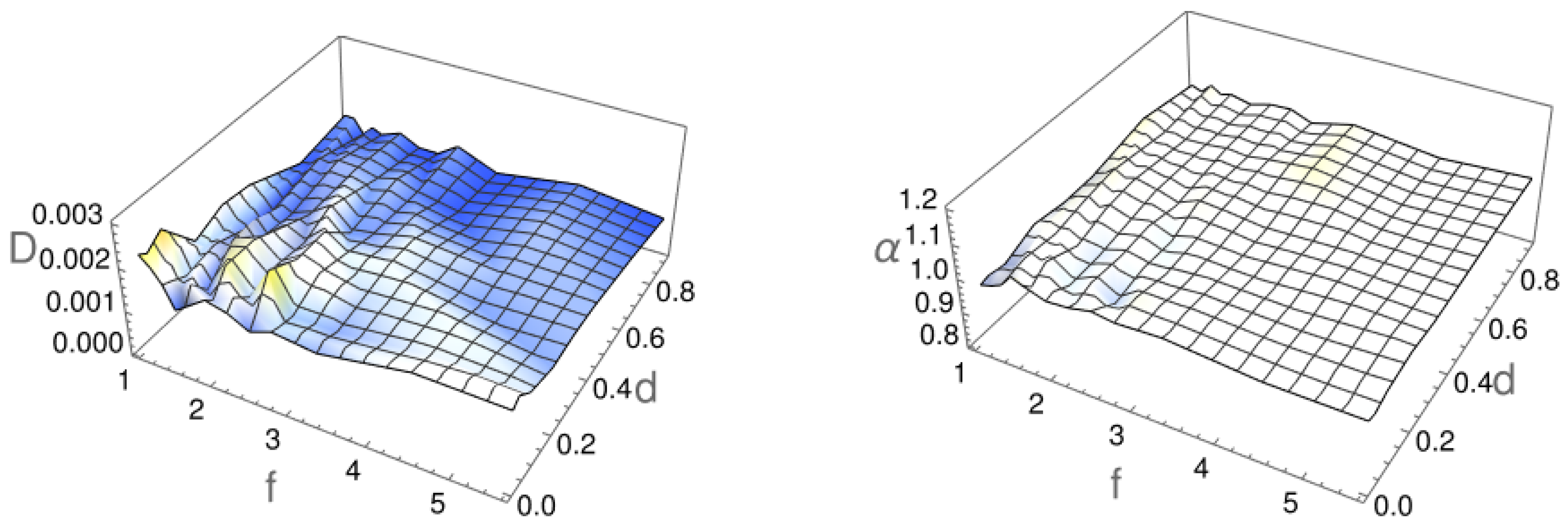
2.1. Diffusion Type
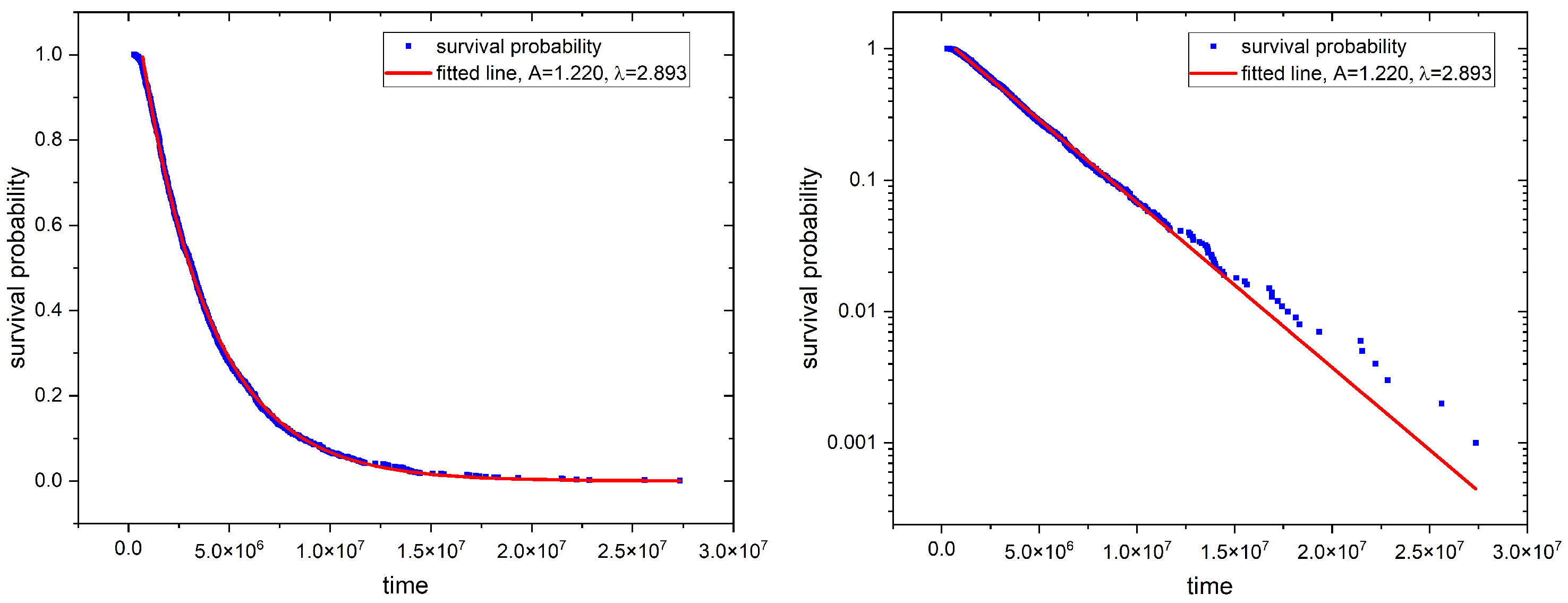
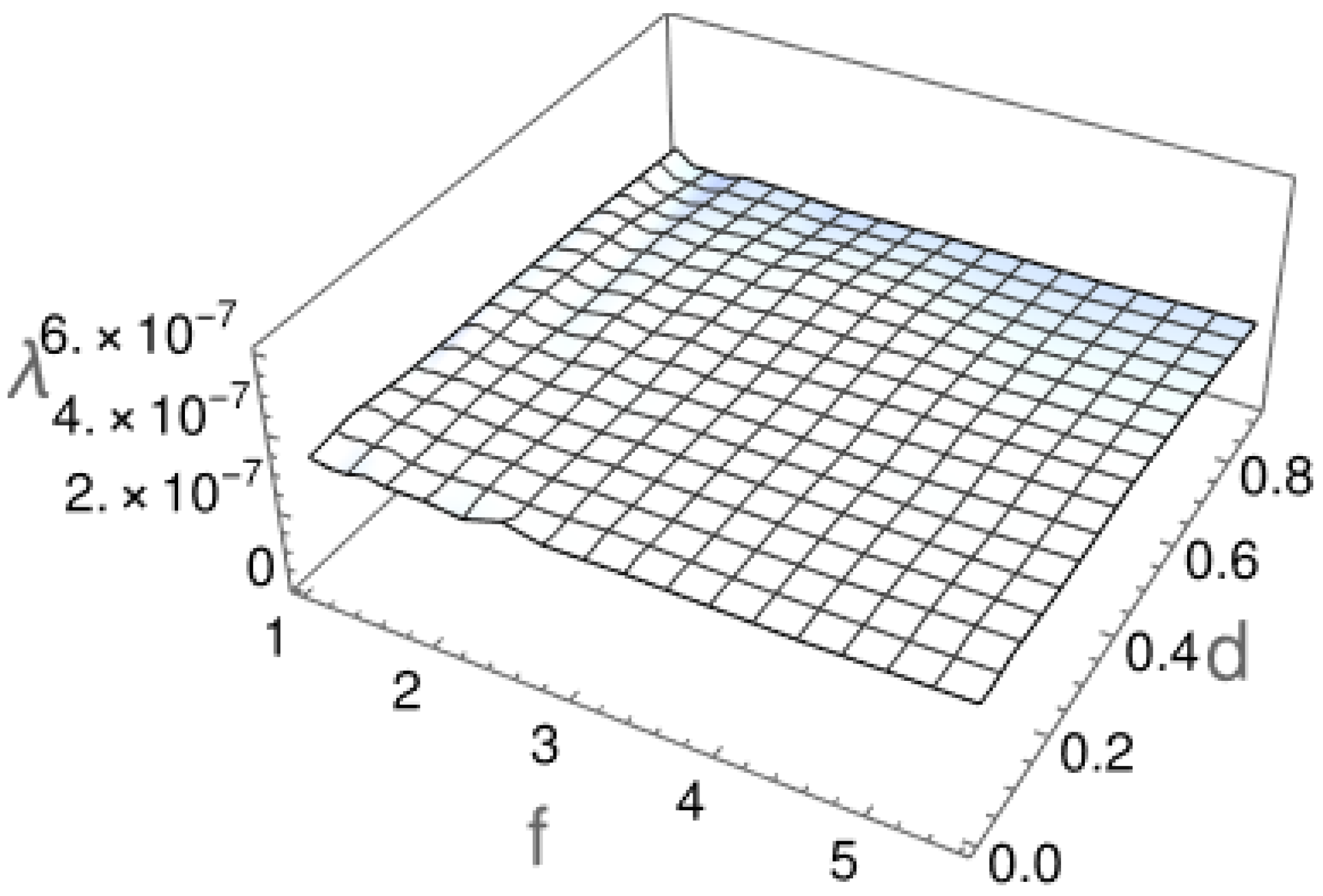
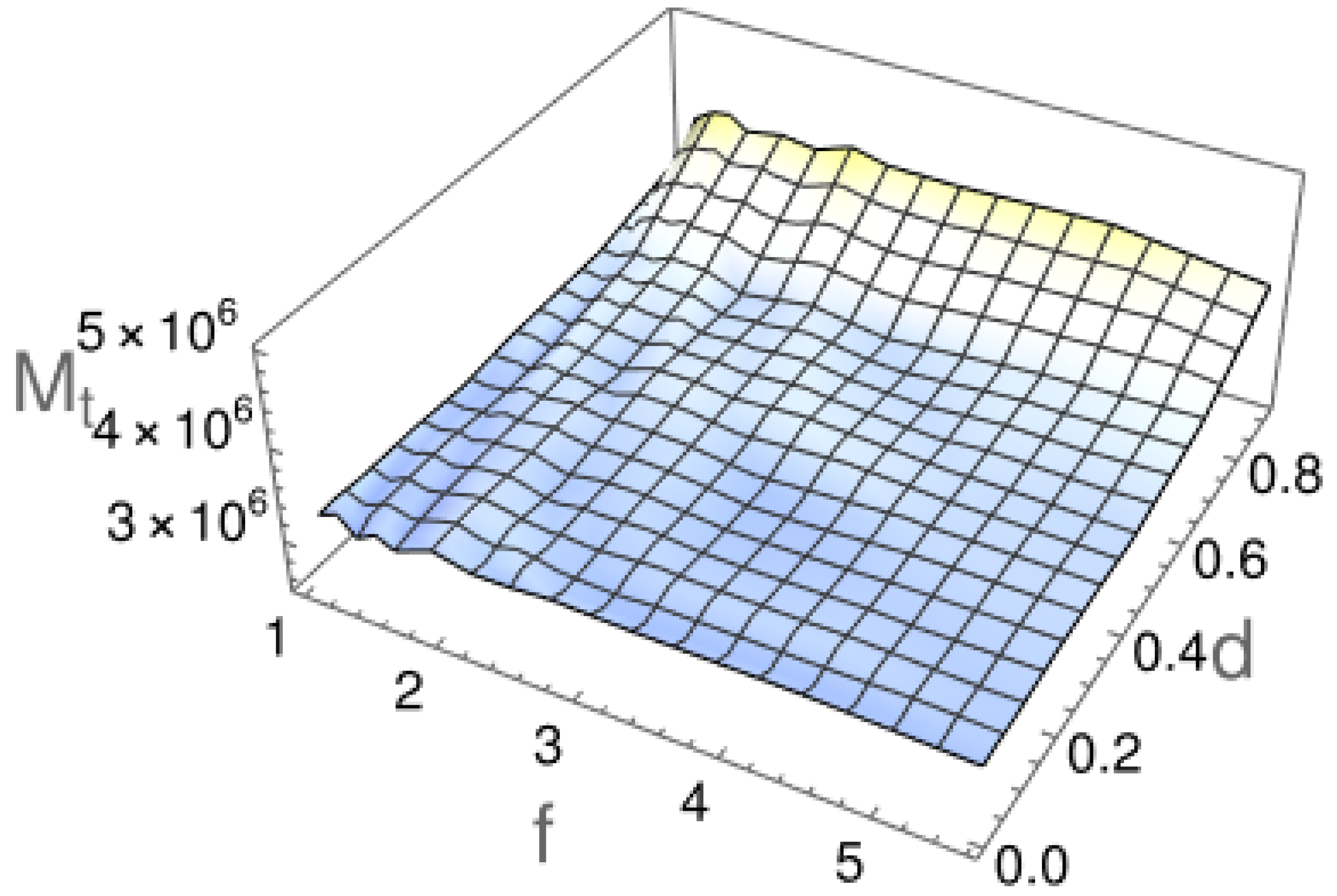
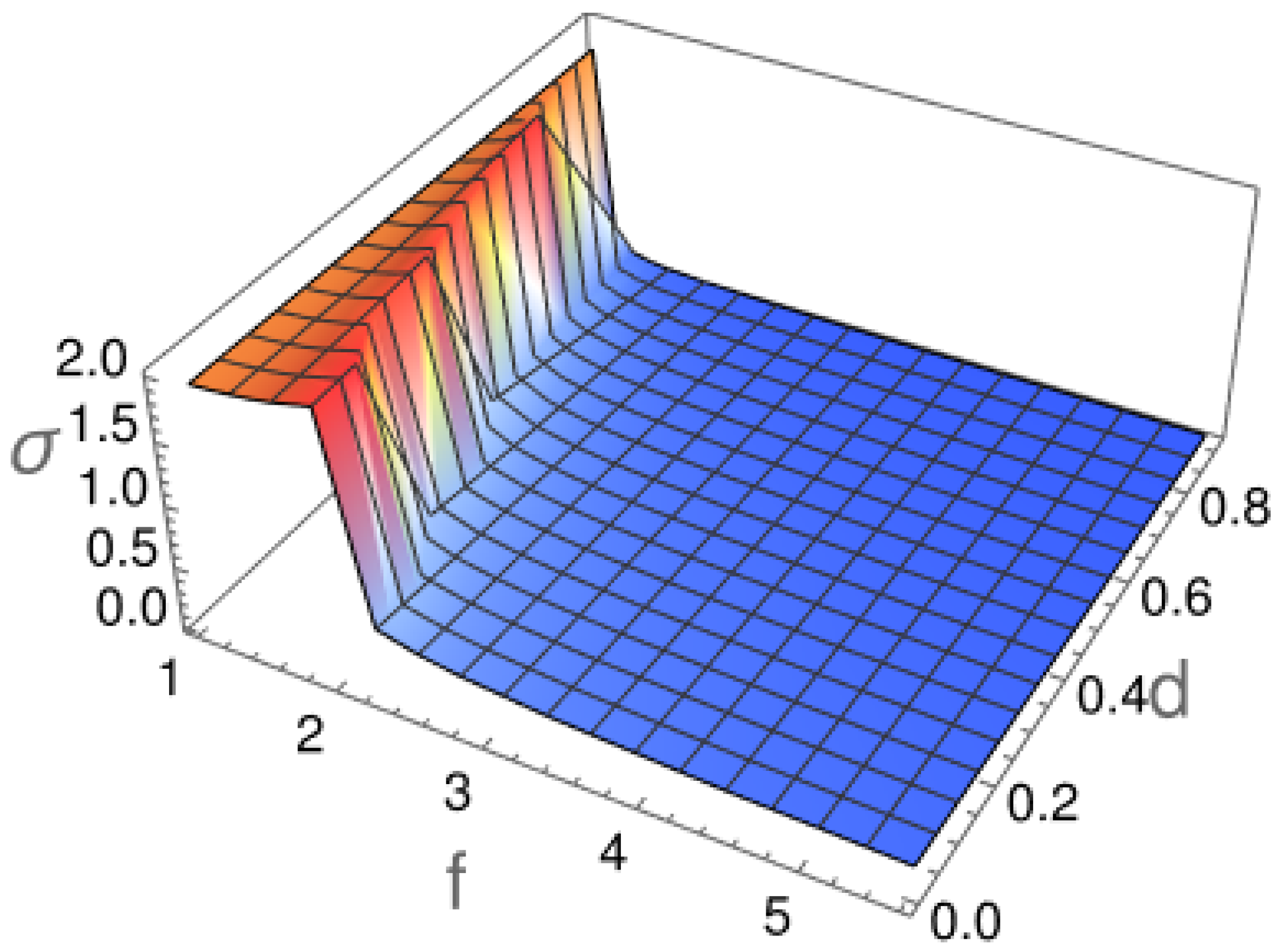
2.2. First Passage Time
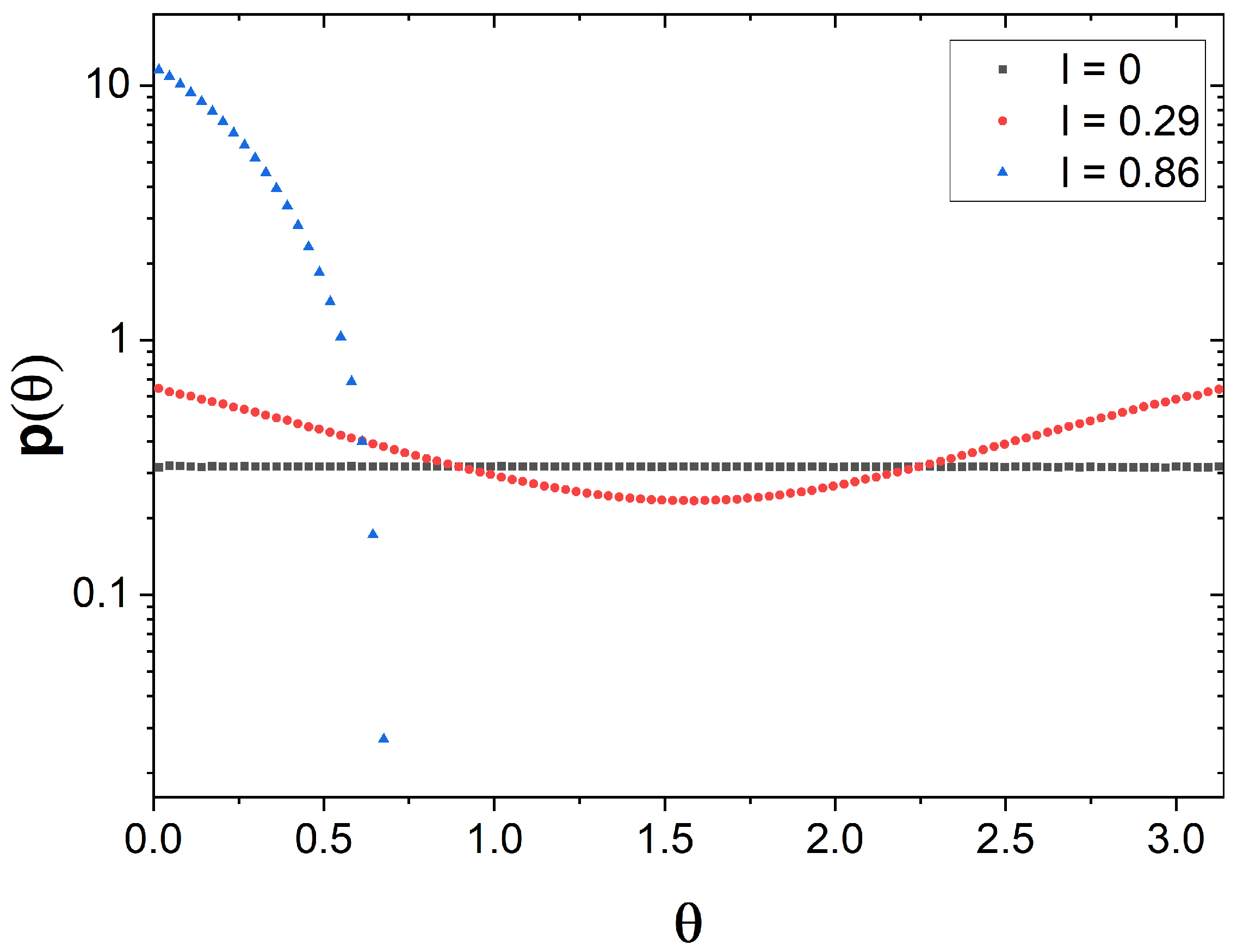
2.3. Angle Distribution
3. Materials and Methods
- Draw a random translation vector with coordinates selected from independent distributions;
- Update the particle position until it does not lead to a collision with channel boundaries, or leaving the particle through the pore entry ();
- Select a random axis of rotation;
- Calculate the particle’s moment of inertia with respect to rotations around the selected axis and the parameter ;
- Draw random angle from the distribution;
- Update the particle orientation if it does not lead to a collision with channel boundaries;
- Increase time;
- Verify if the particle is still within the channel;
- If a particle reaches the exit end of the channel (), record the first passage time (stopping time) and finish the simulation. Otherwise, return to the first step.
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Normal and Anomalous Diffusion
Appendix B. Renormalization of the Angle Distribution
Appendix C. Energy of Rotating (Rigid) Molecule
References
- Hille, B. Ion Channels of Excitable Membranes; Sinauer Associates: Sunderland, MA, USA, 2001. [Google Scholar] [CrossRef]
- Xue, L.; Yamazaki, H.; Ren, R.; Wanunu, M.; Ivanov, A.P.; Edel, J.B. Solid-state nanopore sensors. Nat. Rev. Mater. 2020, 5, 931–951. [Google Scholar] [CrossRef]
- Hou, X.; Guo, W.; Jiang, L. Biomimetic smart nanopores and nanochannels. Chem. Soc. Rev. 2011, 40, 2385–2401. [Google Scholar] [CrossRef] [PubMed]
- Akhtarian, S.; Miri, S.; Doostmohammadi, A.; Brar, S.K.; Rezai, P. Nanopore sensors for viral particle quantification: Current progress and future prospects. Bioengineered 2021, 12, 9189–9215. [Google Scholar] [CrossRef]
- Schmeltzer, A.J.; Peterson, E.M.; Harris, J.M.; Lathrop, D.K.; German, S.R.; White, H.S. Simultaneous Multipass Resistive-Pulse Sensing and Fluorescence Imaging of Liposomes. ACS Nano 2024, 18, 7241–7252. [Google Scholar] [CrossRef] [PubMed]
- Young, Y.W.; Kappler, M.P.; Call, E.D.; Brown, Q.J.; Jacobson, S.C. Integrated In-Plane Nanofluidic Devices for Resistive-Pulse Sensing. Annu. Rev. Anal. Chem. 2024, 17, 221–242. [Google Scholar] [CrossRef]
- Howorka, S.; Siwy, Z. Nanopore analytics: Sensing of single molecules. Chem. Soc. Rev. 2009, 38, 2360–2384. [Google Scholar] [CrossRef] [PubMed]
- Namani, S.; Kavetsky, K.; Lin, C.Y.; Maharjan, S.; Gamper, H.B.; Li, N.S.; Piccirilli, J.A.; Hou, Y.M.; Drndic, M. Unraveling RNA Conformation Dynamics in Mitochondrial Encephalomyopathy, Lactic Acidosis, and Stroke-like Episode Syndrome with Solid-State Nanopores. ACS Nano 2024, 18, 17240–17250. [Google Scholar] [CrossRef] [PubMed]
- Liu, K.; Pan, C.; Kuhn, A.; Nievergelt, A.P.; Fantner, G.E.; Milenkovic, O.; Radenovic, A. Detecting topological variations of DNA at single-molecule level. Nat. Commun. 2019, 10, 3. [Google Scholar] [CrossRef]
- Zhu, J.; Tivony, R.; Bošković, F.; Pereira-Dias, J.; Sandler, S.E.; Baker, S.; Keyser, U.F. Multiplexed Nanopore-Based Nucleic Acid Sensing and Bacterial Identification Using DNA Dumbbell Nanoswitches. J. Am. Chem. Soc. 2023, 145, 12115–12123. [Google Scholar] [CrossRef]
- Henriquez, R.R.; Ito, T.; Sun, L.; Crooks, R.M. The resurgence of Coulter counting for analyzing nanoscale objects. Analyst 2004, 129, 478–482. [Google Scholar] [CrossRef]
- Kozak, D.; Anderson, W.; Vogel, R.; Chen, S.; Antaw, F.; Trau, M. Simultaneous Size and ζ-Potential Measurements of Individual Nanoparticles in Dispersion Using Size-Tunable Pore Sensors. ACS Nano 2012, 6, 6990–6997. [Google Scholar] [CrossRef]
- Bull, R.A.; Adikari, T.N.; Ferguson, J.M.; Hammond, J.M.; Stevanovski, I.; Beukers, A.G.; Naing, Z.; Yeang, M.; Verich, A.; Gamaarachchi, H.; et al. Analytical validity of nanopore sequencing for rapid SARS-CoV-2 genome analysis. Nat. Commun. 2020, 11, 6272. [Google Scholar] [CrossRef] [PubMed]
- Goyal, P.; Goyal, P.; Krasteva, P.V.; Van Gerven, N.; Gubellini, F.; Van den Broeck, I.; Troupiotis-Tsaïlaki, A.; Jonckheere, W.; Péhau-Arnaudet, G.; Pinkner, J.S.; et al. Structural and mechanistic insights into the bacterial amyloid secretion channel CsgG. Nature 2014, 516, 250–253. [Google Scholar] [CrossRef]
- Wanunu, M. Nanopores: A journey towards DNA sequencing. Phys. Life Rev. 2012, 9, 125–158. [Google Scholar] [CrossRef]
- Bayley, H. Sequencing single molecules of DNA. Curr. Opin. Chem. Biol. 2006, 10, 628–637. [Google Scholar] [CrossRef]
- Cherf, G.M.; Lieberman, K.R.; Rashid, H.; Lam, C.E.; Karplus, K.; Akeson, M. Automated forward and reverse ratcheting of DNA in a nanopore at 5-Å precision. Nat. Biotechnol. 2012, 30, 344–348. [Google Scholar] [CrossRef]
- Deamer, D.; Akeson, M.; Branton, D. Three decades of nanopore sequencing. Nat. Biotechnol. 2016, 34, 518–524. [Google Scholar] [CrossRef]
- Hornblower, B.; Coombs, A.; Whitaker, R.D.; Kolomeisky, A.; Picone, S.J.; Meller, A.; Akeson, M. Single-molecule analysis of DNA-protein complexes using nanopores. Nat. Methods 2007, 4, 315–317. [Google Scholar] [CrossRef]
- Manrao, E.A.; Derrington, I.M.; Laszlo, A.H.; Langford, K.W.; Hopper, M.K.; Gillgren, N.; Pavlenok, M.; Niederweis, M.; Gundlach, J.H. Reading DNA at single-nucleotide resolution with a mutant MspA nanopore and phi29 DNA polymerase. Nat. Biotechnol. 2012, 30, 349–353. [Google Scholar] [CrossRef]
- Dorey, A.; Howorka, S. Nanopore DNA sequencing technologies and their applications towards single-molecule proteomics. Nat. Chem. 2024, 16, 314–334. [Google Scholar] [CrossRef]
- Brinkerhoff, H.; Kang, A.S.; Liu, J.; Aksimentiev, A.; Dekker, C. Multiple rereads of single proteins at single–amino acid resolution using nanopores. Science 2021, 374, 1509–1513. [Google Scholar] [CrossRef]
- Ouldali, H.; Sarthak, K.; Ensslen, T.; Piguet, F.; Manivet, P.; Pelta, J.; Behrends, J.C.; Aksimentiev, A.; Oukhaled, A. Electrical recognition of the twenty proteinogenic amino acids using an aerolysin nanopore. Nat. Biotechnol. 2020, 38, 176–181. [Google Scholar] [CrossRef]
- Yuan, Z.; Liu, Y.; Dai, M.; Yi, X.; Wang, C. Controlling DNA Translocation Through Solid-state Nanopores. Nanoscale Res. Lett. 2020, 15, 80. [Google Scholar] [CrossRef]
- Wang, C.; Sensale, S.; Pan, Z.; Senapati, S.; Chang, H.C. Slowing down DNA translocation through solid-state nanopores by edge-field leakage. Nat. Commun. 2021, 12, 140. [Google Scholar] [CrossRef]
- Chien, C.C.; Shekar, S.; Niedzwiecki, D.J.; Shepard, K.L.; Drndić, M. Single-Stranded DNA Translocation Recordings through Solid-State Nanopores on Glass Chips at 10 MHz Measurement Bandwidth. ACS Nano 2019, 13, 10545–10554. [Google Scholar] [CrossRef]
- Yusko, E.C.; Bruhn, B.R.; Eggenberger, O.M.; Houghtaling, J.; Rollings, R.C.; Walsh, N.C.; Nandivada, S.; Pindrus, M.; Hall, A.R.; Sept, D.; et al. Real-time shape approximation and fingerprinting of single proteins using a nanopore. Nat. Nanotechnol. 2017, 12, 360–367. [Google Scholar] [CrossRef] [PubMed]
- Dion, M.B.; Oechslin, F.; Moineau, S. Phage diversity, genomics and phylogeny. Nat. Rev. Microbiol. 2020, 18, 125–138. [Google Scholar] [CrossRef]
- Billaudeau, C.; Chastanet, A.; Yao, Z.; Cornilleau, C.; Mirouze, N.; Fromion, V.; Carballido-López, R. Contrasting mechanisms of growth in two model rod-shaped bacteria. Nat. Commun. 2017, 8, 15370. [Google Scholar] [CrossRef] [PubMed]
- Hattori, S.; Sekido, R.; Leong, I.W.; Tsutsui, M.; Arima, A.; Tanaka, M.; Yokota, K.; Washio, T.; Kawai, T.; Okochi, M. Contrasting mechanisms of growth in two model rod-shaped bacteria. Sci. Rep. 2020, 10, 15525. [Google Scholar] [CrossRef]
- Mitchell, M.J.; Billingsley, M.M.; Haley, R.M.; Wechsler, M.E.; Peppas, N.A.; Langer, R. Engineering precision nanoparticles for drug delivery. Nat. Rev. Drug Discov. 2021, 20, 101–124. [Google Scholar] [CrossRef]
- Golibersuch, D. Observation of Aspherical Particle Rotation in Poiseuille Flow via the Resistance Pulse Technique: I. Application to Human Erythrocytes. Biophys. J. 1973, 13, 265–280. [Google Scholar] [CrossRef] [PubMed]
- Houghtaling, J.; Ying, C.; Eggenberger, O.M.; Fennouri, A.; Nandivada, S.; Acharjee, M.; Li, J.; Hall, A.R.; Mayer, M. Estimation of Shape, Volume, and Dipole Moment of Individual Proteins Freely Transiting a Synthetic Nanopore. ACS Nano 2019, 13, 5231–5242. [Google Scholar] [CrossRef] [PubMed]
- Qiu, Y.; Hinkle, P.; Yang, C.; Bakker, H.E.; Schiel, M.; Wang, H.; Melnikov, D.; Gracheva, M.; Toimil-Molares, M.E.; Imhof, A.; et al. Pores with longitudinal irregularities distinguish objects by shape. ACS Nano 2015, 9, 4390–4397. [Google Scholar] [CrossRef] [PubMed]
- Venta, K.E.; Zanjani, M.B.; Ye, X.; Danda, G.; Murray, C.B.; Lukes, J.R.; Drndić, M. Gold Nanorod Translocations and Charge Measurement through Solid-State Nanopores. Nano Lett. 2014, 14, 5358–5364. [Google Scholar] [CrossRef] [PubMed]
- Maugi, R.; Hauer, P.; Bowen, J.; Ashman, E.; Hunsicker, E.; Platt, M. A methodology for characterising nanoparticle size and shape using nanopores. Nanoscale 2020, 12, 262–270. [Google Scholar] [CrossRef] [PubMed]
- Schiel, M.; Siwy, Z.S. Diffusion and trapping of single particles in pores with combined pressure and dynamic voltage. J. Phys. Chem. C 2014, 118, 19214–19223. [Google Scholar] [CrossRef]
- Gardiner, C.W. Handbook of Stochastic Methods for Physics, Chemistry and Natural Sciences; Springer Verlag: Berlin, Germany, 2009. [Google Scholar]
- Montroll, E.W.; Weiss, G.H. Random walks on lattices II. J. Math. Phys. 1965, 6, 167. [Google Scholar] [CrossRef]
- Montroll, E.W.; Shlesinger, M.F. On the wonderful world of random walks. In Nonequilibrium phenomena II: From Stochastics to Hydrodynamics; Lebowitz, J.L., Montroll, E.W., Eds.; Scientific Research Publishing: Amsterdam, The Netherlands, 1984; pp. 1–121. [Google Scholar]
- Metzler, R.; Klafter, J. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys. Rep. 2000, 339, 1–77. [Google Scholar] [CrossRef]
- Metzler, R.; Klafter, J. The restaurant at the end of the random walk: Recent developments in the description of anomalous transport by fractional dynamics. J. Phys. A: Math. Gen. 2004, 37, R161–R208. [Google Scholar] [CrossRef]
- Meerschaert, M.M.; Scalas, E. Coupled continuous time random walks in finance. Physica A 2006, 370, 114. [Google Scholar] [CrossRef]
- Bartumeus, F.; da Luz, M.G.E.; Viswanathan, G.M.; Catalan, J. Animal search strategies: A quantitative random-walk analysis. Ecology 2005, 86, 3078–3087. [Google Scholar] [CrossRef]
- Viswanathan, G.M.; Da Luz, M.G.; Raposo, E.P.; Stanley, H.E. The Physics of Foraging: An Introduction to Random Searches and Biological Encounters; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar] [CrossRef]
- Collins, J.J.; De Luca, C.J. Random walking during quiet standing. Phys. Rev. Lett. 1994, 73, 764. [Google Scholar] [CrossRef] [PubMed]
- Helmstetter, A.; Sornette, D. Diffusion of epicenters of earthquake aftershocks, Omori’s law, and generalized continuous-time random walk models. Phys. Rev. E 2002, 66, 061104. [Google Scholar] [CrossRef] [PubMed]
- Lacasta, A.M.; Sancho, J.M.; Romero, A.H.; Sokolov, I.M.; Lindenberg, K. From subdiffusion to superdiffusion of particles on solid surfaces. Phys. Rev. E 2004, 70, 051104. [Google Scholar] [CrossRef]
- Kubala, P.; Cieśla, M.; Dybiec, B. Diffusion in crowded environments: Trapped by the drift. Phys. Rev. E 2021, 104, 044127. [Google Scholar] [CrossRef] [PubMed]
- Cieśla, M.; Dybiec, B.; Sokolov, I.; Gudowska-Nowak, E. Taming Lévy flights in confined crowded geometries. J. Chem. Phys. 2015, 142, 164904. [Google Scholar] [CrossRef] [PubMed]
- Strzelewicz, A.; Krasowska, M.; Cieśla, M. Lévy flights diffusion with drift in heterogeneous membranes. Membranes 2023, 13, 417. [Google Scholar] [CrossRef] [PubMed]
- Edwards, S.F.; Evans, K.E. Dynamics of highly entangled rod-like molecules. J. Chem. Soc. Faraday Trans. 2 1982, 78, 113–121. [Google Scholar] [CrossRef]
- Tirado, M.M.; Martínez, C.L.; de la Torre, J.G. Comparison of theories for the translational and rotational diffusion coefficients of rod-like macromolecules. Application to short DNA fragments. J. Chem. Phys. 1984, 81, 2047–2052. [Google Scholar] [CrossRef]
- Pournin, L.; Weber, M.; Tsukahara, M.; Ferrez, J.A.; Ramaioli, M.; Liebling, T.M. Three-dimensional distinct element simulation of spherocylinder crystallization. Granular Mat. 2005, 7, 119–126. [Google Scholar] [CrossRef]
- Pryamitsyn, V.; Ganesan, V. Screening of hydrodynamic interactions in Brownian rod suspensions. J. Chem. Phys. 2008, 128, 134901. [Google Scholar] [CrossRef] [PubMed]
- Zhao, T.; Wang, X. Diffusion of rigid rodlike polymer in isotropic solutions studied by dissipative particle dynamics simulation. Polymer 2013, 54, 5241–5249. [Google Scholar] [CrossRef]
- Hamid, A.; Shakaib, M.; Molina, J.J.; Qasim, M.D.; Fareed, B.; Uzair, M.; Yamamoto, R. Direct numerical simulations of suspension of disk-shaped particles. Phys. Fluids 2024, 36, 043339. [Google Scholar] [CrossRef]
- Straube, A.V.; Höfling, F. Langevin equations and a geometric integration scheme for the overdamped limit of homogeneous rotational Brownian motion. arXiv 2024, arXiv:2403.04501. [Google Scholar]
- Li, D.; Liu, Y.; Luo, H.; Jing, G. Anisotropic Diffusion of Elongated Particles in Active Coherent Flows. Micromachines 2024, 15, 199. [Google Scholar] [CrossRef] [PubMed]
- Chaki, S.; Olsen, K.S.; Löwen, H. Anisotropic Brownian particles under resetting. arXiv 2024, arXiv:2406.17550. [Google Scholar]
- Sokolov, I.M.; Klafter, J. From diffusion to anomalous diffusion: A century after Einstein’s Brownian motion. Chaos 2005, 15, 026103. [Google Scholar] [CrossRef] [PubMed]
- Metzler, R.; Jeon, J.H.; Cherstvy, A.G.; Barkai, E. Anomalous diffusion models and their properties: Non-stationarity, non-ergodicity, and ageing at the centenary of single particle tracking. Phys. Chem. Chem. Phys. 2014, 16, 24128–24164. [Google Scholar] [CrossRef] [PubMed]
- Einstein, A. Über die von der Molekularkinetischen Theorie der Warme Gefordete Bewegung von in ruhenden Flussigkeiten Suspendierten Teilchen. Ann. Phys. 1905, 17, 549–560. [Google Scholar] [CrossRef]
- Sutherland, W. LXXV. A dynamical theory of diffusion for non-electrolytes and the molecular mass of albumin. Philos. Mag. 1905, 9, 781–785. [Google Scholar] [CrossRef]
- Von Smoluchowski, M. Zur kinetischen theorie der brownschen molekularbewegung und der suspensionen. Ann. Phys. 1906, 21, 756–780. [Google Scholar] [CrossRef]
- Tirado, M.M.; de la Torre, J.G. Rotational dynamics of rigid, symmetric top macromolecules. Application to circular cylinders. J. Chem. Phys. 1980, 73, 1986–1993. [Google Scholar] [CrossRef]
- Idema, T. Rotations About an Arbitrary Axis. Available online: https://phys.libretexts.org/Bookshelves/University_Physics/Mechanics_and_Relativity_(Idema)/07%3A_General_Rotational_Motion/7.03%3A_Rotations_About_an_Arbitrary_Axis (accessed on 29 June 2024).
- Caspi, Y.; Zbaida, D.; Cohen, H.; Elbaum, M. Anomalous diffusion of high molecular weight polyisopropylacrylamide in nanopores. Macromolecules 2009, 42, 760–767. [Google Scholar] [CrossRef]
- Coppens, B.; Belpaire, T.E.; Pešek, J.; Steenackers, H.P.; Ramon, H.; Smeets, B. Anomalous diffusion of nanoparticles in the spatially heterogeneous biofilm environment. iScience 2023, 26, 106861. [Google Scholar] [CrossRef]
- Brandani, S.; Hwang, S.; Kärger, J.; Mangano, E. Diffusion anomaly in nanopores as a rich field for theorists and a challenge for experimentalists. Nat. Commun. 2024, 15, 1–3. [Google Scholar] [CrossRef]
- Richardson, L.F. Atmospheric diffusion shown on a distance-neighbour graph. Proc. R. Soc. Lond. Ser. A-Contain. Pap. Math. Phys. Character 1926, 110, 709–737. [Google Scholar] [CrossRef]
- Jeon, J.H.; Leijnse, N.; Oddershede, L.B.; Metzler, R. Anomalous diffusion and power-law relaxation of the time averaged mean squared displacement in worm-like micellar solutions. New J. Phys. 2013, 15, 045011. [Google Scholar] [CrossRef]
- Weigel, A.V.; Simon, B.; Tamkun, M.M.; Krapf, D. Ergodic and nonergodic processes coexist in the plasma membrane as observed by single-molecule tracking. Proc. Natl. Acad. Sci. USA 2011, 108, 6438–6443. [Google Scholar] [CrossRef] [PubMed]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cieśla, M.; Dybiec, B.; Krasowska, M.; Siwy, Z.; Strzelewicz, A. Numerical Modeling of Anisotropic Particle Diffusion through a Cylindrical Channel. Molecules 2024, 29, 3795. https://doi.org/10.3390/molecules29163795
Cieśla M, Dybiec B, Krasowska M, Siwy Z, Strzelewicz A. Numerical Modeling of Anisotropic Particle Diffusion through a Cylindrical Channel. Molecules. 2024; 29(16):3795. https://doi.org/10.3390/molecules29163795
Chicago/Turabian StyleCieśla, Michał, Bartłomiej Dybiec, Monika Krasowska, Zuzanna Siwy, and Anna Strzelewicz. 2024. "Numerical Modeling of Anisotropic Particle Diffusion through a Cylindrical Channel" Molecules 29, no. 16: 3795. https://doi.org/10.3390/molecules29163795
APA StyleCieśla, M., Dybiec, B., Krasowska, M., Siwy, Z., & Strzelewicz, A. (2024). Numerical Modeling of Anisotropic Particle Diffusion through a Cylindrical Channel. Molecules, 29(16), 3795. https://doi.org/10.3390/molecules29163795





