Next Article in Journal
Ab Initio Manganese Kα and Kβ Energy Eigenvalues, Shake-Off Probabilities, Auger Rates, with Convergence Tests
Previous Article in Journal
Analysis of Posidonia oceanica’s Stress Factors in the Marine Environment of Tremiti Islands, Italy
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Molecules
Volume 29
Issue 17
10.3390/molecules29174198
molecules-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Theoretical Study of Metal–Ligand Interactions in Lead Complexes with Radiopharmaceutical Interest †

by
Attila Kovács
1,* and
Zoltán Varga
2
1
European Commission, Joint Research Centre (JRC), 76125 Karlsruhe, Germany
2
Department of Chemistry, Chemical Theory Center, Minnesota Supercomputer Institute, University of Minnesota, Minneapolis, MN 55455, USA
*
Author to whom correspondence should be addressed.
†
Dedicated to the 80th birthday of Prof. Donald Truhlar.
Molecules 2024, 29(17), 4198; https://doi.org/10.3390/molecules29174198
Submission received: 27 June 2024 / Revised: 15 August 2024 / Accepted: 16 August 2024 / Published: 4 September 2024
(This article belongs to the Section Molecular Structure)
Browse Figures
Versions Notes

Abstract

:
The 203Pb and 212Pb lead radioisotopes are attracting growing interest as they can aid in the development of personalized, targeted radionuclide treatment for advanced and currently untreatable cancers. In the present study, the bonding interactions of Pb2+ with twelve macrocyclic ligands, having an octa and nona coordination, were assessed using Density Functional Theory (DFT) calculations. The molecular structures in an aqueous solution were computed utilizing the polarized continuum model. The preference for the twisted square antiprismatic (TSAP) structure was confirmed for ten out of the eleven cyclen-based complexes. The characteristics of the bonding were assessed using a Natural Energy Decomposition Analysis (NEDA). The analysis revealed a strong electrostatic character of the bonding in the complexes, with minor variations in electrical terms. The charge transfer (CT) had a comparable energetic contribution only in the case of neutral ligands, while in general, it showed notable variations regarding the various donor groups. Our data confirmed the general superiority of the carboxylate O and aromatic N donors. The combination of the selected efficient pendant arms pointed out the superiority of the acetate pendant arms and the lack of significant cooperation between the different pendant arms in the probed ligands. Altogether, the combination led only to a marginal enhancement in the total CTs in the complexes.

Graphical Abstract

1. Introduction

The lead radioisotopes 203Pb and 212Pb have recently received growing attention in radiopharmacy. The γ-emitting 203Pb isotope (279 keV, t1/2 = 51.9 h) is suitable for single-photon emission computed tomography (SPECT) imaging [1]. More interesting is the 212Pb isotope, which acts as an α-emitter generator by producing 212Bi (α, t1/2 = 61 min) through its β-decay. The relatively long half-life of 212Pb (β, t1/2 = 10.64 h) [2] can efficiently prolong the presence of the short-lived 212Bi in vivo, where the generated 212Bi isotope should effectively be complexed by the same chelator because its release and subsequent accumulation in off-target sites can lead to toxicity. Altogether, the two Pb radioisotopes form an ideal theranostic pair for radioimaging and targeted cancer radiotherapy [3,4,5] and are currently undergoing clinical trials.
In the above-mentioned pharmaceutical applications, the radionuclides must safely be driven to the biological target in order to avoid the radioactive contamination of other organs, which would lead to toxicity. This targeted delivery (and retention of the radionuclides) is usually performed in the form of chelate complexes, where the ligand is conjugated to a tumor-seeking vector. A strict requirement for these chelate complexes is that they should be thermodynamically highly stable and kinetically inert under in vivo conditions [3,4,6]. Accordingly, the design of appropriate chelators requires an understanding of the relationship between the chelator structure and the stability of the complex.
The main complexing characteristics of Pb2+ are the following: it is a borderline Lewis acid in terms of Hard and Soft Acid and Base (HSAB) theory [7,8,9], and in a solid state, it exhibits various coordinations, from mono- to dodecadentate coordinations, with oxygen, nitrogen, and thiolate groups [10]. Its effective ionic radius in eight-coordinate complexes is 1.29 Å [11], due to which Pb2+ belongs to the largest metal ions. Because its 6d valance orbitals are high in energy, the donor–acceptor interactions are managed by the partially occupied 6p orbitals. In addition, in some complexes, stereochemical activity was attributed to the occupied 6s orbital [12,13].
In terms of radiopharmaceutical research, several traditional and new ligands have been probed for Pb2+. The research includes experimental studies (X-ray crystallography, NMR spectroscopy, potentiometry, radiolabeling, challenge studies with other ligands—mostly EDTA—and metal ions under various solution conditions) [12,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28] as well as a few quantum chemical calculations [12,13,20].
In particular, DFT calculations have been used to study the stereochemical activity of the occupied 6s orbital of Pb2+ [12,13], pointing out the importance of an asymmetric environment around Pb2+ for this feature. In addition, in a few cases, experimental studies have been assisted by DFT calculations on the structural (conformational) properties [20,29] of radiopharmaceutically relevant Pb2+ complexes. To the best of our knowledge, no systematic bonding analysis on such complexes has been reported so far.
In the present study, we selected eleven macrocyclic cyclen-based ligands containing neutral and anionic pendant arms (cf. Figure 1 for notations used in the paper). Some of them have already been probed with Pb2+ (DOTA [15,25], with the current industry standard being DOTAM [16], DO4Py [26], MeDO2PA [20], H2DO2PA [20], and MeDO2Scz [21]). Two other ligands—showing good performance for Bi3+ and Ac3+ [30]—have promising structural properties: DOTPA has extended flexibility due to the longer pendant arms, and DO4Pyd has a modified charge and steric conditions at the aromatic N donor. The ligands with mixed pendant arms (DO2A2AM and DO2A2Py) are well suited to study the competition of two efficient donor groups in the same complex. With DO3APA, where one COO− moiety of DOTA is replaced by a picolinate group, the possibility of nona-coordination with the large Pb2+ ion can be probed. Finally, the twelfth ligand in our comparative analysis is the benzo-substituted [2]-cryptand (CRYPT) macrocycle, which already has some experimental history with Pb2+ [23].
The ligand set presented above promises a versatile assessment of metal–ligand interactions. The Natural Energy Decomposition Analysis (NEDA) [31,32] provides, beyond the net interaction energies, details on the electrostatic, steric, and orbital interaction contributions. The efficiency of the individual donors in the donor–acceptor interactions can be deduced from the second-order perturbation energies obtained from the Natural Bond Orbital (NBO) [33] analysis. The information obtained can help design new efficient ligands for Pb radiopharmaceutical.

2. Results and Discussion

2.1. Structures

Except for CRYPT, the structures of the probed ligands are based on the twelve-membered tetraazamacrocycle cyclen and contain mostly four, while in some cases, two pendant arms (cf. Figure 1). The most stable structures of the complexes with ligands having four identical pendant arms (DOTA, DOTPA, DOTAM, DO4Py, and DO4Pyd) possess C4 symmetry, confirmed by our present calculations for aqueous solutions. The most stable structures of the complexes with ligands having two identical pendant arms (DO2A2AM, DO2A2Py, MeDO2PA, H2DO2PA, and MeDO2Scz) converged to minima with C2 symmetry on the potential energy surface. Two complexes in the set, those formed with ligands DO3APA and CRYPT, have C1 symmetry.
The flexibility of the cyclen-based ligands leads to characteristic stereochemical properties of the complexes [34]. The ethylene groups in the cyclen macrocycle can take up δ- or λ-gauche orientations. The binding of the metal to the four N atoms fixes these to have four identical torsionals: δδδδ or λλλλ, respectively. The rotation of the acetate groups is limited upon coordination with the metal but still allows two opposite helical arrangements, Δ and Λ (Figure 2). The structures with the same helicities of the ring and the acetate groups, Δ(δδδδ) and Λ(λλλλ), respectively, are mirror images. Similarly, the forms with opposite helicities, Λ(δδδδ) and Δ(λλλλ), are enantiomers, too. The structure of the former conformers can be characterized as twisted square antiprismatic, leading to the conventional designation TSAP (or, in some literature, m). The latter conformers have a square antiprismatic coordination geometry (designated as SAP or M in the literature).
As the inversion barrier is rather low, the above enantiomers often appear as racemic mixtures in solutions [19,20,25] (and consequently upon crystallization from solutions [19,20,21]). The structures with the same ring and acetate helicity vs. the ones with opposite helicity are diastereomeric pairs and possess somewhat different spatial properties. The consequence is size selectivity: large metals usually form complexes with the TSAP conformer of these ligands, whereas small metals prefer the SAP conformer [35].
Our computations on the Pb complexes resulted in the energetic preference of the TSAP conformer in an aqueous solution for almost all complexes (cf. Table 1), in agreement with experimental reports for the solid-state structures of some of them [12,18,19,20,21,23,25,26]. The only exception was the Pb(DOTPA)2− complex with a significant energetic preference for the SAP isomer. The DOTPA ligand differs from the other ten cyclen-based ones by its longer pendant arms, forming six-membered chelate rings with the metal. This can facilitate more favorable interactions with large metals in the SAP structures than in the cases of the other ligands forming five-membered chelate rings. It is noteworthy that the TSAP isomers of the ten other cyclen-based complexes are markedly more stable than the SAP ones. The energetic preference dropped below 10 kJ/mol only for the complexes with dipicolinate ligands (MeDO2PA, H2DO2PA, cf. Table 1).
Another characteristic of the cyclen-based complexes with large metals is the possible additional coordination of a small ligand (solvent, counterion, etc.) at a ninth coordination site. For example, in the case of the best-known DOTA with large metal ions (early lanthanides and actinides), such coordination has often been observed in the solid phase [36,37,38,39,40,41,42,43].
As Pb2+ belongs to the largest metal ions (vide supra), we probed the coordination of an H2O molecule at the ninth coordination site of the Pb(DOTA)2− complex in an aqueous solution using the PCM solvation model. First, we constrained the H2O molecule in the middle of the free site; this model structure had a C2 symmetry. The geometry optimization resulted in a rather long Pb-OH2O distance (3.3 Å). Moreover, this structure proved to be a third-order saddle-point on the potential energy surface. Lifting the symmetry constraint, the H2O ligand moved closer to two neighboring pendant arms and established very strong hydrogen bonds with the two carboxylate groups. In this minimum structure, the oxygen of H2O turned away from Pb2+, resulting in a Pb-OH2O distance of 3.6 Å, which prevented any reasonable Pb2+-H2O interaction. Thus, our solvation model calculations do not support bonding of H2O to Pb2+ in the Pb(DOTA)2+ complex due to the stronger competitive effects of hydrogen bonding and outwards stabilization of the H2O oxygen by the polar solvent. Based on this experience, we skipped the study of additional H2O coordination for the other complexes.
Selected structural characteristics are given in Table 1 and Figure 3. We note that comparison of the Pb-O and Pb-N distances with most available X-ray diffraction values is not straightforward: the related crystal structures suffer from intermolecular interactions with counterions and solvent species [12,18,20,21,23] and/or dimer formation [19,21]. The only exception found is the crystal of [PbDO4Py](ClO4)2, in which the complex moiety has only marginal interactions with the ClO4− counterions due to the efficient encapsulation of the metal (the closest ClO4− has a Pb-O contact of 4.55 Å [26]). In addition, the donor N atoms of the pyridyl pendant arms are well shielded against intermolecular interactions. Yet, solid-state effects introduce asymmetry in the molecular structure in the crystal with variations up to 0.11 Å for the four Pb-NPy distances, which are equivalent in the computed structure with C4 symmetry (cf. Table 1). Considering the different conditions, viz., the solution from the calculations while solid phase from the experiment, the average Pb-N distances from the X-ray study and our computations are in reasonably good agreement: 2.641(2) and 2.773(3) [26] vs. 2.693 and 2.765 Å for the cyclen and pyridyl N-s, respectively.
The exchange of pendant arms resulted in several significant changes in the Pb-O and Pb-N bond distances. These also appear in the bonding interactions (vide infra) because the electrostatic interactions are strongly distance-dependent, similar to the overlap of donor and acceptor orbitals for charge transfer.
Due to the C4 symmetry of Pb(DOTPA)2− and Pb(DOTA)2−, Figure 3 clearly demonstrates how the propionate arms in DOTPA pulled the Pb2+ ion out from the cavity of the cyclene ring compared to the parent DOTA complex. The Pb2+ ion readily followed the lengthening of the pendant arm, proving the much stronger character of the carboxylate groups with respect to the cyclen N-s.
The picolinate pendant arm in the DO3APA ligand caused a significant distortion with respect to the C4 parent Pb(DOTA)2− complex. Apparently, due to the larger picolinate group, the space around Pb2+ is more crowded in this complex, which resulted in an increase for most metal–ligand distances as a consequence of the nona-coordination. The increased distances imply a weakening of those metal–ligand interactions. On the other hand, the distortion resulted in the shortening of two Pb-OAc distances, which increased interactions could provide certain compensation for the weakening. Despite their good donor properties, the O and N donors of the picolinate group were positioned relatively far from Pb2+, probably due to steric effects.
Replacement of two acetate O donors of DOTA by neutral O and N in DO2A2AM and DO2A2Py, respectively, decreased both the Pb-OAc and Pb-Ncyc distances, implying a strengthening of these interactions. On the other hand, the distances with the neutral O and N donors were relatively large; they were significantly larger than in their parent DOTAM and DO4Py complexes. It seems that combining the efficient acetate, amide, and pyridyl donor groups did not lead to a synergic cooperation with significant enhancement in the bonding.
The ligands DO4Py and DO4Pyd differ by the meta-positioned N in the pyridazyl arms of the latter ligand. This N is not in an advanced position for bonding interactions with Pb2+ in the complexes, while it influences the charge density of the neighboring N and, consequently, those Pb-N interactions. Pyridazine is known to be less basic than pyridine due to the competitive electron-withdrawing of the two neighboring N-s. On this basis, weaker electrostatic and donor–acceptor interactions with Pb2+ would be expected. Yet, the Pb-N distances in Pb(DO4Pyd)2+ are slightly smaller than in Pb(DO4Py)2+. The explanation lies in the steric conditions: the CH hydrogen at the meta-position in the Py arm exerts a steric repulsion which limits the mutual proximity of the Py groups and, consequently, the access to Pb2+ in the Pb(DO4Py)2+ complex. The replacement of CH with N in Pb(DO4Pyd)2+ allowed a more efficient approach of the pendant arm to Pb2+.
The ligands MeDO2PA and H2DO2PA differ only by the presence of the methyl substituents on the cyclen backbone in the former molecule. Yet, the complex stabilities with Pb2+ are significantly different (log KPbL = 18.44 ± 0.02 and 16.44 ± 0.02, respectively [20]), and similarly, so are the Pb-ligand distances in Figure 3: the Pb-O distances differ by 0.19 Å, whereas the Pb-Ncyc ones differ up to 0.28 Å. The major cause of such drastic differences cannot be explained by the steric effect because both the Me group and NH hydrogen have exo orientations on the cyclen backbone. However, this orientation facilitates NH to form a hydrogen bond with the carboxylate O (2.25 Å), which, in this way, is involved in a second interaction beyond the Pb-O one. The increase in the Pb-O distance by 0.19 Å, with respect to that in the Pb(MeDO2PA) complex, suggests the superiority of the hydrogen bonding. Also, the N donor in the picolinate group has an increased distance to Pb2+ (though only by 0.05 Å) in the Pb(H2DO2PA) complex. In parallel, the NH nitrogen of the cyclen backbone comes very close to Pb2+ (2.55 Å, representing the smallest Pb-N distance in the present set, cf. Figure 3), probably due to the increased polarized character of the NH group upon hydrogen bonding.
Replacing the strong anionic picolinate donor of MeDO2PA with the neutral one in DO2Scz resulted in the expected weakening of the Pb-O and, consequently, some strengthening of the competitive Pb-Ncyc interactions in the Pb(DO2Scz)2+ complex with respect to Pb(MeDO2PA). Coordination of the imido N to Pb2+ proved also to be considerably weaker than that of the picolinate N.
The coordination of the asymmetric CRYPT ligand has one noteworthy structural feature: the Pb(CRYPT)2+ complex has the shortest Pb-O distances (2.55 and 2.61 Å) in the present set formed by the two O-s of the middle bridge. Regarding these O-s being formally neutral donors, the main reason may lie in the spatial conditions that regulate the arrangement of the donor heteroatoms in this macrocycle ligand.

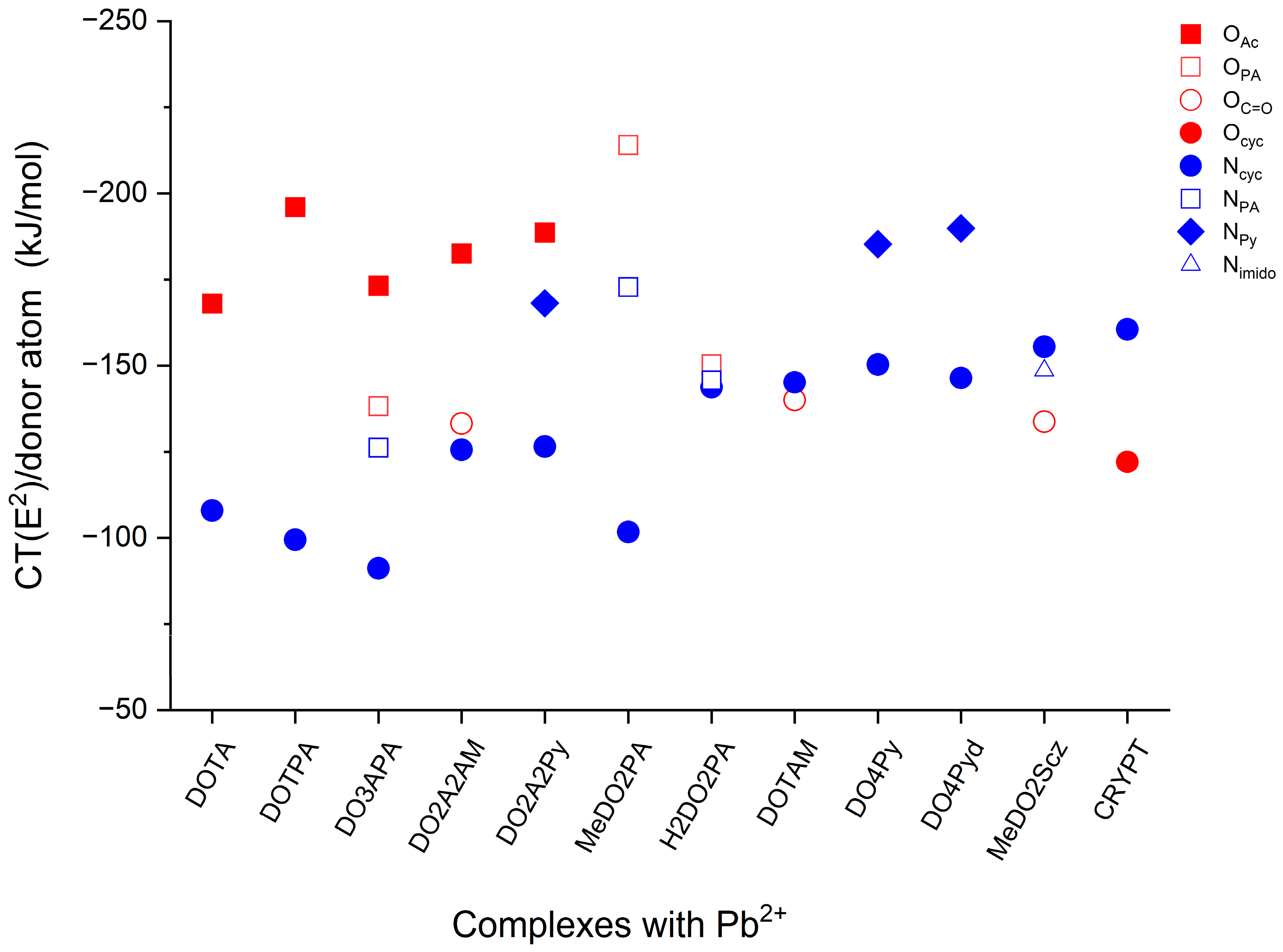
2.2. Bonding Analysis

The energetic properties of metal–ligand interactions were explored with Natural Energy Decomposition Analysis (NEDA) [31,32], which is an energy partitioning approach for molecular interactions applicable to self-consistent field (SCF) wavefunctions and DFT charge densities. The total interaction energy (ΔEINT) between the appropriately selected fragments consists of electrical interaction (EL), charge transfer (CT), and core repulsion (CORE) contributions according to:
ΔEINT = ΔEEL + ΔECT + ΔECORE
An overview of selected NEDA results is presented in Figure 4. While there is no direct relationship between the metal–ligand interaction energy and the complex stability in solution (the latter is strongly influenced by the solvation energy of the free ligand, which has a different structure than in the complex), it is remarkable that the very stable Pb(DOTA)2+ complex (experimental stability constant log KPbL = 25.3 ± 0.2 [25]) has also one of the largest computed interaction energies. Experimental log KPbL data are also available for Pb(DOTAM)2+ and Pb(DOPy4)2+ formed by neutral ligands (log KPbL > 19 [16] and 19.95 ± 0.03 [26], respectively), indicating that a negatively charged ligand is not a prerequisite for complex stability in solution, as these complexes belong to those with the lowest metal–ligand interaction energies in the present set. In contrast, the Pb complexes with the negatively (2−) charged MeDO2PA and H2DO2PA ligands have even lower stabilities in solution (log KPbL determined to be 18.44 ± 0.02 and 16.44 ± 0.02, respectively [20]). Among the latter two complexes, the weaker character of Pb(H2DO2PA) is in line with its lower computed interaction energy.
An interesting question is the efficiency of the nona-coordination in Pb(DO3APA)2−: the ΔEINT data suggest only a marginal improvement of the bonding, as the complex has interaction energies close to those of Pb(DOTA)2− and Pb(DOTPA)2−. As discussed in the previous section, the additional coordination in Pb(DO3APA)2− could only be facilitated by the cost of several increased metal–ligand distances (vide supra in Figure 3), thus weakening those interactions.
The data in Figure 4 demonstrate nicely the dominant role of the free ligand’s charge for the total interaction energies. These ligand charges determine the electrical interaction, which is the major bonding component between Pb2+ and the ligands in the complexes. The portion of ΔEEL within the bonding ΔEEL + ΔECT interactions is between 59 and 78%, the lowest values belonging obviously to the neutral L0 ligands.
In contrast, the covalent charge transfer interactions have close energies (within 200 kJ/mol cf. Figure 4) independently from the charge of the free ligand. Ligands with aromatic N-donor pendant arms (DO4Py, DO4Pyd, DO2A2Py) have somewhat larger CT energy compared with the complexes possessing O-donor pendant arms.
The stronger CT interaction in Pb(DOTPA)2− with respect to Pb(DOTA)2− can be attributed to the flexibility of the longer propionate pendant arm (better orbital overlaps) with respect to the acetate one. In contrast, the spatial conditions for the electrical interactions seem to be more favorable in Pb(DOTA)2−. Yet, this, together with the weaker repulsive core interaction (cf. Table 2), is not enough to compensate for the smaller CT.
The effect of the methyl substituent on the cyclen ring can be assessed by comparing Pb(MeDO2PA) and Pb(H2DO2PA). Both the EL and CT bonding contributions are larger in Pb(MeDO2PA), while the slightly larger core repulsion does not compensate for it; hence, the methyl substitution results in a slightly larger interaction energy in Pb(MeDO2PA). Similar observations can be made for the related DO4Py and DO4Pyd complexes with a slight preference for Pb(DO4Pyd)2+.
The energetic contribution of the various donor atoms to the ΔECT term can be distinguished based on the second-order perturbation energies from Natural Bond Orbital (NBO) analysis [33]. In Table 2, the summed contributions of all the O and N donors, respectively, are shown. The data demonstrate the dominance of the carboxylate O donors in the cases with four COO-type pendant arms. The donation efficiency of the amide C=O groups is weaker, shown by its drop below that of the cyclen N-s in Pb(DOTAM)2+. Substitution of a carboxylate group by picolinate in Pb(DO3APA)2− decreased slightly the summed O-donation with respect to Pb(DOTA)2−, while the additional fifth (picolinate) N donor increased significantly the summed N-donation. Altogether, the nona-coordination in Pb(DO3APA)2− resulted in more favorable CT interactions with respect to the parent Pb(DOTA)2−. The increase in the pendant arms in Pb(DOTPA)2− has a similar consequence.
The effect of the methyl substituent in Pb(MeDO2PA) vs. Pb(H2DO2PA) is the significant increase in the O-donation efficiency for the cost of the N-donation-in agreement with the changes in the Pb-O and Pb-N distances (cf. Figure 3). The N-donation is very efficient in complexes with pyridyl-type ligands (Py, Pyd), exceeding the carboxylate O of DOTA. This efficiency appears also in the mixed Pb(DO2A2Py) complex.
The semicarbazone pendant arms with C=N and C=O donor groups in Pb(MeDO2Scz)2+ show medium CT efficiency, while the ring O and N donors of the cryptand macrocycle in Pb(CRYPT)2+ exert the weakest CT interactions with Pb2+ in the present set of ligands.
The transferred number of electrons in the 12 complexes show relatively small variations (between 0.46 and 0.56 e, cf. Table 2), the trend being more-or-less in qualitative agreement with the CT energies.
The CT efficiency of the individual O and N donors can be followed in Figure 5. The superiority of the acetate/propionate O and aromatic N among these donors is evident. In most ligands, the weakest donors are the cyclen N-s. Exceptions are DOTAM and MeDO2Scz, where they outperform the amide C=O groups and, in the case of MeDO2Scz, also the imido C=N group. In the Pb(CRYPT)2+ complex, the tertiary N outperforms the secondary O donors.
Figure 5 also provides detailed information on the consequences of the probed exchanges of pendant arms. Thus, the replacement of one or more COO− groups of DOTA with CH2COO− (DOTPA), picolinate (DO3APA), amide (DO2A2AM), and pyridyl groups (DO2A2Py) increased the donation efficiency of the carboxylate O in these complexes in agreement with these decreased Pb-OAc distances (vide supra Figure 3). In contrast, the O and N donors in most of the above-added groups perform generally weaker in terms of CT than in their parent Pb(DOTAM)2+ and Pb(DO4Py)2+ or related Pb(MeDO2PA) complexes.
It is noteworthy that the replacement of the methyl groups in the MeDO2PA ligand with hydrogens in H2DO2PA (and the above-discussed hydrogen bonding) more-or-less equalized the CT from the three donor types, whereas these CT-s in the Pb(MeDO2PA) complex differ significantly.
Another enlightening feature appears in the DO4Py vs. DO4Pyd complexes: the decreased Pb-Ncyc and Pb-NPy distances in Pb(DO4Pyd)2+ result only in the case of NPy increased CT energy; the CT performance of the Ncyc donors became slightly weaker.
The natural atomic charges and valence orbital populations of Pb are given in Table S3. The latter data agree with previous findings that the 6p orbitals are the major acceptors in Pb2+. Accordingly, their natural population varies between 0.47 and 0.56 e, following near quantitively the transferred electrons from the ligands. The 6s populations change only marginally, while the 6d natural populations are negligible.

3. Methods

The DFT calculations were carried out with the Gaussian09 suite of programs [44] using the PBE0 exchange-correlation functional [45,46]. This function was selected on the basis of its very good general performance [47,48], particularly for metal complexes [48,49]; therefore, it is applied frequently in such studies [29,50]. For Pb, the small-core relativistic Stuttgart–Cologne pseudopotential (ECP60MDF) [51] in conjunction with a contracted (12s11p8d1f)/[5s4p3d1f] basis set of triple-zeta plus polarization quality [52], whereas for the light atoms the standard 6-311G** basis set was used. The latter bases of O and N were extended by one set of diffuse functions. The dispersion forces were taken into account with the D3 version of Grimme’s dispersion correction [53], applying Becke–Johnson damping [54]. The SuperFine grid was applied for good integration accuracy. It contained 175 radial shells and 974 angular points (175,974) per shell for H, C, O, and N, whereas for Pb, it was 250,974.
In the geometry optimizations the aqueous solution conditions were taken into account by means of the polarizable continuum model (PCM) [55,56]. The initial structures for geometry optimizations of the complexes were taken from the literature when available. In the case of computed literature structures, we chose those of the related Ac complexes based on the similar ionic radii of Pb2+ and Ac3+ [11]: they were the DOTA, DOTPA, DO4Py, DO4Pyd, and MeDO2PA complexes from Ref. [30]. Reported crystal structures of the Pb complexes were used for the DOTAM [19], CRYPT [23], and semicarbazone complexes [21]. The initial structures of the H2DO2PA, DO2A2AM, DO2A2Py, and DO3APA complexes were prepared manually from the optimized structures of the parent complexes. As the geometry optimizations often resulted in structures with C1 symmetry (either because of the crystal initial structures or due to symmetry break during the run), the resulting structures were inspected for possible symmetries and corrected if suited. For analysis of the geometries, the GaussView 5 software [57] was used. The minimum characters of all the optimized structures were confirmed by frequency analyses.
The natural atomic charges and valence orbital populations of Pb, as well as the second-order perturbation energies, were evaluated on the basis of the Natural Bond Orbital (NBO) model [33]. The metal–ligand interactions were further explored with Natural Energy Decomposition Analysis (NEDA) [31,32] using the NBO 7.0 code [58] coupled with Gaussian16 [59].

4. Conclusions

In the present DFT study, the structure and bonding characteristics of twelve complexes of the pharmaceutically important Pb2+ ion with macrocyclic ligands were assessed in an aqueous solution. The bonding analysis was based on NEDA as well as on second-order perturbation energies of the Fock matrix from the NBO model. The obtained computed results facilitated a differentiation between the various pendant arms containing O and N donors for the CT interactions.
With ten out of the eleven cyclen-based ligands, the TSAP conformers proved to be the most stable structures of the Pb complexes. Only the complex with the DOTPA ligand containing extended pendant arms favored the SAP isomer.
The total interaction energies from the NEDA analysis are comparable for the complexes with the same charge. In agreement with the anionic and/or strongly polarized character of the probed ligands, their magnitudes are determined by the electrical term. Its bonding contribution amounts to 59–78% of the total bonding energy (neutral ligands providing the smallest values). The different pendant arms of DOTPA and DO3APA increased marginally the total interaction energy with respect to that of the reference DOTA complex.
Whereas the electrical term depends strongly on the charge of the complex, it varies generally marginally among the complexes with the same charge. In contrast, the CT energies do not show any systematic relation to the charge of the complex but vary more than the EL among the complexes with the same charge. The energetic analysis revealed the CT superiority of the carboxylate O-s. From the N-s, the aromatic ones are generally the most efficient donors.
Combinations of selected efficient O- and N-donor pendant arms were probed in the DO3APA, DO2A2AM, and DO2A2Py complexes with reference to Pb(DOTA)2−—assessing only the CT interactions due to the different charges. While the replacement of one or more carboxylate groups of DOTA by the picolinate, amide, or pyridyl groups increased the donation efficiency of the remaining carboxylate groups, the new donor groups performed worse than in their parent complexes. This shows the superiority of the acetate pendant arms in such ligands and the lack of synergic cooperation between the donor arms. Altogether, the combination led only to marginal enhancement of the total CT in the complexes.
In general, carboxylate donor groups tend to form stronger bonds with Pb2+ than neutral ones, raising the question about a similar or better (?) efficiency of phosphonate and sulfonate groups. On the other hand, the change in the macrocycle moiety could make a significant difference in the bonding. In this direction, the recently reported diaza-18-crown-type [29,60] or bispidine-based ligands [61] may be worth studying.

Supplementary Materials

The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/molecules29174198/s1, Figure S1: 2D structures of the probed ligands; Table S1: Computed Pb-O and Pb-N distances; Table S2: CT energies for the various donor types; Table S3: Natural atomic charge and populations of the 6s, 6p and 6d orbitals of Pb in the complexes; Cartesian coordinates of the optimized TSAP and SAP structures.

Author Contributions

Conceptualization, A.K.; methodology, A.K.; investigation, A.K. and Z.V.; data curation, A.K.; writing—original draft preparation, A.K.; writing—review and editing, A.K. and Z.V.; visualization, A.K.; supervision, A.K.; project administration, A.K. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

All relevant data have been included in the paper and in the Supplementary Materials.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Kvassheim, M.; Revheim, M.-E.R.; Stokke, C. Quantitative SPECT/CT imaging of lead-212: A phantom study. EJNMMI Phys. 2022, 9, 52. [Google Scholar] [CrossRef] [PubMed]
  2. ICRP. Nuclear Decay Data for Dosimetric Calculations; ICRP Publication 107, Annals of the ICRP; International Commission on Radiological Protection: Ottawa, ON, Canada, 2008; Volume 38. [Google Scholar]
  3. Price, E.W.; Orvig, C. Matching chelators to radiometals for radiopharmaceuticals. Chem. Soc. Rev. 2014, 43, 260–290. [Google Scholar] [CrossRef]
  4. Boros, E.; Packard, A.B. Radioactive Transition Metals for Imaging and Therapy. Chem. Rev. 2019, 119, 870–901. [Google Scholar] [CrossRef]
  5. Morgan, K.A.; Rudd, S.E.; Noor, A.; Donnelly, P.S. Theranostic Nuclear Medicine with Gallium-68, Lutetium-177, Copper-64/67, Actinium-225, and Lead-212/203 Radionuclides. Chem. Rev. 2023, 123, 12004–12035. [Google Scholar] [CrossRef] [PubMed]
  6. Ramogida, C.F.; Orvig, C. Tumour targeting with radiometals for diagnosis and therapy. Chem. Commun. 2013, 49, 4720–4739. [Google Scholar] [CrossRef] [PubMed]
  7. Pearson, R.G. Hard and Soft Acids and Bases. J. Am. Chem. Soc. 1963, 85, 3533–3539. [Google Scholar] [CrossRef]
  8. Pearson, R.G. Hard and soft acids and bases, HSAB, part 1: Fundamental principles. J. Chem. Educ. 1968, 45, 581–587. [Google Scholar] [CrossRef]
  9. Pearson, R.G. Hard and soft acids and bases, HSAB, part II: Underlying theories. J. Chem. Educ. 1968, 45, 643–648. [Google Scholar] [CrossRef]
  10. Parr, J. Some recent coordination chemistry of lead(II). Polyhedron 1997, 16, 551–566. [Google Scholar] [CrossRef]
  11. Shannon, R.D. Revised Effective Ionic Radii and Systematic Studies of Interatomic Distances in Halides and Chalcogenides. Acta Cryst. 1976, A32, 751–767. [Google Scholar] [CrossRef]
  12. Nugent, J.W.; Lee, H.-S.; Reibenspies, J.H.; Hancock, R.D. Spectroscopic, structural, and thermodynamic aspects of the stereochemically active lone pair on lead(II): Structure of the lead(II) dota complex. Polyhedron 2015, 91, 120–127. [Google Scholar] [CrossRef]
  13. Moncomble, A.; Cornard, J.-P.; Meyer, M. A quantum chemistry evaluation of the stereochemical activity of the lone pair in PbII complexes with sequestering ligands. J. Mol. Model. 2017, 23, 24. [Google Scholar] [CrossRef]
  14. Mirzadeh, S.; Kumar, K.; Gansow, O.A. The Chemical Fate of 212Bi-DOTA Formed by β− Decay of 212Pb(DOTA)2−. Radiochim. Acta 1993, 60, 1–10. [Google Scholar] [CrossRef]
  15. Pippin, C.G.; McMurry, T.J.; Brechbiel, M.W.; McDonald, M.; Lambrecht, R.; Milenic, D.E.; Roselli, M.; Colcher, D.; Gansow, O.A. Lead(II) complexes of 1,4,7,10-tetraazacyclododecane-N,N′,N″,N‴-tetraacetate: Solution chemistry and application to tumor localization with 203Pb labeled monoclonal antibodies. Inorg. Chim. Acta 1995, 239, 43–51. [Google Scholar] [CrossRef]
  16. Maumela, H.; Hancock, R.D.; Carlton, L.; Reibenspies, J.H.; Wainwright, K.P. The Amide Oxygen as a Donor Group. Metal Ion Complexing Properties of Tetra-N-acetamide Substituted Cyclen: A Crystallographic, NMR, Molecular Mechanics, and Thermodynamic Study. J. Am. Chem. Soc. 1995, 117, 6698–6707. [Google Scholar] [CrossRef]
  17. Chappell, L.L.; Dadachova, E.; Milenic, D.E.; Garmestani, K.; Wu, C.; Brechbiel, M.W. Synthesis, characterization, and evaluation of a novel bifunctional chelating agent for the lead isotopes 203Pb and 212Pb. Nucl. Med. Biol. 2000, 27, 93–100. [Google Scholar] [CrossRef] [PubMed]
  18. Hancock, R.D.; Siddons, C.J.; Oscarson, K.A.; Reibenspies, J.M. The structure of the 11-coordinate barium complex of the pendant-donor macrocycle 1,4,7,10-tetrakis(carbamoylmethyl)-1,4,7,10-tetraazacyclododecane: An analysis of the coordination numbers of barium(II) in its complexes. Inorg. Chim. Acta 2004, 357, 723–727. [Google Scholar] [CrossRef]
  19. Cuenot, F.; Meyer, M.; Espinosa, E.; Bucaille, A.; Burgat, R.; Guilard, R.; Marichal-Westrich, C. New Insights into the Complexation of Lead(II) by 1,4,7,10-Tetrakis(carbamoylmethyl)-1,4,7,10-tetraazacyclododecane (DOTAM): Structural, Thermodynamic, and Kinetic Studies. Eur. J. Inorg. Chem. 2008, 2008, 267–283. [Google Scholar] [CrossRef]
  20. Lima, L.M.P.; Beyler, M.; Delgado, R.; Platas-Iglesias, C.; Tripier, R. Investigating the Complexation of the Pb2+/Bi3+ Pair with Dipicolinate Cyclen Ligands. Inorg. Chem. 2015, 54, 7045–7057. [Google Scholar] [CrossRef]
  21. Lange, J.L.; Davey, P.R.W.J.; Ma, M.T.; White, J.M.; Morgenstern, A.; Bruchertseifer, F.; Blower, P.J.; Paterson, B.M. An octadentate bis(semicarbazone) macrocycle: A potential chelator for lead and bismuth radiopharmaceuticals. Dalton Trans. 2020, 49, 14962–14974. [Google Scholar] [CrossRef]
  22. Ingham, A.; Kostelnik, T.I.; McNeil, B.L.; Patrick, B.O.; Choudhary, N.; de Guadalupe Jaraquemada-Peláez, M.; Orvig, C. Getting a lead on Pb2+-amide chelators for 203/212Pb radiopharmaceuticals. Dalton Trans. 2021, 50, 11579–11595. [Google Scholar] [CrossRef] [PubMed]
  23. McDonagh, A.W.; McNeil, B.L.; Patrick, B.O.; Ramogida, C.F. Synthesis and Evaluation of Bifunctional [2.2.2]-Cryptands for Nuclear Medicine Applications. Inorg. Chem. 2021, 60, 10030–10037. [Google Scholar] [CrossRef] [PubMed]
  24. McNeil, B.L.; Robertson, A.K.H.; Fu, W.; Yang, H.; Hoehr, C.; Ramogida, C.F.; Schaffer, P. Production, purification, and radiolabeling of the 203Pb/212Pb theranostic pair. EJNMMI Radiopharm. Chem. 2021, 6, 6. [Google Scholar] [CrossRef] [PubMed]
  25. Tosato, M.; Lazzari, L.; Marco, V.D. Revisiting Lead(II)-1,4,7,10-tetraazacyclododecane-1,4,7,10-tetraacetic Acid Coordination Chemistry in Aqueous Solutions: Evidence of an Underestimated Thermodynamic Stability. ACS Omega 2022, 7, 15596–15602. [Google Scholar] [CrossRef]
  26. McNeil, B.L.; Kadassery, K.J.; McDonagh, A.W.; Zhou, W.; Schaffer, P.; Wilson, J.J.; Ramogida, C.F. Evaluation of the Effect of Macrocyclic Ring Size on [203Pb]Pb(II) Complex Stability in Pyridyl-Containing Chelators. Inorg. Chem. 2022, 61, 9638–9649. [Google Scholar] [CrossRef]
  27. Grieve, M.L.; Paterson, B.M. The Evolving Coordination Chemistry of Radiometals for Targeted Alpha Therapy. Aust. J. Chem. 2022, 75, 65–88. [Google Scholar] [CrossRef]
  28. Li, M.; Baumhover, N.J.; Liu, D.; Cagle, B.S.; Boschetti, F.; Paulin, G.; Lee, D.; Dai, Z.; Obot, E.R.; Marks, B.M.; et al. Preclinical Evaluation of a Lead Specific Chelator (PSC) Conjugated to Radiopeptides for 203Pb and 212Pb-Based Theranostics. Pharmaceutics 2023, 15, 414. [Google Scholar] [CrossRef]
  29. Blei, M.K.; Waurick, L.; Reissig, F.; Kopka, K.; Stumpf, T.; Drobot, B.; Kretzschmar, J.; Mamat, C. Equilibrium Thermodynamics of Macropa Complexes with Selected Metal Isotopes of Radiopharmaceutical Interest. Inorg. Chem. 2023, 62, 20699–20709. [Google Scholar] [CrossRef]
  30. Kovács, A.; Varga, Z. Metal–ligand interactions in complexes of cyclen-based ligands with Bi and Ac. Struct. Chem. 2021, 32, 1719–1731. [Google Scholar] [CrossRef]
  31. Glendening, E.D.; Streitwieser, A. Natural energy decomposition analysis: An energy partitioning procedure for molecular interactions with application to weak hydrogen bonding, strong ionic, and moderate donor–acceptor interactions. J. Chem. Phys. 1994, 100, 2900–2909. [Google Scholar] [CrossRef]
  32. Glendening, E.D. Natural Energy Decomposition Analysis: Extension to Density Functional Methods and Analysis of Cooperative Effects in Water Clusters. J. Phys. Chem. A 2005, 109, 11936–11940. [Google Scholar] [CrossRef] [PubMed]
  33. Reed, A.E.; Curtiss, L.A.; Weinhold, F. Intermolecular interactions from a natural bond orbital, donor-acceptor viewpoint. Chem. Rev. 1988, 88, 899–926. [Google Scholar] [CrossRef]
  34. Peters, J.A.; Djanashvili, K.; Geraldes, C.F.G.C.; Platas-Iglesias, C. The chemical consequences of the gradual decrease of the ionic radius along the Ln-series. Coord. Chem. Rev. 2020, 406, 213146. [Google Scholar] [CrossRef]
  35. Viola-Villegas, N.; Doyle, R.P. The coordination chemistry of 1,4,7,10-tetraazacyclododecane-N,N′,N″,N‴-tetraacetic acid (H4DOTA): Structural overview and analyses on structure-stability relationships. Coord. Chem. Rev. 2009, 253, 1906–1925. [Google Scholar] [CrossRef]
  36. Spirlet, M.R.; Rebizant, J.; Desreux, J.F.; Loncin, M.F. Crystal and molecular structure of sodium aqua(1,4,7,10-tetraazacyclododecane-1,4,7,10-tetraacetato)europate(III) tetrahydrate Na+(EuDOTA.H2O)−.4H2O, and its relevance to NMR studies of the conformational behavior of the lanthanide complexes formed by the macrocyclic ligand DOTA. Inorg. Chem. 1984, 23, 359–363. [Google Scholar] [CrossRef]
  37. Benetollo, F.; Bombieri, G.; Calabi, L.; Aime, S.; Botta, M. Structural Variations Across the Lanthanide Series of Macrocyclic DOTA Complexes: Insights into the Design of Contrast Agents for Magnetic Resonance Imaging. Inorg. Chem. 2003, 42, 148–157. [Google Scholar] [CrossRef]
  38. Chang, C.A.; Francesconi, L.C.; Malley, M.F.; Kumar, K.; Gougoutas, J.Z.; Tweedle, M.F.; Lee, D.W.; Wilson, L.J. Synthesis, characterization, and crystal structures of M(DO3A) (M = iron, gadolinium) and Na[M(DOTA)] (M = Fe, yttrium, Gd). Inorg. Chem. 1993, 32, 3501–3508. [Google Scholar] [CrossRef]
  39. Aime, S.; Barge, A.; Botta, M.; Fasano, M.; Ayala, J.D.; Bombieri, G. Crystal structure and solution dynamics of the lutetium(III) chelate of DOTA. Inorg. Chim. Acta 1996, 246, 423–429. [Google Scholar] [CrossRef]
  40. Parker, D.; Pulukkody, K.; Smith, F.C.; Batsanov, A.; Howard, J.A.K. Structures of the yttrium complexes of 1,4,7,10-tetraazacyclododecane-N,N′,N″,N‴-tetraacetic acid (H4dota) and N,N″-bis(benzylcarbamoylmethyl)diethylenetriamine-N,N′,N″-triacetic acid and the solution structure of a zirconium complex of H4dota. J. Chem. Soc. Dalton Trans. 1994, 689–693. [Google Scholar] [CrossRef]
  41. Benetollo, F.; Bombieri, G.; Aime, S.; Botta, M. A holmium complex of a macrocyclic ligand (DOTA) and its isostructural europium analogue. Acta Crystallogr. C Cryst. Struct. Commun. 1999, 55, 353–356. [Google Scholar] [CrossRef]
  42. Burai, L.; Tóth, E.; Moreau, G.; Sour, A.; Scopelliti, R.; Merbach, A.E. Novel macrocyclic EuII complexes: Fast water exchange related to an extreme M-Owater distance. Chem. Eur. J. 2003, 9, 1394–1404. [Google Scholar] [CrossRef] [PubMed]
  43. Aime, S.; Barge, A.; Benetollo, F.; Bombieri, G.; Botta, M.; Uggeri, F. A Novel Compound in the Lanthanide(III) DOTA Series. X-ray Crystal and Molecular Structure of the Complex Na[La(DOTA)La(HDOTA)]·10H2O. Inorg. Chem. 1997, 36, 4287–4289. [Google Scholar] [CrossRef]
  44. Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, Revision D. 01; Gaussian, Inc.: Wallingford, CT, USA, 2010. [Google Scholar]
  45. Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865, Erratum in Phys. Rev. Lett. 1997, 78, 1396. [Google Scholar] [CrossRef] [PubMed]
  46. Adamo, C.; Barone, V. Toward reliable density functional methods without adjustable parameters: The PBE0 model. J. Chem. Phys. 1999, 110, 6158–6170. [Google Scholar] [CrossRef]
  47. Mardirossian, N.; Head-Gordon, M. Thirty years of density functional theory in computational chemistry: An overview and extensive assessment of 200 density functionals. Mol. Phys. 2017, 115, 2315–2372. [Google Scholar] [CrossRef]
  48. Bursch, M.; Mewes, J.-M.; Hansen, A.; Grimme, S. Best-Practice DFT Protocols for Basic Molecular Computational Chemistry. Angew. Chem. Int. Ed. 2022, 61, e202205735. [Google Scholar] [CrossRef]
  49. Bühl, M.; Reimann, C.; Pantazis, D.A.; Bredow, T.; Neese, F. Geometries of Third-Row Transition-Metal Complexes from Density-Functional Theory. J. Chem. Theory Comput. 2008, 4, 1449–1459. [Google Scholar] [CrossRef]
  50. Morgenstern, A.; Lilley, L.M.; Stein, B.W.; Kozimor, S.A.; Batista, E.R.; Yang, P. Computer-Assisted Design of Macrocyclic Chelators for Actinium-225 Radiotherapeutics. Inorg. Chem. 2021, 60, 623–632. [Google Scholar] [CrossRef]
  51. Metz, B.; Stoll, H.; Dolg, M. Small-core multiconfiguration-Dirac—Hartree—Fock-adjusted pseudopotentials for post-d main group elements: Application to PbH and PbO. J. Chem. Phys. 2000, 113, 2563–2569. [Google Scholar] [CrossRef]
  52. Peterson, K.A. Systematically convergent basis sets with relativistic pseudopotentials. I. Correlation consistent basis sets for the post-d group 13-15 elements. J. Chem. Phys. 2003, 119, 11099–11112. [Google Scholar] [CrossRef]
  53. Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parameterization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed]
  54. Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the damping function in dispersion corrected density functional theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef]
  55. Tomasi, J.; Mennucci, B.; Cammi, R. Quantum mechanical continuum solvation models. Chem. Rev. 2005, 105, 2999–3093. [Google Scholar] [CrossRef]
  56. Scalmani, G.; Frisch, M.J. Continuous surface charge polarizable continuum models of solvation. I. General formalism. J. Chem. Phys. 2010, 132, 114110. [Google Scholar] [CrossRef] [PubMed]
  57. Dennington, R.; Keith, T.; Millam, J. GaussView, Version 5; Semichem Inc.: Shawnee Mission, KS, USA, 2009. [Google Scholar]
  58. Glendening, E.D.; Landis, C.R.; Weinhold, F. NBO 7.0: New vistas in localized and delocalized chemical bonding theory. J. Comput. Chem. 2019, 40, 2234–2241. [Google Scholar] [CrossRef]
  59. Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision C. 01; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
  60. Fiszbein, D.J.; Brown, V.; Thiele, N.A.; Woods, J.J.; Wharton, L.; MacMillan, S.N.; Radchenko, V.; Ramogida, C.F.; Wilson, J.J. Tuning the Kinetic Inertness of Bi3+ Complexes: The Impact of Donor Atoms on Diaza-18-Crown-6 Ligands as Chelators for 213Bi Targeted Alpha Therapy. Inorg. Chem. 2021, 60, 9199–9211. [Google Scholar] [CrossRef] [PubMed]
  61. Cieslik, P.; Kubeil, M.; Zarschler, K.; Ullrich, M.; Brandt, F.; Anger, K.; Wadepohl, H.; Kopka, K.; Bachmann, M.; Pietzsch, J.; et al. Toward Personalized Medicine: One Chelator for Imaging and Therapy with Lutetium-177 and Actinium-225. J. Am. Chem. Soc. 2022, 144, 21555–21567. [Google Scholar] [CrossRef] [PubMed]
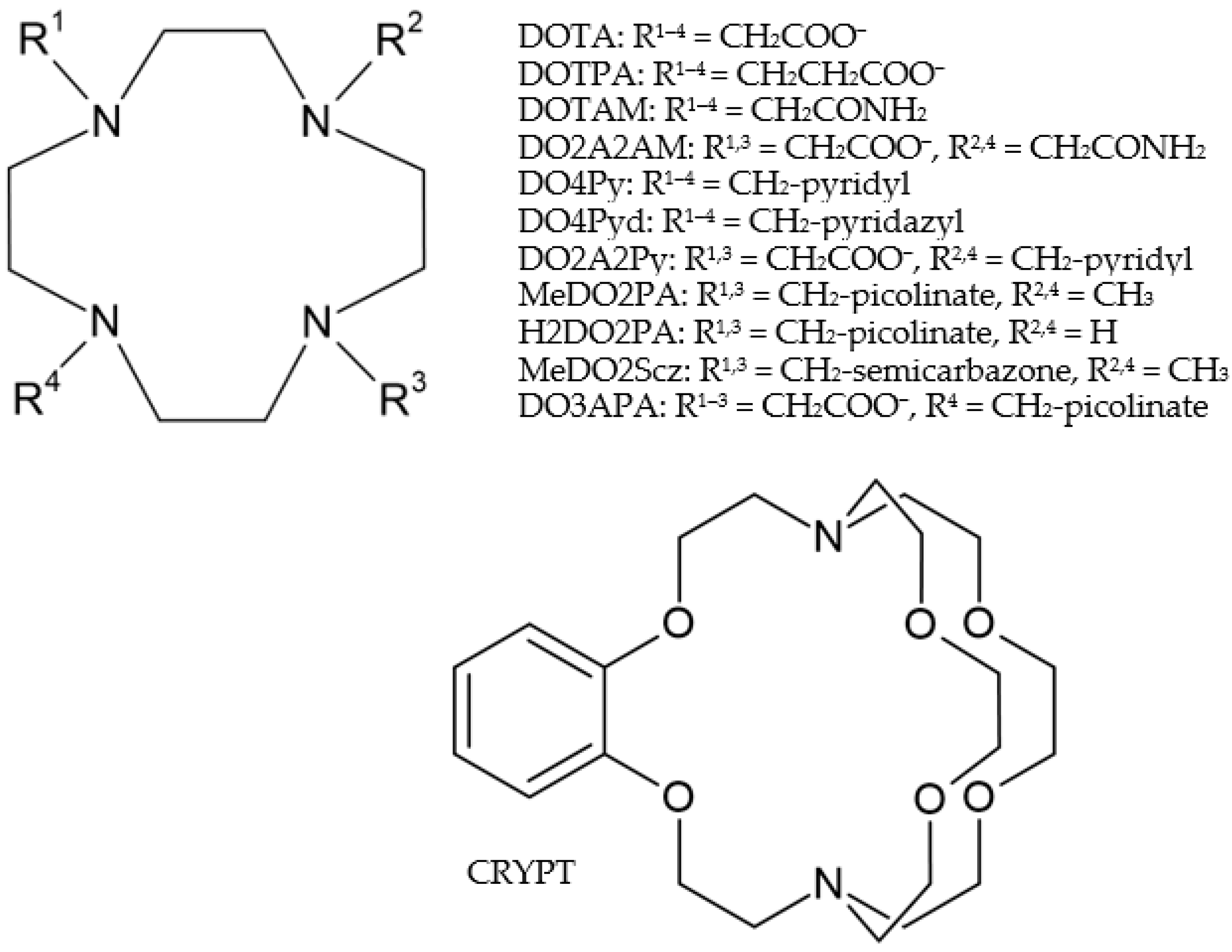
Molecules 29 04198 g001
Figure 1. (Top) Compilation of the eleven cyclen-based ligands (the structure of each ligand is given in Figure S1 of the Supplementary Materials); (Bottom) Benzo substituted [2]-cryptand.
Figure 1. (Top) Compilation of the eleven cyclen-based ligands (the structure of each ligand is given in Figure S1 of the Supplementary Materials); (Bottom) Benzo substituted [2]-cryptand.
Molecules 29 04198 g001
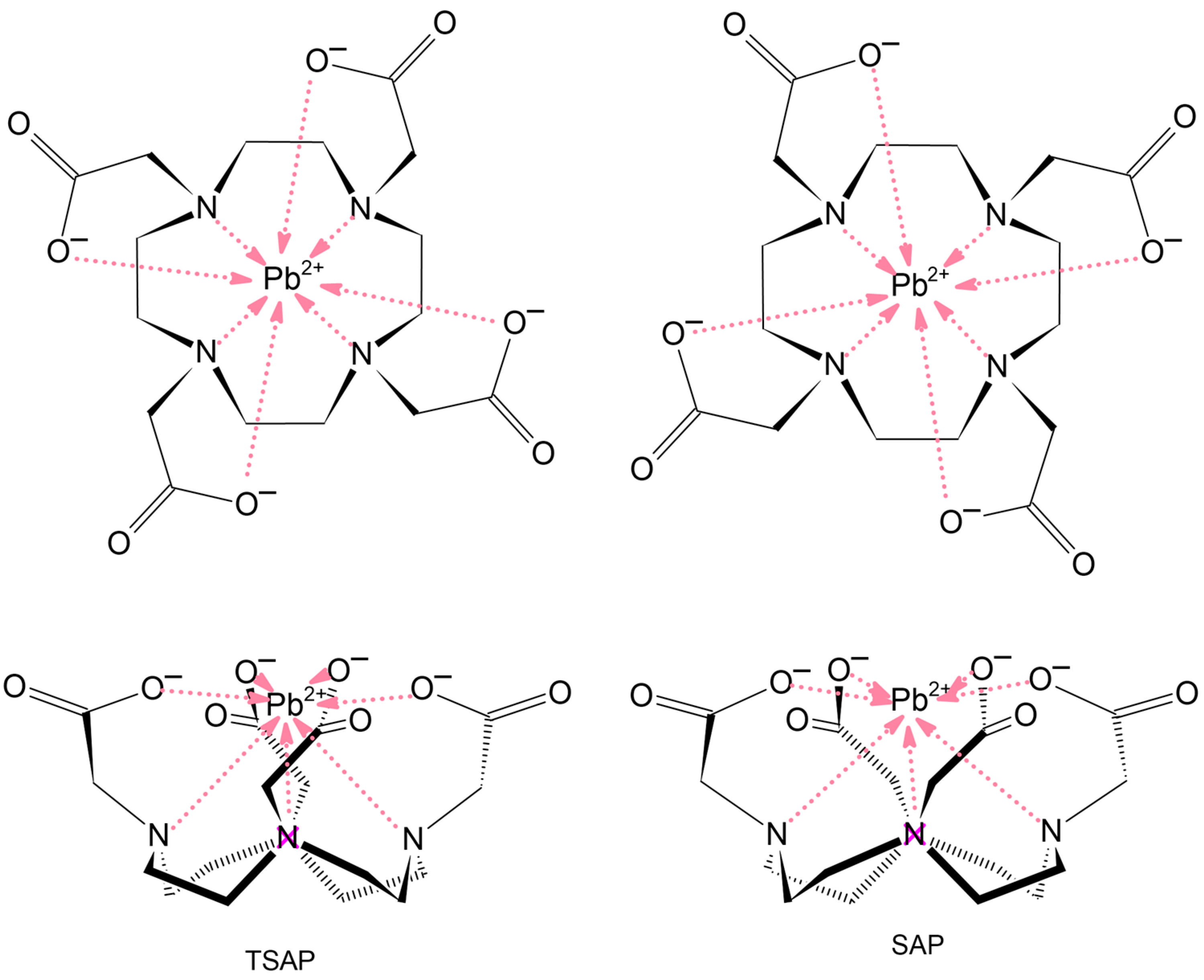
Molecules 29 04198 g002
Figure 2. Schematic presentation of the two significant helical arrangements of (top) the pendant arms and (bottom) cyclen ring for the Pb(DOTA)2− complex. The pink arrows indicate metal-ligand interactions.
Figure 2. Schematic presentation of the two significant helical arrangements of (top) the pendant arms and (bottom) cyclen ring for the Pb(DOTA)2− complex. The pink arrows indicate metal-ligand interactions.
Molecules 29 04198 g002
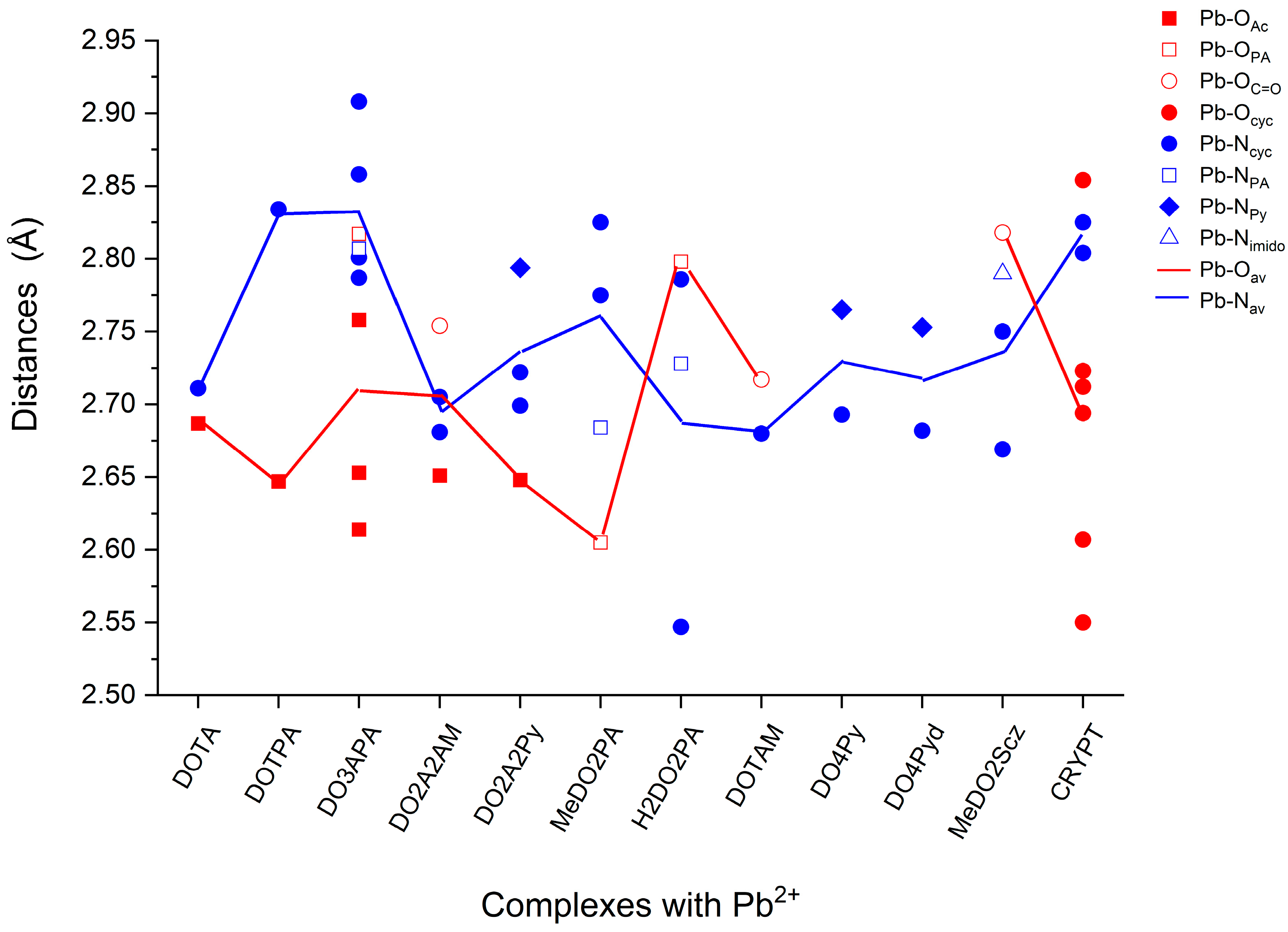
Molecules 29 04198 g003
Figure 3. Individual donor–acceptor (symbols) and the average Pb-O and Pb-N distances (straight lines) in the complexes. The depicted values are given in Table 1 and Table S1.
Figure 3. Individual donor–acceptor (symbols) and the average Pb-O and Pb-N distances (straight lines) in the complexes. The depicted values are given in Table 1 and Table S1.
Molecules 29 04198 g003
Molecules 29 04198 g004
Figure 4. Results of the NEDA analysis grouped according the charges of the free ligands (L4−, L2−, L0). ΔEEL (%) = 100·ΔEEL/(ΔEEL + ΔECT).
Figure 4. Results of the NEDA analysis grouped according the charges of the free ligands (L4−, L2−, L0). ΔEEL (%) = 100·ΔEEL/(ΔEEL + ΔECT).
Molecules 29 04198 g004
Molecules 29 04198 g005
Figure 5. Averaged CT energies (kJ/mol) for the various donor types from the second-order perturbation energies (E2). The depicted values are given in Table S2.
Figure 5. Averaged CT energies (kJ/mol) for the various donor types from the second-order perturbation energies (E2). The depicted values are given in Table S2.
Molecules 29 04198 g005
Table 1. Selected structural characteristics of the Pb complexes in aqueous solution 1.
Table 1. Selected structural characteristics of the Pb complexes in aqueous solution 1.
ComplexΔETSAP-SAPPb-OavPb-NavSymmetry
Pb(DOTA)2−−22.82.6872.711C4
Pb(DOTPA)2−43.72.6472.834C4
Pb(DOTAM)2+−12.82.7172.680C4
Pb(DO2A2AM)−18.92.7022.693C2
Pb(DO4Py)2+−19.0-2.729C4
Pb(DO4Pyd)2+−25.1-2.718C4
Pb(DO2A2Py)−17.72.6482.738C2
Pb(MeDO2PA)−8.52.6052.761C2
Pb(H2DO2PA)−7.42.7982.687C2
Pb(MeDO2Scz)2+−14.72.8182.736C2
Pb(DO3APA)2−−18.62.7112.832C1
Pb(CRYPT)2+-2.6902.815C1
1 Energetic preference of the TSAP structures vs. the SAP ones in terms of electronic energy (kJ/mol); average Pb-O and Pb-N donor–acceptor distances (Å) of the most stable structures (TSAP except for the DOPTA complex); symmetry of the most stable structures.
Table 2. Selected NEDA results and additional NBO characteristics 1.
Table 2. Selected NEDA results and additional NBO characteristics 1.
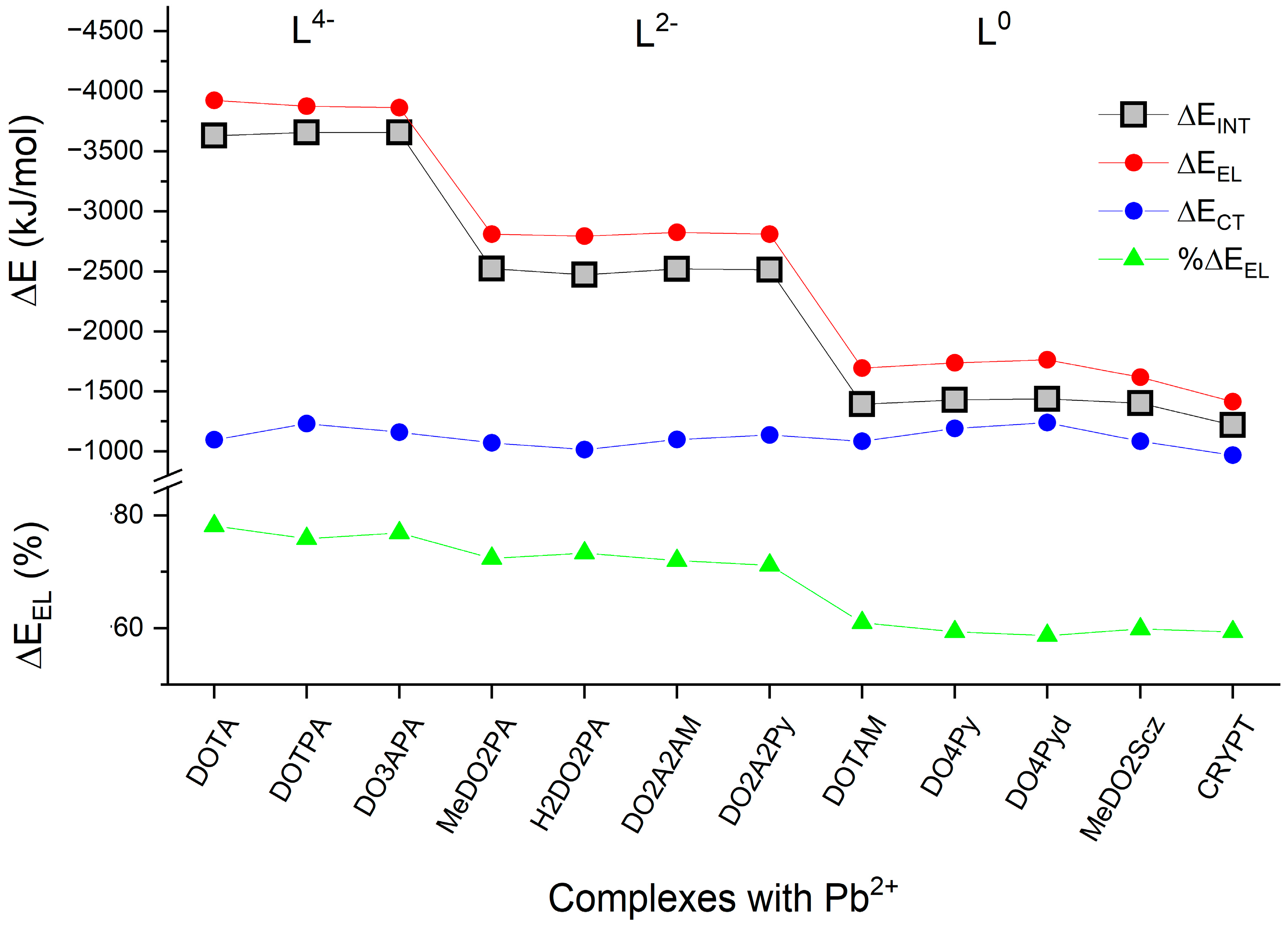
Complex NEDA CT(E2) CT(e)
ΔEINTΔEELΔECOREΔECTO → Pb2+N → Pb2+
Pb(DOTA)2−−3630−39241391−1097−672.1−431.40.49
Pb(DOTPA)2−−3657−38771451−1232−784.1−397.90.51
Pb(DO3APA)2−−3657−38631367−1161−658.0−490.60.52
Pb(MeDO2PA)−2523−28101358−1072−428.0−754.20.50
Pb(H2DO2PA)−2471−27941338−1015−300.7−866.20.51
Pb(DO2A2AM)−2520−28251404−1100−631.4−502.20.50
Pb(DO2A2Py)−2513−28101435−1138−377.1−842.20.53
Pb(DOTAM)2+−1394−16941384−1084−559.8−580.40.49
Pb(DO4Py)2+−1429−17391501−1191-−1342.20.56
Pb(DO4Pyd)2+−1438−17631565−1240-−1344.90.56
Pb(MeDO2Scz)2+−1403−16191302−1086−267.3−919.00.54
Pb(CRYPT)2+−1218−14141164−968−731.9−321.00.46
1 Energy data (kJ/mol) according to ΔEINT = ΔEEL + ΔECT + ΔECORE. ΔEINT means the total interaction energy between the two fragments Pb2+ and ligand consisting of electrical interaction (EL), charge transfer (CT), and core repulsion (CORE) contributions; summed energy consequences (kJ/mol) of the O → Pb2+ and N → Pb2+ charge transfers derived from the second-order perturbation energies between the ligand donor and Pb2+ acceptor orbitals; transferred number of electrons (e) from the ligands to Pb2+.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Kovács, A.; Varga, Z. Theoretical Study of Metal–Ligand Interactions in Lead Complexes with Radiopharmaceutical Interest. Molecules 2024, 29, 4198. https://doi.org/10.3390/molecules29174198

AMA Style

Kovács A, Varga Z. Theoretical Study of Metal–Ligand Interactions in Lead Complexes with Radiopharmaceutical Interest. Molecules. 2024; 29(17):4198. https://doi.org/10.3390/molecules29174198

Chicago/Turabian Style

Kovács, Attila, and Zoltán Varga. 2024. "Theoretical Study of Metal–Ligand Interactions in Lead Complexes with Radiopharmaceutical Interest" Molecules 29, no. 17: 4198. https://doi.org/10.3390/molecules29174198

APA Style

Kovács, A., & Varga, Z. (2024). Theoretical Study of Metal–Ligand Interactions in Lead Complexes with Radiopharmaceutical Interest. Molecules, 29(17), 4198. https://doi.org/10.3390/molecules29174198

Article Metrics

Back to TopTop