The Effects of Omeprazole on the Neuron-like Spiking of the Electrical Potential of Proteinoid Microspheres
Abstract
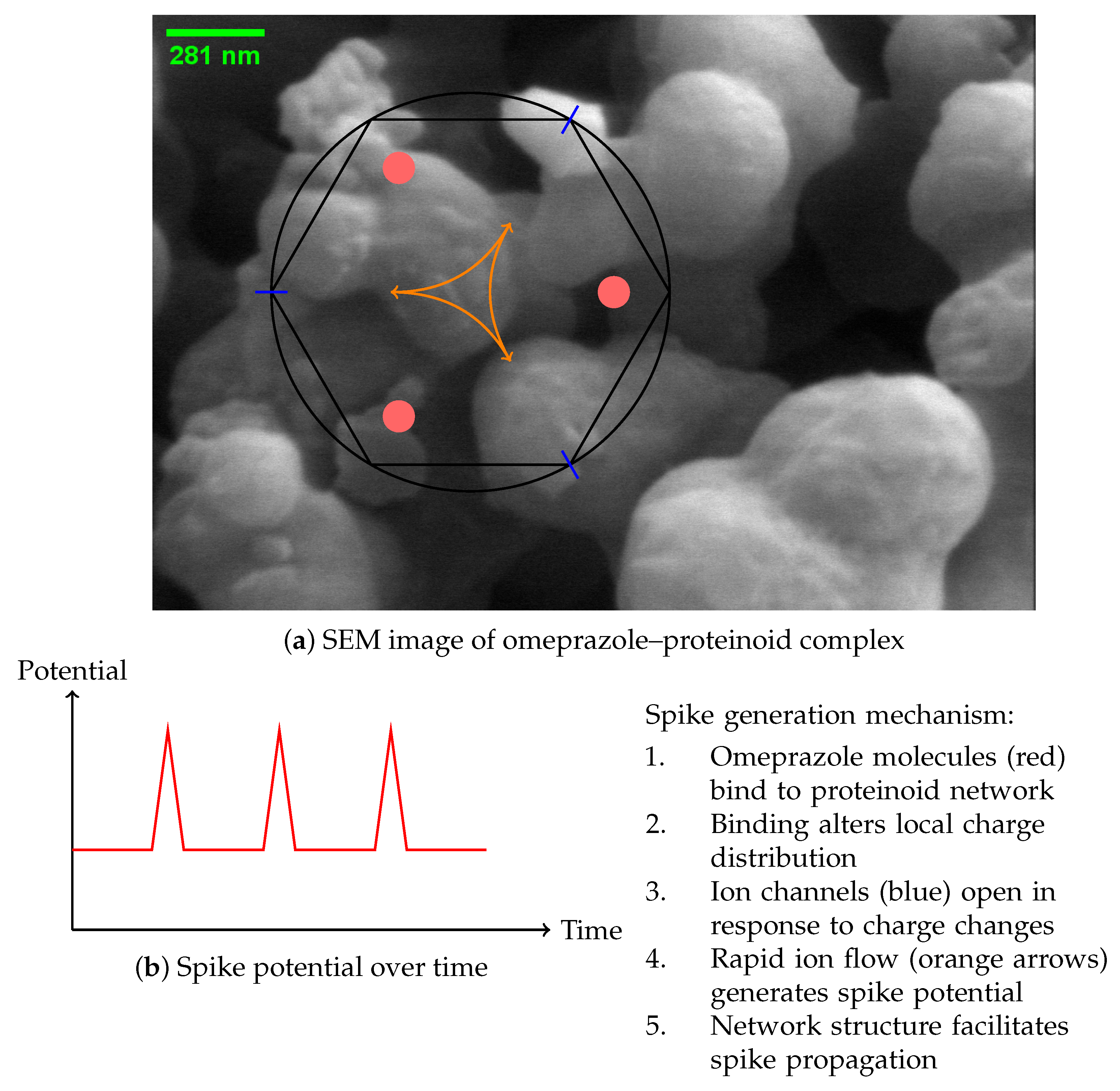
:1. Introduction
- a: the time scale of the recovery variable u;
- b: the sensitivity of the recovery variable u to the subthreshold fluctuations of the membrane potential v;
- c: the after-spike reset value of the membrane potential v;
- d: after-spike reset of the recovery variable u.
2. Materials and Methods
2.1. Synthesis of Omeprazole–Proteinoid Complex
2.2. Electrochemical Analysis of the Omeprazole–Proteinoid Complex
3. Results
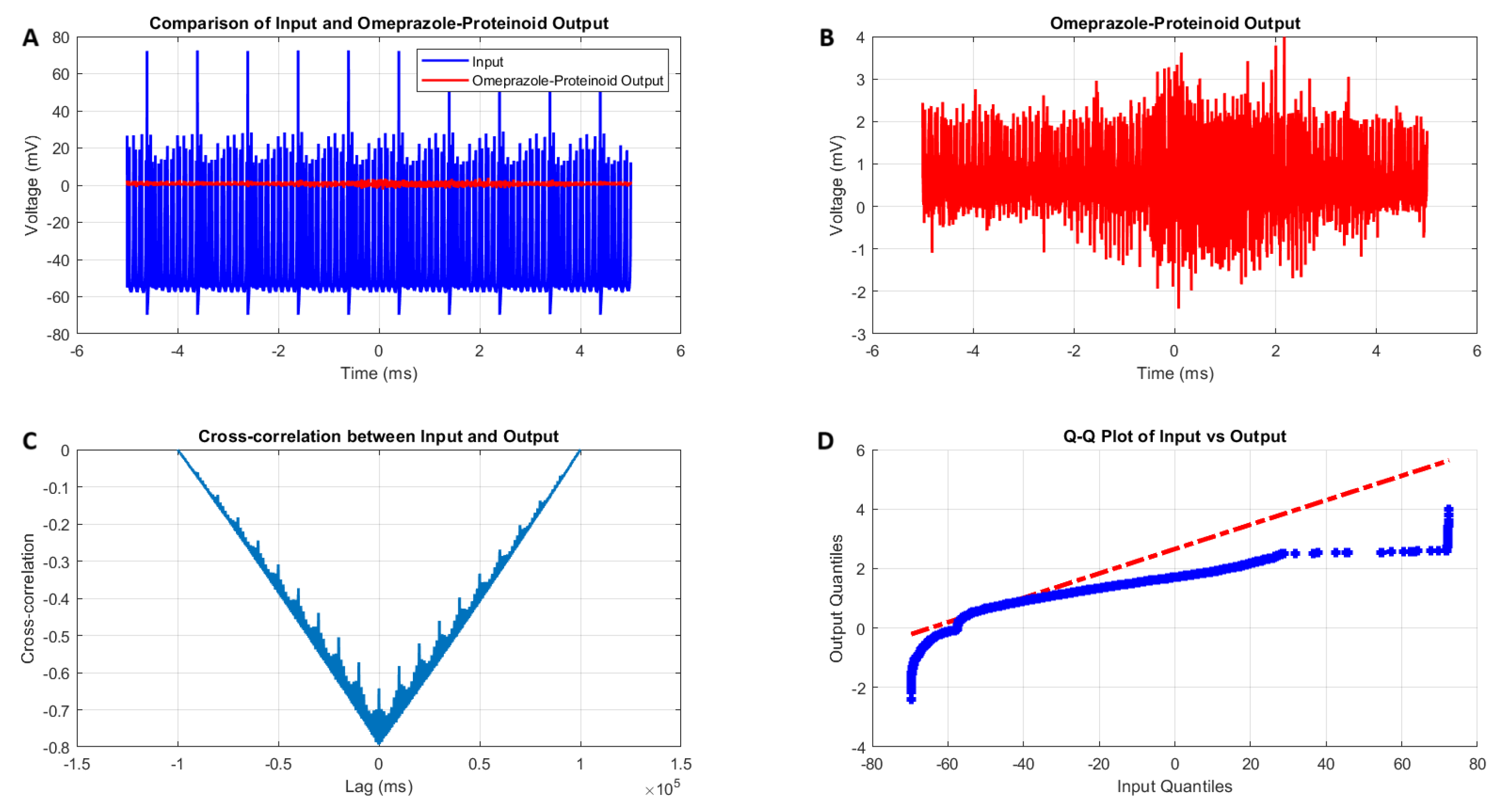
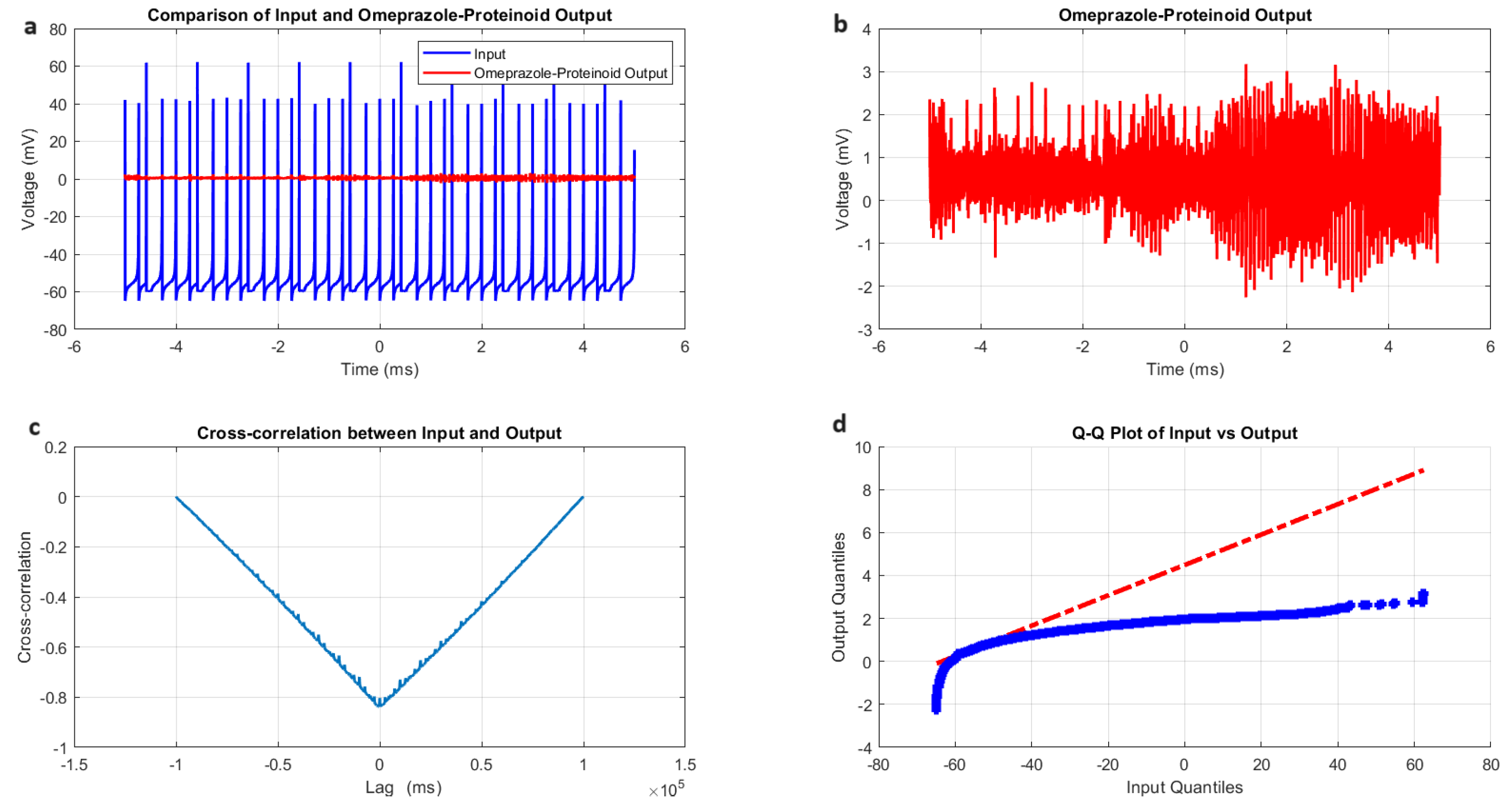
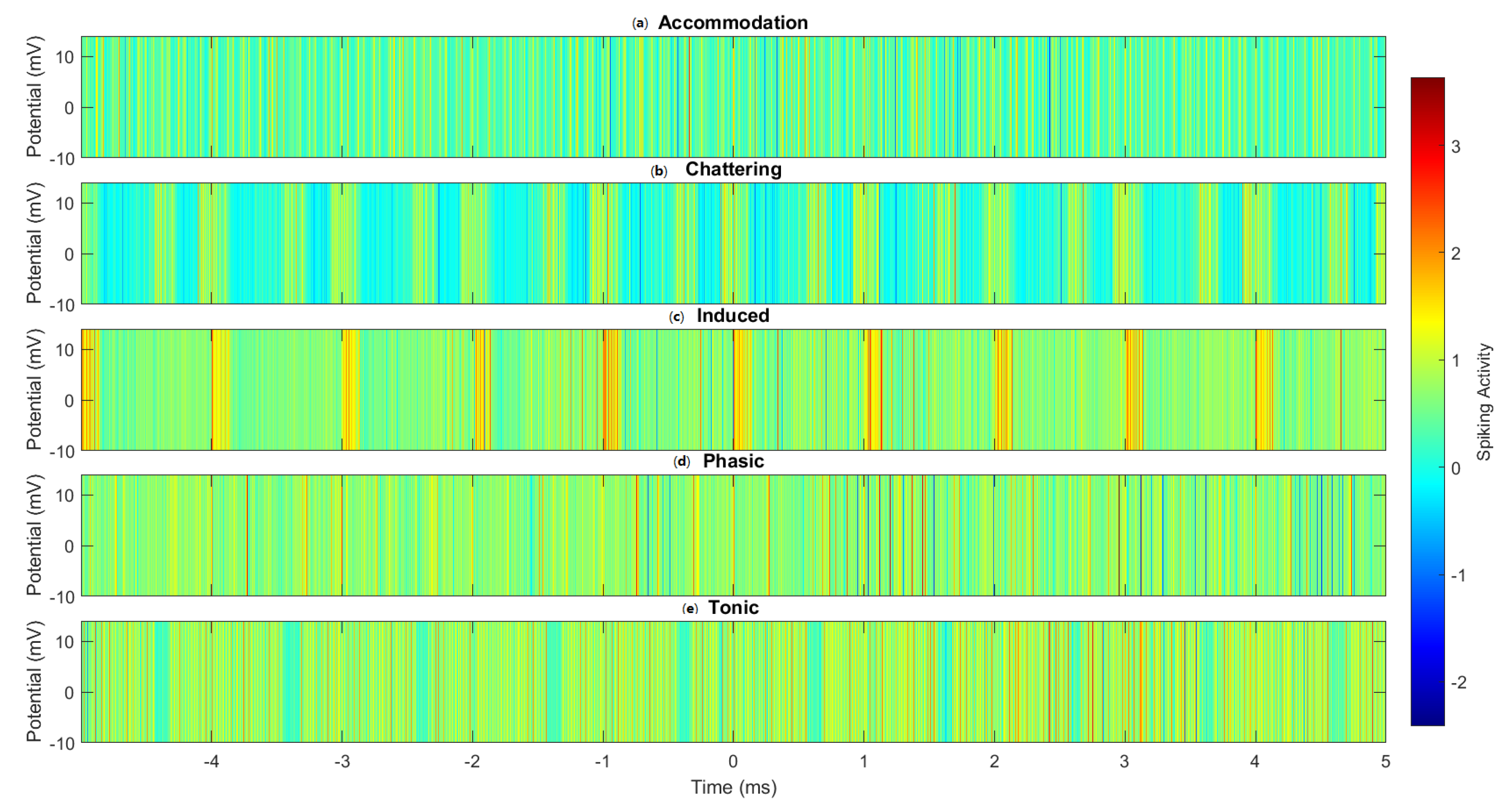
3.1. Accommodation Spiking Modulation by Omeprazole–Proteinoid Complex
Proposed Mechanism of Omeprazole–Proteinoid Modulation
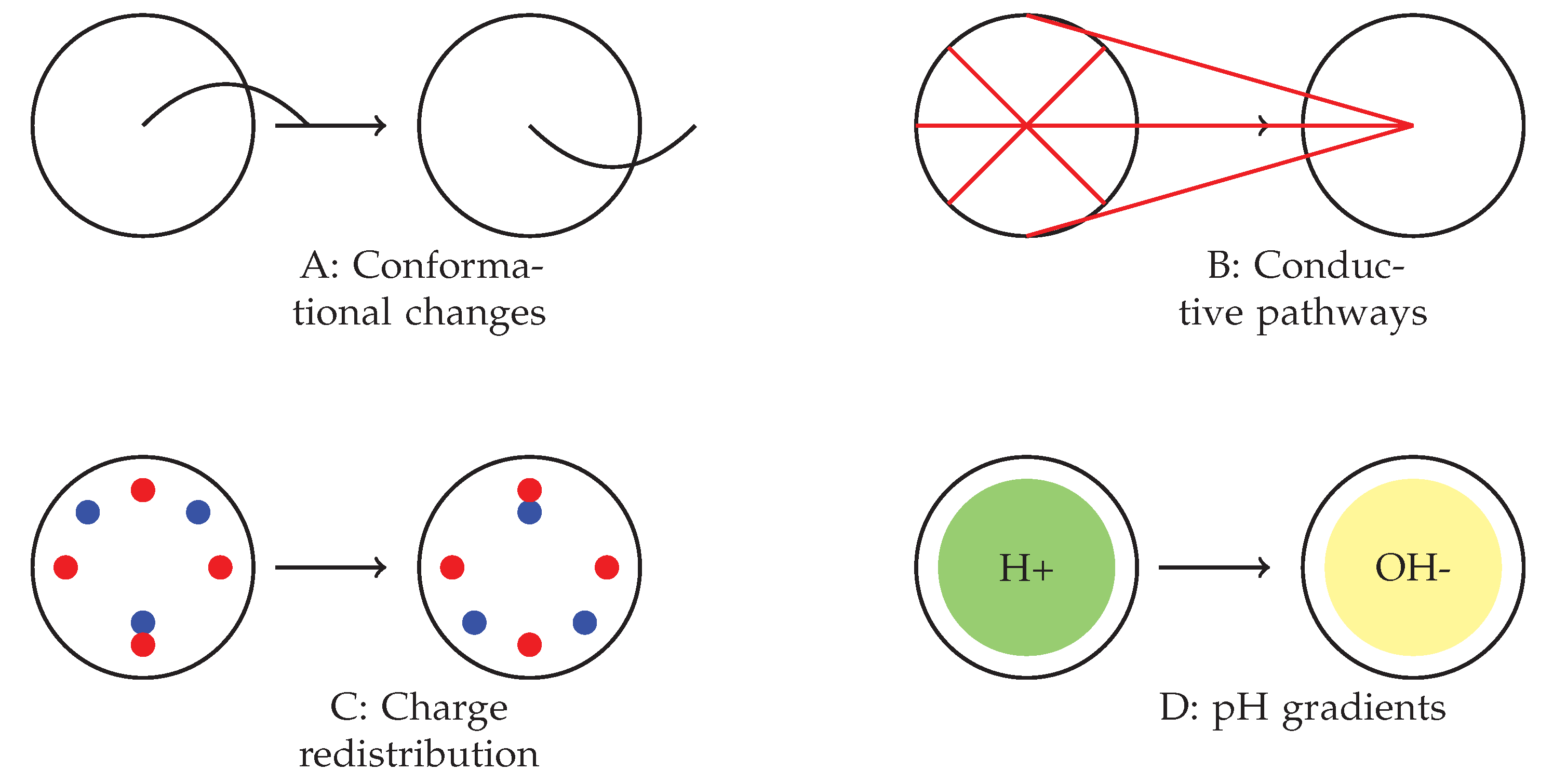
- Membrane capacitance modification: The complex may alter the effective membrane capacitance, , leading to a rescaling of the voltage dynamics [32]:where is the conductance introduced by the omeprazole–proteinoid complex, and is its associated reversal potential.
- Ion channel modulation: Omeprazole, known for its proton pump inhibition [10], may interact with voltage-gated ion channels. We propose a modification to the recovery variable dynamics:where represents the rate of recovery variable attenuation due to the complex.
- Threshold modification: The complex may alter the spiking threshold, affecting the after-spike resetting mechanism:where , , and are the threshold and reset modifications induced by the omeprazole–proteinoid complex.
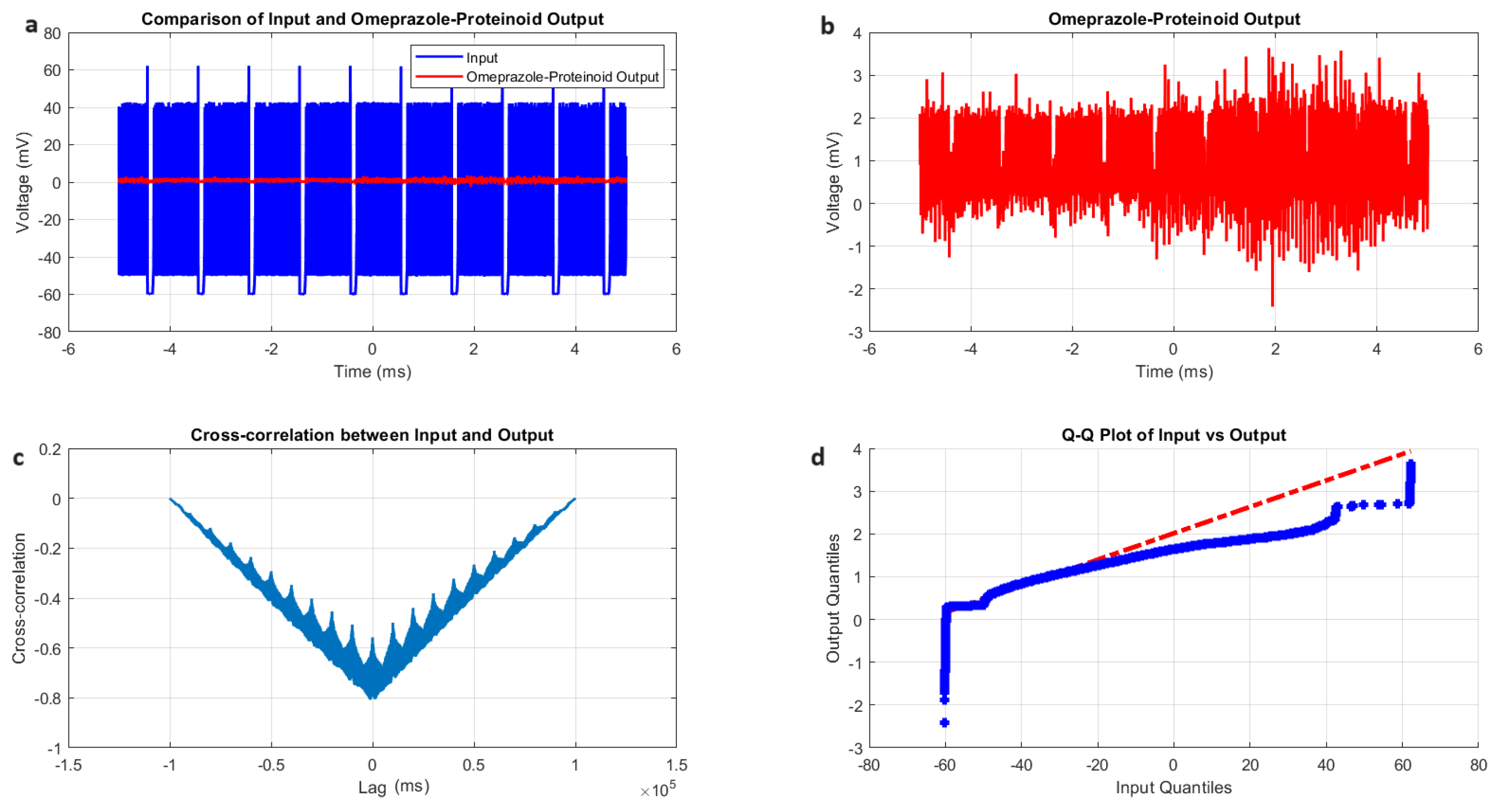
3.2. Izhikevich Model Simulations of Chattering Behaviour in Omeprazole Proteinoid Systems
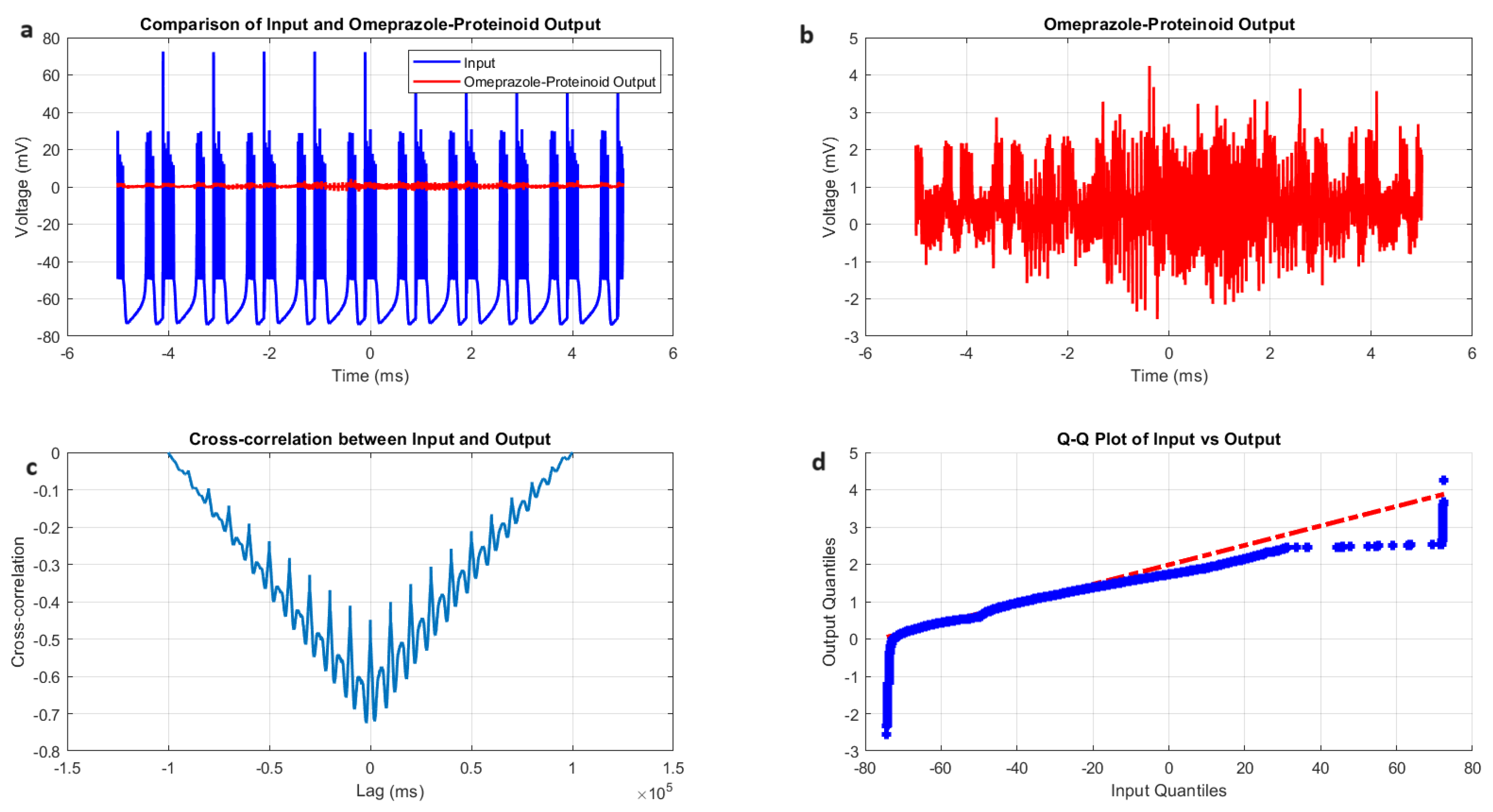
3.3. Induced-Mode Spiking in Omeprazole–Proteinoid Samples: Characterisation and Analysis
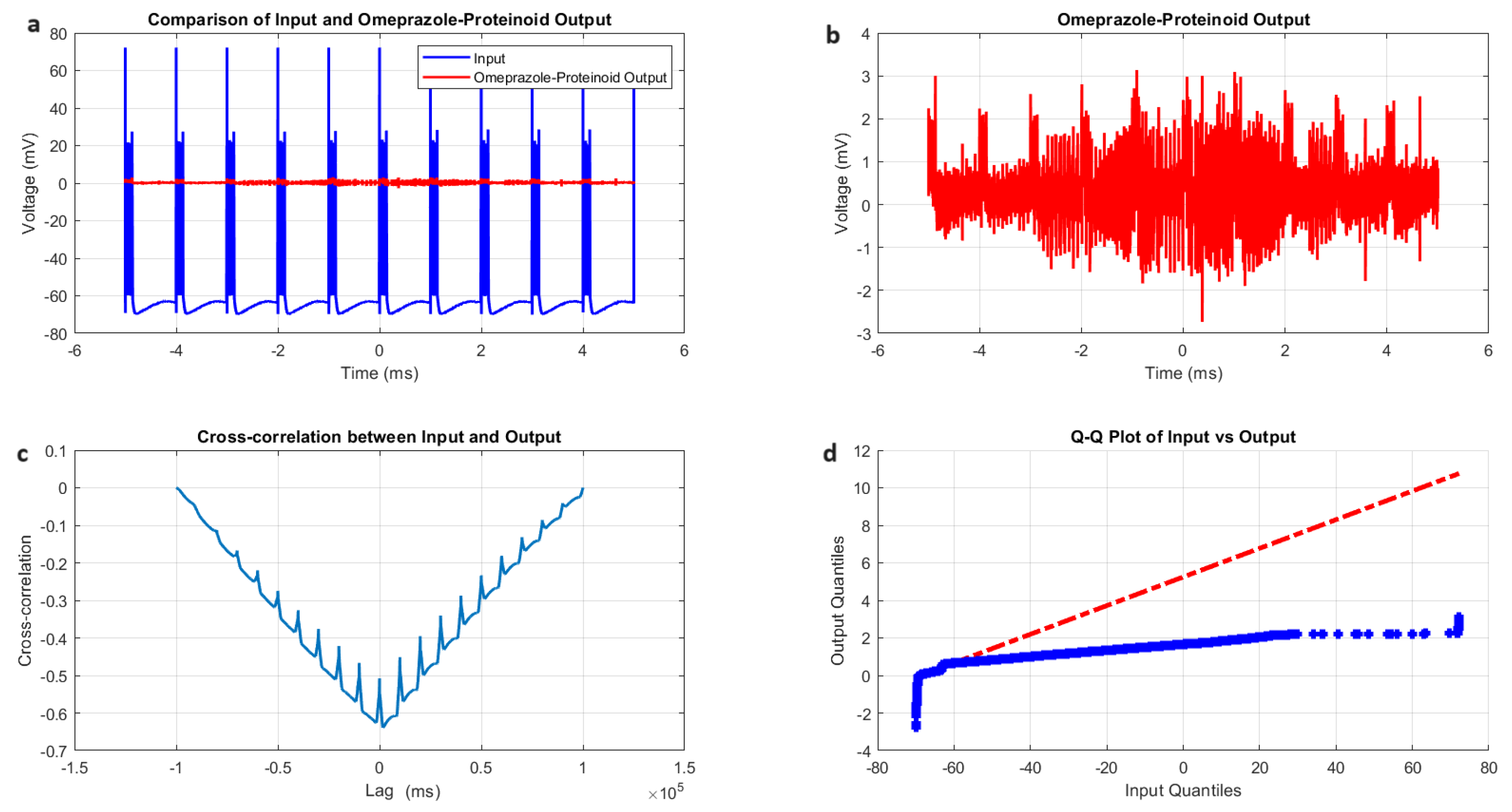
3.4. Phasic Spiking Dynamics in Omeprazole–Proteinoid Complexes: Characterisation of Stimulus–Response Patterns
3.5. Tonic Spiking Behaviour in Omeprazole–Proteinoid Complexes: Sustained Response Characteristics and Signal Processing
4. Discussion
4.1. Comparative Analysis of Spiking Modes
- Amplitude modulation: All modes showed a significant decrease in signal amplitude, with output ranges constantly falling within a range of ±4 mV, whereas input ranges often exceeded ±60 mV. This implies the presence of a strong buffering mechanism that could protect molecular fluctuations downstream from extreme fluctuations in voltage. As seen in Figure 5d, Figure 6d, Figure 7d and Figure 8d The red dashed line depicts the theoretical relationship that would exist if the two distributions were identical, whereas the blue curve shows the relationship that actually exists between the input and output quantiles. Due to the output signal’s narrower range of negative values than the input, the blue curve drops below the red line for input levels below roughly mV. This implies that there is a minimum voltage that the system may produce, or a "floor". Because the output signal has the ability to produce higher positive voltages than those found in the input, the blue curve rises above the red line for input quantities over roughly 70 mV. This indicates the system has some amplification or non-linear response for large positive inputs. The omeprazole-proteinoid system’s non-linear characteristics of the input signal transformation are revealed by these deviations from the red line, especially the asymmetric processing of large positive versus negative inputs.
- Temporal dynamics: The temporal delay between the input and output signals exhibited significant variation across different modes, ranging from ms in the chattering mode to 1590 milliseconds in the induced mode. The negative lag found in accommodation ( ms), phasic ( ms), and tonic ( ms) modes is particularly remarkable. This suggests the presence of anticipatory behaviour, which could have important consequences for information processing and response preparation in biological systems.
- Signal correlation: The correlation between the input and output signals varied from moderate (0.4503 in phasic mode) to strong (0.7937 in chattering mode). This suggests that the complexes effectively modify the input signal while retaining the different levels of the original signal properties.
- Distribution transformation: The Kolmogorov–Smirnov tests consistently revealed significant differences between the distributions of the input and output data in all modes. The KS statistics ranged from 0.9276 (tonic) to 0.9945 (phasic). This implies the use of non-linear processing techniques that have the potential to amplify specific signal characteristics while simultaneously reducing the prominence of others.
4.2. Implications for Molecular Computing
- Multi-modal processing: The diverse reactions to various spiking patterns indicate that these complexes have the ability to function as versatile molecular processors, adjusting their behaviour according to input parameters.
- Non-linear transformation: The persistent non-linear alteration of input signals, as indicated by the results of the KS test and Q-Q plots, suggests that these complexes perform complex signal processing procedures that go beyond mere filtering or amplification.
- Anticipatory behaviour: The presence of negative time delays in several modes indicates the occurrence of predictive processing at the molecular level. These findings could have important consequences for the development of molecular systems that can anticipate events or for understanding the biological reactions that occur before an event.
4.3. Potential Mechanisms and Future Directions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Adamatzky, A. Unconventional Computing: A Volume in the Encyclopedia of Complexity and Systems Science; Springer Publishing Company, Incorporated: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Ziegler, M.; Mussenbrock, T.; Kohlstedt, H. Bio-Inspired Information Pathways: From Neuroscience to Neurotronics; Springer Nature: Berlin/Heidelberg, Germany, 2024. [Google Scholar]
- Woods, D.; Doty, D.; Myhrvold, C.; Hui, J.; Zhou, F.; Yin, P.; Winfree, E. Diverse and robust molecular algorithms using reprogrammable DNA self-assembly. Nature 2019, 567, 366–372. [Google Scholar] [CrossRef] [PubMed]
- Adamatzky, A. A brief history of liquid computers. Philos. Trans. R. Soc. B 2019, 374, 20180372. [Google Scholar] [CrossRef]
- Schuman, C.D.; Potok, T.E.; Patton, R.M.; Birdwell, J.D.; Dean, M.E.; Rose, G.S.; Plank, J.S. A survey of neuromorphic computing and neural networks in hardware. arXiv 2017, arXiv:1705.06963. [Google Scholar]
- Indiveri, G.; Liu, S.C. Memory and information processing in neuromorphic systems. Proc. IEEE 2015, 103, 1379–1397. [Google Scholar] [CrossRef]
- Strand, D.S.; Kim, D.; Peura, D.A. 25 years of proton pump inhibitors: A comprehensive review. Gut Liver 2017, 11, 27. [Google Scholar] [CrossRef] [PubMed]
- Hashioka, S.; Inoue, K.; Hayashida, M.; Wake, R.; Oh-Nishi, A.; Miyaoka, T. Implications of systemic inflammation and periodontitis for major depression. Front. Neurosci. 2018, 12, 483. [Google Scholar] [CrossRef]
- Yoshiyama, H.; Nakamura, H.; Okamoto, T.; Okita, K.; Nakazawa, T. A novel in vitro effect of the mucosal protective agent sofalcone–inhibition of chemotactic motility in Helicobacter pylori. Aliment. Pharmacol. Ther. 2000, 14, 230–236. [Google Scholar] [CrossRef]
- Shin, J.M.; Sachs, G. Pharmacology of proton pump inhibitors. Curr. Gastroenterol. Rep. 2008, 10, 528–534. [Google Scholar] [CrossRef]
- Ortiz-Guerrero, G.; Amador-Muñoz, D.; Calderón-Ospina, C.A.; López-Fuentes, D.; Nava Mesa, M.O. Proton pump inhibitors and dementia: Physiopathological mechanisms and clinical consequences. Neural Plast. 2018, 2018, 5257285. [Google Scholar] [CrossRef]
- Fox, S.W.; Nakashima, T. The assembly and properties of protobiological structures: The beginnings of cellular peptide synthesis. BioSystems 1980, 12, 155–166. [Google Scholar] [CrossRef]
- Adamatzky, A. Advances in Unconventional Computing: Volume 1: Theory; Springer: Berlin/Heidelberg, Germany, 2016; Volume 22. [Google Scholar]
- Mayne, R.; Adamatzky, A. Slime mould foraging behaviour as optically coupled logical operations. Int. J. Gen. Syst. 2015, 44, 305–313. [Google Scholar] [CrossRef]
- Kendon, V.; Sebald, A.; Stepney, S. Heterotic computing: Exploiting hybrid computational devices. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2015, 373, 20150091. [Google Scholar] [CrossRef] [PubMed]
- Cronin, L.; Krasnogor, N.; Davis, B.G.; Alexander, C.; Robertson, N.; Steinke, J.H.; Schroeder, S.L.; Khlobystov, A.N.; Cooper, G.; Gardner, P.M.; et al. The imitation game—A computational chemical approach to recognizing life. Nat. Biotechnol. 2006, 24, 1203–1206. [Google Scholar] [CrossRef] [PubMed]
- Fox, S.W.; Harada, K. Thermal copolymerization of amino acids to a product resembling protein. Science 1958, 128, 1214. [Google Scholar] [CrossRef] [PubMed]
- Izhikevich, E.M. Simple model of spiking neurons. IEEE Trans. Neural Netw. 2003, 14, 1569–1572. [Google Scholar] [CrossRef]
- Izhikevich, E.M. Which model to use for cortical spiking neurons? IEEE Trans. Neural Netw. 2004, 15, 1063–1070. [Google Scholar] [CrossRef]
- Banzhaf, W.; Baumgaertner, B.; Beslon, G.; Doursat, R.; Foster, J.A.; McMullin, B.; De Melo, V.V.; Miconi, T.; Spector, L.; Stepney, S.; et al. Defining and simulating open-ended novelty: Requirements, guidelines, and challenges. Theory Biosci. 2016, 135, 131–161. [Google Scholar] [CrossRef]
- Pettersen, E.F.; Goddard, T.D.; Huang, C.C.; Couch, G.S.; Greenblatt, D.M.; Meng, E.C.; Ferrin, T.E. UCSF Chimera—A visualization system for exploratory research and analysis. J. Comput. Chem. 2004, 25, 1605–1612. [Google Scholar] [CrossRef]
- EM, I. Dynamical Systems in Neuroscience: The Geometry of Excitability and Bursting. In Computational Neuroscience; MIT Press: Cambridge, MA, USA, 2007. [Google Scholar]
- Andersson, T.; Röhss, K.; Bredberg, E.; Hassan-Alin, M. Pharmacokinetics and pharmacodynamics of esomeprazole, the S-isomer of omeprazole. Aliment. Pharmacol. Ther. 2001, 15, 1563–1569. [Google Scholar] [CrossRef]
- Langtry, H.D.; Wilde, M.I. Lansoprazole: An update of its pharmacological properties and clinical efficacy in the management of acid-related disorders. Drugs 1997, 54, 473–500. [Google Scholar] [CrossRef]
- Cheer, S.M.; Prakash, A.; Faulds, D.; Lamb, H.M. Pantoprazole: An update of its pharmacological properties and therapeutic use in the management of acid-related disorders. Drugs 2003, 63, 101–132. [Google Scholar] [CrossRef] [PubMed]
- Prakash, A.; Faulds, D. Rabeprazole. Drugs 1998, 55, 261–267. [Google Scholar] [CrossRef] [PubMed]
- Wu, F.; Gaohua, L.; Zhao, P.; Jamei, M.; Huang, S.-M.; Bashaw, E.D.; Lee, S.-C. Predicting nonlinear pharmacokinetics of omeprazole enantiomers and racemic drug using physiologically based pharmacokinetic modeling and simulation: Application to predict drug/genetic interactions. Pharm. Res. 2014, 31, 1919–1929. [Google Scholar] [CrossRef] [PubMed]
- Mougkogiannis, P.; Adamatzky, A. Learning in ensembles of proteinoid microspheres. R. Soc. Open Sci. 2023, 10, 230936. [Google Scholar] [CrossRef]
- Mougkogiannis, P.; Adamatzky, A. Recognition of sounds by ensembles of proteinoids. Mater. Today Bio 2024, 25, 100989. [Google Scholar] [CrossRef]
- Rao, R.P.; Ballard, D.H. Predictive coding in the visual cortex: A functional interpretation of some extra-classical receptive-field effects. Nat. Neurosci. 1999, 2, 79–87. [Google Scholar] [CrossRef]
- Pessoa, L. Understanding brain networks and brain organization. Phys. Life Rev. 2014, 11, 400–435. [Google Scholar] [CrossRef]
- Hodgkin, A.L.; Huxley, A.F. A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. 1952, 117, 500. [Google Scholar] [CrossRef]
- Mougkogiannis, P.; Adamatzky, A. Proto-Neurons from Abiotic Polypeptides. Encyclopedia 2024, 4, 512–543. [Google Scholar] [CrossRef]
- Poolos, N.P.; Migliore, M.; Johnston, D. Pharmacological upregulation of h-channels reduces the excitability of pyramidal neuron dendrites. Nat. Neurosci. 2002, 5, 767–774. [Google Scholar] [CrossRef]
- Coolen, A.C.; Kühn, R.; Sollich, P. Theory of Neural Information Processing Systems; OUP: Oxford, UK, 2005. [Google Scholar]
- Göpel, W. Chemical sensing, molecular electronics and nanotechnology: Interface technologies down to the molecular scale. Sens. Actuators B Chem. 1991, 4, 7–21. [Google Scholar] [CrossRef]
- Van Drongelen, W. Signal Processing for Neuroscientists; Academic Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Stojanovic, M.N.; Stefanovic, D.; Rudchenko, S. Exercises in molecular computing. Accounts Chem. Res. 2014, 47, 1845–1852. [Google Scholar] [CrossRef]
- Alvarez-Lorenzo, C.; Concheiro, A. Smart drug delivery systems: From fundamentals to the clinic. Chem. Commun. 2014, 50, 7743–7765. [Google Scholar] [CrossRef] [PubMed]
- Stellbrink, J.; Willner, L.; Jucknischke, O.; Richter, D.; Lindner, P.; Fetters, L.J.; Huang, J.S. Self-assembling behavior of living polymers. Macromolecules 1998, 31, 4189–4197. [Google Scholar] [CrossRef]
- Hille, B. Ionic channels in excitable membranes. Current problems and biophysical approaches. Biophys. J. 1978, 22, 283–294. [Google Scholar] [CrossRef] [PubMed]
- Murray, J.D.; Murray, J.D. Mathematical Biology: II: Spatial Models and Biomedical Applications; Springer: Berlin/Heidelberg, Germany, 2003; Volume 18. [Google Scholar]
- Itzhaki, E.; Elias, Y.; Moskovits, N.; Stemmer, S.M.; Margel, S. Proteinoid polymers and nanocapsules for cancer diagnostics, therapy and theranostics: In vitro and in vivo studies. J. Funct. Biomater. 2023, 14, 215. [Google Scholar] [CrossRef]
- Indiveri, G.; Linares-Barranco, B.; Hamilton, T.J.; Schaik, A.v.; Etienne-Cummings, R.; Delbruck, T.; Liu, S.C.; Dudek, P.; Häfliger, P.; Renaud, S.; et al. Neuromorphic silicon neuron circuits. Front. Neurosci. 2011, 5, 73. [Google Scholar] [CrossRef]
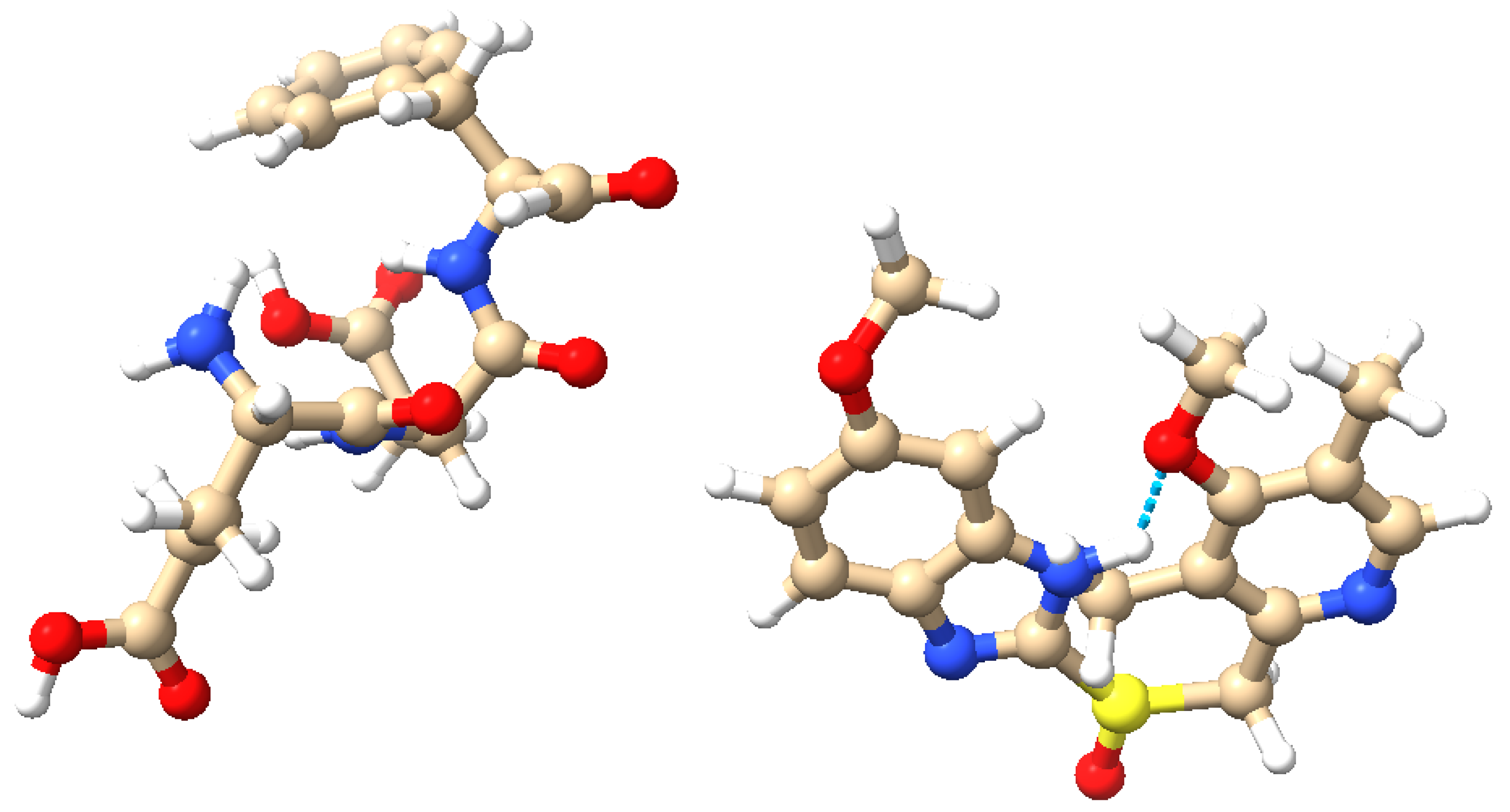


| PPI | Chemical Formula | Half-Life (h) | pKa | Reference |
|---|---|---|---|---|
| Omeprazole | C17H19N3O3S | 1.0 | 4.0 | [10] |
| Esomeprazole | C17H19N3O3S | 1.5 | 4.0 | [23,27] |
| Lansoprazole | C16H14F3N3O2S | 1.5 | 4.0 | [24] |
| Pantoprazole | C16H15F2N3O4S | 1.0 | 3.9 | [25] |
| Rabeprazole | C18H21N3O3S | 1.0 | 4.9 | [26] |
| Metric | Input Signal | Omeprazole–Proteinoid Output |
|---|---|---|
| Mean (mV) | 0.60 | |
| Standard deviation (mV) | 15.30 | 0.43 |
| Maximum (mV) | 72.50 | 3.99 |
| Minimum (mV) | ||
| Comparative Metrics | ||
| Correlation coefficient | 0.6841 | |
| Root mean square error (mV) | 50.4592 | |
| Maximum difference (mV) | 71.92 at 1.39 ms | |
| Time lag (ms) | ||
| Kolmogorov–Smirnov test | ||
| H-value | 1 (distributions are different) | |
| p-value | <0.0001 | |
| KS statistic | 0.9709 | |
| Metric | Input Signal | Omeprazole–Proteinoid Output |
|---|---|---|
| Mean (mV) | 0.48 | |
| Standard deviation (mV) | 19.72 | 0.51 |
| Maximum (mV) | 72.50 | 4.24 |
| Minimum (mV) |
| Metric | Input Signal | Omeprazole–Proteinoid Output |
|---|---|---|
| Mean (mV) | 0.34 | |
| Standard deviation (mV) | 14.20 | 0.40 |
| Maximum (mV) | 72.21 | 3.14 |
| Minimum (mV) | ||
| Comparative Metrics | ||
| Correlation coefficient | 0.6644 | |
| Root mean square error (mV) | 62.8671 | |
| Maximum difference (mV) | 71.91 at 2.00 ms | |
| Time lag (ms) | 1590 | |
| Kolmogorov–Smirnov Test | ||
| H-value | 1 (distributions are different) | |
| p-value | <0.0001 | |
| KS statistic | 0.9844 | |
| Metric | Input Signal | Omeprazole–Proteinoid Output |
|---|---|---|
| Mean (mV) | 0.54 | |
| Standard deviation (mV) | 8.23 | 0.33 |
| Maximum (mV) | 62.46 | 3.17 |
| Minimum (mV) | ||
| Comparative Metrics | ||
| Correlation coefficient | 0.4503 | |
| Root mean square error (mV) | 55.9366 | |
| Maximum difference (mV) | 67.00 at 2.00 ms | |
| Time Lag (ms) | ||
| Kolmogorov–Smirnov Test | ||
| H-value | 1 (distributions are different) | |
| p-value | <0.0001 | |
| KS statistic | 0.9945 | |
| Metric | Input Signal | Omeprazole–Proteinoid Output |
|---|---|---|
| Mean (mV) | 0.80 | |
| Standard deviation (mV) | 20.55 | 0.48 |
| Maximum (mV) | 62.17 | 3.63 |
| Minimum (mV) | ||
| Comparative Metrics | ||
| Correlation coefficient | 0.6823 | |
| Root mean square error (mV) | 43.2821 | |
| Maximum difference (mV) | 62.11 at 0.56 ms | |
| Time lag (ms) | ||
| Kolmogorov–Smirnov Test | ||
| H-value | 1 (distributions are different) | |
| p-value | <0.0001 | |
| KS statistic | 0.9276 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mougkogiannis, P.; Adamatzky, A. The Effects of Omeprazole on the Neuron-like Spiking of the Electrical Potential of Proteinoid Microspheres. Molecules 2024, 29, 4700. https://doi.org/10.3390/molecules29194700
Mougkogiannis P, Adamatzky A. The Effects of Omeprazole on the Neuron-like Spiking of the Electrical Potential of Proteinoid Microspheres. Molecules. 2024; 29(19):4700. https://doi.org/10.3390/molecules29194700
Chicago/Turabian StyleMougkogiannis, Panagiotis, and Andrew Adamatzky. 2024. "The Effects of Omeprazole on the Neuron-like Spiking of the Electrical Potential of Proteinoid Microspheres" Molecules 29, no. 19: 4700. https://doi.org/10.3390/molecules29194700
APA StyleMougkogiannis, P., & Adamatzky, A. (2024). The Effects of Omeprazole on the Neuron-like Spiking of the Electrical Potential of Proteinoid Microspheres. Molecules, 29(19), 4700. https://doi.org/10.3390/molecules29194700








