An Assessment of Dispersion-Corrected DFT Methods for Modeling Nonbonded Interactions in Protein Kinase Inhibitor Complexes
Abstract
1. Introduction
2. Results and Discussion
2.1. Library of 3D Motifs of Nonbonded Interactions
2.2. Energies of Intermolecular Interactions Calculated at the CCSD(T)/CBS Level
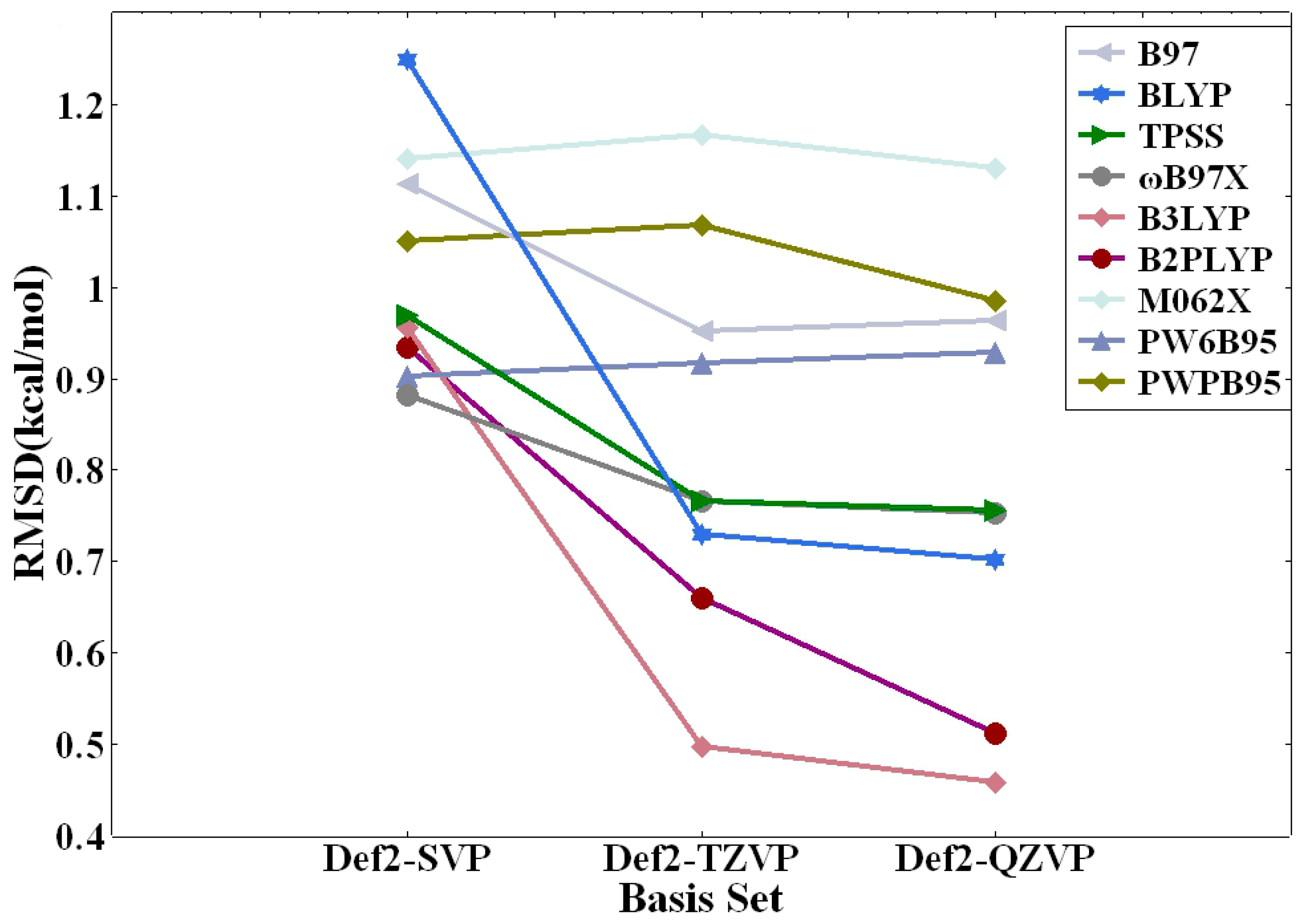
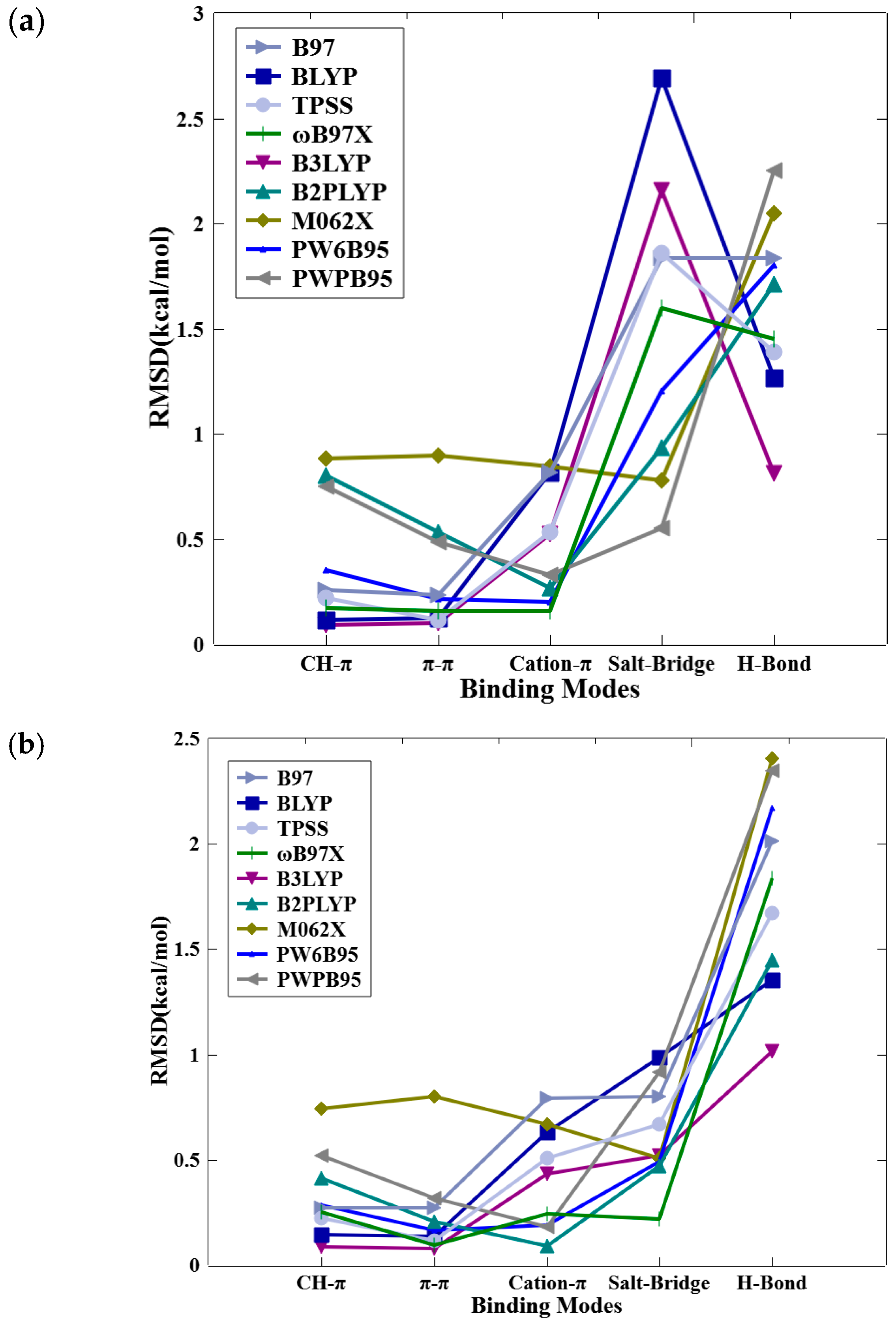
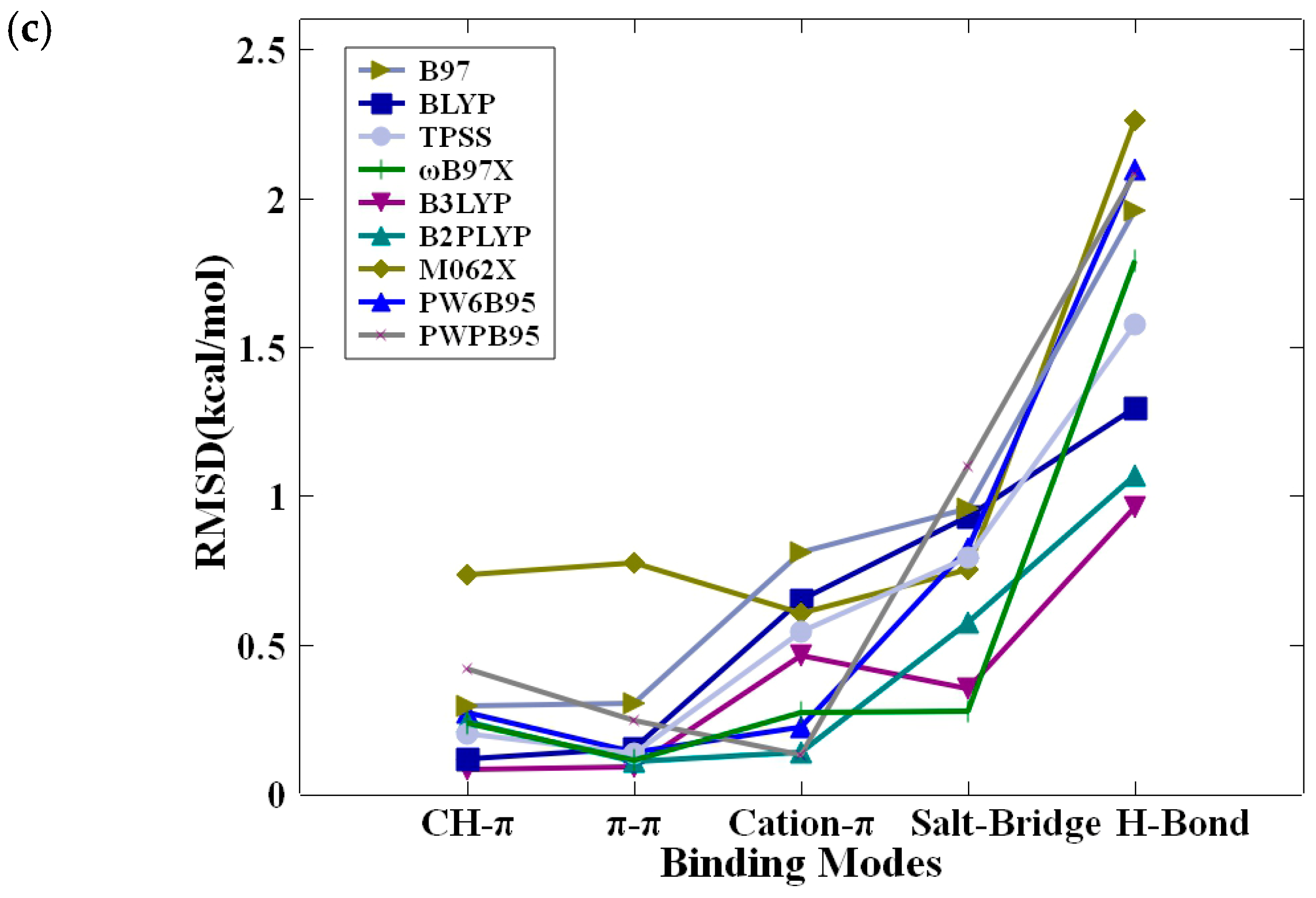
2.3. Benchmarking of DFT Methods
3. Theory and Methods
Quantum Chemical Calculation of Intermolecular Interaction Energies
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Manning, G.; Plowman, G.D.; Hunter, T.; Sudarsanam, S. Evolution of protein kinase signaling from yeast to man. Trends Biochem. Sci. 2002, 27, 514–520. [Google Scholar] [CrossRef] [PubMed]
- Cohen, P.; Cross, D.; Janne, P.A. Kinase drug discovery 20 years after imatinib: Progress and future directions. Nat. Rev. Drug Discov. 2021, 20, 551–569. [Google Scholar] [CrossRef]
- Melnikova, I.; Golden, J. Targeting Protein Kinases; Nature Publishing Group: New York, NY, USA, 2004. [Google Scholar]
- Ayala-Aguilera, C.C.; Valero, T.; Lorente-Macias, A.; Baillache, D.J.; Croke, S.; Unciti-Broceta, A. Small Molecule Kinase Inhibitor Drugs (1995–2021): Medical Indication, Pharmacology, and Synthesis. J. Med. Chem. 2022, 65, 1047–1131. [Google Scholar] [CrossRef] [PubMed]
- Badrinarayan, P.; Sastry, G.N. Rational Approaches Towards Lead Optimization of Kinase Inhibitors: The Issue of Specificity. Curr. Pharm. Des. 2013, 19, 4714–4738. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Y.; Alqahtani, S.; Hu, X.C. Aromatic Rings as Molecular Determinants for the Molecular Recognition of Protein Kinase Inhibitors. Molecules 2021, 26, 1776. [Google Scholar] [CrossRef] [PubMed]
- Persch, E.; Dumele, O.; Diederich, F. Molecular Recognition in Chemical and Biological Systems. Angew. Chem.-Int. Ed. 2015, 54, 3290–3327. [Google Scholar] [CrossRef]
- Bissantz, C.; Kuhn, B.; Stahl, M. A Medicinal Chemist’s Guide to Molecular Interactions. J. Med. Chem. 2010, 53, 5061–5084. [Google Scholar] [CrossRef]
- Hunter, C.A.; Singh, J.; Thornton, J.M. π-π interactions: The geometry and energetics of phenylalanine-phenylalanine interactions in proteins. J. Mol. Biol. 1991, 218, 837–846. [Google Scholar] [CrossRef]
- Nishio, M.; Hirota, M.; Umezawa, Y. The CH/π Interaction: Evidence, Nature, and Consequences; John Wiley & Sons: Hoboken, NJ, USA, 1998. [Google Scholar]
- Gallivan, J.P.; Dougherty, D.A. Cation-π interactions in structural biology. Proc. Natl. Acad. Sci. USA 1999, 96, 9459–9464. [Google Scholar] [CrossRef]
- Zhu, Y.; Hu, X.C. Molecular Recognition of FDA-Approved Small Molecule Protein Kinase Drugs in Protein Kinases. Molecules 2022, 27, 7124. [Google Scholar] [CrossRef]
- Meyer, E.A.; Castellano, R.K.; Diederich, F. Interactions with aromatic rings in chemical and biological recognition. Angew. Chem.-Int. Ed. 2003, 42, 1210–1250. [Google Scholar] [CrossRef]
- Hobza, P. 2 Theoretical studies of hydrogen bonding. Annu. Rep. Sect. “C” (Phys. Chem.) 2004, 100, 3–27. [Google Scholar] [CrossRef]
- Chalasinski, G.; Gutowski, M. Weak Interactions Between Small Systems–Models for Studying the Nature of Intermolecular Forces and Challenging Problems for Ab Initio Calculations. Chem. Rev. 1988, 88, 943–962. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Schwabe, T.; Mück-Lichtenfeld, C. Density functional theory with dispersion corrections for supramolecular structures, aggregates, and complexes of (bio)organic molecules. Org. Biomol. Chem. 2007, 5, 741–758. [Google Scholar] [CrossRef] [PubMed]
- Mao, L.; Wang, Y.; Liu, Y.; Hu, X. Molecular determinants for ATP-binding in proteins: A data mining and quantum chemical analysis. J. Mol. Biol. 2004, 336, 787–807. [Google Scholar] [CrossRef] [PubMed]
- Kristyan, S.; Pulay, P. Can (Semi)Local Density-Functional Theory Account for the London Dispersion Forces. Chem. Phys. Lett. 1994, 229, 175–180. [Google Scholar] [CrossRef]
- Becke, A.D. Density-Functional Exchange-Energy Approximation with Correct Asymptotic Behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef] [PubMed]
- Lee, C.T.; Yang, W.T.; Parr, R.G. Development of the colle-salvetti correlation-energy formula into a functional of the electron-density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Tao, J.M.; Perdew, J.P.; Staroverov, V.N.; Scuseria, G.E. Climbing the density functional ladder: Nonempirical meta-generalized gradient approximation designed for molecules and solids. Phys. Rev. Lett. 2003, 91, 146401. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional thermochemistry.5. Systematic optimization of exchange-correlation functionals. J. Chem. Phys. 1997, 107, 8554–8560. [Google Scholar] [CrossRef]
- Chai, J.-D.; Head-Gordon, M. Systematic optimization of long-range corrected hybrid density functionals. J. Chem. Phys. 2008, 128, 084106. [Google Scholar] [CrossRef] [PubMed]
- Becke, A.D. Density-Functional Thermochemistry.3. The Role of Exact Exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Stephens, P.J.; Devlin, F.J.; Chabalowski, C.F.; Frisch, M.J. Ab-initio calculation of vibrational absorption and circular-dichroism spectra using density-functional force-fields. J. Phys. Chem. 1994, 98, 11623–11627. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar]
- Zhao, Y.; Truhlar, D.G. Design of density functionals that are broadly accurate for thermochemistry, thermochemical kinetics, and nonbonded interactions. J. Phys. Chem. A 2005, 109, 5656–5667. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S. Semiempirical hybrid density functional with perturbative second-order correlation. J. Chem. Phys. 2006, 124, 034108. [Google Scholar] [CrossRef] [PubMed]
- Goerigk, L.; Grimme, S. Efficient and Accurate Double-Hybrid-Meta-GGA Density Functionals-Evaluation with the Extended GMTKN30 Database for General Main Group Thermochemistry, Kinetics, and Noncovalent Interactions. J. Chem. Theory Comput. 2011, 7, 291–309. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
- Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef]
- Dunning, T.H. Gaussian-Basis Sets for Use in Correlated Molecular Calculations: 1. The Atoms Boron through Neon and Hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. [Google Scholar] [CrossRef]
- Neese, F. The ORCA program system. Wiley Interdiscip. Rev.-Comput. Mol. Sci. 2012, 2, 73–78. [Google Scholar] [CrossRef]
- Karton, A.; Martin, J.M.L. Prototypical π-π dimers re-examined by means of high-level CCSDT(Q) composite ab initio methods. J. Chem. Phys. 2021, 154, 124117. [Google Scholar] [CrossRef] [PubMed]
- Rezac, J.; Hobza, P. Benchmark Calculations of Interaction Energies in Noncovalent Complexes and Their Applications. Chem. Rev. 2016, 116, 5038–5071. [Google Scholar] [CrossRef] [PubMed]
- Rezac, J.; Riley, K.E.; Hobza, P. S66: A Well-balanced Database of Benchmark Interaction Energies Relevant to Biomolecular Structures. J. Chem. Theory Comput. 2011, 7, 2427–2438. [Google Scholar] [CrossRef] [PubMed]
- Davies, T.G.; Bentley, J.; Arris, C.E.; Boyle, F.T.; Curtin, N.J.; Endicott, J.A.; Gibson, A.E.; Golding, B.T.; Griffin, R.J.; Hardcastle, I.R. Structure-based design of a potent purine-based cyclin-dependent kinase inhibitor. Nat. Struct. Mol. Biol. 2002, 9, 745. [Google Scholar] [CrossRef]
- Silva-Santisteban, M.C.; Westwood, I.M.; Boxall, K.; Brown, N.; Peacock, S.; McAndrew, C.; Barrie, E.; Richards, M.; Mirza, A.; Oliver, A.W. Fragment-based screening maps inhibitor interactions in the ATP-binding site of checkpoint kinase 2. PLoS ONE 2013, 8, e65689. [Google Scholar] [CrossRef]
- Vulpetti, A.; Casale, E.; Roletto, F.; Amici, R.; Villa, M.; Pevarello, P. Structure-based drug design to the discovery of new 2-aminothiazole CDK2 inhibitors. J. Mol. Graph. Model. 2006, 24, 341–348. [Google Scholar] [CrossRef]
- Schulz, M.N.; Fanghänel, J.; Schäfer, M.; Badock, V.; Briem, H.; Boemer, U.; Nguyen, D.; Husemann, M.; Hillig, R.C. A crystallographic fragment screen identifies cinnamic acid derivatives as starting points for potent Pim-1 inhibitors. Acta Crystallogr. Sect. D Biol. Crystallogr. 2011, 67, 156–166. [Google Scholar] [CrossRef]
- Komander, D.; Kular, G.S.; Schüttelkopf, A.W.; Deak, M.; Prakash, K.; Bain, J.; Elliott, M.; Garrido-Franco, M.; Kozikowski, A.P.; Alessi, D.R. Interactions of LY333531 and other bisindolyl maleimide inhibitors with PDK1. Structure 2004, 12, 215–226. [Google Scholar] [CrossRef]
- Smaill, J.B.; Baker, E.N.; Booth, R.J.; Bridges, A.J.; Dickson, J.M.; Dobrusin, E.M.; Ivanovic, I.; Kraker, A.J.; Lee, H.H.; Lunney, E.A. Synthesis and structure–activity relationships of N-6 substituted analogues of 9-hydroxy-4-phenylpyrrolo [3, 4-c] carbazole-1, 3 (2H, 6H)-diones as inhibitors of Wee1 and Chk1 checkpoint kinases. Eur. J. Med. Chem. 2008, 43, 1276–1296. [Google Scholar] [CrossRef]
- Derewenda, U.; Artamonov, M.; Szukalska, G.; Utepbergenov, D.; Olekhnovich, N.; Parikh, H.I.; Kellogg, G.E.; Somlyo, A.V.; Derewenda, Z.S. Identification of quercitrin as an inhibitor of the p90 S6 ribosomal kinase (RSK): Structure of its complex with the N-terminal domain of RSK2 at 1.8 Å resolution. Acta Crystallogr. Sect. D Biol. Crystallogr. 2013, 69, 266–275. [Google Scholar] [CrossRef] [PubMed]
- Rellos, P.; Pike, A.C.; Niesen, F.H.; Salah, E.; Lee, W.H.; Von Delft, F.; Knapp, S. Structure of the CaMKIIδ/calmodulin complex reveals the molecular mechanism of CaMKII kinase activation. PLoS Biol. 2010, 8, e1000426. [Google Scholar] [CrossRef]
- Aronov, A.M.; Tang, Q.; Martinez-Botella, G.; Bemis, G.W.; Cao, J.; Chen, G.; Ewing, N.P.; Ford, P.J.; Germann, U.A.; Green, J. Structure-guided design of potent and selective pyrimidylpyrrole inhibitors of extracellular signal-regulated kinase (ERK) using conformational control. J. Med. Chem. 2009, 52, 6362–6368. [Google Scholar] [CrossRef] [PubMed]
- Lew, E.D.; Bae, J.H.; Rohmann, E.; Wollnik, B.; Schlessinger, J. Structural basis for reduced FGFR2 activity in LADD syndrome: Implications for FGFR autoinhibition and activation. Proc. Natl. Acad. Sci. USA 2007, 104, 19802–19807. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Meades, C.; Wood, G.; Osnowski, A.; Anderson, S.; Yuill, R.; Thomas, M.; Mezna, M.; Jackson, W.; Midgley, C. 2-Anilino-4-(thiazol-5-yl) pyrimidine CDK inhibitors: Synthesis, SAR analysis, X-ray crystallography, and biological activity. J. Med. Chem. 2004, 47, 1662–1675. [Google Scholar] [CrossRef]
- Richardson, C.M.; Williamson, D.S.; Parratt, M.J.; Borgognoni, J.; Cansfield, A.D.; Dokurno, P.; Francis, G.L.; Howes, R.; Moore, J.D.; Murray, J.B. Triazolo [1, 5-a] pyrimidines as novel CDK2 inhibitors: Protein structure-guided design and SAR. Bioorganic Med. Chem. Lett. 2006, 16, 1353–1357. [Google Scholar] [CrossRef]
- Schonbrunn, E.; Betzi, S.; Alam, R.; Martin, M.P.; Becker, A.; Han, H.; Francis, R.; Chakrasali, R.; Jakkaraj, S.; Kazi, A. Development of highly potent and selective diaminothiazole inhibitors of cyclin-dependent kinases. J. Med. Chem. 2013, 56, 3768–3782. [Google Scholar] [CrossRef]
- Utepbergenov, D.; Derewenda, U.; Olekhnovich, N.; Szukalska, G.; Banerjee, B.; Hilinski, M.K.; Lannigan, D.A.; Stukenberg, P.T.; Derewenda, Z.S. Insights into the inhibition of the p90 ribosomal S6 kinase (RSK) by the flavonol glycoside SL0101 from the 1.5 Å crystal structure of the N-terminal domain of RSK2 with bound inhibitor. Biochemistry 2012, 51, 6499–6510. [Google Scholar] [CrossRef]
- Wu, S.Y.; McNae, I.; Kontopidis, G.; McClue, S.J.; McInnes, C.; Stewart, K.J.; Wang, S.; Zheleva, D.I.; Marriage, H.; Lane, D.P. Discovery of a novel family of CDK inhibitors with the program LIDAEUS: Structural basis for ligand-induced disordering of the activation loop. Structure 2003, 11, 399–410. [Google Scholar] [CrossRef]
- Mohammadi, M.; McMahon, G.; Sun, L.; Tang, C.; Hirth, P.; Yeh, B.K.; Hubbard, S.R.; Schlessinger, J. Structures of the tyrosine kinase domain of fibroblast growth factor receptor in complex with inhibitors. Science 1997, 276, 955–960. [Google Scholar] [CrossRef]
- De Moliner, E.; Moro, S.; Sarno, S.; Zagotto, G.; Zanotti, G.; Pinna, L.A.; Battistutta, R. Inhibition of protein kinase CK2 by anthraquinone-related compounds a structural insight. J. Biol. Chem. 2003, 278, 1831–1836. [Google Scholar] [CrossRef] [PubMed]
- Andersen, C.B.; Wan, Y.; Chang, J.W.; Riggs, B.; Lee, C.; Liu, Y.; Sessa, F.; Villa, F.; Kwiatkowski, N.; Suzuki, M. Discovery of selective aminothiazole aurora kinase inhibitors. ACS Chem. Biol. 2008, 3, 180–192. [Google Scholar] [CrossRef] [PubMed]
- Amaning, K.; Lowinski, M.; Vallee, F.; Steier, V.; Marcireau, C.; Ugolini, A.; Delorme, C.; Foucalt, F.; McCort, G.; Derimay, N. The use of virtual screening and differential scanning fluorimetry for the rapid identification of fragments active against MEK1. Bioorganic Med. Chem. Lett. 2013, 23, 3620–3626. [Google Scholar] [CrossRef]
- Fischmann, T.O.; Hruza, A.; Duca, J.S.; Ramanathan, L.; Mayhood, T.; Windsor, W.T.; Le, H.V.; Guzi, T.J.; Dwyer, M.P.; Paruch, K. Structure-guided discovery of cyclin-dependent kinase inhibitors. Biopolym. Orig. Res. Biomol. 2008, 89, 372–379. [Google Scholar] [CrossRef] [PubMed]
- López-Ramos, M.; Prudent, R.; Moucadel, V.; Sautel, C.F.; Barette, C.; Lafanechère, L.; Mouawad, L.; Grierson, D.; Schmidt, F.; Florent, J.-C. New potent dual inhibitors of CK2 and Pim kinases: Discovery and structural insights. FASEB J. 2010, 24, 3171–3185. [Google Scholar] [CrossRef] [PubMed]
- Homan, K.T.; Wu, E.; Wilson, M.W.; Singh, P.; Larsen, S.D.; Tesmer, J.J. Structural and functional analysis of G protein–coupled receptor kinase inhibition by paroxetine and a rationally designed analog. Mol. Pharmacol. 2014, 85, 237–248. [Google Scholar] [CrossRef]
- Zhao, B.; Bower, M.J.; McDevitt, P.J.; Zhao, H.; Davis, S.T.; Johanson, K.O.; Green, S.M.; Concha, N.O.; Zhou, B.-B.S. Structural basis for Chk1 inhibition by UCN-01. J. Biol. Chem. 2002, 277, 46609–46615. [Google Scholar] [CrossRef]
- Meng, Z.; Ciavarri, J.P.; McRiner, A.; Zhao, Y.; Zhao, L.; Reddy, P.A.; Zhang, X.; Fischmann, T.O.; Whitehurst, C.; Siddiqui, M.A. Potency switch between CHK1 and MK2: Discovery of imidazo [1,2-a] pyrazine-and imidazo [1,2-c] pyrimidine-based kinase inhibitors. Bioorganic Med. Chem. Lett. 2013, 23, 2863–2867. [Google Scholar] [CrossRef]
- Narayana, N.; Diller, T.C.; Koide, K.; Bunnage, M.E.; Nicolaou, K.; Brunton, L.L.; Xuong, N.-H.; Ten Eyck, L.F.; Taylor, S.S. Crystal structure of the potent natural product inhibitor balanol in complex with the catalytic subunit of cAMP-dependent protein kinase. Biochemistry 1999, 38, 2367–2376. [Google Scholar] [CrossRef]
- Kutchukian, P.S.; Wassermann, A.M.; Lindvall, M.K.; Wright, S.K.; Ottl, J.; Jacob, J.; Scheufler, C.; Marzinzik, A.; Brooijmans, N.; Glick, M. Large scale meta-analysis of fragment-based screening campaigns: Privileged fragments and complementary technologies. J. Biomol. Screen. 2015, 20, 588–596. [Google Scholar] [CrossRef]
- Davies, T.G.; Tunnah, P.; Meijer, L.; Marko, D.; Eisenbrand, G.; Endicott, J.A.; Noble, M.E. Inhibitor binding to active and inactive CDK2: The crystal structure of CDK2-cyclin A/indirubin-5-sulphonate. Structure 2001, 9, 389–397. [Google Scholar] [CrossRef]
- Frisch, M.; Trucks, G.; Schlegel, H.; Scuseria, G.; Robb, M.; Cheeseman, J.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.; et al. Gaussian 09, Revision A. 02; Gaussian, Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef] [PubMed]
- Halkier, A.; Klopper, W.; Helgaker, T.; Jorgensen, P.; Taylor, P.R. Basis set convergence of the interaction energy of hydrogen-bonded complexes. J. Chem. Phys. 1999, 111, 9157–9167. [Google Scholar] [CrossRef]
- Halkier, A.; Helgaker, T.; Jorgensen, P.; Klopper, W.; Koch, H.; Olsen, J.; Wilson, A.K. Basis-set convergence in correlated calculations on Ne, N2, and H2O. Chem. Phys. Lett. 1998, 286, 243–252. [Google Scholar] [CrossRef]
- Sherrill, C.D.; Takatani, T.; Hohenstein, E.G. An Assessment of Theoretical Methods for Nonbonded Interactions: Comparison to Complete Basis Set Limit Coupled-Cluster Potential Energy Curves for the Benzene Dimer, the Methane Dimer, Benzene-Methane, and Benzene-H2S. J. Phys. Chem. A 2009, 113, 10146–10159. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Zhu, T.; Hawkins, G.D.; Winget, P.; Liotard, D.A.; Cramer, C.J.; Truhlar, D.G. Extension of the platform of applicability of the SM5. 42R universal solvation model. Theor. Chem. Acc. 1999, 103, 9–63. [Google Scholar] [CrossRef]
- Vahtras, O.; Almlof, J.; Feyereisen, M.W. Integral approximations for lcao-scf calculations. Chem. Phys. Lett. 1993, 213, 514–518. [Google Scholar] [CrossRef]
- Neese, F.; Wennmohs, F.; Hansen, A.; Becker, U. Efficient, approximate and parallel Hartree-Fock and hybrid DFT calculations. A ‘chain-of-spheres’ algorithm for the Hartree-Fock exchange. Chem. Phys. 2009, 356, 98–109. [Google Scholar] [CrossRef]
- Weigend, F. A fully direct RI-HF algorithm: Implementation, optimised auxiliary basis sets, demonstration of accuracy and efficiency. Phys. Chem. Chem. Phys. 2002, 4, 4285–4291. [Google Scholar] [CrossRef]
- Weigend, F. Accurate Coulomb-fitting basis sets for H to Rn. Phys. Chem. Chem. Phys. 2006, 8, 1057–1065. [Google Scholar] [CrossRef]
- Staroverov, V.N.; Scuseria, G.E.; Tao, J.; Perdew, J.P. Comparative assessment of a new nonempirical density functional: Molecules and hydrogen-bonded complexes. J. Chem. Phys. 2003, 119, 12129–12137. [Google Scholar] [CrossRef]
- Hamprecht, F.A.; Cohen, A.J.; Tozer, D.J.; Handy, N.C. Development and assessment of new exchange-correlation functionals. J. Chem. Phys. 1998, 109, 6264–6271. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional thermochemistry. IV. A new dynamical correlation functional and implications for exact-exchange mixing. J. Chem. Phys. 1996, 104, 1040–1046. [Google Scholar] [CrossRef]
- Grimme, S. Improved second-order Møller–Plesset perturbation theory by separate scaling of parallel-and antiparallel-spin pair correlation energies. J. Chem. Phys. 2003, 118, 9095–9102. [Google Scholar] [CrossRef]
- Jung, Y.; Lochan, R.C.; Dutoi, A.D.; Head-Gordon, M. Scaled opposite-spin second order Møller–Plesset correlation energy: An economical electronic structure method. J. Chem. Phys. 2004, 121, 9793–9802. [Google Scholar] [CrossRef]
- Boys, S.F.; Bernardi, F. The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors. Mol. Phys. 1970, 19, 553–566. [Google Scholar] [CrossRef]
- Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the damping function in dispersion corrected density functional theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef]
- Grimme, S. Accurate description of van der Waals complexes by density functional theory including empirical corrections. J. Comput. Chem. 2004, 25, 1463–1473. [Google Scholar] [CrossRef]
- Schmidt, M.W.; Baldridge, K.K.; Boatz, J.A.; Elbert, S.T.; Gordon, M.S.; Jensen, J.H.; Koseki, S.; Matsunaga, N.; Nguyen, K.A.; Su, S.J.; et al. General Atomic and Molecular Electronic-Structure System. J. Comput. Chem. 1993, 14, 1347–1363. [Google Scholar] [CrossRef]
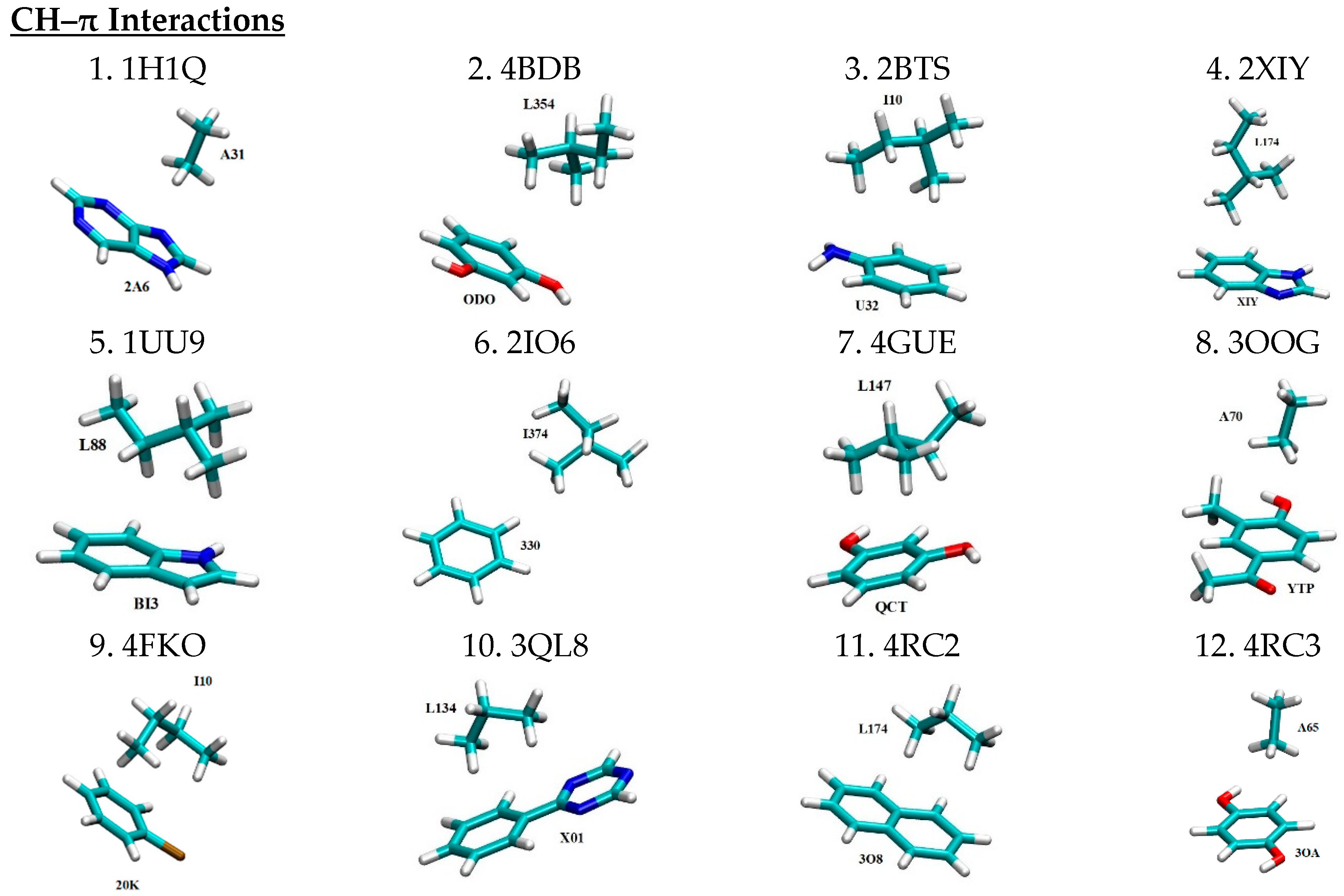
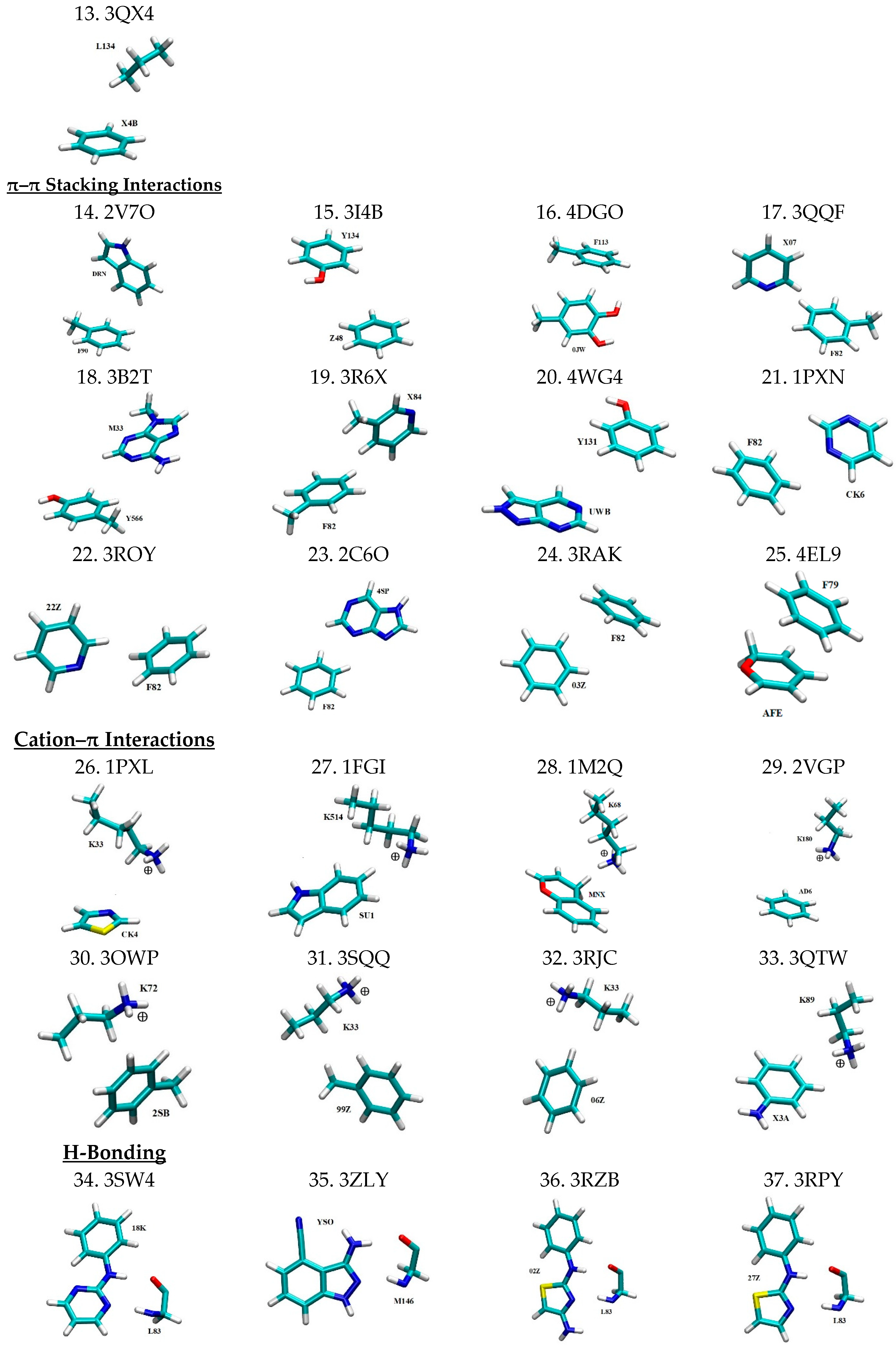


| No. | Mode of Interaction | PDB ID | Intermolecular Pair | Angle | Distance (Å) b | Ref. | ||
|---|---|---|---|---|---|---|---|---|
| 1 | CH–π | 1H1Q | 2A6…A31 | 3.32 | [37] | |||
| 2 | 4BDB | ODO…L354 | - | 3.93 | [38] | |||
| 3 | 2BTS | U32…I10 | - | 3.55 | [39] | |||
| 4 | 2XIY | XIY…L174 | - | 3.57 | [40] | |||
| 5 | 1UU9 | BI3…L88 | - | 3.81 | [41] | |||
| 6 | 2IO6 | 330…I374 | - | 4.41 | [42] | |||
| 7 | 4GUE | QCT…L147 | - | 3.61 | [43] | |||
| 8 | 3OOG | YTP…A70 | - | 3.34 | - | |||
| 9 | 4FKO | 20K…I10 | - | 3.72 | - | |||
| 10 | 3QL8 | X01…L134 | - | 3.23 | - | |||
| 11 | 4RC2 | 3O8…L174 | - | 3.43 | - | |||
| 12 | 4RC3 | 3OA…A56 | - | 3.27 | - | |||
| 13 | 3QX4 | X4B…L134 | - | 3.61 | - | |||
| 14 | π–π stacking | 2V7O | DRN…F90 | 89.64 c | 3.77 | [44] | ||
| 15 | 3I4B | Z48…Y134 | 6.8 | 4.31 | [45] | |||
| 16 | 4DGO | 0JW…F113 | 43.85 | 3.55 | - | |||
| 17 | 3QQF | X07…F82 | 70.14 | 3.76 | - | |||
| 18 | 3B2T | M33…Y566 | 10.09 | 3.83 | [46] | |||
| 19 | 3R6X | X84…F82 | 74.54 | 3.71 | - | |||
| 20 | 4WG4 | UWB…Y131 | 5.57 | 4.08 | - | |||
| 21 | 1PXN | CK6…F82 | 16.8 | 3.62 | [47] | |||
| 22 | 3ROY | 22Z…F82 | 68.31 | 3.75 | - | |||
| 23 | 2C6O | 4SP…F82 | 20.3 | 4.01 | [48] | |||
| 24 | 3RAK | 03Z…F82 | 41.29 | 3.81 | [49] | |||
| 25 | 4EL9 | AFE…F79 | 19.17 | 3.48 | [50] | |||
| 26 | Cation–π | 1PXL | CK4…K33 | - | 4.62 | [51] | ||
| 27 | 1FGI | SU1…K514 | - | 5.15 | [52] | |||
| 28 | 1M2Q | MNX…K68 | - | 4.21 | [53] | |||
| 29 | 2VGP | AD6…K180 | - | 5.06 | [54] | |||
| 30 | 3OWP | 2SB…K72 | - | 3.59 | - | |||
| 31 | 3SQQ | 99Z…K33 | - | 5.12 | [49] | |||
| 32 | 3RJC | 06Z…K33 | - | 4.77 | [49] | |||
| 33 | 3QTW | X3A…K89 | - | 3.51 | [49] | |||
| 34 | H-Bond d | 3SW4 | 18K…L83 | 158.59 | 166.51 | 2.88 | 2.94 | - |
| 35 | 3ZLY | YSO…M146 | 153.12 | 164.48 | 2.97 | 3.26 | [55] | |
| 36 | 3RZB | 02Z…L83 | 143.48 | 162.20 | 2.96 | 3.06 | [49] | |
| 37 | 3RPY | 27Z…L83 | 141.82 | 167.13 | 2.89 | 3.24 | [49] | |
| 38 | 3R28 | XA0…L83 | 155.87 | 134.34 | 2.88 | 2.98 | - | |
| 39 | 3QZI | X72…L83 | 132.02 | 148.51 | 2.98 | 2.98 | - | |
| 40 | 3SXF | BK5…Y131 | 161.45 | 3.14 | ||||
| 41 | 2R3P | 3SC…L83 | 141.41 | 168.79 | 2.82 | 3.35 | [56] | |
| 42 | Salt bridge | 3MA3 | 01I…K67 | - | 3.38 | [57] | ||
| 43 | 4L9I | 8PR…D271 | - | 3.96 | [58] | |||
| 44 | 1NVQ | UCN…E91 | - | 3.48 | [59] | |||
| 45 | 4JIK | 1KO…D148 | - | 3.22 | [60] | |||
| 46 | 1BX6 | BA1…E127 | - | 5.05 | [61] | |||
| 47 | 4WG4 | UWB…E135 | - | 4.16 | - | |||
| 48 | 4MTA | 2D2…K67 | - | 3.67 | [62] | |||
| 49 | 1E9H | INR…K33 | - | 3.65 | [63] | |||
| No. | Mode of Interaction | PDB ID | Intermolecular Pair | (kcal/mol) | ΔEDeh (kcal/mol) | (kcal/mol) a |
|---|---|---|---|---|---|---|
| 1 | CH–π | 1H1Q | 2A6…A31 | −1.9 | 0.5 | −1.4 |
| 2 | 4BDB | ODO…L354 | −2.2 | 0.4 | −1.8 | |
| 3 | 2BTS | U32…I10 | −2.4 | 0.8 | −1.6 | |
| 4 | 2XIY | XIY…L174 | −2.3 | 0.3 | −2.0 | |
| 5 | 1UU9 | BI3…L88 | −3.6 | 0.3 | −3.3 | |
| 6 | 2IO6 | 330…I374 | −0.7 | 0.0 | −0.7 | |
| 7 | 4GUE | QCT…L147 | −3.4 | 0.7 | −2.7 | |
| 8 | 3OOG | YTP…A70 | −1.9 | 0.7 | −1.2 | |
| 9 | 4FKO | 20K…I10 | −2.3 | 0.0 | −2.3 | |
| 10 | 3QL8 | X01…L134 | −2.5 | 0.0 | −2.5 | |
| 11 | 4RC2 | 3O8…L174 | −2.1 | 0.2 | −1.9 | |
| 12 | 4RC3 | 3OA…A56 | −1.0 | −1.0 | −2.0 | |
| 13 | 3QX4 | X4B…L134 | −1.0 | 0.1 | −0.9 | |
| 14 | π–π Stacking | 2V7O | DRN…F90 | −1.3 | 0.0 | −1.3 |
| 15 | 3I4B | Z48…Y134 | −1.0 | 0.3 | −0.7 | |
| 16 | 4DGO | 0JW…F113 | −4.4 | 1.6 | −2.8 | |
| 17 | 3QQF | X07…F82 | −2.4 | 0.7 | −1.7 | |
| 18 | 3B2T | M33…Y566 | −2.0 | 0.5 | −1.5 | |
| 19 | 3R6X | X84…F82 | −1.9 | 0.4 | −1.5 | |
| 20 | 4WG4 | UWB…Y131 | −0.6 | 0.3 | −0.3 | |
| 21 | 1PXN | CK6…F82 | −0.7 | 0.6 | −0.1 | |
| 22 | 3ROY | 22Z…F82 | −2.4 | 0.6 | −1.8 | |
| 23 | 2C6O | 4SP…F82 | −1.1 | 0.8 | −0.3 | |
| 24 | 3RAK | 03Z…F82 | −1.7 | 0.1 | −1.6 | |
| 25 | 4EL9 | AFE…F79 | −1.9 | 0.4 | −1.5 | |
| 26 | Cation–π | 1PXL | CK4…K33 | −6.5 | 5.3 | −1.2 |
| 27 | 1FGI | SU1…K514 | −4.4 | 2.5 | −1.9 | |
| 28 | 1M2Q | MNX…K68 | −2.0 | −0.3 | −2.3 | |
| 29 | 2VGP | AD6…K180 | −1.5 | 1.0 | −0.5 | |
| 30 | 3OWP | 2SB…K72 | −9.2 | 4.5 | −4.7 | |
| 31 | 3SQQ | 99Z…K33 | −2.1 | 0.8 | −1.3 | |
| 32 | 3RJC | 06Z…K33 | −2.1 | 0.5 | −1.6 | |
| 33 | 3QTW | X3A…K89 | −8.4 | 8.6 | 0.2 | |
| 34 | H-Bond | 3SW4 | 18K…L83 | −6.0 | 4.8 | −1.2 |
| 35 | 3ZLY | YSO…M146 | −4.9 | 3.7 | −1.2 | |
| 36 | 3RZB | 02Z…L83 | −7.0 | 5.2 | −1.8 | |
| 37 | 3RPY | 27Z…L83 | −7.0 | 4.4 | −2.6 | |
| 38 | 3R28 | XA0…L83 | −4.8 | 4.0 | −0.8 | |
| 39 | 3QZI | X72…L83 | −4.6 | 0.6 | −4.0 | |
| 40 | 3SXF | BK5…Y131 | −3.8 | 3.1 | −0.7 | |
| 41 | 2R3P | 3SC…L83 | −6.1 | 3.3 | −2.8 | |
| 42 | Salt bridge | 3MA3 | 01I…K67 | −111.0 | 102.6 | −8.4 |
| 43 | 4L9I | 8PR…D271 | −100.3 | 94.5 | −5.8 | |
| 44 | 1NVQ | UCN…E91 | −100.0 | 98.6 | −1.4 | |
| 45 | 4JIK | 1KO…D148 | −115.9 | 112.2 | −3.7 | |
| 46 | 1BX6 | BA1…E127 | −68.2 | 67.5 | −0.7 | |
| 47 | 4WG4 | UWB…E135 | −92.6 | 87.5 | −5.1 | |
| 48 | 4MTA | 2D2…K67 | −106.6 | 99.4 | −7.2 | |
| 49 | 1E9H | INR…K33 | −101.5 | 98.5 | −3.0 |
| Functional | Implementation a | HF Exchange b (%) | Type c | Ex. Functional Corr Functional | Ref. |
|---|---|---|---|---|---|
| BLYP | RI BLYP | 0 | GGA | Becke 1988 Lee-Yang-Parr 1988 | [19,20] |
| TPSS | RI TPSS | 0 | Meta-GGA | TPSS TPSS | [21,74] |
| B97 | RI B97 | 26.93 | hybrid GGA | B97-2 B97-3 | [29,75] |
| ωB97X | ωB97X | 15.77 | range-separated hybrid-GGA | LRC hybrid functionals | [23] |
| B3LYP | B3LYP | 20 | hybrid GGA | Becke 1988 Lee-Yang-Parr 1988 | [19,20] |
| M062X | M062X | 54 | Meta-hybrid GGA | M06-2X M06-2X | [26] |
| PW6B95 | PW6B95 | 28 | Meta-hybrid GGA | PW6B95 PW6B95 | [27] |
| RIJCOSX PW6B95 | |||||
| B2PLYP | RI B2PLYP | 54 | Double-Hybrid-GGA | Becke 1988 | [19,20] |
| RIJK RI B2PLYP | Lee-Yang-Parr 1988 | [28] | |||
| PWPB95 | RI PWPB95 | 50 | Double-Hybrid-Meta GGA | Perdew–Wang32 | [76,77] |
| RIJK RI PWPB95 | Becke9533 | [29,78] |
| DFT Method | RMSD (kcal/mol) | MAE (kcal/mol) | AVG (kcal/mol) | MAX% | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| def2-QZVP | def2-TZVP | def2-SVP | def2-QZVP | def2-TZVP | def2-SVP | def2-QZVP | def2-TZVP | def2-SVP | def2-QZVP | def2-TZVP | def2-SVP | |
| BLYP | 0.70 | 0.73 | 1.25 | 0.48 | 0.48 | 0.76 | 0.15 | 0.09 | −0.28 | 33.2 | 34.0 | 38.1 |
| TPSS | 0.76 | 0.77 | 0.97 | 0.52 | 0.51 | 0.64 | 0.23 | 0.21 | −0.09 | 39.7 | 41.2 | 38.5 |
| B97 | 0.96 | 0.95 | 1.11 | 0.70 | 0.66 | 0.77 | 0.14 | 0.11 | −0.18 | 50.4 | 51.3 | 51.0 |
| ωB97X | 0.75 | 0.77 | 0.88 | 0.43 | 0.43 | 0.55 | 0.23 | 0.20 | 0.01 | 43.1 | 43.5 | 39.8 |
| B3LYP | 0.46 | 0.50 | 0.96 | 0.29 | 0.32 | 0.55 | 0.08 | 0.05 | −0.24 | 25.9 | 26.6 | 26.6 |
| M062X | 1.13 | 1.17 | 1.14 | 0.93 | 0.94 | 1.00 | 0.93 | 0.93 | 0.82 | 103.1 | 106.4 | 118.6 |
| PW6B95 | 0.93 | 0.92 | 0.90 | 0.57 | 0.54 | 0.62 | 0.50 | 0.47 | 0.23 | 46.1 | 47.6 | 54.4 |
| B2PLYP | 0.51 | 0.66 | 0.93 | 0.35 | 0.45 | 0.75 | 0.32 | 0.45 | 0.50 | 26.9 | 43.4 | 76.3 |
| PWPB95 | 0.98 | 1.07 | 1.05 | 0.68 | 0.74 | 0.79 | 0.67 | 0.74 | 0.65 | 51.7 | 61.9 | 86.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Y.; Alqahtani, S.; Hu, X. An Assessment of Dispersion-Corrected DFT Methods for Modeling Nonbonded Interactions in Protein Kinase Inhibitor Complexes. Molecules 2024, 29, 304. https://doi.org/10.3390/molecules29020304
Zhu Y, Alqahtani S, Hu X. An Assessment of Dispersion-Corrected DFT Methods for Modeling Nonbonded Interactions in Protein Kinase Inhibitor Complexes. Molecules. 2024; 29(2):304. https://doi.org/10.3390/molecules29020304
Chicago/Turabian StyleZhu, Yan, Saad Alqahtani, and Xiche Hu. 2024. "An Assessment of Dispersion-Corrected DFT Methods for Modeling Nonbonded Interactions in Protein Kinase Inhibitor Complexes" Molecules 29, no. 2: 304. https://doi.org/10.3390/molecules29020304
APA StyleZhu, Y., Alqahtani, S., & Hu, X. (2024). An Assessment of Dispersion-Corrected DFT Methods for Modeling Nonbonded Interactions in Protein Kinase Inhibitor Complexes. Molecules, 29(2), 304. https://doi.org/10.3390/molecules29020304





