Adsorption and Permeation Events in Molecular Diffusion
Abstract
:1. Introduction
2. Statistics of Adsorption Events
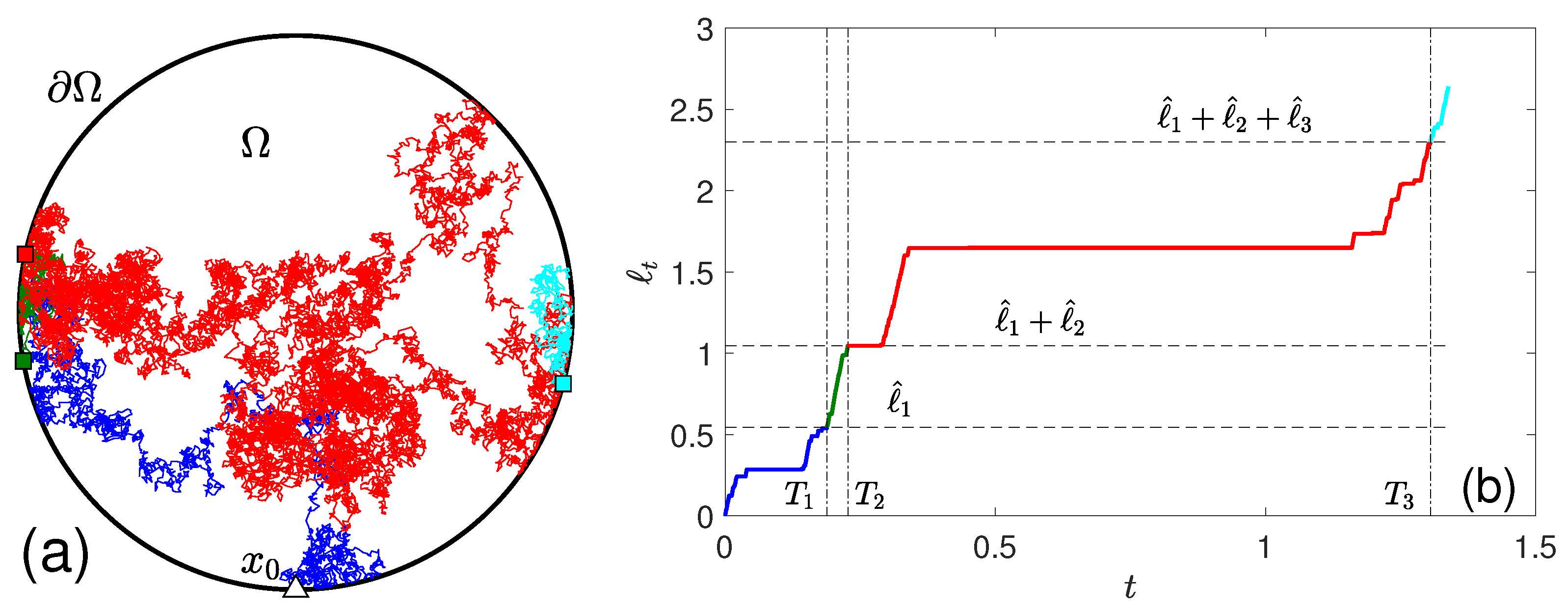
2.1. Encounter-Based Approach
2.2. Long-Time Behavior for Bounded Domains
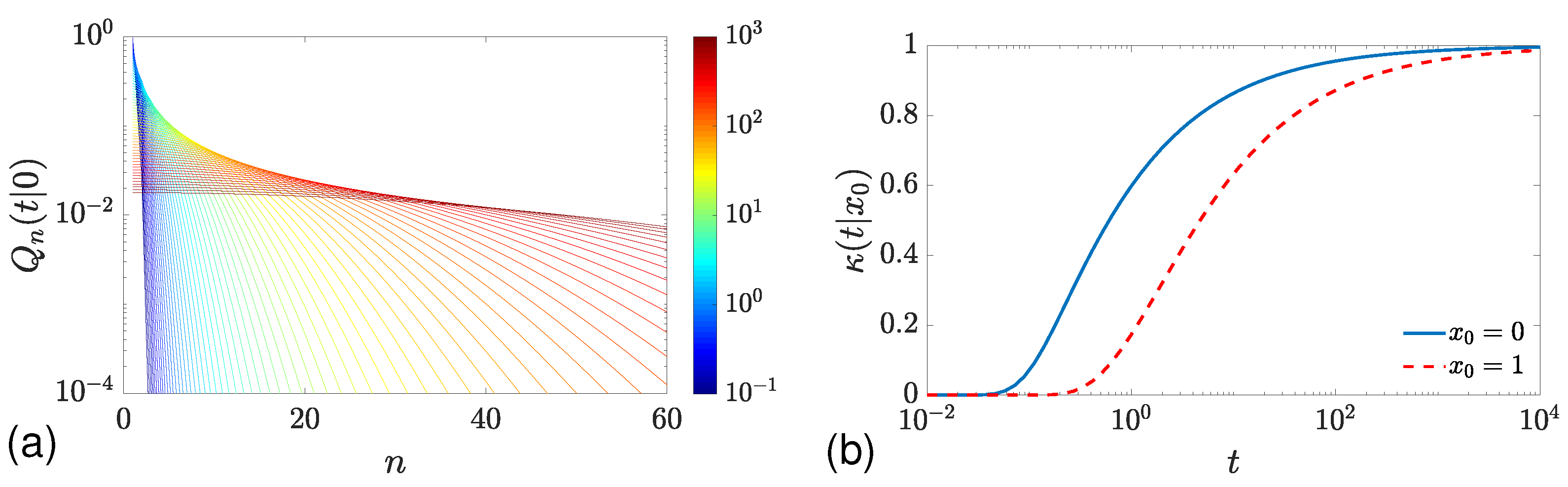
2.2.1. Mean and Standard Deviation
2.2.2. Distribution for the Case
2.2.3. Distribution for the Case
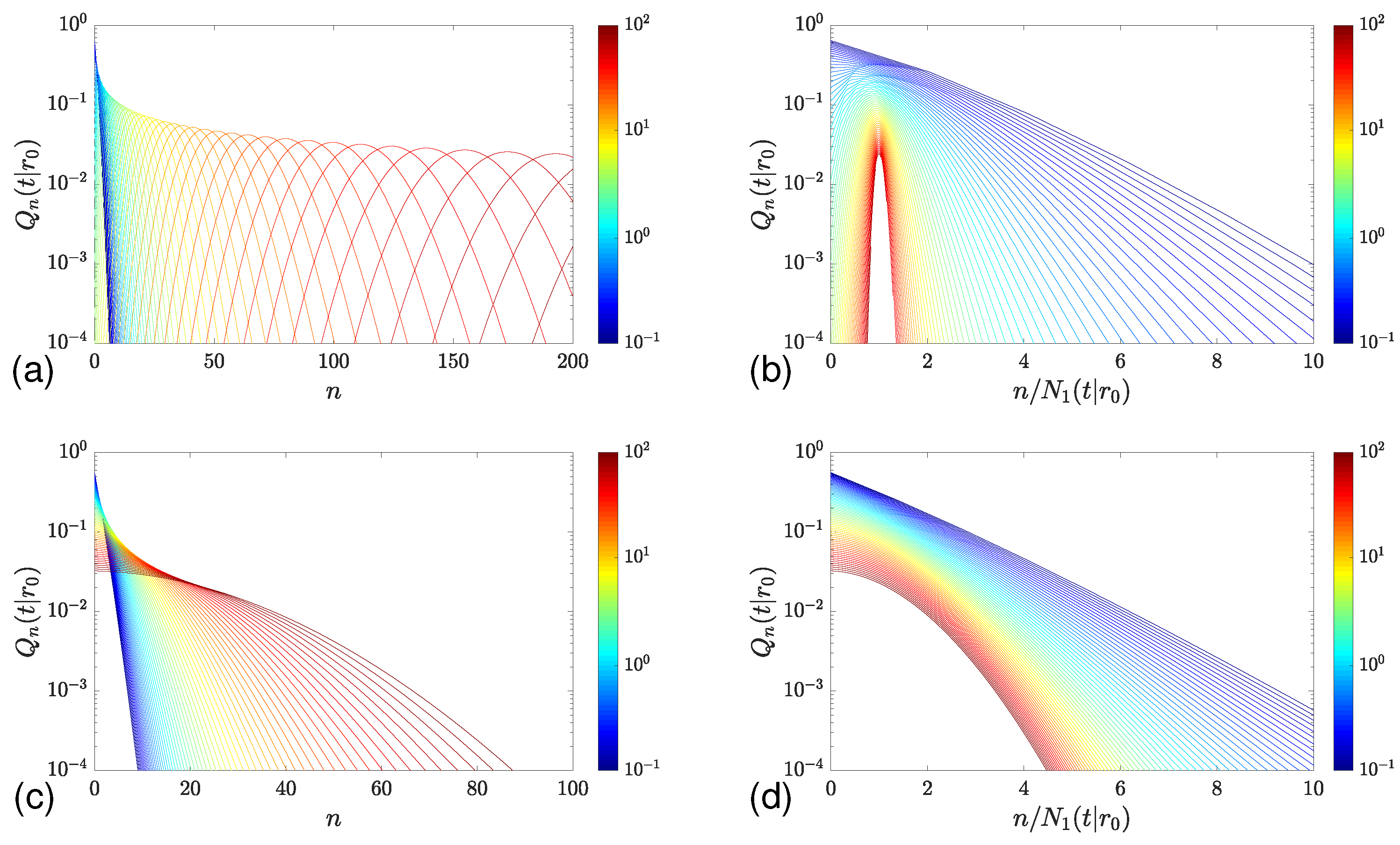
2.3. Long-Time Behavior for Unbounded Domains
3. Statistics of Permeation Events
Spherical Domains
4. Two Relevant Examples
4.1. Flat Surface
4.2. Spherical Surface
5. Discussion and Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Redner, S. A Guide to First Passage Processes; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- House, J.E. Principles of chemical Kinetics, 2nd ed.; Academic Press: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Schuss, Z. Brownian Dynamics at Boundaries and Interfaces in Physics, Chemistry and Biology; Springer: New York, NY, USA, 2013. [Google Scholar]
- Metzler, R.; Oshanin, G.; Redner, S. (Eds.) First-Passage Phenomena and Their Applications; World Scientific: Singapore, 2014. [Google Scholar]
- Masoliver, J. Random Processes: First-Passage and Escape; World Scientific Publishing: Singapore, 2018. [Google Scholar]
- Lindenberg, K.; Oshanin, G.; Metzler, R. (Eds.) Chemical Kinetics: Beyond the Textbook; World Scientific: Hackensack, NJ, USA, 2019. [Google Scholar]
- Dagdug, L.; Peña, J.; Pompa-García, I. Diffusion Under Confinement. A Journey Through Counterintuition; Springer: Berlin/Heidelberg, Germany, 2024. [Google Scholar]
- Weibel, E.B. The Pathway for Oxygen. Structure and Function in the Mammalian Respiratory System; Harvard University Press: Cambridge, MA, USA; London, UK, 1984. [Google Scholar]
- Grebenkov, D.S.; Filoche, M.; Sapoval, B.; Felici, M. Diffusion-Reaction in Branched Structures: Theory and Application to the Lung Acinus. Phys. Rev. Lett. 2005, 94, 050602. [Google Scholar] [CrossRef] [PubMed]
- Serov, A.S.; Salafia, C.; Grebenkov, D.S.; Filoche, M. The Role of Morphology in Mathematical Models of Placental Gas Exchange. J. Appl. Physiol. 2016, 120, 17–28. [Google Scholar] [CrossRef]
- Sapoval, B.; Kang, M.-Y.; Dinh-Xuan, T. Modeling of Gas Exchange in the Lungs. Compr. Physiol. 2021, 11, 1289–1314. [Google Scholar]
- Bénichou, O.; Loverdo, C.; Moreau, M.; Voituriez, R. Intermittent search strategies. Rev. Mod. Phys. 2011, 83, 81–130. [Google Scholar] [CrossRef]
- Kolomeisky, A.B. Physics of protein-DNA interactions: Mechanisms of facilitated target search. Phys. Chem. Chem. Phys. 2011, 13, 2088–2095. [Google Scholar] [CrossRef]
- Sheinman, M.; Bénichou, O.; Kafri, Y.; Voituriez, R. Classes of fast and specific search mechanisms for proteins on DNA. Rep. Prog. Phys. 2012, 75, 026601. [Google Scholar] [CrossRef] [PubMed]
- Bressloff, P.C.; Newby, J. Stochastic models of intracellular transport. Rev. Mod. Phys. 2013, 85, 135–196. [Google Scholar] [CrossRef]
- North, A.M. Diffusion-controlled reactions. Q. Rev. Chem. Soc. 1966, 20, 421–440. [Google Scholar] [CrossRef]
- Wilemski, G.; Fixman, M. General theory of diffusion-controlled reactions. J. Chem. Phys. 1973, 58, 4009–4019. [Google Scholar] [CrossRef]
- Calef, D.F.; Deutch, J.M. Diffusion-Controlled Reactions. Ann. Rev. Phys. Chem. 1983, 34, 493–524. [Google Scholar] [CrossRef]
- Berg, O.G.; von Hippel, P.H. Diffusion-Controlled Macromolecular Interactions. Ann. Rev. Biophys. Biophys. Chem. 1985, 14, 131–160. [Google Scholar] [CrossRef] [PubMed]
- Rice, S. Diffusion-Limited Reactions; Elsevier: Amsterdam, The Netherlands, 1985. [Google Scholar]
- Grebenkov, D.S. Diffusion-Controlled Reactions: An Overview. Molecules 2023, 28, 7570. [Google Scholar] [CrossRef] [PubMed]
- Goodrich, F.C. Random walk with semi-adsorbing barrier. J. Chem. Phys. 1954, 22, 588–594. [Google Scholar] [CrossRef]
- Mysels, K.J. Diffusion-controlled adsorption kinetics. General solution and some applications. J. Phys. Chem. 1982, 86, 4648–4651. [Google Scholar] [CrossRef]
- Agmon, N. Diffusion with back reaction. J. Chem. Phys. 1984, 81, 2811–2817. [Google Scholar] [CrossRef]
- Agmon, N.; Weiss, G.H. Theory of non-Markovian reversible dissociation reactions. J. Chem. Phys. 1989, 91, 6937–6942. [Google Scholar] [CrossRef]
- Agmon, N.; Szabo, A. Theory of reversible diffusion-influenced reactions. J. Chem. Phys. 1990, 92, 5270–5284. [Google Scholar] [CrossRef]
- Kim, H.; Shin, K.J. Exact solution of the reversible diffusion-influenced reaction for an isolated pair in three dimensions. Phys. Rev. Lett. 1999, 82, 1578–1581. [Google Scholar] [CrossRef]
- Prüstel, T.; Tachiya, M. Reversible diffusion-influenced reactions of an isolated pair on some two dimensional surfaces. J. Chem. Phys. 2013, 139, 194103. [Google Scholar] [CrossRef]
- Scher, Y.; Lauber Bonomo, O.; Pal, A.; Reuveni, S. Microscopic theory of adsorption kinetics. J. Chem. Phys. 2023, 158, 094107. [Google Scholar] [CrossRef]
- Sala, F.; Hernández-Cruz, A. Calcium diffusion modeling in a spherical neuron. Relevance of buffering properties. Biophys. J. 1990, 57, 313–324. [Google Scholar] [CrossRef] [PubMed]
- Neher, E.; Sakaba, T. Multiple Roles of Calcium Ions in the Regulation of Neurotransmitter Release. Neuron 2008, 59, 861. [Google Scholar] [CrossRef] [PubMed]
- Holcman, D.; Schuss, Z. Control of flux by narrow passages and hidden targets in cellular biology. Phys. Progr. Rep. 2013, 76, 074601. [Google Scholar] [CrossRef] [PubMed]
- Guerrier, C.; Holcman, D. The First 100 nm Inside the Pre-synaptic Terminal Where Calcium Diffusion Triggers Vesicular Release. Front. Synaptic Neurosci. 2018, 10, 23. [Google Scholar] [CrossRef]
- Reva, M.; DiGregorio, D.; Grebenkov, D.S. A first-passage approach to diffusion-influenced reversible binding and its insights into nanoscale signaling at the presynapse. Sci. Rep. 2021, 11, 5377. [Google Scholar] [CrossRef]
- Dick, D.A.T. The permeability coefficient of water in the cell membrane and the diffusion coefficient in the cell interior. J. Theor. Biol. 1964, 7, 504–531. [Google Scholar] [CrossRef] [PubMed]
- Crick, F. Diffusion in Embryogenesis. Nature 1970, 225, 420. [Google Scholar] [CrossRef]
- Michel, C.C.; Curry, F.E. Microvascular Permeability. Physiol. Rev. 1999, 79, 703. [Google Scholar] [CrossRef]
- Sapoval, B.; Filoche, M.; Weibel, E. Smaller is better–but not too small: A physical scale for the design of the mammalian pulmonary acinus. Proc. Nat. Acad. Sci. USA 2002, 99, 10411. [Google Scholar] [CrossRef]
- Novikov, D.S.; Fieremans, E.; Jensen, J.H.; Helpern, J.A. Random walks with barriers. Nat. Phys. 2011, 7, 508–514. [Google Scholar] [CrossRef]
- Kay, T.; Giuggioli, L. Diffusion through permeable interfaces: Fundamental equations and their application to first-passage and local time statistics. Phys. Rev. Res 2022, 4, L032039. [Google Scholar] [CrossRef]
- Bressloff, P.C. Renewal equation for single-particle diffusion through a semipermeable interface. Phys. Rev. E 2023, 107, 014110. [Google Scholar] [CrossRef] [PubMed]
- Bressloff, P.C. Renewal equations for single-particle diffusion in multilayered media. SIAM J. Appl. Math. 2023, 83, 1518–1545. [Google Scholar] [CrossRef]
- Siepmann, J.; Siepmann, F. Mathematical modeling of drug delivery. Int. J. Pharm. 2008, 364, 328–343. [Google Scholar] [CrossRef] [PubMed]
- Carr, E.J.; Pontrelli, G. Modelling mass diffusion for a multi-layer sphere immersed in a semi-infinite medium: Application to drug delivery. Math. Biosci. 2018, 303, 1–9. [Google Scholar] [CrossRef]
- Rubin, R.J.; Weiss, G.H. Random walks on lattices. The problem of visits to a set of points revisited. J. Math. Phys. 1982, 23, 250. [Google Scholar] [CrossRef]
- Haus, J.W.; Kehr, K.W. Diffusion in regular and disordered lattices. Phys. Rep. 1987, 150, 263. [Google Scholar] [CrossRef]
- Nicolis, C.; Kozak, J.J.; Nicolis, G. Encounter-controlled reactions between interacting walkers in finite lattices: Complex kinetics and many-body effects. J. Chem. Phys. 2001, 115, 663. [Google Scholar] [CrossRef]
- Moreau, M.; Oshanin, G.; Bénichou, O.; Coppey, M. Lattice theory of trapping reactions with mobile species. Phys. Rev. E 2004, 69, 046101. [Google Scholar] [CrossRef]
- Schmit, J.D.; Kamber, E.; Kondev, J. Lattice Model of Diffusion-Limited Bimolecular Chemical Reactions in Confined Environments. Phys. Rev. Lett. 2009, 102, 218302. [Google Scholar] [CrossRef]
- Abad, E.; Kozak, J.J. Competing reaction processes on a lattice as a paradigm for catalyst deactivation. Phys. Rev. E 2015, 91, 022106. [Google Scholar] [CrossRef] [PubMed]
- Giuggioli, L. Exact Spatiotemporal Dynamics of Confined Lattice Random Walks in Arbitrary Dimensions: A Century after Smoluchowski and Polya. Phys. Rev. X 2020, 10, 021045. [Google Scholar] [CrossRef]
- Singer, A.; Schuss, Z.; Holcman, D.; Eisenberg, R.S. Narrow Escape, Part I. J. Stat. Phys. 2006, 122, 437. [Google Scholar] [CrossRef]
- Bénichou, O.; Meyer, B.; Tejedor, V.; Voituriez, R. Zero Constant Formula for First-Passage Observables in Bounded Domains. Phys. Rev. Lett. 2008, 101, 130601. [Google Scholar] [CrossRef]
- Pillay, S.; Ward, M.J.; Peirce, A.; Kolokolnikov, T. An Asymptotic Analysis of the Mean First Passage Time for Narrow Escape Problems. Part I. Two-Dimensional Domains. SIAM Multiscale Model. Simul. 2010, 8, 803. [Google Scholar] [CrossRef]
- Bénichou, O.; Voituriez, R. From first-passage times of random walks in confinement to geometry-controlled kinetics. Phys. Rep. 2014, 539, 225–284. [Google Scholar] [CrossRef]
- Holcman, D.; Schuss, Z. The Narrow Escape Problem. SIAM Rev. 2014, 56, 213–257. [Google Scholar] [CrossRef]
- Grebenkov, D.G. Universal formula for the mean first passage time in planar domains. Phys. Rev. Lett. 2016, 117, 260201. [Google Scholar] [CrossRef]
- Bressloff, P.C. Narrow capture problem: An encounter-based approach to partially reactive targets. Phys. Rev. E 2022, 105, 034141. [Google Scholar] [CrossRef]
- Grebenkov, D.S. Statistics of diffusive encounters with a small target: Three complementary approaches. J. Stat. Mech. 2022, 083205. [Google Scholar] [CrossRef]
- Mörters, P.; Peres, Y. Brownian Motion; Cambridge Series in Statistical and Probabilistic Mathematics; Cambridge University Press: New York, NY, USA, 2010. [Google Scholar]
- Grebenkov, D.S. Residence times and other functionals of reflected Brownian motion. Phys. Rev. E 2007, 76, 041139. [Google Scholar] [CrossRef] [PubMed]
- Bénichou, O.; Grebenkov, D.S.; Levitz, P.E.; Loverdo, C.; Voituriez, R. Optimal Reaction Time for Surface-Mediated Diffusion. Phys. Rev. Lett. 2010, 105, 150606. [Google Scholar] [CrossRef] [PubMed]
- Collins, F.C.; Kimball, G.E. Diffusion-controlled reaction rates. J. Colloid Sci. 1949, 4, 425–437. [Google Scholar] [CrossRef]
- Sano, H.; Tachiya, M. Partially diffusion-controlled recombination. J. Chem. Phys. 1979, 71, 1276–1282. [Google Scholar] [CrossRef]
- Brownstein, K.R.; Tarr, C.E. Importance of Classical Diffusion in NMR Studies of Water in Biological Cells. Phys. Rev. A 1979, 19, 2446–2453. [Google Scholar] [CrossRef]
- Sano, H.; Tachiya, M. Theory of diffusion-controlled reactions on spherical surfaces and its application to reactions on micellar surfaces. J. Chem. Phys. 1981, 75, 2870–2878. [Google Scholar] [CrossRef]
- Agmon, N.; Pines, E.; Huppert, D. Geminate recombination in proton-transfer reactions. II. Comparison of diffusional and kinetic schemes. J. Chem. Phys. 1988, 88, 5631–5638. [Google Scholar] [CrossRef]
- Sapoval, B. General Formulation of Laplacian Transfer Across Irregular Surfaces. Phys. Rev. Lett. 1994, 73, 3314–3316. [Google Scholar] [CrossRef]
- Erban, R.; Chapman, S.J. Reactive boundary conditions for stochastic simulations of reaction-diffusion processes. Phys. Biol. 2007, 4, 16–28. [Google Scholar] [CrossRef] [PubMed]
- Galanti, M.; Fanelli, D.; Traytak, S.D.; Piazza, F. Theory of diffusion-influenced reactions in complex geometries. Phys. Chem. Chem. Phys. 2016, 18, 15950–15954. [Google Scholar] [CrossRef]
- Grebenkov, D.S. Spectral theory of imperfect diffusion-controlled reactions on heterogeneous catalytic surfaces. J. Chem. Phys. 2019, 151, 104108. [Google Scholar] [CrossRef] [PubMed]
- Grebenkov, D.S. Diffusion toward non-overlapping partially reactive spherical traps: Fresh insights onto classic problems. J. Chem. Phys. 2020, 152, 244108. [Google Scholar] [CrossRef] [PubMed]
- Piazza, F. The physics of boundary conditions in reaction-diffusion problems. J. Chem. Phys. 2022, 157, 234110. [Google Scholar] [CrossRef]
- Grebenkov, D.S. Paradigm Shift in Diffusion-Mediated Surface Phenomena. Phys. Rev. Lett. 2020, 125, 078102. [Google Scholar] [CrossRef]
- Grebenkov, D.S. Surface Hopping Propagator: An Alternative Approach to Diffusion-Influenced Reactions. Phys. Rev. E 2020, 102, 032125. [Google Scholar] [CrossRef] [PubMed]
- Bressloff, P.C. A probabilistic model of diffusion through a semipermeable barrier. Proc. Roy. Soc. A 2022, 478, 20220615. [Google Scholar] [CrossRef]
- Grebenkov, D.S. Diffusion-controlled reactions with non-Markovian binding/unbinding kinetics. J. Chem. Phys. 2023, 158, 214111. [Google Scholar] [CrossRef]
- Scher, Y.; Reuveni, S.; Grebenkov, D.S. Escape of a sticky particle. Phys. Rev. Res. 2023, 5, 043196. [Google Scholar] [CrossRef]
- Scher, Y.; Reuveni, S.; Grebenkov, D.S. Escape from textured adsorbing surfaces. J. Chem. Phys. 2024, 160, 184105. [Google Scholar] [CrossRef]
- Grebenkov, D.S. Probability distribution of the boundary local time of reflected Brownian motion in Euclidean domains. Phys. Rev. E 2019, 100, 062110. [Google Scholar] [CrossRef]
- Yuste, S.B.; Abad, E.; Lindenberg, K. Exploration and Trapping of Mortal Random Walkers. Phys. Rev. Lett. 2013, 110, 220603. [Google Scholar] [CrossRef] [PubMed]
- Meerson, B.; Redner, S. Mortality, Redundancy, and Diversity in Stochastic Search. Phys. Rev. Lett. 2015, 114, 198101. [Google Scholar] [CrossRef] [PubMed]
- Grebenkov, D.S.; Rupprecht, J.-F. The escape problem for mortal walkers. J. Chem. Phys. 2017, 146, 084106. [Google Scholar] [CrossRef] [PubMed]
- Levitin, M.; Mangoubi, D.; Polterovich, I. Topics in Spectral Geometry; Graduate Studies in Mathematics; American Mathematical Society: Providence, RI, USA, 2023; Volume 237. [Google Scholar]
- Girouard, A.; Polterovich, I. Spectral geometry of the Steklov problem. J. Spectr. Theory 2017, 7, 321–359. [Google Scholar] [CrossRef] [PubMed]
- Colbois, B.; Girouard, A.; Gordon, C.; Sher, D. Some recent developments on the Steklov eigenvalue problem. Rev. Mat. Complut. 2024, 37, 1–161. [Google Scholar] [CrossRef]
- Kay, T.; Giuggioli, L. Local Time Statistics and Permeable Barrier Crossing: From Poisson to Birth-Death Diffusion Equations. arXiv 2024, arXiv:2406.07142. [Google Scholar]
- Friedlander, L. Some inequalities between Dirichlet and Neumann eigenvalues. Arch. Ration. Mech. Anal. 1991, 116, 153–160. [Google Scholar] [CrossRef]
- Grebenkov, D.S. Statistics of boundary encounters by a particle diffusing outside a compact planar domain. J. Phys. A Math. Theor. 2021, 54, 015003. [Google Scholar] [CrossRef]
- Grebenkov, D.S. Spectral properties of the Dirichlet-to-Neumann operator for spheroids. Phys. Rev. E 2024, 109, 055306. [Google Scholar] [CrossRef]
- Bressloff, P.C. Diffusion-mediated absorption by partially-reactive targets: Brownian functionals and generalized propagators. J. Phys. A Math. Theor. 2022, 55, 205001. [Google Scholar] [CrossRef]
- Chaigneau, A.; Grebenkov, D.S. A numerical study of the generalized Steklov problem in planar domains. J. Phys. A Math. Theor. 2024, 57, 445201. [Google Scholar] [CrossRef]
- Prudnikov, A.P.; Brychkov, Y.A.; Marichev, O.I. Integrals and Series, Vol. 5 Inverse Laplace Transforms; Gordon and Breach Science Publishers: Amsterdam, The Netherlands, 1992. [Google Scholar]
- Equation (13.8.8) of DLMF. Available online: http://dlmf.nist.gov/13.8.E8 (accessed on 1 September 2024).

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grebenkov, D.S. Adsorption and Permeation Events in Molecular Diffusion. Molecules 2024, 29, 5012. https://doi.org/10.3390/molecules29215012
Grebenkov DS. Adsorption and Permeation Events in Molecular Diffusion. Molecules. 2024; 29(21):5012. https://doi.org/10.3390/molecules29215012
Chicago/Turabian StyleGrebenkov, Denis S. 2024. "Adsorption and Permeation Events in Molecular Diffusion" Molecules 29, no. 21: 5012. https://doi.org/10.3390/molecules29215012
APA StyleGrebenkov, D. S. (2024). Adsorption and Permeation Events in Molecular Diffusion. Molecules, 29(21), 5012. https://doi.org/10.3390/molecules29215012





