Aromaticity and Chirality: New Facets of Old Concepts
Abstract
1. Introduction
2. Results and Discussion
2.1. Push–Pull Versus Captodative Aromaticity
2.2. Electron Counting Rules
2.3. Effect of the Electron Density on the Aromatic Ring

2.4. Aromaticity and the Boundaries of the Periodic Table of the Elements: What Is the Connection?
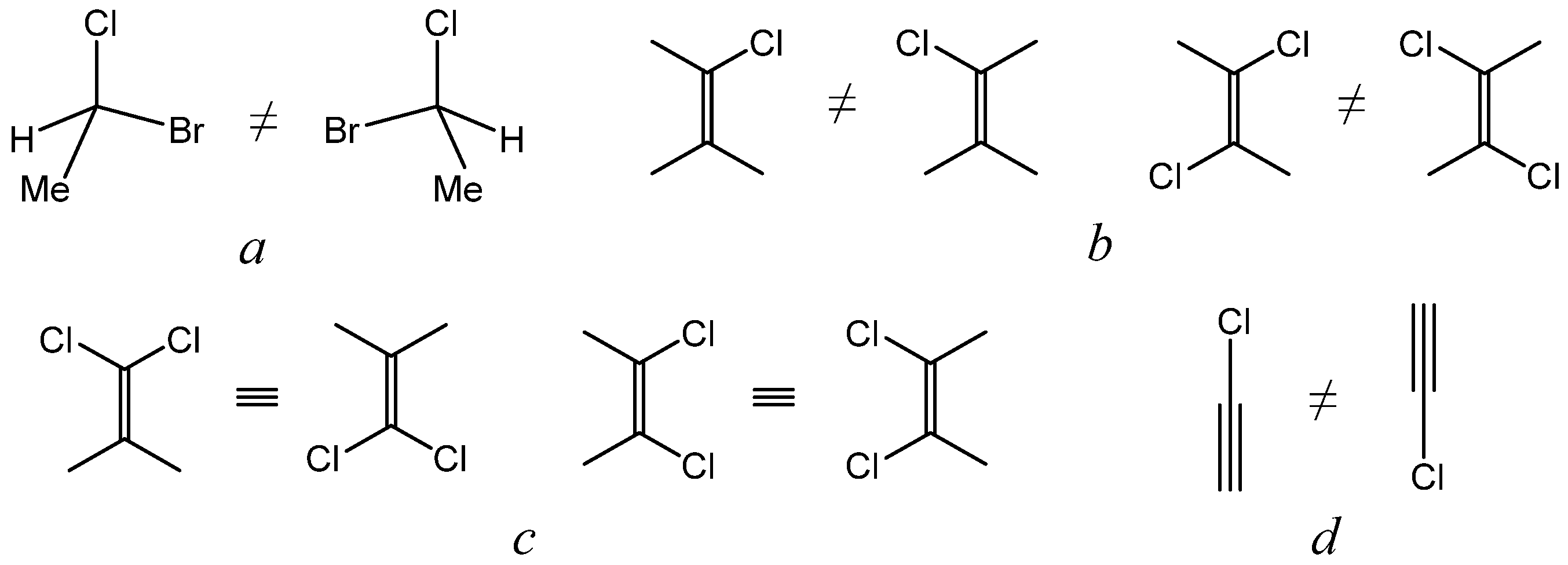
2.5. Chirality and Dimensionality of Space
3. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kekulé, A. Sur la constitution des substances aromatiques. Bull. Mens. Soc. Chim. Paris 1865, 3, 98–111. [Google Scholar]
- Hückel, E. Quantentheoretische Beiträge zum Benzolproblem. Z. Phys. Chem. 1931, 70, 204–286. [Google Scholar] [CrossRef]
- Li, X.; Kuznetsov, A.E.; Zhang, H.-F.; Boldyrev, A.I.; Wang, L.-S. Observation of all-metal aromatic molecules. Science 2001, 291, 859–861. [Google Scholar] [CrossRef] [PubMed]
- Boldyrev, A.I.; Wang, L.-S. All-metal aromaticity and antiaromaticity. Chem. Rev. 2005, 105, 3716–3757. [Google Scholar] [CrossRef] [PubMed]
- Kushvaha, S.K.; Kallenbach, P.; Rohman, S.S.; Pandey, M.K.; Hendi, Z.; Rüttger, F.; Herbst-Irmer, R.; Stalke, D.; Parameswaran, P.; Roesky, H.W. A Neutral Planar Four-Membered Si2B2 2π-Aromatic Ring. J. Am. Chem. Soc. 2023, 145, 25523–25527. [Google Scholar] [CrossRef]
- Pham, H.T.; Duong, L.V.; Nguyen, M.T. Electronic Structure and Chemical Bonding in the Double Ring Tubular Boron Clusters. J. Phys. Chem. C 2014, 118, 24181–24187. [Google Scholar] [CrossRef]
- Duong, L.V.; Pham, H.T.; Tam, N.M.; Nguyen, M.T. A particle on a hollow cylinder: The triple ring tubular cluster B27+. Phys. Chem. Chem. Phys. 2014, 16, 19470–19478. [Google Scholar] [CrossRef]
- Tai, T.B.; Ceulemans, A.; Nguyen, M.T. Disk aromaticity of the planar and fluxional anionic boron clusters B20−/2−. Chem. Eur. J. 2012, 18, 4510–4512. [Google Scholar] [CrossRef]
- Tai, T.B.; Havenith, T.W.; Teunissen, J.L.; Dok, A.R.; Hallaert, S.D.; Nguyen, M.T.; Ceulemans, A. Particle on a boron disk: Ring currents and disk aromaticity in B202−. Inorg. Chem. 2013, 52, 10595–10600. [Google Scholar] [CrossRef]
- Tai, T.; Duong, L.V.; Pham, H.T.; Dang, M.T.T.; Nguyen, M.T. A disk-aromatic bowl cluster B30: Toward formation of boron buckyballs. Chem. Commun. 2014, 50, 1558–1560. [Google Scholar] [CrossRef]
- Cui, P.; Hu, H.-S.; Zhao, B.; Miller, J.T.; Cheng, P.; Li, J. A multicentre-bonded [ZnI]8 cluster with cubic aromaticity. Nat. Commun. 2015, 6, 6331–6336. [Google Scholar] [CrossRef] [PubMed]
- Bühl, M.; Hirsch, A. Spherical Aromaticity of Fullerenes. Chem. Rev. 2001, 101, 1153–1183. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Jiao, H.; Hirsch, A.; Schleyer, P.v.R. Spherical Homoaromaticity. Angew. Chem. Int. Ed. 2002, 41, 4309–4312. [Google Scholar] [CrossRef]
- Wu, S.; Ni, Y.; Han, Y.; Hou, X.; Wang, C.; Hu, W.; Wu, J. Hückel- and Baird-Type Global Aromaticity in a 3D Fully Conjugated Molecular Cage. Angew. Chem. Int. Ed. 2021, 61, e202115571. [Google Scholar] [CrossRef]
- King, R.B. Three-Dimensional Aromaticity in Polyhedral Boranes and Related Molecules. Chem. Rev. 2001, 101, 1119–1152. [Google Scholar] [CrossRef] [PubMed]
- Shainyan, B.A.; Sekiguchi, A. Computational study of tetrasilylcyclobutadiene dianion and its dilithium salt. 6e–6c Three-dimensional aromaticity. J. Mol. Struct. THEOCHEM 2005, 728, 1–5. [Google Scholar] [CrossRef]
- Kleinpeter, E.; Koch, A.; Shainyan, B.A. Cyclobutadiene Dianion Derivatives—Planar 4c,6e or Three-Dimensional 6c,6e Aromaticity? J. Mol. Struct. THEOCHEM 2008, 863, 117–122. [Google Scholar] [CrossRef]
- El Bakouri, O.; Szczepanik, D.W.; Jorner, K.; Ayub, R.; Bultinck, P.; Solà, M.; Ottosson, H. Three-Dimensional Fully π-Conjugated Macrocycles: When 3D-Aromatic and When 2D-Aromatic-in-3D? J. Am. Chem. Soc. 2022, 144, 8560–8575. [Google Scholar] [CrossRef]
- Ren, L.; Han, Y.; Hou, X.; Ni, Y.; Wu, Y. All are aromatic: A 3D globally aromatic cage containing five types of 2D aromatic macrocycles. Chem 2021, 7, 3442–3453. [Google Scholar] [CrossRef]
- Shainyan, B.A. Rules for counting electrons and three-dimensional aromaticity. Russ. J. Org. Chem. 2006, 42, 304–306. [Google Scholar] [CrossRef]
- Shainyan, B.A. Electron-counting rules, three-dimensional aromaticity, and the boundaries of the Periodic Table. J. Phys. Org. Chem. 2011, 24, 619–620. [Google Scholar] [CrossRef]
- Poater, J.; Viñas, C.; Bennour, I.; Escayola, S.; Solà, M.; Teixidor, F. Too Persistent to Give Up: Aromaticity in Boron Clusters Survives Radical Structural Changes. J. Am. Chem. Soc. 2020, 142, 9396–9407. [Google Scholar] [CrossRef] [PubMed]
- Kumar, P. Continuous group and electron-count rules in aromaticity. J. Chem. Sci. 2018, 130, 17. [Google Scholar] [CrossRef]
- Solà, M. Why Aromaticity Is a Suspicious Concept? Why? Front. Chem. 2017, 5, 22. [Google Scholar] [CrossRef] [PubMed]
- Merino, G.; Solà, M.; Fernández, I.; Foroutan-Nejad, C.; Lazzeretti, P.; Frenking, G.; Anderson, H.L.; Sundholm, D.; Cossío, F.P.; Petrukhina, M.A.; et al. Aromaticity: Quo Vadis. Chem. Sci. 2023, 14, 5569–5576. [Google Scholar] [CrossRef]
- Agranat, I. Aromaticity—A theoretical notion. Struct. Chem. 2024, 35, 715–720. [Google Scholar] [CrossRef]
- Shainyan, B.A.; Fettke, A.; Kleinpeter, E. Push-pull vs. Captodative Aromaticity. J. Phys. Chem. A 2008, 112, 10895–10903. [Google Scholar] [CrossRef]
- Scott, A.P.; Agranat, I.; Biedermann, P.U.; Riggs, N.V.; Radom, L. Fulvalenes, Fulvenes, and Related Molecules: An ab Initio Study. J. Org. Chem. 1997, 62, 2026–2038. [Google Scholar] [CrossRef]
- Shainyan, B.A. Aromaticity of tropylium derivatives: When and why might captodative structures be preferred over the isomeric push-pull structures? Int. J. Quantum Chem. 2024, 124, e27449. [Google Scholar] [CrossRef]
- Shainyan, B.A. Captodative versus push-pull aromatic cyclopentadienyl derivatives. Int. J. Quantum Chem. 2024, 124, e27490. [Google Scholar] [CrossRef]
- Hirsch, A.; Chen, Z.; Jiao, H. Spherical Aromaticity in Ih Symmetrical Fullerenes: The 2(N+1)2 Rule. Angew. Chem. Int. Ed. 2000, 39, 3915–3917. [Google Scholar] [CrossRef]
- Chen, Z.; Jiao, H.; Hirsch, A.; Thiel, W. The 2(N+1)2 rule for spherical aromaticity: Further validation. Mol. Model. Annu. 2001, 7, 161–163. [Google Scholar] [CrossRef]
- Hirsch, A.; Chen, Z.; Jiao, H. Spherical Aromaticity of Inorganic Cage Molecules. Angew. Chem. Int. Ed. 2001, 40, 2834–2838. [Google Scholar] [CrossRef]
- Chen, Z.; King, R.B. Spherical Aromaticity: Recent Work on Fullerenes, Polyhedral Boranes, and Related Structures. Chem. Rev. 2005, 105, 3613–3642. [Google Scholar] [CrossRef]
- Wade, K. The structural significance of the number of skeletal bonding electron-pairs in carboranes, the higher boranes and borane anions, and various transition-metal carbonyl cluster compounds. Chem. Commun. 1971, 792–793. [Google Scholar] [CrossRef]
- Mingos, D.M.P. A General Theory for Cluster and Ring Compounds of the Main Group and Transition Elements. Nat. Phys. Sci. 1972, 236, 99–102. [Google Scholar] [CrossRef]
- King, R.B.; Silaghi-Dumitrescu, I. The role of “external” lone pairs in the chemical bonding of bare post-transition element clusters: The Wade–Mingos rules versus the jellium model. Dalton Trans. 2008, 6083–6088. [Google Scholar] [CrossRef]
- Poater, J.; Solà, M. Open-shell spherical aromaticity: The 2N2 + 2N + 1 (with S = N + ½) rule. Chem. Commun. 2011, 47, 11647–11649. [Google Scholar] [CrossRef]
- Rubin, M.A.; Ordóñez, C.R. Eigenvalues and degeneracies for n-dimensional tensor spherical harmonics. J. Math. Phys. 1984, 25, 2888–2894. [Google Scholar] [CrossRef]
- Ciesielski, A.; Cyrański, M.K.; Krygowski, T.M.; Fowler, P.W.; Lillington, M. Super-Delocalized Valence Isomer of Coronene. J. Org. Chem. 2006, 71, 6840–6845. [Google Scholar] [CrossRef]
- Chen, Z.; Jiao, H.; Moran, D.; Hirsch, A.; Thiel, W.; Schleyer, P.v.R. Aromatic stabilization in heterofullerenes C48X12 (X = N, P, B, Si). J. Phys. Org. Chem. 2003, 16, 726–730. [Google Scholar] [CrossRef]
- Duong, L.V.; Matito, E.; Solà, M.; Behzadi, H.; Momenie, M.J.; Nguyen, M.T. The electronic structure and stability of germanium tubes Ge30H12 and Ge33H12. Phys. Chem. Chem. Phys. 2018, 20, 23467–23479. [Google Scholar] [CrossRef] [PubMed]
- Johansson, M.P.; Jusélius, J.; Sundholm, D. Sphere Currents of Buckminsterfullerene. Angew. Chem. Int. Ed. 2005, 44, 1843–1846. [Google Scholar] [CrossRef] [PubMed]
- Sidorov, L.N.; Yurovskaya, M.A.; Borshchevskii, A.Y.; Trushkov, I.V.; Ioffe, I.N. Fullerenes; Ekzamen: Moscow, Russia, 2005; 687p. [Google Scholar]
- Reiher, M.; Hirsch, A. From Rare Gas Atoms to Fullerenes: Spherical Aromaticity Studied From the Point of View of Atomic Structure Theory. Chem. Eur. J. 2003, 9, 5442–5452. [Google Scholar] [CrossRef] [PubMed]
- King, R.B.; Silaghi-Dumitrescu, I.; Lupan, A. Density functional theory study of eight-atom germanium clusters: Effect of electron count on cluster geometry. Dalton Trans. 2005, 1858–1864. [Google Scholar] [CrossRef]
- An, W.; Bulusu, S.; Gao, Y.; Zeng, X.C. Relative stability of planar versus double-ring tubular isomers of neutral and anionic boron cluster B20 and B20−. J. Chem. Phys. 2006, 124, 154310. [Google Scholar] [CrossRef]
- Najafian, K.; Schleyer, P.v.R.; Tidwell, T.T. Stability and Three-Dimensional Aromaticity of closo-NBn-1Hn Azaboranes, n = 5–12. Inorg. Chem. 2003, 42, 4190–4203. [Google Scholar] [CrossRef]
- Okazaki, T.; Galembeck, S.E.; Laali, K.K. Novel Examples of Three-Dimensional Aromaticity: 1,3-Dehydro-silaadamantane Dications. A Theoretical (DFT, GIAO NMR, NICS) Study. J. Org. Chem. 2003, 67, 8721–8725. [Google Scholar] [CrossRef]
- Rzepa, H.S. Möbius aromaticity and delocalization. Chem. Rev. 2005, 105, 3697–3715. [Google Scholar] [CrossRef]
- Soncini, A.; Viglione, R.G.; Zanasi, R.; Fowler, P.W.; Jenneskens, L.W. Efficient mapping of ring currents in fullerenes and other curved carbon networks. C. R. Chim. 2006, 9, 1085–1093. [Google Scholar] [CrossRef]
- Torres-Vega, J.J.; Vásquez-Espinal, A.; Ruiz, L.; Fernández-Herrera, M.A.; Alvarez-Thon, L.; Merino, G.; Tiznado, M. Revisiting Aromaticity and Chemical Bonding of Fluorinated Benzene Derivatives. ChemistryOpen 2015, 4, 302–307. [Google Scholar] [CrossRef] [PubMed]
- Krygowski, T.M.; Ejsmont, K.; Stepień, B.T.; Cyrański, M.K.; Poater, J.; Solà, M. Relation between the Substituent Effect and Aromaticity. J. Org. Chem. 2004, 69, 6634–6640. [Google Scholar] [CrossRef] [PubMed]
- Krygowski, T.M.; Stepień, B.T. Sigma- and Pi-Electron Delocalization: Focus on Substituent Effects. Chem. Rev. 2005, 105, 3482–3512. [Google Scholar] [CrossRef] [PubMed]
- Voronkov, M.G.; Shainyan, B.A.; Trofimova, O.M. Effect of N-Silatranylmethyl Group on the Aromaticity of Pyrrole, Indole, and Carbazole. Dokl. Chem. 2004, 396, 127–131. [Google Scholar] [CrossRef]
- Eliav, E.; Shmulyian, S.; Kaldor, U.; Ishikawa, Y. Transition energies of lanthanum, actinium, and eka-actinium (element 121). J. Chem. Phys. 1998, 109, 3954–3958. [Google Scholar] [CrossRef]
- Shainyan, B.A. Aromaticity, chirality and dimensionality of space. New J. Chem. 2023, 47, 9560–9563. [Google Scholar] [CrossRef]
- Zeilinger, A.; Svozil, K. Measuring the Dimension of Space-Time. Phys. Rev. Lett. 1985, 54, 2553–2555. [Google Scholar] [CrossRef]
- Kak, S. Information theory and dimensionality of space. Sci. Rep. 2020, 10, 20733. [Google Scholar] [CrossRef]
- Bhatia, B.; Sholl, D.S. Enantiospecific Chemisorption of Small Molecules on Intrinsically Chiral Cu Surfaces. Angew. Chem. Int. Ed. 2005, 44, 7761–7764. [Google Scholar] [CrossRef]
- Miložič, N.; Lubej, M.; Lakner, M.; Žnidaršič-Plazl, P.; Plazl, I. Theoretical and experimental study of enzyme kinetics in a microreactor system with surface-immobilized biocatalyst. Chem. Eng. J. 2017, 313, 374–381. [Google Scholar] [CrossRef]
- Valikhani, D.; Bolivar, J.M.; Pfeiffer, M.; Nidetzky, B. Multivalency Effects on the Immobilization of Sucrose Phosphorylase in Flow Microchannels and Their Use in the Development of a High-Performance Biocatalytic Microreactor. ChemCatChem 2017, 9, 161–166. [Google Scholar] [CrossRef]
- Prinz, J.; Gröning, O.; Brune, H.; Widmer, R. Highly Enantioselective Adsorption of Small Prochiral Molecules on a Chiral Intermetallic Compound. Angew. Chem. Int. Ed. 2015, 54, 3902–3906. [Google Scholar] [CrossRef] [PubMed]
- Shukla, N.; Gellman, A.J. Chiral metal surfaces for enantioselective processes. Nat. Mater. 2020, 19, 939–945. [Google Scholar] [CrossRef] [PubMed]
- Gellman, A.J. An Account of Chiral Metal Surfaces and Their Enantiospecific Chemistry. Acc. Mater. Res. 2021, 2, 1024–1032. [Google Scholar] [CrossRef]
- Wang, C.; Hao, H.; Hashizume, D.; Tajima, K. Surface-induced enantiomorphic crystallization of achiral fullerene derivatives in thin films. Chem. Sci. 2020, 11, 4702. [Google Scholar] [CrossRef]
- Nakanishi, T.; Yamakawa, N.; Asahi, T.; Shibata, N.; Ohtani, B.; Osaka, T. Chiral discrimination between thalidomide enantiomers using a solid surface with two-dimensional chirality. Chirality 2004, 16 (Suppl. S1), S36–S39. [Google Scholar] [CrossRef]


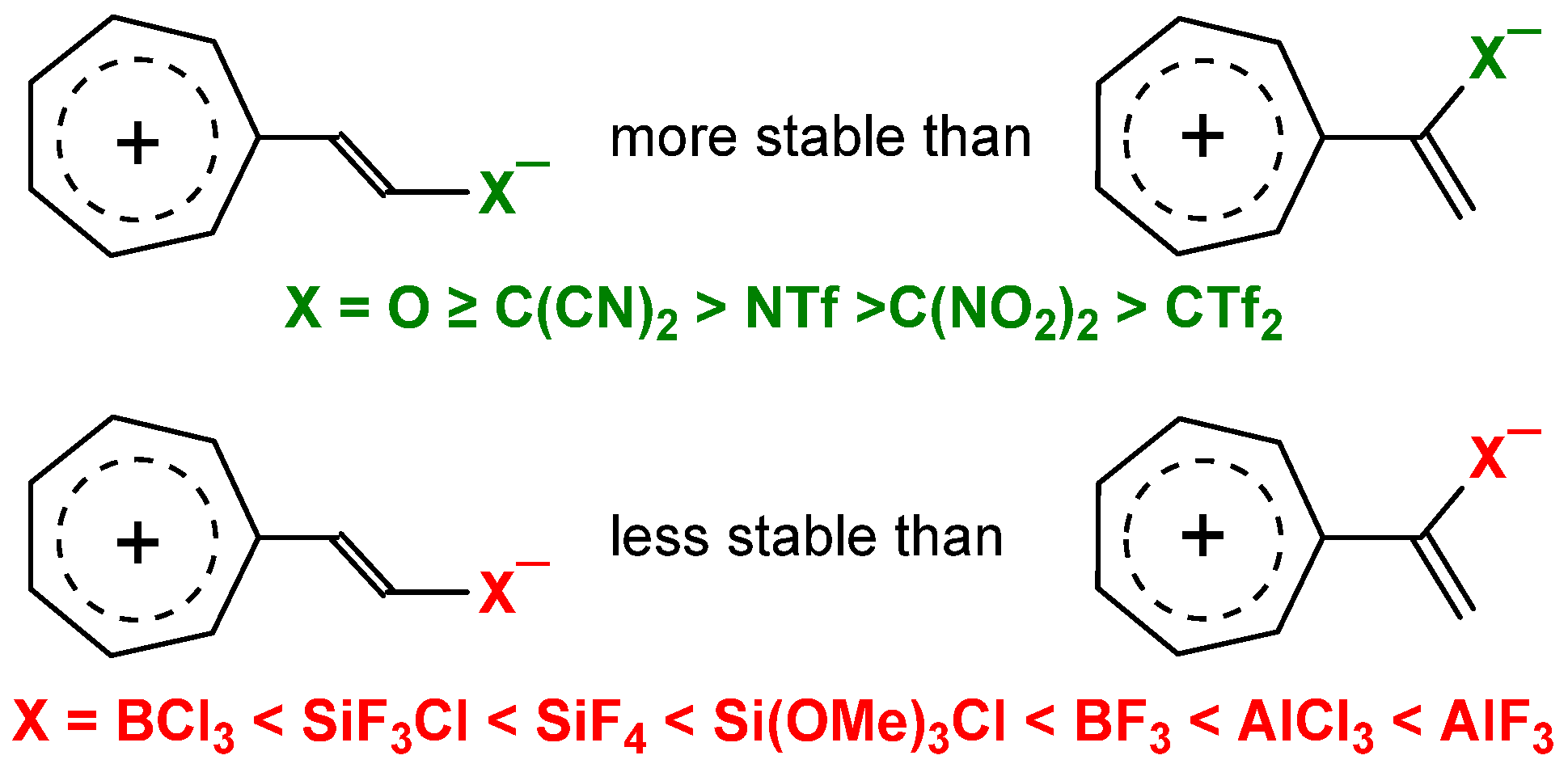
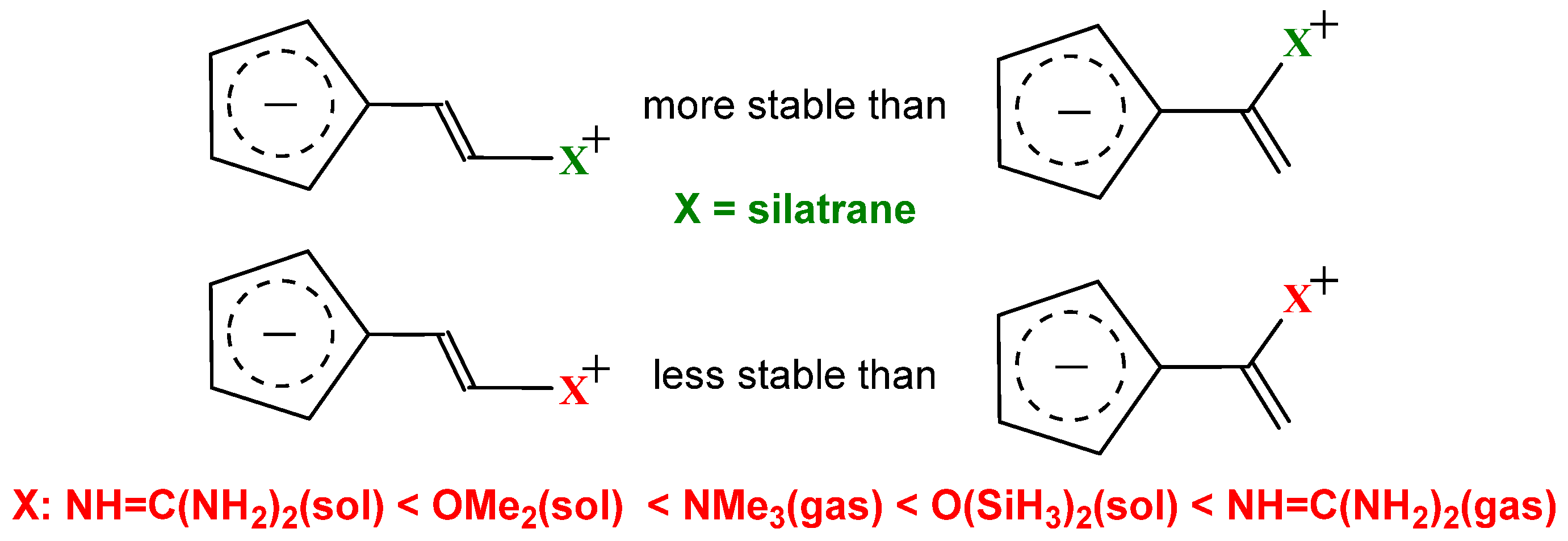
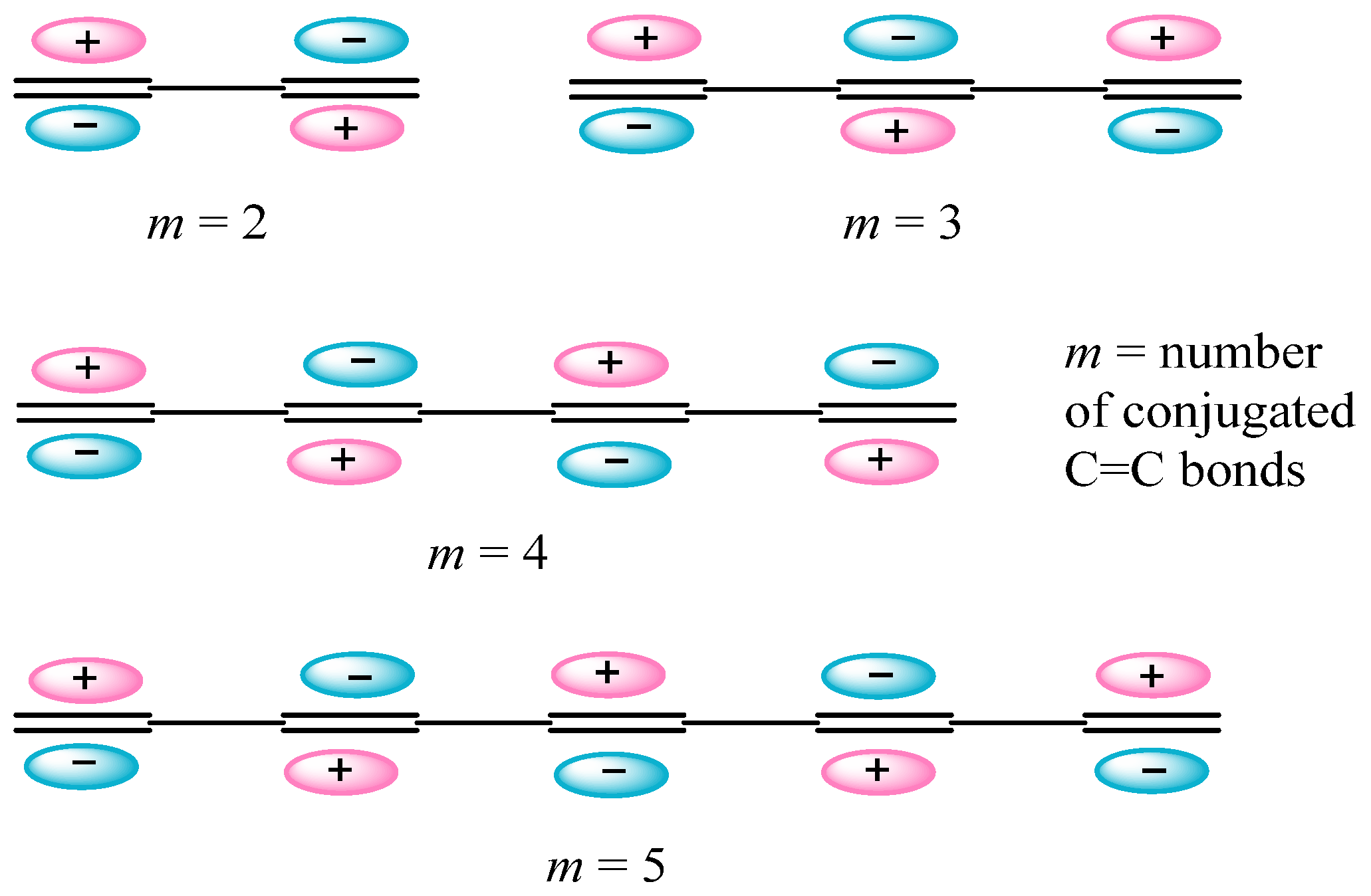
| Molecule | –NICS | ASE | ||
|---|---|---|---|---|
| 0.0 Å | 1.0 Å | 2.0 Å | ||
| Hexamethylbenzene | 12.19 | 10.98 | 5.13 | 51.80 |
| Hexacyanobenzene | 9.00 | 10.57 | 5.34 | 3.97 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shainyan, B.A. Aromaticity and Chirality: New Facets of Old Concepts. Molecules 2024, 29, 5394. https://doi.org/10.3390/molecules29225394
Shainyan BA. Aromaticity and Chirality: New Facets of Old Concepts. Molecules. 2024; 29(22):5394. https://doi.org/10.3390/molecules29225394
Chicago/Turabian StyleShainyan, Bagrat A. 2024. "Aromaticity and Chirality: New Facets of Old Concepts" Molecules 29, no. 22: 5394. https://doi.org/10.3390/molecules29225394
APA StyleShainyan, B. A. (2024). Aromaticity and Chirality: New Facets of Old Concepts. Molecules, 29(22), 5394. https://doi.org/10.3390/molecules29225394







