Temperature-Induced Restructuring of Mycolic Acid Bilayers Modeling the Mycobacterium tuberculosis Outer Membrane: A Molecular Dynamics Study
Abstract
:1. Introduction
2. Results and Discussion
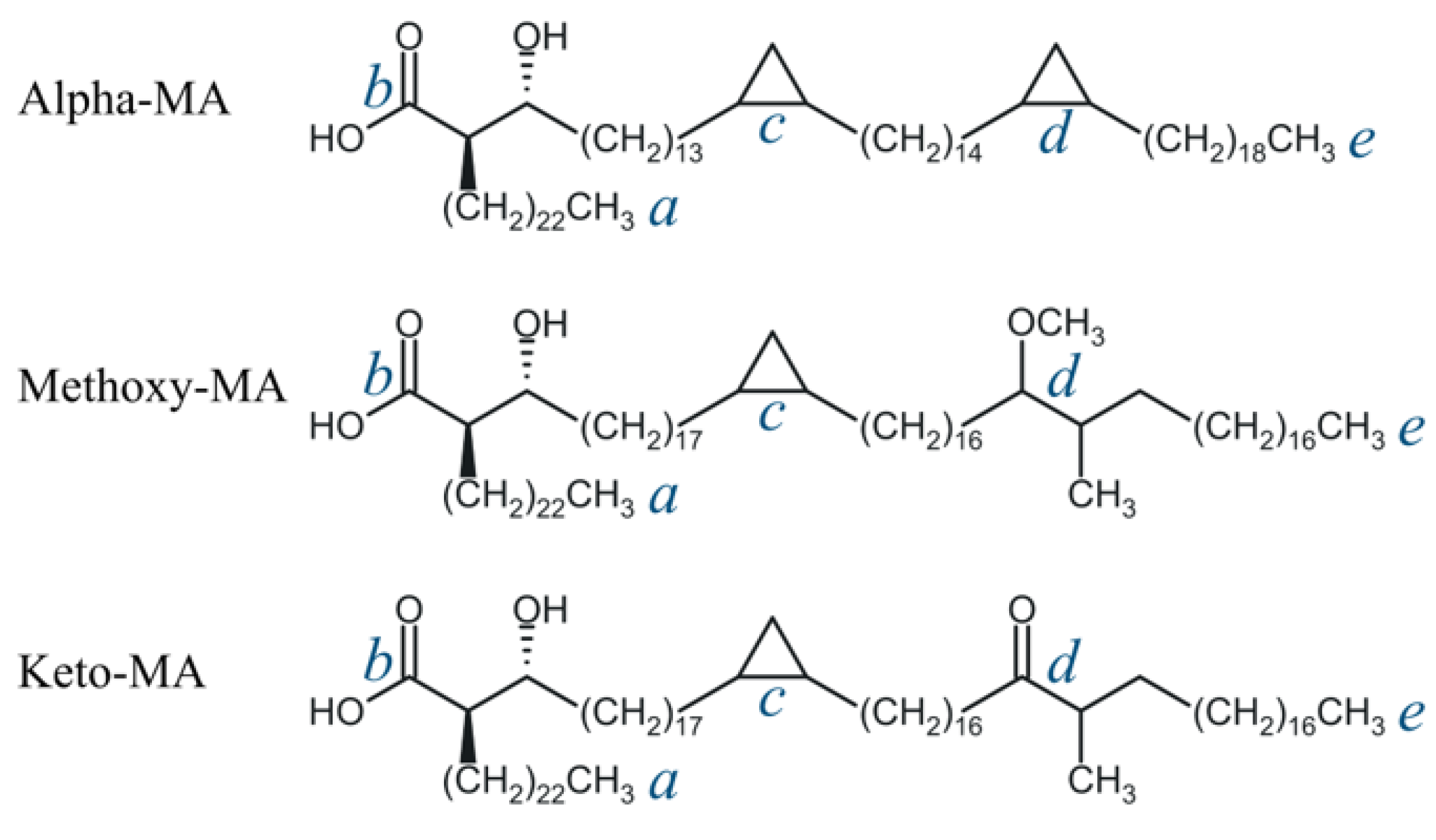
2.1. Model Systems and Conditions
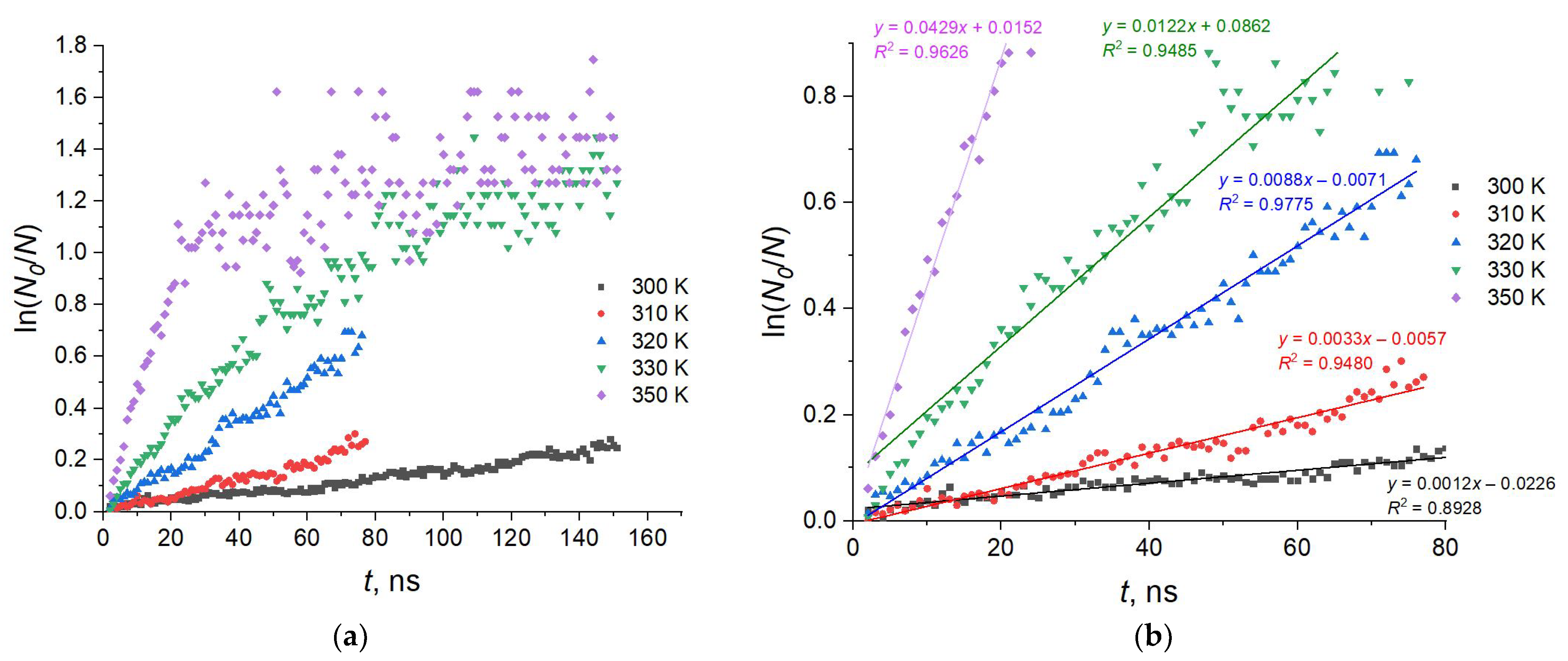
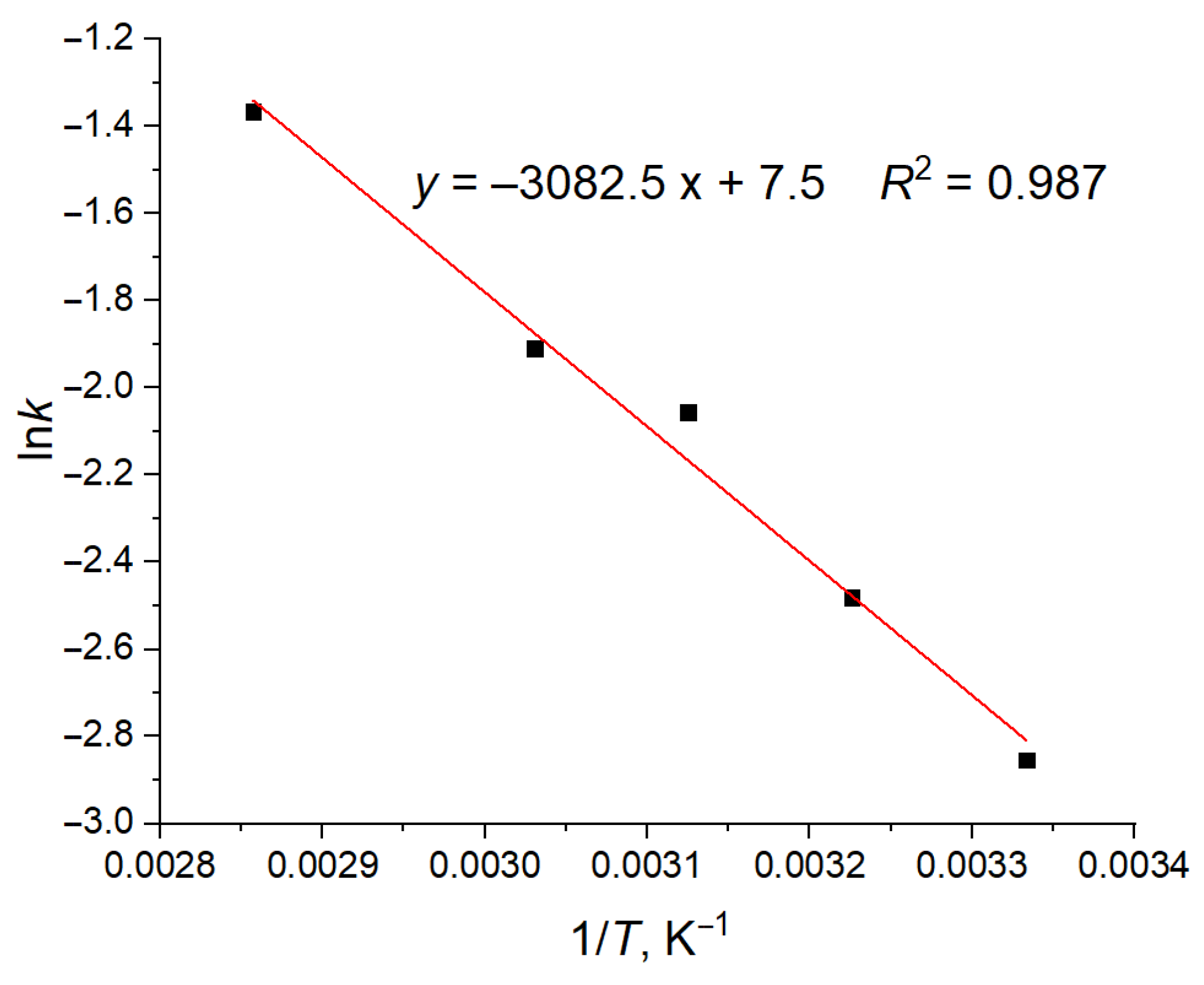
2.2. Temperature-Induced Conformational Changes in the MA Membranes and Their Activation Energies
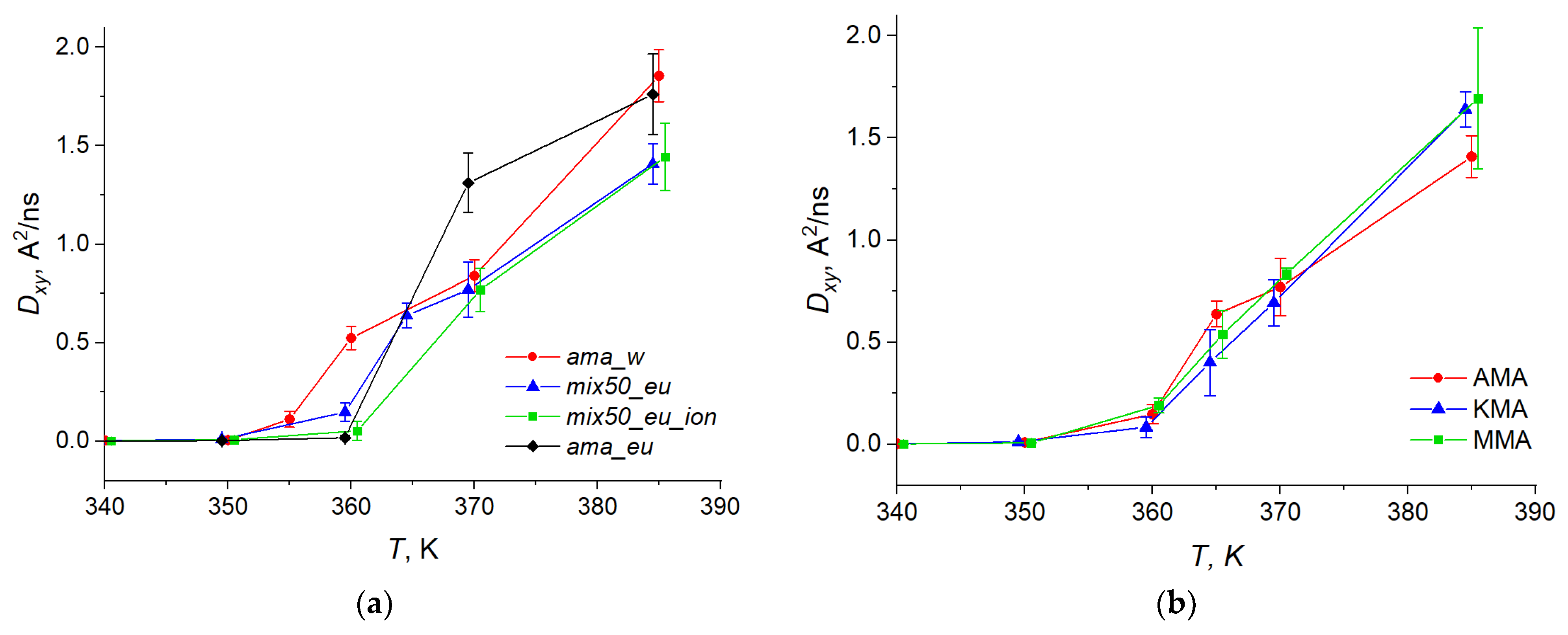
2.3. MA Self-Diffusion in Bilayer Membranes
2.4. Temperature-Induced Structural Reordering in MA Membranes
3. Materials and Methods
3.1. Model Membranes
3.2. Molecular Dynamics Simulations
3.3. MA Self-Diffusion in Bilayer Membranes
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- World Health Organization. Global Tuberculosis Report 2022; World Health Organization: Geneva, Switzerland, 2022; ISBN 978-92-4-006172-9. [Google Scholar]
- Joint United Nations Programme on HIV/AIDS. The Path That Ends AIDS: UNAIDS Global AIDS Update; Joint United Nations Programme on HIV/AIDS: Geneva, Switzerland, 2023. [Google Scholar]
- Houben, R.M.G.J.; Dodd, P.J. The global burden of latent tuberculosis infection: A re-estimation using mathematical modelling. PLoS Med. 2016, 13, e1002152. [Google Scholar] [CrossRef] [PubMed]
- Rao, M.; Ippolito, G.; Mfinanga, S.; Ntoumi, F.; Yeboah-Manu, D.; Vilaplana, C.; Zumla, A.; Maeurer, M. Latent TB Infection (LTBI)–Mycobacterium tuberculosis pathogenesis and the dynamics of the granuloma battleground. Int. J. Infect. Dis. 2019, 80, S58–S61. [Google Scholar] [CrossRef] [PubMed]
- Dulberger, C.L.; Rubin, E.J.; Boutte, C.C. The mycobacterial cell envelope—A moving target. Nat. Rev. Microbiol. 2020, 18, 47–59. [Google Scholar] [CrossRef] [PubMed]
- Bansal-Mutalik, R.; Nikaido, H. Mycobacterial outer membrane is a lipid bilayer and the inner membrane is unusually rich in diacyl phosphatidylinositol dimannosides. Proc. Natl. Acad. Sci. USA 2014, 111, 4958–4963. [Google Scholar] [CrossRef] [PubMed]
- Chiaradia, L.; Lefebvre, C.; Parra, J.; Marcoux, J.; Burlet-Schiltz, O.; Etienne, G.; Tropis, M.; Daffé, M. Dissecting the mycobacterial cell envelope and defining the composition of the native mycomembrane. Sci. Rep. 2017, 7, 12807. [Google Scholar] [CrossRef]
- Gutiérrez, A.V.; Viljoen, A.; Ghigo, E.; Herrmann, J.-L.; Kremer, L. Glycopeptidolipids, a double-edged sword of the Mycobacterium abscessus complex. Front. Microbiol. 2018, 9, 1145. [Google Scholar] [CrossRef]
- Craggs, P.D.; de Carvalho, L.P.S. Bottlenecks and opportunities in antibiotic discovery against Mycobacterium tuberculosis. Curr. Opin. Microbiol. 2022, 69, 102191. [Google Scholar] [CrossRef]
- Bhat, Z.S.; Rather, M.A.; Maqbool, M.; Lah, H.U.; Yousuf, S.K.; Ahmad, Z. Cell wall: A versatile fountain of drug targets in Mycobacterium tuberculosis. Biomed. Pharmacother. 2017, 95, 1520–1534. [Google Scholar] [CrossRef]
- Jones, A.; Lee, O.Y.-C.; Minnikin, D.E.; Baird, M.S.; Al Dulayymi, J.R. A re-investigation of the mycolic acids of Mycobacterium avium. Chem. Phys. Lipids 2020, 230, 104928. [Google Scholar] [CrossRef]
- Batt, S.M.; Minnikin, D.E.; Besra, G.S. The thick waxy coat of mycobacteria, a protective layer against antibiotics and the host’s immune system. Biochem. J. 2020, 477, 1983–2006. [Google Scholar] [CrossRef] [PubMed]
- Minnikin, D.E.; Brennan, P.J. Lipids of clinically significant mycobacteria. In Health Consequences of Microbial Interactions with Hydrocarbons, Oils, and Lipids; Goldfine, H., Ed.; Springer International Publishing: Cham, Switzerland, 2020; pp. 1–76. ISBN 978-3-319-72473-7. [Google Scholar] [CrossRef]
- Marrakchi, H.; Lanéelle, M.-A.; Daffé, M. Mycolic acids: Structures, biosynthesis, and beyond. Chem. Biol. 2014, 21, 67–85. [Google Scholar] [CrossRef]
- Watanabe, M.; Aoyagi, Y.; Ridell, M.; Minnikin, D.E. Separation and characterization of individual mycolic acids in representative mycobacteria. Microbiology 2001, 147, 1825–1837. [Google Scholar] [CrossRef] [PubMed]
- Takayama, K.; Wang, C.; Besra, G.S. Pathway to synthesis and processing of mycolic acids in Mycobacterium tuberculosis. Clin. Microbiol. Rev. 2005, 18, 81–101. [Google Scholar] [CrossRef] [PubMed]
- Villeneuve, M.; Kawai, M.; Watanabe, M.; Aoyagi, Y.; Hitotsuyanagi, Y.; Takeya, K.; Gouda, H.; Hirono, S.; Minnikin, D.E.; Nakahara, H. Differential conformational behaviors of α-mycolic acids in Langmuir monolayers and computer simulations. Chem. Phys. Lipids 2010, 163, 569–579. [Google Scholar] [CrossRef] [PubMed]
- Lambert, P.A. Cellular impermeability and uptake of biocides and antibiotics in Gram-positive bacteria and mycobacteria: Antimicrobial penetration of walls. J. Appl. Microbiol. 2002, 92, 46S–54S. [Google Scholar] [CrossRef] [PubMed]
- Gebhardt, H.; Meniche, X.; Tropis, M.; Krämer, R.; Daffé, M.; Morbach, S. The key role of the mycolic acid content in the functionality of the cell wall permeability barrier in Corynebacterineae. Microbiology 2007, 153, 1424–1434. [Google Scholar] [CrossRef] [PubMed]
- Daffé, M.; Draper, P. The envelope layers of mycobacteria with reference to their pathogenicity. In Advances in Microbial Physiology; Elsevier: Amsterdam, The Netherlands, 1997; Volume 39, pp. 131–203. ISBN 978-0-12-027739-1. [Google Scholar] [CrossRef]
- Magnuson, K.; Jackowski, S.; Rock, C.O.; Cronan, J.E. Regulation of fatty acid biosynthesis in Escherichia coli. Microbiol. Rev. 1993, 57, 522–542. [Google Scholar] [CrossRef] [PubMed]
- Marr, A.G.; Ingraham, J.L. Effect of temperature on the composition of fatty acids in Escherichia coli. J. Bacteriol. 1962, 84, 1260–1267. [Google Scholar] [CrossRef] [PubMed]
- Kremer, L.; Guérardel, Y.; Gurcha, S.S.; Locht, C.; Besra, G.S. Temperature-induced changes in the cell-wall components of Mycobacterium thermoresistibile. Microbiology 2002, 148, 3145–3154. [Google Scholar] [CrossRef]
- Brown, D.A.; London, E. Structure and function of sphingolipid- and cholesterol-rich membrane rafts. J. Biol. Chem. 2000, 275, 17221–17224. [Google Scholar] [CrossRef]
- Park, J.-W.; Ahn, D.J. Temperature effect on nanometer-scale physical properties of mixed phospholipid monolayers. Colloids Surf. B Biointerfaces 2008, 62, 157–161. [Google Scholar] [CrossRef] [PubMed]
- Seeger, H.M.; Marino, G.; Alessandrini, A.; Facci, P. Effect of physical parameters on the main phase transition of supported lipid bilayers. Biophys. J. 2009, 97, 1067–1076. [Google Scholar] [CrossRef] [PubMed]
- Sullan, R.M.A.; Li, J.K.; Hao, C.; Walker, G.C.; Zou, S. Cholesterol-dependent nanomechanical stability of phase-segregated multicomponent lipid bilayers. Biophys. J. 2010, 99, 507–516. [Google Scholar] [CrossRef] [PubMed]
- Simons, K.; Sampaio, J.L. Membrane organization and lipid rafts. Cold Spring Harb. Perspect. Biol. 2011, 3, a004697. [Google Scholar] [CrossRef] [PubMed]
- Alessandrini, A.; Seeger, H.M.; Caramaschi, T.; Facci, P. Dynamic force spectroscopy on supported lipid bilayers: Effect of temperature and sample preparation. Biophys. J. 2012, 103, 38–47. [Google Scholar] [CrossRef]
- Nicolson, G.L. The Fluid—Mosaic model of membrane structure: Still relevant to understanding the structure, function and dynamics of biological membranes after more than 40 years. Biochim. Biophys. Acta Biomembr. 2014, 1838, 1451–1466. [Google Scholar] [CrossRef]
- Bag, N.; Yap, D.H.X.; Wohland, T. Temperature dependence of diffusion in model and live cell membranes characterized by imaging fluorescence correlation spectroscopy. Biochim. Biophys. Acta Biomembr. 2014, 1838, 802–813. [Google Scholar] [CrossRef]
- Nguyen, H.T.H.; Madec, M.-N.; Ong, L.; Kentish, S.E.; Gras, S.L.; Lopez, C. The dynamics of the biological membrane surrounding the buffalo milk fat globule investigated as a function of temperature. Food Chem. 2016, 204, 343–351. [Google Scholar] [CrossRef] [PubMed]
- Murthy, A.V.R.; Guyomarc’h, F.; Lopez, C. The temperature-dependent physical state of polar lipids and their miscibility impact the topography and mechanical properties of bilayer models of the milk fat globule membrane. Biochim. Biophys. Acta Biomembr. 2016, 1858, 2181–2190. [Google Scholar] [CrossRef] [PubMed]
- Sugahara, K.; Shimokawa, N.; Takagi, M. Thermal stability of phase-separated domains in multicomponent lipid membranes with local anesthetics. Membranes 2017, 7, 33. [Google Scholar] [CrossRef]
- Bhojoo, U.; Chen, M.; Zou, S. Temperature induced lipid membrane restructuring and changes in nanomechanics. Biochim. Biophys. Acta Biomembr. 2018, 1860, 700–709. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Barry, C.E.; Besra, G.S.; Nikaido, H. Mycolic acid structure determines the fluidity of the mycobacterial cell wall. J. Biol. Chem. 1996, 271, 29545–29551. [Google Scholar] [CrossRef] [PubMed]
- Adhyapak, P.; Srivatsav, A.T.; Mishra, M.; Singh, A.; Narayan, R.; Kapoor, S. Dynamical organization of compositionally distinct inner and outer membrane lipids of mycobacteria. Biophys. J. 2020, 118, 1279–1291. [Google Scholar] [CrossRef] [PubMed]
- Villeneuve, M.; Kawai, M.; Kanashima, H.; Watanabe, M.; Minnikin, D.E.; Nakahara, H. Temperature dependence of the Langmuir monolayer packing of mycolic acids from Mycobacterium tuberculosis. Biochim. Biophys. Acta Biomembr. 2005, 1715, 71–80. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Rosenberg, E.Y.; Nikaido, H. Fluidity of the lipid domain of cell wall from Mycobacterium chelonae. Proc. Natl. Acad. Sci. USA 1995, 92, 11254–11258. [Google Scholar] [CrossRef]
- Hong, X.; Hopfinger, A.J. Construction, molecular modeling, and simulation of Mycobacterium tuberculosis cell walls. Biomacromolecules 2004, 5, 1052–1065. [Google Scholar] [CrossRef] [PubMed]
- Hong, X.; Hopfinger, A.J. Molecular modeling and simulation of Mycobacterium tuberculosis cell wall permeability. Biomacromolecules 2004, 5, 1066–1077. [Google Scholar] [CrossRef]
- Rath, P.; Saurel, O.; Czaplicki, G.; Tropis, M.; Daffé, M.; Ghazi, A.; Demange, P.; Milon, A. Cord factor (trehalose 6,6′-dimycolate) forms fully stable and non-permeable lipid bilayers required for a functional outer membrane. Biochim. Biophys. Acta Biomembr. 2013, 1828, 2173–2181. [Google Scholar] [CrossRef]
- Menon, A.P.; Dong, W.; Lee, T.-H.; Aguilar, M.-I.; Duan, M.; Kapoor, S. Mutually exclusive interactions of rifabutin with spatially distinct mycobacterial cell envelope membrane layers offer insights into membrane-centric therapy of infectious diseases. ACS Bio. Med. Chem. Au 2022, 2, 395–408. [Google Scholar] [CrossRef]
- Savintseva, L.A.; Steshin, I.S.; Avdoshin, A.A.; Panteleev, S.V.; Rozhkov, A.V.; Shirokova, E.A.; Livshits, G.D.; Vasyankin, A.V.; Radchenko, E.V.; Ignatov, S.K.; et al. Conformational dynamics and stability of bilayers formed by mycolic acids from the Mycobacterium tuberculosis outer membrane. Molecules 2023, 28, 1347. [Google Scholar] [CrossRef]
- Kumar, G.; Kapoor, S. Targeting mycobacterial membranes and membrane proteins: Progress and limitations. Bioorg. Med. Chem. 2023, 81, 117212. [Google Scholar] [CrossRef]
- Mehta, K.; Sharma, P.; Mujawar, S.; Vyas, A. Role of antimicrobial peptides in treatment and prevention of Mycobacterium tuberculosis: A review. Int. J. Pept. Res. Ther. 2022, 28, 132. [Google Scholar] [CrossRef]
- Modak, B.; Girkar, S.; Narayan, R.; Kapoor, S. Mycobacterial membranes as actionable targets for lipid-centric therapy in tuberculosis. J. Med. Chem. 2022, 65, 3046–3065. [Google Scholar] [CrossRef]
- Jacobo-Delgado, Y.M.; Rodríguez-Carlos, A.; Serrano, C.J.; Rivas-Santiago, B. Mycobacterium tuberculosis cell-wall and antimicrobial peptides: A mission impossible? Front. Immunol. 2023, 14, 1194923. [Google Scholar] [CrossRef] [PubMed]
- Steshin, I.S.; Vasyankin, A.V.; Shirokova, E.A.; Rozhkov, A.V.; Livshits, G.D.; Panteleev, S.V.; Radchenko, E.V.; Ignatov, S.K.; Palyulin, V.A. Free energy barriers for passive drug transport through the Mycobacterium tuberculosis outer membrane: A molecular dynamics study. Int. J. Mol. Sci. 2024, 25, 1006. [Google Scholar] [CrossRef] [PubMed]
- Filippov, A.; Orädd, G.; Lindblom, G. Influence of cholesterol and water content on phospholipid lateral diffusion in bilayers. Langmuir 2003, 19, 6397–6400. [Google Scholar] [CrossRef]
- Filippov, A.; Orädd, G.; Lindblom, G. The effect of cholesterol on the lateral diffusion of phospholipids in oriented bilayers. Biophys. J. 2003, 84, 3079–3086. [Google Scholar] [CrossRef] [PubMed]
- Gaede, H.C.; Gawrisch, K. Lateral diffusion rates of lipid, water, and a hydrophobic drug in a multilamellar liposome. Biophys. J. 2003, 85, 1734–1740. [Google Scholar] [CrossRef] [PubMed]
- Scheidt, H.A.; Huster, D.; Gawrisch, K. Diffusion of cholesterol and its precursors in lipid membranes studied by 1H pulsed field gradient magic angle spinning NMR. Biophys. J. 2005, 89, 2504–2512. [Google Scholar] [CrossRef] [PubMed]
- Wu, H.-L.; Tsao, H.-K.; Sheng, Y.-J. Dynamic and mechanical properties of supported lipid bilayers. J. Chem. Phys. 2016, 144, 154904. [Google Scholar] [CrossRef]
- Koynova, R.; Tenchov, B. Phase transitions and phase behavior of lipids. In Encyclopedia of Biophysics; Roberts, G.C.K., Ed.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 1841–1854. ISBN 978-3-642-16711-9. [Google Scholar] [CrossRef]
- Minnikin, D.E. Chemical principles in the organization of lipid components in the mycobacterial cell envelope. Res. Microbiol. 1991, 142, 423–427. [Google Scholar] [CrossRef] [PubMed]
- Meniche, X.; Labarre, C.; De Sousa-d’Auria, C.; Huc, E.; Laval, F.; Tropis, M.; Bayan, N.; Portevin, D.; Guilhot, C.; Daffé, M.; et al. Identification of a stress-induced factor of Corynebacterineae that is involved in the regulation of the outer membrane lipid composition. J. Bacteriol. 2009, 191, 7323–7332. [Google Scholar] [CrossRef] [PubMed]
- Koga, Y. Thermal adaptation of the archaeal and bacterial lipid membranes. Archaea 2012, 2012, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Minnikin, D.E.; Minnikin, S.M.; Parlett, J.H.; Goodfellow, M.; Magnusson, M. Mycolic acid patterns of some species of Mycobacterium. Arch. Microbiol. 1984, 139, 225–231. [Google Scholar] [CrossRef] [PubMed]
- Zhuang, X.; Makover, J.R.; Im, W.; Klauda, J.B. A systematic molecular dynamics simulation study of temperature dependent bilayer structural properties. Biochim. Biophys. Acta Biomembr. 2014, 1838, 2520–2529. [Google Scholar] [CrossRef] [PubMed]
- Akhunzada, M.J.; Sagresti, L.; Catte, A.; Bhattacharjee, N.; D’Agostino, T.; Brancato, G. Temperature dependence of the structure and dynamics of a dye-labeled lipid in a planar phospholipid bilayer: A computational study. J. Membr. Biol. 2019, 252, 227–240. [Google Scholar] [CrossRef] [PubMed]
- Huang, J.; MacKerell, A.D. CHARMM36 all-atom additive protein force field: Validation based on comparison to NMR data. J. Comput. Chem. 2013, 34, 2135–2145. [Google Scholar] [CrossRef] [PubMed]
- Marrink, S.J.; Corradi, V.; Souza, P.C.T.; Ingólfsson, H.I.; Tieleman, D.P.; Sansom, M.S.P. Computational modeling of realistic cell membranes. Chem. Rev. 2019, 119, 6184–6226. [Google Scholar] [CrossRef]
- Lee, J.; Cheng, X.; Swails, J.M.; Yeom, M.S.; Eastman, P.K.; Lemkul, J.A.; Wei, S.; Buckner, J.; Jeong, J.C.; Qi, Y.; et al. CHARMM-GUI input generator for NAMD, GROMACS, AMBER, OpenMM, and CHARMM/OpenMM simulations using the CHARMM36 additive force field. J. Chem. Theory Comput. 2016, 12, 405–413. [Google Scholar] [CrossRef]
- Jo, S.; Cheng, X.; Lee, J.; Kim, S.; Park, S.-J.; Patel, D.S.; Beaven, A.H.; Lee, K.I.; Rui, H.; Park, S.; et al. CHARMM-GUI 10 years for biomolecular modeling and simulation. J. Comput. Chem. 2017, 38, 1114–1124. [Google Scholar] [CrossRef]
- Abraham, M.J.; Murtola, T.; Schulz, R.; Páll, S.; Smith, J.C.; Hess, B.; Lindahl, E. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 2015, 1–2, 19–25. [Google Scholar] [CrossRef]
- Smith, D.J.; Klauda, J.B.; Sodt, A.J. Simulation best practices for lipid membranes. LiveCoMS 2019, 1, 5966. [Google Scholar] [CrossRef]
- Vögele, M.; Hummer, G. Divergent diffusion coefficients in simulations of fluids and lipid membranes. J. Phys. Chem. B 2016, 120, 8722–8732. [Google Scholar] [CrossRef]
- Pettersen, E.F.; Goddard, T.D.; Huang, C.C.; Couch, G.S.; Greenblatt, D.M.; Meng, E.C.; Ferrin, T.E. UCSF Chimera—A visualization system for exploratory research and analysis. J. Comput. Chem. 2004, 25, 1605–1612. [Google Scholar] [CrossRef]
- Qian, H.; Sheetz, M.P.; Elson, E.L. Single particle tracking. Analysis of diffusion and flow in two-dimensional systems. Biophys. J. 1991, 60, 910–921. [Google Scholar] [CrossRef]
- Wieser, S.; Schütz, G.J. Tracking single molecules in the live cell plasma membrane—Do’s and Don’t’s. Methods 2008, 46, 131–140. [Google Scholar] [CrossRef] [PubMed]
- Michalet, X. Mean square displacement analysis of single-particle trajectories with localization error: Brownian motion in an isotropic medium. Phys. Rev. E 2010, 82, 041914. [Google Scholar] [CrossRef] [PubMed]
- Von Bülow, S.; Bullerjahn, J.T.; Hummer, G. Systematic errors in diffusion coefficients from long-time molecular dynamics simulations at constant pressure. J. Chem. Phys. 2020, 153, 021101. [Google Scholar] [CrossRef] [PubMed]
- Bullerjahn, J.T.; Von Bülow, S.; Hummer, G. Optimal estimates of self-diffusion coefficients from molecular dynamics simulations. J. Chem. Phys. 2020, 153, 024116. [Google Scholar] [CrossRef] [PubMed]
- Bullerjahn, J.T.; Von Bülow, S.; Heidari, M.; Hénin, J.; Hummer, G. Unwrapping NPT simulations to calculate diffusion coefficients. J. Chem. Theory Comput. 2023, 19, 3406–3417. [Google Scholar] [CrossRef] [PubMed]
- Pranami, G.; Lamm, M.H. Estimating error in diffusion coefficients derived from molecular dynamics simulations. J. Chem. Theory Comput. 2015, 11, 4586–4592. [Google Scholar] [CrossRef] [PubMed]
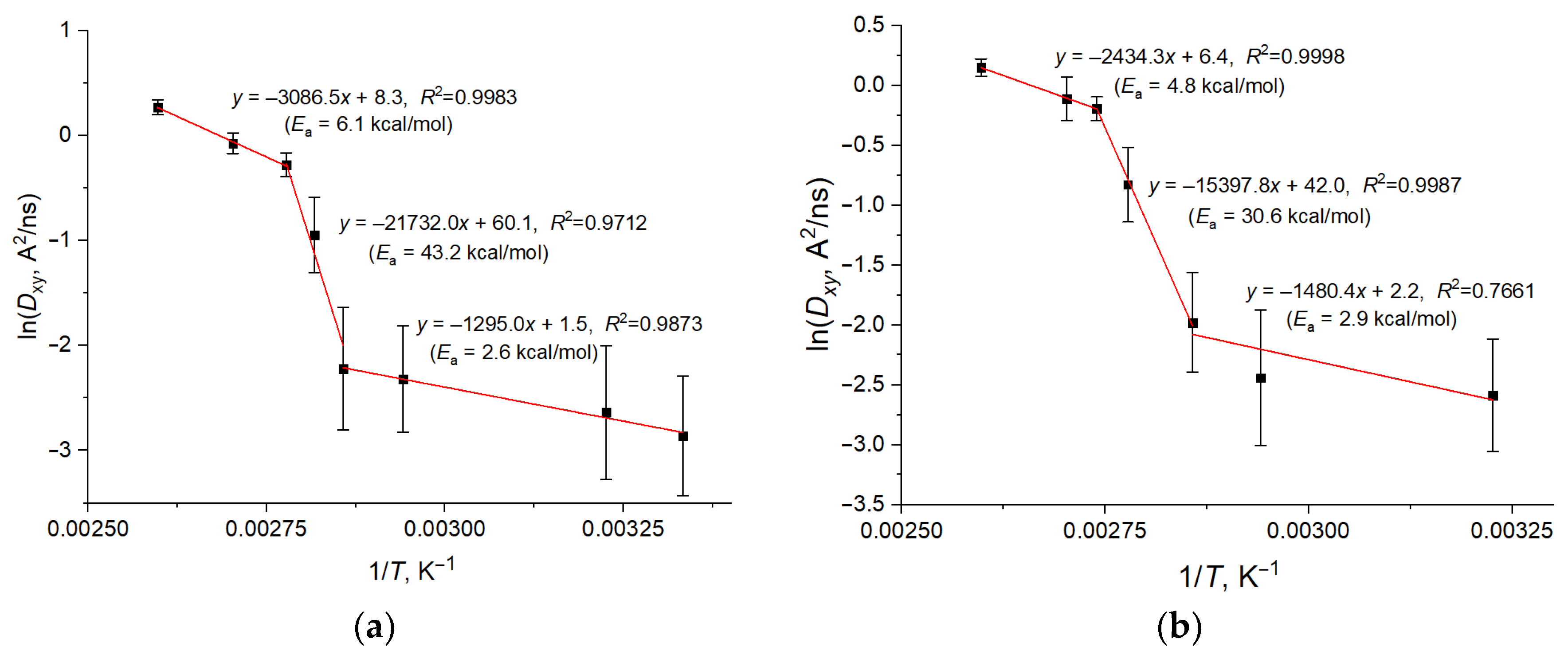
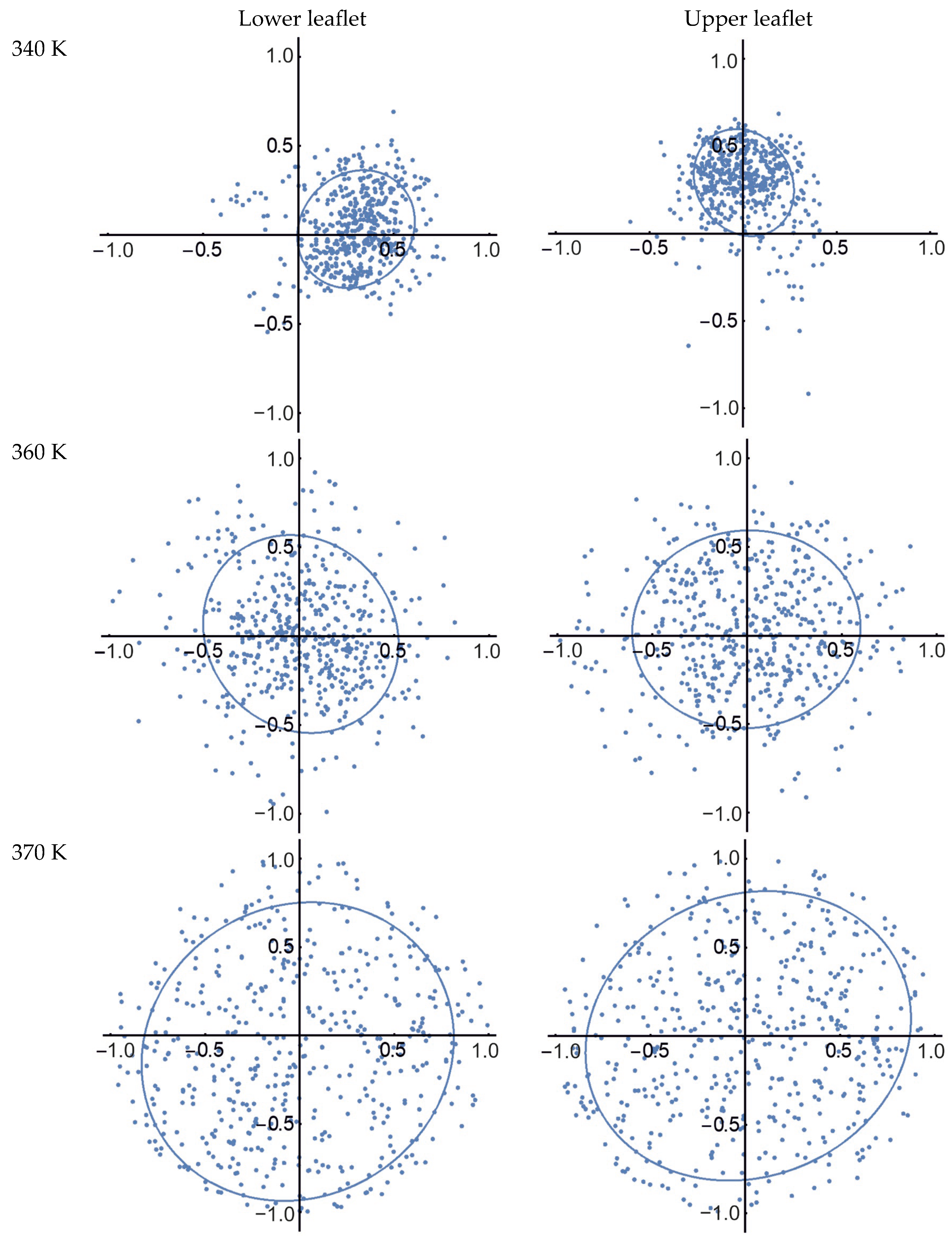


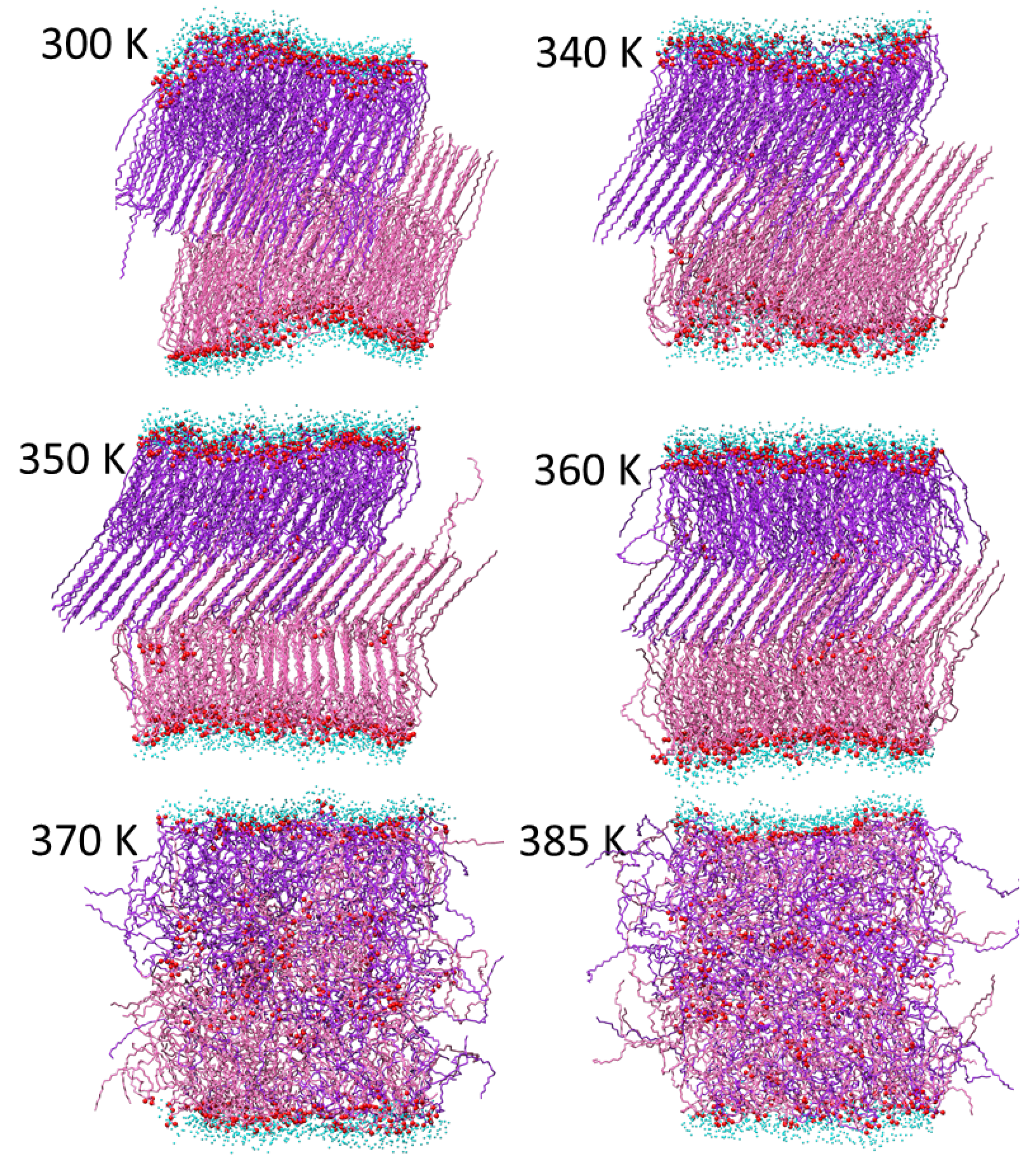

| T, K | Dx, Å2/ns | Dxy, Å2/ns | D, Å2/ns |
|---|---|---|---|
| AMA in AMA_W | |||
| 300 | 0.001 ± 0.001 | 0.001 ± 0.001 | 0.003 ± 0.011 |
| 310 | 0.002 ± 0.002 | 0.002 ± 0.002 | 0.003 ± 0.003 |
| 340 | 0.004 ± 0.003 | 0.005 ± 0.002 | 0.006 ± 0.004 |
| 350 | 0.007 ± 0.003 | 0.006 ± 0.004 | 0.008 ± 0.006 |
| 355 | 0.131 ± 0.061 | 0.112 ± 0.040 | 0.086 ± 0.034 |
| 360 | 0.470 ± 0.083 | 0.524 ± 0.058 | 0.359 ± 0.044 |
| 370 | 0.802 ± 0.180 | 0.840 ± 0.082 | 0.601 ± 0.055 |
| 385 | 1.731 ± 0.375 | 1.856 ± 0.132 | 1.299 ± 0.087 |
| AMA in AMA_eU | |||
| 310 | 0.005 ± 0.002 | 0.004 ± 0.002 | 0.005 ± 0.003 |
| 340 | 0.001 ± 0.001 | 0.001 ± 0.001 | 0.001 ± 0.001 |
| 350 | 0.004 ± 0.003 | 0.004 ± 0.002 | 0.003 ± 0.002 |
| 360 | 0.019 ± 0.012 | 0.018 ± 0.010 | 0.013 ± 0.007 |
| 370 | 1.329 ± 0.163 | 1.312 ± 0.151 | 0.998 ± 0.129 |
| 385 | 1.822 ± 0.235 | 1.761 ± 0.204 | 1.366 ± 0.166 |
| AMA in Mix50_eU | |||
| 310 | 0.002 ± 0.002 | 0.003 ± 0.001 | 0.003 ± 0.002 |
| 340 | 0.003 ± 0.002 | 0.004 ± 0.002 | 0.003 ± 0.002 |
| 350 | 0.010 ± 0.005 | 0.010 ± 0.004 | 0.008 ± 0.004 |
| 360 | 0.129 ± 0.042 | 0.148 ± 0.046 | 0.106 ± 0.036 |
| 365 | 0.598 ± 0.051 | 0.638 ± 0.063 | 0.478 ± 0.047 |
| 370 | 0.738 ± 0.179 | 0.770 ± 0.140 | 0.589 ± 0.113 |
| 385 | 1.442 ± 0.120 | 1.408 ± 0.102 | 1.065 ± 0.100 |
| (AMA + AMA−) in Mix50_eU_ion | |||
| 310 | 0.001 ± 0.002 | 0.003 ± 0.001 | 0.003 ± 0.003 |
| 340 | 0.002 ± 0.001 | 0.002 ± 0.001 | 0.002 ± 0.001 |
| 350 | 0.010 ± 0.009 | 0.010 ± 0.009 | 0.007 ± 0.008 |
| 360 | 0.060 ± 0.027 | 0.054 ± 0.036 | 0.042 ± 0.029 |
| 370 | 0.635 ± 0.095 | 0.789 ± 0.108 | 0.575 ± 0.064 |
| 385 | 1.406 ± 0.261 | 1.526 ± 0.040 | 1.107 ± 0.050 |
| T, K | Dx, Å2/ns | Dxy, Å2/ns | D, Å2/ns |
|---|---|---|---|
| KMA in Mix50_eU | |||
| 310 | 0.002 ± 0.002 | 0.003 ± 0.001 | 0.003 ± 0.002 |
| 340 | 0.002 ± 0.002 | 0.002 ± 0.001 | 0.002 ± 0.001 |
| 350 | 0.011 ± 0.006 | 0.012 ± 0.003 | 0.009 ± 0.003 |
| 360 | 0.071 ± 0.038 | 0.084 ± 0.050 | 0.074 ± 0.032 |
| 365 | 0.323 ± 0.149 | 0.402 ± 0.161 | 0.314 ± 0.115 |
| 370 | 0.755 ± 0.246 | 0.694 ± 0.113 | 0.503 ± 0.076 |
| 385 | 1.358 ± 0.325 | 1.641 ± 0.087 | 1.195 ± 0.083 |
| MMA in Mix50_eU | |||
| 310 | 0.003 ± 0.003 | 0.003 ± 0.001 | 0.003 ± 0.002 |
| 340 | 0.002 ± 0.003 | 0.003 ± 0.002 | 0.002 ± 0.002 |
| 350 | 0.005 ± 0.005 | 0.007 ± 0.003 | 0.006 ± 0.003 |
| 360 | 0.195 ± 0.036 | 0.192 ± 0.037 | 0.146 ± 0.033 |
| 365 | 0.476 ± 0.130 | 0.539 ± 0.118 | 0.385 ± 0.109 |
| 370 | 1.075 ± 0.085 | 0.837 ± 0.027 | 0.623 ± 0.035 |
| 385 | 1.897 ± 0.224 | 1.694 ± 0.344 | 1.274 ± 0.288 |
| Membrane | AMA_W | AMA_eU | Mix50_eU | Mix50_eU_ion |
|---|---|---|---|---|
| Number of MA molecules in a box AMA:KMA:MMA | 200:0:0 | 200:0:0 | 100:50:50 | 100:50:50 |
| Initial conformations of AMA:KMA:MMA | W:–:– | eU:–:– | eU:W:W | eU:W:W |
| Number of ionized molecules AMA+KMA+MMA | 0 | 0 | 0 | 20 |
| Time of equilibration, ns | 1200 | 300 | 300 | 100 a |
| Thickness after equilibration, nm | 4.4 | 7.8 | 5.0 | 5.1 |
| Density after equilibration, kg/m3 | 863 | 907 | 877 | 873 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vasyankin, A.V.; Panteleev, S.V.; Steshin, I.S.; Shirokova, E.A.; Rozhkov, A.V.; Livshits, G.D.; Radchenko, E.V.; Ignatov, S.K.; Palyulin, V.A. Temperature-Induced Restructuring of Mycolic Acid Bilayers Modeling the Mycobacterium tuberculosis Outer Membrane: A Molecular Dynamics Study. Molecules 2024, 29, 696. https://doi.org/10.3390/molecules29030696
Vasyankin AV, Panteleev SV, Steshin IS, Shirokova EA, Rozhkov AV, Livshits GD, Radchenko EV, Ignatov SK, Palyulin VA. Temperature-Induced Restructuring of Mycolic Acid Bilayers Modeling the Mycobacterium tuberculosis Outer Membrane: A Molecular Dynamics Study. Molecules. 2024; 29(3):696. https://doi.org/10.3390/molecules29030696
Chicago/Turabian StyleVasyankin, Alexander V., Sergey V. Panteleev, Ilya S. Steshin, Ekaterina A. Shirokova, Alexey V. Rozhkov, Grigory D. Livshits, Eugene V. Radchenko, Stanislav K. Ignatov, and Vladimir A. Palyulin. 2024. "Temperature-Induced Restructuring of Mycolic Acid Bilayers Modeling the Mycobacterium tuberculosis Outer Membrane: A Molecular Dynamics Study" Molecules 29, no. 3: 696. https://doi.org/10.3390/molecules29030696
APA StyleVasyankin, A. V., Panteleev, S. V., Steshin, I. S., Shirokova, E. A., Rozhkov, A. V., Livshits, G. D., Radchenko, E. V., Ignatov, S. K., & Palyulin, V. A. (2024). Temperature-Induced Restructuring of Mycolic Acid Bilayers Modeling the Mycobacterium tuberculosis Outer Membrane: A Molecular Dynamics Study. Molecules, 29(3), 696. https://doi.org/10.3390/molecules29030696






