Approximated Uncertainty Propagation of Correlated Independent Variables Using the Ordinary Least Squares Estimator
Abstract
:1. Introduction
2. Theory
2.1. Least Squares Methods
2.2. Variance–Covariance Matrix of the Regression Coefficient
2.3. Propagation of Variance–Covariance of the Regression Coefficients
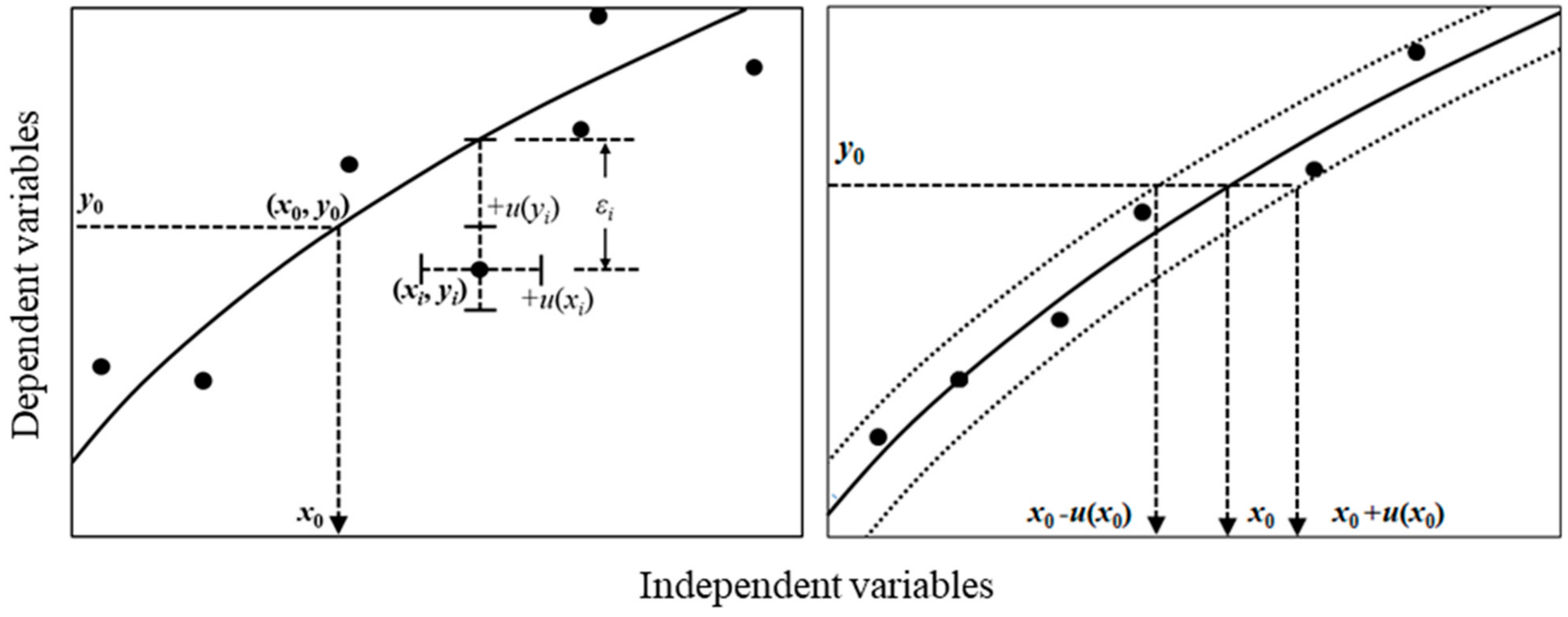
2.4. Propagation of the Measurement Uncertainty of the Calibration Target
2.5. Propagation of Uncertainty of the Independent Variable
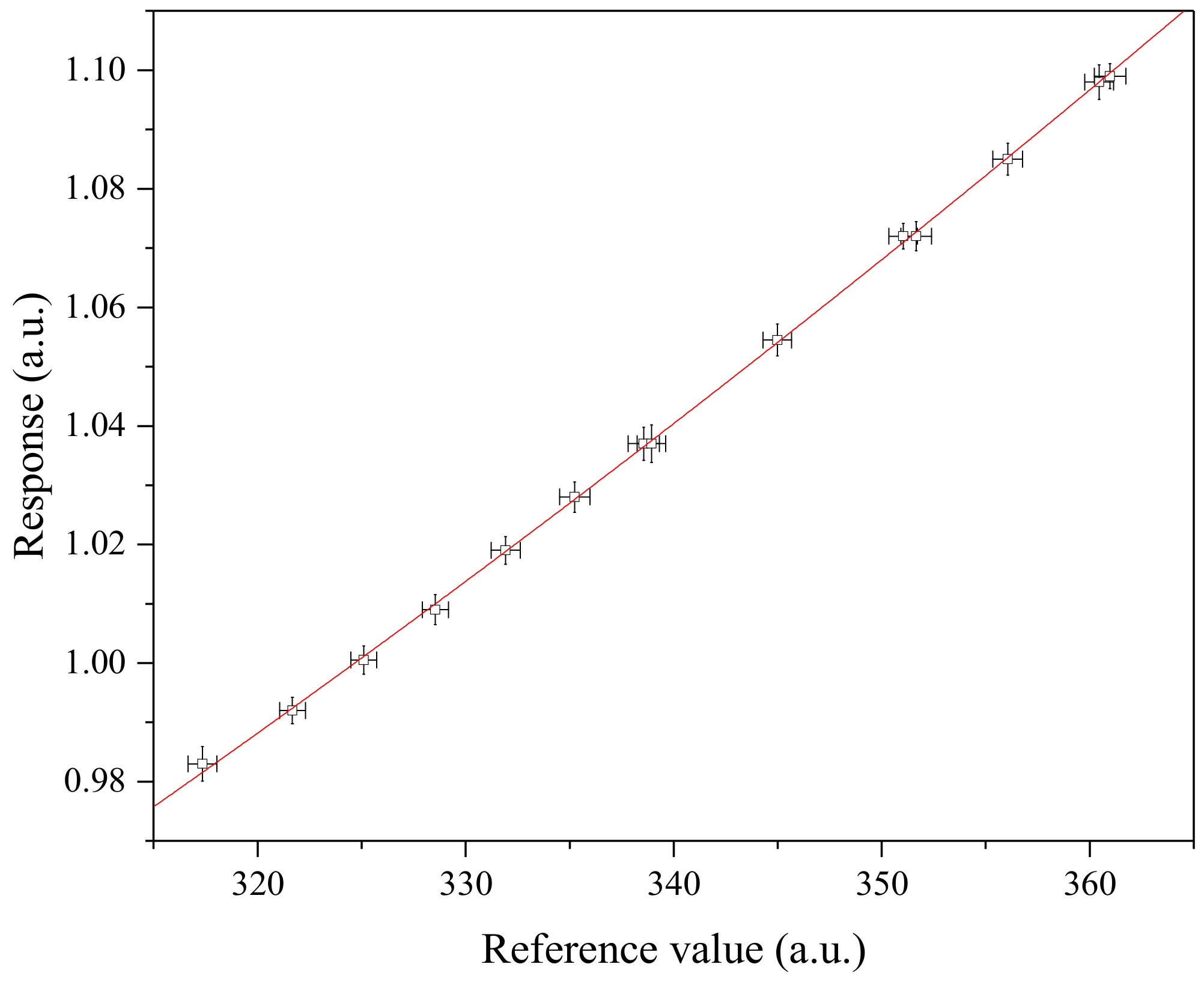
| Reference (xi) | u (xi) | Response | u(yi) | ||
|---|---|---|---|---|---|
| Set A | Set B | Set C | |||
| 317.35 | 0.231 | 0.983 | 0.00098 | 0.00098 | |
| 321.68 | 0.206 | 0.992 | 0.00074 | 0.00074 | 0.00041 |
| 325.11 | 0.208 | 1.001 | 0.00080 | ||
| 328.54 | 0.209 | 1.009 | 0.00085 | 0.00085 | |
| 331.92 | 0.233 | 1.019 | 0.00077 | 0.00077 | 0.00042 |
| 335.24 | 0.243 | 1.028 | 0.00085 | ||
| 338.56 | 0.252 | 1.037 | 0.00093 | 0.00093 | |
| 338.93 | 0.231 | 1.037 | 0.00106 | 0.00106 | 0.00058 |
| 344.98 | 0.230 | 1.055 | 0.00089 | ||
| 351.03 | 0.229 | 1.072 | 0.00072 | 0.00072 | |
| 351.66 | 0.246 | 1.072 | 0.00082 | 0.00082 | 0.00045 |
| 356.06 | 0.239 | 1.085 | 0.00090 | ||
| 360.45 | 0.232 | 1.098 | 0.00098 | 0.00098 | |
| 360.97 | 0.253 | 1.099 | 0.00069 | 0.00069 | 0.00038 |
| 364.85 | 0.241 | 1.111 | 0.00085 | ||
| Target | (p = 1) | 1.003 | n = 15 | n = 10 | n = 5 |
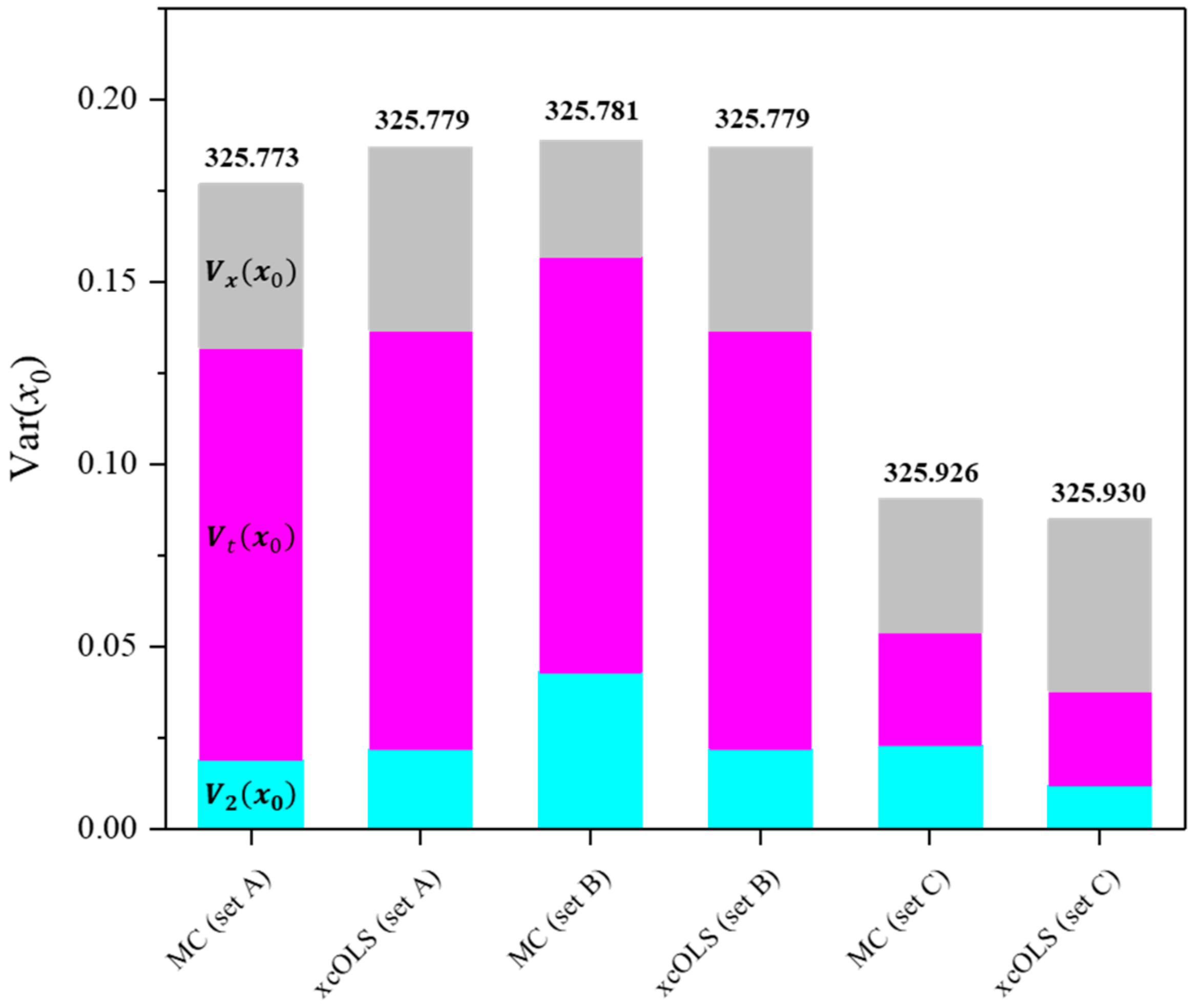
3. Discussions
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tellinghuisen, J. Least squares methods for treating problems with uncertainty in x and y. Anal. Chem. 2020, 92, 10863–10871. [Google Scholar] [CrossRef] [PubMed]
- Tellinghuisen, J. Calibration: Detection, quantification, and confidence limits are (almost) exact when the data variance function is known. Anal. Chem. 2019, 91, 8715–8722. [Google Scholar] [CrossRef] [PubMed]
- Riu, J.; Ruis, F.X. Assessing the accuracy of analytical methods using linear regression with errors in both axes. Anal. Chem. 1996, 68, 1851–1857. [Google Scholar] [CrossRef]
- Tellinghuisen, J. A simple, All-purpose nonlinear algorithm for univariate calibration. Analyst 2000, 125, 1045–1048. [Google Scholar] [CrossRef]
- Tellinghuisen, J. Weighted least-squares in calibration: What difference does it make? Analyst 2007, 132, 536–543. [Google Scholar] [CrossRef] [PubMed]
- Tellinghuisen, J. Least squares in calibration: Dealing with uncertainty in x. Analyst 2010, 135, 1961–1969. [Google Scholar] [CrossRef]
- Tellinghuisen, J. Least-squares analysis of data with uncertainty in x and y: A Monte Carlo methods comparison. Chem. Int. Lab. Syst. 2010, 103, 160–169. [Google Scholar] [CrossRef]
- Francios, N.; Govaerts, B.; Boulanger, B. Optimal designs for inverse prediction in univariate nonlinear calibration models. Chem. Int. Lab. Syst. 2004, 74, 283–292. [Google Scholar] [CrossRef]
- Tellinghuisen, J. Simple algorithms for nonlinear calibration by the classical and standard additions methods. Analyst. 2005, 130, 370–378. [Google Scholar] [CrossRef]
- Mulholland, M.; Hibbert, D.B. Linearity and the limitations of least squares calibration. J. Chrom. A. 1997, 762, 73–82. [Google Scholar] [CrossRef]
- Rehman, Z.; Zhang, S. Three-dimensional elasto-plastic damage model for gravelly soil-structure interface considering the shear coupling effect. Comput. Geotech. 2021, 129, 103868. [Google Scholar] [CrossRef]
- Rehman, Z.; Khalid, U.; Ijaz, N.; Mujtaba, H.; Haider, A.; Farooq, K.; Ijaz, Z. Machine learning-based intelligent modeling of hydraulic conductivity of sandy soils considering a wide range of grain sizes. Eng. Geol. 2022, 311, 106899. [Google Scholar] [CrossRef]
- Ni, Y.; Wang, H.; Hu, S. Linear Fitting of Time-Varying Signals in Static Noble Gas Mass Spectrometry Should Be Avoided. Anal. Chem. 2023, 95, 3917–3921. [Google Scholar] [CrossRef] [PubMed]
- Bremser, W.; Viallon, J.; Wielgosz, R.I. Influence of correlation on the assessment of measurement result compatibility over a dynamic range. Metrologia 2007, 44, 495–504. [Google Scholar] [CrossRef]
- Cox, M.G.; Jones, H.M. An algorithm for least-squares circle fitting to data with specified uncertainty ellipses. IMA J. Numer. Anal. 1981, 1, 3–22. [Google Scholar] [CrossRef]
- Tellinghuisen, J. Goodness-of-Fit Tests in Calibration: Are They Any Good for Selecting Least-Squares weighting formula. Anal. Chem. 2022, 94, 15997–16005. [Google Scholar] [CrossRef]
- Milton, M.J.T.; Harris, P.M.; Smith, I.M.; Brown, A.S.; Goody, B.A. Implementation of a generalized least-squares method for determining calibration curves from data with general uncertainty structures. Metrologia 2006, 43, S291–S298. [Google Scholar] [CrossRef]
- Markovsky, I.; Van Huffel, S. Overview of total least-squares methods. Signal Process 2007, 87, 2283–2302. [Google Scholar] [CrossRef]
- Malengo, A.; Pennecchi, F. A weighted total least-squares algorithm for any fitting model with correlated variables. Metrologia 2013, 50, 654–662. [Google Scholar] [CrossRef]
- Krystek, M.; Anton, M. A weighted total least-squares algorithm for fitting a straight line. Meas. Sci. Technol. 2007, 18, 3438–3442. [Google Scholar] [CrossRef]
- Amiri-Simkooei, A.R.; Zangeneh-Nejad, F.; Asgari, J. On the covariance matrix of weighted total least-squares estimates. J. Surv. Eng. 2016, 142, 04015014. [Google Scholar] [CrossRef]
- Krystek, M.; Anton, M. A least-squares algorithm for fitting data points with mutually correlated coordinates to a straight line. Meas. Sci. Technol. 2011, 22, 035101. [Google Scholar] [CrossRef]
- Bremser, W.; Hasselbarth, W. Controlling uncertainty in calibration. Anal. Chim. Acta 1997, 348, 61–69. [Google Scholar] [CrossRef]
- Forbes, A.B. Generalised regression problems in metrology. Numer. Algorithms 1993, 5, 523–534. [Google Scholar] [CrossRef]
- ISO 6143:2001(E); Gas Analysis—Comparison Methods for Determining and Checking the Composition of Calibration Gas Mixtures, 2nd ed. ISO: Geneva, Switzerland, 2001.
- ISO/TS 28037:2010(E); Determination and Use of Straight Line Calibration Functions, 1st ed. ISO: Geneva, Switzerland, 2010.
- DIN 1319-4 1985; Basic Concepts of Measurements; Treatment of Uncertainties in the Evaluation of Measurements. DIN: Berlin, Germany, 1985.
- Malengo, A.; Pennecchi, F.; Spazzini, P.G. Calibration Curve Computing (CCC) software v2.0: A new release of the INRIM regression tool. Meas. Sci. Technol. 2015, 31, 114004. [Google Scholar] [CrossRef]
- Smith, I.M.; Onakunle, F.O. XLGENLINE, Software for Generalized Least Squares Fitting. 2007. Available online: https://www.npl.co.uk/resources/software/xlgenline-and-xgenline (accessed on 27 February 2024).
- XGENLINE. Software for Generalized Least Squares Fitting. Available online: https://www.npl.co.uk/resources/software/xgenline (accessed on 27 February 2024).
- Software to Support ISO/TS 28037:2010(E). Available online: https://www.npl.co.uk/resources/software/iso-ts-28037-2010e (accessed on 27 February 2024).
- Bremser, W. Calibration Tool B LEAST Software Supporting Implementation of ISO Standard 6143. 2001. Available online: https://www.iso.org/obp/ui/es/#iso:std:iso:6143:dis:ed-3:v1:en:sec:C (accessed on 27 February 2024).
- Klauenberg, K.; Martens, S.; Bošnjaković, A.; Cox, M.G.; van der Veen, A.M.H.; Elster, C. The GUM perspective on straight-line errors-in-variables regression. Measurement 2022, 187, 110340. [Google Scholar] [CrossRef]
- Khalid, U.; Rehman, Z.; Liao, C.; Farooq, K.; Mujtaba, H. Compressibility of Compacted Clays Mixed with a Wide Range of Bentonite for Engineered Barriers. Arab. J. Sci. Eng. 2019, 44, 5027–5042. [Google Scholar] [CrossRef]
- Johnson, R.A.; Wichern, D.W. Applied Multivariate Statistical Analysis, 6th ed.; Pearson: London, UK, 2002; Chapter 7; pp. 360–538. [Google Scholar]
- Hill, C.; Griffiths, W.E.; Lim, G.C. Principles of Econometrics, 4th ed.; John Wiley & Sons: Hoboken, NJ, USA, 1971; pp. 119–124. [Google Scholar]
- Rao, C.R.; Toutenburg, H.; Shalabh; Heumann, C. Linear Models and Generalizations, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 36–38. [Google Scholar]
- Walpole, R.E.; Myers, R.H.; Myers, S.L.; Ye, K.E. Probability and Statistics for Engineers and Scientists, 9th ed.; Pearson: London, UK, 2014; 501p. [Google Scholar]
- DIN 1319-4:1999-02; Fundamentals of Metrology: Part 4. Evaluation of Measurements; Uncertainty of Measurement. DIN: Berlin, Germany, 1999.
- ISO/IEC Guide 98-3:2008/Suppl.1:2008; Propagation of Distributions Using a Monte Carlo Method. ISO: Geneva, Switzerland, 2008.

| Dataset | Method | Regression Coefficients (Uncertainty) | ||
|---|---|---|---|---|
| β0 | β1 | β2 | ||
| A | MC | 0.7643 (0.1441) | −0.001084 (0.000844) | 0.0000056 (0.0000012) |
| xcOLS | 0.7642 (0.1445) | −0.001084 (0.000846) | 0.0000056 (0.0000012) | |
| B | MC | 0.8084 (0.2368) | −0.001338 (0.001394) | 0.0000059 (0.0000020) |
| xcOLS | 0.8080 (0.1724) | −0.001336 (0.001015) | 0.0000059 (0.0000015) | |
| C | MC | 0.6767 (0.1866) | −0.000565 (0.001089) | 0.0000048 (0.0000016) |
| xcOLS | 0.6785 (0.1355) | −0.000576 (0.000794) | 0.0000048 (0.0000012) | |
| Polynomial Order | |
|---|---|
| m > l | |
| m = 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lim, J.S.; Kim, Y.D.; Woo, J.-C. Approximated Uncertainty Propagation of Correlated Independent Variables Using the Ordinary Least Squares Estimator. Molecules 2024, 29, 1248. https://doi.org/10.3390/molecules29061248
Lim JS, Kim YD, Woo J-C. Approximated Uncertainty Propagation of Correlated Independent Variables Using the Ordinary Least Squares Estimator. Molecules. 2024; 29(6):1248. https://doi.org/10.3390/molecules29061248
Chicago/Turabian StyleLim, Jeong Sik, Yong Doo Kim, and Jin-Chun Woo. 2024. "Approximated Uncertainty Propagation of Correlated Independent Variables Using the Ordinary Least Squares Estimator" Molecules 29, no. 6: 1248. https://doi.org/10.3390/molecules29061248







