State-to-State Quantum Dynamics Study of Intramolecular Isotope Effects on Be(1S) + HD (v0 = 2, j0 = 0) → BeH/BeD + H/D Reaction
Abstract
:1. Introduction
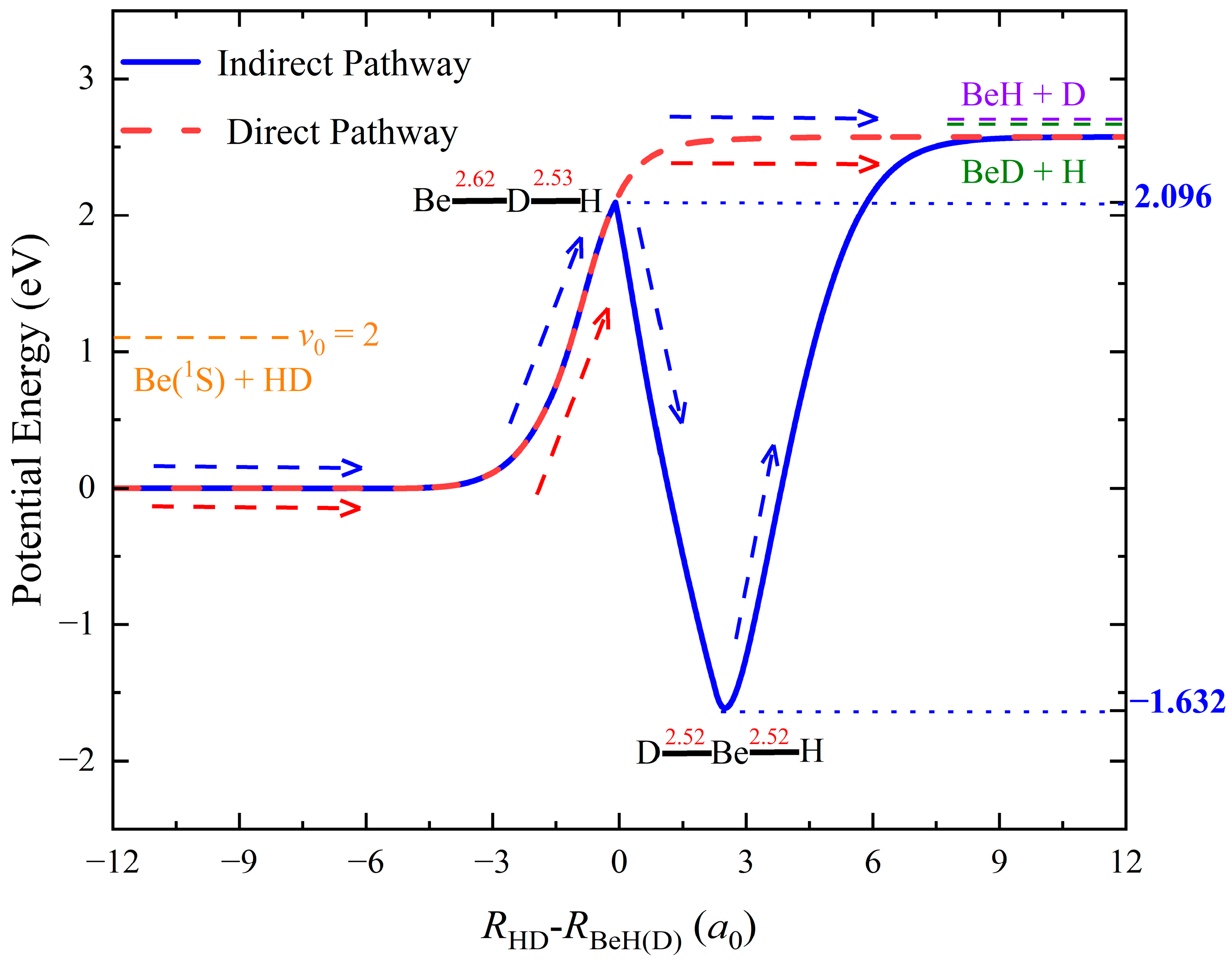
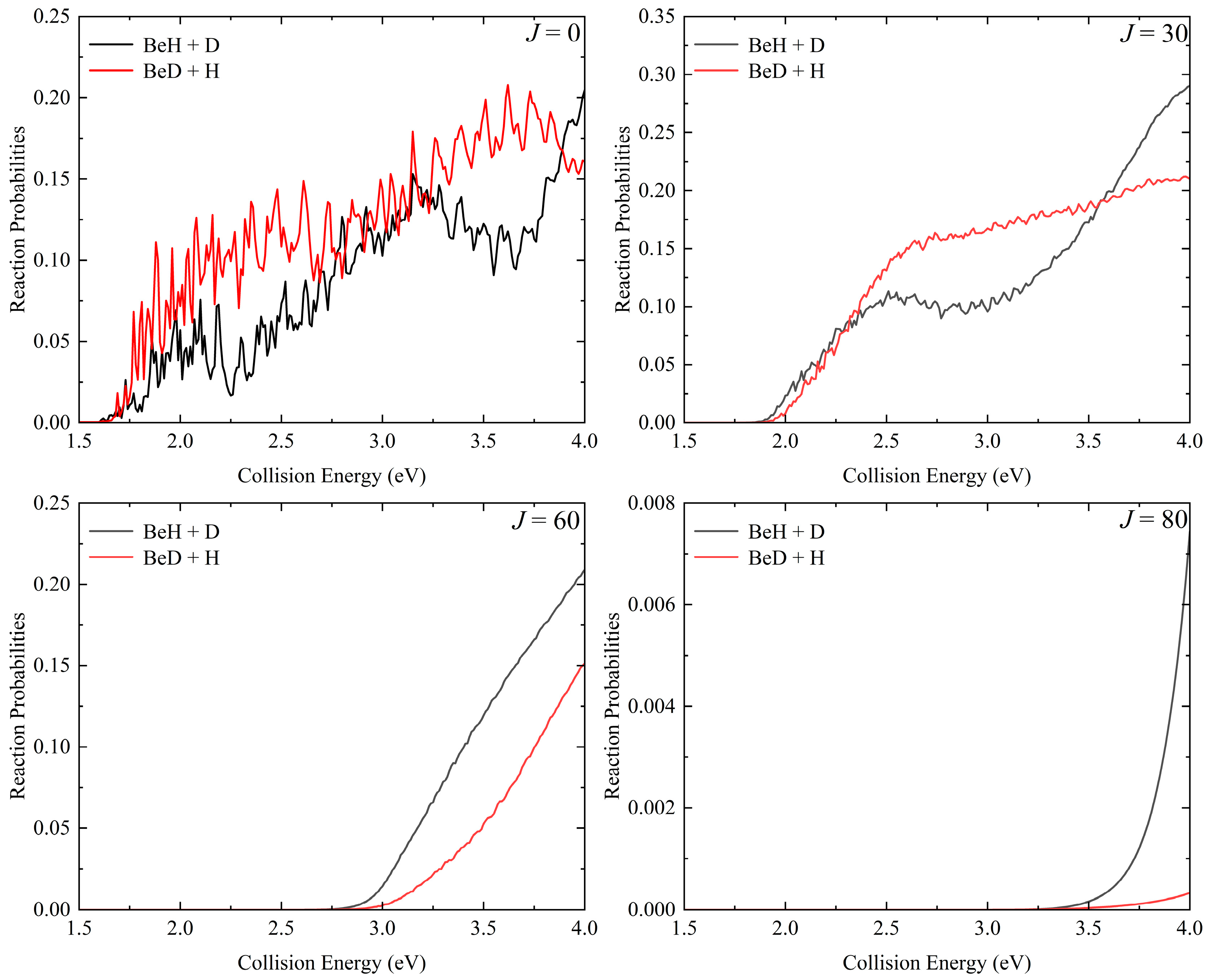
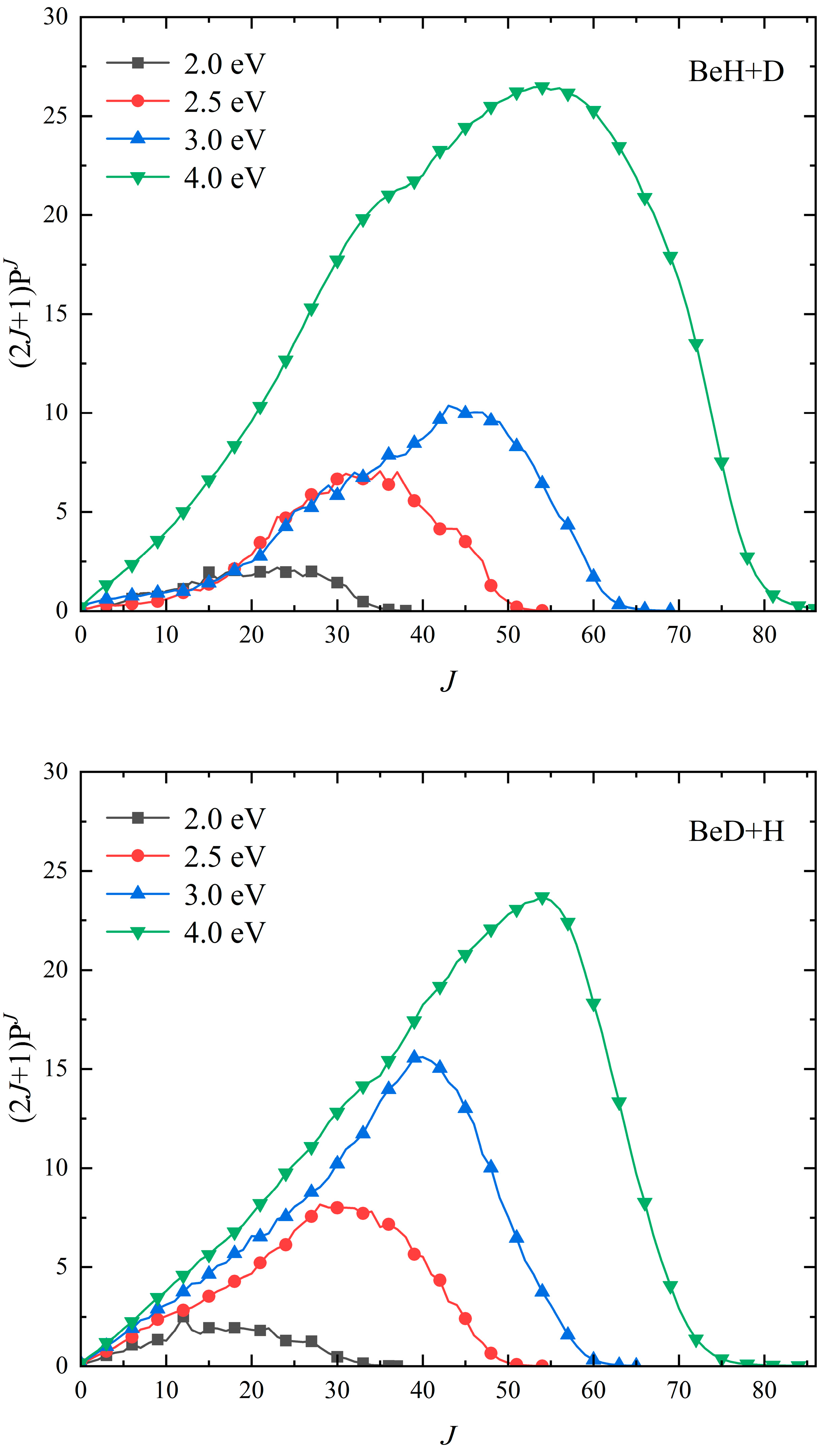
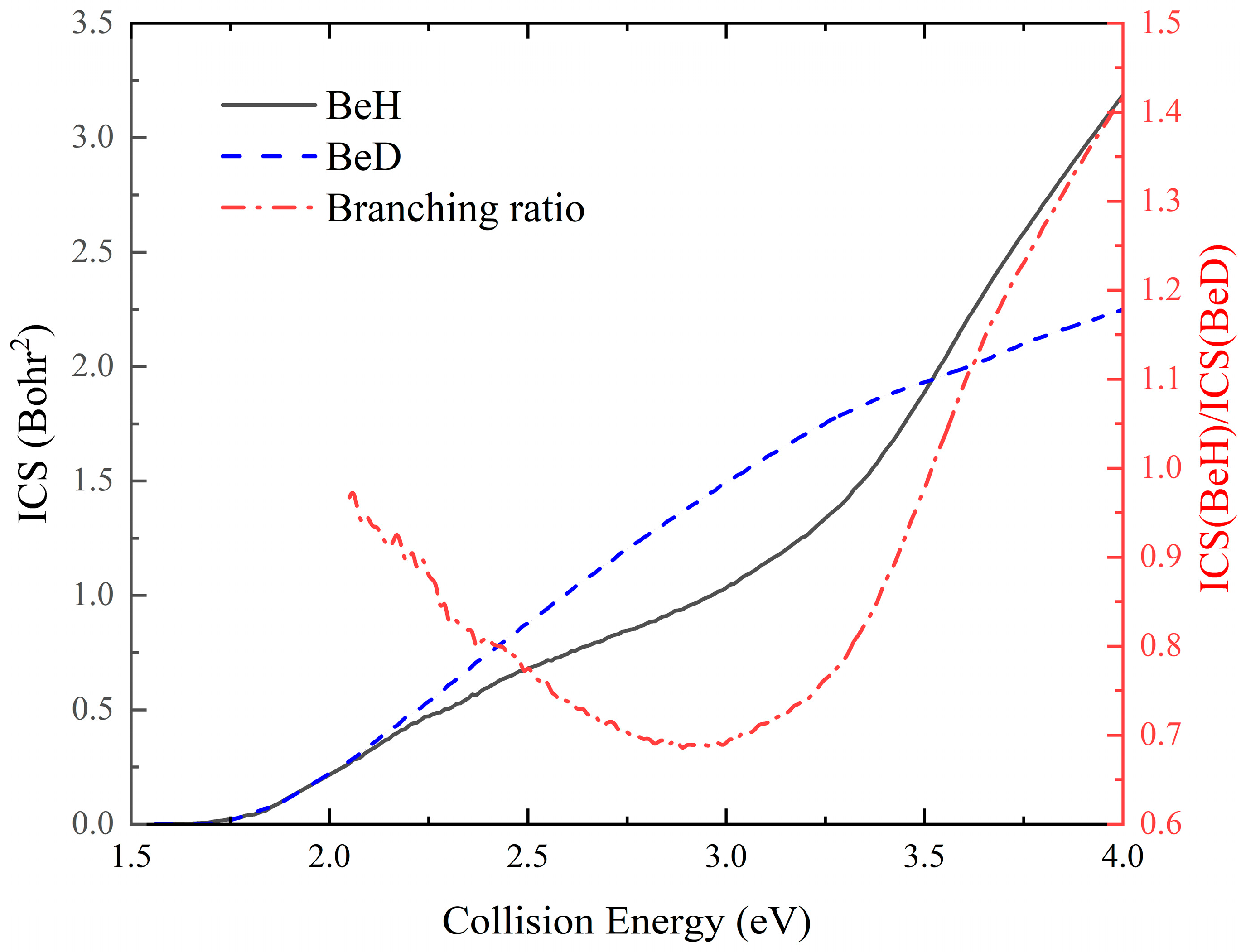
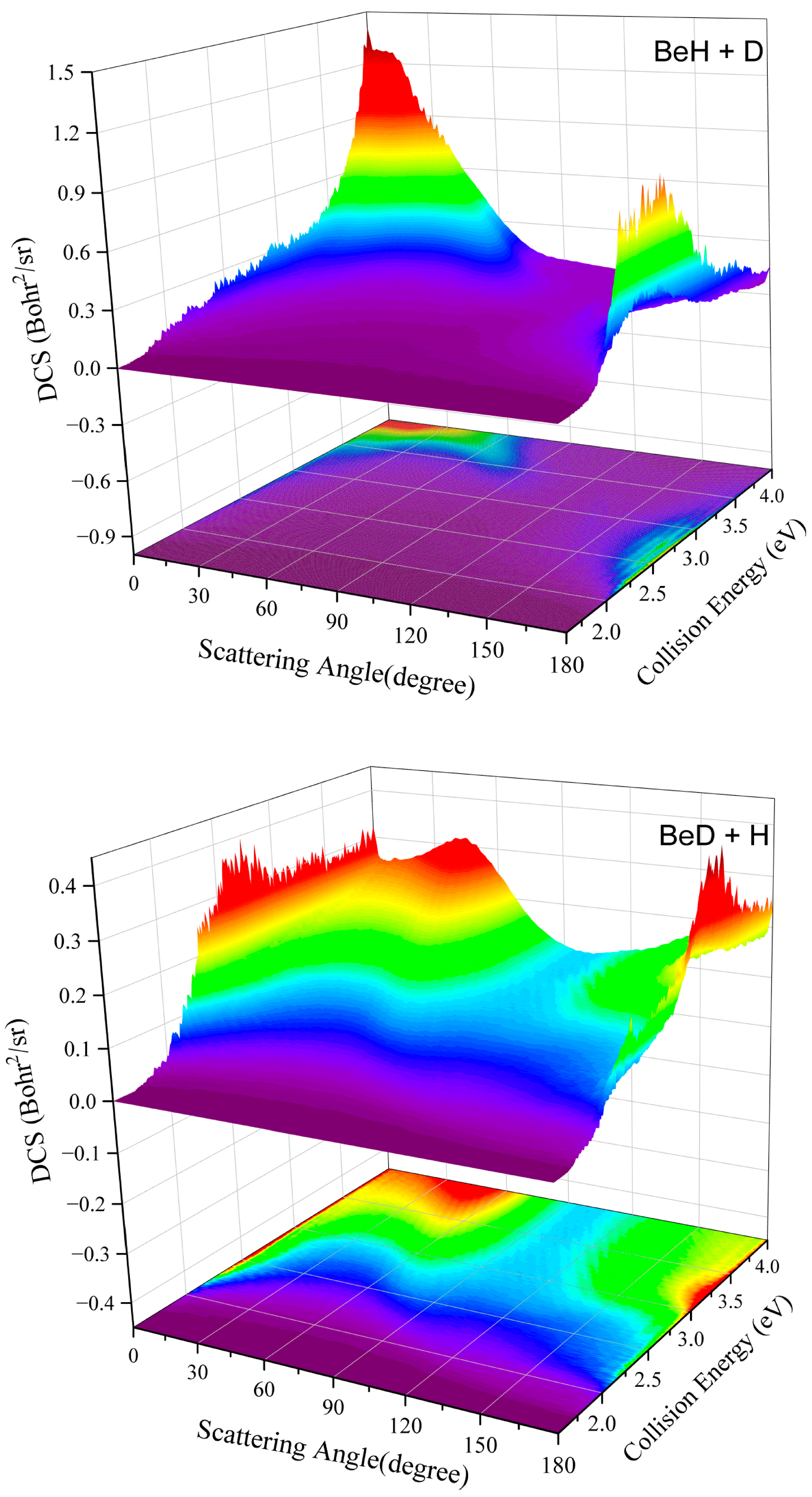
2. Results and Discussion
3. Methods
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zare, R.N. Laser control of chemical reactions. Science 1998, 279, 1875–1879. [Google Scholar] [CrossRef] [PubMed]
- Song, H.W.; Lee, S.Y.; Lu, Y.P.; Guo, H. Full-Dimensional Quantum Dynamical Studies of the Cl + HOD → HCl/DCl + OD/OH Reaction: Bond Selectivity and Isotopic Branching Ratio. J. Phys. Chem. A 2015, 119, 12224–12230. [Google Scholar] [CrossRef] [PubMed]
- Xin, R.; Pan, M.Y.; Song, H.W.; Yang, M.H. Mode- and Bond-Selected Reaction of H with Local Mode Molecule HDS. J. Phys. Chem. A 2020, 124, 10162–10170. [Google Scholar] [CrossRef] [PubMed]
- Crim, F.F. State-Selected and Bond-Selected Unimolecular Reactions. Science 1990, 249, 1387–1392. [Google Scholar] [CrossRef] [PubMed]
- Li, J.Q.; Tu, Z.; Xiang, H.P.; Li, Y.; Song, H.W. Theoretical studies on the kinetics and dynamics of the BeH+ + H2O reaction: Comparison with the experiment. Phys. Chem. Chem. Phys. 2023, 25, 20997–21005. [Google Scholar] [CrossRef] [PubMed]
- Yang, T.G.; Zhao, B.; Chen, G.K.; Guo, H.; Campbell, W.C.; Hudson, E.R. Determining reaction pathways at low temperatures by isotopic substitution: The case of BeD+ + H2O. New J. Phys. 2021, 23, 115004. [Google Scholar] [CrossRef]
- Nuñez-Reyes, D.; Hickson, K.M.; Larrégaray, P.; Bonnet, L.; González-Lezana, T.; Bhowmick, S.; Suleimanov, Y.V. Experimental and Theoretical Study of the O(1D) + HD Reaction. J. Phys. Chem. A 2019, 123, 8089–8098. [Google Scholar] [CrossRef] [PubMed]
- Tsukiyama, K.; Katz, B.; Bersohn, R. Isotopic branching ratio for the reaction A+HD→AD(H)+H(D). J. Chem. Phys. 1985, 83, 2889–2893. [Google Scholar] [CrossRef]
- Hickson, K.M.; Larrégaray, P.; Bonnet, L.; González-Lezana, T. The kinetics of X + H2 reactions (X = C(1D), N(2D), O(1D), S(1D)) at low temperature: Recent combined experimental and theoretical investigations. Int. Rev. Phys. Chem. 2021, 40, 457–493. [Google Scholar] [CrossRef]
- Buren, B.; Yang, Z.J.; Chen, M.D. Dynamics study on the non-adiabatic Na(3p) + HD → NaH/NaD plus D/H reaction: Insertion-abstraction mechanism. Phys. Chem. Chem. Phys. 2020, 22, 3633–3642. [Google Scholar] [CrossRef] [PubMed]
- Yang, H.; Han, K.L.; Schatz, G.C.; Lee, S.H.; Liu, K.; Smith, S.C.; Hankel, M. Integral and differential cross sections for the S(1D) + HD reaction employing the ground adiabatic electronic state. Phys. Chem. Chem. Phys. 2009, 11, 11587–11595. [Google Scholar] [CrossRef] [PubMed]
- González-Lezana, T.; Larrégaray, P.; Bonnet, L. Statistical investigations of the S(1D) + HD reaction in the quantum regime. Chem. Phys. Lett. 2021, 763, 138228. [Google Scholar] [CrossRef]
- Saez-Rabanos, V.; Verdasco, J.E.; Aoiz, F.J.; Herrero, V.J. The F + HD(v = 0, 1; j = 0, 1) reactions: Stereodynamical properties of orbiting resonances. Phys. Chem. Chem. Phys. 2021, 23, 8002–8012. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.J.; Demireva, M.; Kim, J.; De Jong, W.A.; Armentrout, P.B. Reactions of U+ with H2, D2 and HD Studied by Guided Ion Beam Tandem Mass Spectrometry and Theory. J. Phys. Chem. A 2021, 125, 7825–7839. [Google Scholar] [CrossRef] [PubMed]
- González-Lezana, T.; Hily-Blant, P.; Faure, A. A statistical investigation of the rate constants for the H+ + HD reaction at temperatures of astrophysical interest. J. Chem. Phys. 2022, 157, 214302. [Google Scholar] [CrossRef] [PubMed]
- Xu, X.X.; Yang, Z.J.; Buren, B.; Chen, M.D. Analysis of Ca+(2S) + HD (v0 = 0, j0 = 0) → CaH+ /CaD+ + D/H reaction dynamics using time-dependent wave packet method. Chem. Phys. Lett. 2024, 835, 140997. [Google Scholar] [CrossRef]
- Skouteris, D.; Manolopoulos, D.E.; Bian, W.S.; Werner, H.J.; Lai, L.H.; Liu, K.P. van der Waals interactions in the Cl + HD reaction. Science 1999, 286, 1713–1716. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.N.; Cao, J.W.; Bian, W.S. Quantum Dynamics Study of the C(1D) + HD Reaction on the A′ and A″ Potential Energy Surfaces. J. Phys. Chem. A 2020, 124, 801–809. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z.J.; Mao, Y.; Chen, M.D. Quantum Dynamics Studies of the Significant IntramolecularIsotope Effects on the Nonadiabatic Be+(2P) + HD → BeH+/BeD+ + D/H Reaction. J. Phys. Chem. A 2021, 125, 235–242. [Google Scholar] [CrossRef] [PubMed]
- Mao, Y.; Yuan, J.C.; Yang, Z.J.; Chen, M.D. Quantum dynamics studies of isotope effects in the Mg(3p) + HD → MgH/MgD + D/H insertion reaction. Sci. Rep. 2020, 10, 3410. [Google Scholar] [CrossRef]
- Staanum, P.F.; Højbjerre, K.; Wester, R.; Drewsen, M. Probing isotope effects in chemical reactions using single ions. Phys. Rev. Lett. 2008, 100, 243003. [Google Scholar] [CrossRef]
- Li, H.; Le Roy, R.J. An accurate ab initio potential energy surface and calculated spectroscopic constants for BeH2, BeD2, and BeHD. J. Chem. Phys. 2006, 125, 044307. [Google Scholar] [CrossRef]
- Koput, J.; Peterson, K.A. Ab initio prediction of the potential energy surface and vibration-rotation energy levels of BeH2. J. Chem. Phys. 2006, 125, 044306. [Google Scholar] [CrossRef]
- Koput, J. Ab initio prediction of the potential energy surface and vibrational-rotational energy levels of calcium dihydride, CaH2. J. Phys. Chem. A 2005, 109, 4410–4414. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Xie, D.Q.; Guo, H. An Ab Initio Potential Energy Surface and Vibrational States of MgH2(11A′). J. Chem. Phys. 2004, 121, 4156–4163. [Google Scholar] [CrossRef] [PubMed]
- Li, A.Y.; Li, J.; Guo, H. Quantum Manifestation of Roaming in H + MgH → Mg + H2: The Birth of Roaming Resonances. J. Phys. Chem. A 2013, 117, 5052–5060. [Google Scholar] [CrossRef] [PubMed]
- Guo, H. Quantum dynamics of complex-forming bimolecular reactions. Int. Rev. Phys. Chem. 2012, 31, 1–68. [Google Scholar] [CrossRef]
- Motallebipour, M.S.; Shayesteh, A. Determination of fundamental band origin for BeH2 and BeD2 from deperturbation analysis of hot bands. J. Chem. Phys. 2016, 145, 074310. [Google Scholar] [CrossRef] [PubMed]
- Bernath, P.F.; Shayesteh, A.; Tereszchuk, K.; Colin, R. The vibration-rotation emission spectrum of free BeH2. Science 2002, 297, 1323–1324. [Google Scholar] [CrossRef] [PubMed]
- Sampath, S.; Lantzky, K.M.; Benmore, C.J.; Neuefeind, J.; Siewenie, J.E.; Egelstaff, P.A.; Yarger, J.L. Structural quantum isotope effects in amorphous beryllium hydride. J. Chem. Phys. 2003, 119, 12499–12502. [Google Scholar] [CrossRef]
- Iddir, H.; Zapol, P.; Kolesnikov, A.I. Theoretical investigation of the vibrational properties of BeH2 and Li2BeH4. Phys. Rev. B 2009, 80, 134111. [Google Scholar] [CrossRef]
- Hrenar, T.; Werner, H.J.; Rauhut, G. Towards accurate calculations on the vibrational modes of the alkaline earth metal hydrides. Phys. Chem. Chem. Phys. 2005, 7, 3123–3125. [Google Scholar] [CrossRef]
- Yang, Z.J.; Chen, M.D. A globally accurate potential energy surface and quantum dynamics calculations on the Be(1S) + H2(v0 = 0, j0 = 0) → BeH + H reaction. Front. Phys. 2022, 10, 1022222. [Google Scholar] [CrossRef]
- Jiang, B.; Li, J.; Guo, H. Potential energy surfaces from high fidelity fitting of ab initio points: The permutation invariant polynomial—Neural network approach. Int. Rev. Phys. Chem. 2016, 35, 479–506. [Google Scholar] [CrossRef]
- Jiang, B.; Guo, H. Permutation invariant polynomial neural network approach to fitting potential energy surfaces. J. Chem. Phys. 2013, 139, 054112. [Google Scholar] [CrossRef]
- Sun, Z.G.; Zhang, D.H.; Xu, C.X.; Zhou, S.L.; Xie, D.Q.; Lendvay, G.; Lee, S.Y.; Lin, Y.; Guo, H. State-to-State Dynamics of H + O2 Reaction, Evidence for Nonstatistical Behavior. J. Am. Chem. Soc. 2008, 130, 14962–14963. [Google Scholar] [CrossRef]
- Larrégaray, P.; Bonnet, L. Quantum state-resolved differential cross sections for complex-forming chemical reactions: Asymmetry is the rule, symmetry the exception. J. Chem. Phys. 2015, 143, 144113. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Zhao, B.; Xie, D.Q.; Guo, H. Advances and New Challenges to Bimolecular Reaction Dynamics Theory. J. Phys. Chem. Lett. 2020, 11, 8844–8860. [Google Scholar] [CrossRef]
- Li, Q.; Yang, M.J.; Song, H.W.; Li, Y.L. Reaction dynamics for the Cl(2P) + XCl → XCl + Cl(2P) (X = H, D, Mu) reaction on a high-fidelity ground state potential energy surface. J. Chem. Phys. 2023, 158, 234301. [Google Scholar] [CrossRef]
- Wang, H.; Fang, J.H.; Yang, H.; Song, J.N.; Li, Y.L. Ring-polymer molecular dynamical benchmarks for X + H2 insertion reactions. Chem. Phys. Lett. 2019, 730, 227–233. [Google Scholar] [CrossRef]
- Sun, Z.G.; Lee, S.Y.; Guo, H.; Zhang, D.H. Comparison of second-order split operator and Chebyshev propagator in wave packet based state-to-state reactive scattering calculations. J. Chem. Phys. 2009, 130, 174102. [Google Scholar] [CrossRef]
- Sun, Z.G.; Guo, H.; Zhang, D.H. Extraction of state-to-state reactive scattering attributes from wave packet in reactant Jacobi coordinates. J. Chem. Phys. 2010, 132, 084112. [Google Scholar] [CrossRef]
- Buren, B.; Chen, M.D.; Sun, Z.G.; Guo, H. Quantum Wave Packet Treatment of Cold Nonadiabatic Reactive Scattering at the State-To-State Level. J. Phys. Chem. A 2021, 125, 10111–10120. [Google Scholar] [CrossRef]
- Huang, J.Y.; Liu, S.; Zhang, D.H.; Krems, R.V. Time-Dependent Wave Packet Dynamics Calculations of Cross Sections for Ultracold Scattering of Molecules. Phys. Rev. Lett. 2018, 120, 143401. [Google Scholar] [CrossRef] [PubMed]
- Sathyamurthy, N.; Mahapatra, S. Time-dependent quantum mechanical wave packet dynamics. Phys. Chem. Chem. Phys. 2021, 23, 7586–7614. [Google Scholar] [CrossRef]
- Zhao, B.; Sun, Z.G.; Guo, H. A reactant-coordinate-based approach to state-to-state differential cross sections for tetratomic reactions. J. Chem. Phys. 2016, 145, 184106. [Google Scholar] [CrossRef]
- Li, X.M.; Sun, Z.G. Dynamical resonances in F + H2/HD reaction scattering. Theor. Chem. Acc. 2018, 137, 19. [Google Scholar] [CrossRef]
- Lu, D.D.; Guo, H. Quantum and Semiclassical Dynamics of Nonadiabatic Electronic Excitation of C(3P) to C(1D) by Hyperthermal Collisions with N2. J. Phys. Chem. A 2023, 127, 3190–3199. [Google Scholar] [CrossRef] [PubMed]
- Lu, D.D.; Galvao, B.R.L.; Varandas, A.J.C.; Guo, H. Quantum and semiclassical studies of nonadiabatic electronic transitions between N(4S) and N(2D) by collisions with N2. Phys. Chem. Chem. Phys. 2023, 25, 15656–15665. [Google Scholar] [CrossRef]
- Wang, Z.M.; Hou, S.T.; Xie, C.J. Nonadiabatic quantum dynamics of the charge transfer reaction H+ + NO(X2Π) → H + NO+(X1Σ+). Phys. Chem. Chem. Phys. 2023, 25, 23808–23818. [Google Scholar] [CrossRef]
- Chen, H.H.; Buren, B.; Yang, Z.J.; Chen, M.D. An effective approximation of Coriolis coupling in reactive scattering: Application to the time-dependent wave packet calculations. Phys. Chem. Chem. Phys. 2023, 25, 22927–22940. [Google Scholar] [CrossRef]
- Mao, Y.; Buren, B.; Yang, Z.J.; Chen, M.D. Time-dependent wave packet dynamics study of the resonances in the H + LiH+(v=0, j=0) → Li+ + H2 reaction at low collision energies. Phys. Chem. Chem. Phys. 2022, 24, 15532–15539. [Google Scholar] [CrossRef]
- Yang, Z.J.; Chen, H.H.; Mao, Y.; Chen, M.D. A neural network potential energy surface and quantum dynamics studies for the Ca+(2S) + H2 → CaH+ + H reaction. Phys. Chem. Chem. Phys. 2022, 24, 19209–19217. [Google Scholar] [CrossRef] [PubMed]
- Mao, Y.; Chen, H.H.; Yang, Z.J.; Buren, B.; Chen, M.D. Quantum State-resolved Nonadiabatic Dynamics of the H + NaF → Na + HF reaction. Chin. Phys. Lett. 2024. [Google Scholar] [CrossRef]
- Yang, Z.J.; Chen, H.H.; Buren, B.; Chen, M.D. Globally Accurate Gaussian Process Potential Energy Surface and Quantum Dynamics Studies on the Li(2S) + Na2 → LiNa + Na Reaction at Low Collision Energies. Molecules 2023, 28, 2938. [Google Scholar] [CrossRef]
- Feit, M.D.; Fleck, J.A.; Steiger, A. Solution of the schrodinger-equation by a spectral method. J. Comput. Phys. 1982, 47, 412–433. [Google Scholar] [CrossRef]
- Sun, Z.G.; Lin, X.; Lee, S.Y.; Zhang, D.H. A Reactant-Coordinate-Based Time-Dependent Wave Packet Method for Triatomic State-to-State Reaction Dynamics: Application to the H + O-2 Reaction. J. Phys. Chem. A 2009, 113, 4145–4154. [Google Scholar] [CrossRef]
- Gómez-Carrasco, S.; Roncero, O. Coordinate transformation methods to calculate state-to-state reaction probabilities with wave packet treatments. J. Chem. Phys. 2006, 125, 054102. [Google Scholar] [CrossRef]


| Parameter | Value |
|---|---|
| R r Rotational basisInitial wave packet | R ∈ [0.1, 15.0], NR = 199, = 129 r ∈ [0.01, 16.0], νInt = 159, νAsy = 15 jInt = 139, jAsy = 39 Rc = 10.0, δ = 0.3, Ec = 2.7 eV |
| Absorbing potential | R: Ca = 0. 06, Cb = 0.12, Ra = 11.0, Rb = 15.0 |
| r: Ca = 0.04, Cb = 0.12, ra = 12.0, rb = 15.0 | |
| Propagation time Matching plane | Ttot = 40000, Δt = 10 R0′ = 8.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, H.; Yang, Z. State-to-State Quantum Dynamics Study of Intramolecular Isotope Effects on Be(1S) + HD (v0 = 2, j0 = 0) → BeH/BeD + H/D Reaction. Molecules 2024, 29, 1263. https://doi.org/10.3390/molecules29061263
Xu H, Yang Z. State-to-State Quantum Dynamics Study of Intramolecular Isotope Effects on Be(1S) + HD (v0 = 2, j0 = 0) → BeH/BeD + H/D Reaction. Molecules. 2024; 29(6):1263. https://doi.org/10.3390/molecules29061263
Chicago/Turabian StyleXu, Hongtai, and Zijiang Yang. 2024. "State-to-State Quantum Dynamics Study of Intramolecular Isotope Effects on Be(1S) + HD (v0 = 2, j0 = 0) → BeH/BeD + H/D Reaction" Molecules 29, no. 6: 1263. https://doi.org/10.3390/molecules29061263
APA StyleXu, H., & Yang, Z. (2024). State-to-State Quantum Dynamics Study of Intramolecular Isotope Effects on Be(1S) + HD (v0 = 2, j0 = 0) → BeH/BeD + H/D Reaction. Molecules, 29(6), 1263. https://doi.org/10.3390/molecules29061263






