Thermo-Structural Characterization of Phase Transitions in Amorphous Griseofulvin: From Sub-Tg Relaxation and Crystal Growth to High-Temperature Decomposition
Abstract
:1. Introduction
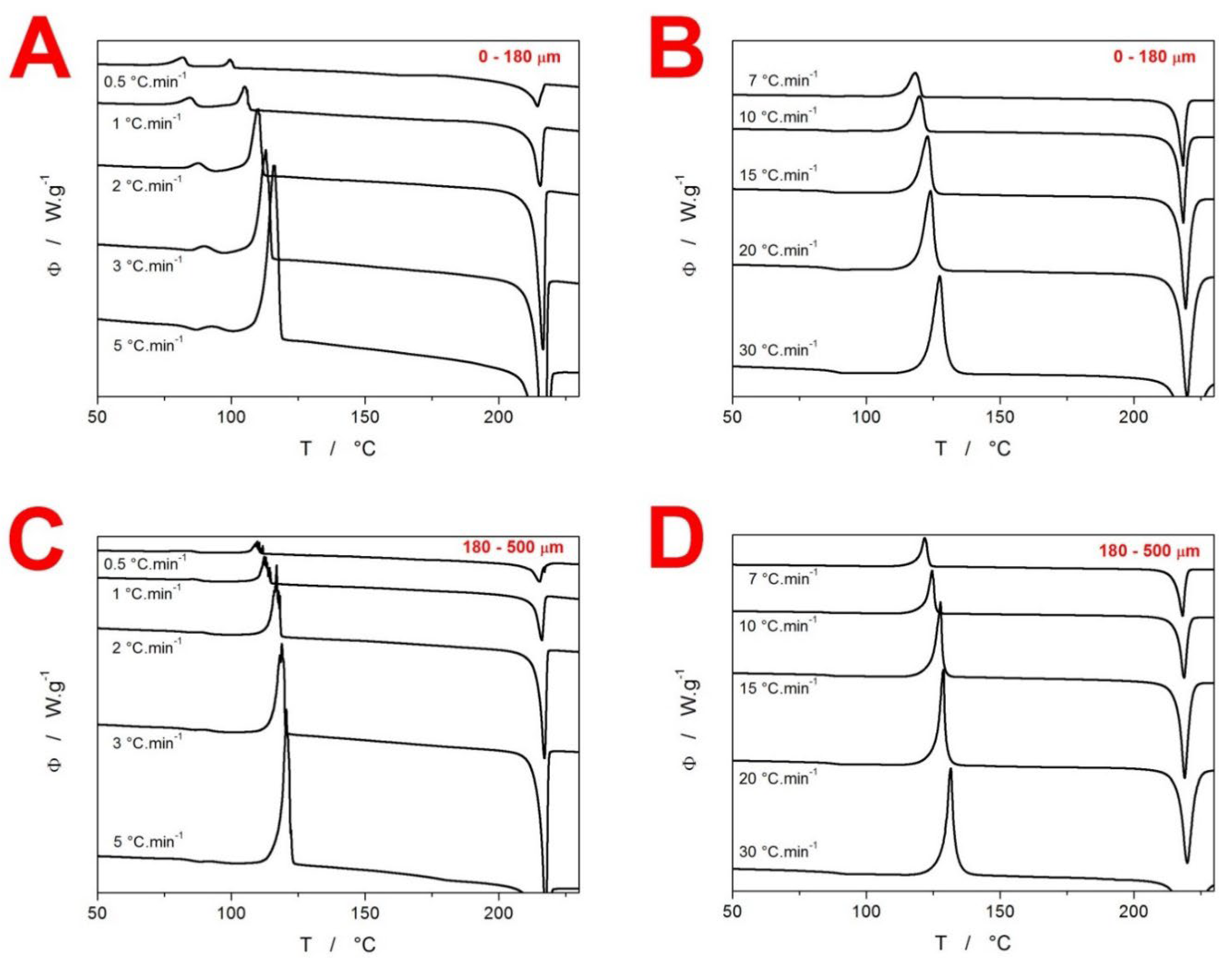
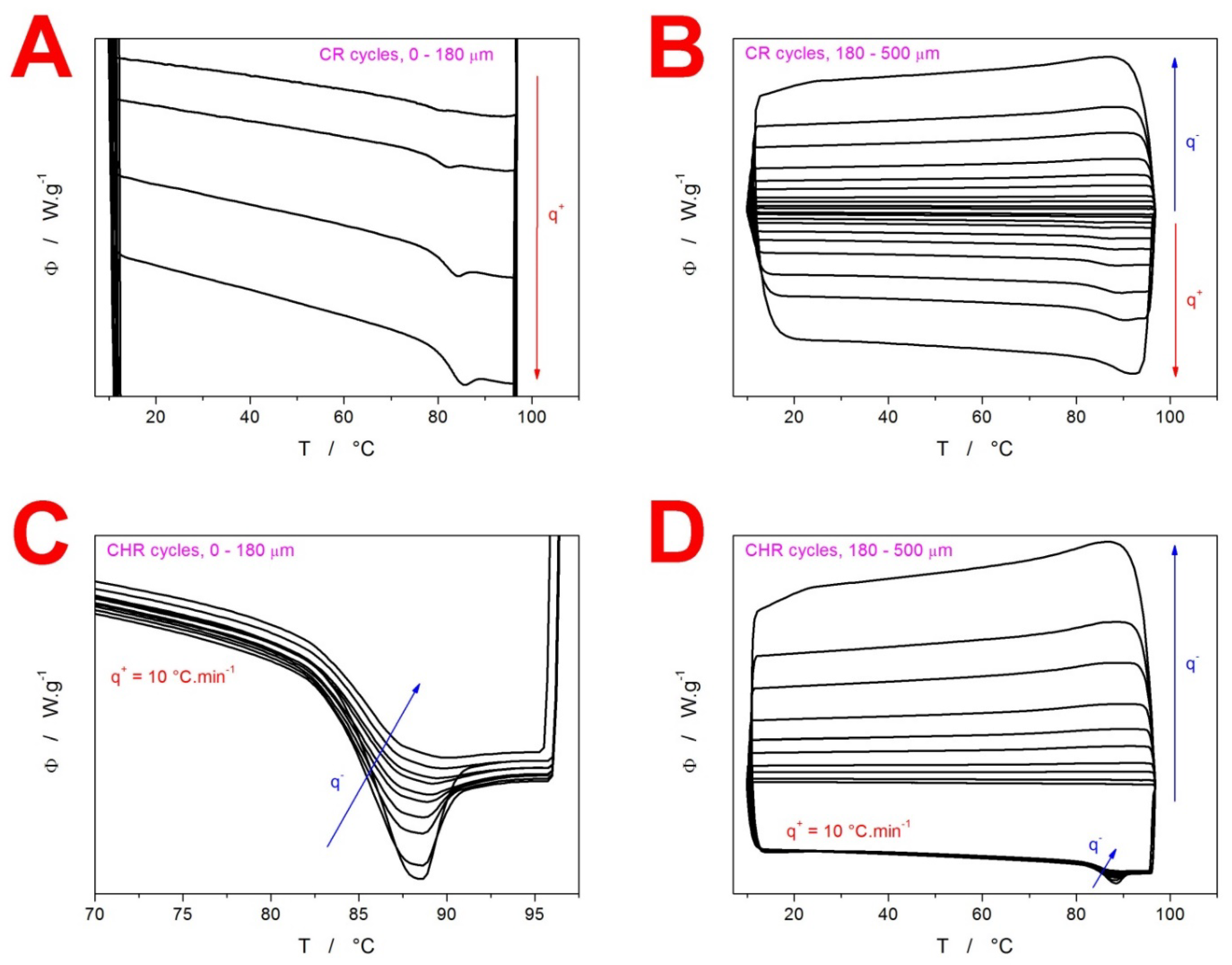
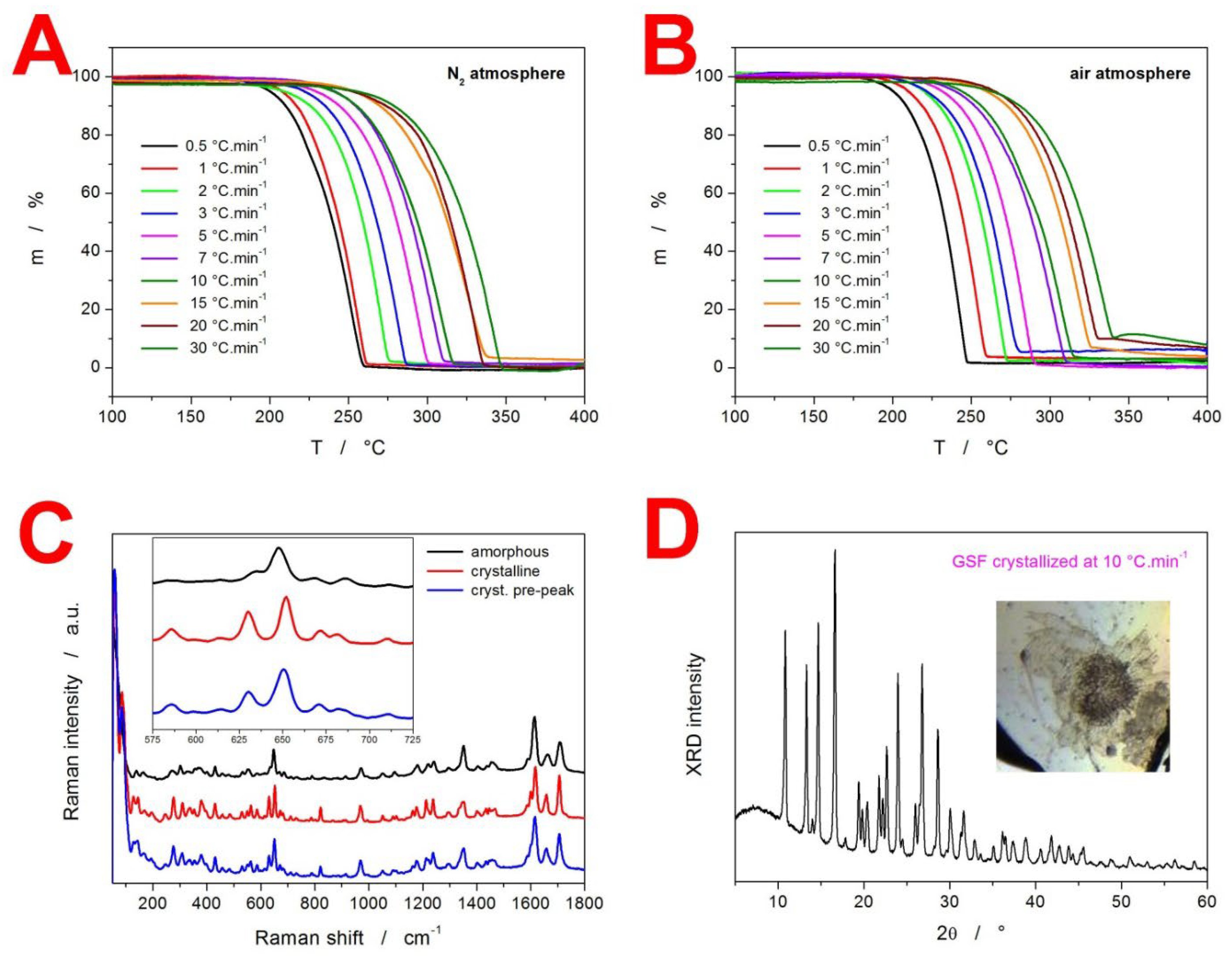
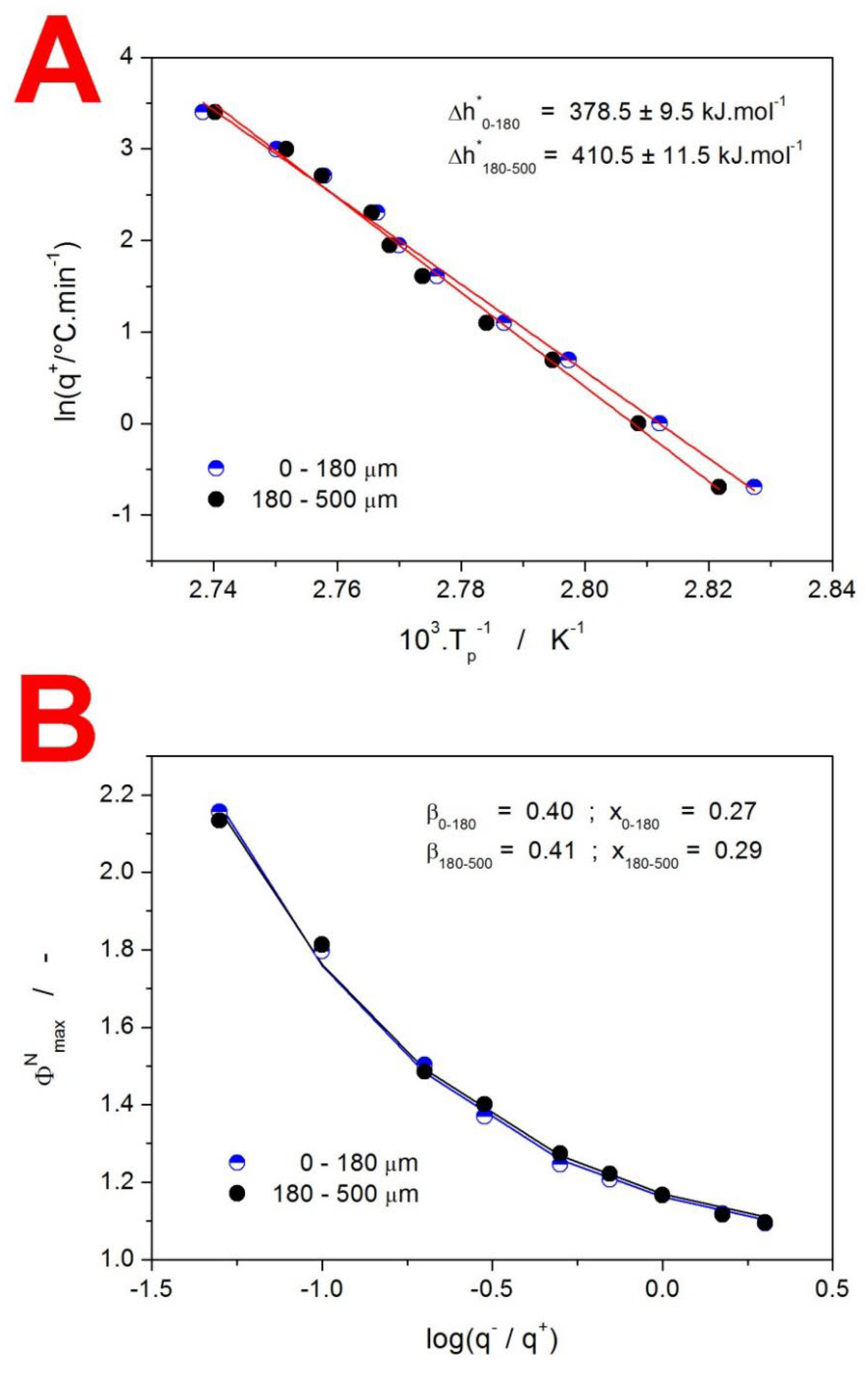
2. Results
3. Discussion
3.1. Kinetics of Structural Relaxation in Amorphous GSF
3.2. Kinetics of Crystallization in Amorphous GSF
3.3. Kinetics of GSF Thermal Decomposition
3.4. Mutual Relationships between Structural Relaxation, Microscopic and Macroscopic Crystal Growth
4. Experimental
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Grandner, J.; Cacho, R.; Tang, Y.; Houk, K. Mechanism of the p450-catalyzed oxidative cyclization in the biosynthesis of griseofulvin. ACS Catal. 2016, 6, 4506–4511. [Google Scholar] [CrossRef]
- Duldulao, P.; Ortega, A.; Delgadillo, X. Mycotic and bacterial infections. Clin. Colon Rectal Surg. 2019, 32, 333–339. [Google Scholar] [CrossRef]
- Otto, D.; Otto, A.; Villiers, M. In vitro skin delivery of griseofulvin by layer-by-layer nanocoated emulsions stabilized by whey protein and polysaccharides. Pharmaceutics 2022, 14, 554. [Google Scholar] [CrossRef]
- Schmeel, L.; Schmeel, F.; Kim, Y.; Blaum-Feder, S.; Schmidt-Wolf, I. Griseofulvin efficiently induces apoptosis in in vitro treatment of lymphoma and multiple myeloma. Anticancer Res. 2017, 37, 2289–2295. [Google Scholar] [CrossRef]
- Grigalunas, M.; Patil, S.; Krzyzanowski, A.; Pahl, A.; Flegel, J.; Schölermannet, B.; Xie, J.; Sievers, S.; Ziegler, S.; Waldmann, H. Unprecedented combination of polyketide natural product fragments identifies the new hedgehog signaling pathway inhibitor grismonone. Chem. Eur. J. 2022, 28, e2022021642022. [Google Scholar] [CrossRef]
- Smith, C.; Jerkovic, A.; Truong, T.; Foote, S.; McCarthy, J.; McMorran, B. Griseofulvin impairs intraerythrocytic growth of plasmodium falciparum through ferrochelatase inhibition but lacks activity in an experimental human infection study. Sci. Rep. 2017, 7, 41975. [Google Scholar] [CrossRef]
- Ricci, A.; Pierro, E.; Marcacci, M.; Ventura, P. Mechanisms of neuronal damage in acute hepatic porphyrias. Diagnostics 2021, 11, 2205. [Google Scholar] [CrossRef]
- Hee-Jeong, K.; Sang-Do, Y. Liquid antisolvent crystallization of griseofulvin from organic solutions. Chem. Eng. Res. Des. 2015, 97, 68–76. [Google Scholar]
- Chen, H.; Wang, C.; Sun, C.C. Profoundly Improved Plasticity and Tabletability of Griseofulvin by in Situ Solvation and Desolvation during Spherical Crystallization. Cryst. Growth Des. 2019, 19, 2350–2357. [Google Scholar] [CrossRef]
- Shi, Q.; Zhang, C.; Su, Y.; Zhang, J.; Zhou, D.; Cai, T. Acceleration of Crystal Growth of Amorphous Griseofulvin by Low-Concentration Poly(ethylene oxide): Aspects of Crystallization Kinetics and Molecular Mobility. Mol. Pharm. 2017, 14, 2262–2272. [Google Scholar] [CrossRef]
- Rahman, M.; Ahmad, S.; Tarabokija, J.; Parker, N.; Bilgili, E. Spray-Dried Amorphous Solid Dispersions of Griseofulvin in HPC/Soluplus/SDS: Elucidating the Multifaceted Impact of SDS as a Minor Component. Pharmaceutics 2020, 12, 197. [Google Scholar] [CrossRef]
- Chakravarty, P.; Famili, A.; Nagapudi, K.; Al-Sayah, M. Using supercritical fluid technology as a green alternative during the preparation of drug delivery systems. Pharmaceutics 2019, 11, 629. [Google Scholar] [CrossRef]
- Kumar, R.; Dalvi, S.; Siril, P. Nanoparticle-based drugs and formulations: Current status and emerging applications. ACS Appl. Nano Mater. 2020, 3, 4944–4961. [Google Scholar] [CrossRef]
- Liu, Q.; Mao, L.; Liu, C.; Yin, J.; Zhu, X.; Chen, D. Continuous synthesis of polymer-coated drug nanoparticles by heterogeneous nucleation in a hollow-fiber membrane module. Ind. Eng. Chem. Res. 2021, 61, 349–358. [Google Scholar] [CrossRef]
- Bhujbal, S.; Mitra, B.; Jain, U.; Gong, Y.; Agrawal, A.; Karkiet, S.; Taylor, L.S.; Kumar, S.; Zhou, Q.T. Pharmaceutical amorphous solid dispersion: A review of manufacturing strategies. Acta Pharm. Sin. B 2021, 11, 2505–2536. [Google Scholar] [CrossRef]
- Willart, J.F.; Dudognon, E.; Mahieu, A.; Eddleston, M.; Jones, W.; Descamps, M. The role of cracks in the crystal nucleation process of amorphous griseofulvin. Eur. Phys. J. Spec. Top. 2017, 226, 837–847. [Google Scholar] [CrossRef]
- Willart, J.F.; Carpentier, L.; Danède, F.; Descamps, M. Solid-state vitrification of crystalline griseofulvin by mechanical milling. J. Pharm. Sci. 2012, 101, 1570–1577. [Google Scholar] [CrossRef]
- Brian, C.W.; Yu, L. Surface self-diffusion of organic glasses. J. Phys. Chem. A 2013, 117, 13303–13309. [Google Scholar] [CrossRef]
- Zhu, L.; Jona, J.; Nagapudi, K.; Wu, T. Fast surface crystallization of amorphous griseofulvin below Tg. Pharm. Res. 2010, 27, 1558–1567. [Google Scholar] [CrossRef]
- Huang, C.; Ruan, S.; Cai, T.; Yu, L. Fast Surface Diffusion and Crystallization of Amorphous Griseofulvin. J. Phys. Chem. B 2017, 121, 9463–9468. [Google Scholar] [CrossRef]
- Zhou, D.; Zhang, G.G.Z.; Law, D.; Grant, D.J.W.; Schmitt, E.A. Thermodynamics, Molecular Mobility and Crystallization Kinetics of Amorphous Griseofulvin. Mol. Pharm. 2008, 5, 927–936. [Google Scholar] [CrossRef]
- Trenfield, S.; Awad, A.; Goyanes, Á.; Gaisford, S.; Basit, A. 3d printing pharmaceuticals: Drug development to frontline care. Trends Pharmacol. Sci. 2018, 39, 440–451. [Google Scholar] [CrossRef]
- Vithani, K.; Goyanes, Á.; Jannin, V.; Basit, A.; Gaisford, S.; Boyd, B. A proof of concept for 3d printing of solid lipid-based formulations of poorly water-soluble drugs to control formulation dispersion kinetics. Pharm. Res. 2019, 36, 102. [Google Scholar] [CrossRef]
- Hong, X.; Han, X.; Li, X.; Li, J.; Wang, Z.; Zheng, A. Binder jet 3d printing of compound lev-pn dispersible tablets: An innovative approach for fabricating drug systems with multicompartmental structures. Pharmaceutics 2021, 13, 1780. [Google Scholar] [CrossRef]
- Mathew, E.; Pitzanti, G.; Larrañeta, E.; Lamprou, D. 3d printing of pharmaceuticals and drug delivery devices. Pharmaceutics 2020, 12, 266. [Google Scholar] [CrossRef] [PubMed]
- Buyukgoz, G.; Kossor, C.; Davé, R. Enhanced supersaturation via fusion-assisted amorphization during fdm 3d printing of crystalline poorly soluble drug loaded filaments. Pharmaceutics 2021, 13, 1857. [Google Scholar] [CrossRef]
- Renterghem, J.; Vervaet, C.; Beer, T. Rheological characterization of molten polymer-drug dispersions as a predictive tool for pharmaceutical hot-melt extrusion processability. Pharm. Res. 2017, 34, 2312–2321. [Google Scholar] [CrossRef] [PubMed]
- Shu, L.; Tian, Y.; Jones, D.; Andrews, G. Optimising drug solubilisation in amorphous polymer dispersions: Rational selection of hot-melt extrusion processing parameters. Aaps Pharmscitech 2016, 17, 200–213. [Google Scholar] [CrossRef]
- Figueroa, F.; Espinell, J.; Hernández, M.; López-Mejías, V.; Stelzer, T. Polymorphic phase transformations in crystalline solid dispersions: The combined effect of pressure and temperature. Cryst. Growth Des. 2022, 22, 2903–2909. [Google Scholar] [CrossRef]
- Gupta, S.; Solanki, N.; Serajuddin, A. Investigation of thermal and viscoelastic properties of polymers relevant to hot melt extrusion, iv: Affinisol™ hpmc hme polymers. Aaps Pharmscitech 2015, 17, 148–157. [Google Scholar] [CrossRef]
- Chamberlain, R.; Windolf, H.; Geissler, S.; Quodbach, J.; Breitkreutz, J. Precise dosing of pramipexole for low-dosed filament production by hot melt extrusion applying various feeding methods. Pharmaceutics 2022, 14, 216. [Google Scholar] [CrossRef]
- Ma, X.; Müller, F.; Huang, S.; Lowinger, M.; Liu, X.; Schooleret, R.; Williams, R.O., III. Influence of carbamazepine dihydrate on the preparation of amorphous solid dispersions by hot melt extrusion. Pharmaceutics 2020, 12, 379. [Google Scholar] [CrossRef] [PubMed]
- Yi, S.; Wang, J.; Liu, Y.; Ma, R.; Gao, Q.; Liuet, S.; Xiong, S. Novel hot melt extruded matrices of hydroxypropyl cellulose and amorphous felodipine–plasticized hydroxypropyl methylcellulose as controlled release systems. Aaps Pharmscitech 2019, 20, 219. [Google Scholar] [CrossRef] [PubMed]
- Kawakami, K. Crystallization Tendency of Pharmaceutical Glasses: Relevance to Compound Properties, Impact of Formulation Process, and Implications for Design of Amorphous Solid Dispersions. Pharmaceutics 2019, 11, 202. [Google Scholar] [CrossRef] [PubMed]
- Ediger, M.D.; Harrowell, P.; Yu, L. Crystal growth kinetics exhibit a fragility-dependent decoupling from viscosity. J. Chem. Phys. 2008, 128, 034709. [Google Scholar] [CrossRef] [PubMed]
- Musumeci, D.; Hasebe, M.; Yu, L. Crystallization of Organic Glasses: How Does Liquid Flow Damage Surface Crystal Growth? Cryst. Growth Des. 2016, 16, 2931–2936. [Google Scholar] [CrossRef]
- Swallen, S.F.; Ediger, M.D. Self-diffusion of the amorphous pharmaceutical indomethacin near Tg. Soft Matter 2011, 7, 10339–10344. [Google Scholar] [CrossRef]
- Svoboda, R.; Macháčková, J.; Nevyhoštěná, M.; Komersová, A. Thermal stability of amorphous nimesulide: From glass formation to crystal growth and thermal degradation. Phys. Chem Chem. Phys. 2024, 26, 856–872. [Google Scholar] [CrossRef] [PubMed]
- Svoboda, R.; Košťálová, D.; Krbal, M.; Komersová, A. Indomethacin: The Interplay between Structural Relaxation, Viscous Flow and Crystal Growth. Molecules 2022, 27, 5668. [Google Scholar] [CrossRef]
- Svoboda, R.; Málek, J. Evaluation of glass-stability criteria for chalcogenide glasses: Effect of experimental conditions. J. Non-Cryst. Sol. 2015, 413, 39–45. [Google Scholar] [CrossRef]
- Svoboda, R.; Kincl, M.; Málek, J. Thermal characterization of Se-Te thin films. J. Alloys Compd. 2015, 644, 40–46. [Google Scholar] [CrossRef]
- Ou, X.; Li, S.; Chen, Y.; Rong, H.; Li, A.; Lu, M. Polymerphism in Griseofulvin: New Story between an Old Drug and Polyethylene Glycol. Cryst. Growth Des. 2022, 22, 3778–3785. [Google Scholar] [CrossRef]
- Svoboda, R.; Koutná, N.; Košťálová, D.; Krbal, M.; Komersová, A. Indomethacin: Effect of Diffusionless Crystal Growth on Thermal Stability during Long-Term Storage. Molecules 2023, 28, 1568. [Google Scholar] [CrossRef]
- Martin, J.D.; Hillis, B.G.; Hou, F. Transition Zone Theory Compared to Standard Models: Reexamining the Theory of Crystal Growth from Melts. J. Phys. Chem. C 2020, 124, 18724–18740. [Google Scholar] [CrossRef]
- Berthier, L.; Chandler, D.; Garrahan, J.P. Length scale for the onset of Fickian diffusion in supercooled liquids. Europhys. Lett. 2005, 69, 320. [Google Scholar] [CrossRef]
- Chong, S.-H.; Kob, W. Coupling and Decoupling between Translational and Rotational Dynamics in a Supercooled Molecular Liquid. Phys. Rev. Lett. 2009, 102, 025702. [Google Scholar] [CrossRef]
- Scherer, G.W. Theories of relaxation. J. Non-Cryst. Sol. 1990, 123, 75–89. [Google Scholar] [CrossRef]
- Hodge, I.M. Enthalpy relaxation and recovery in amorphous materials. J. Non-Cryst. Sol. 1994, 169, 211–266. [Google Scholar] [CrossRef]
- Rozo, J.I.J.; Zarow, A.; Zhou, B.; Pinal, R.; Iqbal, Z.; Romañach, R.J. Complementary near-infrared and raman chemical imaging of pharmaceutical thin films. J. Pharm. Sci. 2011, 100, 4888–4895. [Google Scholar] [CrossRef]
- Smith, G.P.S.; Huff, G.S.; Gordon, K.C. Investigating Crystallinity Using Low Frequency Raman Spectroscopy: Applications in Pharmaceutical Analysis. Spectroscopy 2016, 31, 42–50. [Google Scholar]
- Tool, A.Q. Relation between inelastic deformability and thermal expansion of glass in its annealing range. J. Am. Ceram. Soc. 1946, 29, 240–253. [Google Scholar] [CrossRef]
- Narayanaswamy, O.S. A Model of Structural Relaxation in Glass. J. Am. Ceram. Soc. 1971, 54, 491–498. [Google Scholar] [CrossRef]
- Moynihan, C.T.; Easteal, A.J.; De Bolt, M.A.; Tucker, J. Dependence of the Fictive Temperature of Glass on Cooling Rate. J. Am. Ceram. Soc. 1976, 59, 12–16. [Google Scholar] [CrossRef]
- Svoboda, R.; Málek, J. Description of enthalpy relaxation dynamics in terms of TNM model. J. Non-Cryst. Solids 2013, 378, 186–195. [Google Scholar] [CrossRef]
- Svoboda, R. Utilization of “q+/q−=const.” DSC cycles for physical aging studies. Eur. Polym. J. 2014, 59, 180–188. [Google Scholar] [CrossRef]
- Svoboda, R. Novel equation to determine activation energy of enthalpy relaxation. J. Therm. Anal. 2015, 121, 895–899. [Google Scholar] [CrossRef]
- Svoboda, R.; Málek, J. Enthalpy relaxation in Ge–Se glassy system. J. Therm. Anal. 2012, 113, 831–842. [Google Scholar] [CrossRef]
- Hodge, I.M.; Berens, A.R. Effects of annealing and prior history on enthalpy relaxation in glassy polymers. 2. Mathematical modeling. Macromolecules 1982, 15, 762–770. [Google Scholar] [CrossRef]
- Šesták, J. Thermophysical Properties of Solids, Their Measurements and Theoretical Analysis; Elsevier: Amsterdam, The Netherlands, 1984. [Google Scholar]
- Šesták, J. Science of Heat and Thermophysical Studies: A Generalized Approach to Thermal Analysis; Elsevier: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Johnson, W.A.; Mehl, K.F. Reaction kinetics in processes of nucleation and growth. Trans. Am. Inst. Min. (Met.) Eng. 1939, 135, 416–442. [Google Scholar]
- Avrami, M. Kinetics of phase change I–general theory. J. Chem. Phys. 1939, 7, 1103–1112. [Google Scholar] [CrossRef]
- Avrami, M. Kinetics of phase change. II–transformation-time relations for random distribution of nuclei. J. Chem. Phys. 1940, 7, 212–224. [Google Scholar] [CrossRef]
- Avrami, M. Granulation, phase change, and microstructure—Kinetics of phase change III. J. Chem. Phys. 1941, 7, 177–184. [Google Scholar] [CrossRef]
- Vyazovkin, S.; Burnham, A.K.; Criado, J.M.; Pérez-Maqueda, L.A.; Popescu, C.; Sbirrazzuoli, N. ICATC Kinetics Committee recommendations for performing kinetic computations on thermal analysis data. Thermochim. Acta 2011, 520, 1–19. [Google Scholar] [CrossRef]
- Kissinger, H.E. Reaction kinetics in differential thermal analysis. Anal.Chem. 1957, 29, 1702–1706. [Google Scholar] [CrossRef]
- Friedman, H.L. Kinetics of Thermal Degradation of Char-Forming Plastics from Thermogravimetry. Application to a Phenolic Plastic; Wiley, Inc.: Hoboken, NJ, USA, 1964. [Google Scholar]
- Starink, M.J. The determination of activation energy from linear heating rate experiments: A comparison of the accuracy of isoconversion methods. Thermochim. Acta 2003, 404, 163–176. [Google Scholar] [CrossRef]
- Svoboda, R. Crystallization of glasses—When to use the Johnson-Mehl-Avrami kinetics? J. Eur. Ceram. Soc. 2021, 41, 7862–7867. [Google Scholar]
- Svoboda, R.; Chovanec, J.; Slang, S.; Beneš, L.; Konrád, P. Single-curve multivariate kinetic analysis: Application to the crystallization of commercial Fe-Si-Cr-B amorphous alloys. J. Alloys Compd. 2021, 889, 161672. [Google Scholar] [CrossRef]
- Shi, Q.; Cai, T. Fast Crystal Growth of Amorphous Griseofulvin: Relations between Bulk and Surface Growth Modes. Cryst. Growth Des. 2016, 16, 3279–3286. [Google Scholar] [CrossRef]
- Li, F.; Xin, J.; Shi, Q. Diffusion-controlled and “diffusionless” crystal growth: Relation between liquid dynamics and growth kinetics of griseofulvin. J. Appl. Cryst. 2021, 54, 142–147. [Google Scholar] [CrossRef]
- Stevenson, J.D.; Wolynes, P.G. On the surface of glasses. J. Chem. Phys. 2008, 129, 234514. [Google Scholar] [CrossRef]
- Svoboda, R. Utilization of constant heating rate DSC cycles for enthalpy relaxation studies and their influenceability by erroneous experimental operations. J. Non-Cryst. Solids 2015, 408, 115–122. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Svoboda, R.; Kozlová, K. Thermo-Structural Characterization of Phase Transitions in Amorphous Griseofulvin: From Sub-Tg Relaxation and Crystal Growth to High-Temperature Decomposition. Molecules 2024, 29, 1516. https://doi.org/10.3390/molecules29071516
Svoboda R, Kozlová K. Thermo-Structural Characterization of Phase Transitions in Amorphous Griseofulvin: From Sub-Tg Relaxation and Crystal Growth to High-Temperature Decomposition. Molecules. 2024; 29(7):1516. https://doi.org/10.3390/molecules29071516
Chicago/Turabian StyleSvoboda, Roman, and Kateřina Kozlová. 2024. "Thermo-Structural Characterization of Phase Transitions in Amorphous Griseofulvin: From Sub-Tg Relaxation and Crystal Growth to High-Temperature Decomposition" Molecules 29, no. 7: 1516. https://doi.org/10.3390/molecules29071516





