1H NMR Relaxation Processes in Lung Tissues at Low Magnetic Fields
Abstract
1. Introduction
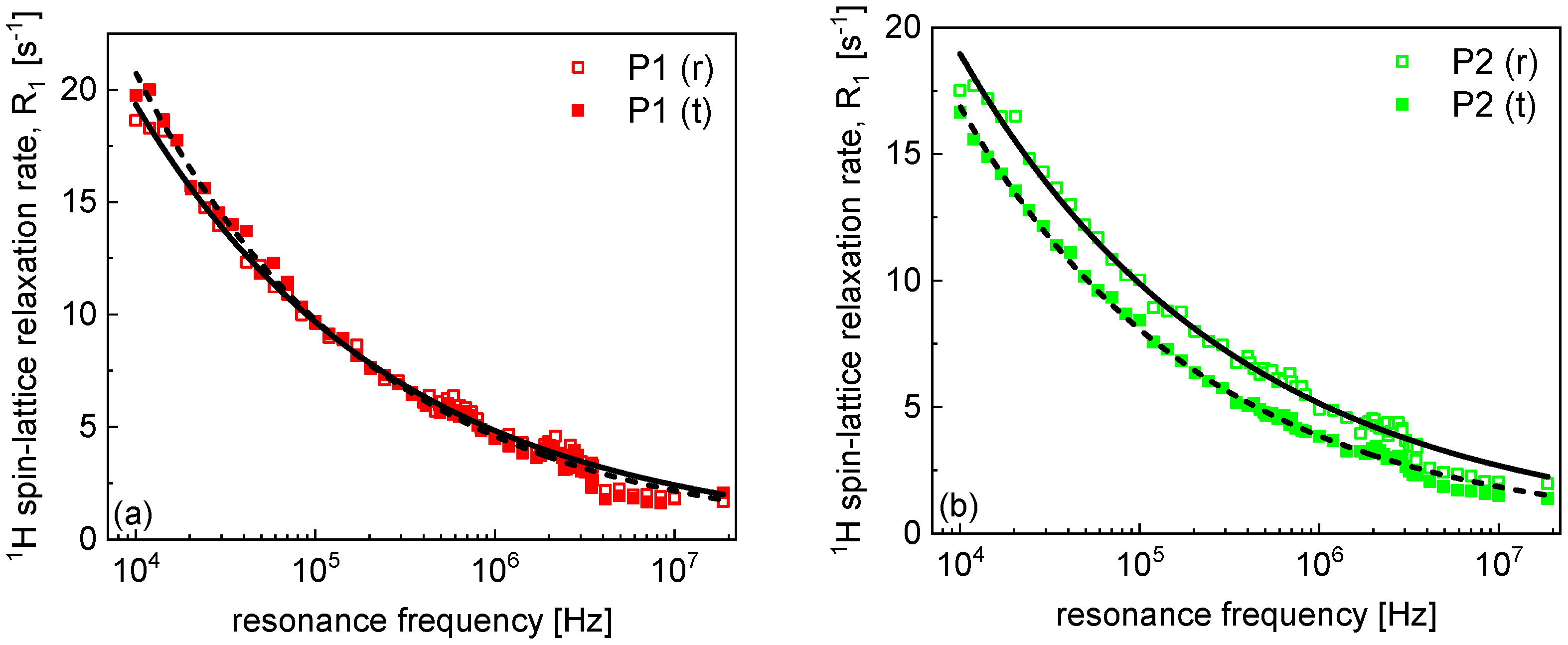
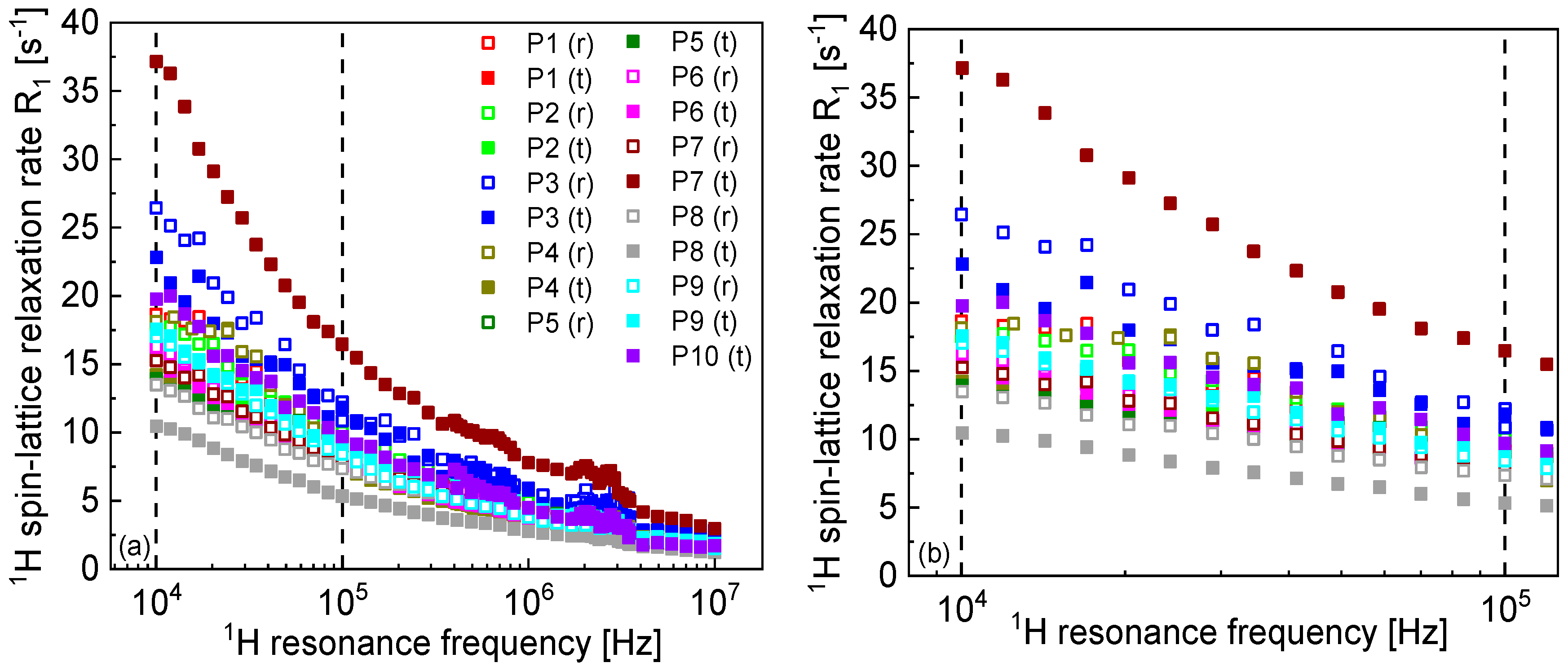
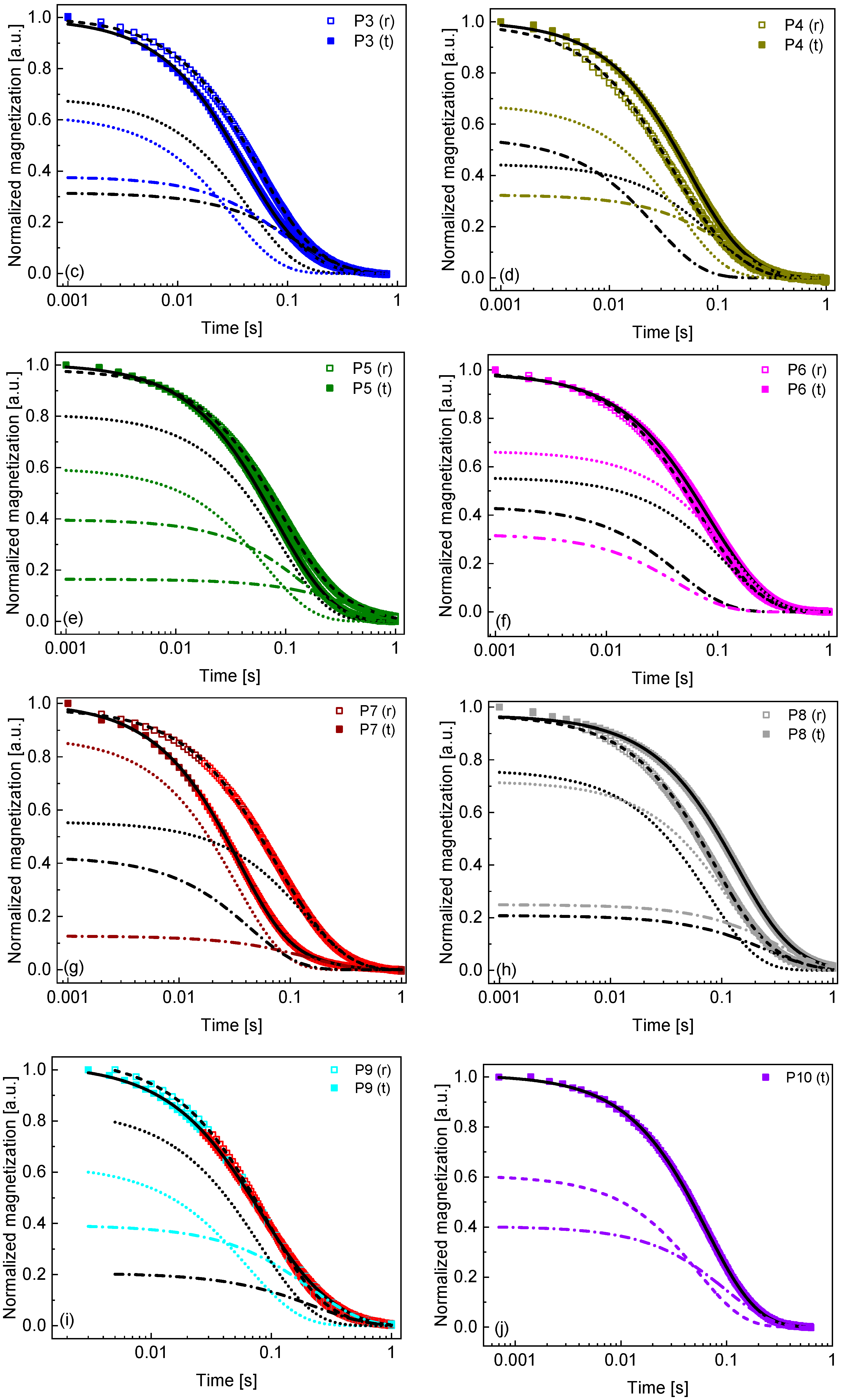
2. Results and Analysis
3. Discussion
4. Materials and Methods
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Siddiqui, F.; Vaqar, S.; Siddiqui, A.H. Lung Cancer; StatPearls Publishing: Treasure Island, FL, USA, 2025. [Google Scholar]
- Lorigan, P.; Radford, J.; Howell, A.; Thatcher, N. Lung cancer after treatment for Hodgkin’s lymphoma: A systematic review. Lancet Oncol. 2005, 6, 773–779. [Google Scholar] [CrossRef]
- Burns, D.M. Primary prevention, smoking, and smoking cessation: Implications for future trends in lung cancer prevention. Cancer 2000, 89, 2506–2509. [Google Scholar] [CrossRef] [PubMed]
- Cagle, P.T.; Allen, T.C.; Olsen, R.J. Lung cancer biomarkers: Present status and future developments. Arch. Pathol. Lab. Med. 2013, 137, 1191–1198. [Google Scholar] [CrossRef]
- Lindeman, N.I.; Cagle, P.T.; Beasley, M.B.; Chitale, D.A.; Dacic, S.; Giaccone, G.; Jenkins, R.B.; Kwiatkowski, D.J.; Saldivar, J.S.; Squire, J.; et al. Molecular testing guideline for selection of lung cancer patients for EGFR and ALK tyrosine kinase inhibitors: Guideline from the College of American Pathologists, International Association for the Study of Lung Cancer, and Association for Molecular Pathology. J. Mol. Diagn. 2013, 15, 415–453. [Google Scholar] [CrossRef]
- Lindeman, N.I.; Cagle, P.T.; Aisner, D.L.; Arcila, M.E.; Beasley, M.B.; Bernicker, E.H.; Colasacco, C.; Dacic, S.; Hirsch, F.R.; Kerr, K.; et al. Updated Molecular Testing Guideline for the Selection of Lung Cancer Patients for Treatment with Targeted Tyrosine Kinase Inhibitors: Guideline From the College of American Pathologists, the International Association for the Study of Lung Cancer, and the Association for Molecular Pathology. J. Mol. Diagn. 2018, 20, 129–159. [Google Scholar] [CrossRef]
- Collins, L.G.; Haines, C.; Perkel, R.; Enck, R.E. Lung cancer: Diagnosis and management. Am. Fam. Physician 2007, 75, 56–63. [Google Scholar] [PubMed]
- Hendriks, L.E.L.; Remon, J.; Faivre-Finn, C.; Garassino, M.C.; Heymach, J.V.; Kerr, K.M.; Tan, D.S.W.; Veronesi, G.; Reck, M. Non-small-cell lung cancer. Nat. Rev. Dis. Prim. 2024, 10, 71. [Google Scholar] [CrossRef]
- Slichter, C.P. Principles of Magnetic Resonance, 3rd ed.; Springer: Berlin, Germany, 1990. [Google Scholar]
- Chen, C.C.; Wan, Y.L.; Wai, Y.Y.; Liu, H.L. Quality Assurance of Clinical MRI Scanners Using ACR MRI Phantom: Preliminary Results. J. Digit. Imaging 2004, 17, 279–284. [Google Scholar] [CrossRef]
- Levitt, M.H. Spin Dynamics: Basics of Nuclear Magnetic Resonance, 2nd ed.; Wiley: Chichester, UK, 2008. [Google Scholar]
- Kruk, D.; Masiewicz, E.; Lotarska, S.; Markiewicz, R.; Jurga, S. Relationship between Translational and Rotational Dynamics of Alkyltriethylammonium-Based Ionic Liquids. Int. J. Mol. Sci. 2022, 23, 1688. [Google Scholar] [CrossRef]
- Kruk, D.; Masiewicz, E.; Borkowska, A.M.; Rochowski, P.; Fries, P.H.; Broche, L.M.; Lurie, D.J. Dynamics of Solid Proteins by Means of Nuclear Magnetic Resonance Relaxometry. Biomolecules 2019, 9, 652. [Google Scholar] [CrossRef] [PubMed]
- Bryant, R.G. Dynamics of water in and around proteins characterized by 1H-spin-lattice relaxometry. C. R. Phys. 2010, 11, 128–135. [Google Scholar] [CrossRef]
- Parigi, G.; Ravera, E.; Fragai, M.; Luchinat, C. Unveiling protein dynamics in solution with field-cycling NMR relaxometry. Prog. Nucl. Magn. Reson. Spectrosc. 2021, 124–125, 85–98. [Google Scholar] [CrossRef]
- Ravera, E.; Parigi, G.; Mainz, A.; Religa, T.L.; Reif, B.; Luchinat, C. Experimental Determination of Microsecond Reorientation Correlation Times in Protein Solutions. J. Phys. Chem. B 2013, 117, 3548–3553. [Google Scholar] [CrossRef]
- Kruk, D.; Grunin, L.; Stankiewicz, A.; Kolodziejski, K.; Ilhan, E.; Oztop, M.H. Molecular Dynamics of Jelly Candies by Means of Nuclear Magnetic Resonance Relaxometry. Molecules 2023, 28, 2230. [Google Scholar] [CrossRef]
- Kruk, D.; Florek-Wojciechowska, M.; Oztop, M.; Ilhan, E.; Wieczorek, Z. Water dynamics in eggs by means of Nuclear Magnetic Resonance relaxometry. J. Magn. Reson. 2021, 327, 106976. [Google Scholar] [CrossRef]
- Stankiewicz, A.; Kasparek, A.; Masiewicz, E.; Kruk, D. Diffusion of Water Molecules on the Surface of Silica Nanoparticles—Insights from Nuclear Magnetic Resonance Relaxometry. J. Phys. Chem. B 2024, 128, 1535–1543. [Google Scholar] [CrossRef]
- Bitonto, V.; Ruggiero, M.R.; Pittaro, A.; Castellano, I.; Bussone, R.; Broche, L.M.; Lurie, D.J.; Aime, S.; Baroni, S.; Crich, S.G. Low-Field NMR Relaxometry for Intraoperative Tumour Margin Assessment in Breast-Conserving Surgery. Cancers 2021, 13, 4141. [Google Scholar] [CrossRef] [PubMed]
- Mallikourti, V.; Ross, P.J.; Maier, O.; Hana, K.; Husain, H.; Davies, G.R.; Lurie, D.J.; Lip, G.; Lahrech, H.; Masannat, Y.; et al. Field cycling imaging to characterise breast cancer at low and ultra-low magnetic fields below 0.2 T. Commun. Med. 2024, 4, 221. [Google Scholar] [CrossRef] [PubMed]
- Ruggiero, M.R.; Baroni, S.; Bitonto, V.; Ruiu, R.; Rapisadra, S.; Aime, S.; Crich, S.G. Intracellular Water Lifetime as a Tumor Biomarker to Monitor Doxorubicin Treatment via FFC-Relaxometry in a Breast Cancer Model. Front. Oncol. 2021, 11, 778823. [Google Scholar] [CrossRef] [PubMed]
- Petit, M.; Leclercq, M.; Pierre, S.; Ruggeiro, M.R.; El Atifi, M.; Bouttonat, J.; Fries, P.H.; Berger, F.; Lahrech, H. Fast-field-cycling NMR at very low magnetic fields: Water molecular dynamic biomarkers of glioma cell invasion and migration. NMR Biomed. 2022, 35, e4677. [Google Scholar] [CrossRef]
- Ruggiero, M.R.; Baroni, S.; Aime, S.; Crich, S.G. Relaxometric investigations addressing the determination of intracellular water lifetime: A novel tumour biomarker of general applicability. Mol. Phys. 2018, 117, 968–974. [Google Scholar] [CrossRef]
- Ruggiero, M.R.; Baroni, S.; Pezzana, S.; Ferrante, G.; Crich, S.G.; Aime, S. Evidence for the Role of Intracellular Water Lifetime as a Tumour Biomarker Obtained by In Vivo Field-Cycling Relaxometry. Angew. Chem. Int. Ed. Engl. 2018, 57, 7468–7472. [Google Scholar] [CrossRef] [PubMed]
- Broche, L.M.; Ashcroft, G.P.; Lurie, D.J. Detection of osteoarthritis in knee and hip joints by fast field-cycling NMR. Magn. Reson. Med. 2012, 68, 358–362. [Google Scholar] [CrossRef]
- Broche, L.M.; Kennedy, B.W.; MacEachern, C.; Ashcroft, G.P.; Lurie, D.J. Fast field-cycling NMR of cartilage: A way toward molecular imaging. Osteoarthr. Cartil. 2014, 22, S66–S67. [Google Scholar] [CrossRef]
- Masiewicz, E.; Ashcroft, G.P.; Boddie, D.; Boddie, D.; Dundas, S.R.; Kruk, D.; Broche, L.M. Towards applying NMR relaxometry as a diagnostic tool for bone and soft tissue sarcomas: A pilot study. Sci. Rep. 2020, 10, 14207. [Google Scholar] [CrossRef] [PubMed]
- Kolodziejski, K.; Masiewicz, E.; Alamri, A.; Zampetoulas, V.; Samuel, L.; Murray, G.; Lurie, D.J.; Broche, L.M.; Kruk, D. Markers of low field NMR relaxation features of tissues. Sci. Rep. 2024, 14, 24901. [Google Scholar] [CrossRef]
- Broche, L.M.; Ross, P.J.; Davies, G.R.; MacLeod, M.-J.; Lurie, D.J. A whole-body Fast Field-Cycling scanner. Sci. Rep. 2019, 9, 10402. [Google Scholar] [CrossRef]
- Gradišek, A.; Domenici, V.; Apih, T.; Novotná, V.; Sebastião, P.J. 1H NMR Relaxometric Study of Molecular Dynamics in a de Vries Liquid Crystal. J. Phys. Chem. B 2016, 120, 4706–4714. [Google Scholar] [CrossRef]
- Fries, P.H.; Belorizky, E. Simple expressions of the nuclear relaxation rate enhancement due to quadrupole nuclei in slowly tumbling molecules. J. Chem. Phys. 2015, 143, 044202. [Google Scholar] [CrossRef]
- Kimmich, R.; Fatkullin, N. Polymer chain dynamics & NMR. Adv. Pol. Sci. 2004, 170, 1–113. [Google Scholar] [CrossRef]
- Kimmich, R.; Anoardo, E. Field-cycling NMR relaxometry. Prog. Nucl. Magn. Reson. Spectrosc. 2004, 44, 257–320. [Google Scholar] [CrossRef]
- Kresse, B.; Hofmann, M.; Privalov, A.F.; Fatkullin, N.; Fujara, F.; Rössler, E.A. All polymer diffusion regimes covered by combining field-cycling and field-gradient 1H NMR. Macromolecules 2015, 48, 4491–4502. [Google Scholar] [CrossRef]
- Bormuth, A.; Hofmann, M.; Henritzi, P.; Vogel, M.; Rössler, E.A. Chain-length dependence of polymer dynamics: A comparison of results from molecular dynamics simulations and field-cycling 1H NMR. Macromolecules 2013, 46, 7805–7811. [Google Scholar] [CrossRef]
- Hofmann, M.; Kresse, B.; Privalov, A.F.; Willner, L.; Fatkullin, N.; Fujara, F.; Rossler, E.A. Field-cycling NMR relaxometry probing the microscopic dynamics in polymer melts. Macromolecules 2014, 47, 7917–7929. [Google Scholar] [CrossRef]
- Masiewicz, E.; Ullah, F.; Mieloch, A.; Godlewski, J.; Kruk, D. Dynamical properties of solid and hydrated collagen: Insight from nuclear magnetic resonance relaxometry. J. Chem. Phys. 2024, 160, 165101. [Google Scholar] [CrossRef]
- Calucci, L.; Forte, C. Proton longitudinal relaxation coupling in dynamically heterogeneous soft systems. Prog. Nucl. Magn. Reson. Spectrosc. 2009, 55, 296–323. [Google Scholar] [CrossRef]
- Bryant, R.G.; Korb, J.-P. Nuclear magnetic resonance and spin relaxation in biological systems. Magn. Reson. Imaging 2005, 23, 167–173. [Google Scholar] [CrossRef]
- Kiihne, S.; Bryant, R.G. Protein-Bound Water Molecule Counting by Resolution of 1H Spin-Lattice Relaxation Mechanisms. Biophys. J. 2000, 78, 2163–2171. [Google Scholar] [CrossRef] [PubMed]
- Ratiney, H.; Albers, M.J.; Rabeson, H.; Kurhanewicz, J. Semi-parametric time-domain quantification of HR-MAS data from prostate tissue. NMR Biomed. 2010, 23, 1146–1151. [Google Scholar] [CrossRef] [PubMed]
- Schumacher, S.U.; Rothenhäusler, B.; Willmann, A.; Thun, J.; Moog, R.; Kuentz, M. Time domain NMR as a new process monitoring method for characterization of pharmaceutical hydrates. J. Pharm. Biomed. Anal. 2017, 137, 96–103. [Google Scholar] [CrossRef]



| Case | SUV | Tumor Size (mm × mm) | Description |
|---|---|---|---|
| P1 | 2.9 | 2.8 × 2.8 | Organized hematoma |
| P2 | 17.3 | 84 × 30 | Squamous cell carcinoma |
| P3 | 25.0 | 48 × 35 | Squamous cell carcinoma |
| P4 | 19.9 | 56 × 46 | Adenocarcinoma |
| P5 | 2.0 | 25 × 29 | Benign tumor from epithelioid cells |
| P6 | 9.6 | 80 × 90 | Squamous cell carcinoma |
| P7 | 14.2 | 84 × 57 | Adenocarcinoma |
| P8 | 12.2 | 65 × 51 | Squamous cell carcinoma |
| P9 | 26.7 | 53 × 50 | Pleomorphic lung cancer |
| P10 | 12.0 | 50 × 43 | Squamous cell carcinoma |
| Case | |||||||
|---|---|---|---|---|---|---|---|
| P1 (r) | 0.30 ± 0.01 | 48 | 10.8 ± 0.1 | 24.1 ± 0.77 | 46 | 2.2 | 6.4 |
| P1 (t) | 0.33 ± 0.01 | 54 | 5.6 ± 0.2 | 15.3 ± 0.20 | 36 | 2.7 | 2.7 |
| P2 (r) | 0.28 ± 0.01 | 43 | 11.99 ± 0.04 | 37.1 ± 0.89 | 26 | 3.1 | 6.1 |
| P2 (t) | 0.32 ± 0.01 | 55 | 6.4 ± 0.1 | 12.4 ± 0.11 | 38 | 1.9 | 4.6 |
| P3 (r) | 0.33 ± 0.01 | 59 | 7.5 ± 0.1 | 22.26 ± 0.04 | 46 | 3.0 | 3.2 |
| P3 (t) | 0.31 ± 0.01 | 53 | 10.11 ± 0.08 | 31.4 ± 0.3 | 61 | 3.2 | 4.7 |
| P4 (r) | 0.33 ± 0.01 | 50 | 10.9 ± 0.1 | 37.3 ± 0.7 | 81 | 3.4 | 7.0 |
| P4 (t) | 0.30 ± 0.01 | 51 | 7.62 ± 0.06 | 22.5 ± 0.2 | 48 | 2.9 | 5.4 |
| P5 (r) | 0.29 ± 0.01 | 44 | 6.72 ± 0.05 | 15.5 ± 0.2 | 66 | 2.3 | 4.9 |
| P5 (t) | 0.29 ± 0.01 | 49 | 2.37 ± 0.02 | 11.04 ± 0.04 | 20 | 4.7 | 1.7 |
| P6 (r) | 0.29 ± 0.01 | 52 | 6.61 ± 0.08 | 16.1 ± 0.1 | 36 | 2.4 | 4.4 |
| P6 (t) | 0.30 ± 0.01 | 53 | 7.49 ± 0.03 | 18.2 ± 0.2 | 76 | 2.4 | 5.1 |
| P7 (r) | 0.28 ± 0.01 | 49 | 6.68 ± 0.04 | 18.8 ± 0.2 | 88 | 2.8 | 4.5 |
| P7 (t) | 0.33 ± 0.01 | 58 | 5.91 ± 0.06 | 28.8 ± 0.1 | 19 | 4.9 | 2.7 |
| P8 (r) | 0.27 ± 0.01 | 47 | 3.91 ± 0.04 | 12.8 ± 0.1 | 27 | 3.3 | 2.9 |
| P8 (t) | 0.29 ± 0.01 | 51 | 2.95 ± 0.02 | 8.40 ± 0.04 | 35 | 2.9 | 2.8 |
| P9 (r) | 0.33 ± 0.01 | 51 | 4.18 ± 0.04 | 11.89 ± 0.05 | 21 | 2.8 | 3.4 |
| P9 (t) | 0.30 ± 0.01 | 48 | 4.38 ± 0.03 | 14.6 ± 0.1 | 34 | 3.3 | 2.9 |
| P10 (t) | 0.33 ± 0.01 | 52 | 10.1 ± 0.1 | 18.8 ± 0.2 | 66 | 1.9 | 5.2 |
| Avg. (t) | 0.31 ± 0.02 | 52 ± 3 | 6.3 ± 0.2 | 18.2 ± 0.7 | 43 ± 19 | 3.2 ± 0.9 | 3.7 ± 1.3 |
| Avg. (r) | 0.30 ± 0.02 | 49 ± 4 | 7.7 ± 0.3 | 21.8 ± 0.9 | 49 ± 24 | 2.8 ± 0.4 | 4.8 ± 1.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kołodziejski, K.; Ullah, F.; Klepacki, Ł.; Gielecki, J.; Kruk, D. 1H NMR Relaxation Processes in Lung Tissues at Low Magnetic Fields. Molecules 2025, 30, 4002. https://doi.org/10.3390/molecules30194002
Kołodziejski K, Ullah F, Klepacki Ł, Gielecki J, Kruk D. 1H NMR Relaxation Processes in Lung Tissues at Low Magnetic Fields. Molecules. 2025; 30(19):4002. https://doi.org/10.3390/molecules30194002
Chicago/Turabian StyleKołodziejski, Karol, Farman Ullah, Łukasz Klepacki, Jerzy Gielecki, and Danuta Kruk. 2025. "1H NMR Relaxation Processes in Lung Tissues at Low Magnetic Fields" Molecules 30, no. 19: 4002. https://doi.org/10.3390/molecules30194002
APA StyleKołodziejski, K., Ullah, F., Klepacki, Ł., Gielecki, J., & Kruk, D. (2025). 1H NMR Relaxation Processes in Lung Tissues at Low Magnetic Fields. Molecules, 30(19), 4002. https://doi.org/10.3390/molecules30194002






