Absorption Spectrum of Hydroperoxymethyl Thioformate: A Computational Chemistry Study
Abstract
:1. Introduction
- -
- Studying the structural parameters of HPMTF in both the gas and aqueous phases;
- -
- Calculating the absorption spectra of HPMTF in the gas phase and in the aqueous phase;
- -
- Performing a critical analysis of the approximations used in the literature for the spectroscopic and photochemical properties of HPMTF;
- -
- Estimating the photolytic behavior by calculating photolysis constants based on our computed spectra.
2. Results and Discussion
2.1. Geometrical Analyses
2.1.1. Selection of Computational Method
2.1.2. Conformational Study of HPMTF
2.1.3. Water Clusters and Aqueous Solution
2.2. Excitation Properties: Nature, Energies, and Oscillator Strengths
2.2.1. Isolated Molecule
2.2.2. Solvatochromic Shifts
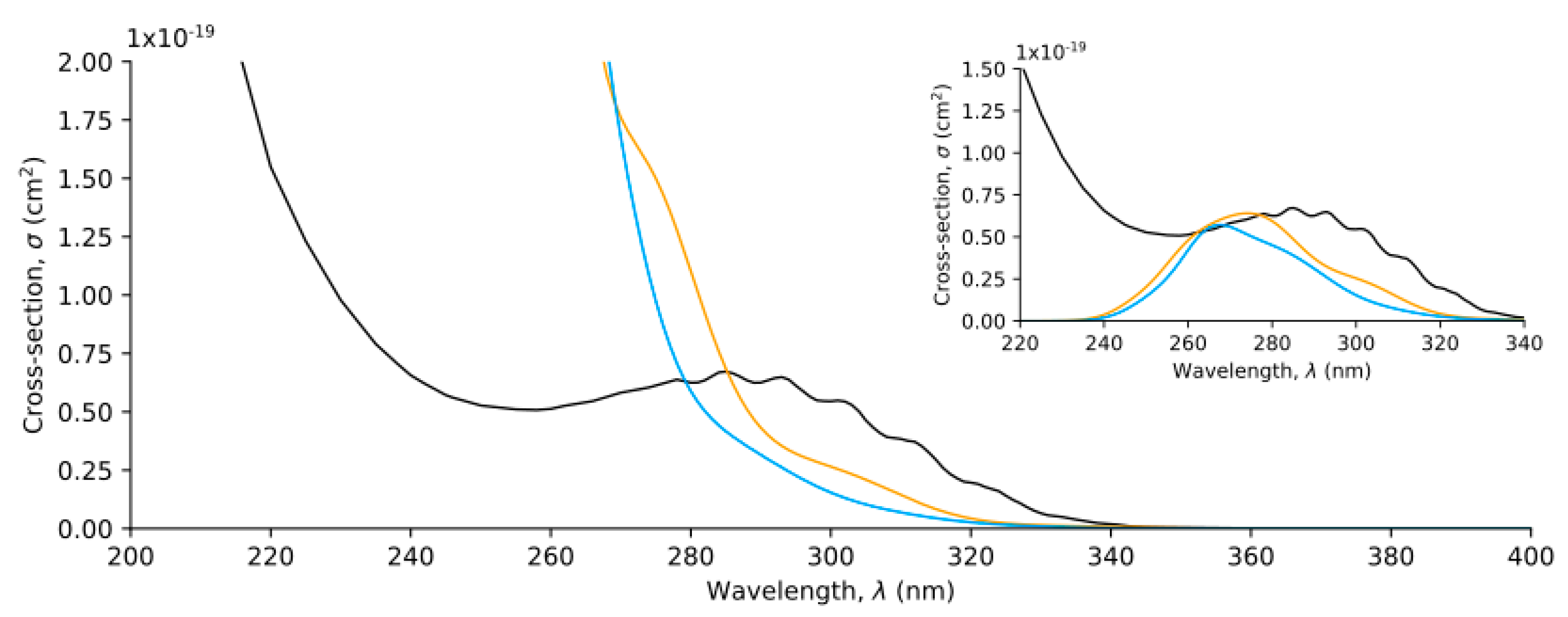
2.3. Absorption Electronic Spectra
2.3.1. Cross-Sections in the Gas Phase
2.3.2. Cross-Sections in Aqueous Solution
2.4. Estimated Photolysis, Atmospheric Implications, and Future Perspectives
3. Materials and Methods
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Charlson, R.J.; Lovelock, J.E. Oceanic phytoplankton, atmospheric sulphur, cloud albedo and climate. Nature 1987, 326, 655–661. [Google Scholar] [CrossRef]
- Likens, G.E.; Bormann, F.H. Acid Rain. Environ. Sci. Policy Sustain. Dev. 1972, 14, 33–40. [Google Scholar] [CrossRef]
- Charlson, R.J.; Schwartz, S.E. Climate forcing by anthropogenic aerosols. Science 1992, 255, 423–430. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Wang, H. Global source attribution of sulfate concentration and direct and indirect radiative forcing. Atmos. Chem. Phys. 2017, 17, 8903–8922. [Google Scholar] [CrossRef]
- Wu, R.; Wang, S. New Mechanism for the Atmospheric Oxidation of Dimethyl Sulfide. The Importance of Intramolecular Hydrogen Shift in a CH3SCH2OO Radical. J. Phys. Chem. A 2015, 119, 112–117. [Google Scholar] [CrossRef]
- Berndt, T.; Scholz, W. Fast Peroxy Radical Isomerization and OH Recycling in the Reaction of OH Radicals with Dimethyl Sulfide. J. Phys. Chem. Lett. 2019, 10, 6478–6483. [Google Scholar] [CrossRef] [PubMed]
- Veres, P.R.; Neuman, J.A. Global airborne sampling reveals a previously unobserved dimethyl sulfide oxidation mechanism in the marine atmosphere. Proc. Natl. Acad. Sci. USA 2020, 117, 4505–4510. [Google Scholar] [CrossRef] [PubMed]
- Khan, M.A.H.; Bannan, T.J. Impacts of Hydroperoxymethyl Thioformate on the Global Marine Sulfur Budget. ACS Earth Space Chem. 2021, 5, 2577–2586. [Google Scholar] [CrossRef]
- Khan, M.A.H.; Gillespie, S.M.P. A modelling study of the atmospheric chemistry of DMS using the global model, STOCHEM-CRI. Atmos. Environ. 2016, 127, 69–79. [Google Scholar] [CrossRef]
- Jernigan, C.; Bertram, T.H. Laboratory measurements of reduced and oxidized sulfur formed from dimethyl sulfide oxidation under low NOx concentrations. AGU Fall Meet. Abstr. 2019, 2019, A43Q-3122. [Google Scholar]
- Besler, B.H.; Scuseria, G.E. A systematic theoretical study of harmonic vibrational frequencies: The single and double excitation coupled cluster (CCSD) method. J. Chem. Phys. 1988, 89, 306–366. [Google Scholar] [CrossRef]
- Borrego-Sánchez, A.; Zemmouche, M. Multiconfigurational Quantum Chemistry Determinations of Absorption Cross Sections (σ) in the Gas Phase and Molar Extinction Coefficients (ε) in Aqueous Solution and Air–Water Interface. J. Chem. Theory Comput. 2021, 17, 3571–3582. [Google Scholar] [CrossRef]
- Master Chemical Mechanism (MCM) v3.3.1. Photolysis Parameters. Available online: https://mcm.york.ac.uk/MCM/rates/photolysis (accessed on 22 November 2024).
- Rao, Z.; Li, X. Spontaneous Oxidation of Thiols and Thioether at the Air–Water Interface of a Sea Spray Microdroplet. J. Am. Chem. Soc. 2023, 145, 10839–10846. [Google Scholar] [CrossRef]
- Møller, C.; Plesset, M.S. Note on an Approximation Treatment for Many-Electron Systems. Phys. Rev. 1934, 46, 618. [Google Scholar] [CrossRef]
- Bartlett, R.J. Many-Body Perturbation Theory and Coupled Cluster Theory for Electron Correlation in Molecules. Ann. Rev. Phys. Chem. 1981, 32, 359–401. [Google Scholar] [CrossRef]
- Purvis, G.D., III; Bartlett, R.J. A full coupled-cluster singles and doubles model: The inclusion of disconnected triples. J. Chem. Phys. 1982, 76, 1910–1918. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785. [Google Scholar] [CrossRef]
- Vosko, S.H.; Wilk, L. Accurate spin-dependent electron liquid correlation energies for local spin density calculations: A critical analysis. Can. J. Phys. 1980, 58, 1200–1211. [Google Scholar] [CrossRef]
- Stephens, J.; Devlin, F.J. Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields. J. Phys. Chem. 1994, 98, 11623–11627. [Google Scholar] [CrossRef]
- Krishnan, R.; Binkley, J.S. Self-consistent molecular orbital methods. XX. A basis set for correlated wave functions. J. Chem. Phys. 1980, 72, 650–654. [Google Scholar] [CrossRef]
- Clark, T.; Chandrasekhar, J. Efficient diffuse function-augmented basis sets for anion calculations. III. The 3-21+G basis set for first-row elements, Li-F. J. Comput. Chem. 1983, 4, 294–301. [Google Scholar] [CrossRef]
- McLean, A.D.; Chandler, G.S. Contracted Gaussian basis sets for molecular calculations. I. Second row atoms, Z=11-18. J. Chem. Phys. 1980, 72, 5639–5648. [Google Scholar] [CrossRef]
- Francl, M.M.; Pietro, W.J. Self-consistent molecular orbital methods. XXIII. A polarization-type basis set for second-row elements. J. Chem. Phys. 1982, 77, 3654–3665. [Google Scholar] [CrossRef]
- Spitznagel, G.W.; Clark, T. An evaluation of the performance of diffuse function-augmented basis sets for second row elements. J. Comput. Chem. 1987, 8, 1109–1116. [Google Scholar] [CrossRef]
- Pracht, P.; Bohle, F. Automated exploration of the low-energy chemical space with fast quantum chemical methods. Phys. Chem. Chem. Phys. 2020, 22, 7169–7192. [Google Scholar] [CrossRef]
- Grimme, S. Exploration of Chemical Compound, Conformer, and Reaction Space with Meta-Dynamics Simulations Based on Tight-Binding Quantum Chemical Calculations. J. Chem. Theory Comput. 2019, 15, 2847–2862. [Google Scholar] [CrossRef]
- Pracht, P.; Grimme, S. CREST—A program for the exploration of low-energy molecular chemical space. J. Chem. Phys. 2024, 160, 114110. [Google Scholar] [CrossRef]
- Spicher, S.; Grimme, S. Robust Atomistic Modeling of Materials, Organometallic, and Biochemical Systems. Angew. Chem. 2020, 59, 15665–15673. [Google Scholar] [CrossRef]
- Tomasi, J.; Mennucci, B. Quantum Mechanical Continuum Solvation Models. Chem. Rev. 2005, 105, 2999–3094. [Google Scholar] [CrossRef]
- Miertuš, S.; Scrocco, E. Electrostatic interaction of a solute with a continuum. A direct utilizaion of AB initio molecular potentials for the prevision of solvent effects. Chem. Phys. 1981, 55, 117–129. [Google Scholar] [CrossRef]
- Miertuš, S.; Tomasi, J. Approximate evaluations of the electrostatic free energy and internal energy changes in solution processes. Chem. Phys. 1982, 65, 239–245. [Google Scholar] [CrossRef]
- Pascual-ahuir, J.L.; Silla, E. GEPOL: An improved description of molecular surfaces. III. A new algorithm for the computation of a solvent-excluding surface. J. Comput. Chem. 1994, 15, 1127–1138. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed]
- Frisch, M.J.; Trucks, G.W. Gaussian 16, revision C.01; Gaussian Inc.: Wallingford, CT, USA, 2016.
- Crespo-Otero, R.; Barbatti, M. Spectrum simulation and decomposition with nuclear ensemble: Formal derivation and application to benzene, furan and 2-phenylfuran. Theor. Chem. Acc. 2012, 131, 1237. [Google Scholar] [CrossRef]
- Multispec, Tool for Predicting Electronic Spectra with Multiconfigurational Quantum Chemistry and Nuclear Ensemble Approaches. Available online: https://github.com/qcexval/multispec (accessed on 22 November 2024).
- Wigner, E. On the Quantum Correction For Thermodynamic Equilibrium. Phys. Rev. 1932, 40, 749. [Google Scholar] [CrossRef]
- Barbatti, M.; Bondanza, M. Newton-X Platform: New Software Developments for Surface Hopping and Nuclear Ensembles. J. Chem. Theory Comput. 2022, 18, 6851–6865. [Google Scholar] [CrossRef] [PubMed]
- Case, D.A.; Aktulga, H.M. AmberTools. J. Chem. Inf. Model. 2023, 63, 6183–6191. [Google Scholar] [CrossRef] [PubMed]
- Case, D.A.; Aktulga, H.M. Amber22, version 2022; University of California: San Francisco, CA, USA, 2022.
- Wang, J.; Wolf, R.M. Development and testing of a general amber force field. J. Comput. Chem. 2004, 25, 1157–1174. [Google Scholar] [CrossRef] [PubMed]
- Jorgensen, W.L.; Chandrasekhar, J. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Miyamoto, S.; Kollman, P.A. Settle: An analytical version of the SHAKE and RATTLE algorithm for rigid water models. J. Comput. Chem. 1992, 13, 952–962. [Google Scholar] [CrossRef]
- Singh, U.C.; Kollman, P.A. An approach to computing electrostatic charges for molecules. J. Comput. Chem. 1984, 5, 129–145. [Google Scholar] [CrossRef]
- Besler, B.H.; Merz, K.M. Atomic charges derived from semiempirical methods. J. Comput. Chem. 1990, 11, 431–439. [Google Scholar] [CrossRef]
- Darden, T.; York, D. Particle mesh Ewald: An N⋅log(N) method for Ewald sums in large systems. J. Chem. Phys. 1993, 98, 10089–10092. [Google Scholar] [CrossRef]
- Essmann, U.; Perera, L. A smooth particle mesh Ewald method. J. Chem. Phys. 1995, 103, 8577–8593. [Google Scholar] [CrossRef]
- Olsen, J. The CASSCF Method: A perspective and Commentary. Int. J. Quantum Chem. 2011, 111, 3267–3272. [Google Scholar] [CrossRef]
- Finley, J.; Malmqvist, P.Å. The multi-state CASPT2 method. Chem. Phys. Lett. 1998, 288, 299–306. [Google Scholar] [CrossRef]
- Widmark, P.O.; Malmqvist, P.Å. Density matrix averaged atomic natural orbital (ANO) basis sets for correlated molecular wave functions. Theoret. Chim. Acta 1990, 77, 291–306. [Google Scholar] [CrossRef]
- Widmark, P.O.; Persson, B.J. Density matrix averaged atomic natural orbital (ANO) basis sets for correlated molecular wave functions. Theoret. Chim. Acta 1991, 79, 419–432. [Google Scholar] [CrossRef]
- Ghigo, G.; Roos, B.O. A modified definition of the zeroth-order Hamiltonian in multiconfigurational perturbation theory (CASPT2). Chem. Phys. Lett. 2004, 396, 142–149. [Google Scholar] [CrossRef]
- Roos, B.O.; Andersson, K. Multiconfigurational perturbation theory with level shift—The Cr2 potential revisited. Chem. Phys. Lett. 1995, 245, 215–223. [Google Scholar] [CrossRef]
- Roos, B.O.; Andersson, K. Applications of level shift corrected perturbation theory in electronic spectroscopy. Chem. Phys. Lett. 1996, 388, 257–276. [Google Scholar] [CrossRef]
- Forsberg, N.; Malmqvist, P.Å. Multiconfiguration perturbation theory with imaginary level shift. Chem. Phys. Lett. 1997, 274, 196–204. [Google Scholar] [CrossRef]
- Aquilante, F.; Autschbach, J. Modern quantum chemistry with [Open]Molcas. J. Chem. Phys. 2020, 152, 214117. [Google Scholar] [CrossRef]
- Galván, I.F.; Vacher, M. OpenMolcas: From Source Code to Insight. J. Chem. Theory Comput. 2019, 15, 5925–5964. [Google Scholar] [CrossRef] [PubMed]
- Manni, G.L.; Galván, I.F. The OpenMolcas Web: A Community-Driven Approach to Advancing Computational Chemistry. J. Chem. Theory Comput. 2023, 19, 6933–6991. [Google Scholar] [CrossRef] [PubMed]
- ACOM: Quick TUV. Available online: https://www.acom.ucar.edu/Models/TUV/Interactive_TUV (accessed on 15 June 2023).
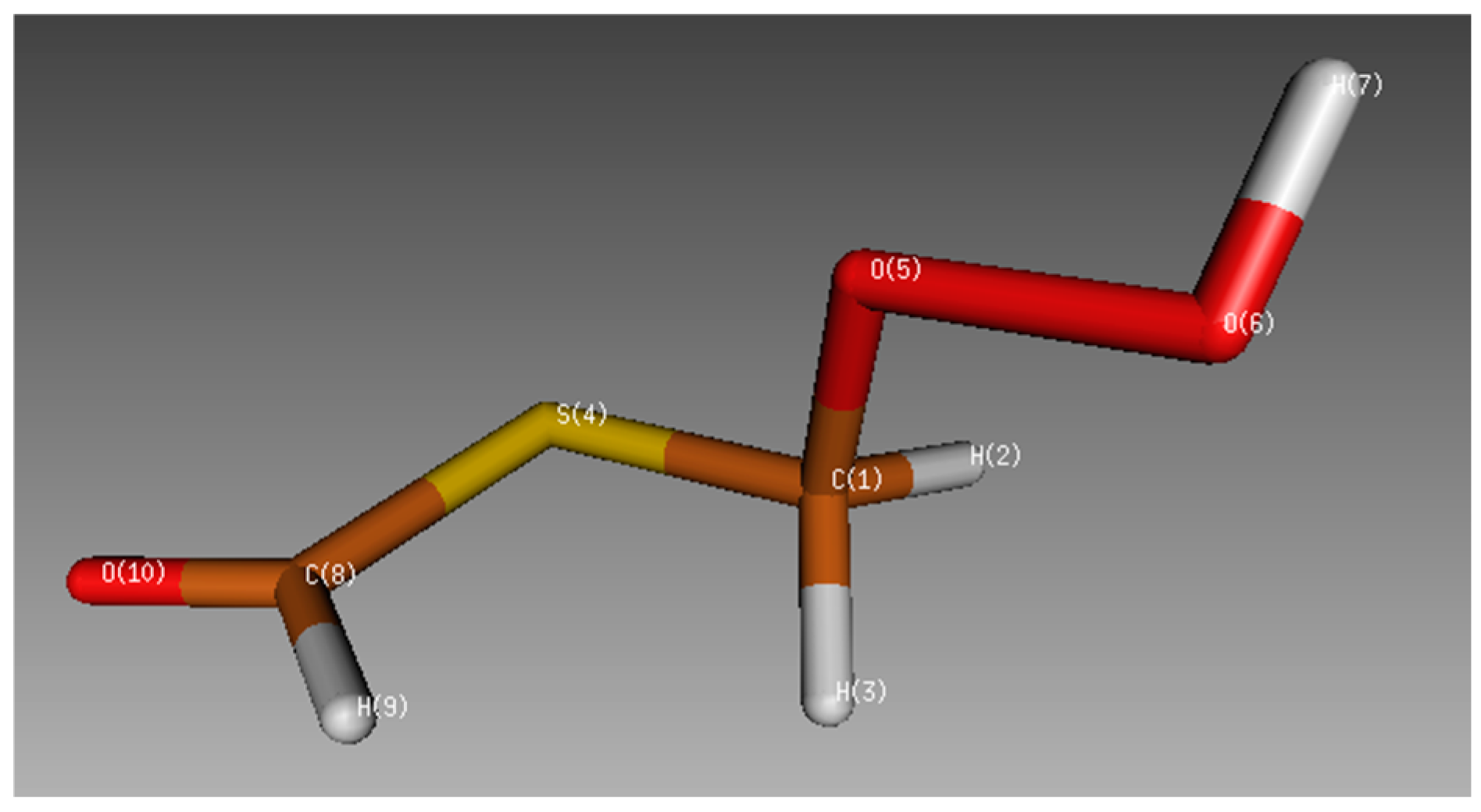
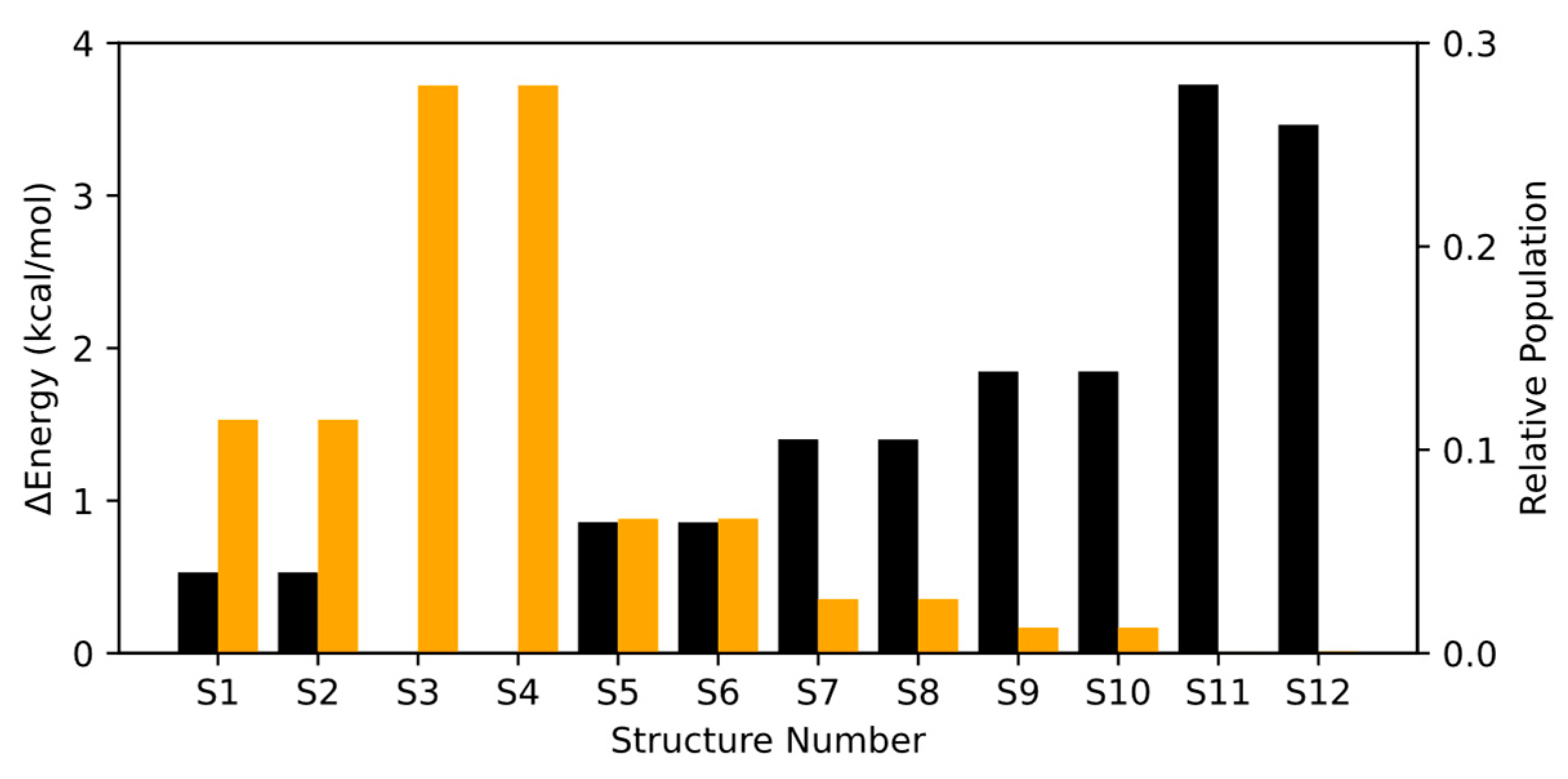

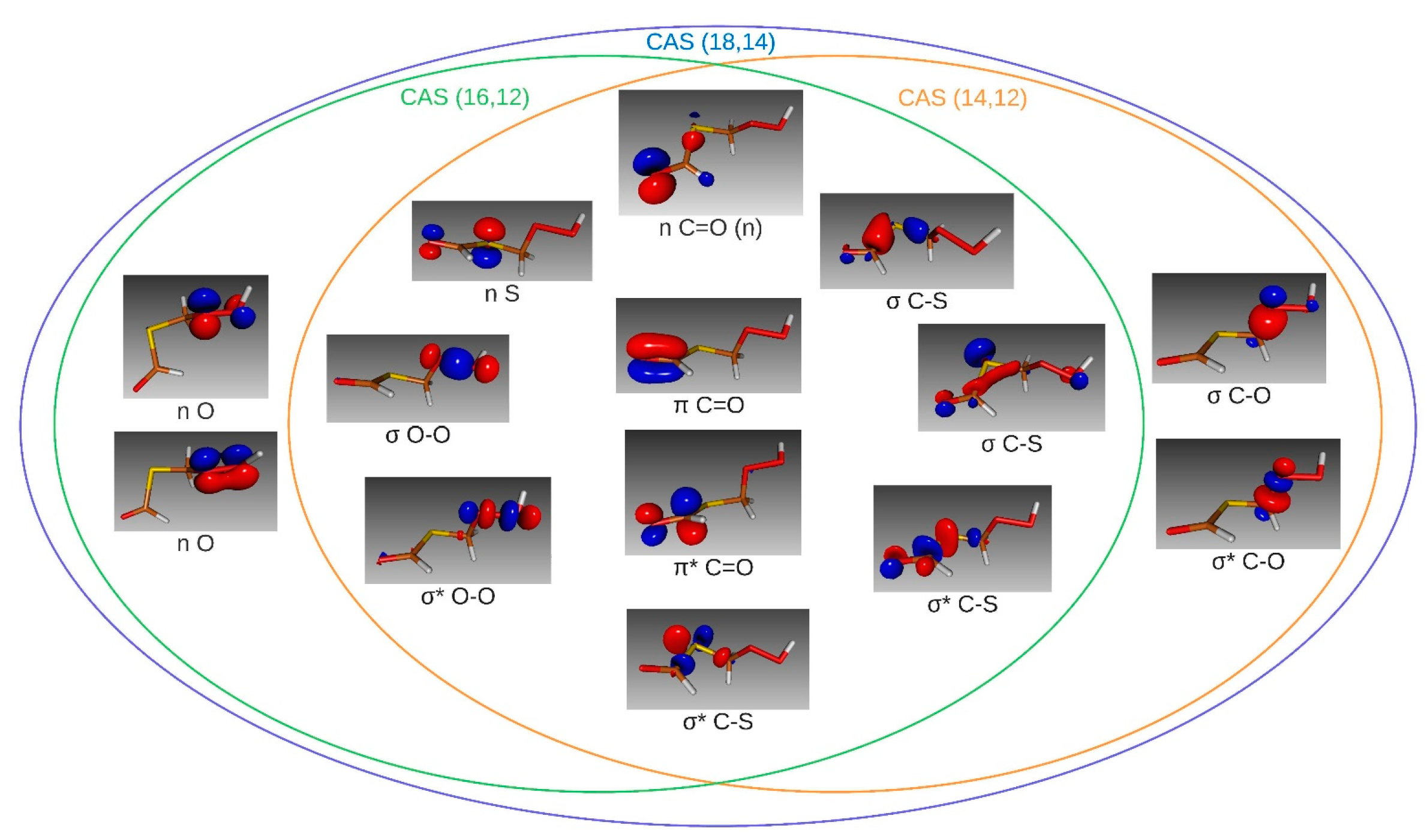
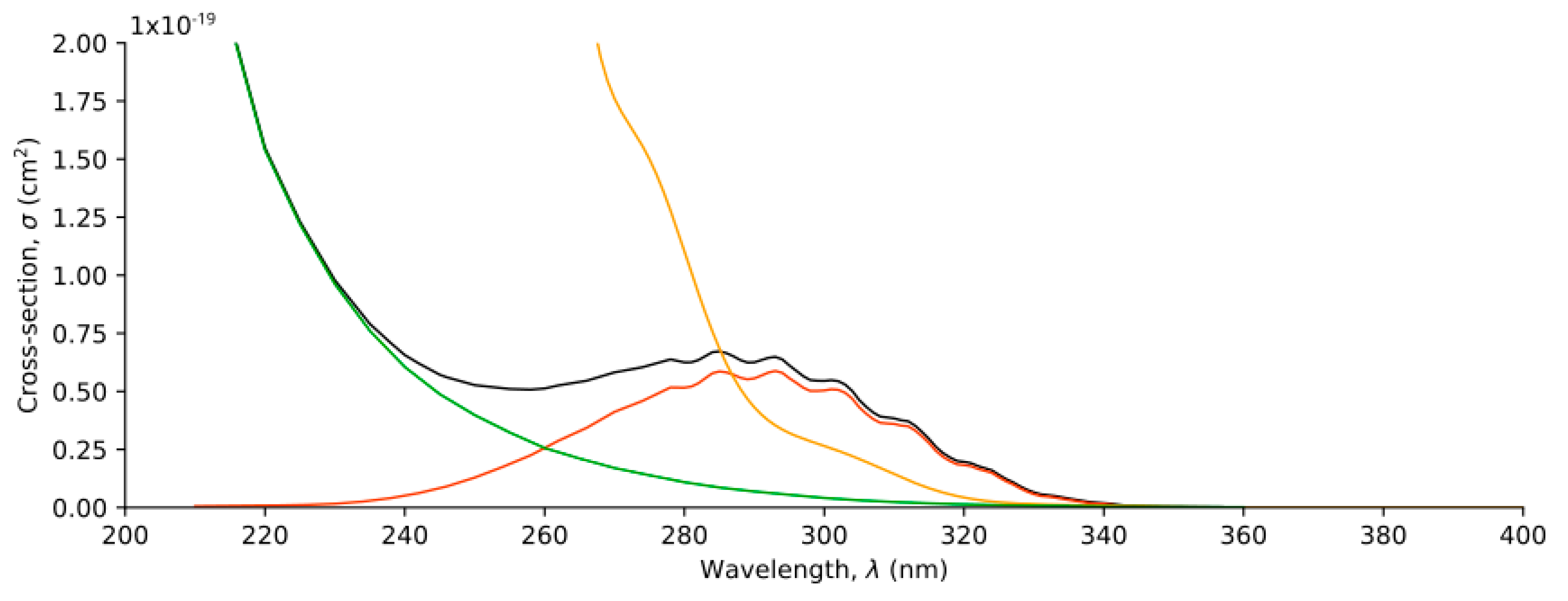
| HF | DFT | MP2 | CCSD | ||
|---|---|---|---|---|---|
| Bond Distances (Å) | O10-C8 * | 1.173 | 1.195 | 1.205 | 1.198 |
| C8-H9 | 1.093 | 1.106 | 1.107 | 1.107 | |
| C8-S4 | 1.781 | 1.801 | 1.779 | 1.787 | |
| S4-C1 | 1.799 | 1.812 | 1.791 | 1.800 | |
| C1-H2 | 1.083 | 1.093 | 1.093 | 1.095 | |
| C1-H3 | 1.083 | 1.094 | 1.095 | 1.095 | |
| C1-O5 | 1.398 | 1.419 | 1.417 | 1.418 | |
| O5-O6 | 1.385 | 1.466 | 1.460 | 1.446 | |
| O6-H7 | 0.944 | 0.968 | 0.966 | 0.964 | |
| Bond Angles (°) | O10-C8-S4 | 122.4 | 123.0 | 123.5 | 123.1 |
| C8-S4-C1 | 99.9 | 99.2 | 97.5 | 97.8 | |
| S4-C1-O5 | 108.4 | 106.7 | 106.3 | 106.9 | |
| C1-O5-O6 | 107.0 | 105.5 | 104.7 | 105.2 | |
| O5-O6-H7 | 102.7 | 99.9 | 99.0 | 100.0 | |
| Dihedral Angles (°) | O10-C8-S4-C1 | 178.7 | 178.6 | 176.8 | 177.0 |
| C8-S4-C1-O5 | −73.9 | −81.6 | −77.1 | −75.9 | |
| S4-C1-O5-O6 | 178.2 | −179.3 | 178.5 | 178.4 | |
| C1-O5-O6-H7 | 126.7 | 130.6 | 130.0 | 127.8 | |
| Vibrational Mode | DFT | MP2 | CCSD | Vibrational Mode | DFT | MP2 | CCSD |
|---|---|---|---|---|---|---|---|
| 1 | 57.3 | 63.9 | 64.4 | 13 | 963.0 | 989.1 | 993.0 |
| 2 | 103.3 | 116.9 | 113.2 | 14 | 1020.7 | 1069.2 | 1087.1 |
| 3 | 167.6 | 170.1 | 161.2 | 15 | 1219.9 | 1247.8 | 1256.0 |
| 4 | 188.1 | 216.4 | 223.0 | 16 | 1313.3 | 1336.6 | 1362.4 |
| 5 | 228.9 | 249.5 | 247.9 | 17 | 1356.8 | 1380.8 | 1407.5 |
| 6 | 273.9 | 288.0 | 291.9 | 18 | 1373.0 | 1406.6 | 1419.1 |
| 7 | 369.0 | 388.5 | 390.6 | 19 | 1492.5 | 1505.4 | 1515.2 |
| 8 | 475.0 | 495.8 | 497.4 | 20 | 1788.6 | 1746.6 | 1806.1 |
| 9 | 741.0 | 788.2 | 785.3 | 21 | 2929.9 | 2990.9 | 2990.7 |
| 10 | 772.4 | 823.4 | 820.5 | 22 | 3033.8 | 3090.1 | 3078.5 |
| 11 | 879.8 | 877.5 | 926.5 | 23 | 3092.2 | 3156.8 | 3135.2 |
| 12 | 924.3 | 934.3 | 940.2 | 24 | 3778.9 | 3830.8 | 3854.7 |
| Electronic State | CAS (18,14) | CAS (16,12) | CAS (14,12) | |||
|---|---|---|---|---|---|---|
| ΔE (eV) | Osc. Str. | ΔE (eV) | Osc. Str. | ΔE (eV) | Osc. Str. | |
| S0 | 0.0000 | 0.0000 | 0.0000 | |||
| S1 | 4.5869 | 1.33 × 10−4 | 4.5821 | 1.26 × 10−4 | 4.6182 | 1.40 × 10−4 |
| S2 | 5.5525 | 5.95 × 10−3 | 5.5657 | 3.53 × 10−3 | 5.7950 | 6.33 × 10−2 |
| S3 | 5.7562 | 8.73 × 10−2 | 5.7931 | 8.12 × 10−2 | 6.1512 | 1.13 × 10−3 |
| S4 | 6.1793 | 7.68 × 10−4 | 6.1035 | 8.01 × 10−4 | 6.9595 | 9.07 × 10−2 |
| S5 | 6.9185 | 8.83 × 10−2 | 6.9377 | 1.12 × 10−1 | 8.0963 | 1.14 × 10−2 |
| S6 | 7.5116 | 2.22 × 10−4 | 7.5587 | 1.78 × 10−4 | 9.2233 | 7.90 × 10−2 |
| S7 | 7.8580 | 1.00 × 10−2 | 8.0324 | 1.55 × 10−2 | 10.3142 | 6.76 × 10−4 |
| Electronic State | 8 Roots | 10 Roots | 12 Roots | |||
|---|---|---|---|---|---|---|
| ΔE (eV) | Osc. Str. | ΔE (eV) | Osc. Str. | ΔE (eV) | Osc. Str. | |
| S0 | 0.0000 | 0.0000 | 0.0000 | |||
| S1 | 4.5821 | 1.26 × 10−4 | 4.5798 | 1.22 × 10−4 | 4.6082 | 9.65 × 10−5 |
| S2 | 5.5657 | 3.53 × 10−3 | 5.5101 | 4.51 × 10−3 | 5.4983 | 5.02 × 10−3 |
| S3 | 5.7931 | 8.12 × 10−2 | 5.7570 | 8.90 × 10−2 | 5.7677 | 7.41 × 10−2 |
| S4 | 6.1035 | 8.01 × 10−4 | 6.2168 | 7.34 × 10−4 | 6.2052 | 1.15 × 10−3 |
| S5 | 6.9377 | 1.12 × 10−1 | 6.9639 | 1.01 × 10−1 | 6.9461 | 9.87 × 10−2 |
| S6 | 7.5587 | 1.78 × 10−4 | 7.6567 | 3.20 × 10−3 | 7.4712 | 1.90 × 10−3 |
| S7 | 8.0324 | 1.55 × 10−2 | 7.7128 | 1.48 × 10−3 | 7.7658 | 2.69 × 10−4 |
| S8 | 8.1640 | 1.41 × 10−2 | 8.0708 | 1.29 × 10−2 | ||
| S9 | 8.7098 | 2.06 × 10−3 | 8.1414 | 1.37 × 10−2 | ||
| S10 | 8.7480 | 1.48 × 10−3 | ||||
| S11 | 9.3123 | 7.55 × 10−2 | ||||
| Electronic State | No Field | Field | ||
|---|---|---|---|---|
| ΔE (eV) | Osc. Str. | ΔE (eV) | Osc. Str. | |
| S0 | 0.0000 | 0.0000 | ||
| S1 | 4.4374 | 6.17 × 10−5 | 4.5649 | 2.54 × 10−4 |
| S2 | 5.5770 | 9.64 × 10−2 | 5.6615 | 1.15 × 10−1 |
| S3 | 5.9234 | 1.14 × 10−3 | 5.8150 | 4.02 × 10−4 |
| S4 | 5.9779 | 1.49 × 10−3 | 6.4215 | 1.68 × 10−3 |
| S5 | 6.8171 | 7.66 × 10−2 | 7.1528 | 7.61 × 10−2 |
| S6 | 7.3893 | 5.79 × 10−4 | 7.3539 | 1.86 × 10−3 |
| S7 | 8.0283 | 1.52 × 10−2 | 7.7733 | 1.41 × 10−2 |
| Photolysis Rate | Lifetime (Hours) | |
|---|---|---|
| Chromophore Approximation | 6.14 × 10−5 | 4.52 |
| Gas Phase | 1.93 × 10−5 | 14.37 |
| Aqueous Phase | 1.02 × 10−5 | 27.18 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Catalán-Fenollosa, D.; Carmona-García, J.; Borrego-Sánchez, A.; Saiz-Lopez, A.; Roca-Sanjuán, D. Absorption Spectrum of Hydroperoxymethyl Thioformate: A Computational Chemistry Study. Molecules 2025, 30, 338. https://doi.org/10.3390/molecules30020338
Catalán-Fenollosa D, Carmona-García J, Borrego-Sánchez A, Saiz-Lopez A, Roca-Sanjuán D. Absorption Spectrum of Hydroperoxymethyl Thioformate: A Computational Chemistry Study. Molecules. 2025; 30(2):338. https://doi.org/10.3390/molecules30020338
Chicago/Turabian StyleCatalán-Fenollosa, David, Javier Carmona-García, Ana Borrego-Sánchez, Alfonso Saiz-Lopez, and Daniel Roca-Sanjuán. 2025. "Absorption Spectrum of Hydroperoxymethyl Thioformate: A Computational Chemistry Study" Molecules 30, no. 2: 338. https://doi.org/10.3390/molecules30020338
APA StyleCatalán-Fenollosa, D., Carmona-García, J., Borrego-Sánchez, A., Saiz-Lopez, A., & Roca-Sanjuán, D. (2025). Absorption Spectrum of Hydroperoxymethyl Thioformate: A Computational Chemistry Study. Molecules, 30(2), 338. https://doi.org/10.3390/molecules30020338








