Potential Push-Pull Carbon Superbases Based on Methyl Substitution of Rare Tautomers of Imines
Abstract
:1. Introduction
2. Results and Discussion
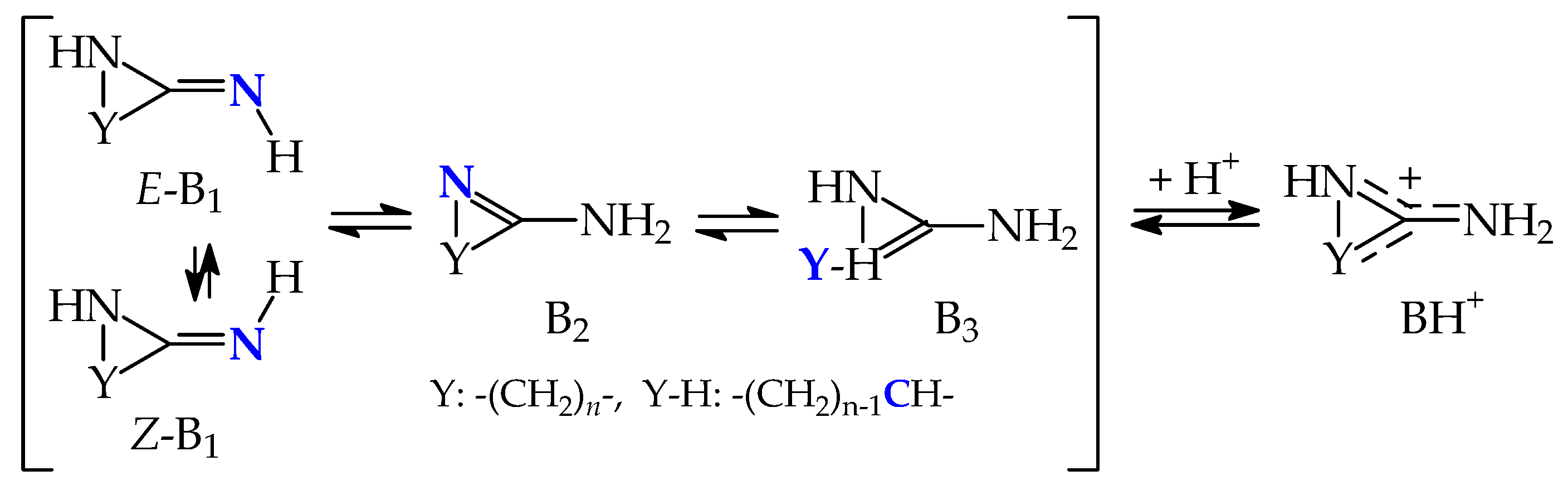
2.1. Basicity of Acyclic Tautomeric System 1 Containing the Amidine Group
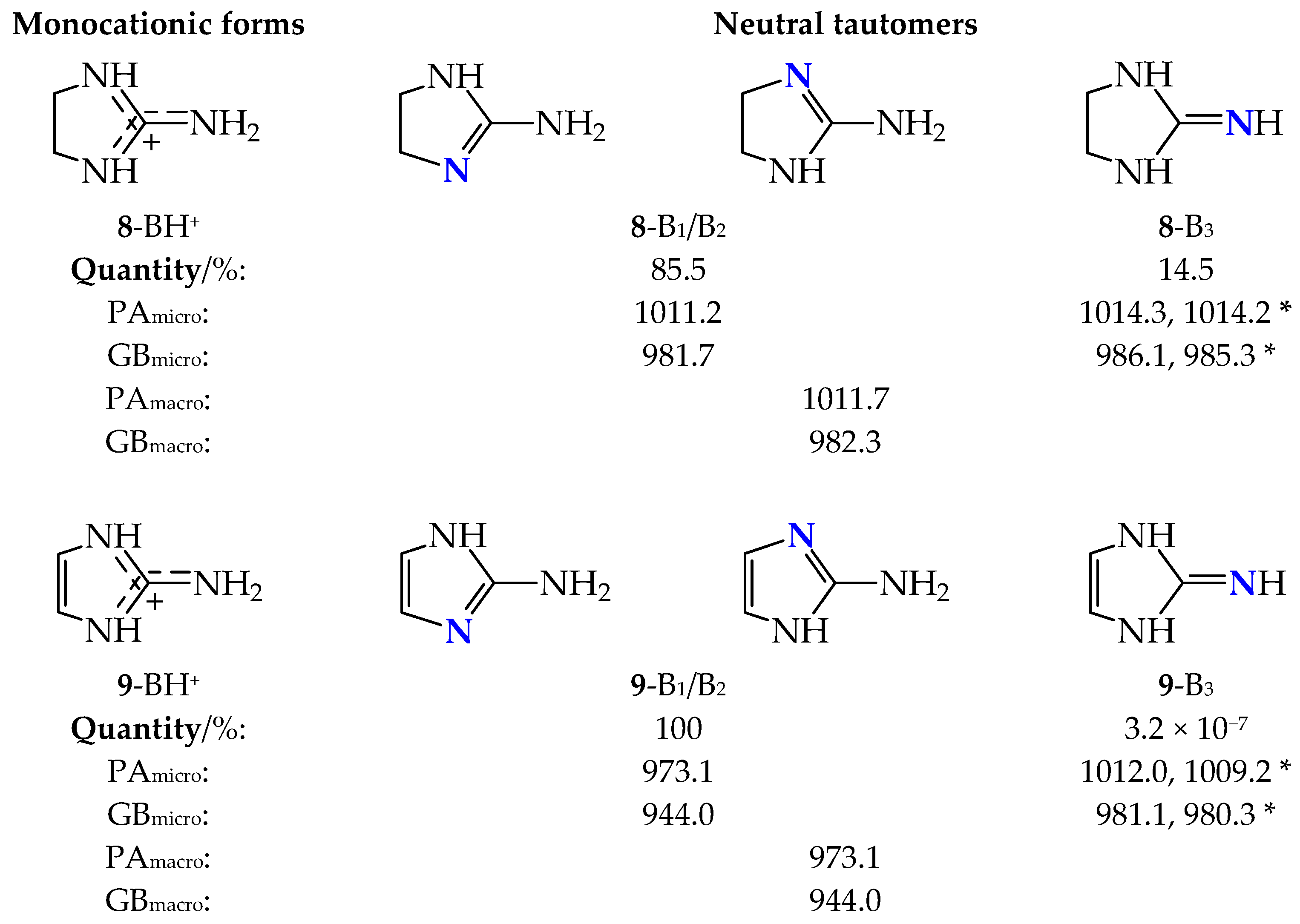
2.2. Basicity of Cyclic Tautomeric Systems 2–7 Containing the Amidine Group
2.3. Basicity of Tautomeric Cyclic Systems Containing the Guanidine Group
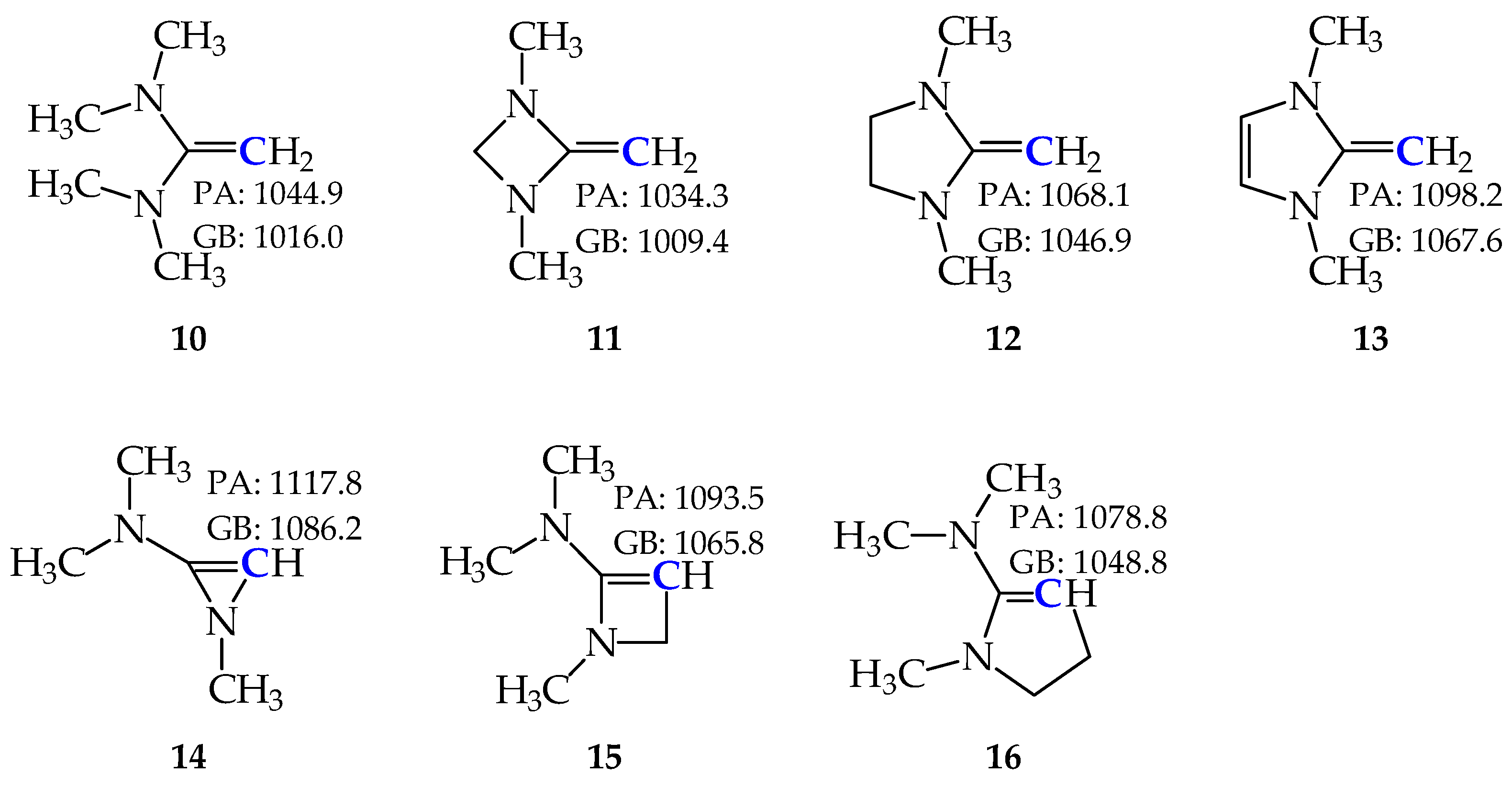
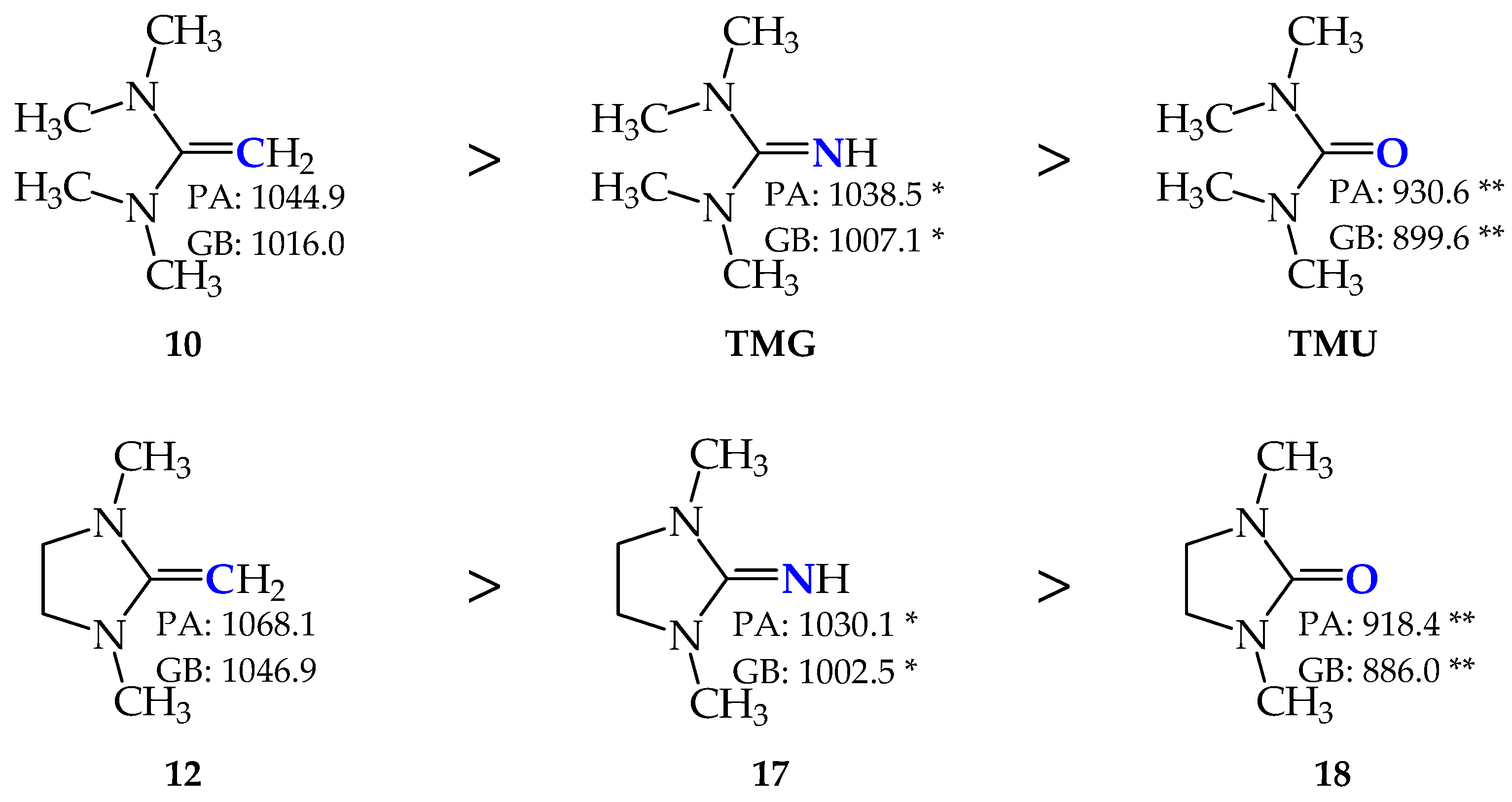
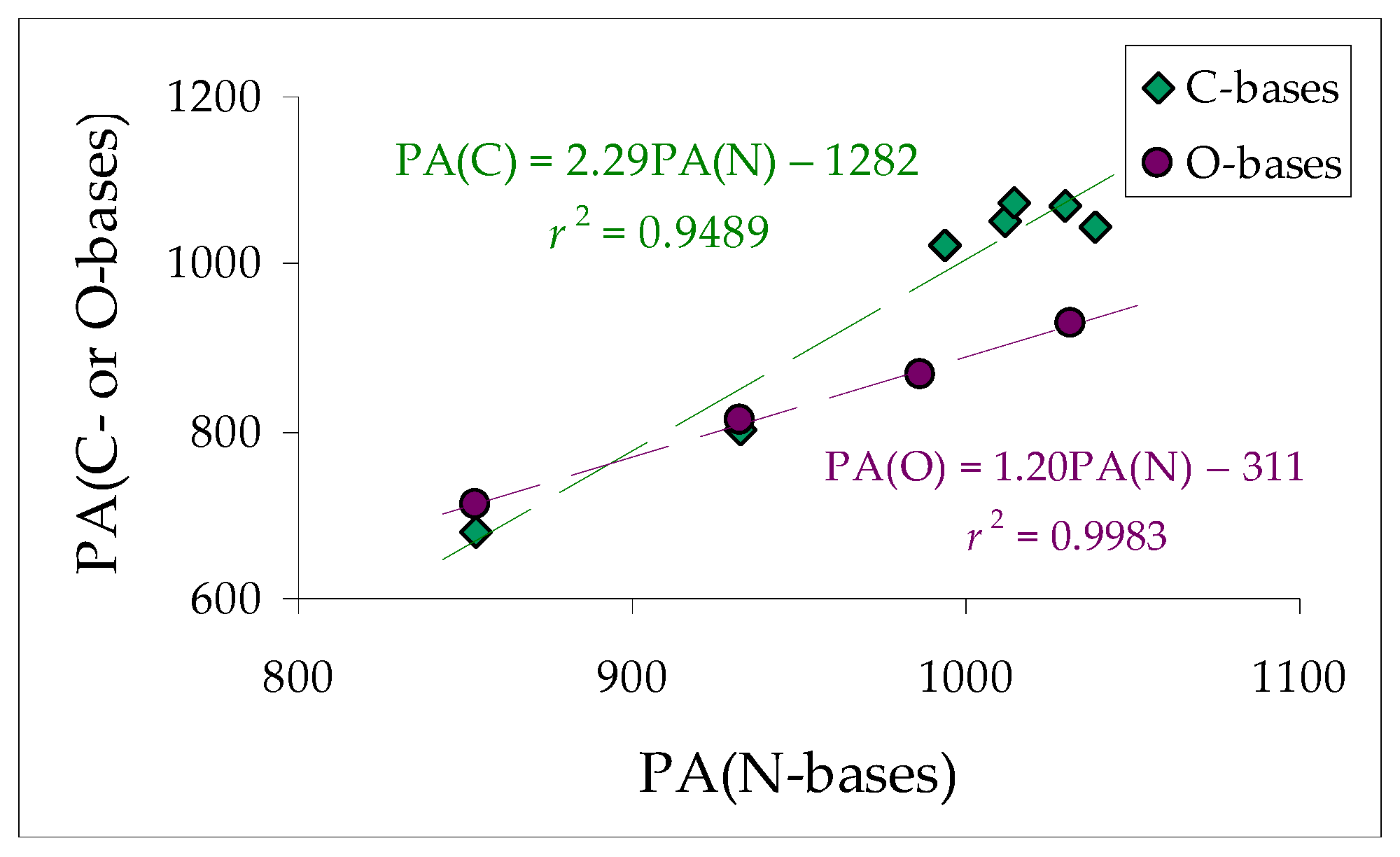
2.4. Basicity of Methyl Derivatives with the Framework of Rare Tautomers of Amidines 1–7
3. Methodology
H298(Bi) + H298(H+) − H298(BiH+)
G298(Bi) + G298(H+) − G298(BiH+) = PA − TΔS
[x1B1 ⇌ x2B2 ⇌ x3B3 ⇌ …] + H+
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
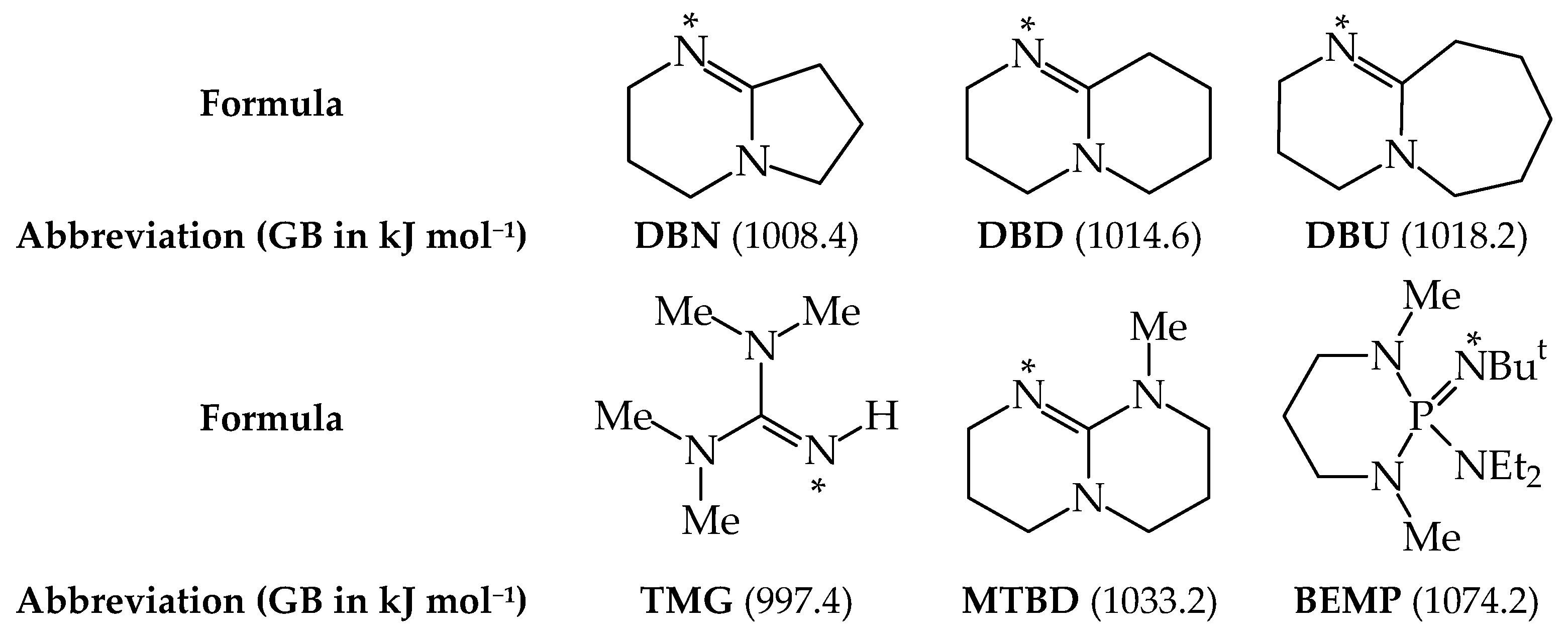
Abbreviations
| A | acceptor |
| B | neutral base |
| Bi | tautomer of B |
| BEMP | 2-tert-butylimino-2-diethylamino-1,3-dimethylperhydro-1,3,2-diazaphosporine |
| BH+ | conjugate acid of B |
| Bu | buthyl group |
| D | donor |
| DBD | 1,5-diazabicyclo[4.4.0]dec-5-ene |
| DBN | 1,5-diazabicyclo[4.3.0]non-5-ene |
| DBU | 1,8-diazabicyclo[5.4.0]undec-7-ene |
| DFT | density functional theory |
| DMAN | 1,8-bis(dimethylamino)naphthalene |
| E | energy |
| Et | ethyl group |
| FT-ICR | Fourier transform mode of ICR |
| G | Gibbs energy |
| G2 | Gaussian-2 theory |
| G2MP2 | MP2 variant of Gaussian-2 theory |
| G3B3 | Gaussian-3 theory with B3LYP structures and frequencies |
| G4MP2 | MP2 variant of Gaussian-4 theory |
| Gn | Gaussian-n theory |
| GB | gas-phase basicity |
| H | enthalpy |
| K | equilibrium constant |
| Me | methyl group |
| MP2 | second-order Møller-Plesset (perturbation theory) |
| MTBD | 7-methyl-1,5,7-triazabicyclo[4.4.0]dec-7,9-ene |
| PA | proton affinity |
| R | molar gas constant |
| S | entropy |
| T | temperature |
| TMG | N1,N1,N3,N3-tetramethylguanidine |
| TMU | N,N,N’,N’-tetramethylurea |
| xi | molar fraction of B isomer |
| yi | molar fraction of BH+ isomer |
| ZPE | zero-point energy |
References
- Raczyńska, E.D.; Gal, J.-F.; Maria, P.-C. Strong Bases and beyond: The Prominent Contribution of Neutral Push-Pull Organic Molecules towards Superbases in the Gas-Phase. Int. J. Mol. Sci. 2024, 25, 5591. [Google Scholar] [CrossRef] [PubMed]
- Raczyńska, E.D.; Gal, J.-F.; Maria, P.-C. Enhanced Basicity of Push-Pull Nitrogen Bases in the Gas Phase. Chem. Rev. 2016, 116, 13454–13511. [Google Scholar] [PubMed]
- Leito, I.; Koppel, I.A.; Koppel, I.; Kaupmees, K.; Tshepelevitsh, S.; Saame, J. Basicity Limits of Neutral Organic Superbases. Angew. Chem. Int. Ed. 2015, 54, 9262–9265. [Google Scholar] [CrossRef]
- Maksić, Z.B.; Kovačević, B.; Vianello, R. Advances in Determining the Absolute Proton Affinities of Neutral Organic Molecules in the Gas Phase and Their Interpretation: A Theoretical Account. Chem. Rev. 2012, 112, 5240–5270. [Google Scholar] [CrossRef]
- Tortajada, J.; Leon, E.; Luna, A.; Mó, O.; Yáñez, M. Ab Initio Calculations on Formamidine-X+ (X = H, Li, Na, Mg, and Al) Complexes. J. Phys. Chem. 1994, 98, 12919–12926. [Google Scholar] [CrossRef]
- Bouchoux, G.; Eckert-Maksić, M. Gas Phase Basicities of Polyfunctional Molecules. Part 5: Non-Aromatic sp2 Nitrogen Containing Compounds. Mass Spectrom. Rev. 2016, 37, 139–170. [Google Scholar] [CrossRef]
- Hunter, E.P.L.; Lias, S.G. Evaluated Gas Phase Basicities and Proton Affinities of Molecules: An Update. J. Phys. Chem. Ref. Data 1998, 27, 413–656. [Google Scholar] [CrossRef]
- Amekraz, B.; Tortajada, J.; Morizur, J.-P.; Gonzalez, A.I.; Mó, O.; Yáñez, M.; Leito, I.; Maria, P.-C.; Gal, J.-F. Experimental and Theoretical Study of the Basicity of Guanidine. The Performance of DFT Calculations vs. High Level Ab Initio Approaches. New J. Chem. 1996, 20, 1011–1021. [Google Scholar]
- González, A.I.; Mó, O.; Yáñez, M.; Léon, E.; Tortajada, J.; Morizur, J.P.; Leito, I.; Maria, P.-C.; Gal, J.F. Basicity of Acetamidine. Experimental and Theoretical Study. J. Phys. Chem. 1996, 100, 10490–10496. [Google Scholar] [CrossRef]
- Maksić, Z.B.; Vianello, R. Quest for the Origin of Basicity: Initial vs Final State Effects in Neutral Nitrogen Bases. J. Phys. Chem. A 2002, 105, 419–430. [Google Scholar] [CrossRef]
- Kolomeitsev, A.A.; Koppel, I.A.; Rodima, T.; Barten, J.; Lork, E.; Röschenthaler, G.-V.; Kaljurand, I.; Kütt, A.; Koppel, I.; Mäemets, V.; et al. Guanidinophosphazenes: Design, Synthesis, and Basicity in THF and in the Gas Phase. J. Am. Chem. Soc. 2005, 127, 17656–17666. [Google Scholar] [CrossRef] [PubMed]
- Despotović, I.; Maksić, Z.B.; Vianello, R. Computational Design of Brønsted Neutral Organic Superbases—[3]Iminoradialenes and Quinonimines Are Important Synthetic Targets. New J. Chem. 2007, 31, 52–62. [Google Scholar] [CrossRef]
- Kunetskiy, R.A.; Polyakova, S.M.; Vavřík, J.; Císařová, I.; Saame, J.; Roos Nerut, E.; Koppel, I.; Koppel, I.A.; Kütt, A.; Leito, I.; et al. A New Class of Organosuperbases, N-Alkyl- and A-Aryl-1,3-dialkyl-4,5-dimethyloimidazol-2-ylidine Amines: Synthesis, Structure, pKBH+ Measurements, and Properties. Chem. Eur. J. 2012, 18, 3621–3630. [Google Scholar] [CrossRef] [PubMed]
- Polyakova, S.M.; Kunetskiy, R.A.; Schröder, D. Proton Affinities of 2-Iminoimidazolines with Bulky N-Alkyl-Substituents. Int. J. Mass Spectrom. 2012, 314, 13–17. [Google Scholar] [CrossRef]
- Maksić, Z.B.; Kovačević, B. Toward Organic Superbases: The Electronic Structure and the Absolute Proton Affinity of Quinodiimines and Some Related Compounds. J. Phys. Chem. A 1998, 102, 7324–7328. [Google Scholar] [CrossRef]
- Maksić, Z.B.; Glosovac, Z.; Despotović, I. Predicted High Proton Affinity of Poly-2,5-dihydropyrrolimines¾the Aromatic Domino Effect. J. Phys. Org. Chem. 2002, 15, 499–508. [Google Scholar] [CrossRef]
- Koneshlou, T.; Rouhani, M.; Saeidian, H.; Aliabad, J.M. Super/Hyperbasicity of Novel Diquinonimino Derivatives of Guanidine in Gas Phase. Chem. Phys. Lett. 2022, 804, 139915. [Google Scholar] [CrossRef]
- Khazali, M.; Rouhani, M.; Saeidian, H. Utilizing the Synergistic Effect between Imidazole Aromaticity and Guanidine Structure for the Computational Design of Novel Uncharged Organic Superbases. J. Mol. Struct. 2023, 1273, 134348. [Google Scholar] [CrossRef]
- Miranda, M.S.; Esteves da Silva, J.C.G.; Castillo, A.; Frank, A.T.; Greer, A.; Brown, J.A.; Davis, B.C.; Liebman, J.F. Amino, Ammonio and Aminoethenes: A Theoretical Study of Their Structure and Energetics. J. Phys. Org. Chem. 2013, 26, 613–625. [Google Scholar] [CrossRef]
- Bouchoux, G. Gas Phase Basicities of Polyfunctional Molecules. Part 3: Amino Acids. Mass Spectrom. Rev. 2012, 31, 391–435. [Google Scholar] [CrossRef]
- Patai, S.; Rappoport, Z. (Eds.) The Chemistry of Amidines and Imidates; Wiley: London, UK, 1991; Volume 2. [Google Scholar]
- Koppel, I.A.; Schwesinger, R.; Breuer, T.; Burk, P.; Herodes, K.; Koppel, I.; Leito, I.; Mishima, M. Intrinsic Basicities of Phosphorus Imines and Ylides: A Theoretical Study. J. Phys. Chem. A 2001, 105, 9575–9586. [Google Scholar] [CrossRef]
- Raczyńska, E.D. Quantum-Chemical Studies of the Consequences of One-Electron Oxidation and One-Electron Reduction for Imidazole in the Gas Phase and Water. Comput. Theor. Chem. 2012, 993, 73–79. [Google Scholar] [CrossRef]
- Raczyńska, E.D. On Some Origins of Tautomeric Preferences in Neutral Creatinine in Vacuo: Search for Analogies and Differences in Cyclic Azoles and Azines. Symmetry 2024, 16, 98. [Google Scholar] [CrossRef]
- NIST Chemistry WebBook, NIST Standard Reference Database No. 69; Linstrom, P.J., Mallard, W.G., Eds.; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2014. Available online: http://webbook.nist.gov/chemistry (accessed on 15 March 2024).
- Parr, R.G.; Yang, W. Density Functional Theory of Atoms and Molecular Orbital Theory; Oxford University Press: New York, NY, USA, 1989. [Google Scholar]
- Becke, A.D. Density-Functional Thermochemistry. III. The Role of Exact Exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Hehre, W.J.; Radom, L.; Schleyer, P.v.R.; Pople, J.A. Ab Initio Molecular Theory; Wiley: New York, NY, USA, 1986. [Google Scholar]
- Curtiss, L.A.; Redfern, P.C.; Raghavachari, K. Gn theory. WIREs Comput. Mol. Sci. 2011, 1, 810–825. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Montgomery, J.A., Jr.; Vreven, T.; Kudin, K.N.; Burant, J.C.; et al. Gaussian-03, Revision E.01; Gaussian, Inc.: Wallingford, CT, USA, 2004. [Google Scholar]
- Bartmess, J.E. Thermodynamics of the Electron and the Proton. J. Phys. Chem. 1994, 98, 6420–6424, Erratum in J. Phys. Chem. 1995, 99, 6755. [Google Scholar] [CrossRef]
- Fifen, J.J.; Dhaouadi, Z.; Nsangou, M. Revision of the Thermodynamics of the Proton in the Gas Phase. J. Phys. Chem. A 2014, 118, 11090–11097. [Google Scholar] [CrossRef]
- Guthrie, J.P. Use of DFT Method for the Calculation of the Entropy of Gas Phase Organic Molecules: An Examination of the Quality of Results from a Simple Approach. J. Phys. Chem. A 2001, 105, 8495–8499. [Google Scholar] [CrossRef]
- Raczyńska, E.D.; Gal, J.-F.; Maria, P.-C. The Guanylated Bioamine Agmatine—A Theoretical Investigation of Its Structure and Exceptional High Basicity in the Gas Phase. Comput. Theor. Chem. 2017, 1109, 10–18. [Google Scholar] [CrossRef]
- Raczyńska, E.D.; Gal, J.-F.; Maria, P.-C.; Michalec, P.; Zalewski, M. Exceptionally High Proton and Lithium Cation Gas-Phase Basicity of the Anti-Diabetic Drug Metformin. J. Phys. Chem. A 2017, 121, 8706–8718. [Google Scholar] [CrossRef] [PubMed]
- Raczyńska, E.D.; Gal, J.F.; Pierre-Charles Maria, P.-C.; Fontaine-Vive, F. Biguanide Antidiabetic Drugs: Imeglimin Exhibits Higher Proton Basicity but Smaller Lithium-Cation Basicity than Metformin in Vacuo. ACS Omega 2018, 3, 17842–17852. [Google Scholar] [CrossRef]
- Puleo, T.R.; Sujansky, S.J.; Wright, S.E.; Bandar, J.S. Organic Superbases in Recent Synthetic Methodology Research. Chem. Eur. J. 2021, 27, 4216–4229. [Google Scholar] [CrossRef] [PubMed]
- Vazdar, K.; Margetić, D.; Kovačević, B.; Sundermeyer, J.; Leito, I.; Jahn, U. Design of Novel Uncharged Organic Superbases: Merging Basicity and Functionality. Acc. Chem. Res. 2021, 54, 3108–3123. [Google Scholar] [CrossRef] [PubMed]
- Wei, H.; Cheng, Z.; Wu, T.; Liu, Y.; Guo, J.; Chen, P.A.; Xia, J.; Xie, H.; Qiu, X.; Liu, T.; et al. Novel Organic Superbase Dopants for Ultraefficient N-Doping of Organic Semiconductors. Adv. Mater. 2023, 35, 2300084. [Google Scholar] [CrossRef]
- Nishinaka, M.; Harada, I.; Akaike, K.; Wei, Q.; Koshiba, Y.; Horike, S.; Ishida, K. Electrochemical Charge-Carrier Modulation of Carbon Nanotubes Using Ionic Liquids Derived from Organic Superbases for Stable Thermoelectric Materials. Carbon 2024, 218, 118667. [Google Scholar] [CrossRef]
- Zhang, K.; Wang, R. A Critical Review on New and Efficient Adsorbents for CO2 Capture. Chem. Eng. J. 2024, 485, 149495. [Google Scholar] [CrossRef]
- Elsayed, S.; Hummel, M.; Sawada, D.; Guizani, C.; Rissanen, M.; Sixta, H. Superbase-Based Protic Ionic Liquids for Cellulose Filament Spinning. Cellulose 2021, 28, 533–547. [Google Scholar] [CrossRef]
- Clerc, M.; Sandlass, S.; Rifaie-Graham, O.; Peterson, J.A.; Bruns, N.; Read de Alaniz, J.; Boesel, L.F. Visible Light-Responsive Materials: The (Photo)Chemistry and Applications of Donor–Acceptor Stenhouse Adducts in Polymer Science. Chem. Soc. Rev. 2023, 52, 8245–8294. [Google Scholar] [CrossRef]
- Wang, J.; Gadenne, V.; Patrone, L.; Raimundo, J.-M. Self-Assembled Monolayers of Push–Pull Chromophores as Active Layers and Their Applications. Molecules 2024, 29, 559. [Google Scholar] [CrossRef]
- Jing, Q.; Mei, Z.; Sheng, X.; Zou, X.; Xu, Q.; Wang, L.; Guo, H. Tuning the Bonding Behavior of d-p Orbitals to Enhance Oxygen Reduction through Push–Pull Electronic Effects. Adv. Funct. Mat. 2024, 34, 2307002. [Google Scholar] [CrossRef]
- Ma, J.; Sun, R.; Xia, K.; Xia, Q.; Liu, Y.; Zhang, X. Design and Application of Fluorescent Probes to Detect Cellular Physical Microenvironments. Chem. Rev. 2024, 124, 1738–1861. [Google Scholar] [CrossRef]
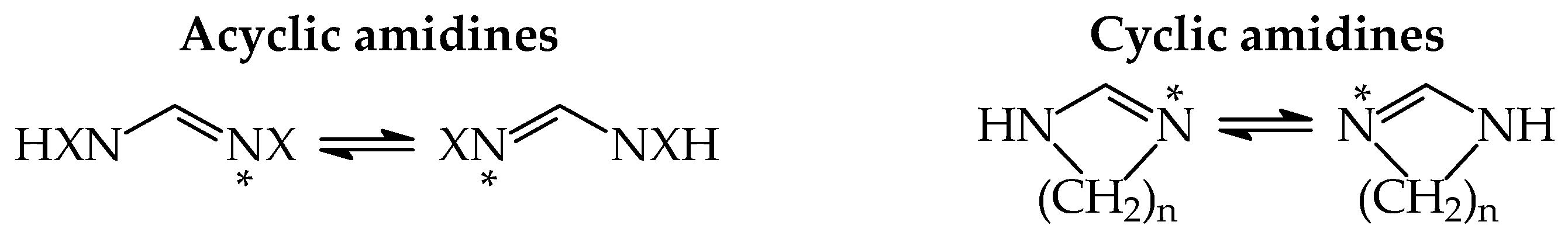

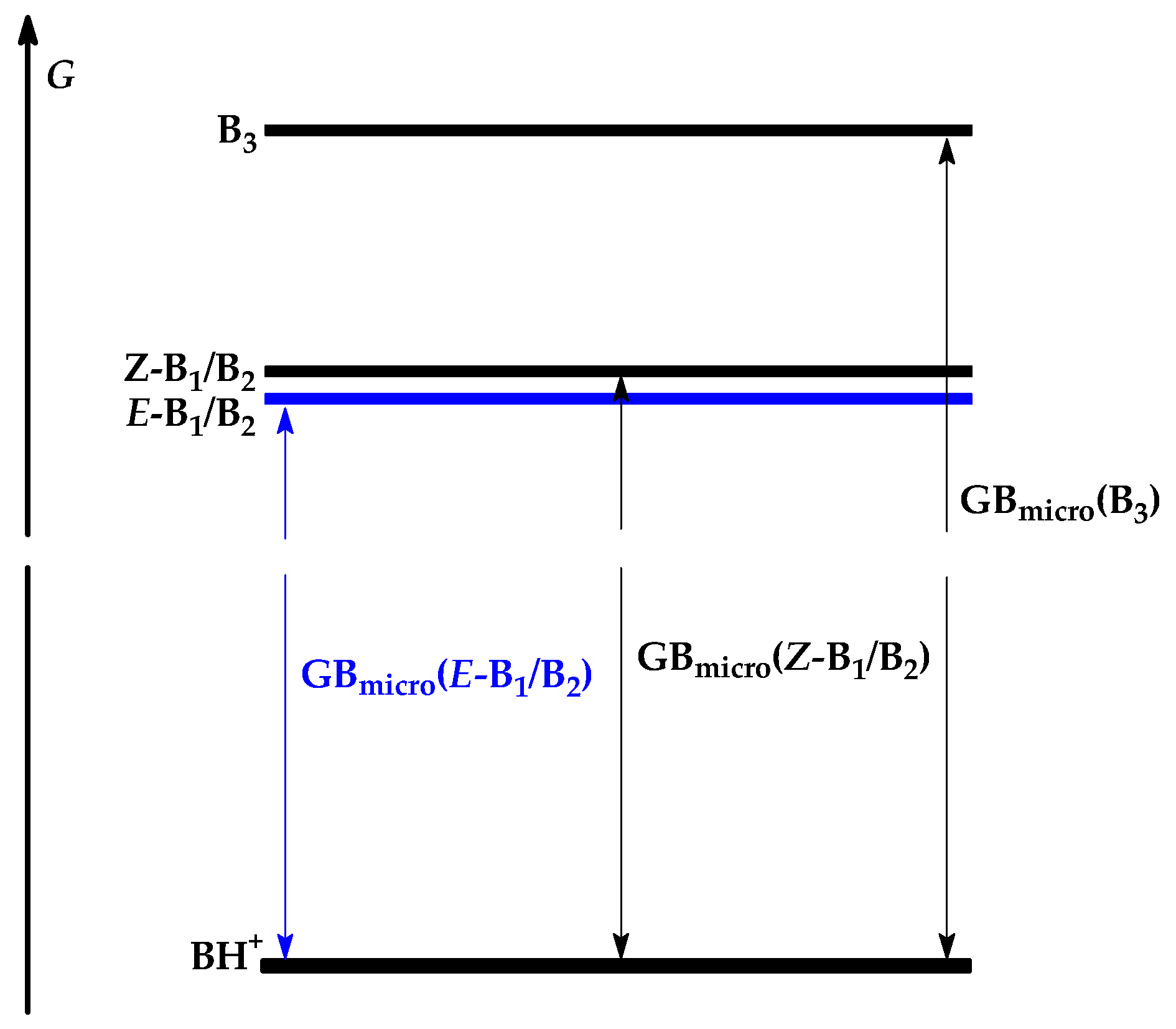
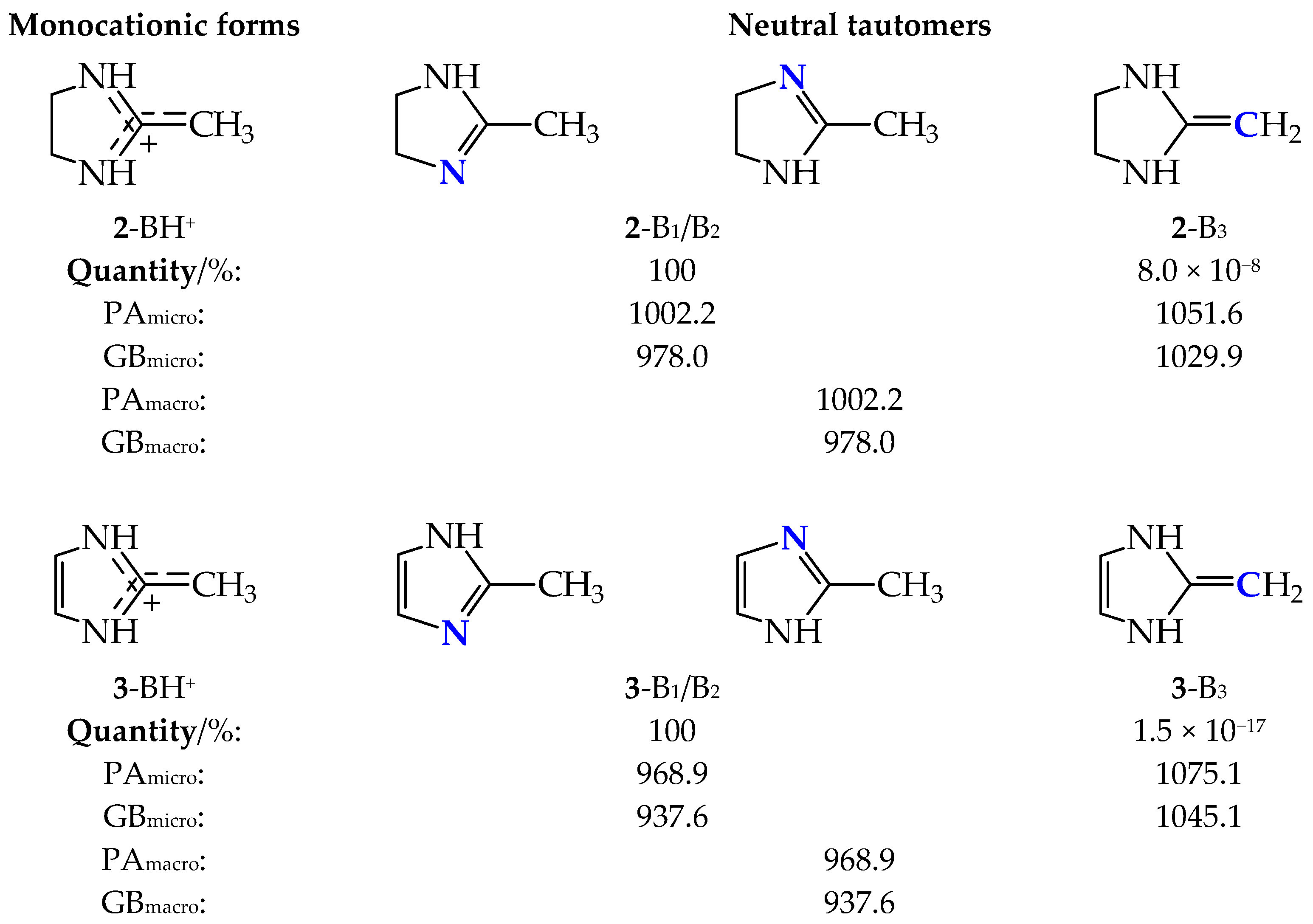
| Method | Quantity | E-B1/B2 | Z-B1/B2 | B3 | Quantity | Mixture |
|---|---|---|---|---|---|---|
| DFT a | PAmicro | 982.2 | 986.2 | 1021.6 1021.7 b | PAmacro | 982.6 |
| GBmicro | 950.9 | 995.0 | 993.0 993.3 b | GBmacro | 951.2 | |
| % | 84.2 | 15.8 | 3.5 × 10−6 | |||
| G2 a | PAmicro | 975.8 975.7 c | 979.9 | 1018.5 | PAmacro | 976.4 |
| GBmicro | 945.8 | 950.1 | 990.6 | GBmacro | 946.4 | |
| % | 85.3 | 14.7 | 1.2 × 10−6 | |||
| G2MP2 a | PAmicro | 975.7 975.7 c | 979.8 | 1018.4 | PAmacro | 976.3 |
| GBmicro | 945.6 | 950.0 | 990.4 | GBmacro | 946.3 | |
| % | 85.5 | 14.5 | 1.2 × 10−6 | |||
| G3B3 a | PAmicro | 977.5 | 981.5 | 1017.4 | PAmacro | 978.1 |
| GBmicro | 946.8 | 951.3 | 989.2 | GBmacro | 947.4 | |
| % | 86.2 | 13.8 | 3.2 × 10−6 | |||
| G4MP2 d | PA | 975.1 | ||||
| Experiment e | PAexp | 970.7 | ||||
| GBexp | 938.2 |
| Amidine | Method | Quantity | E-B1 | Z-B1 | B2 | B3 | Quantity | Mixture |
|---|---|---|---|---|---|---|---|---|
| 4 | DFT | PAmicro | 923.8 | 924.7 | 902.0 | 1056.9 | PAmacro | 902.0 |
| GBmicro | 893.6 | 894.4 | 869.3 | 1022.2 | GBmacro | 869.3 | ||
| % | 0.005 | 0.004 | 99.991 | 1.6 × 10−25 | ||||
| G2 | PAmicro | 916.3 | 917.0 | 894.1 | 1052.4 | PAmacro | 894.1 | |
| GBmicro | 886.6 | 887.2 | 862.4 | 1020.6 | GBmacro | 862.4 | ||
| % | 0.006 | 0.004 | 99.990 | 3.4 × 10−26 | ||||
| G2MP2 | PAmicro | 916.2 | 916.3 | 894.8 | 1055.1 | PAmacro | 894.8 | |
| GBmicro | 886.5 | 887.2 | 863.1 | 1019.0 | GBmacro | 863.1 | ||
| % | 0.008 | 0.006 | 99.986 | 4.8 × 10−26 | ||||
| G3B3 | PAmicro | 918.2 | 918.5 | 895.2 | 1052.6 | PAmacro | 895.2 | |
| GBmicro | 887.9 | 888.2 | 863.1 | 1018.2 | GBmacro | 863.1 | ||
| % | 0.004 | 0.004 | 99.992 | 6.4 × 10−26 | ||||
| 5 | DFT | PAmicro | 982.6 | 985.3 | 990.3 | 1049.2 | PAmacro | 983.5 |
| GBmicro | 950.5 | 953.2 | 958.0 | 1017.0 | GBmacro | 951.4 | ||
| % | 72.5 | 23.9 | 3.6 | 2.2 × 10−12 | ||||
| G2 | PAmicro | 977.7 | 980.4 | 981.3 | 1042.8 | PAmacro | 978.9 | |
| GBmicro | 946.1 | 948.7 | 949.2 | 1010.9 | GBmacro | 947.2 | ||
| % | 61.2 | 21.3 | 17.5 | 2.7 × 10−10 | ||||
| G2MP2 | PAmicro | 977.7 | 980.4 | 981.3 | 1042.8 | PAmacro | 978.7 | |
| GBmicro | 946.1 | 948.7 | 949.2 | 1010.9 | GBmacro | 947.0 | ||
| % | 66.5 | 22.7 | 10.8 | 3.1 × 10−10 | ||||
| 6 | DFT | PAmicro | 1005.8 | 1009.8 | 999.5 | 1061.5 | PAmacro | 1000.1 |
| GBmicro | 973.9 | 977.9 | 967.4 | 1029.0 | GBmacro | 968.0 | ||
| % | 6.6 | 1.3 | 92.1 | 1.2 × 10−9 | ||||
| 7 | DFT | PAmicro | 1015.2 | 1021.0 | 1010.9 | 1056.0 | PAmacro | 1011.5 |
| GBmicro | 984.4 | 989.9 | 979.3 | 1021.13 | GBmacro | 980.0 | ||
| % | 11.4 | 1.2 | 87.4 | 3.8 × 10−6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Raczyńska, E.D.; Gal, J.-F.; Maria, P.-C. Potential Push-Pull Carbon Superbases Based on Methyl Substitution of Rare Tautomers of Imines. Molecules 2025, 30, 474. https://doi.org/10.3390/molecules30030474
Raczyńska ED, Gal J-F, Maria P-C. Potential Push-Pull Carbon Superbases Based on Methyl Substitution of Rare Tautomers of Imines. Molecules. 2025; 30(3):474. https://doi.org/10.3390/molecules30030474
Chicago/Turabian StyleRaczyńska, Ewa Daniela, Jean-François Gal, and Pierre-Charles Maria. 2025. "Potential Push-Pull Carbon Superbases Based on Methyl Substitution of Rare Tautomers of Imines" Molecules 30, no. 3: 474. https://doi.org/10.3390/molecules30030474
APA StyleRaczyńska, E. D., Gal, J.-F., & Maria, P.-C. (2025). Potential Push-Pull Carbon Superbases Based on Methyl Substitution of Rare Tautomers of Imines. Molecules, 30(3), 474. https://doi.org/10.3390/molecules30030474








