Hydrogenated Planar Aluminum Clusters: A Density Functional Theory Study
Abstract
:1. Introduction
2. Result and Discussion
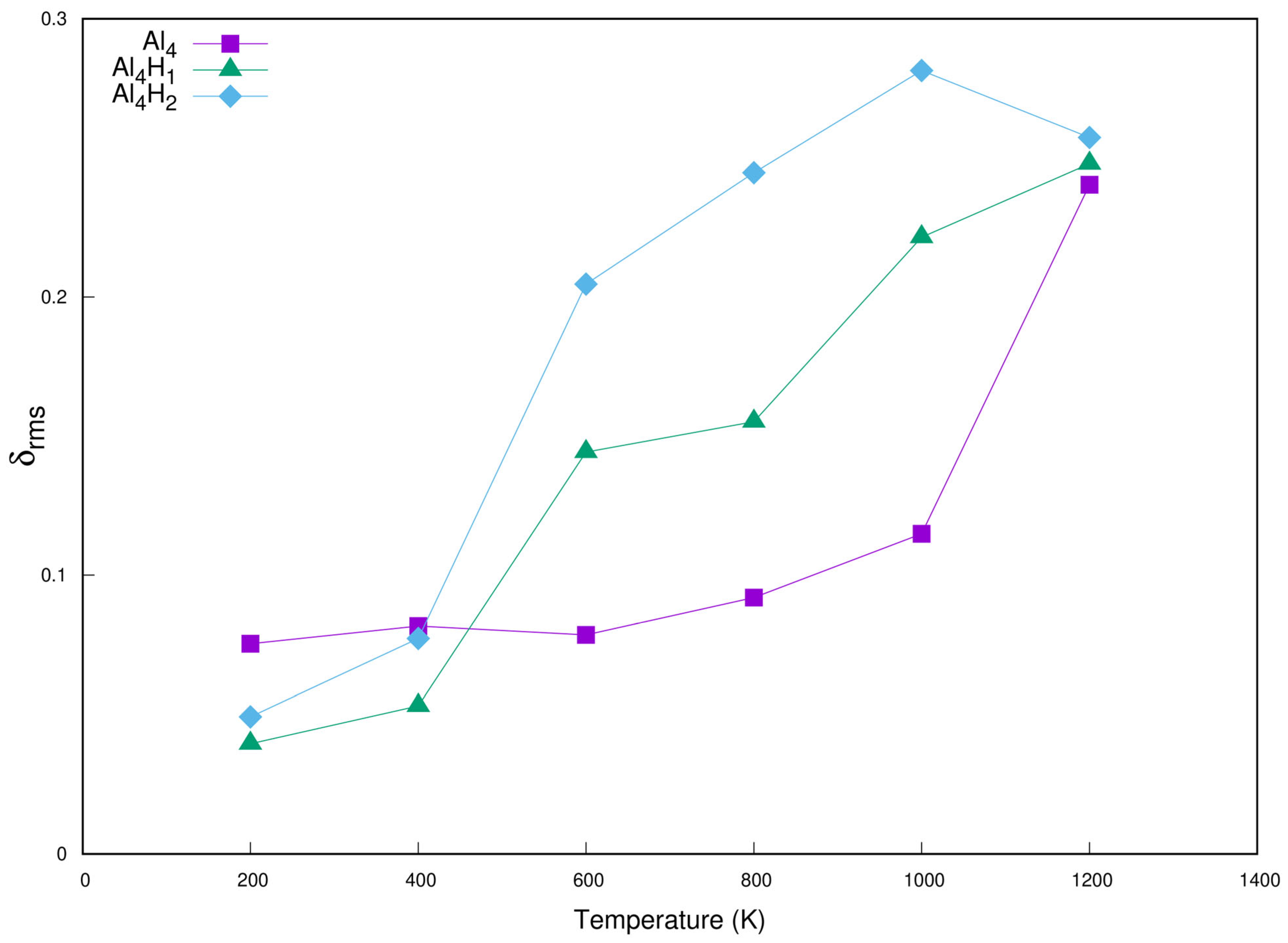
2.1. Structures of the Small Planar Aln (n = 3–10) Clusters
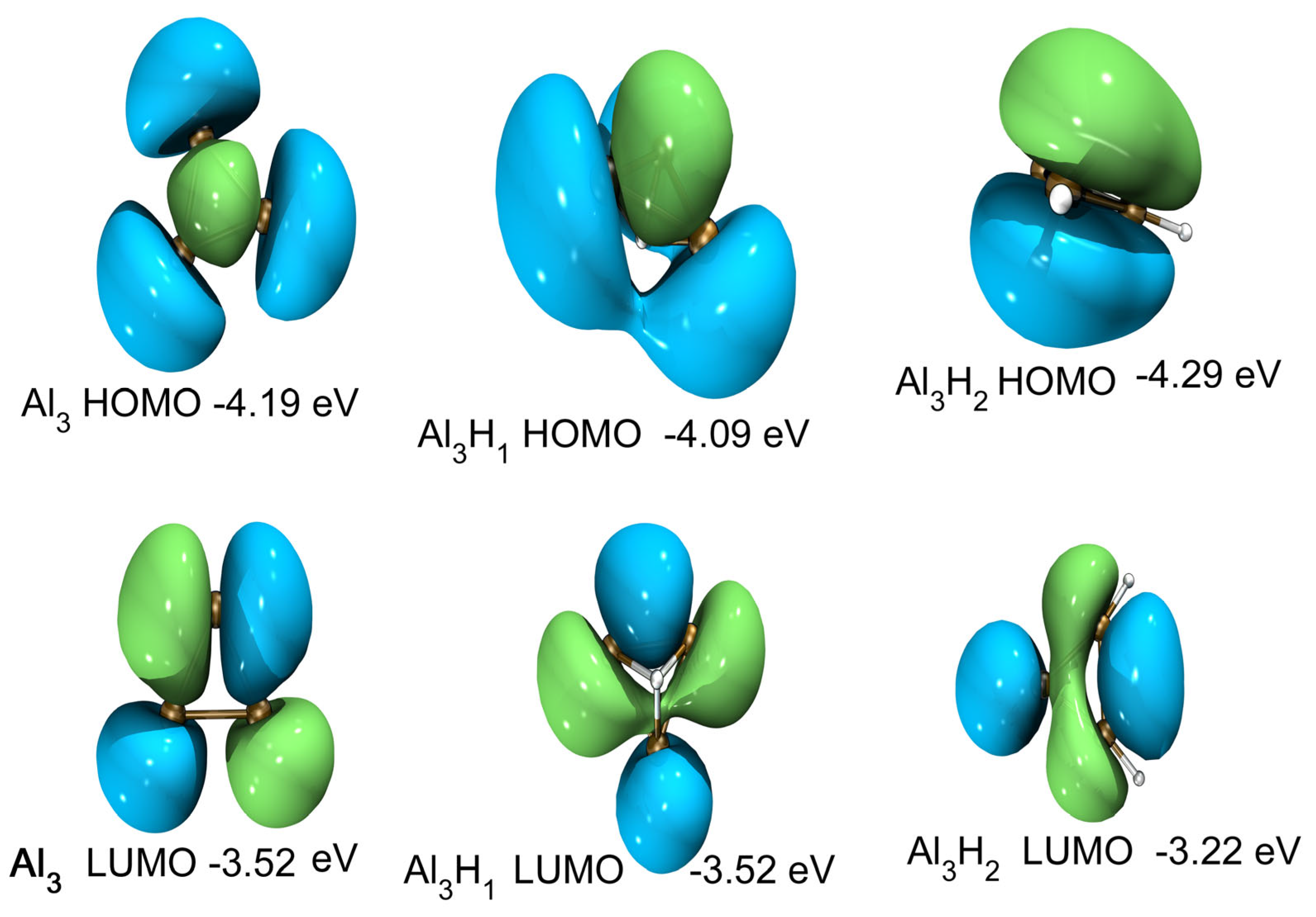
2.2. Structures of One or Two Hydrogen Atoms Adsorbed on Small Planar Aln Clusters
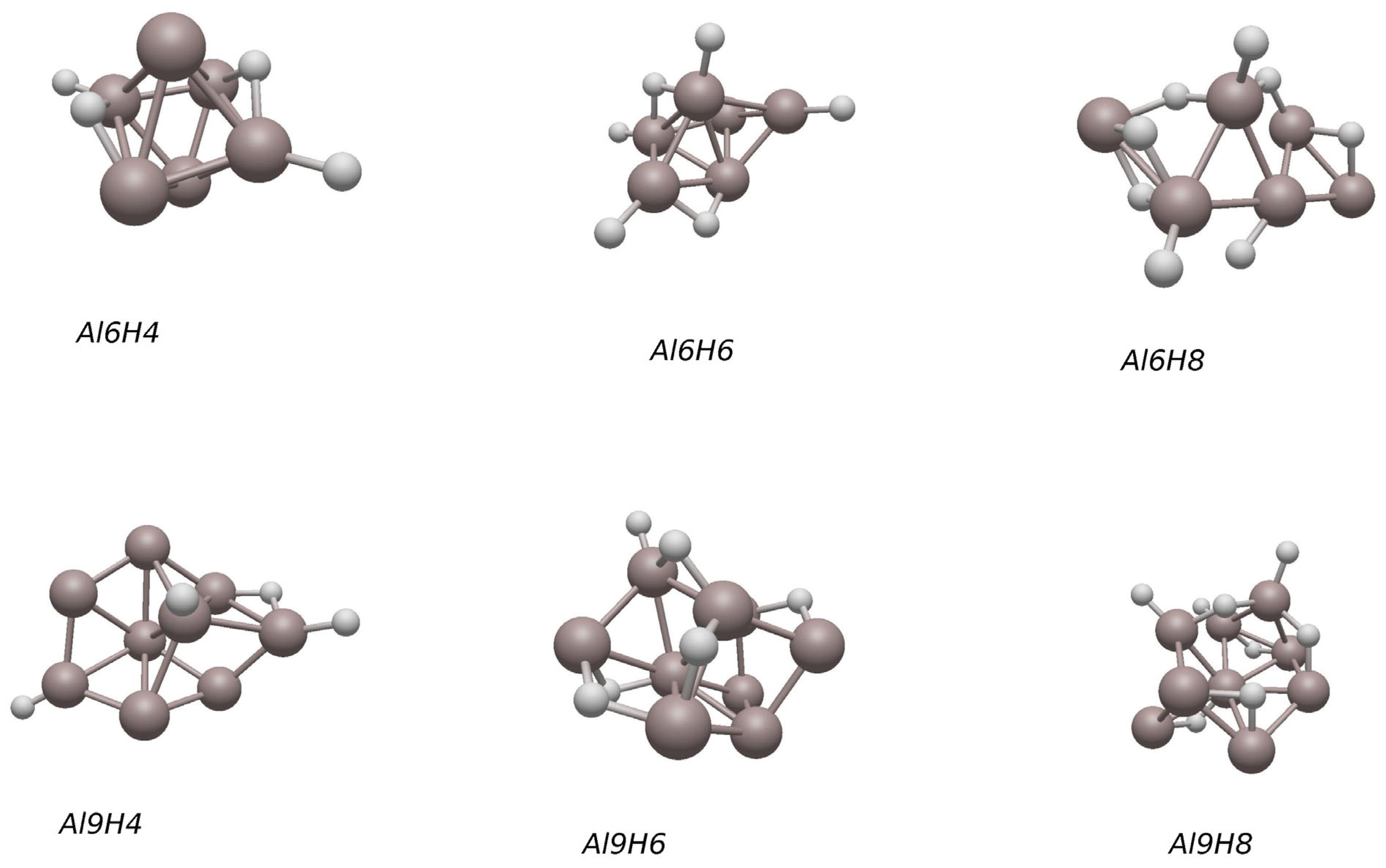
2.3. Lowest-Energy Structures of AlnHm (n = 6–10, m = 0–2)
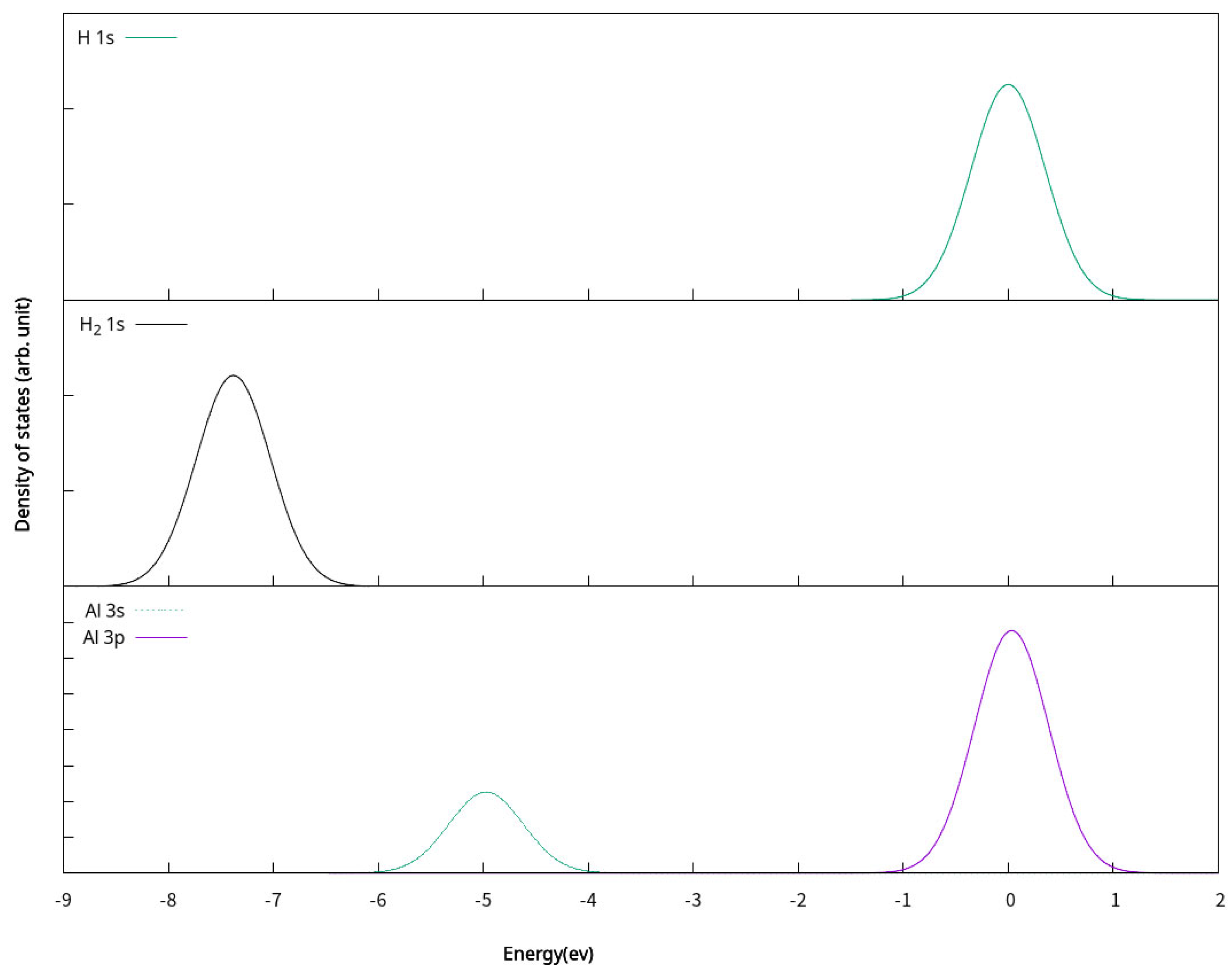
2.4. Electronic Properties
3. Materials and Methods
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lan, N.T.; Mai, N.T.; Cuong, N.T.; Van, P.T.H.; La, D.D.; Tam, N.M.; Ngo, S.T.; Tung, N.T. Density Functional Study of Size-Dependent Hydrogen Adsorptionon AgnCr (n = 1–12) Clusters. ACS Omega 2022, 7, 37379–37387. [Google Scholar] [CrossRef] [PubMed]
- Ma, L.; Zhou, T.; Li, J.; Chen, H. Aluminum-Silicon Hydride Clusters for Prospective Hydrogen Storage. Int. J. Hydrogen Energy 2019, 44, 26459–26468. [Google Scholar] [CrossRef]
- Zhang, J.; Sun, J.; Liu, Y.; Li, J.; Liang, X.; Duan, H. The First-Principles Study of Al12X (X = Sc-Zn) Clusters and Their Adsorption of H, O and N. AIP Adv. 2016, 6, 075312. [Google Scholar] [CrossRef]
- Ichikawa, K.; Ikeda, Y.; Terashima, R.; Tachibana, A. Aluminum Hydride Clusters as Hydrogen Storage Materials and Their Electronic Stress Tensor Analysis. Mater. Sci. Forum 2012, 706–709, 1539–1544. [Google Scholar] [CrossRef]
- Xu, B.; Liu, J.; Zhao, L.; Yan, L. Theoretical Study on the Structure and Stability of Aluminum Hydride (AlnH3n) Clusters. J. Mater. Sci. 2013, 48, 2647–2658. [Google Scholar] [CrossRef]
- Tang, C.; Chen, S.; Zhu, W.; Zhang, A.; Zhang, K.; Liu, M. The High-Capacity Hydrogen Storage Abilities of the Ti Atoms Coated Si@Al12 Clusters. Chem. Phys. Lett. 2013, 586, 116–120. [Google Scholar] [CrossRef]
- Fernández Albanesi, L.; Garroni, S.; Arneodo Larochette, P.; Nolis, P.; Mulas, G.; Enzo, S.; Baró, M.D.; Gennari, F.C. Role of Aluminum Chloride on the Reversible Hydrogen Storage Properties of the Li–N–H System. Int. J. Hydrogen Energy 2015, 40, 13506–13517. [Google Scholar] [CrossRef]
- Antsiburov, I.; Schütz, M.; Bühler, R.; Muhr, M.; Stephan, J.; Gemel, C.; Klein, W.; Kahlal, S.; Saillard, J.-Y.; Fischer, R.A. All-Hydrocarbon-Ligated Superatomic Gold/Aluminum Clusters. Inorg. Chem. 2024, 63, 3749–3756. [Google Scholar] [CrossRef]
- Higino Damasceno, J.; Teixeira Rabelo, J.N.; Cândido, L. A Quantum Monte Carlo Study on Electron Correlation Effects in Small Aluminum Hydride Clusters. New J. Chem. 2015, 39, 2195–2201. [Google Scholar]
- Loukhovitski, B.I.; Torokhov, S.A.; Loukhovitskaya, E.E.; Sharipov, A.S. DFT Study of Small Aluminum and Boron Hydrides: Isomeric Composition and Physical Properties. Struct. Chem. 2018, 29, 49–68. [Google Scholar] [CrossRef]
- Elsayed, M.; Staab, T.E.M.; Čížek, J.; Krause-Rehberg, R. Monovacancy-Hydrogen Interaction in Pure Aluminum: Experimental and Ab-Initio Theoretical Positron Annihilation Study. Acta Mater. 2023, 248, 118770. [Google Scholar] [CrossRef]
- Vanbuel, J.; Jia, M.; Ferrari, P.; Gewinner, S.; Schöllkopf, W.; Nguyen, M.T.; Fielicke, A.; Janssens, E. Competitive Molecular and Dissociative Hydrogen Chemisorption on Size Selected Doubly Rhodium Doped Aluminum Clusters. Top. Catal. 2018, 61, 62–70. [Google Scholar] [CrossRef]
- Vanbuel, J.; Fernández, E.M.; Ferrari, P.; Gewinner, S.; Schöllkopf, W.; Balbás, L.C.; Fielicke, A.; Janssens, E. Hydrogen Chemisorption on Singly Vanadium-Doped Aluminum Clusters. Chem. Eur. J. 2017, 23, 15638–15643. [Google Scholar] [CrossRef] [PubMed]
- Roach, P.J.; Reber, A.C.; Woodward, W.H.; Khanna, S.N.; Castleman, A.W. Al4H7− Is a Resilient Building Block for Aluminum Hydrogen Cluster Materials. Proc. Natl. Acad. Sci. USA. 2007, 104, 14565–14569. [Google Scholar] [CrossRef]
- Xu, J.; Zhang, X.; Wang, H.; Fu, L.; Li, X.; Grubisic, A.; Harris, R.M.; Eichhorn, B.; Gantefoer, G.; Ding, Y.; et al. A Combined Theoretical and Photoelectron Spectroscopy Study of Al3Hn− (n = 1–9) Clusters. Z. Anorg.Allg. Chem. 2021, 647, 1840–1848. [Google Scholar] [CrossRef]
- Maatallah, M.; Guo, M.; Cherqaoui, D.; Jarid, A.; Liebman, J.F. Aluminium Clusters for Molecular Hydrogen Storage and the Corresponding Alanes as Fuel Alternatives: A Structural and Energetic Analysis. Int. J. Hydrogen Energy 2013, 38, 5758–5767. [Google Scholar] [CrossRef]
- Mañanes, A.; Duque, F.; Méndez, F.; López, M.J.; Alonso, J.A. Analysis of the Bonding and Reactivity of H and the Al13 Cluster Using Density Functional Concepts. J. Chem. Phys. 2003, 119, 5128–5141. [Google Scholar] [CrossRef]
- Maatallah, M.; Cherqaoui, D.; Jarid, A.; Liebman, J.F. Are Closed Clusters Expected from the (n + 1) Skeletal Electron Pairs Rule in Alanes and Gallanes? A DFT Structural Study of AnHn+2 (A = Al, Ga, and n = 4–6). Polyhedron 2011, 30, 1080–1084. [Google Scholar] [CrossRef]
- Duque, F.; Molina, L.M.; López, M.J.; Mananes, A.; Alonso, J.A. Assembling of Hydrogenated Aluminum Clusters. Eur. Phys. J. D-At. Mol. Opt. Plasma Phys. 2001, 16, 285–288. [Google Scholar] [CrossRef]
- Kawamura, H.; Kumar, V.M.; Sun, Q.; Kawazoe, Y. Bonding Character of Hydrogen in Aluminum Clusters. Mater. Trans. 2001, 42, 2175–2179. [Google Scholar] [CrossRef]
- Muz, İ.; Atiş, M. Boron-Doped Hydrogenated Al3 Clusters: A Material for Hydrogen Storage. J. Alloys Compd. 2016, 667, 275–281. [Google Scholar] [CrossRef]
- Charkin, O.P.; Klimenko, N.M.; Charkin, D.O. DFT Modeling of Successive Hydrogenated Subnano-Size Aluminum Clusters. Chem. Phys. 2019, 522, 112–122. [Google Scholar] [CrossRef]
- Henry, D.J.; Yarovsky, I. Dissociative Adsorption of Hydrogen Molecule on Aluminum Clusters: Effect of Charge and Doping. J. Phys. Chem. A 2009, 113, 2565–2571. [Google Scholar] [CrossRef] [PubMed]
- Gandhi, K.; Kumar Dixit, D.; Kumar Dixit, B. Hydrogen Desorption Energies of Aluminum Hydride (AlnH3n) Clusters. Phys. B: Condens. Matter 2010, 405, 3075–3081. [Google Scholar] [CrossRef]
- Kiran, B.; Jena, P.; Li, X.; Grubisic, A.; Stokes, S.T.; Ganteför, G.F.; Bowen, K.H.; Burgert, R.; Schnöckel, H. Magic Rule for AlnHm Magic Clusters. Phys. Rev. Lett. 2007, 98, 256802. [Google Scholar] [CrossRef]
- Pino, I.; Kroes, G.J.; Van Hemert, M.C. Hydrogen Dissociation on Small Aluminum Clusters. J. Chem. Phys. 2010, 133, 184304. [Google Scholar] [CrossRef]
- Moc, J. Physisorption and Dissociative Chemisorption of H2 on Sub-Nanosized Al13− Anion Cluster: Ab Initio Study. Eur. Phys. J. D 2011, 61, 397–402. [Google Scholar] [CrossRef]
- Yamamura, H.; Ohishi, Y.; Katsura, Y.; Kimura, K.; Uchida, N.; Kanayama, T. Stability and Bonding Nature for Icosahedral or Planar Cluster of Hydrogenated Boron or Aluminum. AIP Adv. 2019, 9, 115117. [Google Scholar] [CrossRef]
- Ichikawa, K.; Ikeda, Y.; Wagatsuma, A.; Watanabe, K.; Szarek, P.; Tachibana, A. Theoretical Study of Hydrogenated Tetrahedral Aluminum Clusters. Int. J. Quantum Chem. 2011, 111, 3548–3555. [Google Scholar] [CrossRef]
- Varano, A.; Henry, D.J.; Yarovsky, I. Role of Hydrogen in Dimerizaton of Aluminum Clusters: A Theoretical Study. J. Phys. Chem. A 2011, 115, 7734–7743. [Google Scholar] [CrossRef]
- He, C.; Shao, J.; Shi, R.; Zhu, X. A Theoretical Study on Structures, Stabilities, and Potential Energy Surfaces of Planar BnP2 (n = 1–7). Comput. Theor. Chem. 2011, 964, 121–132. [Google Scholar] [CrossRef]
- Hao-Ping, Z.; Jing-An, H. Ab Initio Study of the Electronic Properties of the Planar Ga5N5 Cluster. Chin. Phys. 2005, 14, 529–532. [Google Scholar] [CrossRef]
- Buendía, F.; Pham, H.T.; Barquera-Lozada, J.E.; Beltrán Sanchez, M.R.; Nguyen, M.T. Formation of the Quasi-Planar B56 Boron Cluster: Topological Path from B12 and Disk Aromaticity. Phys. Chem. Chem. Phys. 2022, 24, 21822–21832. [Google Scholar] [CrossRef] [PubMed]
- Pettersson, L.G.M.; Bauschlicher, C.W.; Halicioglu, T. Small Al Clusters. II. Structure and Binding in Aln (n = 2–6, 13). J. Chem. Phys. 1987, 87, 2205–2213. [Google Scholar] [CrossRef]
- Jones, R.O. Simulated Annealing Study of Neutral and Charged Clusters. J. Chem. Phys. 1993, 99, 1194–1206. [Google Scholar] [CrossRef]
- Yang, S.H.; Drabold, D.A.; Adams, J.B.; Sachdev, A. First-Principles Local-Orbital Density-Functional Study of Al Clusters. Phys. Rev. B 1993, 47, 1567–1576. [Google Scholar] [CrossRef] [PubMed]
- Ueno, J.; Hoshino, T.; Hata, M.; Tsuda, M. Stable Structures of Al Micro-Clusters and Their Characteristics for Electric Charging. Appl. Surf. Sci. 2000, 162–163, 440–444. [Google Scholar] [CrossRef]
- Chuang, F.-C.; Wang, C.Z.; Ho, K.H. Structure of Neutral Aluminum Clusters Aln (2 ≤ n ≤ 23): Genetic Algorithm Tight-Binding Calculations. Phys. Rev. B 2006, 73, 125431. [Google Scholar] [CrossRef]
- Kiohara, V.O.; Carvalho, E.F.V.; Paschoal, C.W.A.; Machado, F.B.C.; Roberto-Neto, O. DFT and CCSD(T) Electronic Properties and Structures of Aluminum Clusters: Alnx (n = 1–9, x = 0, ±1). Chem. Phys. Lett. 2013, 568–569, 42–48. [Google Scholar] [CrossRef]
- Tan, L.-P.; Die, D.; Zheng, B.-X. Growth Mechanism, Electronic Properties and Spectra of Aluminum Clusters. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2022, 267, 120545. [Google Scholar] [CrossRef]
- Rotteger, C.H.; Jarman, C.K.; Sutton, S.F.; Sayres, S.G. Size Onset of Metallic Behavior in Neutral Aluminum Clusters. Nanoscale 2024, 16, 13516–13524. [Google Scholar] [CrossRef]
- Rao, B.K.; Jena, P. Evolution of the Electronic Structure and Properties of Neutral and Charged Aluminum Clusters: A Comprehensive Analysis. J. Chem. Phys. 1999, 111, 1890–1904. [Google Scholar] [CrossRef]
- Ahlrichs, R.; Elliott, S.D. Clusters of Aluminium, a Density Functional Study. Phys. Chem. Chem. Phys. 1999, 1, 13–21. [Google Scholar] [CrossRef]
- Tam, N.M.; Duong, L.V.; Cuong, N.T.; Nguyen, M.T. Structure, Stability, Absorption Spectra and Aromaticity of the Singly and Doubly Silicon Doped Aluminum Clusters AlnSim0/+ with n = 3–16 and m = 1, 2. RSC Adv. 2019, 9, 27208–27223. [Google Scholar] [CrossRef]
- Neese, F.; Wennmohs, F.; Becker, U.; Riplinger, C. The ORCA Quantum Chemistry Program Package. J. Chem. Phys. 2020, 152, 224108. [Google Scholar] [CrossRef]
- Neese, F. Software Update: The ORCA Program System, Version4.0. WIREs Comput. Mol. Sci. 2018, 8, e1327. [Google Scholar] [CrossRef]
- Neese, F. The ORCA Program System. WIREs Comput. Mol. Sci. 2012, 2, 73–78. [Google Scholar] [CrossRef]
- Weigend, F.; Ahlrichs, R. Balanced Basis Sets of Split Valence, Triple Zeta Valence and Quadruple Zeta Valence Quality for H to Rn: Design and Assessment of Accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297. [Google Scholar] [CrossRef]
- Kawamura, H.; Kumar, V.; Sun, Q.; Kawazoe, Y. Magic Behavior and Bonding Nature in Hydrogenated Aluminum Clusters. Phys. Rev. B 2001, 65, 045406. [Google Scholar] [CrossRef]
- Bursch, M.; Mewes, J.; Hansen, A.; Grimme, S. Best-Practice DFT Protocols for Basic Molecular Computational Chemistry. Angew. Chem. Int. Ed. 2022, 61, e202205735. [Google Scholar] [CrossRef]
- Akola, J.; Manninen, M.; Häkkinen, H.; Landman, U.; Li, X.; Wang, L.-S. Aluminum Cluster Anions: Photoelectron Spectroscopy and Ab Initio Simulations. Phys. Rev. B 2000, 62, 13216–13228. [Google Scholar] [CrossRef]
- Schriver, K.E.; Persson, J.L.; Honea, E.C.; Whetten, R.L. Electronic Shell Structure of Group-III A Metal Atomic Clusters. Phys. Rev. Lett. 1990, 64, 2539–2542. [Google Scholar] [CrossRef] [PubMed]
- Taylor, K.J.; Pettiette, C.L.; Craycraft, M.J.; Chesnovsky, O.; Smalley, R.E. Ups of Negative Aluminum Clusters. Chem. Phys. Lett. 1988, 152, 347–352. [Google Scholar] [CrossRef]
- Li, X.; Wu, H.; Wang, X.-B.; Wang, L.-S. S-p Hybridization and Electron Shell Structures in Aluminum Clusters: A Photoelectron Spectroscopy Study. Phys. Rev. Lett. 1998, 81, 1909–1912. [Google Scholar] [CrossRef]
- Yao, C.H.; Li, Y.D. Geometries and Electronic Structures of Pn−1Al (n = 20–40) Cages: A DFT Study. Comput. Theor. Chem. 2022, 1217, 113922. [Google Scholar] [CrossRef]
- Hanwell, M.D.; Curtis, D.E.; Lonie, D.C.; Vandermeersch, T.; Zurek, E.; Hutchison, G.R. Avogadro: An Advanced Semantic Chemical Editor, Visualization, and Analysis Platform. J. Cheminform. 2012, 4, 17. [Google Scholar] [CrossRef]
- De, H.S.; Krishnamurty, S.; Mishra, D.; Pal, S. Finite Temperature Behavior of Gas Phase Neutral Aun (3 ≤ n ≤ 10) Clusters: A First Principles Investigation. J. Phys. Chem. C 2011, 115, 17278–17285. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual Molecular Dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Lu, T.; Chen, F. Multiwfn: A Multi functional Wavefunction Analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef]
- Fallah-Bagher-Shaidaei, H.; Wannere, C.S.; Corminboeuf, C.; Puchta, R.; Schleyer, P.V.R. Which NICS Aromaticity Index for Planar π Rings Is Best? Org. Lett. 2006, 8, 863–866. [Google Scholar] [CrossRef]
- Poater, J.; Viñas, C.; Solà, M.; Teixidor, F. 3D and 2D Aromatic Units Behave like Oil and Water in the Case of Benzocarborane Derivatives. Nat.Commun. 2022, 13, 3844. [Google Scholar] [CrossRef] [PubMed]
- Lu, W.; Do, D.C.H.; Kinjo, R. A Flat Carborane with Multiple Aromaticity beyond Wade–Mingos’ Rules. Nat.Commun. 2020, 11, 3370. [Google Scholar] [CrossRef] [PubMed]
- Buzsáki, D.; Kovács, M.B.; Hümpfner, E.; Harcsa-Pintér, Z.; Kelemen, Z. Conjugation between 3D and 2D Aromaticity: Does It Really Exist? The Case of Carborane-Fused Heterocycles. Chem. Sci. 2022, 13, 11388–11393. [Google Scholar] [CrossRef] [PubMed]
- Buzsáki, D.; Gál, D.; Harcsa-Pintér, Z.; Kalabay, L.; Kelemen, Z. The Possible Aromatic Conjugation via the Different Edges of (Car) Borane Clusters: Can the Relationship Between 3D and 2D Aromatic Systems Be Reconciled? Chem. A Eur. J 2024, 30, e202402970. [Google Scholar] [CrossRef]
- Jeilani, Y.A.; Van Duong, L.; Al Qahtani, O.M.S.; Nguyen, M.T. A Reinvestigation of the Boron Cluster B15+/0/−: A Benchmark of Density Functionals and Consideration of Aromaticity Models. Phys. Chem. Chem. Phys. 2024, 26, 11347–11359. [Google Scholar] [CrossRef]
- Li, X.; Kuznetsov, A.E.; Zhang, H.F.; Boldyrev, A.I.; Wang, L.-S. Observation of All-Metal Aromatic Molecules. Science 2001, 291, 859–861. [Google Scholar] [CrossRef]
- Soler, J.M.; Artacho, E.; Gale, J.D.; García, A.; Junquera, J.; Ordejón, P.; Sánchez-Portal, D. The SIESTA Method for Ab Initio Order-N Materials Simulation. J. Phys. Condens. Matter 2002, 14, 2745–2779. [Google Scholar] [CrossRef]
- Junquera, J.; Paz, O.; Sanchez-Portal, D.; Artacho, E. Numerical Atomic Orbitals for Linear Scaling. Phys. Rev. B 2001, 64, 235111. [Google Scholar] [CrossRef]
- Hammer, B.; Hansen, L.B.; Nørskov, J.K. Improved Adsorption Energetics with in Density-Functional Theory Using Revised Perdew-Burke-Ernzerh of Functionals. Phys. Rev. B 1999, 59, 7413–7421. [Google Scholar] [CrossRef]
- Troullier, N.; Martins, J.L. Efficient Pseudopotentials for Plane-Wave Calculations. II. Operators for Fast Iterative Diagonalization. Phys. Rev. B 1991, 43, 8861–8869. [Google Scholar] [CrossRef]
- Hestenes, M.R.; Stiefel, E.L. Methods of Conjugate Gradients for Solving Linear Systems. J. Res. Nat. Bur. Stand. 1952, 49, 409–436. [Google Scholar] [CrossRef]
- Cai, M.F.; Dzugan, T.P.; Bondybey, V.E. Fluorescence Studies of Laser Vaporized Aluminum: Evidence for A3 Piu Ground State of Aluminum Dimer. Chem. Phys. Lett. 1989, 155, 430–436. [Google Scholar]
- Yao, C.H.; Li, Y.D. Evolution of the Structural and Electronic Properties of Aln P13−n (n = 0–13) Clusters. Theor. Chem. Acc. 2022, 141, 53. [Google Scholar] [CrossRef]

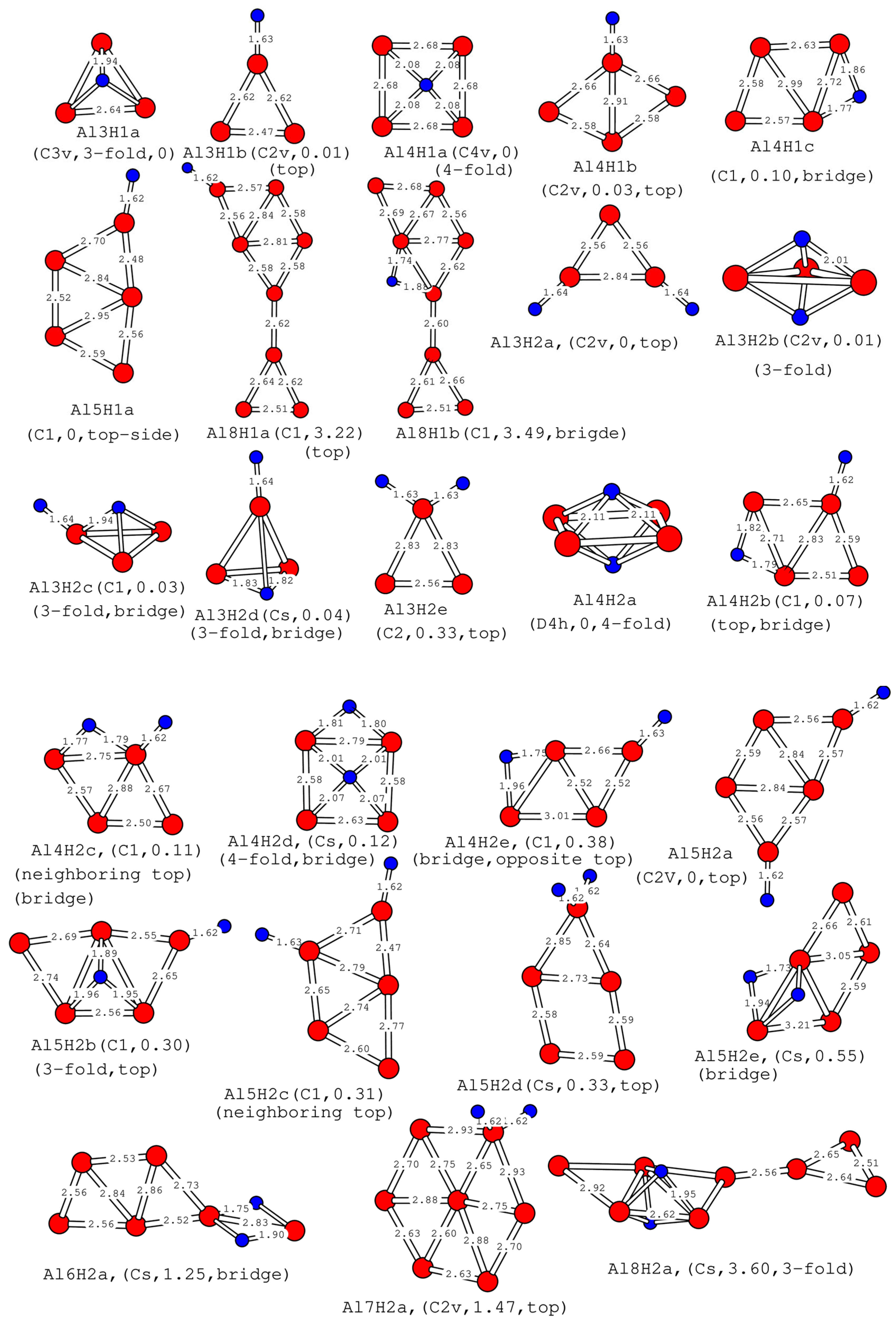
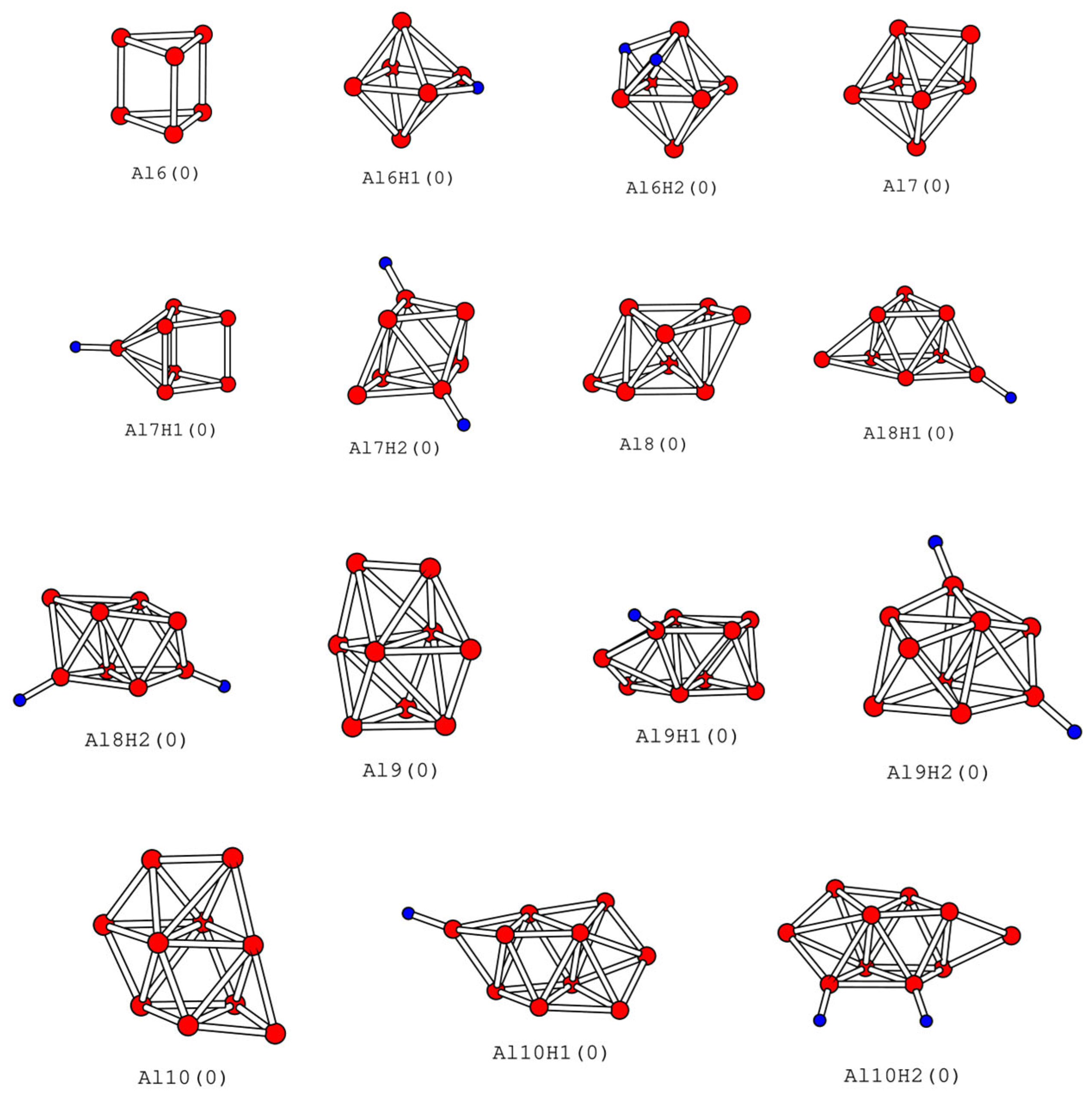
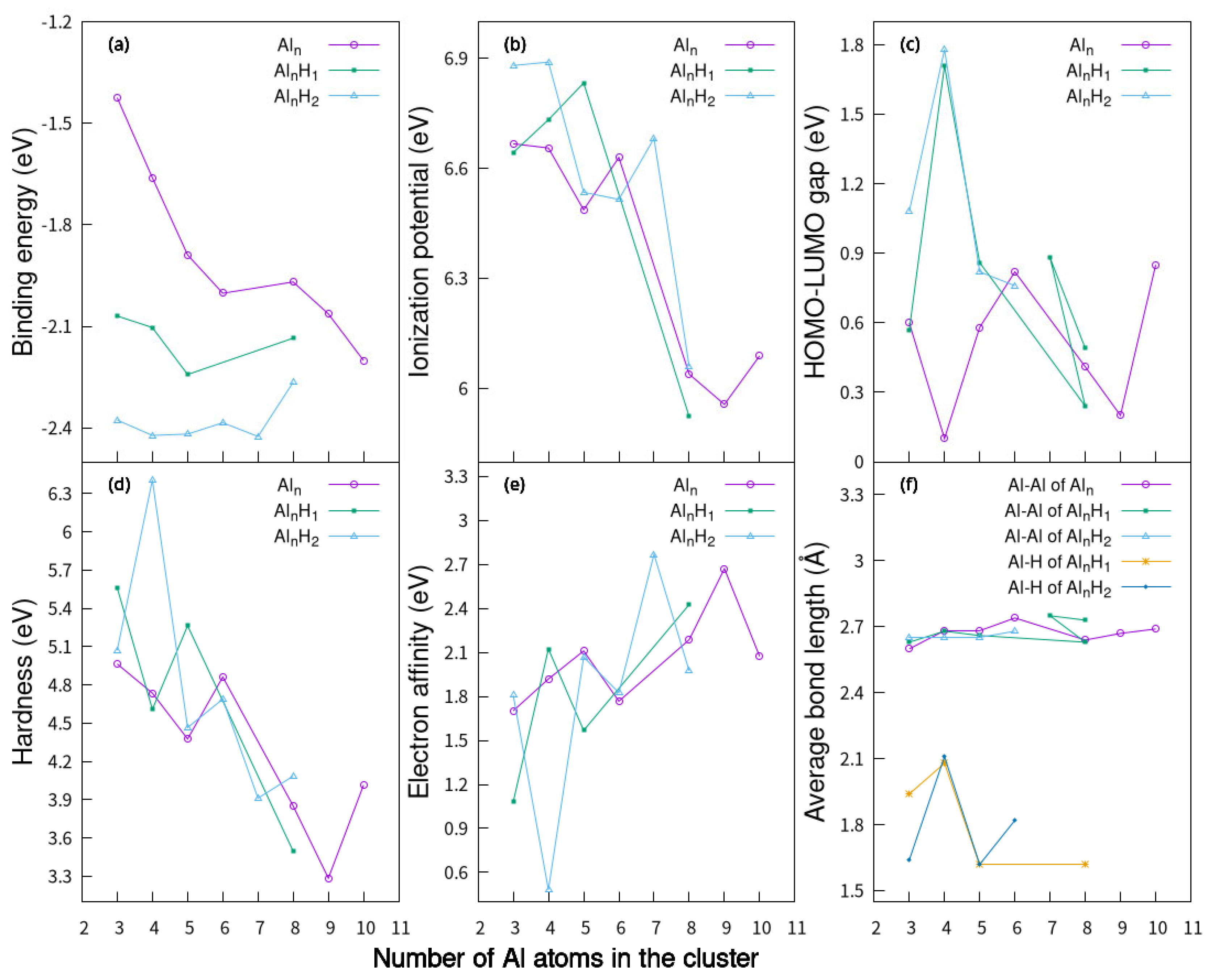
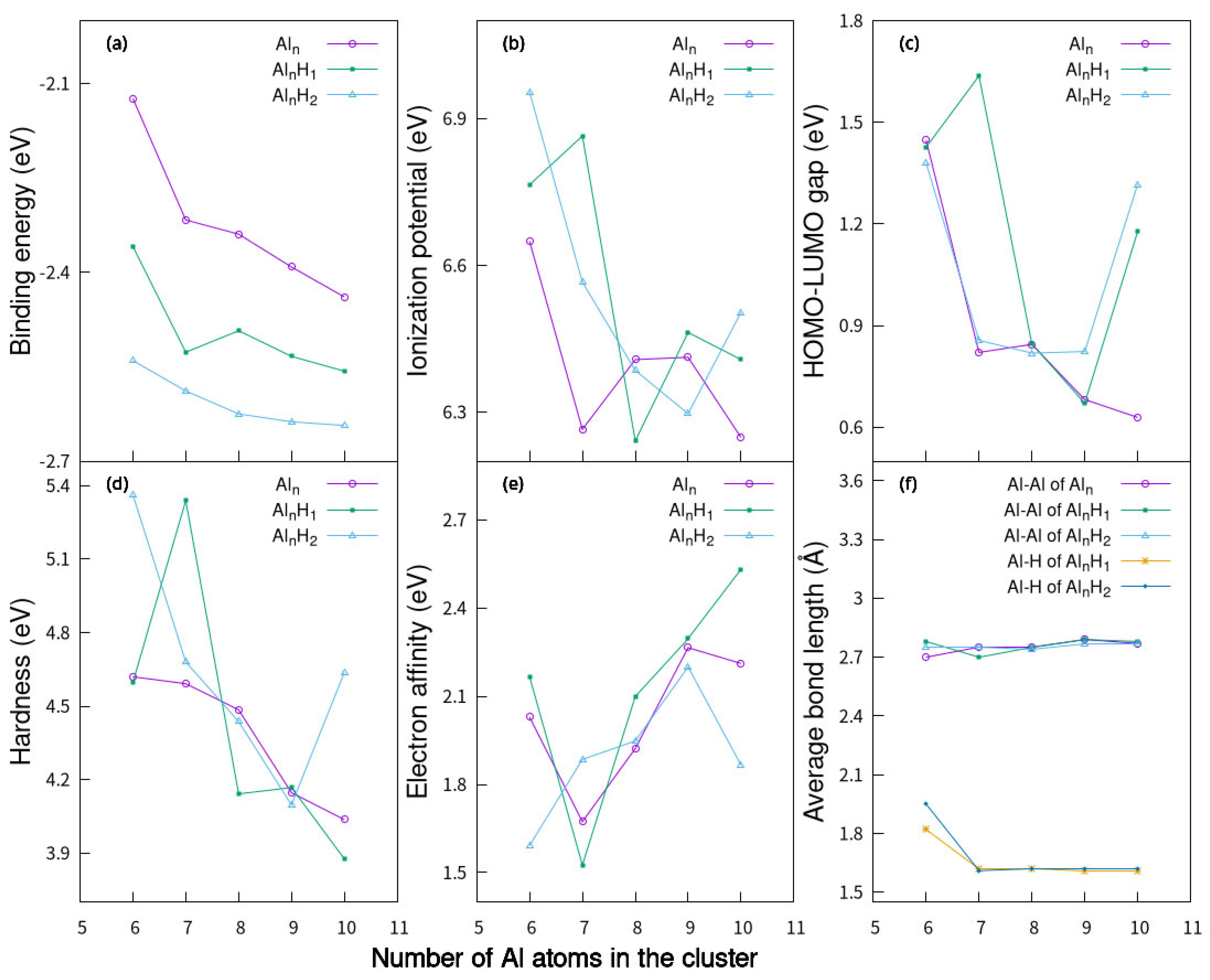

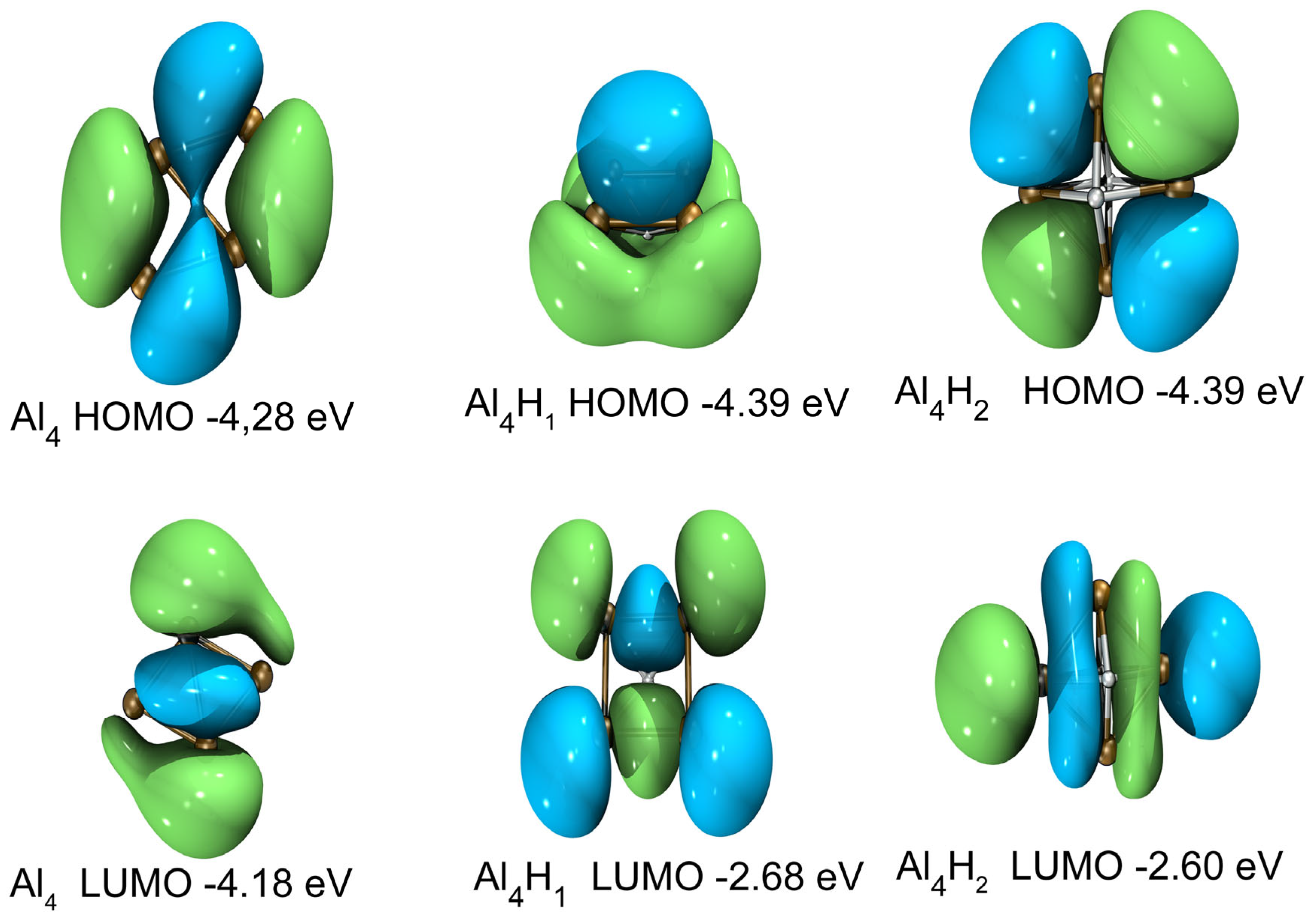
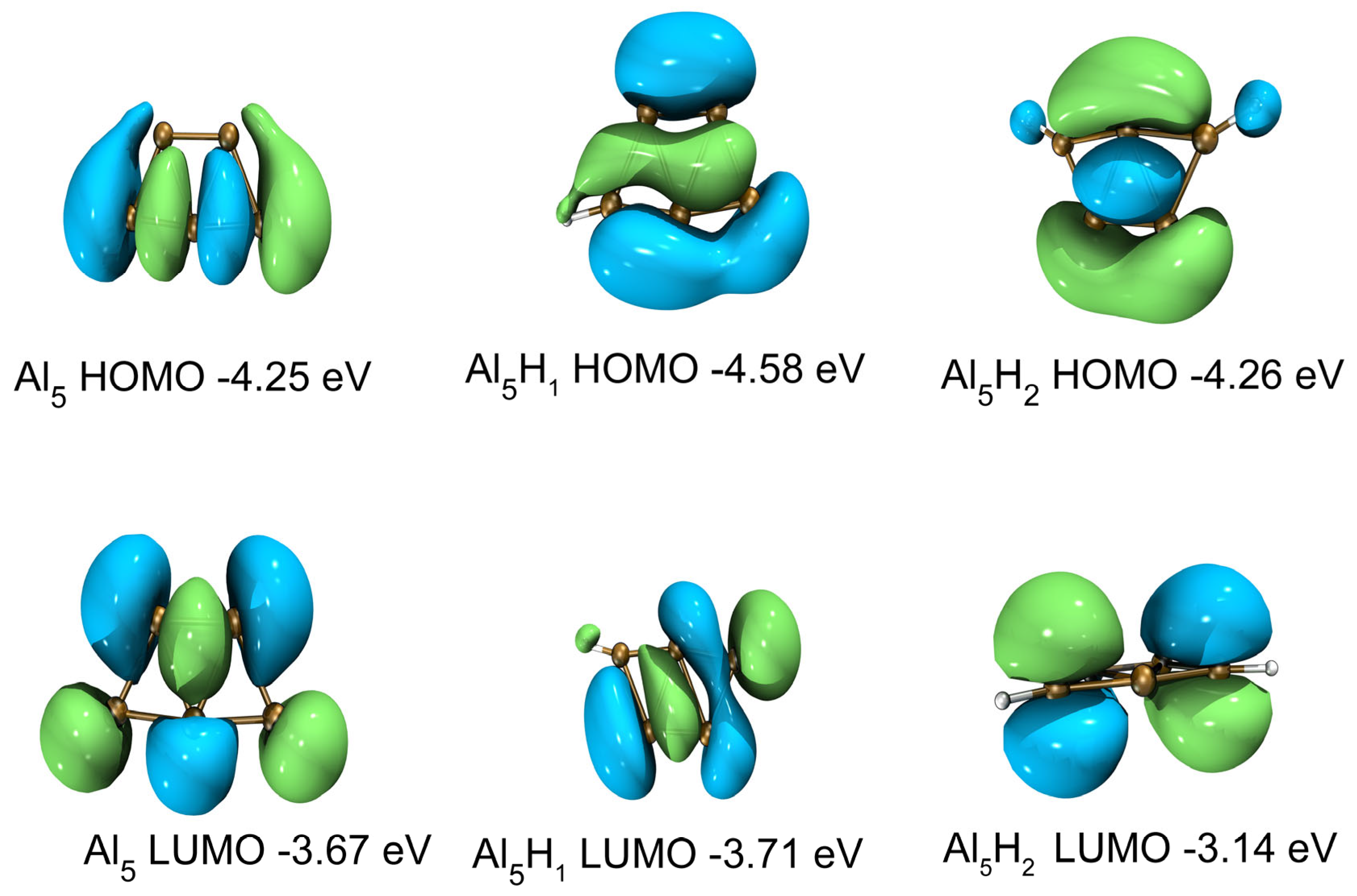
| Cluster | (Å) | BE (eV) | IP (eV) | EA (eV) | η (eV) | Gap (eV) |
|---|---|---|---|---|---|---|
| Al3a | 2.60 | −1.42 (−1.47, −1.50) | 6.67 | 1.70 | 4.96 | 0.60 |
| Al4a | 2.68 | −1.66 (−1.72, −1.74) | 6.66 | 1.92 | 4.74 | 0.10 |
| Al5a | 2.68 | −1.89 (−1.95, −1.97) | 6.49 | 2.11 | 4.38 | 0.58 |
| Al6a | 2.74 | −2.00 (−2.07, −2.08) | 6.63 | 1.77 | 4.86 | 0.82 |
| Al8a | 2.64 | −1.97 (−2.03, −2.05) | 6.04 | 2.19 | 3.85 | 0.41 |
| Al9a | 2.67 | −2.06 (−2.13, −2.15) | 5.96 | 2.67 | 3.29 | 0.20 |
| Al10a | 2.69 | −2.20 (−2.27, −2.29) | 6.09 | 2.07 | 4.02 | 0.85 |
| Cluster | (Å) | (Å) | BE (eV) | IP (eV) | EA (eV) | η (eV) | Gap (eV) | Location of H |
|---|---|---|---|---|---|---|---|---|
| Al3H1a | 2.63 | 1.94 | −2.07 (−2.11, −2.14) | 6.64 | 1.08 | 5.56 | 0.57 | 3 |
| Al4H1a | 2.68 | 2.08 | −2.10 (−2.16, −2.18) | 6.73 | 2.12 | 4.61 | 1.71 | 4 |
| Al5H1a | 2.66 | 1.62 | −2.24 (−2.30, −2.31) | 6.83 | 1.57 | 5.26 | 0.86 | t |
| Al8H1a | 2.63 | 1.62 | −2.13 (−2.19, −2.21) | 5.92 | 2.43 | 3.49 | 0.24 | t |
| Al3H2a | 2.65 | 1.64 | −2.38 (−2.41, −2.43) | 6.88 | 1.81 | 5.07 | 1.08 | t, t |
| Al4H2a | 2.65 | 2.11 | −2.42 (−2.48, −2.51) | 6.89 | 0.48 | 6.41 | 1.78 | 4, o |
| Al5H2a | 2.65 | 1.62 | −2.42 (−2.47, −2.48) | 6.53 | 2.07 | 4.47 | 0.82 | t, t |
| Al6H2a | 2.68 | 1.82 | −2.38 (−2.44, −2.46) | 6.52 | 1.83 | 4.69 | 0.76 | t, n |
| Al7H2a | 2.75 | 1.62 | −2.43 (−2.49, −2.50) | 6.68 | 2.77 | 3.91 | 0.88 | t, n |
| Al8H2a | 2.73 | 1.94 | −2.27 (−2.32, −2.44) | 6.06 | 1.97 | 4.09 | 0.49 | 3, o |
| Cluster | (Å) | (Å) | BE (eV) | IP (eV) | EA (eV) | η (eV) | Gap (eV) | Location of H |
|---|---|---|---|---|---|---|---|---|
| Al6 | 2.70 | −2.12 (−2.19, −2.21) | 6.55 | 2.03 | 4.62 | 1.45 | ||
| Al6H1 | 2.78 | 1.82 | −2.36 (−2.43, −2.45) | 6.76 | 2.17 | 4.60 | 1.43 | B |
| Al6H2 | 2.75 | 1.95 | −2.54 (−2.61, −2.64) | 6.95 | 1.59 | 5.36 | 1.38 | 3, 3 |
| Al7 | 2.75 | −2.32 (−2.39, −2.43) | 6.26 | 1.67 | 4.59 | 0.82 | ||
| Al7H1 | 2.70 | 1.62 | −2.52 (−2.60, −2.63) | 6.86 | 1.53 | 5.34 | 1.64 | T |
| Al7H2 | 2.75 | 1.61 | −2.59 (−2.66, −2.69) | 6.57 | 1.89 | 4.68 | 0.86 | t, t |
| Al8 | 2.75 | −2.34 (−2.42, −2.45) | 6.41 | 1.92 | 4.49 | 0.84 | ||
| Al8H1 | 2.75 | 1.62 | −2.49 (−2.57, −2.60) | 6.24 | 2.10 | 4.14 | 0.85 | T |
| Al8H2 | 2.74 | 1.62 | −2.63 (−2.70, −2.73) | 6.39 | 1.95 | 4.44 | 0.82 | t, t |
| Al9 | 2.79 | −2.39 (−2.48, −2.51) | 6.41 | 2.27 | 4.15 | 0.68 | ||
| Al9H1 | 2.79 | 1.61 | −2.53 (−2.62, −2.65) | 6.46 | 2.29 | 4.17 | 0.67 | T |
| Al9H2 | 2.77 | 1.62 | −2.64 (−2.72, −2.75) | 6.30 | 2.20 | 4.10 | 0.82 | t, t |
| Al10 | 2.77 | −2.44 (−2.53, −2.56) | 6.25 | 2.21 | 4.04 | 0.63 | ||
| Al10H1 | 2.78 | 1.61 | −2.56 (−2.64, −2.68) | 6.41 | 2.53 | 3.88 | 1.18 | T |
| Al10H2 | 2.77 | 1.62 | −2.64 (−2.73, −2.76) | 6.50 | 1.87 | 4.64 | 1.32 | t, t |
| Structure | Ead (eV) | Structure | Ead (eV) | Structure | Ead (eV) | Structure | Ead (eV) |
|---|---|---|---|---|---|---|---|
| Al3H2a | 1.15 | Al6H4 | 1.95 | Al8H2 | 1.08 | Al9H8 | 1.28 |
| Al4H2a | 1.43 | Al6H6 | 2.75 | Al8H4 | 1.34 | Al10H2 | 0.87 |
| Al5H2a | 1.02 | Al6H8 | 2.14 | Al9H2 | 1.03 | ||
| Al6H2a | 0.61 | Al7H2 | 0.62 | Al9H4 | 1.15 | ||
| Al6H2 | 1.12 | Al8H2a | 0.44 | Al9H6 | 1.28 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, C.; Wang, M.; Cao, L. Hydrogenated Planar Aluminum Clusters: A Density Functional Theory Study. Molecules 2025, 30, 1389. https://doi.org/10.3390/molecules30061389
Yao C, Wang M, Cao L. Hydrogenated Planar Aluminum Clusters: A Density Functional Theory Study. Molecules. 2025; 30(6):1389. https://doi.org/10.3390/molecules30061389
Chicago/Turabian StyleYao, Changhong, Meijiao Wang, and Lianzhen Cao. 2025. "Hydrogenated Planar Aluminum Clusters: A Density Functional Theory Study" Molecules 30, no. 6: 1389. https://doi.org/10.3390/molecules30061389
APA StyleYao, C., Wang, M., & Cao, L. (2025). Hydrogenated Planar Aluminum Clusters: A Density Functional Theory Study. Molecules, 30(6), 1389. https://doi.org/10.3390/molecules30061389







