Periodic Density Functional Theory Investigation of the Uranyl Ion Sorption on Three Mineral Surfaces: A Comparative Study
Abstract
:1. Introduction
2. Computational Details
2.1. TiO2 bulk
2.2. Al(OH)3 bulk
2.3. Ni bulk
3. H2O Interaction with Mineral Surfaces
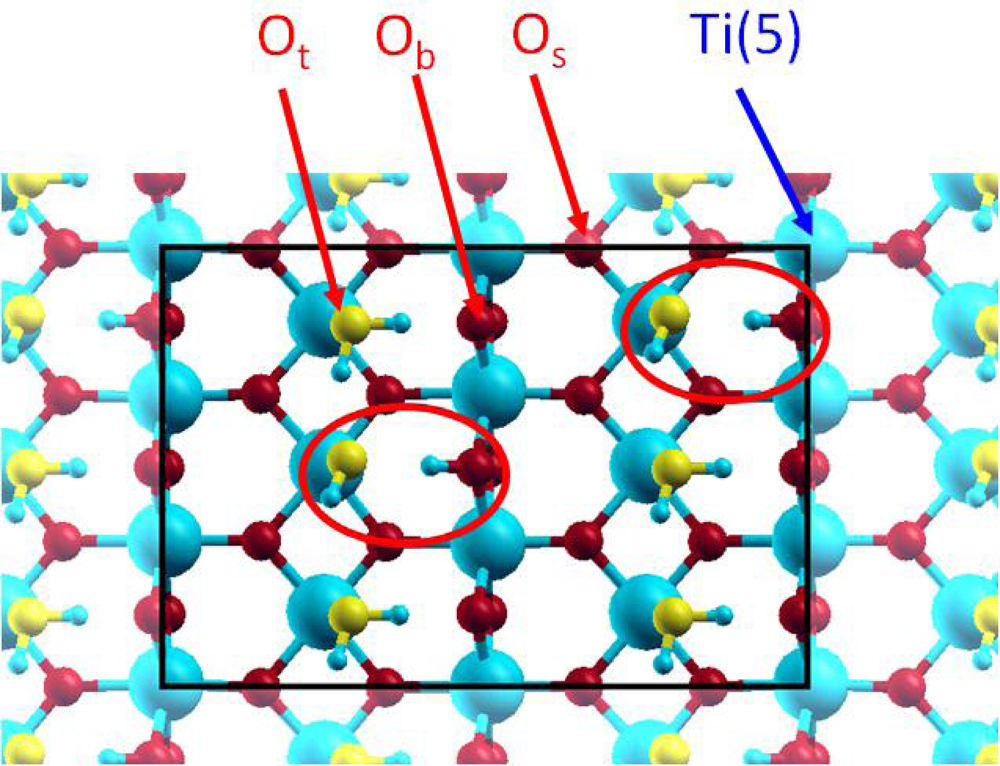
3.1. H2O / TiO2(111)
- The average destabilisation energy due to the partial dissociation was calculated using Equation (1):Where was the destabilisation energy per dissociated water molecule, Eref was the total energy of the supercell with the six molecular water molecules adsorbed on the six Ti(5) atoms, Esup ercell was the total energy of the considered supercell and was the number of dissociated water molecules.
- The destabilisation of each dissociated water molecule can also be calculated using Equation (2):Where was the destabilisation energy due to the nth dissociation, was the total energy of the supercell with (n−1) dissociated water molecules and was the total energy of the supercell with n dissociated water molecules.
3.2. H2O / γ-Al(OH)3 (001)
3.2.1. Adsorption at low water coverage
- Figure 4 (a) corresponds to adsorption on a “two out-of-plane hydrogen site”, with Eads =−0.64 eV. Distances are the following: d(HH2O−Osurface)=1.63 Å, d(OH2O−Hsurface)=1.88 – 1.99 Å.
- Figure 4 (b) shows the adsorption configuration on a “one in-plane hydrogen site”, with Eads=−0.54 eV. Water molecule is linked to the surface with two strong hydrogen bonds (d(HH2O−Osurface)=1.70 Å and d(OH2O−Hsurface)=1.85 Å) and a weaker third one (d(HH2O−Osurface)= 2.46 Å).
3.2.2. Adsorption at high water coverage
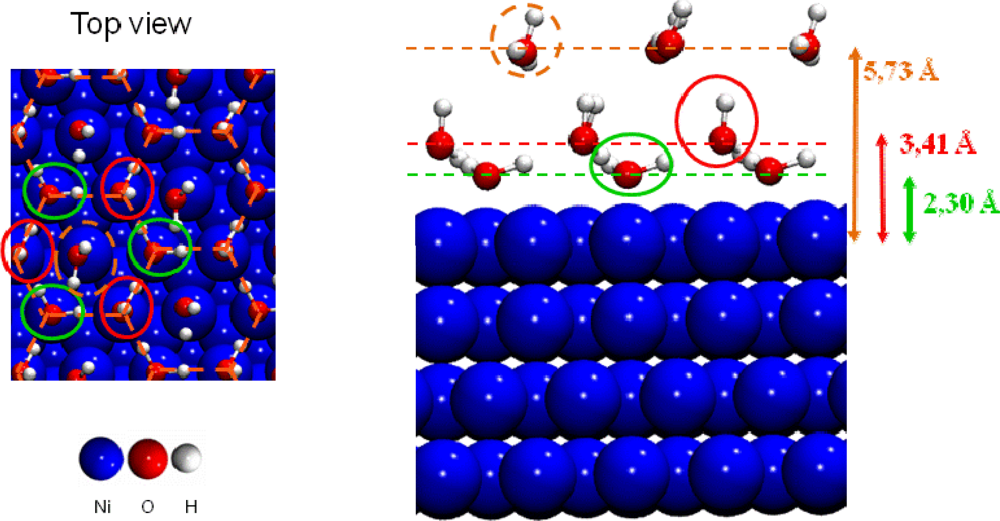
3.3. H2O / Ni(111)
- For surface coverage lower than 2/3 ML, the adsorption energies were in the range of isolated water molecules (≈ −0.3 eV)).
- For 2/3 ML surface coverage distances between water molecules were ∼2.5 Å and hydrogen bonds were created stabilizing the water network. Water molecules were organized in a bilayer H-up-hexamer structure which will be detailed below.
- For higher coverage than 2/3 ML water molecules pushed back themselves, which led to the formation of a third layer. The three water layers are displayed in Figure 7.
3.4. Conclusion of the water part
4. Uranyl Interaction on the Hydrated Mineral Surfaces
4.1. Uranyl / hydrated-TiO2(111)
4.2. Uranyl / hydrated-γ-Al(OH)3(001)
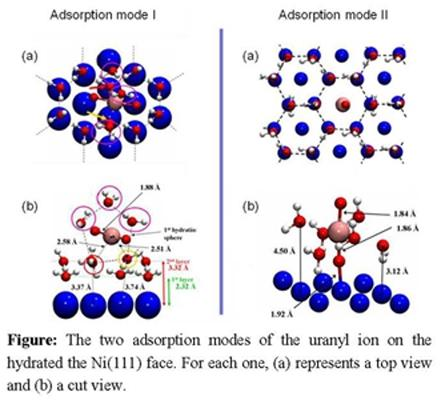
4.3. Uranyl / hydrated-Ni(111)
5. Conclusions
Acknowledgments
References
- Guillaumont, R. Radiochemical approches to the migration of elements from a radwaste repository. Radiochim Acta 1994, 66/67, 231–242. [Google Scholar]
- Silva, RJ; Nitsche, H. Actinide environmental chemistry. Radiochim Acta 1995, 70/71, 377–396. [Google Scholar]
- Fruzzetti, K; Wood, CJ. International Conference on Water Chemistry of Nuclear Reactor Systems, Jeju, Republic of Korea, October 23–26; 2006.
- Sandler, YL. Structure of PWR primary corrosion products. Corrosion 1979, 35, 205–208. [Google Scholar]
- Vandenborre, J. Etude multi-échelle des mécanismes d'interaction des ions aquo uranyle avec des surfaces de l'oxyde de titane; Thesis, Paris 11 University: Paris, France, 2005. [Google Scholar]
- Moskaleva, LV; Nasluzov, VA; Rösch, N. Modeling adsorption of the uranyl dication on the hydroxylated alpha-Al2O3 (0001) surface in an aqueous medium. Density functional study. Langmuir 2006, 22, 2141–2145. [Google Scholar]
- Sherman, DM; Peacock, CL; Hubbard, CG. Surface complexation of U(VI) on goethite (α-FeOOH). Geochim. Cosmochim. Acta 2008, 72, 298–310. [Google Scholar]
- Greathouse, JA; O’Brien, RJ; Bemis, G; Pabalan, RT. Molecular dynamics study of aqueous uranyl interactions with quartz (010). J. Phys. Chem. B 2002, 106, 1646–1655. [Google Scholar]
- Greathouse, JA; Stellalevinsohn, HR; Denecke, MA; Bauer, A; Paballan, RT. Uranyl surface complexes in mixed-charge montmorillonite: Monte Carlo computer simulation and polarized XAFS results. Clays Clay Miner 2005, 53, 278–286. [Google Scholar]
- Zaidan, OF; Greathouse, JA; Pabalan, RT. Monte Carlo and molecular dynamics simulation of uranyl adsorption on montmorillonite clay. Clays Clay Miner 2003, 51, 372–381. [Google Scholar]
- Jones, P; Hockey, JA. Infra-red studies of rutile surfaces. Part 1. Trans. Faraday Soc 1971, 67, 2669–2678. [Google Scholar]
- Jones, P; Hockey, JA. Infra-red studies of rutile surfaces. Part 2. Hydroxylation, hydration and structure of rutile surfaces. Trans. Faraday Soc 1971, 67, 2679–2685. [Google Scholar]
- Onishi, H; Iwasawa, Y. STM-imaging of formate intermediates adsorbed on a TiO2(110) surface. Chem. Phys. Lett 1994, 226, 111–114. [Google Scholar]
- Parfitt, GD. The surface of titanium dioxide. Prog. Surf. Membr. Sci 1976, 11, 181–226. [Google Scholar]
- Den Auwer, C; Drot, R; Simoni, E; Conradson, SD; Gailhanou, M; de Leon, MJ. Grazing incidence XAFS spectroscopy of uranyl sorbed onto TiO2 rutile surfaces. New J. Chem 2003, 27, 648–655. [Google Scholar]
- Dossot, M; Cremel, S; Vandenborre, J; Grausem, J; Humbert, B; Drot, R; Simoni, E. Sorption of uranyl cations on a rutile (001) single-crystal monitored by surface second harmonic generation. Langmuir 2006, 22, 140–148. [Google Scholar]
- Vandenborre, J; Drot, R; Simoni, E. Interaction mechanisms between uranium(VI) and rutile titanium dioxide: From single crystal to powder. Inorg. Chem 2006, 46, 1291–1296. [Google Scholar]
- Hiemstra, T; Riemsdijk, WHV. On the relationship between charge distribution, surface hydration, and the structure of the interface of metal hydroxides. J. Coll. Inter. Sci 2006, 301, 1–18. [Google Scholar]
- Hiemstra, T; Venema, P; Riemsdijk, WHV. Intrinsic proton affinity of reactive surface groups of metal (hydr)oxides: The bond valence principle. J. Coll. Inter. Sci 1996, 184, 680–692. [Google Scholar]
- Hiemstra, T; Yong, H; Riemsdijk, WHV. Interfacial charging phenomena of aluminium (hydr)oxides. Langmuir 1999, 15, 5942–5955. [Google Scholar]
- Hiemstra, T; Riemsdijk, WHV; Bolt, GH. Multisite proton adsorption modeling at the solid/interface of (hydr)oxides: A new approach I: Model description and evaluation of intrinsic reaction constants. J. Coll. Inter. Sci 1989, 133, 91–104. [Google Scholar]
- Hiemstra, T; Wit, JCMD; Riemsdijk, WHV. Multisite proton adsorption modeling at the solid/interface of (hydr)oxides: A new approach II: Application to various important (hydr)oxides. J. Coll. Inter. Sci 1989, 133, 105–117. [Google Scholar]
- Jodin, MC; Gaboriaud, F; Humbert, B. Limitations of potentiometric studies to determine the surface charge of gibbsite γ-Al(OH)3 particles. J. Coll. Inter. Sci 2005, 287, 581–591. [Google Scholar]
- Chang, H-S; Korshin, GV; Wang, Z; Zachara, JM. Adsorption of uranyl on gibbsite: A time-resolved laser-induced fluorescence spectroscopy study. Environ. Sci. Technol 2006, 40, 1244–1249. [Google Scholar]
- Baumann, N; Brendler, V; Arnold, T; Geipel, G; Bernhard, G. Uranyl sorption onto gibbsite studied by time-resolved laser-induced fluorescence spectroscopy (TRLFS). J. Coll. Inter. Sci 2005, 290, 318–324. [Google Scholar]
- Froideval, A; Gaillard, C; Barillon, R; Rossini, I; Hazemann, JL. Uranyl sorption species at low coverage on Al-hydroxide: TRLFS and XAFS studies. Geochim. Cosmochim. Acta 2006, 70, 5270–5284. [Google Scholar] [Green Version]
- Hongxia, Z; Yongxin, X; Zuyi, T. Sorption of uranyl ions on gibbsite: effects of contact time, pH, ionic strength, concentration and anion of electrolyte. Coll. Surf. A 2005, 252, 1–5. [Google Scholar]
- Kresse, G; Hafner, J. Ab initio molecular dynamics for open-shell transition metals. Phys. Rev. B 1993, 48, 13115–13118. [Google Scholar]
- Kresse, G; Hafner, J. Ab initio molecular-dynamics simulation of the liquid-metal–amorphous-semiconductor transition in germanium. Phys. Rev. B 1994, 49, 14251–14269. [Google Scholar]
- Kresse, G; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comp. Mater. Sci 1996, 6, 15–50. [Google Scholar]
- Kresse, G; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar]
- Perdew, JP; Wang, Y. Accurate and simple analytic representation of the electron-gas correlation energy. Phys. Rev. B 1992, 45, 13244–13249. [Google Scholar]
- Perdew, JP; Chevary, JA; Vosko, SH; Jackson, KA; Pederson, MR; Singh, DJ; Fiolhais, C. Atoms, molecules, solids, and surfaces: Applications of the generalized gradient approximation for exchange and correlation. Phys. Rev. B 1992, 46, 6671–6687. [Google Scholar]
- Blöchl, PE. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar]
- Kresse, G; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar]
- Perron, H; Domain, C; Roques, J; Drot, R; Simoni, E; Catalette, H. Optimisation of accurate rutile TiO2 (110), (100), (101) and (001) surface models from periodic DFT calculations. Theor. Chem. Acc 2007, 117, 565–574. [Google Scholar]
- Muscat, J; Swamy, V; Harrison, NM. First-principles calculations of the phase stability of TiO2. Phys. Rev. B 2002, 65, 224112. [Google Scholar]
- Giese, RF. Hydroxyl orientations in gibbsite and bayerite. Acta Crystallogra. B 1976, 32, 1719–1723. [Google Scholar]
- Saalfeld, H; Weede, M. Refinement of the crystal structure of gibbsite, Al(OH)3. Zeit. fur Kristall 1974, 139, 129–135. [Google Scholar]
- Mercury, JMR; Pena, P; deAza, AH; Sheptayakov, D; Turrillas, X. On the decomposition of synthetic gibbsite studied by neutron thermodiffractometry. J. Am. Ceram. Soc 2006, 89, 3728–3733. [Google Scholar]
- Veilly, E; Roques, J; Jodin-Caumon, MC; Humbert, B; Drot, R; Simoni, E. Uranyl interaction with the hydrated (001) basal face of gibbsite: A combined theoretical and spectroscopic study. J. Chem. Phys 2008, 129, 244704. [Google Scholar] [Green Version]
- Digne, M; Sautet, P; Raybaud, P; Toulhoat, H; Emilio, A. Structure and stability of aluminium hydroxides: A theoretical study. J. Phys Chem. B 2002, 106, 5155–5162. [Google Scholar]
- Kittel, C. Introduction to Solid State Physics; Dunod university: France, 1996. [Google Scholar]
- Levesque, M; Roques, J; Domain, C; Perron, H; Veilly, E; Simoni, E; Catalette, H. Uranyl interaction with the hydrated (111) nickel face: A periodic density functional theory investigation. Surf. Sci 2008, 602, 3331–3337. [Google Scholar]
- Mittendorfer, F; Eichler, A; Hafner, J. Structural, electronic and magnetic properties of nickel surfaces. Surf. Sci 1999, 423, 1–11. [Google Scholar]
- Perron, H; Domain, C; Roques, J; Drot, R; Simoni, E; Catalette, H. Optimisation of accurate rutile TiO2 (110), (100), (101) and (001) surface models from periodic DFT calculations. Theor Chem Acc 2007. [Google Scholar]
- Perron, H; Vandenborre, J; Domain, C; Roques, J; Drot, R; Simoni, E; Ehrhardt, J-J; Catalette, H. Combined investigation of water sorption on TiO2 rutile (110) single crystal face: XPS vs. periodic DFT. Surf. Sci 2007, 601, 518–527. [Google Scholar]
- Lindan, PJD; Harrison, NM; Gillan, MJ. Mixed dissociative and molecular adsorption of water on the rutile (110) surface. Phys. Rev. Lett 1998, 80, 762–765. [Google Scholar]
- Bezrodna, T; Puchkovska, G; Shymanovska, V; Baran, J; Ratajczak, H. IR-analysis of H-bonded H2O on the pure TiO2 surface. J. Mol. Struct 2004, 700, 175–181. [Google Scholar]
- Primet, M; Pichat, P; Mathieu, MV. Infrared study of the surface of titanium dioxides. I. Hydroxyl groups. J. Phys. Chem 1971, 75, 1216–1220. [Google Scholar]
- Brinkley, D; Dietrich, M; Engel, T; Farrall, P; Gantner, G; Schafer, A; Szuchmacher, A. A modulated molecular beam study of the extent of H2O dissociation on TiO2(110). Surf. Sci 1998, 395, 292–306. [Google Scholar]
- Jodin, MC. De la prise en compte des hétérogénéités morphologiques et structurales vers l’interprétation de la réactivité globale d’un hydroxyde d’aluminium; Thesis, Henri Poincaré University, Nancy: France, 2004. [Google Scholar]
- Molis, E; Barrès, O; Marchand, H; Sauzéat, E; Humbert, B; Thomas, F. Initial steps of ligand-promoted dissolution of gibbsite. Coll. Surf. A 2000, 163, 283–292. [Google Scholar]
- Teppen, BJ; Rasmussen, K; Bertsch, PM; Miller, DM; Schafer, L. Molecular dynamics modeling of clay minerals. 1. Gibbsite, Kaolinite, Pyrophyllite, and Beidellite. J. Phys. Chem. B 1997, 101, 1579–1587. [Google Scholar]
- Wang, J; Kalinichev, AG; Kirkpatrick, RJ. Effects of substrate structure and composition on the structure, dynamics, and energetics of water at mineral surfaces: A molecular dynamics modeling study. Geochim. Cosmochim. Acta 2006, 70, 562–582. [Google Scholar]
- Tunega, D; Gerzabek, MH; Lischka, H. Ab initio molecular dynamics study of a monomolecular water layer on octahedral and tetrahedral kaolinite surface. J. Phys. Chem. B 2004, 108, 5930–5936. [Google Scholar]
- Eichler, A. CO adsorption on Ni(111): A density functional theory study. Surf. Sci 2002, 526, 332–340. [Google Scholar]
- Roques, J; Anderson, AB. Electrode potential-dependent stages in OHads formation on the Pt3Cr alloy (111) surface. J. Electrochem. Soc 2004, 151, E340–E347. [Google Scholar]
- Roques, J; Anderson, AB. Theory for the Potential Shift of OHads Formation on the Pt Skin on Pt3Cr(111)n Acid. J. Electrochemi. Soc 2004, 151, E85–E91. [Google Scholar]
- Lu, HC; Gusev, EP; Garfunkel, E; Gustafsson, T. A MEIS study of thermal effects on the Ni(111) surface. Surf Sci 1996, 352–354, 21–24. [Google Scholar]
- Sebastiani, D; Site, DL. Adsorption of water molecules on flat and stepped nickel surfaces from first principles. J. Chem. Theory Comput 2005, 1, 78–82. [Google Scholar]
- Pache, T; Steinrück, H-P; Huber, W; Menzel, D. The adsorption of H2O on clean and oxygen precovered Ni(111) studied by ARUPS and TPD. Surf. Sci 1989, 224, 195–214. [Google Scholar]
- Yang, H; Whitten, JL. The adsorption of water and hydroxyl on Ni(111). Surf. Sci 1989, 223, 131–150. [Google Scholar]
- Schulze, M; Reissner, R; Bolwin, K; Kuch, W. Interaction of water with clean and oxygen precovered nickel surfaces. Fresenius' J. Anal. Chem 1995, 353, 661–665. [Google Scholar]
- Li, J; Zhu, S; Li, Y; Oguzie, EE; Wang, F. Electronic structure of monomeric water adsorption on Ni{111}: Beyond the general model. J. Phys. Chem. C 2008, 12, 8294–8300. [Google Scholar]
- Nakamura, M; Ito, M. Monomer and tetramer water clusters adsorbed on Ru(0001). Chem. Phys. Lett 2000, 325, 293–298. [Google Scholar]
- Michaelides, A; Alavi, A; King, DA. Insight into H2O-ice adsorption and dissociation on metal surfaces from first-principles simulations. Phys Rev B 2004, 69. [Google Scholar]
- Michaelides, A. Density functional theory simulations of water–metal interfaces: Waltzing waters, a novel 2D ice phase, and more. Appl. Phys. A 2006, 85, 415–425. [Google Scholar]
- Nakamura, M; Ito, M. Coadsorption of water dimer and ring-hexamer clusters on M(111) (M =Cu, Ni, Pt) and Ru(001) surfaces at 25 K as studied by infrared reflection absorption spectroscopy. Chem. Phys. Lett 2005, 404, 346–350. [Google Scholar]
- Michaelides, A; Alavi, A; King, DA. Different surface chemistries of water on Ru{0001}: From monomer adsorption to partially dissociated bilayers. J. Am. Chem. Soc 2003, 125, 2746–2755. [Google Scholar]
- Meng, S; Wang, EG; Gao, S. Water adsorption on metal surfaces: A general picture from density functional theory studies. Phys. Rev. B 2004, 69, 195404. [Google Scholar]
- Perron, H; Roques, J; Domain, C; Drot, R; Simoni, E; Catalette, H. Theoretical investigation of the uranyl ion sorption on the rutile TiO2(110) face. Inorg. Chem 2008, 47, 10991–10997. [Google Scholar]
- Clavaguéra-Sarrio, C; Ismail, N; Marsden, CJ; Bégué, D; Pouchan, C. Calculation of harmonic and anharmonic vibrational wavenumbers for triatomic uranium compounds XUY. Chem. Phys 2004, 302, 1–11. [Google Scholar]
- Clavaguéra-Sarrio, C; Brenner, V; Hoyau, S; Marsden, CJ; Millié, P; Dognon, J-P. Modeling of uranyl cation-water clusters. J. Phys. Chem. B 2003, 107, 3051–3060. [Google Scholar]
- Ismail, N; Heully, J-L; Saue, T; Daudey, J-P; Marsden, CJ. Theoretical studies of the actinides: Method calibration for the UO22+ and PuO22+ ions. J. Chem. Phys. Lett 1999, 300, 296–302. [Google Scholar]
- Hiemstra, T; Riemsdijk, WHV. A surface structural approach to ion adsorption: The charge distribution (CD) model. J. Coll. Inter. Sci 1996, 179, 488–508. [Google Scholar]
- Perron, H; Domain, C; Roques, J; Drot, R; Simoni, E; Catalette, H. Theoretical first step towards an understanding of the uranyl ion sorption on the rutile TiO2 (110) face: A DFT periodic and cluster study. Radiochim. Acta 2006, 94, 601–607. [Google Scholar]
- Perron, H. Simulation par la théorie de la fonctionnelle de la densité de l’interaction de l’ion uranyle avec les surfaces de TiO2 et de NiFe2O4; Thesis, Paris 11 University: Paris, France, 2007. [Google Scholar]
- Perron, H; Domain, C; Roques, J; Drot, R; Simoni, E; Catalette, H. Periodic density functional theory investigation of the uranyl ion sorption on the TiO2 rutile (110) face. Inorg. Chem 2006, 45, 6568–6570. [Google Scholar]
- Kowal-Fouchard, A; Drot, R; Simoni, E; Marmier, N; Fromage, F; Ehrhardt, J-J. Structural identification of europium(III) adsorption complexes on montmorillonite. New J. Chem 2004, 28, 864–869. [Google Scholar]
- Xu, D; Ning, QL; Zhou, X; Chen, CL; Wu, AD; Wang, XK. Sorption and desorption of Eu(III) on alumina. J. Radioanal. Nucl. Chem 2005, 266, 419–424. [Google Scholar]
- Fairhurst, AJ; Warwick, P; Richardson, S. The influence of humic acid on the adsorption of europium onto inorganic colloids as a function of pH. Coll. Surf. A 1995, 99, 187–199. [Google Scholar]
- Dong, WM; Wang, XK; Bian, XY; Wang, AX; Du, JZ; Tao, ZY. Comparative study on sorption/desorption of radioeuropium on alumina, bentonite and red earth: Effects of pH, ionic strength, fulvic acid, and iron oxides in red earth. Appl. Rad. Isot 2001, 54, 603–610. [Google Scholar]
- Silvestrelli, S; Parrinello, M. Structural, electronic, and bonding properties of liquid water from first principles. J. Chem. Phys 1999, 111, 3572–3580. [Google Scholar]










| Parameter | This worka | Calculatedb | Experimentalc |
|---|---|---|---|
| a (Å) | 8.736 | 8.765 | 8.684 |
| b (Å) | 5.099 | 5.083 | 5.078 |
| c (Å) | 9.628 | 9.594 | 9.736 |
| β (°) | 92.83 | 92.63 | 94.54 |
| V (Å3) | 428.4 | 427.0 | 428.0 |
| M / D Percentage | 6 / 0 0% | 5 / 1 17% | 4 / 2 33% | 3 / 3 50% | 2 / 4 66% | 1 / 5 83% | 0 / 6 100% |
|---|---|---|---|---|---|---|---|
| 0.00 | −0.03 | −0.02 | −0.06 | −0.08 | −0.11 | −0.13 | |
| 0.00 | −0.03 | −0.01 | −0.14 | −0.13 | −0.23 | −0.25 |
| Eads | ΔEads | Eads GGA [61] | Eads exp.[62] | Eads exp.[63] | Eads exp.[64] | |
|---|---|---|---|---|---|---|
| (1) on top | −0.34 | 0 | −0.25 | −0.42 | −0.48 | −0.53 |
| (2) fcc | −0.24 | +0.10 | – | – | – | – |
| (3) bridge | −0.18 | +0.16 | −0.10 | – | – | – |
| (4) hcp | −0.14 | +0.20 | – | – | – | – |
| bb | bt | tt | EXAFSe | |
|---|---|---|---|---|
| U=O | 1.91 | 1.90 | 1.86 | 1.78 ± 0.02 |
| O=U=O | 166.1 | 172.4 | 176.1 | 180 |
| U–Osurface | 2.30 | 2.21a / 2.28b | 2.17 | 2.31 ± 0.02 |
| U–Owater | 2.60c | 2.62c | 2.64c | 2.46 ± 0.02 |
| Erelatived | 0.0 | 85 | 175 |
| d(U-Osurf) | d(U=O-yl) | d(O-yl••••H) | Θ(O=U=O) | ΔE | |
|---|---|---|---|---|---|
| Protonated sites | |||||
| Site I | 2.61–2.70 | 1.88–1.96 | 1.81-1.82-2.32 | 169.6 | 0.28 |
| Site II | 2.53–2.87 | 1.92–1.94 | 1.71-1.75-1.79 | 176.0 | 0 |
| Site III | 2.60–2.70 | 1.92–1.95 | 1.61-1.72-2.32 | 168.4 | 0.24 |
| Deprotonated sites | |||||
| Site I | 2.11–2.21 | 1.87–1.92 | 1.95-2.04-2.31 | 146.9 | 0.58 |
| Site II | 2.10–2.24 | 1.87–1.89 | 1.74-1.77-1.83 | 162.9 | 0 |
| Site III | 2.12–2.17 | 1.90–1.92 | 1.69-1.79-2.08 | 150.8 | 0.40 |
| (1) top | (2) hcp | (3) bridge | (4) hcp | |
|---|---|---|---|---|
| E (eV) | −8.89 | −8.66 | −8.62 | −8.03 |
| ΔE (eV) | 0.00 | +0.23 | +0.27 | +0.86 |
© 2009 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Roques, J.; Veilly, E.; Simoni, E. Periodic Density Functional Theory Investigation of the Uranyl Ion Sorption on Three Mineral Surfaces: A Comparative Study. Int. J. Mol. Sci. 2009, 10, 2633-2661. https://doi.org/10.3390/ijms10062633
Roques J, Veilly E, Simoni E. Periodic Density Functional Theory Investigation of the Uranyl Ion Sorption on Three Mineral Surfaces: A Comparative Study. International Journal of Molecular Sciences. 2009; 10(6):2633-2661. https://doi.org/10.3390/ijms10062633
Chicago/Turabian StyleRoques, Jérôme, Edouard Veilly, and Eric Simoni. 2009. "Periodic Density Functional Theory Investigation of the Uranyl Ion Sorption on Three Mineral Surfaces: A Comparative Study" International Journal of Molecular Sciences 10, no. 6: 2633-2661. https://doi.org/10.3390/ijms10062633
APA StyleRoques, J., Veilly, E., & Simoni, E. (2009). Periodic Density Functional Theory Investigation of the Uranyl Ion Sorption on Three Mineral Surfaces: A Comparative Study. International Journal of Molecular Sciences, 10(6), 2633-2661. https://doi.org/10.3390/ijms10062633