Chemical Interactions and Their Role in the Microphase Separation of Block Copolymer Thin Films
Abstract
:1. Introduction and Background
1.1. The Thermodynamics of Self-Assembly
1.2. The Intermolecular Forces Involved in Self-Assembly
2. Microphase Separation and Self-Organisation Block Copolymers
2.1. Intermolecular Forces in Microphase Separation of Block Copolymers
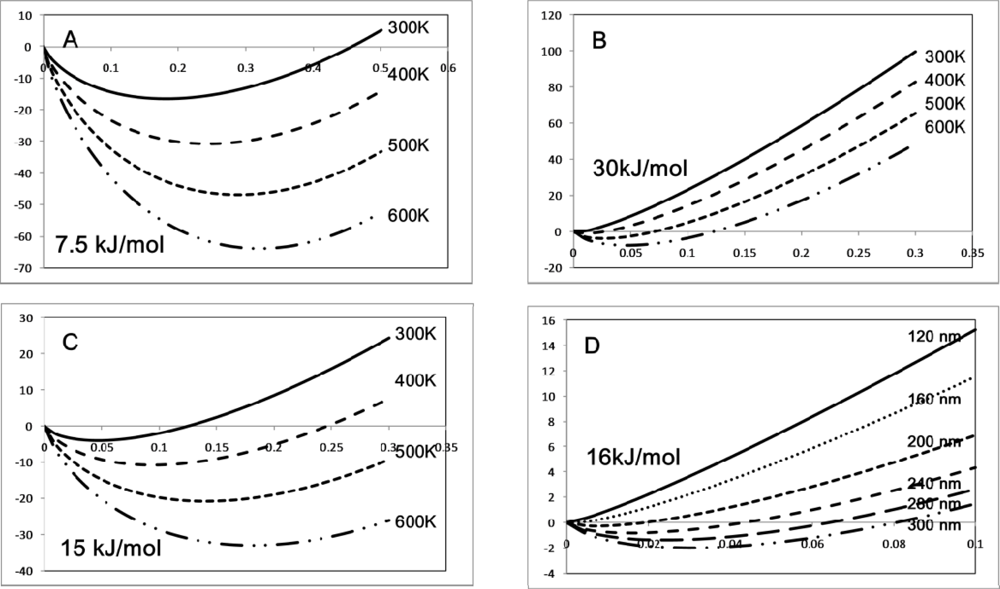
2.2. The Solubility Parameter and the Thermodynamics of Microphase Separation
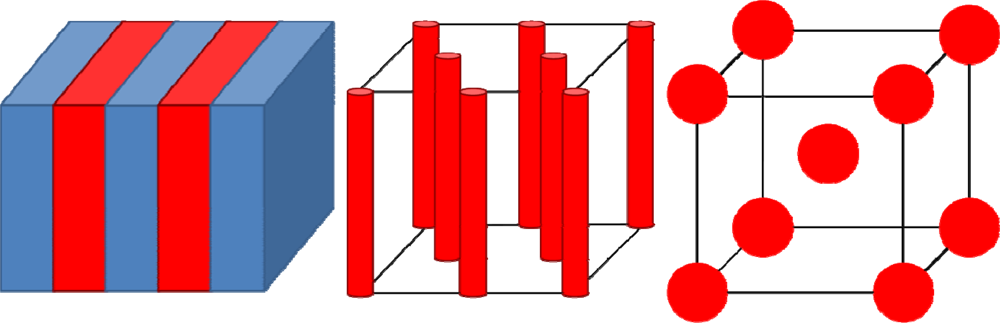
2.3. Phase Diagrams
2.4. Applications of Microphase Separation—SURFACE Pattern Formations
3. Surface, Interface and Related Effects
3.1. Surface Interface Effects
3.2. Solvent Interface Effects
3.3. Solvent Casting Effects
4. Alignment of Microphase Separated BCP Features
4.1. Pattern Alignment Control
4.2. Chemical Patterning
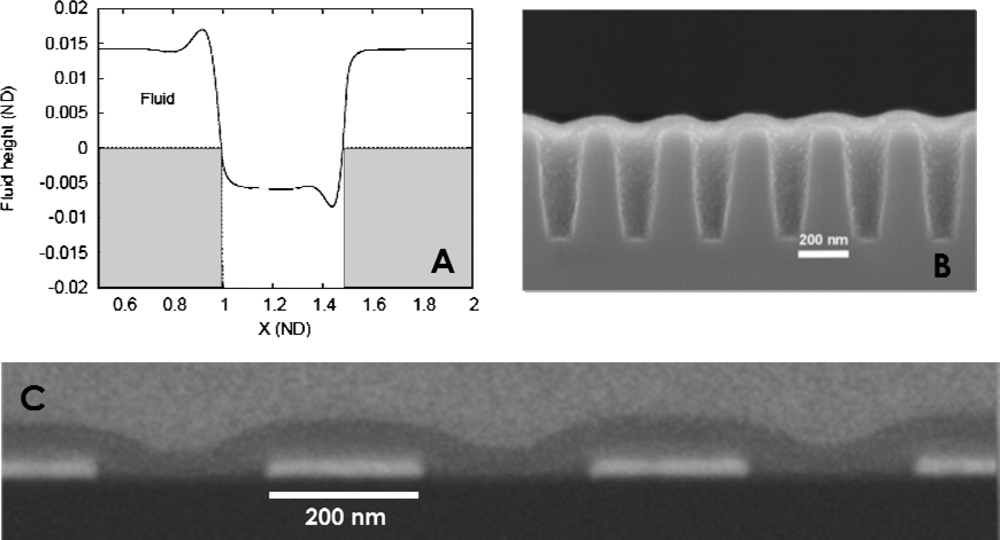
4.3. Graphoepitaxy for Patterning
5. Defect Formation
5.1. Intrinsic Defects in Block Copolymer Nanopatterned Surfaces
5.1.1. Equilibrium Defects
5.1.2. Non-Equilibrium Defects
5.2. Extrinsic Defects in Block Copolymer Nanopatterned Surfaces
6. Concluding Remarks
Acknowledgments
References
- Whitesides, GM; Grzybowski, B. Self-assembly at all scales. Science 2002, 295, 2418–2421. [Google Scholar]
- Whitesides, GM; Mathias, JP; Seto, CT. Molecular self-assembly and nanochemistry: A chemical strategy for the synthesis of nanostructures. Science 1991, 254, 1312–1319. [Google Scholar]
- Murray, CB; Kagan, CR; Bawendi, MG. Self-organization of CdSe nanocrystallites into three-dimensional quantum dot superlattices. Science 1995, 270, 1335. [Google Scholar]
- Schwarz, DK. Mechanisms and kinetics of self-assembled monolayer formation. Annu. Rev. Phys. Chem 2001, 52, 107–137. [Google Scholar]
- Svenson, S. Controlling surfactant self-assembly. Curr. Opin. Colloid Interface Sci 2004, 9, 201–212. [Google Scholar]
- Kresge, CT; Leonowicz, ME; Roth, WJ; Vartuli, JC; Beck, JS. Ordered mesoporous molecular sieves synthesized by a liquid-crystal mechanism. Nature 1992, 359, 710–712. [Google Scholar]
- Holmes, JD; Morris, MA; Ryan, KM. Self Assembly—The Future, 1st ed; Robinson, BH, Ed.; Elsevier: Amsterdam, The Netherlands, 2003; Chapter 2; p. 175. [Google Scholar]
- Misteli, T. The concept of self-organization in cellular architecture. J. Cell Biol 2001, 155, 181–185. [Google Scholar]
- Care, CM; Dalby, T. Packing entropy in micelle self-assembly. Europhys. Lett 1999, 45, 38–42. [Google Scholar]
- Yodh, AG; Lin, K-H; Crockery, JC; Dinsmorez, AD; Verma, R; Kaplan, PD. Entropically driven self-assembly and interaction in suspension. Phil. Trans. R. Soc. Lond A 2001, 359, 921–937. [Google Scholar]
- Huie, JC. Guided molecular self-assembly: A review of recent efforts. Smart Mater. Struct 2003, 12, 264–271. [Google Scholar]
- Neidle, S. Oxford Handbook of Nucleic Acid; Structure Oxford University Press: Oxford, UK, 1999. [Google Scholar]
- Ninham, B. Self Assembly; Robinson, BH, Ed.; IOS Press: Amsterdam, The Netherlands, 2003; p. 11. [Google Scholar]
- Würthner, F. Perylene bisimide dyes as versatile building blocks for functional supramolecular architectures. Chem. Commun 2004, 14, 1574. [Google Scholar]
- Olenyuk, B; Whiteford, JA; Stang, PJ. Self-assembly of nanoscale cuboctahedra by coordination chemistry. Nature 1990, 398, 796–799. [Google Scholar]
- Lindgård, P-A. Reflections on the protein-folding problem. J. Phys.: Condens. Matter 2003, 15, S1779–S1786. [Google Scholar]
- Israelachivili, J. Intermolecular and surface forces, 2nd ed; Academic Press: NY, USA, 1991; pp. 1–130. [Google Scholar]
- Leclère, Ph; Surin, M; Brocorens, P; Cavallini, M; Biscarini, F; Lazzaroni, R. Supramolecular assembly of conjugated polymers: From molecular engineering to solid-state properties. Mater. Sci. Eng. R 2006, 55, 1–56. [Google Scholar]
- D’Errico, G. Encyclopaedia of Surface and Colloid Science; Somasundaran, P, Ed.; CRC Press: Boca Raton, FL, USA, 2006; pp. 3840–3848. [Google Scholar]
- Ryan, KM; Coleman, NRB; Lyons, DM; Morris, MA; Steytler, DC; Heenan, RK; Holmes, JD. Control of pore morphology in mesoporous silica synthesized from triblock copolymer templates. Langmuir 2002, 18, 4996–5001. [Google Scholar]
- Carraher, CE, Jr. Introduction to Polymer Chemistry; CRC Press: New York, NY, USA, 2007. [Google Scholar]
- Hamley, IW. Developments in Block Copolymer Science and Technology; Wiley: Hoboken, NJ, USA, 2004. [Google Scholar]
- Lazzari, M; Liu, G; Lecommandoux, S. Block Copolymers in Nanoscience; Wiley-VCH. Weinheim: Berlin, DE, Germany, 2006. [Google Scholar]
- Kim, G; Libera, M. Microstructural development in solvent-cast polystyrene-polybutadiene-polystyrene (SBS) triblock copolymer thin films. Macromolecules 1998, 31, 2569–2577. [Google Scholar]
- Burke, GM; Woscholski, R; Yaliraki, SN. Differential hydrophobicity drives self-assembly in Huntington’s disease. Proc. Nat. Acad. Sci. USA 2003, 100, 13928–13933. [Google Scholar]
- Hildebrand, JH. The Solubility of Non-Electrolytes; Reinhold Publishing Corporation: New York, NY, USA, 1936. [Google Scholar]
- Burke, J. Solubility parameters: Theory and application. AIC Book and Paper Group Annual 1984, 3, 13–58. [Google Scholar]
- Barton, AFM. Handbook of Polymer-liquid Interaction Parameters and Solubility Parameters; CRC Press: Boca Raton, FL, USA, 1990. [Google Scholar]
- Hansen, CM. The three dimensional solubility parameter key to paint component affinities: 1. Solvents, plasticizers, polymers, and resins. J. Paint Technol 1967, 39, 104–117. [Google Scholar]
- Hansen, CM. The universality of the solubility parameter concept. Ind. Eng. Chem. Prod. Res. Dev 1969, 8, 2–11. [Google Scholar]
- Bates, FS. Polymer-polymer phase behaviour. Science 1991, 251, 898–905. [Google Scholar]
- Flory, PJ. Thermodynamics of high polymer solutions. J. Chem. Phys 1942, 10, 51–61. [Google Scholar]
- Huggins, ML. Theories of solutions of high polymers. J. Am. Chem. Soc 1942, 74, 1712–1719. [Google Scholar]
- Matsen, MW; Bates, FS. Unifying weak- and strong-segregation block copolymer theories. Macromolecules 1996, 28, 1091–1098. [Google Scholar]
- Leibler, L. Theory of microphase separation in block copolymers. Macromolecules 1980, 13, 1602–1617. [Google Scholar]
- Grason, GM. The packing of soft materials: Molecular asymmetry, geometric frustration and optimal lattices in block copolymer melts. Phys. Rep 2006, 433, 1–64. [Google Scholar]
- Khandpur, AK; Förster, S; Bates, FS; Hamley, IW; Ryan, AJ; Bras, W; Almdal, K; Mortensen, K. A small-angle neutron scattering study of orientational order in the nematic phase of a thermotropic liquid crystal. Macromolecules 1995, 28, 8796–8806. [Google Scholar]
- Melenkevitz, J; Muthukumar, M. Density functional theory of lamellar ordering in diblock copolymers. Macromolecules 1991, 24, 4199–4205. [Google Scholar]
- Bates, FS; Fredrickson, GH. Block copolymers—Designer soft materials. Phys. Today 1998, 52, 32–38. [Google Scholar]
- Grason, GM. Continuous crystallization in hexagonally ordered materials. Phys. Rev. Letts 2008, 101, 105702–105706. [Google Scholar]
- Hajduk, DA; Takenouchi, H; Hillmyer, MA; Bates, FS; Vigild, ME; Almdal, K. Stability of the perforated layer (PL) phase in diblock copolymer melts. Macromolecules 1997, 30, 3788–3795. [Google Scholar]
- Hamley, IW; Koppi, KA; Rosedale, JH; Bates, FS; Almdal, K; Mortensen, K. Hexagonal mesophases between lamellae and cylinders in a diblock copolymer melt. Macromolecules 1993, 26, 5959–5970. [Google Scholar]
- Knoll, A; Horvat, A; Lyakhova, KS; Krausch, G; Sevink, GJA; Zvelindovsky, AV; Magerle, R. Phase behavior in thin films of cylinder-forming block copolymers. Phys. Rev. Letts 2002, 89, 035501–035505. [Google Scholar]
- Castelletto, V; Hamley, IW. Morphologies of block copolymer melts. Current Opinion in Sol. State Mater. Sci 2004, 8, 426–438. [Google Scholar]
- Rice, R; Arnold, DC; Shaw, MT; Lacopina, I; Quinn, AJ; Amenitsch, H; Holmes, JD; Morris, MA. Ordered mesoporous silicate structures as potential templates for nanowire growth. Adv. Funct. Mater 2007, 17, 133–141. [Google Scholar]
- Petkov, N; Platschek, B; Morris, MA; Holmes, JD; Bein, T. Oriented growth of metal and semiconductor nanostructures within aligned mesoporous channels. Chem. Mater 2007, 19, 1376–1381. [Google Scholar]
- Pileni, MP. Nanocrystal self-assemblies: Fabrication and collective properties. J. Phys. Chem. B 2001, 105, 3358–3371. [Google Scholar]
- Lodge, TP. Block copolymers: Past successes and future challenges. Macromol. Chem. Phys 2003, 204, 265–273. [Google Scholar]
- Fasolka, M; Mayes, AM. Block copolymer thin films—Physics and applications. Ann. Rev. Mater. Res 2001, 31, 323–355. [Google Scholar]
- Soo, PP; Huang, BY; Jang, YI; Chiang, YM; Sadoway, DR; Mayes, AM. Rubbery block copolymer electrolytes. J. Electrochem. Soc 1999, 146, 32–37. [Google Scholar]
- Ulbricht, M. Advanced functional polymer membranes. Polymer 2006, 47, 2217–2262. [Google Scholar]
- Park, C; Yoon, J; Thomas, EL. Enabling nanotechnology with self assembled block copolymer patterns. Polymer 2003, 44, 6725–6760. [Google Scholar]
- Chen, VZH; Hoffman, J; Lee, VY; Latrou, H; Avgeropoulus, A; Hadjichristidis, N; Miller, RD; Thomas, EL. Ordered bicontinuous nanoporous and nanorelief ceramic films from self assembling polymer precursors. Science 1999, 286, 1716–1719. [Google Scholar]
- Farrell, RA; Petkov, N; Cherkaoui, K; Hurley, P; Amenitsch, H; Holmes, JD; Morris, MA. Thin and continuous films with controlled bi- and tri-modal porosities by embedment of zeolite nanoparticles in a mesoporous Matrix. J. Mat. Chem 2008, 18, 2213–2220. [Google Scholar]
- Farrell, RA; Cherkaoui, K; Petkov, N; Amenitsch, H; Holmes, JD; Hurley, PK; Morris, MA. Physical and electrical properties of low dielectric constant self-assembled mesoporous silica thin films. Microelectron. Reliab 2007, 47, 759–763. [Google Scholar]
- Cheng, JY; Ross, CA; Chan, VZH; Thomas, EL; Robb, GH; Lammertink, RGH; Vancso, GJ. Formation of a cobalt magnetic dot array via block copolymer lithography. Adv. Mater 2001, 13, 1174–1178. [Google Scholar]
- Edrington, AC; Urbas, AM; DeRege, P; Chen, CX; Swager, TM; Hadjichristidis, N; Xenidou, M; Fetters, LJ; Joannopoulos, JD; Fink, Y; Thomas, EL. Polymer-based photonic crystals. Adv. Mater 2001, 13, 421–425. [Google Scholar]
- Pease, RF; Chou, SY. Lithography and other patterning techniques for future electronics. Pro. IEEE 2008, 96, 248–270. [Google Scholar]
- Del Campo, A; Artz, E. Fabrication approaches for generating complex micro- and nanopatterns on polymeric surfaces. Chem. Rev 2008, 108, 911–945. [Google Scholar]
- Bloomstein, TM; Marchant, MF; Deneault, S; Hardy, DE; Rothschild, M. 22-NM immersion interference lithography. Opt. Express 2006, 14, 6434–6443. [Google Scholar]
- Davari, B; Dennard, RH; Shahidi, GG. CMOS scaling for high performance and low power-the next ten years. Proc. IEEE 1995, 83, 595–606. [Google Scholar]
- ITRS roadmap 2005 [Online].
- Whitesides, GM; Mathias, JP; Seto, CT. Molecular self-assembly and nanochemistry—A chemical strategy for the synthesis of nanostructures. Science 1991, 254, 1312–1319. [Google Scholar]
- Hillenius, S; Herr, D; Weitzman, B; Welser, J. SRC collaborations paving the way. IEEE Nanotechnol. Mag 2007, 1, 6–12. [Google Scholar]
- Jeong, SJ; Xia, G; Kim, BH; Shin, DO; Kwon, SH; Kang, SW; Kim, OS. Universal block copolymer lithography for metals, semiconductors, ceramics, and polymers. Adv. Mater 2008, 20, 1898–1904. [Google Scholar]
- Yamaguchi, T; Yamaguchi, H. Block copolymer lithography toward 16-nm-technology nodes and beyond. NTT Tech. Rev 2006, 4, 17–24. [Google Scholar]
- Stoykovich, MP; Nealey, PF. Block copolymers and conventional lithography. Mater. Today 2006, 9, 20–29. [Google Scholar]
- Cheng, JY; Sanders, DP; Kim, HC; Sundberg, LK. Integration of polymer self-assembly for lithographic application. Proc SPIE 2008, 6921, 692127/1–692127/8. [Google Scholar]
- Aizawa, M; Buriak, JM. Block copolymer templated chemistry for the formation of metallic nanoparticle arrays on semiconductor surfaces. Chem. Mater 2007, 19, 5090–5101. [Google Scholar]
- Krishnamoorthy, S; Hinderling, C; Heinzelmann, H. Nanoscale patterning with block copolymers. Mater. Today 2002, 9, 40–47. [Google Scholar]
- Segalman, RA. Patterning with block copolymer thin films. Mater. Sci. Eng. R 2005, 48, 191–226. [Google Scholar]
- Qi, S; Wang, ZG. On the nature of the perforated layer phase in undiluted diblock copolymers. Macromolecules 1997, 30, 4491–4497. [Google Scholar]
- Knoll, A; Lyakhova, KS; Horvat, A; Krausch, G; Sevink, GJA; Zvelindovsky, AV; Magerle, R. Direct imaging and mesoscale modelling of phase transitions in a nanostructured fluid. Nat. Mater 2004, 3, 886–891. [Google Scholar]
- Seo, YA; Kim, E; Kwon, SY; Jing, H; Shin, K. AFM study of phase-separated morphology in immiscible blend thin films. Ultramicroscopy 2008, 10, 1186–1190. [Google Scholar]
- Green, PF; Limary, R. Block copolymer thin films: Pattern formation and phase behaviour. Adv. Colloid Interface Sci 2001, 94, 53–81. [Google Scholar]
- Suh, JY; Kim, YS; Lee, HH. Parallel and vertical morphologies in block copolymers of cylindrical domains. J. Chem. Phys 1998, 108, 1253–1256. [Google Scholar]
- Fasolka, MJ; Harris, DJ; Mayes, AM; Yoon, M; Mochrie, SGJ. Observed substrate topography-mediated lateral patterning of diblock copolymer films. Phys. Rev. Lett 1997, 79, 3018–3021. [Google Scholar]
- Sohn, BH; Yun, SH. Perpendicular lamellae induced at the interface of neutral self-assembled monolayers in thin diblock copolymer films. Polymer 2002, 43, 2507–2512. [Google Scholar]
- Mansky, P; Liu, Y; Huang, E; Russell, TP; Hawker, CJ. Controlling polymer-surface interactions with random copolymer brushes. Science 1997, 275, 1458–1460. [Google Scholar]
- In, I; La, YH; Park, SM; Nealey, PF; Gopalan, P. Side-chain-grafted random copolymer brushes as neutral surfaces for controlling the orientation of block copolymer microdomains in thin films. Langmuir 2006, 22, 7855–7860. [Google Scholar]
- Sperling, LH. Introduction to Physical Polymer Science, 4th ed; Wiley: Hoboken, NJ, USA, 2006. [Google Scholar]
- Schott, H. Swelling kinetics of polymers. J. Macromol. Sci. Part B 1992, 3, 1–9. [Google Scholar]
- Fukunaga, K; Elbs, H; Magerle, R; Krausch, G. Large-scale alignment of ABC block copolymer microdomains via solvent vapor treatment. Macromolecules 2000, 33, 947–953. [Google Scholar]
- Niu, SJ; Saraf, RF. Stability of order in solvent-annealed block copolymer thin films. Macromolecules 2003, 36, 2428–2440. [Google Scholar]
- Cavicchi, KA; Russell, TP. Solvent annealed thin films of asymmetric polyisoprene-polylactide diblock copolymers. Macromolecules 2001, 40, 1181–1186. [Google Scholar]
- Lin, Z; Kim, DH; Wu, X; Boosahda, L; Stone, D; LaRose, L; Russell, TP. A rapid route to arrays of nanostructures in thin films. Adv. Mater 2002, 14, 1373–1376. [Google Scholar]
- Kim, SH; Misner, MJ; Xu, T; Kimura, M; Russell, TP. Highly oriented and ordered arrays from block copolymers via solvent evaporation. Adv. Mater 2004, 16, 226–231. [Google Scholar]
- Gutierrez, MH; Ford, WT. The glass-to-gel transition in solvent-swollen polystyrene networks. J. Polym. Sci., Part B: Polym. Chem 2003, 24, 655–663. [Google Scholar]
- Hildebrand, JH; Scott, RL. The Solubility of Nonelectrolytes, 3rd ed; Reinhold Publishing Corporation: New York, NY, USA, 1950. [Google Scholar]
- Tassin, JF; Siemans, RL; Tang, WT; Hadziioannou, G; Swalen, JD; Smith, BA. Kinetics of adsorption of block copolymers revealed by surface plasmons. J. Phys. Chem 1989, 93, 2106–2111. [Google Scholar]
- Cheng, F; Yang, X; Peng, H; Chen, D; Jing, M. Well-controlled formation of polymeric micelles with a nanosized aqueous core and their applications as nanoreactors. Macromolecules 2007, 40, 8007–8014. [Google Scholar]
- Fitzgerald, TG; Farrell, RA; O’Driscoll, S; O’Mahony, CT; Holmes, JD; Morris, MA. Orientation and translational control of PS-b-PEO/PS thin films via solvent annealing and graphoepitaxy techniques. e-J. Surf. Sci. Nanotech 2009, 7, 741–745. [Google Scholar]
- Scriven, LE. Physics and applications of dip coating and spin coating. Mater. Res. Soc. Symp. Proc 1998, 121, 717–729. [Google Scholar]
- Liquid Film Coating: Scientific Principles and Their Technological Implications, 1st ed; Kistler, SF; Schweizer, PM (Eds.) Chapman and Hall: London, UK, 1997.
- Weill, A; Francou, JM; Dechenaux, E. Photoresist spin coating mechanism related to polymer solution rheology. Microelectron. Eng 1987, 6, 427–431. [Google Scholar]
- Yimsiria, P; Mackley, MR. Spin and dip coating of light-emitting polymer solutions: Matching experiment with modelling. Chem. Eng. Sci 2006, 61, 3496–3505. [Google Scholar]
- Matar, OK; Sisoev, GM; Lawrence, CJ. Thin film flow over spinning discs: The effect of surface topography and flow rate modulation. Chem. Eng. Sci 2008, 63, 2225–2232. [Google Scholar]
- Fitzgerald, TG; Farrell, RA; O’Driscoll, S; O’Mahony, CT; Holmes, JD; Morris, MA. Orientation and translational control of PS-b-PEO/PS thin films via solvent annealing and graphoepitaxy techniques. e-J. Surf. Sci. Nanotech 2009, 7, 471–475. [Google Scholar]
- Fitzgerald, TG; Farrell, RA; Petkov, N; Shaw, MT; Charpin, J; Gleeson, JP; Holmes, JD; Morris, MA. A study on the combined effects of solvent evaporation and polymer flow upon block copolymer self-assembly and alignment on topographic patterns. Langmuir.
- Perlich, J; Körstgens, V; Metwalli, E; Schulz, L; Georgii, R; Müller-Buschbaum, P. Solvent content in thin spin-coated polystyrene homopolymer films. Macromolecules 2009, 42, 337–344. [Google Scholar]
- Harrison, C; Adamson, H; Cheng, Z; Sebastian, JM; Sethuraman, S; Huse, DA; Register, A; Chaikin, PM. Mechanisms of ordering in striped patterns. Science 2000, 290, 1558–1560. [Google Scholar]
- Darling, SB. Directing the self-assembly of block copolymers. Prog. Polym. Sci 2007, 32, 1152–1204. [Google Scholar]
- Kim, HC; Hinsberg, WD. Surface patterns from block copolymer self-assembly. J. Vac. Sci. Technol. A 2008, 26, 1369–1382. [Google Scholar]
- Thurn-Albrecht, T; DeRouchey, J; Russell, TP; Kolb, R. Pathways toward electric field induced alignment of block copolymers. Macromolecules 2002, 35, 8106–8110. [Google Scholar]
- Amundsen, K; Helfand, E; Quan, XN; Hudson, SD; Smith, SD. Alignment of lamellar block copolymer microstructure in an electric field. 2. Mechanisms of alignment. Macromolecules 1994, 27, 6559–6570. [Google Scholar]
- Morkved, TL; Lu, M; Urbas, AM; Ehrichs, EE; Jaeger, HM; Mansky, P; Russell, TP. Local control of microdomain orientation in diblock copolymer thin films with electric fields. Science 1996, 273, 931–933. [Google Scholar]
- Mansky, P; DeRouchey, J; Mays, J; Pitsikalis, M; Morkved, T; Russell, TP. Large-area domain alignment in block copolymer thin films using electric fields. Macromolecules 1998, 31, 4399–4401. [Google Scholar]
- Angelescu, DE; Waller, JH; Adamson, DA; Deshpandle, P; Chou, SY; Register, RA; Chaikin, PM. Macroscopic orientation of block copolymer cylinders in single-layer films by shearing. Adv. Mater 2004, 16, 1736–1740. [Google Scholar]
- Kimura, M; Misner, MJ; Xu, T; Kim, SH; Russell, TP. Long-range ordering of diblock copolymers induced by droplet pinning. Langmuir 2003, 19, 9910–9913. [Google Scholar]
- Petermann, J; Gohil, RM. New method for the preparation of high modulus thermoplastic films. J. Mater. Sci 1979, 14, 2260–2264. [Google Scholar]
- Park, C; Rosa, CD; Thomas, EL. Large area orientation of block copolymer microdomains in thin films via directional crystallization of a solvent. Macromolecules 2001, 34, 2602–2606. [Google Scholar]
- Park, C; Rosa, CD; Lotz, B; Fetters, LJ; Thomas, EL. Molecular and microdomain orientation in semicrystalline block copolymer thin films by directional crystallization of the solvent and epitaxy. Macromol. Chem. Phys 2003, 204, 1514–1523. [Google Scholar]
- Kim, SO; Solak, HH; Stoykovich, MP; Ferrier, NJ; de Pablo, JJ; Nealey, PF. Epitaxial self-assembly of block copolymers on lithographically defined nanopatterned substrates. Nature 2003, 424, 411–414. [Google Scholar]
- Chen, H; Chakrabarti, J. Morphology of thin block copolymer films on chemically patterned substrates. J. Chem. Phys 1998, 108, 6897–6905. [Google Scholar]
- Pereira, GG; Williams, DRM. Diblock copolymer thin film melts on striped, heterogeneous surfaces: Parallel, perpendicular and mixed lamellar morphologies. Macromolecules 1999, 32, 758–764. [Google Scholar]
- Rockford, I; Liu, Y; Mansky, P; Russell, TP; Yoon, M; Mochrie, SGJ. Polymers on nanoperiodic, heterogeneous surfaces. Phys. Rev. Lett 1999, 82, 2602–2605. [Google Scholar]
- Peters, RD; Yang, XM; Wang, Q; de Pablo, JJ; Nealey, PF. Combining advanced lithographic techniques and self-assembly of thin films of diblock copolymers to produce templates for nanofabrication. J. Vac. Sci. Tech B 2000, 18, 3530–3534. [Google Scholar]
- Kim, TK; Yang, XM; Peters, RD; Sohn, BH; Nealey, PF. Chemical modification of self-assembled monolayers by exposure to soft X-rays in air. J. Phys. Chem. B 2000, 104, 7403–7410. [Google Scholar]
- Stoykovich, MP; Müller, M; Kim, SO; Solak, HH; Edward, EW; de Pablo, JJ; Nealey, PF. Directed assembly of block copolymer blends into nonregular device-oriented structures. Science 2005, 308, 1442–1446. [Google Scholar]
- Cheng, JY; Rettner, CT; Sanders, DP; Kim, HC; Hinsberg, WD. Dense self-assembly on sparse chemical patterns: Rectifying and multiplying lithographic patterns using block copolymers. Adv. Mater 2008, 20, 3155–3158. [Google Scholar]
- Ruiz, R; Kang, H; Detcheverry, FA; Dobisz, F; Kercher, D; Albrecht, TR; de Pablo, JJ; Nealey, PF. Density multiplication and improved lithography by directed block copolymer assembly. Science 2008, 321, 936–939. [Google Scholar]
- Smith, HI; Flanders, DC. Orientated crystal-growth on amorphous substrates using artificial surface-relief gratings. Appl. Phys. Letts 1978, 32, 349–350. [Google Scholar]
- Whittmann, JC; Smith, P. Highly orientated thin-films of poly(tetrafluoroethylene) as a substrate for orientated growth of materials. Nature 1991, 353, 414–417. [Google Scholar]
- Segalman, RA; Yokoyama, H; Kramer, EJ. Graphoepitaxy of spherical domain block copolymer films. Adv. Mater 2001, 13, 1152–1155. [Google Scholar]
- Cheng, JY; Ross, CA; Thomas, EL; Smith, HI; Vancso, GJ. Fabrication of nanostructures with long-range order using block copolymer lithography. Appl. Phys. Lett 2002, 81, 3657–3659. [Google Scholar]
- Xiao, S; Yang, XM; Edwards, EW; La, WH; Nealey, PF. Graphoepitaxy of cylinder-forming block copolymers for use as templates to pattern magnetic metal dot arrays. Nanotechnology 2005, 16, S324–S329. [Google Scholar]
- Chen, F; Akasaka, S; Inoue, T; Takenaka, M; Hasegawa, H; Yoshida, H. Ordering cylindrical microdomains for binary blends of block copolymers with graphoepitaxy. Macromol. Rapid Commun 2007, 28, 2137–2144. [Google Scholar]
- Cheng, JY; Mayes, AM; Ross, CA. Nanostructure engineering by templated self-assembly of block copolymers. Nat. Mater 2004, 3, 823–828. [Google Scholar]
- Bosworth, JK; Paik, MY; Ruiz, R; Schwartz, EL; Huang, JQ; Ko, AW; Smilgies, DM; Black, CT; Ober, CK. Control of self-assembly of lithographically patternable block copolymer films. ACS Nano 2008, 2, 1396–1402. [Google Scholar]
- Bita, I; Yang, JKW; Jung, YS; Ross, CA; Thomas, EL; Berggren, KK. Graphoepitaxy of self-assembled block copolymers on two-dimensional periodic patterned templates. Science 2008, 321, 939–943. [Google Scholar]
- Rudenko, T; Kilchytska, V; Collaert, N; Nazarov, AN; Jurczak, M; Flandre, D. Electrical characterization and special properties of FINFET structures. In Nanoscaled Semiconductor-On-Insulator Structures and Devices, 1st ed; Springer Verlag: Berlin, Germany, 2007. [Google Scholar]
- Black, CT; Ruiz, Z; Bretya, G; Cheng, JY; Colburn, ME; Guarini, KW; Kim, HC; Zhang, Y. Polymer self assembly in semiconductor microelectronics. IBM J. Res. Dev 2007, 51, 605–633. [Google Scholar]
- Segalman, RA; Schaefer, KE; Fredrickson, GH; Kramer, EJ; Mogonov, S. Topographic templating of islands and holes in highly asymmetric block copolymer films. Macromolecules 2003, 36, 4498–4506. [Google Scholar]
- Park, SM; Stoykovich, MP; Ruiz, R; Zhang, Y; Black, CT; Nealey, PF. Directed assembly of lamellae-forming block copolymers by using chemically and topographically patterned substrates. Adv. Mater 2007, 19, 607–611. [Google Scholar]
- Ruiz, R; Sandstrom, RL; Black, CT. Induced orientational order in symmetric diblock copolymer thin films. Adv. Mater 2007, 19, 587–591. [Google Scholar]
- Fitzgerald, TG; Borsetto, F; O’Callaghan, JM; Kosmala, B; Shaw, MT; Holmes, JD; Morris, MA. Polymer nanostructures in sub-micron lithographically defined channels: Film-thickness effects on structural alignment of a small feature size polystyrene-polyisoprene-polystyrene block copolymer. Soft Matter 2007, 2, 916–921. [Google Scholar]
- Scheel, HJ; Fukuda, T. Crystal Growth Technology, 1st ed; John Wiley & Sons, Inc: London, UK, 2003. [Google Scholar]
- Hammond, MR; Cochran, E; Fredrickson, GH; Kramer, EJ. Temperature dependence of order, disorder, and defects in laterally confined diblock copolymer cylinder monolayers. Macromolecules 2005, 38, 6575–6585. [Google Scholar]
- Chastek, TQ; Lodge, TP. Twinning and growth kinetics of lamellar grains in a diblock copolymer solution. J. Polym. Sci., Part B: Polym. Phys 2005, 44, 405–412. [Google Scholar]
- Harrison, C; Angelescu, DE; Trawick, M; Zhengdong, C; Huse, DA; Chaikin, PM; Vega, DA; Sebastian, JM; Register, RA; Adamson, DH. Pattern coarsening in a 2D hexagonal system. Europhys. Lett 2004, 67, 800–806. [Google Scholar]
- Segalman, RA; Hexemer, A; Kramer, EJ. Edge effects on the order and freezing of a 2D Array of block copolymer spheres. Phys Rev Letts 2003, 91, 196101/1-4. [Google Scholar]
- Hahm, J; Lopes, WA; Jaeger, HM; Sibener, SJ. Defect evolution in ultrathin films of polystyrene-block-polymethylmethacrylate diblock copolymers observed by atomic force microscopy. J. Chem. Phys 1998, 109, 10111–10114. [Google Scholar]
- Hahm, J; Sibener, SJ. Time-resolved atomic force microscopy imaging studies of asymmetric PS-b-PMMA ultrathin films: Dislocation and disclination transformations, defect mobility, and evolution of nanoscale morphology. J. Chem. Phys 2001, 114, 4730–4740. [Google Scholar]
- Tsarkova, L; Horvat, A; Krausch, G; Zvelindovsky, AV; Sevink, GJA; Magerle, R. Defect evolution in block copolymer thin films via temporal phase transitions. Langmuir 2006, 22, 8089–8095. [Google Scholar]
- Stoykovich, MP; Kang, H; Daoulas, KC; Liu, G; Liu, CC; de Pablo, JJ; Müller, M; Nealey, PF. Directed self-assembly of block copolymers for nanolithography: Fabrication of isolated features and essential integrated circuit geometries. ACS Nano 2007, 1, 168–175. [Google Scholar]
- Roerdink, M; Hempenius, MA; Gunst, U; Arlinghaus, HF; Vancso, GJ. Substrate wetting and topographically induced ordering of amorphous PI-b-PFS block-copolymer domains. Small 2007, 3, 1415–1423. [Google Scholar]
- Welander, AM; Nealey, PF; Cao, H; Bristol, R. Impact of trench width roughness on the graphoepitaxial assembly of block copolymers. J. Vac. Sci. Tech. B 2008, 26, 2484–2488. [Google Scholar]
- Park, SM; Craig, GSW; La, YK; Nealey, PF. Morphological reconstruction and ordering in films of sphere-forming block copolymers on striped chemically patterned surfaces. Macromolecules 2008, 41, 9124–9129. [Google Scholar]
- Huck, WTS. Effects of nanoconfinement on the morphology and reactivity of organic materials. Chem. Comm 2005, 41, 4143–4148. [Google Scholar]
- Black, CT. Self-aligned self assembly of multi-nanowire silicon field effect transistors. Appl. Phys. Lett 2005, 87, 163116. [Google Scholar]
- Ruiz, R; Ruiz, N; Sandstrom, RL; Black, CT. Local defectivity control of 2D self-assembled block copolymer patterns. Adv. Mater 2007, 19, 2157–2162. [Google Scholar]










© 2009 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Farrell, R.A.; Fitzgerald, T.G.; Borah, D.; Holmes, J.D.; Morris, M.A. Chemical Interactions and Their Role in the Microphase Separation of Block Copolymer Thin Films. Int. J. Mol. Sci. 2009, 10, 3671-3712. https://doi.org/10.3390/ijms10093671
Farrell RA, Fitzgerald TG, Borah D, Holmes JD, Morris MA. Chemical Interactions and Their Role in the Microphase Separation of Block Copolymer Thin Films. International Journal of Molecular Sciences. 2009; 10(9):3671-3712. https://doi.org/10.3390/ijms10093671
Chicago/Turabian StyleFarrell, Richard A., Thomas G. Fitzgerald, Dipu Borah, Justin D. Holmes, and Michael A. Morris. 2009. "Chemical Interactions and Their Role in the Microphase Separation of Block Copolymer Thin Films" International Journal of Molecular Sciences 10, no. 9: 3671-3712. https://doi.org/10.3390/ijms10093671
APA StyleFarrell, R. A., Fitzgerald, T. G., Borah, D., Holmes, J. D., & Morris, M. A. (2009). Chemical Interactions and Their Role in the Microphase Separation of Block Copolymer Thin Films. International Journal of Molecular Sciences, 10(9), 3671-3712. https://doi.org/10.3390/ijms10093671



