Comparative Study of the Dissociative Ionization of 1,1,1 Trichloroethane Using Nanosecond and Femtosecond Laser Pulses
Abstract
:1. Introduction
2. Experimental Setup
2.1. Femtosecond Laser System
2.2. Nanosecond Laser System
2.3. Time of Flight Mass Spectrometer
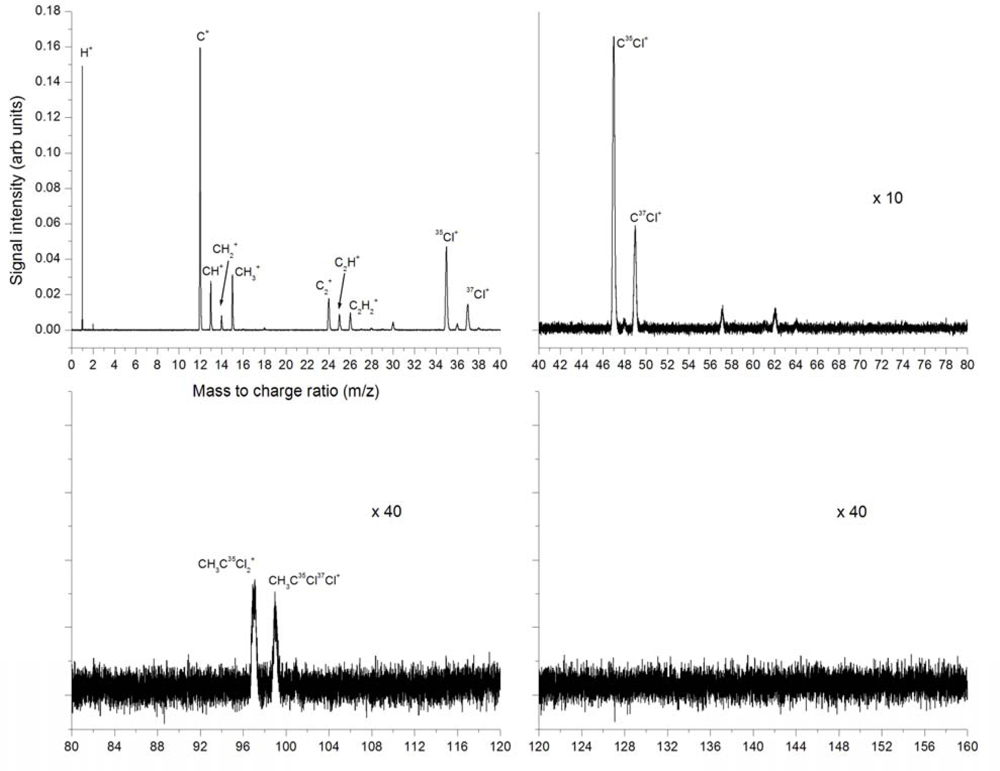
3. Results
3.1. Nanosecond Ionization
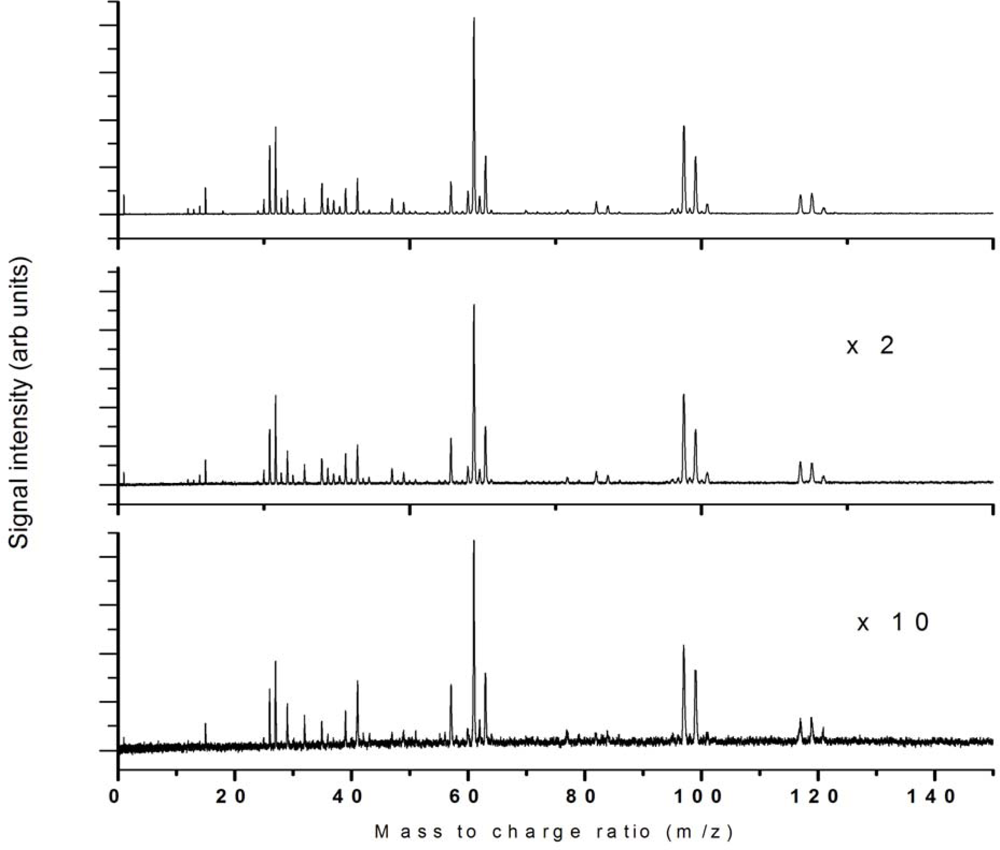
3.1.1. Nanosecond Ionization 532 nm
3.1.2. Nanosecond Ionization 355 nm
3.1.3. Nanosecond Ionization 266 nm
3.2. Femtosecond Ionization
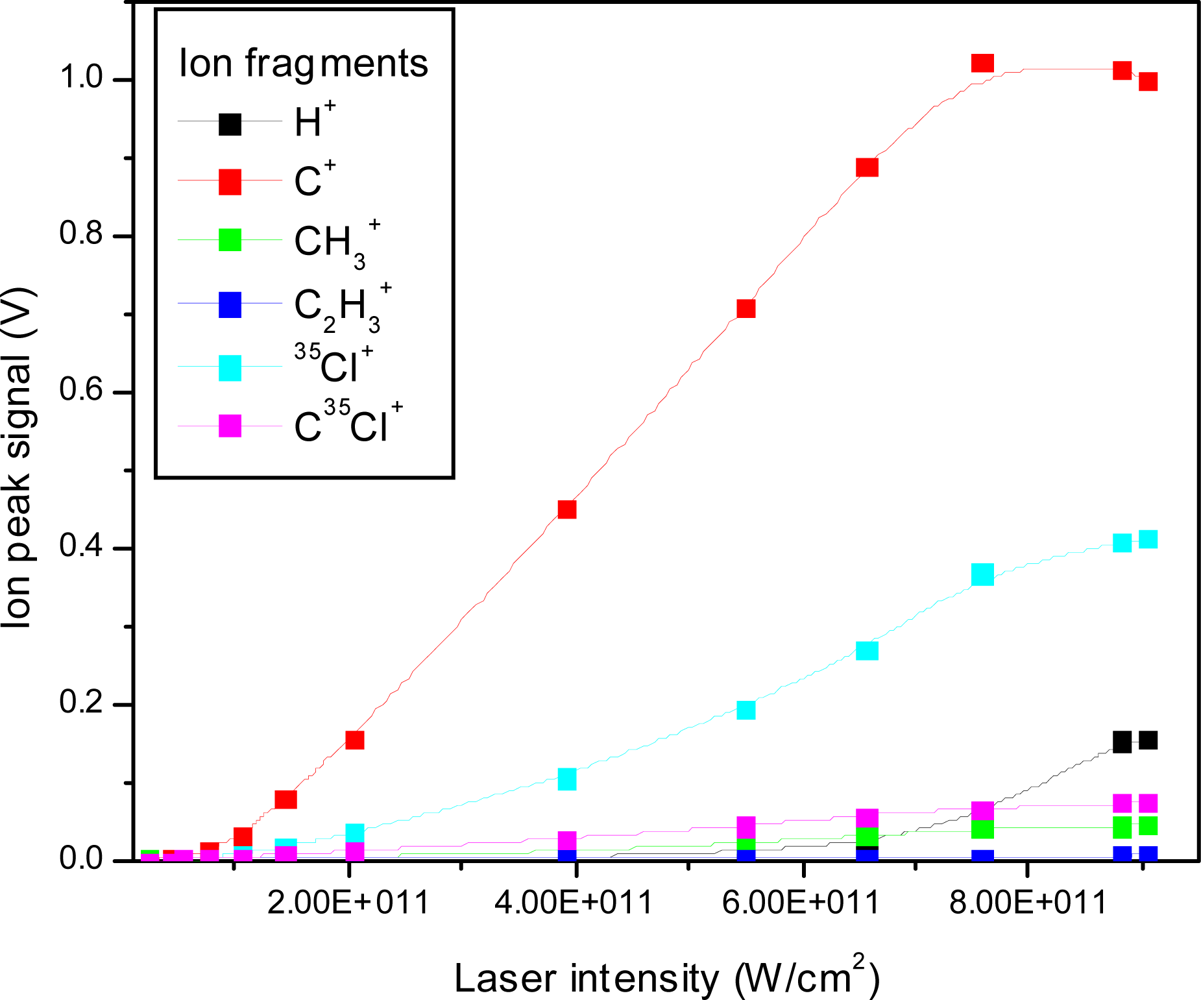
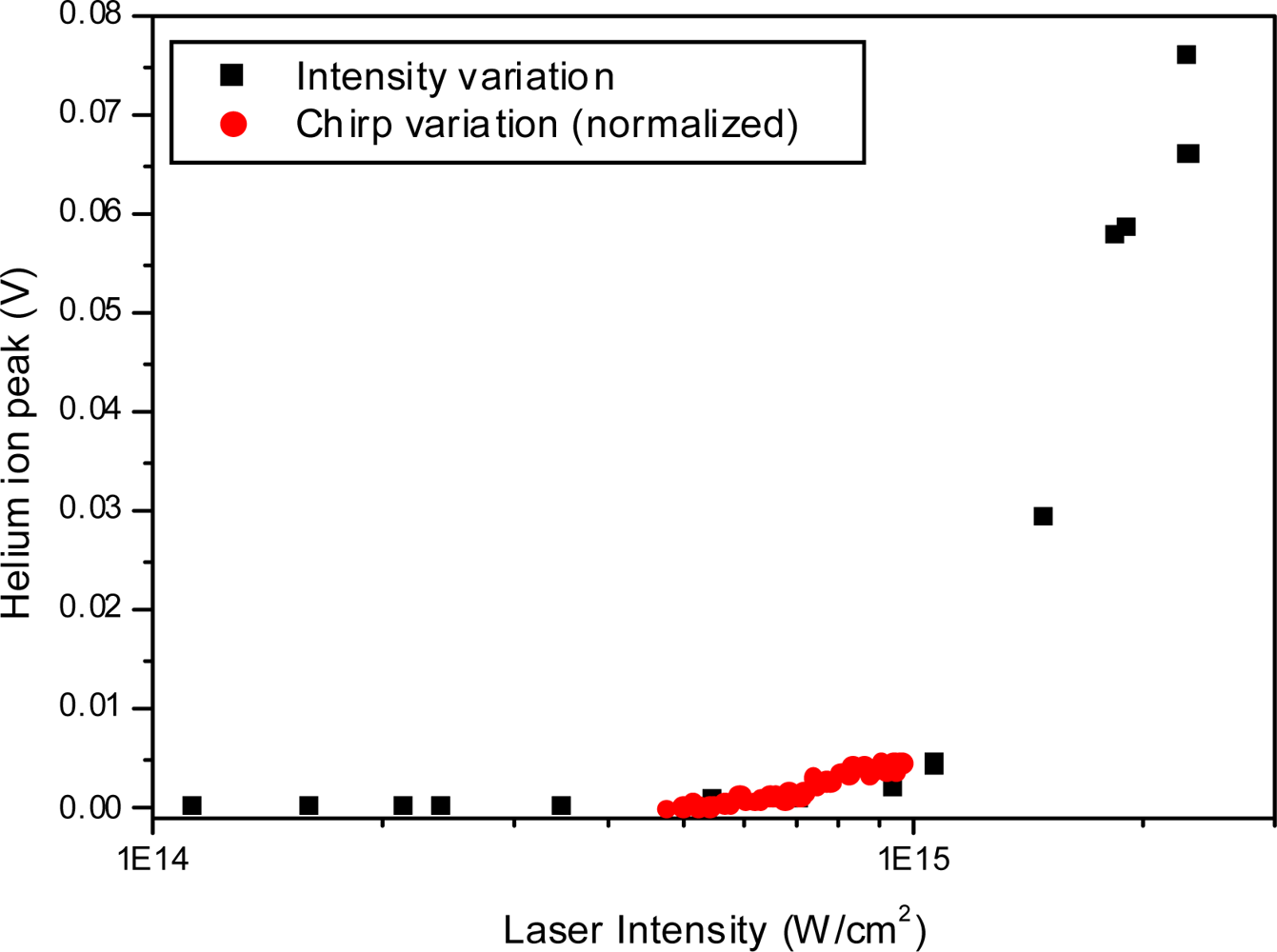
3.2.1. Femtosecond 795 nm Ionization
3.2.2. Femtosecond 397 nm Ionization
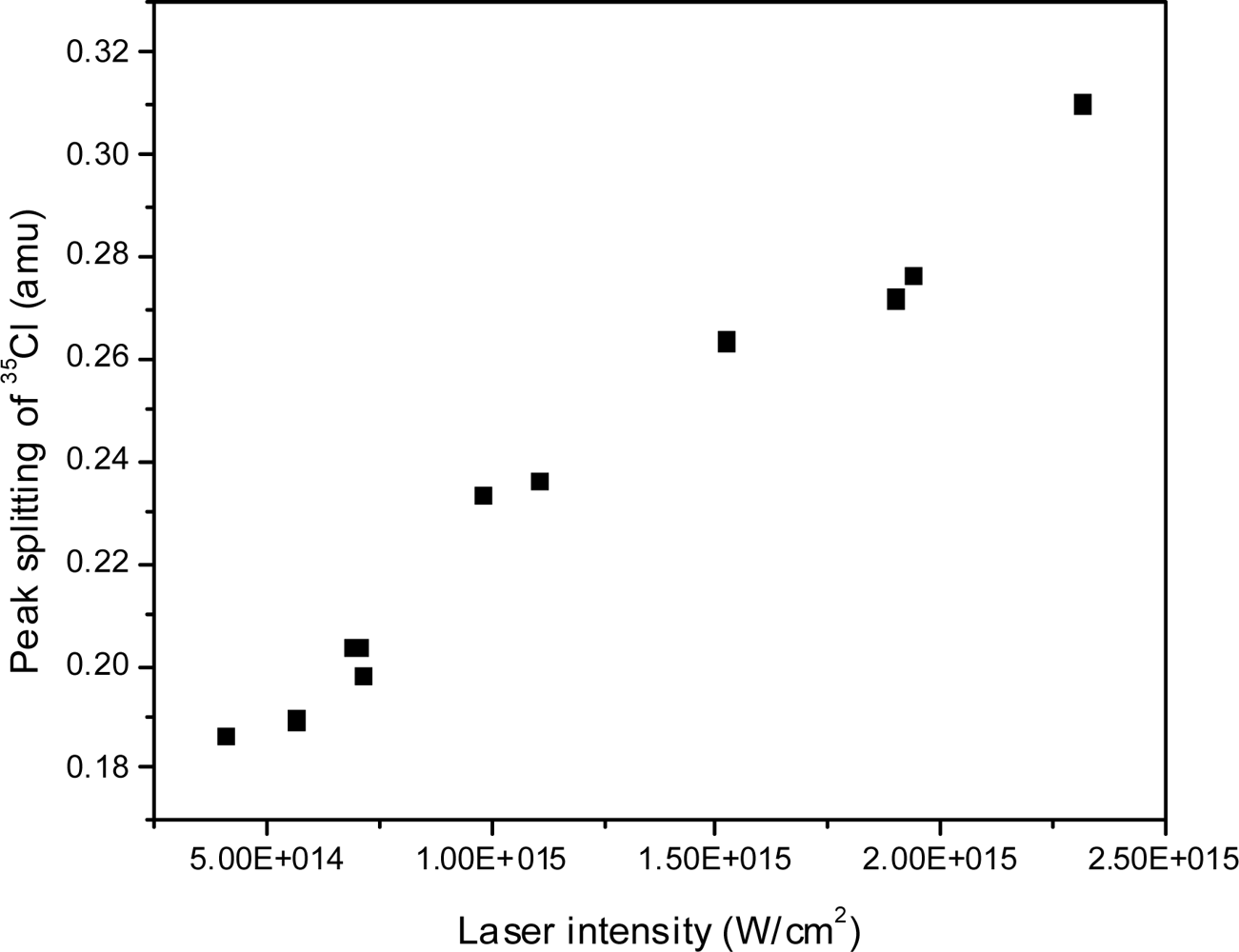
3.2.3. Explosive Dissociation
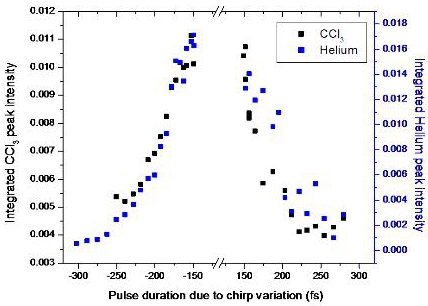
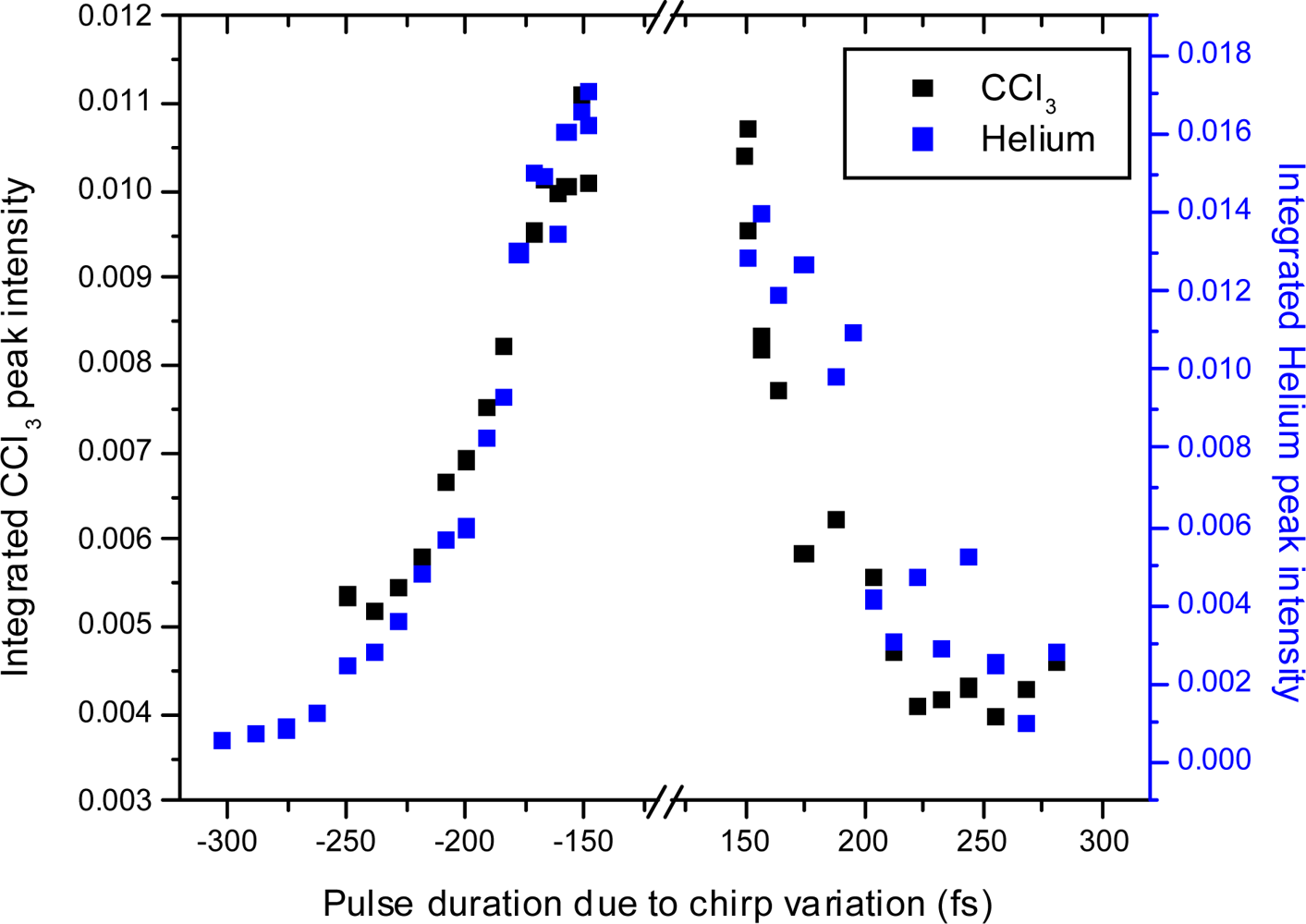
3.2.4. Open loop Control Example with Linear Chirp
4. Discussion
5. Conclusions
References
- Dantus, M; Lozovoy, VV. Experimental coherent laser control of physicochemical processes. Chem. Rev 2004, 104, 1813–1859. [Google Scholar]
- Lozovoy, VV; Dantus, M. Laser control of physicochemical processes; experiments and applications. Annu. Rep. Prog. Chem.: C 2006, 102, 227–258. [Google Scholar]
- Lozovoy, VV; Zhu, X; Gunaratne, TC; Harris, DA; Shane, JC; Dantus, M. Control of molecular fragmentation using shaped femtosecond pulses. J. Phys. Chem. A 2008, 112, 3790–3811. [Google Scholar]
- Assion, A; Baumert, T; Bergt, M; Brixner, T; Kiefer, B; Sayfried, V; Strehle, M; Gerber, G. Control of chemical reactions by feedback-optimized phase-shaped femtosecond laser pulses. Science 1998, 282, 919–922. [Google Scholar]
- Damrauer, NH; Dietl, C; Krampert, G; Lee, S-H; Jung, K-H; Gerber, G. Control of bond-selective photochemistry in CH2BrCl using adaptive femtosecond pulse shaping. Eur. Phys. J. D 2002, 20, 71–76. [Google Scholar]
- Graham, P; Menkir, G; Levis, RJ. An investigation of the effects of experimental parameters on the closed-loop control of photoionization/dissociation processes in acetophenone. Spectrochim. Acta B 2002, 58, 1097–1108. [Google Scholar]
- Cardoza, D; Baertschy, M; Weinacht, T. Interpreting closed-loop learning control of molecular fragmentation in terms of wave-packet dynamics and enhanced molecular ionization. J. Chem. Phys 2005, 123, 074315, doi:10.1063/1.2008257.. [Google Scholar]
- Cardoza, D; Trallero-Herrero, C; Langhojer, F; Rabitz, H; Weinacht, T. Transformations to diagonal bases in closed-loop quantum learning control experiments. J. Chem. Phys 2005, 122, 124306:1–124306:7. [Google Scholar]
- Cardoza, D; Baertschy, M; Weinacht, T. Understanding learning control of molecular fragmentation. Chem. Phys. Lett 2005, 411, 311–315. [Google Scholar]
- Ledingham, KWD; Singhal, RP. High intensity laser mass spectrometry - a review. Int. J. Mass Spectrom. Ion Proc 1997, 163, 149–168. [Google Scholar]
- Weinkauf, R; Aicher, P; Wesley, G; Grotemeyer, J; Schlag, EW. Femtosecond versus nanosecond multiphoton ionization and dissociation of large molecules. J. Phys. Chem 1994, 98, 8381–8391. [Google Scholar]
- Levis, RJ; DeWitt, MJ. Photoexcitation, ionization, and dissociation of molecules using intense near-infrared radiation of femtosecond duration. J. Phys. Chem. A 1999, 103, 6493–6507. [Google Scholar]
- Nakashima, N; Shimizu, S; Yatsuhashi, T; Sakabe, S; Izawa, Y. Large molecules in high-intensity laser fields. J. Photochem. Photobiol. C: Photochem. Rev 2000, 1, 131–143. [Google Scholar]
- Harada, H; Shimizu, S; Yatsuhashi, T; Sakabe, S; Izawa, Y; Nakashima, N. A key factor in parent and fragment ion formation on irradiation with an intense femtosecond laser pulse. Chem. Phys. Lett 2001, 342, 563–570. [Google Scholar]
- Robson, L; Ledingham, KWD; Tasker, AD; McKenna, P; McCanny, T; Kosmidis, C; Jaroszynski, DA; Jones, DR; Issac, RC; Jamieson, S. Ionisation and fragmentation of polycyclic aromatic hydrocarbons by femtosecond laser pulses at wavelengths resonant with cation transitions. Chem. Phys. Lett 2002, 360, 382–389. [Google Scholar]
- Posthumus, JH; Giles, AJ; Thompson, MR; Codling, K. Field-ionization, Coulomb explosion of diatomic molecules in intense laser fields. J. Phys. B: At. Mol. Opt. Phys 1996, 29, 5811–5829. [Google Scholar]
- Vanlaethem-Meurée, N; Wisenberg, J; Simon, PC. Ultraviolet absorption spectrum of methylchloroform in the vapor phase. Geophys. Res. Lett 1979, 6, 451–54. [Google Scholar]
- Nayak, AK; Kurylo, MJ; Fahr, A. UV absorption cross sections of methylchloroform: Temperature-dependent gas and liquid phase measurements. J. Geophys. Res 1995, 100, 11185–11189. [Google Scholar]
- Hubrich, C; Stuhl, F. The ultraviolet absorption of some halogenated methanes and ethanes of atmospheric interest. J. Photochem 1980, 12, 93–107. [Google Scholar]
- Katsumata, S; Kimura, K. Photoelectron spectra and sum rule consideration. Effect of chlorine substitution on ionization energies for chloroethanes, chloroacetaldehydes and chloroacetyl chlorides. J. Electron. Spectrosc. Relat. Phenom 1975, 6, 309–319. [Google Scholar]
- Wu, YG; Bozzelli, JW. Pyrolysis and oxidation of 1,1,1-Trichloroethane in methane/oxygen/argon. Hazard. Waste Hazard. Mater 1993, 10, 381–395. [Google Scholar]
- Ogura, H. CO2 Laser-induced Decomposition of 1,1,2-Trichloroethane. Bull. Chem. Soc. Jpn 1985, 58, 3528–3534. [Google Scholar]
- Posthumus, JH. The dynamics of small molecules in intense laser fields. Rep. Prog. Phys 2004, 67, 623–665. [Google Scholar]
- Ma, J; Ding, L; Fang, L; Zheng, H; Gu, X; Zhang, W. The dynamics of small molecules in intense laser fields. Opt. Appl 2005, XXXV, 395–402. [Google Scholar]
- Castillejo, M; Martin, M; de Nalda, R; Couris, S; Koudoumas, E. Dissociative ionization of halogenated ethylenes in intense femtosecond laser pulses. Chem. Phys. Lett 2002, 353, 295–303. [Google Scholar]
- Tzallas, P; Kosmidis, C; Graham, P; Ledingham, KWD; McCanny, T; Hankin, SM; Singhal, RP; Taday, PF; Langley, AJ. Coulomb explosion in aromatic molecules and their deuterated derivatives. Chem. Phys. Lett 2000, 332, 236–242. [Google Scholar]
- Kaziannis, S; Kosmidis, C. The ejection anisotropy in the Coulomb explosion of some alkyl halide molecules under strong ps laser fields. Chem. Phys. Lett 2009, 467, 281–286. [Google Scholar]
- Kong, F; Luo, Q; Xu, H; Sharafi, M; Song, D; Chin, SL. Explosive photodissociation of methane induced by ultrafast intense laser. J. Chem. Phys 2006, 125, 133320:1–133320:5. [Google Scholar]




















| Pulse duration | Wavelength (nm) | Max pulse energy (mJ) | Focal spot size (μm) | Max pulse fluence (J/cm2) | Max peak intensity (W/cm2) |
|---|---|---|---|---|---|
| 8 ns | 1064 nm | 120 | 19.1 | 20,900 | 2.6 × 1012 |
| 8 ns | 532 nm | 32 | 9.5 | 22,500 | 2.8 × 1012 |
| 8 ns | 355 nm | 6 | 8.5 | 5,400 | 6.8 × 1011 |
| 8 ns | 266 nm | 6 | 7.6 | 7,200 | 9 × 1011 |
| 150 fs | 795 nm | 1 | 13.7 | 350 | 2.3 × 1015 |
| 150 fs | 397 nm | 0.012 | 8.2 | 11 | 7.6 × 1013 |
© 2010 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Du Plessis, A.; Strydom, C.; Botha, L. Comparative Study of the Dissociative Ionization of 1,1,1 Trichloroethane Using Nanosecond and Femtosecond Laser Pulses. Int. J. Mol. Sci. 2010, 11, 1114-1140. https://doi.org/10.3390/ijms11031114
Du Plessis A, Strydom C, Botha L. Comparative Study of the Dissociative Ionization of 1,1,1 Trichloroethane Using Nanosecond and Femtosecond Laser Pulses. International Journal of Molecular Sciences. 2010; 11(3):1114-1140. https://doi.org/10.3390/ijms11031114
Chicago/Turabian StyleDu Plessis, Anton, Christien Strydom, and Lourens Botha. 2010. "Comparative Study of the Dissociative Ionization of 1,1,1 Trichloroethane Using Nanosecond and Femtosecond Laser Pulses" International Journal of Molecular Sciences 11, no. 3: 1114-1140. https://doi.org/10.3390/ijms11031114
APA StyleDu Plessis, A., Strydom, C., & Botha, L. (2010). Comparative Study of the Dissociative Ionization of 1,1,1 Trichloroethane Using Nanosecond and Femtosecond Laser Pulses. International Journal of Molecular Sciences, 11(3), 1114-1140. https://doi.org/10.3390/ijms11031114