Calculated Third Order Rate Constants for Interpreting the Mechanisms of Hydrolyses of Chloroformates, Carboxylic Acid Halides, Sulfonyl Chlorides and Phosphorochloridates
Abstract
:1. Introduction
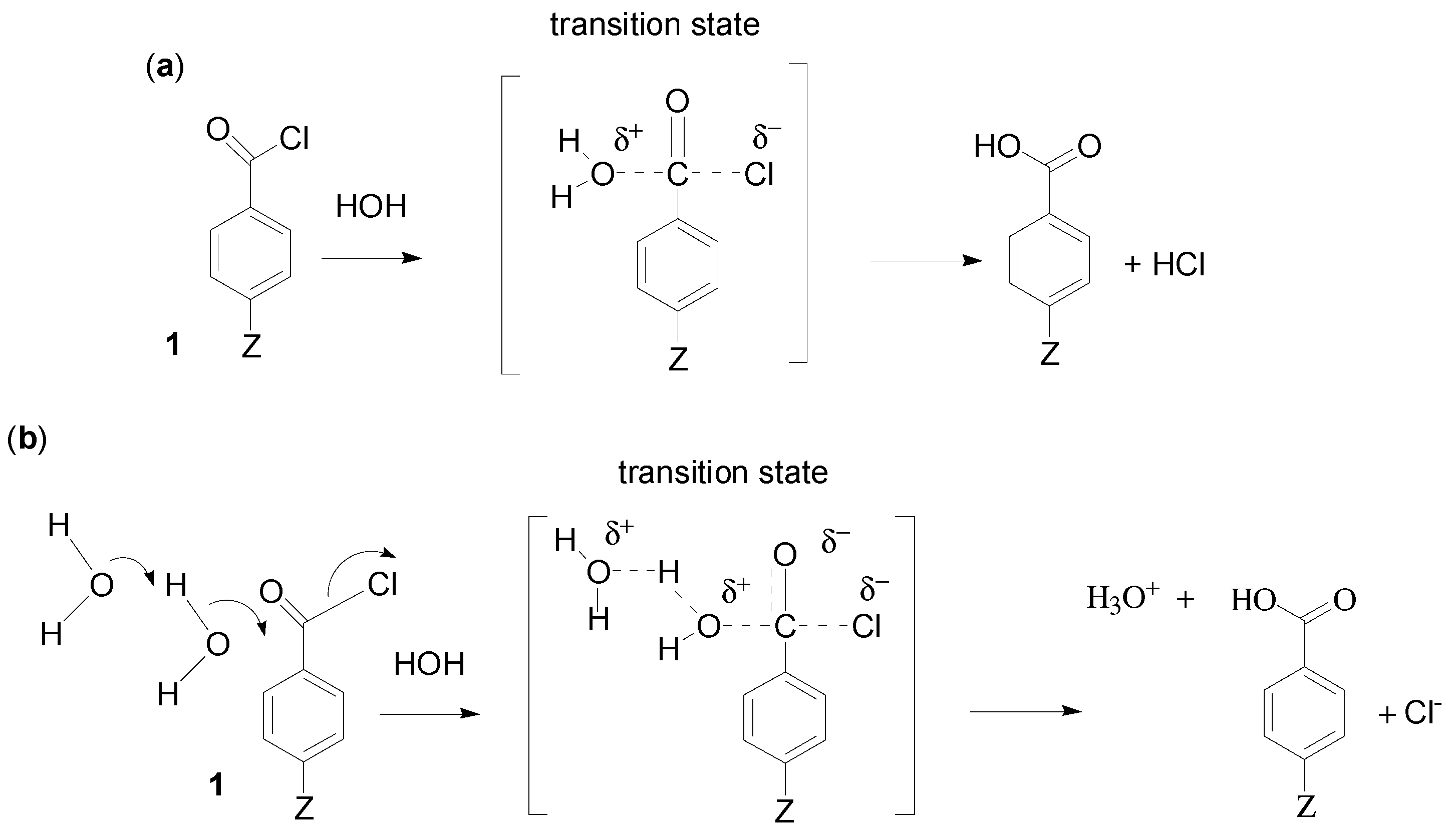
2. Results and Discussion

2.1. Choice of Equation for Correlating Solvolysis Rates

2.2. Evidence for the Third Order (Addition-Elimination) Reaction Channel from Correlations Using Equation (3) and Kinetic Solvent Isotope Effects
2.2.1. Chloroformates
| Acetone (% v/v) | 5, R = Et a 24.2 °C | 6, Z = H b 25 °C | 6, Z = Me b 25 °C | 6, Z = OMe b 25 °C | 5, R = CH2CCl3 Reference c, 35 °C |
|---|---|---|---|---|---|
| 95 | −7.01 | ||||
| 90 | −7.01 | −5.11 d | −4.62 | ||
| 80 | −7.11 | −5.20 | −5.43 | −5.47 | −4.82 |
| 70 | −5.35 | −5.54 | −5.55 | −4.83 | |
| 60 | −7.13 | −5.40 | −5.59 | −5.60 | −4.86 |
| 50 | −5.43 | −5.59 | −5.58 | −4.82 | |
| 40 | −7.06 | −5.41 | −5.56 | −5.53 | −4.78 |
| 30 | −5.36 | −5.51 | −5.47 | −4.67 | |
| 20 | −6.96 | −5.34 | −5.46 | −5.43 | −4.62 |
| 10 | −5.34 | −5.45 | −5.39 | ||
| water | −6.96 | −5.37 | −5.46 | −5.55 |

2.2.2. Fluoroformates (7)
2.2.3. Carboxylic Acid Halides

2.2.4. Sulfonyl Chlorides
| Substrate | Slope | Intercept | R2 | Std. Error | Range (%) | KSIE a | KSIE b |
|---|---|---|---|---|---|---|---|
| Me2NSO2Cl c | 0.36 ± 0.01 | −7.16 ± 0.03 | 0.990 | 0.06 | 80–0 | 1.33 c,1.29 d | |
| 9 e,f | 0.16 ± 0.02 | −6.05 ± 0.04 | 0.882 | 0.11 | 90–0 g | 1.46 | 1.76 |
| i-PrSO2Cl h | 0.07 ± 0.02 | −8.18 ± 0.03 | 0.770 | 0.06 | 80–0 | 1.66 | 2.54 |
| MeSO2Cl i | −0.07 ± 0.02 | −6.81 ± 0.03 | 0.788 | 0.06 | 80–0 | 1.81 | 1.62 |
| PhCH2SO2Cl j | −0.07 ± 0.02 | −6.25 ± 0.04 | 0.688 | 0.08 | 90–20 | 2.34 | |
| 2, Z = NO2 k | −0.11 ± 0.01 | −5.56 ± 0.03 | 0.922 | 0.06 | 90–0 | 1.76 l | 2.31 l |
| 2, Z = Cl m | 0.04 ± 0.02 | −6.32 ± 0.03 | 0.461 | 0.07 | 90–0 | 1.65 l | 1.89 l |
| 2, Z = H m | 0.13 ± 0.03 | −6.56 ± 0.06 | 0.781 | 0.13 | 90–0 | 1.59 l | 1.79 l |
| CF3SO2Cl e,n | −0.42 ± 0.03 | −6.14 ± 0.06 | 0.971 | 0.11 | 80–0 | 2.24 | 3.08 |
2.2.5. Anhydrides
2.2.6. Phosphorus Halides
| Substrate | Slope | Intercept | R2 | Std. Error | Range (%) | KSIE a | KSIE b |
|---|---|---|---|---|---|---|---|
| (Me2N)2POCl c | 0.17 ± 0.03 | −6.28 ± 0.06 | 0.930 | 0.09 | 80–0 | 1.34 d | |
| 11 e | 0.15 ± 0.06 f | −6.55 ± 0.12 | 0.463 | 0.30 | 90–0 | ||
| (MeO)2POCl g | 0.07 ± 0.01 | −5.08 ± 0.01 | 0.979 | 0.02 | 90–60 | ||
| 12 h | 0.16 ± 0.03 | −4.22 ± 0.04 | 0.884 | 0.10 | 90–20 | ||
| 13 h,i | −0.06 ± 0.02 | −6.22 ± 0.04 | 0.597 | 0.08 | 80–0 | ||
| (PhO)2POCl j | 0 k | 95–0 | 2.9 l | 3.06 | |||
| Ph2POCl m | 0 n | 95–50 | |||||
| Ph2PSCl o | 0.28 ± 0.03 | −4.90 ± 0.04 | 0.967 | 0.09 | 95–50 | 1.83 | |
| (MeO)2PSCl g | 0.08 ± 0.03 | −6.67 ± 0.06 | 0.503 | 0.15 | 90–0 |
2.3. Deviations from Equation (3) as Evidence for Mechanistic Changes
2.3.1. Carboxylic Acid Chlorides

2.3.2. Chloroformates



2.3.3. Sulfonyl Chlorides
| Sulfonyl Chloride | KSIE (MeOH) | KSIE (Water) a | Equation (3) Plot |
|---|---|---|---|
| p-methoxybenzene (2, Z = OMe) | 1.58 a | 1.37 a | Figure 10 |
| Dansyl (16) | 1.88 b | (1.34) b,c | Figure 10 |
| Mesityl (10, Z = Me) | 1.68 d | 1.34 d | Figure 11 |
| p-methoxy (10, Z = OMe) | 1.58 e | 1.41 a | Figure 11 |

2.4. Multi-Parameter Equations
2.5. Mechanistic Insights from Theoretical Calculations

2.6. Comments on Mechanistic Details


3. Experimental Section
4. Conclusions
Acknowledgments
Conflicts of Interest
References
- Streitwieser, A. Solvolytic displacement reactions at saturated carbon atoms. Chem. Rev. 1956, 56, 571–752. [Google Scholar] [CrossRef]
- Bentley, T.W.; Schleyer, P.v.R. Medium effects on the rates and mechanisms of solvolytic reactions. Adv. Phys. Org. Chem. 1976, 8, 1–67. [Google Scholar]
- Williams, A. Free Energy Relationships in Organic and Bioorganic Chemistry; The Royal Society of Chemistry: Cambridge, UK, 2003. [Google Scholar]
- Grunwald, E.; Winstein, S. Correlation of solvolysis rates. J. Am. Chem. Soc. 1948, 70, 846–854. [Google Scholar] [CrossRef]
- Schadt, F.L.; Bentley, T.W.; Schleyer, P.v.R. The SN2-SN1 spectrum 2. Quantitative treatments of nucleophilic solvent assistance. A scale of solvent nucleophilicities. J. Am. Chem. Soc. 1976, 98, 7667–7674. [Google Scholar] [CrossRef]
- Ruff, F.; Farkas, O. Concerted SN2 mechanism for the hydrolysis of acid chlorides: comparisons of reactivities calculated by density functional theory with experimental data. J. Phys. Org. Chem. 2011, 24, 480–491. [Google Scholar] [CrossRef]
- Yamabe, S.; Zeng, G.; Guan, W.; Sakaki, S. SN1-SN2 and SN2-SN3 mechanistic changes revealed by transition states of the hydrolyses of benzyl and benzenesulfonyl chlorides. J. Comput. Chem. 2014, 35, 1140–1148. [Google Scholar] [CrossRef] [PubMed]
- Bentley, T.W.; Jones, R.O.; Kang, D.H.; Koo, I.S. The SN3-SN2 spectrum. Rate constants and product selectivities for solvolyses of benzenesulphonyl chlorides in aqueous alcohols. J. Phys. Org. Chem. 2009, 22, 799–806. [Google Scholar] [CrossRef]
- Song, B.D.; Jencks, W.P. Mechanisms of solvolysis of substituted benzoyl halides. J. Am. Chem. Soc. 1989, 111, 8470–8479. [Google Scholar] [CrossRef]
- Kevill, D.N.; D’Souza, M.J. Correlation of the rates of solvolysis of benzoyl fluoride and a consideration of leaving group effects. J. Org. Chem. 2004, 69, 7044–7050. [Google Scholar] [CrossRef] [PubMed]
- Kevill, D.N.; Ryu, Z.H. Reaction mechanism studies involving the correlation of the rates of solvolysis of benzoyl and p-nitrobenzoyl p-toluenesulfonates. J. Chem. Res. 2014, 38, 387–395. [Google Scholar] [CrossRef]
- Johnson, S.L. General base and nucleophilic catalysis of ester hydrolysis and related reactions. Adv. Phys. Org. Chem. 1967, 5, 237–330. [Google Scholar]
- Koo, I.S.; Lee, I.; Oh, J.; Yang, K.; Bentley, T.W. Substituent effects on the kinetic solvent isotope effect in solvolyses of arenesulfonyl chlorides. J. Phys. Org. Chem. 1993, 6, 223–227. [Google Scholar] [CrossRef]
- Koo, I.S.; Yang, K.; Kang, K.; Lee, I. Transition state variation in solvolyses of para-substituted phenyl chloroformates in alcohol-water mixtures. Bull. Korean Chem. Soc. 1998, 19, 968–973. [Google Scholar]
- Bentley, T.W.; Koo, I.S.; Norman, S.J. Distinguishing between solvation effects and mechanistic changes. Effects due to differences in solvation between aromatic rings and alkyl groups. J. Org. Chem. 1991, 56, 1604–1609. [Google Scholar] [CrossRef]
- Bentley, T.W.; Llewellyn, G.; Ryu, Z.H. Solvolytic reactions in fluorinated alcohols. Role of nucleophilic and other solvations effects. J. Org. Chem. 1998, 63, 4654–4659. [Google Scholar] [CrossRef]
- Fainberg, A.H.; Winstein, S. Correlation of solvolysis rates. III. t-Butyl chloride in a wide range of solvent mixtures. J. Am. Chem. Soc. 1956, 78, 2770–2777. [Google Scholar]
- Kevill, D.N.; D’Souza, M.J. Sixty years of the Grunwald-Winstein equation: Development and recent applications. J. Chem. Res. 2008, 2008, 61–66. [Google Scholar] [CrossRef]
- Bentley, T.W.; Llewellyn, G. YX scales of solvent ionizing power. Prog. Phys. Org. Chem. 1990, 17, 121–158. [Google Scholar]
- Bentley, T.W.; Koo, I.S.; Llewellyn, G.; Norman, S.J. Similarity models for solvent effects on reactivity. The dissociative channel for solvolyses of sulfonyl chlorides in binary aqueous mixtures. Croat. Chem. Acta 1992, 65, 575–583. [Google Scholar]
- Bentley, T.W. Structural effects on the solvolytic reactivity of carboxylic and sulfonic acid chlorides. Comparisons with gas phase data for cation formation. J. Org. Chem. 2008, 73, 6251–6257. [Google Scholar] [CrossRef] [PubMed]
- Swain, C.G. Kinetic evidence for a termolecular reaction in displacement reactions of triphenyl methyl halides in benzene solution. J. Am. Chem. Soc. 1948, 70, 1119–1128. [Google Scholar] [CrossRef]
- Kevill, D.N.; D’Souza, M.J. Concerning the two reaction channels for solvolyses of ethyl chloroformate and ethyl chlorothioformate. J. Org. Chem. 1998, 63, 2120–2124. [Google Scholar] [CrossRef]
- Koh, H.J.; Kang, S.J. Correlation of the rates of solvolysis on 2,2,2-trichloroethyl chloroformate using the extended Grunwald-Winstein equation. Bull. Korean Chem. Soc. 2012, 33, 1729–1733. [Google Scholar] [CrossRef]
- Kevill, D.N.; Koyoshi, F.; D’Souza, M.J. Correlation of specific rates of solvolysis of solvolysis of aromatic carbamoyl chlorides, chloroformates, chlorothionoformates, and chlorodithiono-formates revisited. Int. J. Mol. Sci. 2007, 8, 346–362. [Google Scholar] [CrossRef]
- Koh, H.J.; Kang, S.J.; Kevill, D.N. Kinetic studies of the solvolyses of 2,2,2-trichloroethyl-1,1-dimethyl chloroformate. Bull. Korean Chem. Soc. 2010, 21, 835–839. [Google Scholar] [CrossRef]
- Koo, I.S.; Yang, K.; Kang, K.; Lee, I.; Bentley, T.W. Stoichiometric solvation effects. Part 3. Product-rate correlations for solvolyses of p-nitrophenyl chloroformate in alcohol-water mixtures. J. Chem. Soc. Perkin Trans. 1998, 2, 1179–1183. [Google Scholar] [CrossRef]
- D’Souza, M.J.; Kevill, D.N. Application of the Grunwald-Winstein equations to studies of solvolytic reactions of chloroformate and fluoroformate esters. Recent Res. Dev. Org. Chem. 2013, 13, 1–38. [Google Scholar] [PubMed]
- Kevill, D.N.; D’Souza, M.J. Correlation of the rates of solvolysis of n-octyl fluoroformate and a comparison with n-octyl chloroformate. J. Chem. Soc. Perkin Trans 2002, 2, 240–243. [Google Scholar] [CrossRef]
- Lee, Y.W.; Seong, M.H.; Kyong, J.B.; Kevill, D.N. Correlation of the rates of solvolysis of t-butyl fluoroformate using the extended Grunwald-Winstein equation. Bull. Korean Chem. Soc. 2010, 31, 3366–3370. [Google Scholar] [CrossRef]
- Kevill, D.N.; Kyong, J.B. Multiple pathways in the solvolyses of 1-adamantyl fluoroformate. J. Org. Chem. 1992, 57, 258–265. [Google Scholar] [CrossRef]
- D’Souza, M.J.; McAneny, M.J.; Kevill, D.N.; Kyong, J.B.; Choi, S.H. Kinetic evaluation of the solvolysis of isobutyl chloro- and thiochloroformate esters. Beilstein J. Org. Chem. 2011, 7, 543–552. [Google Scholar] [CrossRef] [PubMed]
- Bentley, T.W.; Harris, H.C. Separation of mass law and solvent effects in the kinetics of solvolyses of p-nitrobenzoyl chloride in aqueous binary mixtures. J. Org. Chem. 1988, 53, 724–728. [Google Scholar] [CrossRef]
- Bentley, T.W.; Harris, H.C.; Ryu, Z.H.; Lim, G.T.; Sung, D.D.; Szajda, S.R. Mechanisms of solvolyses of acid chlorides and chloroformates. Chloroacetyl and phenylacetyl chloride as similarity models. J. Org. Chem. 2005, 70, 8963–8970. [Google Scholar] [CrossRef]
- Bentley, T.W.; Jones, R.O. Stoichiometric solvation effects. Part 1. New equations relating product selectivities to alcohol-water solvent compositions for hydrolyses of p-nitrobenzoyl chloride. J. Chem. Soc. Perkin Trans. 1993, 2, 2351–2357. [Google Scholar] [CrossRef]
- Koo, I.S.; Lee, S.I.; An, S.K.; Yang, K.; Lee, I. Nucleophilic substitution reaction of α-methoxy-α-(trifluoromethyl)phenylacetyl chloride in alcohol-water mixtures. Bull. Korean Chem. Soc. 1999, 20, 1451–1456. [Google Scholar]
- Bunton, C.A.; Fendler, J.H. The hydrolysis of acetyl fluoride. J. Org. Chem. 1966, 31, 2307–2312. [Google Scholar] [CrossRef]
- Rogne, O. Solvolysis of dimethylsulphamoyl chloride in water and aqueous acetone. J. Chem. Soc. B 1969, 663–665. [Google Scholar] [CrossRef]
- Ko, E.C.F.; Robertson, R.E. The hydrolysis of sulfamoyl chlorides. I. Hydrolysis of dimethylsulfamoyl choride. Heat capacity of activation, the secondary γ-deuterium isotope effects, and solvent isotope effect. J. Am. Chem. Soc. 1972, 94, 573–575. [Google Scholar] [CrossRef]
- Ryu, Z.H.; Lee, S.W.; D’Souza, M.J.; Yaakoubd, L.; Feld, S.E.; Kevill, D.N. Correlation of the rates of solvolysis of two arenesulfonyl chlorides and of trans-β-styrenylsulfonyl chloride—Precursors in the development of new pharmaceuticals. Int. J. Mol. Sci. 2008, 9, 2639–2657. [Google Scholar] [CrossRef] [PubMed]
- Koo, I.S.; Yang, K.; Shin, H.B.; An, S.K.; Lee, J.P.; Lee, I. Stoichiometric solvation effects. Solvolysis of isopropylsulfonyl chloride. Bull. Korean Chem. Soc. 2004, 25, 699–703. [Google Scholar] [CrossRef]
- Koo, I.S.; Yang, K.; An, S.K.; Lee, C-K.; Lee, I. Stoichiometric solvation effects. Solvolysis of methanesulfonyl chloride. Bull. Korean Chem. Soc. 2000, 21, 1011–1014. [Google Scholar]
- Koh, H.J.; Kang, S.J. Application of the extended Grunwald-Winstein equation to solvolyses of phenylmethanesulfonyl chloride in aqueous binary mixtures. Bull. Korean Chem. Soc. 2011, 32, 1897–1901. [Google Scholar] [CrossRef]
- Bentley, T.W.; Jones, R.O.; Koo, I.S. Stoichiometric solvation effects. Part 2. A new product-rate correlation for solvolyses of p-nitrobenzene sulfonyl chloride in alcohol-water mixtures. J. Chem. Soc. Perkin Trans. 1994, 2, 753–759. [Google Scholar] [CrossRef]
- Koo, I.S.; Yang, K.; Park, J.K.; Woo, M.Y.; Cho, J.M.; Lee, J.P.; Lee, I. Stoichiometric solvation effects. Solvolyses of trifluoromethane sulfonyl chloride. Bull. Korean Chem. Soc. 2001, 26, 1241–1245. [Google Scholar]
- Kevill, D.N.; Park, B.-C.; Park, K.-H.; D’Souza, M.J.; Yaakoubd, L.; Mlynarski, S.L.; Kyong, J.B. Rate and product studies in the solvolyses of N,N-dimethylsulfamoyl chloride and 2-propanesulfonyl chloride. Org. Biomol. Chem. 2006, 4, 1580–1586. [Google Scholar] [CrossRef] [PubMed]
- D’Souza, M.J.; Yaakoubd, L.; Mlynarski, S.L.; Kevill, D.N. Concerted solvent processes for common sulfonyl chloride precursors used in the synthesis of sulphonamide-based drugs. Int. J. Mol. Sci. 2008, 9, 914–925. [Google Scholar] [CrossRef] [PubMed]
- Jenkins, F.E.; Hambly, A.N. Solvolyses of sulfonyl halides. I. The hydrolysis of aromatic sulfonyl chlorides in aqueous dioxan and aqueous acetone. Aust. J. Chem. 1961, 14, 190–204. [Google Scholar] [CrossRef]
- Kim, W.K.; Lee, I. Nucleophilic displacement at sulfur center (II). Solvolysis of benzenesulfonyl chloride in acetone-water mixtures. J. Korean Chem. Soc. 1973, 17, 163–168. [Google Scholar]
- Kevill, D.N.; Ryu, Z.H. Correlation of the rates of solvolysis of acetyl p-toluenesulfonate (acetyl tosylate) and a comparison with acetyl halides. J. Phys. Org. Chem. 2013, 26, 983–988. [Google Scholar] [CrossRef]
- Kevill, D.N.; Ryu, Z.H.; Niedermeyer, M.A.; Koyoshi, F.; D’Souza, M.J. Rate and product studies in the solvolyses of methanesulfonic acid anhydride and a comparison with methane sulfonyl chloride solvolyses. J. Phys. Org. Chem. 2007, 20, 431–438. [Google Scholar] [CrossRef]
- Kevill, D.N.; Ryu, Z.H. Rate and product studied in solvolyses of two arenesulfonic acid anhydrides. J. Chem. Res. 2007, 365–369. [Google Scholar] [CrossRef]
- Christensen, N.H. Kinetic solvent isotope effect in the hydrolyses of sulfonic anhydrides. Acta Chem. Scand. 1967, 21, 899–904. [Google Scholar] [CrossRef]
- Christensen, N.H. Kinetic studies of the hydrolysis of aromatic sulfonic anhydrides. Acta Chem. Scand. 1966, 20, 1955–1964. [Google Scholar] [CrossRef]
- Bentley, T.W.; Carter, G.E.; Roberts, K. Solvent ionizing power. Comparisons of solvolyses of 1-adamantyl chlorides, bromides, iodides and tosylates in protic solvents. J. Org. Chem. 1984, 49, 5183–5189. [Google Scholar] [CrossRef]
- Kevill, D.N.; Miller, B. Application of the NT solvent nucleophilicity scale to attack at phosphorus. Solvolyses of N,N,N',N'-tetramethyl diamidophosphorochloridate. J. Org. Chem. 2002, 67, 7399–7406. [Google Scholar] [CrossRef] [PubMed]
- Traylor, P.S.; Westheimer, F.H. Mechanism of hydrolysis of phosphorodiamidic chlorides. J. Am. Chem. Soc. 1965, 87, 553–559. [Google Scholar] [CrossRef]
- Choi, H.; Yang, K.; Koh, H.J.; Koo, I.S. Solvolysis reaction kinetics, rates and mechanisms for phenyl N-phenyl phosphoamidochloridate. Bull. Korean Chem. Soc. 2014, 35, 2465–2470. [Google Scholar] [CrossRef]
- Kevill, D.N.; Carver, J.S. Rate and product studies with dimethyl phosphorochloridate and phosphorochloridothionate. Org. Biomol. Chem. 2004, 2, 2040–2043. [Google Scholar] [CrossRef] [PubMed]
- Koh, H.J.; Kang, S.J.; Kevill, D.N. Rate and product studies in the solvolyses of two cyclic phosphorochoridate esters. Phosphorus Sulfur Silicon 2010, 185, 1404–1415. [Google Scholar] [CrossRef]
- Bentley, T.W.; Ebdon, D.; Llewellyn, G.; Abduljaber, M.H.; Miller, B.; Kevill, D.N. Chlorophosphate solvolyses. Evaluation of third order rate laws and rate-product correlations for solvolyses of diphenylphosphorochloridate in aqueous alcohols. J. Chem. Soc. Dalton Trans 1997, 3819–3825. [Google Scholar] [CrossRef]
- Kevill, D.N.; Koh, H.J. Correlation of the rates of solvolysis of diphenylphosphinyl chloride using an extended form of the Grunwald-Winstein equation. J. Phys. Org. Chem. 2007, 20, 88–92. [Google Scholar] [CrossRef]
- Koh, H.J.; Kang, S.J.; Kevill, D.N. Correlation of the rates of solvolysis of diphenyl-thiophosphinyl chloride using an extended form of the Grunwald-Winstein equation. Bull. Korean Chem. Soc. 2008, 29, 1927–1931. [Google Scholar] [CrossRef]
- Dostrovsky, I.; Halman, M. Kinetic studies in the phosphinyl chloride and phosphochloridate series. Part 1. Solvolytic reactions. J. Chem. Soc. 1953, 502–507. [Google Scholar] [CrossRef]
- Lee, O.-S.; Yang, K.; Kang, K.D.; Koo, I.S.; Kim, C.-K.; Lee, I. Ab initio and DFT studies on hydrolyses of phosphorus halides. J. Comput. Chem. 2004, 25, 1740–1748. [Google Scholar] [CrossRef] [PubMed]
- Bentley, T.W.; Llewellyn, G.; McAlister, J.A. SN2 mechanism for alcoholysis, aminolysis and hydrolysis of acetyl chloride. J. Org. Chem. 1996, 61, 7927–7932. [Google Scholar] [CrossRef] [PubMed]
- Bentley, T.W.; Carter, G.E.; Harris, H.C. SN2 character of hydrolysis of benzoyl chloride. J. Chem. Soc. Chem. Commun. 1984, 387–389. [Google Scholar] [CrossRef]
- Bentley, T.W.; Carter, G.E.; Harris, H.C. Competing SN2 and carbonyl addition pathways for solvolyses of benzoyl chloride in aqueous media. J. Chem. Soc. Perkin Trans. 1985, 2, 983–990. [Google Scholar] [CrossRef]
- Bentley, T.W.; Koo, I.S. Trends in selectivity. Evidence from rates and products for simultaneous reaction channels in solvolyses of benzoyl chloride and substituted derivatives. J. Chem. Soc. Perkin Trans. 1989, 2, 1385–1392. [Google Scholar] [CrossRef]
- Bentley, T.W.; Shim, C.B. Dual reaction channels for solvolyses of acyl chlorides in alcohol-water mixtures. J. Chem. Soc. Perkin Trans. 1993, 2, 1659–1663. [Google Scholar] [CrossRef]
- Queen, A. Kinetics of the hydrolysis of acyl chlorides in water. Can. J. Chem. 1967, 45, 1619–1629. [Google Scholar] [CrossRef]
- D’Souza, M.J.; Reed, D.N.; Erdman, K.J.; Kyong, J.B.; Kevill, D.N. Grunwald-Winstein analysis—Isopropyl chloroformate solvolysis revisited. Int. J. Mol. Sci. 2009, 10, 862–879. [Google Scholar] [CrossRef] [PubMed]
- Lim, G.T.; Lee, Y.H.; Ryu, Z.H. Further kinetic studies of solvolytic reactions of isobutyl chloroformate in solvents of high ionizing power under conductometric conditions. Bull. Korean Chem. Soc. 2013, 34, 615–621. [Google Scholar] [CrossRef]
- Koh, H.J.; Kang, S.J. A kinetic study on solvolysis of 9-fluorenylmethyl chloroformate. Bull. Korean Chem. Soc. 2011, 32, 3799–3801. [Google Scholar] [CrossRef]
- Koo, I.S.; Yang, K.; Kang, D.H.; Park, H.J.; Kang, K.; Lee, I. Transition state variation in the solvolyses of phenylchlorothionoformate in alcohol-water mixtures. Bull. Korean Chem. Soc. 1999, 20, 577–580. [Google Scholar]
- Ryu, Z.H.; Lee, Y.H.; Oh, Y. Stoichiometric effects. Correlation of the rates of solvolysis of isopropenyl chloroformate. Bull. Korean Chem. Soc. 2005, 26, 1761–1766. [Google Scholar] [CrossRef]
- Koh, H.J.; Kang, S.J. Kinetic studies of solvolyses of isopropenyl chloroformate. Bull. Korean Chem. Soc. 2010, 31, 1793–1796. [Google Scholar] [CrossRef]
- D’Souza, M.J.; Shuman, K.E.; Omondi, A.O.; Kevill, D.N. Detailed analysis for the solvolysis of isopropenyl chloroformate. Eur. J. Chem. 2011, 2, 130–135. [Google Scholar] [CrossRef] [PubMed]
- Koh, H.J.; Kang, S.J. Rate and product studies of 5-dimethylamino-naphthalene-1-sulfonyl chloride under solvolytic conditions. Bull. Korean Chem. Soc. 2014, 35, 2285–2289. [Google Scholar] [CrossRef]
- Koo, I.S.; Bentley, T.W.; Kang, D.H.; Lee, I. Limitations of the transition state variation model. Part 2. Dual reaction channels for solvolyses of 2,4,6-trimethylbenzenesulfonyl chloride. J. Chem. Soc. Perkin Trans 1991, 2, 175–179. [Google Scholar] [CrossRef]
- Koo, I.S.; Bentley, T.W.; Llewellyn, G.; Yang, K. Limitations of the transition state variation model. Part 3. Solvolyses of electron-rich benzenesulfonyl chlorides. J. Chem. Soc. Perkin Trans 1991, 2, 1175–1179. [Google Scholar] [CrossRef]
- Koo, I.S.; Lee, O-K.; Lee, I. Limitations of the transition state variation model (5) dual reaction channels for solvolysis of dansyl chloride. Bull. Korean Chem. Soc. 1992, 13, 395–398. [Google Scholar]
- Bentley, T.W.; Garley, M.S. Correlations and predictions of solvent effects on reactivity: some limitations of multi-parameter equations and comparisons with similarity models based on one parameter. J. Phys. Org. Chem. 2006, 19, 341–349. [Google Scholar] [CrossRef]
- Bentley, T.W. A comprehensive N+ scale of nucleophilicity in an equation including a Swain-Scott selectivity parameter. J. Phys. Org. Chem. 2013, 26, 977–982. [Google Scholar] [CrossRef]
- Kevill, D.N.; Anderson, S.W. An improved scale of solvent nucleophilicity based on solvolyses of S-methyldibenzothiophenium ion. J. Org. Chem. 1991, 56, 1845–1850. [Google Scholar] [CrossRef]
- Kevill, D.N. Development and uses of scales of solvent nucleophilicity. In Advances in Quantitative Structure-Property Relationships; Charton, M., Ed.; Jai Press: Greenwich, CT, USA, 1996; Volume 1, pp. 81–115. [Google Scholar]
- D’Souza, M.J.; Mahon, B.P.; Kevill, D.N. Analysis of the nucleophilic solvation effects in isopropyl chlorothioformate solvolyses. Int. J. Mol. Sci. 2010, 11, 2597–2611. [Google Scholar] [CrossRef] [PubMed]
- Kevill, D.N.; D’Souza, M.J. Correlation of the rates of solvolysis of phenyl chloroformate. J. Chem. Soc. Perkin Trans. 1997, 2, 1721–1724. [Google Scholar] [CrossRef]
- D’Souza, M.J.; Deol, J.K.; Pavey, M.T.; Kevill, D.N. Statistical methods for the investigation of solvolysis mechanisms illustrated by the chlorides of the carbomethoxy protecting groups NVOC and FMOC. J. Anal. Methods Chem. 2015. [CrossRef]
- Yew, K.H.; Koh, H.J.; Lee, H.W.; Lee, I. Nucleophilic substitution reactions of phenyl chloroformates. J. Chem. Soc. Perkin Trans. 1995, 2, 2263–2268. [Google Scholar] [CrossRef]
- Ba-Saif, S.; Luthra, A.K.; Williams, A. Concertedness in acyl group transfer in solution: A single transition state for acetyl group transfer between phenolate ion nucleophiles. J. Am. Chem. Soc. 1987, 109, 6362–6368. [Google Scholar] [CrossRef]
- Renfrew, A.H.M.; Rettura, D.; Taylor, J.A.; Whitmore, J.M.J.; Williams, A. Stepwise vs. concerted mechanisms at trigonal carbon. Transfer of the 1,3,5-triazinyl group between aryl oxide ions in aqueous solution. J. Am. Chem. Soc. 1995, 109, 5484–5491. [Google Scholar]
- Marlier, J.F. Heavy atom isotope effects on the alkaline hydrolysis of methyl formate the role of hydroxide ion in ester hydrolysis. J. Am. Chem. Soc. 1993, 115, 5953–5956. [Google Scholar] [CrossRef]
- Mata-Segreda, J.F. Hydroxide as general base in the saponification of ethyl acetate. J. Am. Chem. Soc. 2002, 124, 2259–2262. [Google Scholar] [CrossRef] [PubMed]
- Bentley, T.W.; Morris, P.J.; Taylor, J.A. Alkoxide-catalysed hydrolysis of a chlorotriazine in alcohol-water mixtures: A new indirect probe for hydroxide-catalysed hydrolysis. J. Chem. Soc. Perkin Trans. 2000, 2, 2171–2176. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bentley, T.W. Calculated Third Order Rate Constants for Interpreting the Mechanisms of Hydrolyses of Chloroformates, Carboxylic Acid Halides, Sulfonyl Chlorides and Phosphorochloridates. Int. J. Mol. Sci. 2015, 16, 10601-10623. https://doi.org/10.3390/ijms160510601
Bentley TW. Calculated Third Order Rate Constants for Interpreting the Mechanisms of Hydrolyses of Chloroformates, Carboxylic Acid Halides, Sulfonyl Chlorides and Phosphorochloridates. International Journal of Molecular Sciences. 2015; 16(5):10601-10623. https://doi.org/10.3390/ijms160510601
Chicago/Turabian StyleBentley, T. William. 2015. "Calculated Third Order Rate Constants for Interpreting the Mechanisms of Hydrolyses of Chloroformates, Carboxylic Acid Halides, Sulfonyl Chlorides and Phosphorochloridates" International Journal of Molecular Sciences 16, no. 5: 10601-10623. https://doi.org/10.3390/ijms160510601
APA StyleBentley, T. W. (2015). Calculated Third Order Rate Constants for Interpreting the Mechanisms of Hydrolyses of Chloroformates, Carboxylic Acid Halides, Sulfonyl Chlorides and Phosphorochloridates. International Journal of Molecular Sciences, 16(5), 10601-10623. https://doi.org/10.3390/ijms160510601






