Anomalous Behavior of Hyaluronan Crosslinking Due to the Presence of Excess Phospholipids in the Articular Cartilage System of Osteoarthritis
Abstract
:1. Introduction
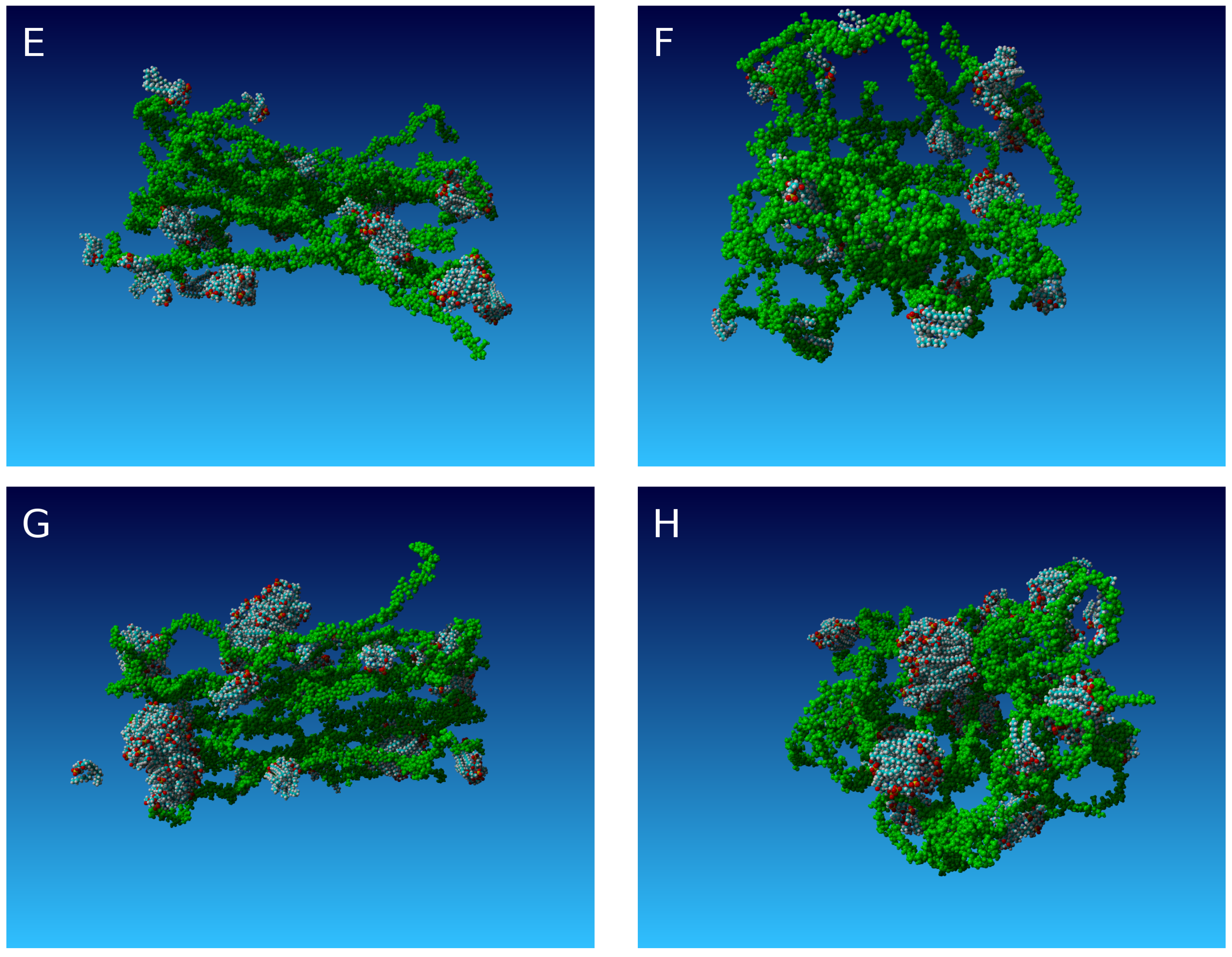
2. Results
3. Theoretical Considerations
4. Discussion
5. Materials and Methods
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| SF | Synovial Fluid |
| AC | Articular Cartilage |
| HA | Hyaluronic acid |
| PL | Phospholipids |
| OA | Ostheoarthritis |
References
- Hari, G.G.; Hales, C.A. Chemistry and Biology of Hyaluronan; Elsevier Science: Amsterdam, The Netherlands, 2008; ISBN 9780080472225. [Google Scholar]
- Jung, S.; Petelska, A.; Bełdowski, P.; Augé, W.K.; Casey, T.; Walczak, D.; Lemke, K.; Gadomski, A. Hyaluronic acid and phospholipid interactions useful for repaired articular cartilage surfaces–a mini review toward tribological surgical adjuvants. Colloid Polym. Sci. 2017, 295, 403–412. [Google Scholar] [CrossRef] [PubMed]
- Siódmiak, J.; Bełdowski, P.; Augé, W.K., II; Ledziński, D.; Śmigiel, S.; Gadomski, A. Molecular Dynamic Analysis of Hyaluronic Acid and Phospholipid Interaction in Tribological Surgical Adjuvant Design for Osteoarthritis. Molecules 2017, 22, 1436. [Google Scholar] [CrossRef]
- Ganguly, K.; McRury, I.D.; Goodwin, P.M.; Morgan, R.E.; Augé, W.K. Native chondrocyte viability during cartilage lesion progression: Normal to surface fibrillation. Cartilage 2010, 1, 306–311. [Google Scholar] [CrossRef] [PubMed]
- Augé, W.K. Conceptualization of surface-confined nano-assemblies as a biophysical battery circuit during tissue rescue: A bridge to accessing genomic control mechanisms. Int. J. Nanosyst. 2012, 5, 1–18. [Google Scholar]
- Augé, W.K. Inverse mass ratio batteries: An in situ energy source generated from motive proton delivery gradients. Nano Energy 2012, 1, 309–315. [Google Scholar] [CrossRef]
- Kwiecinski, J.J.; Dorosz, S.G.; Ludwig, T.E.; Abubacker, S.; Cowman, M.K.; Schmidt, T.A. The effect of molecular weight on hyaluronan’s cartilage boundary lubricating ability—Alone and in combination with proteoglycan 4. Osteoarthr. Cartil. 2011, 19, 1356–1362. [Google Scholar] [CrossRef] [PubMed]
- Temple-Wong, M.M.; Ren, S.; Quach, P.; Hansen, B.C.; Chen, A.C.; Hasegawa, A.; D’Lima, D.D.; Koziol, J.; Masuda, K.; Lotz, M.K.; et al. Hyaluronan concentration and size distribution in human knee synovial fluid: Variations with age and cartilage degeneration. Arthritis Res. Ther. 2016, 18, 18. [Google Scholar] [CrossRef] [PubMed]
- Snelling, S.; Rout, R.; Davidson, R.; Clark, I.; Carr, A.; Hulley, P.A.; Price, A.J. A gene expression study of normal and damaged cartilage in anteromedial gonarthrosis, a phenotype of osteoarthritis. Osteoarthr. Cartil. 2014, 22, 334–343. [Google Scholar] [CrossRef] [PubMed]
- Band, P.A.; Heeter, J.; Wisniewski, H.G.; Liublinska, V.; Pattanayak, C.W.; Karia, R.J.; Stabler, T.; Balazs, E.A.; Kraus, V.B. Hyaluronan molecular weight distribution is associated with the risk of knee osteoarthritis progression. Osteoarthr. Cartil. 2015, 23, 70–76. [Google Scholar] [CrossRef] [PubMed]
- Bełdowski, P.; Augé, W.K.; Andrysiak, T.; Mrela, A.; Pawlak, Z.; Gadomski, A. The structural dependence of surface active phospholipid on hyaluronan molecular mass and concentration in model synovial joint organ systems. Polymers 2018. Submitted for publication. [Google Scholar]
- Pasquali-Ronchetti, I.; Quaglino, D.; Mori, G.; Bacchelli, B.; Ghosh, P. Hyaluronan–phospholipid interactions. J. Struct. Biol. 1997, 120, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Goychuk, I.; Hänggi, P. Fractional diffusion modeling of ion channel gating. Phys. Rev. E 2004, 70, 051915. [Google Scholar] [CrossRef] [PubMed]
- Goychuk, I.; Hänggi, P. The role of conformational diffusion in ion channel gating. Phys. A 2004, 325, 9–18. [Google Scholar] [CrossRef]
- Glöckle, W.G.; Nonnenmacher, T.F. A Fractional Calculus Approach to Self-Similar Protein Dynamics. Biophys. J. 1995, 68, 46–53. [Google Scholar] [CrossRef]
- Ślȩzak, J.; Weron, K. Revised approach to statistical analysis of ionic current fluctuations. Acta Phys. Pol. B 2012, 43, 1215–1226. [Google Scholar] [CrossRef]
- Gadomski, A.; Rubi, J.M.; Łuczka, J.; Ausloos, M. On temperature and space-dimension dependent matter agglomerations in mature growing stage. Chem. Phys. 2005, 310, 153–161. [Google Scholar] [CrossRef]
- Sorkin, R.; Kampf, N.; Zhu, L.; Klein, J. Hydration lubrication and shear-induced self-healing of lipid bilayer boundary lubricants in phosphatidylcholine dispersions. Soft Matter 2016, 12, 2773–2784. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; Liu, C.; Thormann, E.; Dédinaité, A. Hyaluronan and phospholipid association in biolubrication. Biomacromolecules 2013, 14, 4198–4206. [Google Scholar] [CrossRef] [PubMed]
- Kosińska, M.K.; Liebisch, G.; Lochnit, G.; Wilhelm, J.; Klein, H.; Kaesser, U.; Lasczkowski, G.; Rickert, M.; Schmitz, G.; Steinmeyer, J. A lipidomic study of phospholipid classes and species in human synovial fluid. Arthritis Rheum. 2013, 65, 2323–2333. [Google Scholar] [CrossRef] [PubMed]
- Kosińska, M.; Ludwig, T.E.; Liebisch, G.; Zhang, R.; Siebert, H.C.; Wilhelm, J.; Kaesser, U.; Dettmeyer, R.B.; Klein, H.; Ishaque, B.; et al. Articular joint lubricants during osteoarthritis and rheumatoid arthritis display altered levels and molecular species. PLoS ONE 2015, 10, e0125192. [Google Scholar] [CrossRef] [PubMed]
- Ermakov, S.; Beletskii, A.; Eismont, O.; Nikolaev, V. Liquid Crystals in Biotribology, Synovial Joint Treatment. Biological and Medicinal Physics; Biomedical Engineering; Springer International Publishing AG: Cham, Switzerland, 2016; ISBN 978-3-319-20348-5. [Google Scholar]
- Das, S.; Banquy, X.; Zappone, B.; Israelachvili, J. Synergistic interactions between grafted hyaluronic acid and lubricin provide enhanced wear protection and lubrication. Biomacromolecules 2013, 14, 1669–1677. [Google Scholar] [CrossRef] [PubMed]
- Wierzcholski, K. Joint cartilage lubrication with phospholipid bilayer. Tribologia 2016, 2, 145–157. [Google Scholar]
- Dédinaité, A. Biomimetic lubrication. Soft Matter 2012, 8, 273–284. [Google Scholar] [CrossRef]
- Hills, B.A. Boundary lubrication in vivo. Proc. Inst. Mech. Eng. H 2000, 214, 83–94. [Google Scholar] [CrossRef] [PubMed]
- Greene, G.W.; Banquy, X.; Lee, D.W.; Lowrey, D.D.; Yu, J.; Israelachvili, J. Adaptive mechanically controlled lubrication mechanism found in articular joints. Proc. Nat. Acad. Sci. USA 2011, 108, 5255–5259. [Google Scholar] [CrossRef] [PubMed]
- Matej, D. Boundary cartilage lubrication: Review of current concepts. Wien. Med. Wochenschr. 2014, 164, 88–94. [Google Scholar]
- Wieland, D.C.F.; Degen, P.; Zander, T.; Gayer, S.; Raj, A.; An, J.; Dédinaité, A.; Claesson, P.; Willumeit-Römer, R. Structure of DPPC-hyaluronan interfacial layers—Effects of molecular weight and ion composition. Soft Matter 2016, 12, 729–740. [Google Scholar] [CrossRef] [PubMed]
- Scott, J.E.; Heatley, F. Biological Properties of Hyaluronan in Aqueous Solution Are Controlled and Sequestered by Reversible Tertiary Structures, Defined by NMR Spectroscopy. Biomacromolecules 2002, 3, 547–553. [Google Scholar] [CrossRef] [PubMed]
- Jenkins, S.; Jacob, K.I.; Kumar, S. The effect of hydrogen bonding on the physical and mechanical properties of rigid-rod polymers. J. Polym. Sci. Part B Polym. Phys. 2000, 38, 3053–3061. [Google Scholar] [CrossRef]
- Chen, Y.; Crawford, R.W.; Oloyede, A. Unsaturated phosphatidylcholines lining on the surface of cartilage and its possible physiological roles. J. Orthop. Surg. Res. 2007, 2, 14. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lee, D.W.; Banquy, X.; Das, S.; Cadirov, N.; Jay, G.; Israelachvili, J. Effects of molecular weight of grafted hyaluronic acid on wear initiation. J. Acta Biomater. 2014, 10, 1817–1823. [Google Scholar] [CrossRef] [PubMed]
- Banquy, X.; Lee, D.W.; Das, S.; Israelachvili, J. Shear-induced aggregation of mammalian synovial fluid components under boundary lubrication conditions. Adv. Funct. Mater. 2014, 24, 3152–3161. [Google Scholar] [CrossRef]
- Nitzan, D.W.; Nitzan, U.; Dan, P.; Yedgar, S. The role of hyaluronic acid in protecting surface-active phospholipids from lysis by exogenous phospholipase A2. Rheumatology 2001, 40, 335–340. [Google Scholar] [CrossRef]
- Pathak, P.; London, F. The effect of membrane lipid composition on the formation of lipid ultrananodomains. Biophys. J. 2015, 109, 1630–1638. [Google Scholar] [CrossRef] [PubMed]
- Raj, A.; Wang, M.; Zander, T.; Wieland, D.C.F.; Liu, X.; An, J.; Garamus, V.M.; Willumeit-Römer, R.; Fielden, M.; Claesson, P.M.; et al. Lubrication synergy: Mixture of hyaluronan and dipalmitoylphosphatidylcholine (DPPC) vesicles. J. Colloid Inter. Sci. 2017, 488, 225–233. [Google Scholar] [CrossRef] [PubMed]
- Goudoulas, T.B.; Kastrinakis, E.G.; Nychas, S.G.; Papazoglou, L.G.; Kazakos, G.M.; Kosmas, P.V. Rheological study of synovial fluid obtained from dogs: Healthy, pathological, and post-surgery, after spontaneous rupture of cranial cruciate ligament. Ann. Biomed. Eng. 2010, 38, 57–65. [Google Scholar] [CrossRef] [PubMed]
- Bełdowski, P.; Winkler, R.G.; Hładyszowski, J.; Jung, S.; Gadomski, A. Shape Change of Micelles Dragged with Constant Velocity as Addressed in Terms of Biolubrication Application. Acta Phys. Pol. A 2016, 129, 188–189. [Google Scholar] [CrossRef]
- Gadomski, A.; Pawlak, Z.; Oloyede, A. Directed ion transport as virtual cause of some facilitated friction-lubrication mechanism prevailing in articular cartilage: A hypothesis. Tribol. Lett. 2008, 30, 83–90. [Google Scholar] [CrossRef]
- Bełdowski, P.; Winkler, R.G.; Augé, W.K.; Hładyszowski, J.; Gadomski, A. Micelle confined in aqueous environment: Lubrication at the nanoscale and its nonlinear characteristics. In Dynamical Systems: Modelling; Springer Proceedings in Mathematics and Statistics; Springer International Publishing AG: Cham, Switzerland, 2016; pp. 73–80. ISBN 978-3-319-42401-9. [Google Scholar]
- Bełdowski, P.; Augé, W.K.; Gadomski, A. Nanoscale friction requirements for the boundary lubrication behavior of model articular systems. In Current Topics in Quantum Biology; Michalak, K., Nawrocka-Bogusz, H., Eds.; Publishing House of Adam Mickiewicz University of Poznań: Poznań, Poland, 2014; pp. 79–93. ISBN 978-83-232-2775-5. [Google Scholar]
- Gadomski, A.; Bełdowski, P.; Rubi, J.M.; Urbaniak, W.; Augé, W.K.; Santamaria-Holek, I.; Pawlak, Z. Some conceptual thoughts toward nanoscale oriented friction in a model of articular cartilage. Math. Biosci. 2013, 244, 188–200. [Google Scholar] [CrossRef] [PubMed]
- Seror, J.; Zhu, L.; Goldberg, R.; Day, A.J.; Klein, J. Supramolecular synergy in the boundary lubrication of synovial joints. Nat. Commun. 2015, 6, 6497. [Google Scholar] [CrossRef] [PubMed]
- Bonnevie, E.D.; Delco, M.L.; Jasty, N.; Bartell, L.; Fortier, L.A.; Cohen, I.; Bonassar, L.J. Chondrocyte death and mitochondrial dysfunction are mediated by cartilage friction and shear strain. Ostheoarthr. Cartil. 2016, 24, S46. [Google Scholar] [CrossRef]
- Connoly, M.L. Analytical molecular surface calculation. J. Appl. Cryst. 1983, 16, 548–558. [Google Scholar] [CrossRef]
- Richmond, T.J. Solvent accessible surface area and excluded volume in proteins. Analytical equations for overlapping spheres and implications for the hydrophobic effect. J. Mol. Biol. 1984, 178, 63–89. [Google Scholar] [CrossRef]













| Case | ||||
|---|---|---|---|---|
| 0.9754 | 0.9634 | 0.9916 | 0.9783 | |
| 0.826 | 0.8456 | 0.9073 | 0.7581 |
| Case | ||||
|---|---|---|---|---|
| 0.9792 | 0.9684 | 0.9626 | 0.9654 | |
| 0.9247 | 0.9855 | 0.8715 | 0.8601 |
| Case | ||||
|---|---|---|---|---|
| 0.9958 | 0.9987 | 0.9977 | 0.9962 | |
| 0.9882 | 1.005 | 0.9748 | 1.06 | |
| 6.201 | 5.506 | 7.400 | 6.121 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bełdowski, P.; Weber, P.; Andrysiak, T.; Augé II, W.K.; Ledziński, D.; De Leon, T.; Gadomski, A. Anomalous Behavior of Hyaluronan Crosslinking Due to the Presence of Excess Phospholipids in the Articular Cartilage System of Osteoarthritis. Int. J. Mol. Sci. 2017, 18, 2779. https://doi.org/10.3390/ijms18122779
Bełdowski P, Weber P, Andrysiak T, Augé II WK, Ledziński D, De Leon T, Gadomski A. Anomalous Behavior of Hyaluronan Crosslinking Due to the Presence of Excess Phospholipids in the Articular Cartilage System of Osteoarthritis. International Journal of Molecular Sciences. 2017; 18(12):2779. https://doi.org/10.3390/ijms18122779
Chicago/Turabian StyleBełdowski, Piotr, Piotr Weber, Tomasz Andrysiak, Wayne K. Augé II, Damian Ledziński, Tristan De Leon, and Adam Gadomski. 2017. "Anomalous Behavior of Hyaluronan Crosslinking Due to the Presence of Excess Phospholipids in the Articular Cartilage System of Osteoarthritis" International Journal of Molecular Sciences 18, no. 12: 2779. https://doi.org/10.3390/ijms18122779
APA StyleBełdowski, P., Weber, P., Andrysiak, T., Augé II, W. K., Ledziński, D., De Leon, T., & Gadomski, A. (2017). Anomalous Behavior of Hyaluronan Crosslinking Due to the Presence of Excess Phospholipids in the Articular Cartilage System of Osteoarthritis. International Journal of Molecular Sciences, 18(12), 2779. https://doi.org/10.3390/ijms18122779







