Comparative Evaluation of Machine Learning Strategies for Analyzing Big Data in Psychiatry
Abstract
1. Introduction
2. Results
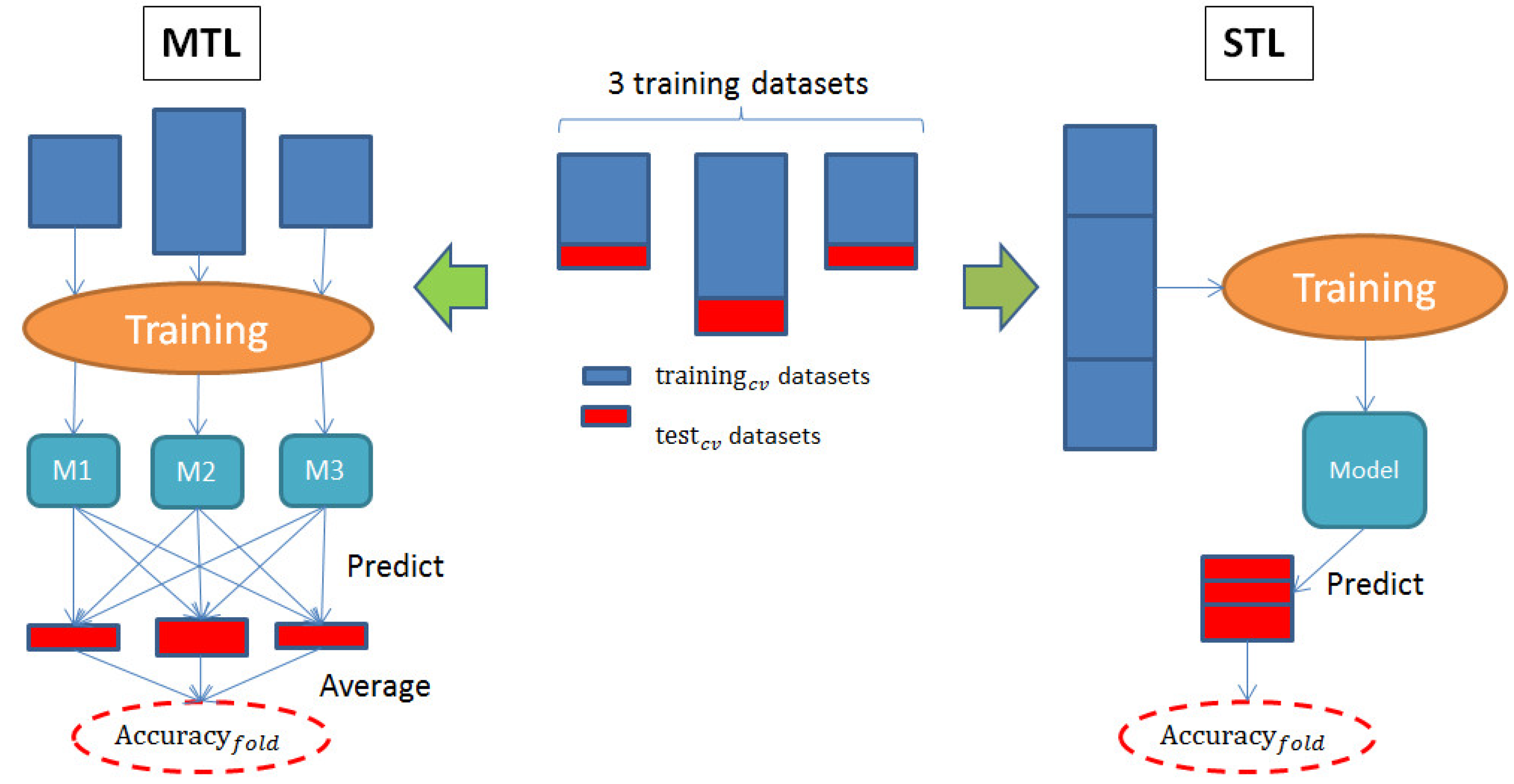
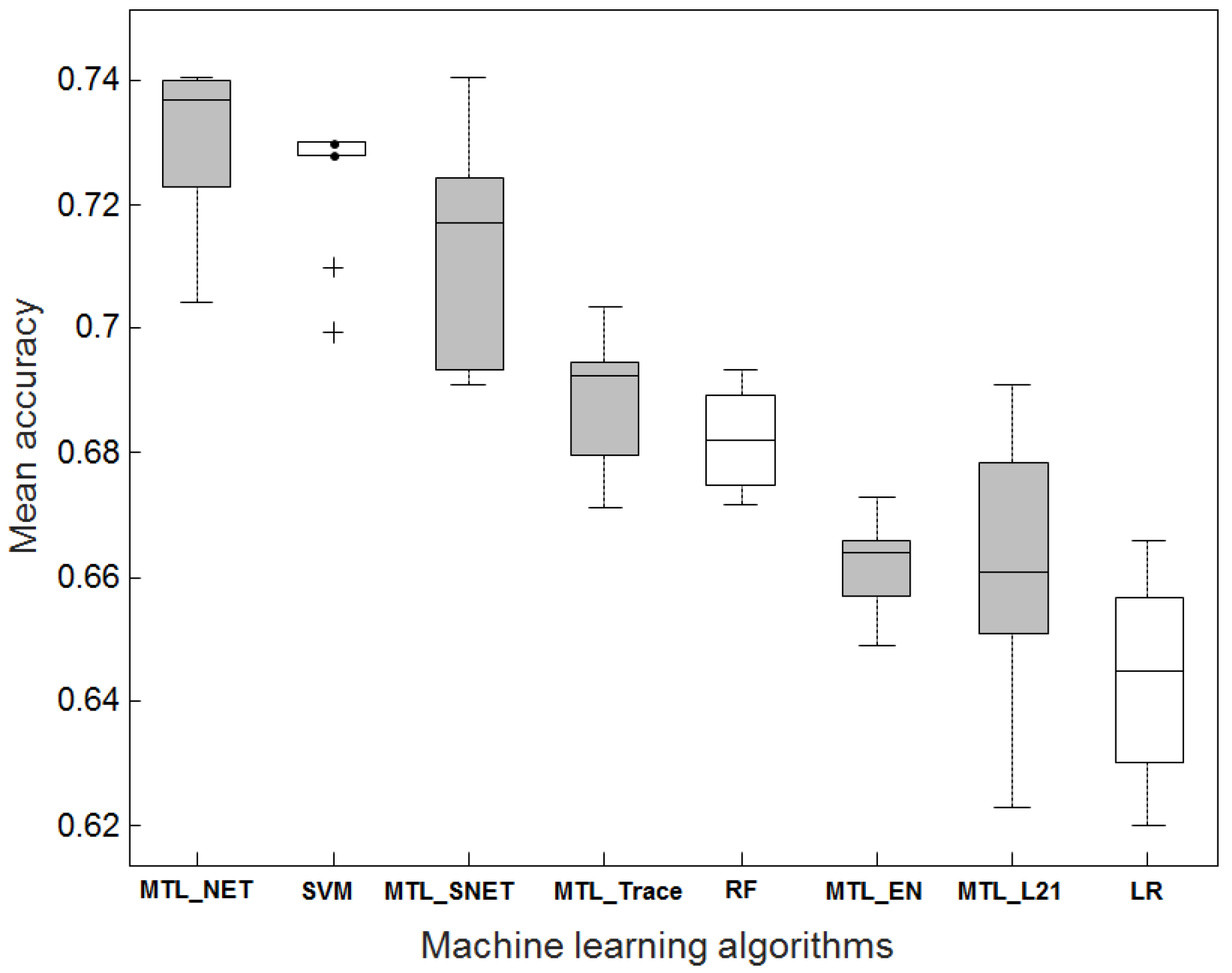
2.1. Accuracy Comparison Between MTL and STL
2.2. Dependency of Classification Performance on the Number of Training Datasets
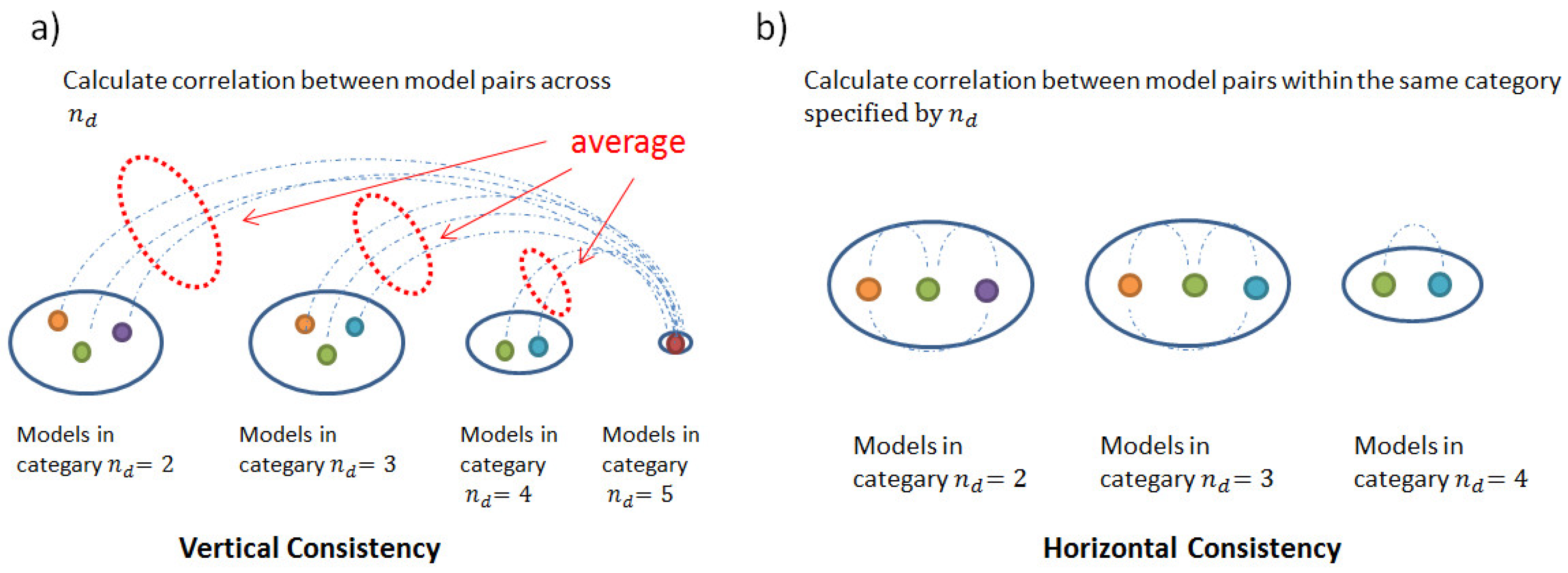
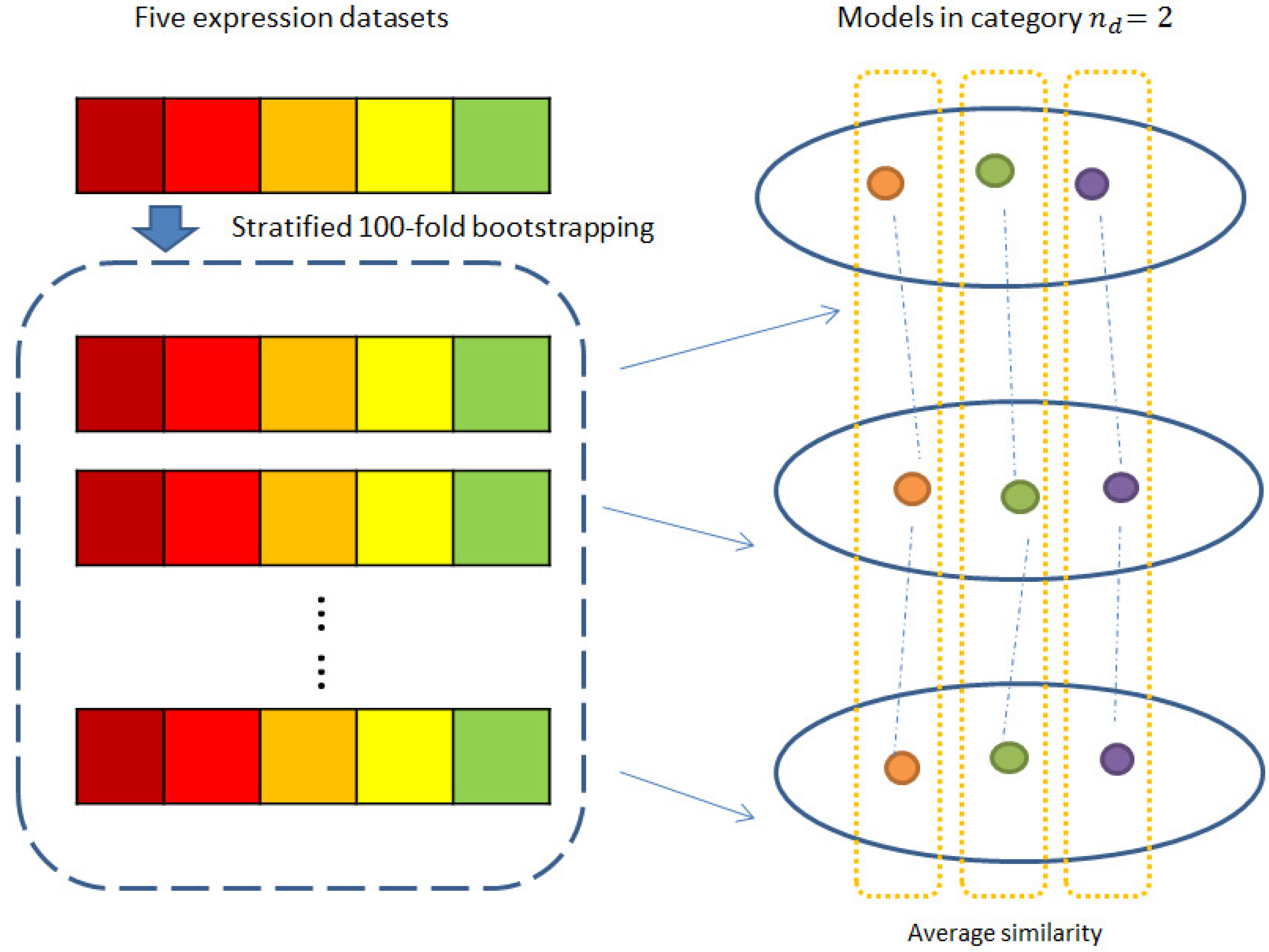
2.3. Consistency and Stability of Trained Models
3. Discussion
4. Materials and Methods
4.1. Datasets
4.2. Preprocessing
4.3. Machine Learning Approaches
4.3.1. Multi-Task Learning
4.3.2. Conventional, Single-Task Machine Learning
4.3.3. Assessment of Predictive Performance
4.3.4. Consistency and Stability Analysis
5. Limitations and Future Work
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| MTL | Multi-task learning |
| STL | Single-task learning |
| RF | Random Forests |
| SVM | Support Vector Machine |
Appendix A
- The model pairs trained using different (overlapping or non-overlapping) combinations of datasets were represented as and , respectively (i.e., represented the model trained using the training set, ; was trained using a different dataset combination, for example, or )
- The notation of an algorithm: , (i.e., = MTL_NET, = SVM)
- The index of the bootstrapping sample: and . For computational efficiency, bootstrapping was performed across all datasets, , and data subsets were selected from this sampling.
Appendix B
References
- Sullivan, P.F. The psychiatric GWAS consortium: Big science comes to psychiatry. Neuron 2010, 68, 182–186. [Google Scholar] [CrossRef] [PubMed]
- Passos, I.C.; Mwangi, B.; Kapczinski, F. Big data analytics and machine learning: 2015 and beyond. Lancet Psychiatry 2016, 3, 13–15. [Google Scholar] [CrossRef]
- Schizophrenia Working Group of the Psychiatric Genomics Consortium. Biological insights from 108 schizophrenia-associated genetic loci. Nature 2014, 511, 421–427. [Google Scholar] [CrossRef] [PubMed]
- Major Depressive Disorder Working Group of the Psychiatric GWAS Consortium; Ripke, S.; Wray, N.R.; Lewis, C.M.; Hamilton, S.P.; Weissman, M.M.; Breen, G.; Byrne, E.M.; Blackwood, D.H.; Boomsma, D.I.; et al. A mega-analysis of genome-wide association studies for major depressive disorder. Mol. Psychiatry 2013, 18, 497–511. [Google Scholar] [PubMed]
- Wolfers, T.; Buitelaar, J.K.; Beckmann, C.F.; Franke, B.; Marquand, A.F. From estimating activation locality to predicting disorder: A review of pattern recognition for neuroimaging-based psychiatric diagnostics. Neurosci. Biobehav. Rev. 2015, 57, 328–349. [Google Scholar] [CrossRef] [PubMed]
- Franke, B.; Stein, J.L.; Ripke, S.; Anttila, V.; Hibar, D.P.; van Hulzen, K.J.E.; Arias-Vasquez, A.; Smoller, J.W.; Nichols, T.E.; Neale, M.C.; et al. Genetic influences on schizophrenia and subcortical brain volumes: Large-scale proof of concept. Nat. Neurosci. 2016, 19, 420–431. [Google Scholar] [CrossRef] [PubMed]
- de Wit, S.J.; Alonso, P.; Schweren, L.; Mataix-Cols, D.; Lochner, C.; Menchón, J.M.; Stein, D.J.; Fouche, J.P.; Soriano-Mas, C.; Sato, J.R.; et al. Multicenter voxel-based morphometry mega-analysis of structural brain scans in obsessive-compulsive disorder. Am. J. Psychiatry 2014, 171, 340–349. [Google Scholar] [CrossRef] [PubMed]
- Jordan, M.I.; Mitchell, T.M. Machine learning: Trends, perspectives, and prospects. Science 2015, 349, 255–260. [Google Scholar] [CrossRef] [PubMed]
- Iniesta, R.; Stahl, D.; McGuffin, P. Machine learning, statistical learning and the future of biological research in psychiatry. Psychol. Med. 2016, 46, 2455–2465. [Google Scholar] [CrossRef] [PubMed]
- Vilhjalmsson, B.J.; Yang, J.; Finucane, H.K.; Gusev, A.; Lindström, S.; Ripke, S.; Genovese, G.; Loh, P.R.; Bhatia, G.; Do, R.; et al. Modeling Linkage Disequilibrium Increases Accuracy of Polygenic Risk Scores. Am. J. Hum. Genet. 2015, 97, 576–592. [Google Scholar] [CrossRef] [PubMed]
- Vos, T.; Flaxman, A.D.; Naghavi, M.; Lozano, R.; Michaud, C.; Ezzati, M.; Shibuya, K.; Salomon, J.A.; Abdalla, S.; et al. Years lived with disability (YLDs) for 1160 sequelae of 289 diseases and injuries 1990-2010: A systematic analysis for the Global Burden of Disease Study 2010. Lancet 2012, 380, 2163–2196. [Google Scholar] [CrossRef]
- Whelan, R.; Watts, R.; Orr, C.A.; Althoff, R.R.; Artiges, E.; Banaschewski, T.; Barker, G.J.; Bokde, A.L.; Büchel, C.; Carvalho, F.M.; et al. Neuropsychosocial profiles of current and future adolescent alcohol misusers. Nature 2014, 512, 185–189. [Google Scholar] [CrossRef] [PubMed]
- Xia, C.H.; Ma, Z.; Ciric, R.; Gu, S.; Betzel, R.F.; Kaczkurkin, A.N.; Calkins, M.E.; Cook, P.A.; García de la Garza, A.; Vandekar, S.N.; et al. Linked dimensions of psychopathology and connectivity in functional brain networks. Nat. Commun. 2018, 9, 3003. [Google Scholar] [CrossRef] [PubMed]
- Caruana, R. Multitask Learning. In Learning to Learn; Springer: Boston, MA, USA, 1998; pp. 95–133. [Google Scholar]
- Widmer, C.; Rätsch, G. Multitask Learning in Computational Biology. In Proceedings of the ICML Workshop on Unsupervised and Transfer Learning, PMLR, Bellevue, WA, USA, 2 July 2012; Volume 27, pp. 207–216. [Google Scholar]
- Li, Y.; Wang, J.; Ye, J.P.; Reddy, C.K. A Multi-Task Learning Formulation for Survival Analysis. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016. [Google Scholar]
- Yuan, H.; Paskov, I.; Paskov, H.; González, J.A.; Leslie, S.C. Multitask learning improves prediction of cancer drug sensitivity. Sci. Rep. 2016, 6, 31619. [Google Scholar] [CrossRef] [PubMed]
- Feriante, J. Massively Multitask Deep Learning for Drug Discovery. Master’s Thesis, University of Wisconsin-Madison, Madison, WI, USA, 2015. [Google Scholar]
- Xu, Q.; Pan, S.J.; Xue, H.H.; Yang, Q. Multitask Learning for Protein Subcellular Location Prediction. IEEE/ACM Trans. Comput. Biol. Bioinform. 2011, 8, 748–759. [Google Scholar] [PubMed]
- Zhou, J.; Liu, J.; Narayan, V.A.; Ye, J.; Alzheimer’s Disease Neuroimaging Initiative. Modeling disease progression via multi-task learning. Neuroimage 2013, 78, 233–248. [Google Scholar] [PubMed]
- Collobert, R.; Weston, J. A unified architecture for natural language processing: Deep neural networks with multitask learning. In Proceedings of the 25th International Conference on Machine Learning, New York, NY, USA, 5–9 July 2008. [Google Scholar]
- Wu, Z.; Valentini-Botinhao, C.; Watts, O.; King, S. Deep neural networks employing Multi-Task Learning and stacked bottleneck features for speech synthesis. In Proceedings of the 2015 IEEE International Conference on Acoustics, Speech and Signal Processing, Brisbane, Australia, 19–24 April 2015. [Google Scholar]
- Wang, X.; Zhang, C.; Zhang, Z. Boosted multi-task learning for face verification with applications to web image and video search. In Proceedings of the 2009 IEEE International Conference on on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009. [Google Scholar]
- Zhang, Z.; Luo, P.; Loy, C.C.; Tang, X. Facial Landmark Detection by Deep Multi-task Learning. In Proceedings of the European Conference on Computer Vision, Zurich, Switzerland, 6–12 September 2014. [Google Scholar]
- Chapelle, O.; Shivaswamy, P.; Vadrevu, P.; Weinberger, K.; Zhang, Y. Multi-task learning for boosting with application to web search ranking. In Proceedings of the 16th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Washington, DC, USA, 25–28 July 2010. [Google Scholar]
- Ahmed, A.; Aly, M.; Das, A.; Smola, J.A.; Anastasakos, T. Web-scale multi-task feature selection for behavioral targeting. In Proceedings of the 21st ACM International Conference on Information and Knowledge Management, Maui, HI, USA, 29 October–2 November 2012. [Google Scholar]
- Marquand, A.F.; Brammer, M.; Williams, S.C.; Doyle, O.M. Bayesian multi-task learning for decoding multi-subject neuroimaging data. Neuroimage 2014, 92, 298–311. [Google Scholar] [CrossRef] [PubMed]
- Jing, W.; Zhang, Z.L.; Yan, J.W.; Li, T.Y.; Rao, D.B.; Fang, S.F.; Kim, S.; Risacher, L.S.; Saykin, J.A.; Shen, L. Sparse Bayesian multi-task learning for predicting cognitive outcomes from neuroimaging measures in Alzheimer’s disease. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012. [Google Scholar]
- Wang, H.; Nie, F.; Huang, H.; Kim, S.; Nho, K.; Risacher, S.L.; Saykin, A.J.; Shen, L.; Alzheimer’s Disease Neuroimaging Initiative. Identifying quantitative trait loci via group-sparse multitask regression and feature selection: An imaging genetics study of the ADNI cohort. Bioinformatics 2012, 28, 229–237. [Google Scholar] [CrossRef] [PubMed]
- Lin, D.; Zhang, J.; Li, J.; He, H.; Deng, H.W.; Wang, Y.P. Integrative analysis of multiple diverse omics datasets by sparse group multitask regression. Front. Cell Dev. Biol. 2014, 2, 62. [Google Scholar] [CrossRef] [PubMed]
- Xu, Q.; Xue, H.; Yang, Q. Multi-platform gene-expression mining and marker gene analysis. Int. J. Data Min. Bioinform. 2011, 5, 485–503. [Google Scholar] [CrossRef] [PubMed]
- O′Brien, C.M. Statistical Learning with Sparsity: The Lasso and Generalizations. Int. Stat. Rev. 2016, 84, 156–157. [Google Scholar] [CrossRef]
- Gandal, M.J.; Haney, J.R.; Parikshak, N.N.; Leppa, V.; Ramaswami, G.; Hartl, C.; Schork, A.J.; Appadurai, V.; Buil, A.; Werge, T.M.; et al. Shared molecular neuropathology across major psychiatric disorders parallels polygenic overlap. Science 2018, 359, 693–697. [Google Scholar] [CrossRef] [PubMed]
- Bulik-Sullivan, B.; Finucane, H.K.; Anttila, V.; Gusev, A.; Day, F.R.; Loh, P.R.; ReproGen Consortium; Psychiatric Genomics Consortium; Genetic Consortium for Anorexia Nervosa of the Wellcome Trust Case Control Consortium; Duncan, L.; et al. An atlas of genetic correlations across human diseases and traits. Nat. Genet. 2015, 47, 1236–1241. [Google Scholar] [CrossRef] [PubMed]
- Cross-Disorder Group of the Psychiatric Genomics Consortium; Lee, S.H.; Ripke, S.; Neale, B.M.; Faraone, S.V.; Purcell, S.M.; Perlis, R.H.; Mowry, B.J.; Thapar, A.; Goddard, M.E.; et al. Genetic relationship between five psychiatric disorders estimated from genome-wide SNPs. Nat. Genet. 2013, 45, 984–994. [Google Scholar] [CrossRef] [PubMed]
- International Schizophrenia Consortium; Purcell, S.M.; Wray, N.R.; Stone, J.L.; Visscher, P.M.; O′Donovan, M.C.; Sullivan, P.F.; Sklar, P. Common polygenic variation contributes to risk of schizophrenia and bipolar disorder. Nature 2009, 460, 748–752. [Google Scholar] [CrossRef] [PubMed]
- Harris, L.W.; Wayland, M.; Lan, M.; Ryan, M.; Giger, T.; Lockstone, H.; Wuethrich, I.; Mimmack, M.; Wang, L.; Kotter, M.; et al. The cerebral microvasculature in schizophrenia: A laser capture microdissection study. PLoS ONE 2008, 3, e3964. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.; Cheng, L.; Grennan, K.; Pibiri, F.; Zhang, C.; Badner, J.A.; Members of the Bipolar Disorder Genome Study (BiGS) Consortium; Gershon, E.S.; Liu, C. Two gene co-expression modules differentiate psychotics and controls. Mol. Psychiatry 2013, 18, 1308–1314. [Google Scholar] [CrossRef] [PubMed]
- Maycox, P.R.; Kelly, F.; Taylor, A.; Bates, S.; Reid, J.; Logendra, R.; Barnes, M.R.; Larminie, C.; Jones, N.; Lennon, M.; et al. Analysis of gene expression in two large schizophrenia cohorts identifies multiple changes associated with nerve terminal function. Mol. Psychiatry 2009, 14, 1083–1094. [Google Scholar] [CrossRef] [PubMed]
- Barnes, M.R.; Huxley-Jones, J.; Maycox, P.R.; Lennon, M.; Thornber, A.; Kelly, F.; Bates, S.; Taylor, A.; Reid, J.; Jones, N.; et al. Transcription and pathway analysis of the superior temporal cortex and anterior prefrontal cortex in schizophrenia. J. Neurosci. Res. 2011, 89, 1218–1227. [Google Scholar] [CrossRef] [PubMed]
- Narayan, S.; Tang, B.; Head, S.R.; Gilmartin, T.J.; Sutcliffe, J.G.; Dean, B.; Thomas, E.A. Molecular profiles of schizophrenia in the CNS at different stages of illness. Brain Res. 2008, 1239, 235–248. [Google Scholar] [CrossRef] [PubMed]
- Irizarry, R.A.; Hobbs, B.; Collin, F.; Beazer-Barclay, Y.D.; Antonellis, K.J.; Scherf, U.; Speed, T.P. Exploration, normalization, and summaries of high density oligonucleotide array probe level data. Biostatistics 2003, 4, 249–264. [Google Scholar] [CrossRef] [PubMed]
- Leek, J.T.; Johnson, W.E.; Parker, H.S.; Jaffe, A.E.; Storey, J.D. The sva package for removing batch effects and other unwanted variation in high-throughput experiments. Bioinformatics 2012, 28, 882–883. [Google Scholar] [CrossRef] [PubMed]
- Zhou, J.; Chen, J.; Ye, J. MALSAR: Multi-tAsk Learning via StructurAl Regularization; Arizona State University: Tempe, AZ, USA, 2012. [Google Scholar]
- Evgeniou, T.; Pontil, M. Regularized multi-task learning. In Proceedings of the Tenth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Seattle, WA, USA, 22–25 August 2004. [Google Scholar]
- Tibshirani, R.J. The lasso problem and uniqueness. Electron. J. Statist. 2013, 7, 1456–1490. [Google Scholar] [CrossRef]
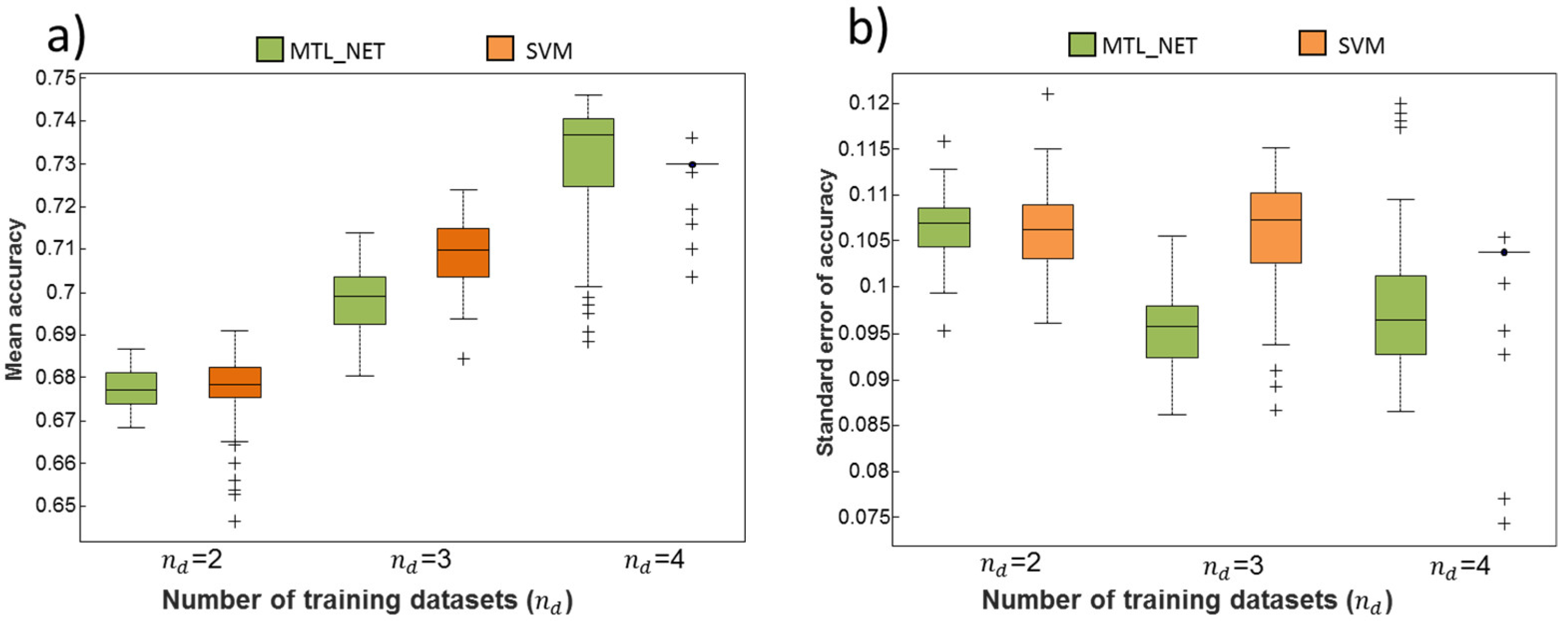

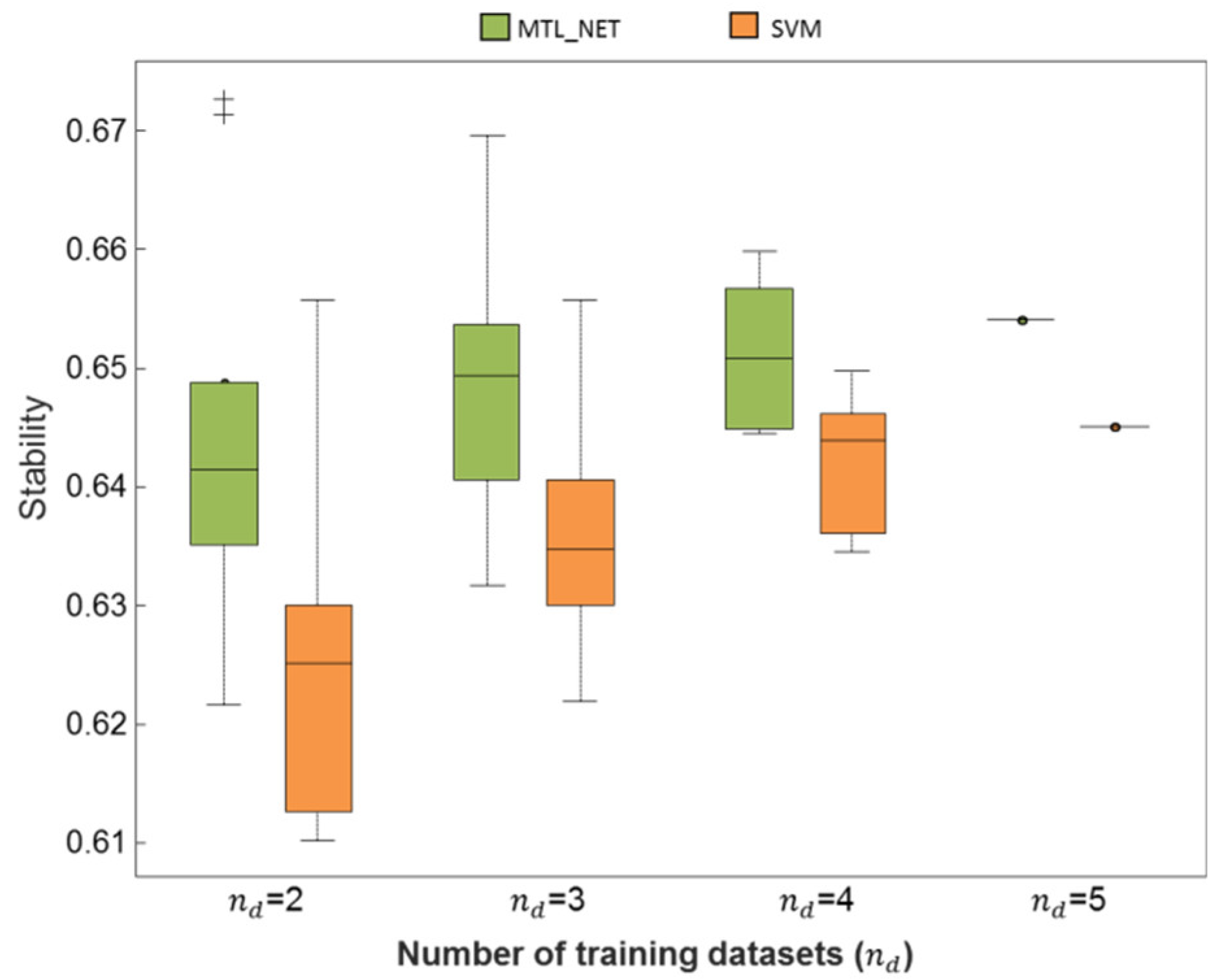
| MTL_NET/SVM | nd = 2 | nd = 3 | nd = 4 | nd = 5 |
|---|---|---|---|---|
| Horizontal consistency | 0.26/0.24 | 0.39/0.37 | 0.51/0.49 | - |
| Vertical consistency | 0.22/0.21 | 0.35/0.33 | 0.49/0.46 | - |
| Stability | 0.64/0.63 | 0.65/0.64 | 0.65/0.64 | 0.654/0.645 |
| Success rate (horizontal consistency) | 1 | 1 | 1 | - |
| Success rate (vertical consistency) | 1 | 1 | 1 | - |
| Success rate (stability) | 1 | 1 | 1 | 1 |
| GSE12679 | GSE35977 | GSE17612 | GSE21935 | GSE21138 | |
|---|---|---|---|---|---|
| Reference | [37] | [38] | [39] | [40] | [41] |
| n SZ | 11 | 50 | 22 | 19 | 29 |
| n HC | 11 | 50 | 22 | 19 | 29 |
| age SZ | 46.1 ± 5.9 | 42.4 ± 9.9 | 76 ± 12.9 | 77.6 ± 11.4 | 43.3 ± 17.3 |
| age HC | 41.7 ± 7.9 | 45.5 ± 9 | 68 ± 21.5 | 67.7 ± 22.2 | 44.7 ± 16.1 |
| sex SZ (m/f) | 7/4 | 37/13 | 16/6 | 11/8 | 23/6 |
| sex HC (m/f) | 8/3 | 35/15 | 11/11 | 10/9 | 24/5 |
| PMI SZ | 33 ± 6.7 | 31.8 ± 15.4 | 6.2 ± 4.1 | 5.5 ± 2.6 | 38.1 ± 10.8 |
| PMI HC | 24.2 ± 15.7 | 27.3 ± 11.8 | 10.1 ± 4.3 | 9.1 ± 4.3 | 40.5 ± 14 |
| brain pH SZ | NA | 6.4 ± 0.3 | 6.1 ± 0.2 | 6.1 ± 0.2 | 6.2 ± 0.2 |
| brain pH HC | NA | 6.5 ± 0.3 | 6.5 ± 0.3 | 6.5 ± 0.3 | 6.3 ± 0.2 |
| Genechip | HGU | HuG | HGU | HGU | HGU |
| Brain Region | PFC | PC | APC | STC | PFC |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, H.; Meyer-Lindenberg, A.; Schwarz, E. Comparative Evaluation of Machine Learning Strategies for Analyzing Big Data in Psychiatry. Int. J. Mol. Sci. 2018, 19, 3387. https://doi.org/10.3390/ijms19113387
Cao H, Meyer-Lindenberg A, Schwarz E. Comparative Evaluation of Machine Learning Strategies for Analyzing Big Data in Psychiatry. International Journal of Molecular Sciences. 2018; 19(11):3387. https://doi.org/10.3390/ijms19113387
Chicago/Turabian StyleCao, Han, Andreas Meyer-Lindenberg, and Emanuel Schwarz. 2018. "Comparative Evaluation of Machine Learning Strategies for Analyzing Big Data in Psychiatry" International Journal of Molecular Sciences 19, no. 11: 3387. https://doi.org/10.3390/ijms19113387
APA StyleCao, H., Meyer-Lindenberg, A., & Schwarz, E. (2018). Comparative Evaluation of Machine Learning Strategies for Analyzing Big Data in Psychiatry. International Journal of Molecular Sciences, 19(11), 3387. https://doi.org/10.3390/ijms19113387




