Inferring the Disease-Associated miRNAs Based on Network Representation Learning and Convolutional Neural Networks
Abstract
1. Introduction
2. Results and Discussion
2.1. Evaluation Metrics
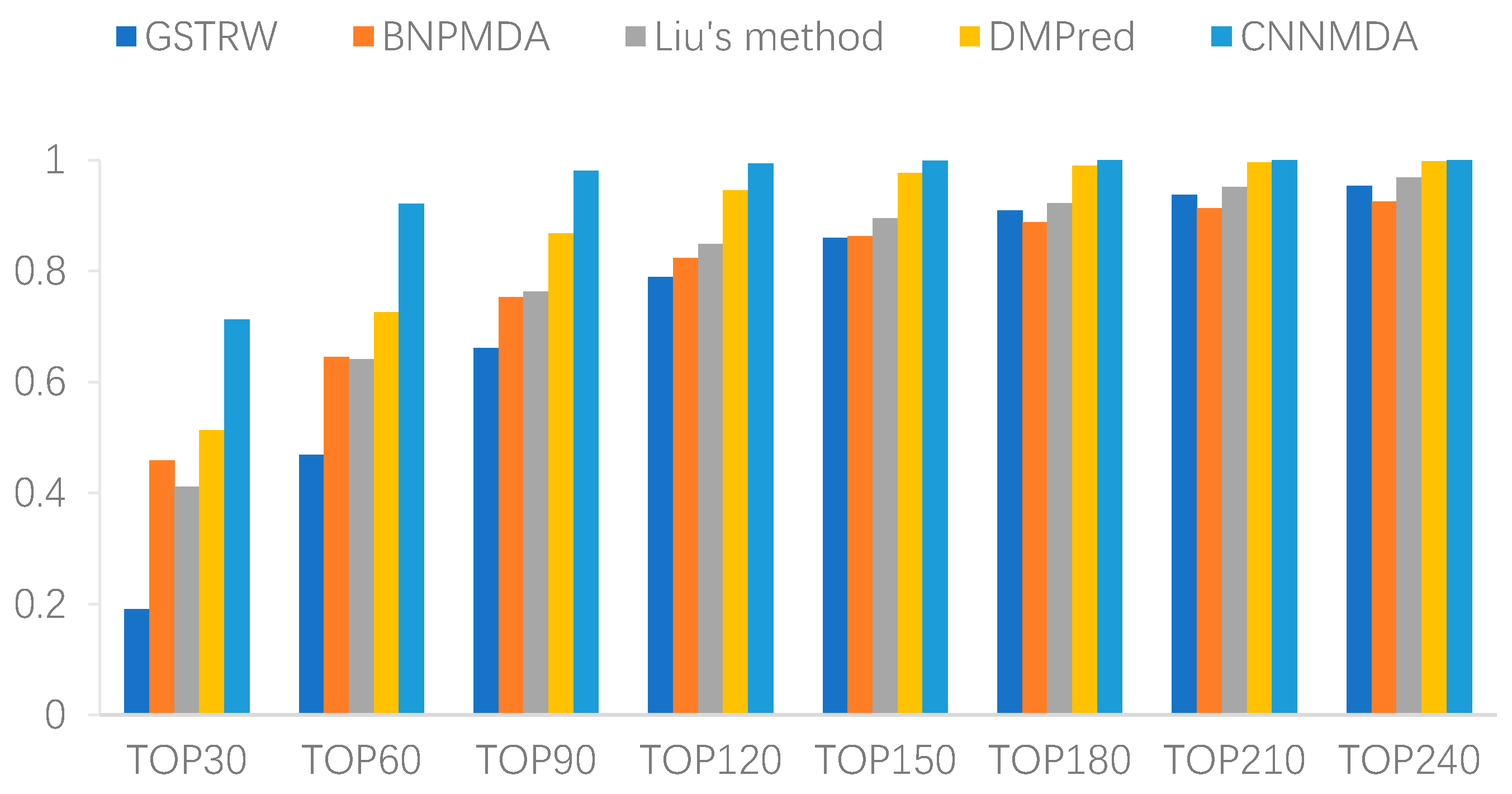
2.2. Comparison with Other Method
2.3. Case Studies of Lung Neoplasms, Breast Neoplasms, and Pancreatic Neoplasms
3. Materials and Methods
3.1. Dataset
3.2. Representation of miRNA and Disease Heterogeneous Data
3.2.1. MiRNA Similarity Measure
3.2.2. Disease Similarity Measure
3.2.3. miRNA-Disease Associations
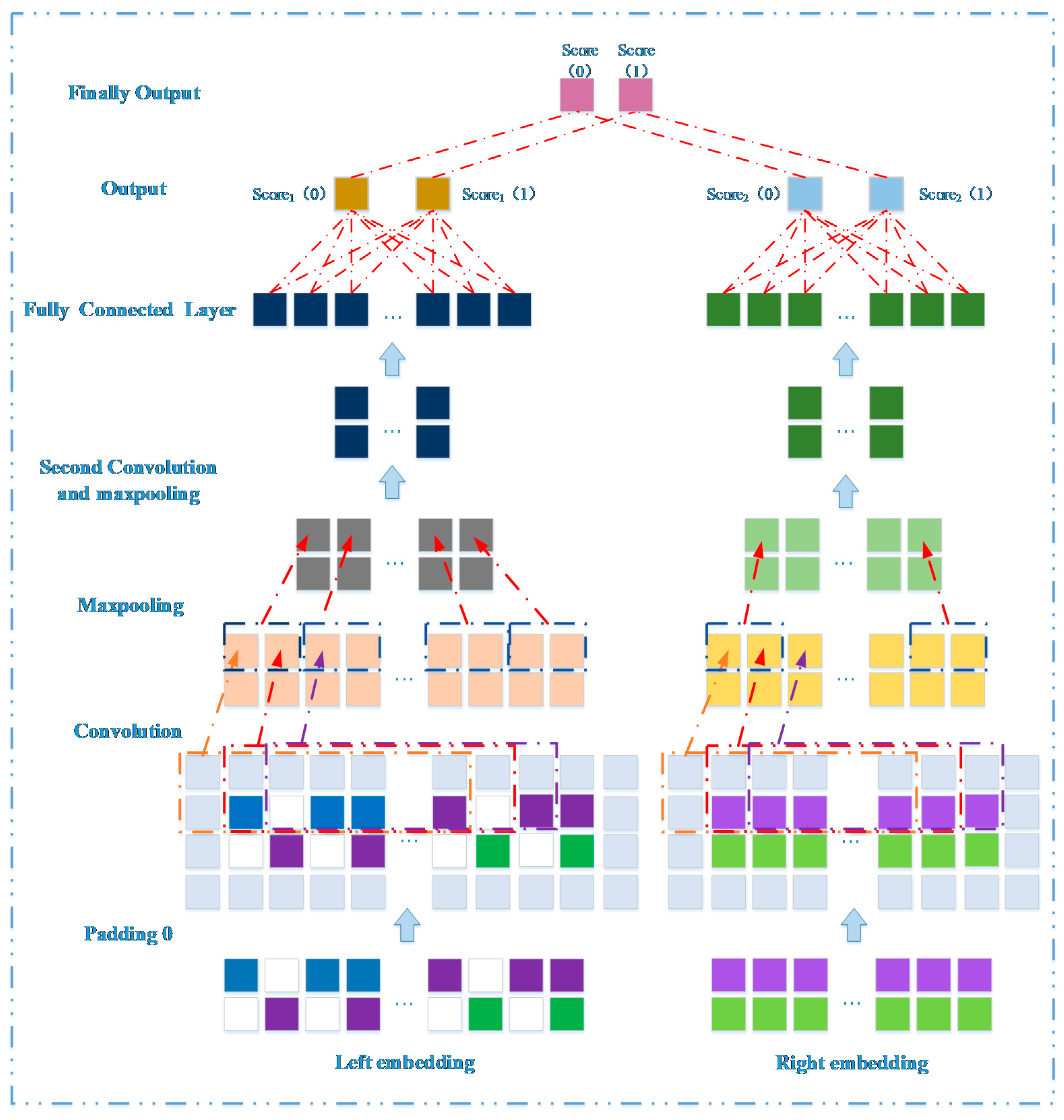
3.3. Prediction Model Based on Network Representation Learning and Dual CNN
3.3.1. Embedding Layer on the Left
3.3.2. Embedding Layer on the Right
3.3.3. Convolutional Module on the Left
3.3.4. Convolutional Module on the Right
3.3.5. Combined Strategy
3.4. Predicting Novel Disease-Related miRNAs
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Chen, K.; Rajewsky, N. The evolution of gene regulation by transcription factors and microRNAs. Nat. Rev. Genet. 2007, 8, 93–103. [Google Scholar] [CrossRef] [PubMed]
- Subramanian, S.; Fu, Y.; Sunkar, R.; Barbazuk, W.B.; Zhu, J.-K.; Yu, O. Novel and nodulation-regulated microRNAs in soybean roots. BMC Genom. 2008, 9, 160. [Google Scholar] [CrossRef] [PubMed]
- Zhang, B.; Wang, Q.; Pan, X. MicroRNAs and their regulatory roles in animals and plants. J. Cell. Physiol. 2007, 210, 279–289. [Google Scholar] [CrossRef] [PubMed]
- Calin, G.A.; Croce, C.M. MicroRNA signatures in human cancers. Nat. Rev. Cancer 2006, 6, 857–866. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Xie, D.; Zhao, Q.; You, Z.-H. MicroRNAs and complex diseases: From experimental results to computational models. Brief. Bioinform. 2017, 20, 515–539. [Google Scholar] [CrossRef] [PubMed]
- Gaur, A.; Jewell, D.A.; Liang, Y.; Ridzon, D.; Moore, J.H.; Chen, C.; Ambros, V.R.; Israel, M.A. Characterization of microRNA expression levels and their biological correlates in human cancer cell lines. Cancer Res. 2007, 67, 2456–2468. [Google Scholar] [CrossRef] [PubMed]
- Meola, N.; Gennarino, V.A.; Banfi, S. microRNAs and genetic diseases. Pathogenetics 2009, 2, 7. [Google Scholar] [CrossRef] [PubMed]
- Bartel, D.P. MicroRNAs: Genomics, biogenesis, mechanism, and function. Cell 2004, 116, 281–297. [Google Scholar] [CrossRef]
- Jiang, Q.; Hao, Y.; Wang, G.; Juan, L.; Zhang, T.; Teng, M.; Liu, Y.; Wang, Y. Prioritization of disease microRNAs through a human phenome-microRNAome network. BMC Syst. Biol. 2010, 4, S2. [Google Scholar] [CrossRef]
- Qabaja, A.; Alshalalfa, M.; Bismar, T.A.; Alhajj, R. Protein network-based Lasso regression model for the construction of disease-miRNA functional interactions. EURASIP J. Bioinform. Syst. Biol. 2013, 2013, 3. [Google Scholar] [CrossRef]
- Shi, H.; Xu, J.; Zhang, G.; Xu, L.; Li, C.; Wang, L.; Zhao, Z.; Jiang, W.; Guo, Z.; Li, X. Walking the interactome to identify human miRNA-disease associations through the functional link between miRNA targets and disease genes. BMC Syst. Biol. 2013, 7, 101. [Google Scholar] [CrossRef] [PubMed]
- Xu, C.; Ping, Y.; Li, X.; Zhao, H.; Wang, L.; Fan, H.; Xiao, Y.; Li, X. Prioritizing candidate disease miRNAs by integrating phenotype associations of multiple diseases with matched miRNA and mRNA expression profiles. Mol. Biosyst. 2014, 10, 2800–2809. [Google Scholar] [CrossRef] [PubMed]
- Kertesz, M.; Iovino, N.; Unnerstall, U.; Gaul, U.; Segal, E. The role of site accessibility in microRNA target recognition. Nat. Genet. 2007, 39, 1278–1284. [Google Scholar] [CrossRef] [PubMed]
- Lewis, B.P.; Shih, I.-h.; Jones-Rhoades, M.W.; Bartel, D.P.; Burge, C.B. Prediction of mammalian microRNA targets. Cell 2003, 115, 787–798. [Google Scholar] [CrossRef]
- Bandyopadhyay, S.; Mitra, R.; Maulik, U.; Zhang, M.Q. Development of the human cancer microRNA network. Silence 2010, 1, 6. [Google Scholar] [CrossRef] [PubMed]
- Barabási, A.-L.; Gulbahce, N.; Loscalzo, J. Network medicine: A network-based approach to human disease. Nat. Rev. Genet. 2011, 12, 56–68. [Google Scholar] [CrossRef] [PubMed]
- Paci, P.; Colombo, T.; Fiscon, G.; Gurtner, A.; Pavesi, G.; Farina, L. SWIM: A computational tool to unveiling crucial nodes in complex biological networks. Sci. Rep. 2017, 7, 44797. [Google Scholar] [CrossRef] [PubMed]
- Fiscon, G.; Conte, F.; Farina, L.; Paci, P. Network-based approaches to explore complex biological systems towards network medicine. Genes 2018, 9, 437. [Google Scholar] [CrossRef]
- Fiscon, G.; Conte, F.; Farina, L.; Pellegrini, M.; Russo, F.; Paci, P. Identification of Disease–miRNA Networks Across Different Cancer Types Using SWIM. In MicroRNA Target Identification; Humana Press: New York, NY, USA, 2019; pp. 169–181. [Google Scholar]
- Xu, J.; Li, C.-X.; Lv, J.-Y.; Li, Y.-S.; Xiao, Y.; Shao, T.-T.; Huo, X.; Li, X.; Zou, Y.; Han, Q.-L. Prioritizing candidate disease miRNAs by topological features in the miRNA target–dysregulated network: Case study of prostate cancer. Mol. Cancer Ther. 2011, 10, 1857–1866. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Liu, M.-X.; Yan, G.-Y. RWRMDA: Predicting novel human microRNA–disease associations. Mol. BioSyst. 2012, 8, 2792–2798. [Google Scholar] [CrossRef] [PubMed]
- Xuan, P.; Han, K.; Guo, Y.; Li, J.; Li, X.; Zhong, Y.; Zhang, Z.; Ding, J. Prediction of potential disease-associated microRNAs based on random walk. Bioinformatics 2015, 31, 1805–1815. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Zeng, X.; He, Z.; Zou, Q. Inferring microRNA-disease associations by random walk on a heterogeneous network with multiple data sources. IEEE/ACM Trans. Comput. Biol. Bioinform. 2016, 14, 905–915. [Google Scholar] [CrossRef] [PubMed]
- Luo, J.; Xiao, Q. A novel approach for predicting microRNA-disease associations by unbalanced bi-random walk on heterogeneous network. J. Biomed. Inform. 2017, 66, 194–203. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Huang, L. LRSSLMDA: Laplacian regularized sparse subspace learning for MiRNA-disease association prediction. PLoS Comput. Biol. 2017, 13, e1005912. [Google Scholar] [CrossRef] [PubMed]
- Shen, Z.; Zhang, Y.-H.; Han, K.; Nandi, A.K.; Honig, B.; Huang, D.-S. miRNA-disease association prediction with collaborative matrix factorization. Complexity 2017, 2017, 2498957. [Google Scholar] [CrossRef]
- Xiao, Q.; Luo, J.; Liang, C.; Cai, J.; Ding, P. A graph regularized non-negative matrix factorization method for identifying microRNA-disease associations. Bioinformatics 2017, 34, 239–248. [Google Scholar] [CrossRef]
- Xuan, P.; Shen, T.; Wang, X.; Zhang, T.; Zhang, W. Inferring disease-associated microRNAs in heterogeneous networks with node attributes. IEEE/ACM Trans. Comput. Biol. Bioinform. 2018. [Google Scholar] [CrossRef]
- Zhong, Y.; Xuan, P.; Wang, X.; Zhang, T.; Li, J.; Liu, Y.; Zhang, W. A non-negative matrix factorization based method for predicting disease-associated miRNAs in miRNA-disease bilayer network. Bioinformatics 2017, 34, 267–277. [Google Scholar] [CrossRef]
- Zeng, X.; Liu, L.; Lü, L.; Zou, Q. Prediction of potential disease-associated microRNAs using structural perturbation method. Bioinformatics 2018, 34, 2425–2432. [Google Scholar] [CrossRef]
- Luo, J.; Ding, P.; Liang, C.; Cao, B.; Chen, X. Collective prediction of disease-associated miRNAs based on transduction learning. IEEE/ACM Trans. Comput. Biol. Bioinform. 2016, 14, 1468–1475. [Google Scholar] [CrossRef]
- Chen, X.; Wang, L.; Qu, J.; Guan, N.-N.; Li, J.-Q. Predicting miRNA–disease association based on inductive matrix completion. Bioinformatics 2018, 34, 4256–4265. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Xie, D.; Wang, L.; Zhao, Q.; You, Z.-H.; Liu, H. BNPMDA: Bipartite network projection for MiRNA–disease association prediction. Bioinformatics 2018, 34, 3178–3186. [Google Scholar] [CrossRef] [PubMed]
- Che, K.; Guo, M.; Wang, C.; Liu, X.; Chen, X. Predicting MiRNA-Disease Association by Latent Feature Extraction with Positive Samples. Genes 2019, 10, 80. [Google Scholar] [CrossRef] [PubMed]
- Saito, T.; Rehmsmeier, M. The precision-recall plot is more informative than the ROC plot when evaluating binary classifiers on imbalanced datasets. PLoS ONE 2015, 10, e0118432. [Google Scholar] [CrossRef] [PubMed]
- Xuan, P.; Sun, C.; Zhang, T.; Ye, Y.; Shen, T.; Dong, Y. Gradient Boosting Decision Tree-Based Method for Predicting Interactions Between Target Genes and Drugs. Front. Genet. 2019, 10. [Google Scholar] [CrossRef] [PubMed]
- Chen, M.; Liao, B.; Li, Z. Global Similarity Method Based on a Two-tier Random Walk for the Prediction of microRNA–Disease Association. Sci. Rep. 2018, 8, 6481. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z.; Ren, F.; Liu, C.; He, S.; Sun, G.; Gao, Q.; Yao, L.; Zhang, Y.; Miao, R.; Cao, Y. dbDEMC: A database of differentially expressed miRNAs in human cancers. BMC Genom. 2010, 11, S5. [Google Scholar] [CrossRef] [PubMed]
- Ruepp, A.; Kowarsch, A.; Schmidl, D.; Buggenthin, F.; Brauner, B.; Dunger, I.; Fobo, G.; Frishman, G.; Montrone, C.; Theis, F.J. PhenomiR: A knowledgebase for microRNA expression in diseases and biological processes. Genome Biol. 2010, 11, R6. [Google Scholar] [CrossRef] [PubMed]
- Xie, B.; Ding, Q.; Han, H.; Wu, D. miRCancer: A microRNA–cancer association database constructed by text mining on literature. Bioinformatics 2013, 29, 638–644. [Google Scholar] [CrossRef]
- Tomczak, K.; Czerwińska, P.; Wiznerowicz, M. The Cancer Genome Atlas (TCGA): An immeasurable source of knowledge. Contemp. Oncol. 2015, 19, A68–A77. [Google Scholar] [CrossRef]
- Chen, L.-T.; Xu, S.-D.; Xu, H.; Zhang, J.-F.; Ning, J.-F.; Wang, S.-F. MicroRNA-378 is associated with non-small cell lung cancer brain metastasis by promoting cell migration, invasion and tumor angiogenesis. Med. Oncol. 2012, 29, 1673–1680. [Google Scholar] [CrossRef] [PubMed]
- Daugaard, I.; Sanders, K.; Idica, A.; Vittayarukskul, K.; Hamdorf, M.; Krog, J.; Chow, R.; Jury, D.; Hansen, L.; Hager, H. miR-151a induces partial EMT by regulating E-cadherin in NSCLC cells. Oncogenesis 2017, 6, e366. [Google Scholar] [CrossRef] [PubMed]
- Hu, L.; Ai, J.; Long, H.; Liu, W.; Wang, X.; Zuo, Y.; Li, Y.; Wu, Q.; Deng, Y. Integrative microRNA and gene profiling data analysis reveals novel biomarkers and mechanisms for lung cancer. Oncotarget 2016, 7, 8441–8454. [Google Scholar] [CrossRef] [PubMed]
- Shen, W.; Liu, J.; Zhao, G.; Fan, M.; Song, G.; Zhang, Y.; Weng, Z.; Zhang, Y. Repression of Toll-like receptor-4 by microRNA-149-3p is associated with smoking-related COPD. Int. J. Chronic Obstr. Pulm. Dis. 2017, 12, 705–715. [Google Scholar] [CrossRef] [PubMed]
- Tang, Y.; Cui, Y.; Li, Z.; Jiao, Z.; Zhang, Y.; He, Y.; Chen, G.; Zhou, Q.; Wang, W.; Zhou, X. Radiation-induced miR-208a increases the proliferation and radioresistance by targeting p21 in human lung cancer cells. J. Exp. Clin. Cancer Res. 2016, 35, 7. [Google Scholar] [CrossRef]
- Bandi, N.; Vassella, E. miR-34a and miR-15a/16 are co-regulated in non-small cell lung cancer and control cell cycle progression in a synergistic and Rb-dependent manner. Mol. Cancer 2011, 10, 55. [Google Scholar] [CrossRef] [PubMed]
- Zhao, M.; Xu, P.; Liu, Z.; Zhen, Y.; Chen, Y.; Liu, Y.; Fu, Q.; Deng, X.; Liang, Z.; Li, Y. Dual roles of miR-374a by modulated c-Jun respectively targets CCND1-inducing PI3K/AKT signal and PTEN-suppressing Wnt/β-catenin signaling in non-small-cell lung cancer. Cell Death Dis. 2018, 9, 78. [Google Scholar] [CrossRef]
- Isobe, T.; Hisamori, S.; Hogan, D.J.; Zabala, M.; Hendrickson, D.G.; Dalerba, P.; Cai, S.; Scheeren, F.; Kuo, A.H.; Sikandar, S.S. miR-142 regulates the tumorigenicity of human breast cancer stem cells through the canonical WNT signaling pathway. Elife 2014, 3, e01977. [Google Scholar] [CrossRef]
- Zhu, Q.-N.; Renaud, H.; Guo, Y. Bioinformatics-based identification of miR-542-5p as a predictive biomarker in breast cancer therapy. Hereditas 2018, 155, 17. [Google Scholar] [CrossRef]
- D’aiuto, F.; Callari, M.; Dugo, M.; Merlino, G.; Musella, V.; Miodini, P.; Paolini, B.; Cappelletti, V.; Daidone, M. miR-30e* is an independent subtype-specific prognostic marker in breast cancer. Br. J. Cancer 2015, 113, 290–298. [Google Scholar] [CrossRef]
- Gui, Z.; Li, S.; Liu, X.; Xu, B.; Xu, J. Oridonin alters the expression profiles of microRNAs in BxPC-3 human pancreatic cancer cells. BMC Complement. Altern. Med. 2015, 15, 117. [Google Scholar] [CrossRef] [PubMed]
- Yu, J.; Li, A.; Hong, S.-M.; Hruban, R.H.; Goggins, M. MicroRNA alterations of pancreatic intraepithelial neoplasias. Clin. Cancer Res. 2012, 18, 981–992. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Zhang, Z.; Lu, Y.; Song, K.; Liu, X.; Xia, F.; Sun, W. Downregulation of ULK 1 by micro RNA-372 inhibits the survival of human pancreatic adenocarcinoma cells. Cancer Sci. 2017, 108, 1811–1819. [Google Scholar] [CrossRef] [PubMed]
- Hao, J.; Zhang, S.; Zhou, Y.; Hu, X.; Shao, C. MicroRNA 483-3p suppresses the expression of DPC4/Smad4 in pancreatic cancer. FEBS Lett. 2011, 585, 207–213. [Google Scholar] [CrossRef] [PubMed]
- Backes, C.; Khaleeq, Q.T.; Meese, E.; Keller, A. miEAA: microRNA enrichment analysis and annotation. Nucleic Acids Res. 2016, 44, W110–W116. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Han, X.; Wan, Y.; Zhang, S.; Zhao, Y.; Fan, R.; Cui, Q.; Zhou, Y. TAM 2.0: Tool for MicroRNA set analysis. Nucleic Acids Res. 2018, 46, W180–W185. [Google Scholar] [CrossRef] [PubMed]
- Fan, Y.; Habib, M.; Xia, J. Xeno-miRNet: A comprehensive database and analytics platform to explore xeno-miRNAs and their potential targets. PeerJ 2018, 6, e5650. [Google Scholar] [CrossRef] [PubMed]
- Park, M.-T.; Lee, S.-J. Cell cycle and cancer. J. Biochem. Mol. Biol. 2003, 36, 60–65. [Google Scholar] [CrossRef] [PubMed]
- Collins, K.; Jacks, T.; Pavletich, N.P. The cell cycle and cancer. Proc. Natl. Acad. Sci. USA 1997, 94, 2776–2778. [Google Scholar] [CrossRef]
- Eymin, B.; Gazzeri, S. Role of cell cycle regulators in lung carcinogenesis. Cell Adhes. Migr. 2010, 4, 114–123. [Google Scholar] [CrossRef]
- Visvader, J.E. Cells of origin in cancer. Nature 2011, 469, 314–322. [Google Scholar] [CrossRef] [PubMed]
- Martin-Belmonte, F.; Perez-Moreno, M. Epithelial cell polarity, stem cells and cancer. Nat. Rev. Cancer 2012, 12, 23–38. [Google Scholar] [CrossRef] [PubMed]
- Deng, X.; Tannehill-Gregg, S.H.; Nadella, M.V.; He, G.; Levine, A.; Cao, Y.; Rosol, T.J. Parathyroid hormone-related protein and ezrin are up-regulated in human lung cancer bone metastases. Clin. Exp. Metastasis 2007, 24, 107–119. [Google Scholar] [CrossRef] [PubMed]
- Domagala-Kulawik, J.; Osinska, I.; Hoser, G. Mechanisms of immune response regulation in lung cancer. Transl. Lung Cancer Res. 2014, 3, 15–22. [Google Scholar] [PubMed]
- Liu, G.; Pei, F.; Yang, F.; Li, L.; Amin, A.; Liu, S.; Buchan, J.; Cho, W. Role of autophagy and apoptosis in non-small-cell lung cancer. Int. J. Mol. Sci. 2017, 18, 367. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Qiu, C.; Tu, J.; Geng, B.; Yang, J.; Jiang, T.; Cui, Q. HMDD v2. 0: A database for experimentally supported human microRNA and disease associations. Nucleic Acids Res. 2013, 42, D1070–D1074. [Google Scholar] [CrossRef] [PubMed]
- Hoehndorf, R.; Schofield, P.N.; Gkoutos, G.V. The role of ontologies in biological and biomedical research: A functional perspective. Brief. Bioinform. 2015, 16, 1069–1080. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.; Wang, J.; Lu, M.; Song, F.; Cui, Q. Inferring the human microRNA functional similarity and functional network based on microRNA-associated diseases. Bioinformatics 2010, 26, 1644–1650. [Google Scholar] [CrossRef] [PubMed]
- Hosoda, K.; Watanabe, M.; Wersing, H.; Körner, E.; Tsujino, H.; Tamura, H.; Fujita, I. A model for learning topographically organized parts-based representations of objects in visual cortex: Topographic nonnegative matrix factorization. Neural Comput. 2009, 21, 2605–2633. [Google Scholar] [CrossRef]
- Zheng, C.-H.; Huang, D.-S.; Zhang, L.; Kong, X.-Z. Tumor clustering using nonnegative matrix factorization with gene selection. IEEE Trans. Inf. Technol. Biomed. 2009, 13, 599–607. [Google Scholar] [CrossRef] [PubMed]
- Facchinei, F.; Kanzow, C.; Sagratella, S. Solving quasi-variational inequalities via their KKT conditions. Math. Program. 2014, 144, 369–412. [Google Scholar] [CrossRef]




| Diseases Name | AUC CNNMDA | GSTRW | DMPred | BNPMDA | Liu’s Method |
|---|---|---|---|---|---|
| Breast neoplasms | 0.991 | 0.822 | 0.939 | 0.906 | 0.896 |
| Hepatocellular carcinoma | 0.978 | 0.770 | 0.899 | 0.784 | 0.846 |
| Renal cell carcinoma | 0.960 | 0.801 | 0.897 | 0.830 | 0.785 |
| Squamous cell carcinoma | 0.932 | 0.821 | 0.894 | 0.793 | 0.897 |
| Colorectal neoplasms | 0.924 | 0.742 | 0.882 | 0.724 | 0.864 |
| Glioblastoma | 0.916 | 0.821 | 0.906 | 0.781 | 0.828 |
| Heart failure | 0.986 | 0.823 | 0.984 | 0.929 | 0.816 |
| Acute myeloid leukemia | 0.969 | 0.817 | 0.894 | 0.784 | 0.924 |
| Lung neoplasms | 0.987 | 0.795 | 0.941 | 0.903 | 0.931 |
| Melanoma | 0.994 | 0.788 | 0.909 | 0.909 | 0.859 |
| Ovarian neoplasms | 0.955 | 0.831 | 0.934 | 0.924 | 0.855 |
| Pancreatic neoplasms | 0.971 | 0.853 | 0.913 | 0.725 | 0.892 |
| Prostatic neoplasms | 0.982 | 0.828 | 0.947 | 0.896 | 0.895 |
| Stomach neoplasms | 0.994 | 0.781 | 0.922 | 0.740 | 0.838 |
| Urinary bladder neoplasms | 0.982 | 0.821 | 0.921 | 0.879 | 0.870 |
| Diseases Name | AUPR CNNMDA | GSTRW | DMPred | BNPMDA | Liu’s Method |
|---|---|---|---|---|---|
| Breast neoplasms | 0.919 | 0.261 | 0.681 | 0.245 | 0.378 |
| Hepatocellular carcinoma | 0.871 | 0.234 | 0.539 | 0.574 | 0.335 |
| Renal cell carcinoma | 0.549 | 0.127 | 0.325 | 0.328 | 0.152 |
| Squamous cell carcinoma | 0.290 | 0.104 | 0.191 | 0.272 | 0.170 |
| Colorectal neoplasms | 0.425 | 0.136 | 0.279 | 0.177 | 0.273 |
| Glioblastoma | 0.277 | 0.142 | 0.270 | 0.452 | 0.166 |
| Heart failure | 0.874 | 0.160 | 0.669 | 0.451 | 0.157 |
| Acute myeloid leukemia | 0.262 | 0.118 | 0.236 | 0.367 | 0.207 |
| Lung neoplasms | 0.706 | 0.140 | 0.481 | 0.480 | 0.343 |
| Melanoma | 0.896 | 0.157 | 0.410 | 0.477 | 0.309 |
| Ovarian neoplasms | 0.543 | 0.152 | 0.453 | 0.386 | 0.239 |
| Pancreatic neoplasms | 0.593 | 0.133 | 0.308 | 0.136 | 0.283 |
| Prostatic neoplasms | 0.673 | 0.150 | 0.414 | 0.175 | 0.231 |
| Stomach neoplasms | 0.881 | 0.207 | 0.503 | 0.306 | 0.303 |
| Urinary bladder neoplasms | 0.694 | 0.134 | 0.331 | 0.292 | 0.229 |
| p-Value between CNNMDA and Another Method | DMPred | GSTRW | BNPMDA | Liu’s Method |
|---|---|---|---|---|
| p-values of ROC curves | 3.3219 × 10−5 | 8.5916 × 10−23 | 5.4483 × 10−10 | 2.0247 × 10−10 |
| p-values of PR curves | 1.4386 × 10−8 | 2.7951 × 10−13 | 1.181 × 10−2 | 2.9012 × 10−8 |
| Rank | miRNA Name | Evidence |
|---|---|---|
| 1 | hsa-mir-106b | dbDEMC, PhenomiR |
| 2 | hsa-mir-15a | Literature [47] |
| 3 | hsa-mir-16 | dbDEMC, PhenomiR, miRCancer |
| 4 | hsa-mir-130a | dbDEMC, PhenomiR |
| 5 | hsa-mir-193b | dbDEMC, PhenomiR, TCGA |
| 6 | hsa-mir-520d | dbDEMC |
| 7 | hsa-mir-429 | dbDEMC, miRCancer |
| 8 | hsa-mir-122 | dbDEMC, PhenomiR, miRCancer |
| 9 | hsa-mir-149 | dbDEMC, PhenomiR |
| 10 | hsa-mir-424 | dbDEMC, PhenomiR |
| 11 | hsa-mir-451a | dbDEMC |
| 12 | hsa-mir-378a | Literature [42] |
| 13 | hsa-mir-708 | dbDEMC |
| 14 | hsa-mir-20b | dbDEMC, PhenomiR, TCGA |
| 15 | hsa-mir-15b | dbDEMC, PhenomiR, miRCancer |
| 16 | hsa-mir-520a | dbDEMC, TCGA |
| 17 | hsa-mir-10a | dbDEMC |
| 18 | hsa-mir-520b | dbDEMC |
| 19 | hsa-mir-625 | dbDEMC |
| 20 | hsa-mir-141 | dbDEMC, PhenomiR, miRCancer |
| 21 | hsa-mir-449a | dbDEMC, PhenomiR, miRCancer |
| 22 | hsa-mir-99a | dbDEMC, PhenomiR, TCGA |
| 23 | hsa-mir-195 | dbDEMC, PhenomiR, miRCancer |
| 24 | hsa-mir-151a | Literature [43] |
| 25 | hsa-mir-296 | Literature [44] |
| 26 | hsa-mir-449b | dbDEMC, PhenomiR, miRCancer |
| 27 | hsa-mir-28 | dbDEMC, PhenomiR |
| 28 | hsa-mir-342 | dbDEMC, PhenomiR |
| 29 | hsa-mir-372 | dbDEMC, PhenomiR, TCGA |
| 30 | hsa-mir-345 | dbDEMC, PhenomiR |
| 31 | hsa-mir-92b | dbDEMC, PhenomiR |
| 32 | hsa-mir-328 | dbDEMC, PhenomiR |
| 33 | hsa-mir-367 | dbDEMC, PhenomiR |
| 34 | hsa-mir-373 | dbDEMC, PhenomiR |
| 35 | hsa-mir-302b | dbDEMC, PhenomiR, miRCancer |
| 36 | hsa-mir-194 | dbDEMC, PhenomiR |
| 37 | hsa-mir-1258 | dbDEMC |
| 38 | hsa-mir-320a | dbDEMC, PhenomiR |
| 39 | hsa-mir-152 | dbDEMC, PhenomiR |
| 40 | hsa-mir-302c | dbDEMC, PhenomiR |
| 41 | hsa-mir-151b | dbDEMC |
| 42 | hsa-mir-204 | dbDEMC, PhenomiR |
| 43 | hsa-mir-23b | dbDEMC, PhenomiR |
| 44 | hsa-mir-129 | dbDEMC, PhenomiR, TCGA |
| 45 | hsa-mir-451b | Literature [45] |
| 46 | hsa-mir-374a | Literature [48] |
| 47 | hsa-mir-211 | dbDEMC, PhenomiR |
| 48 | hsa-mir-208a | Literature [46] |
| 49 | hsa-mir-1254 | dbDEMC, miRCancer |
| 50 | hsa-mir-337 | dbDEMC, PhenomiR, TCGA |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xuan, P.; Sun, H.; Wang, X.; Zhang, T.; Pan, S. Inferring the Disease-Associated miRNAs Based on Network Representation Learning and Convolutional Neural Networks. Int. J. Mol. Sci. 2019, 20, 3648. https://doi.org/10.3390/ijms20153648
Xuan P, Sun H, Wang X, Zhang T, Pan S. Inferring the Disease-Associated miRNAs Based on Network Representation Learning and Convolutional Neural Networks. International Journal of Molecular Sciences. 2019; 20(15):3648. https://doi.org/10.3390/ijms20153648
Chicago/Turabian StyleXuan, Ping, Hao Sun, Xiao Wang, Tiangang Zhang, and Shuxiang Pan. 2019. "Inferring the Disease-Associated miRNAs Based on Network Representation Learning and Convolutional Neural Networks" International Journal of Molecular Sciences 20, no. 15: 3648. https://doi.org/10.3390/ijms20153648
APA StyleXuan, P., Sun, H., Wang, X., Zhang, T., & Pan, S. (2019). Inferring the Disease-Associated miRNAs Based on Network Representation Learning and Convolutional Neural Networks. International Journal of Molecular Sciences, 20(15), 3648. https://doi.org/10.3390/ijms20153648





