Self-Association of Antimicrobial Peptides: A Molecular Dynamics Simulation Study on Bombinin
Abstract
1. Introduction
2. Results
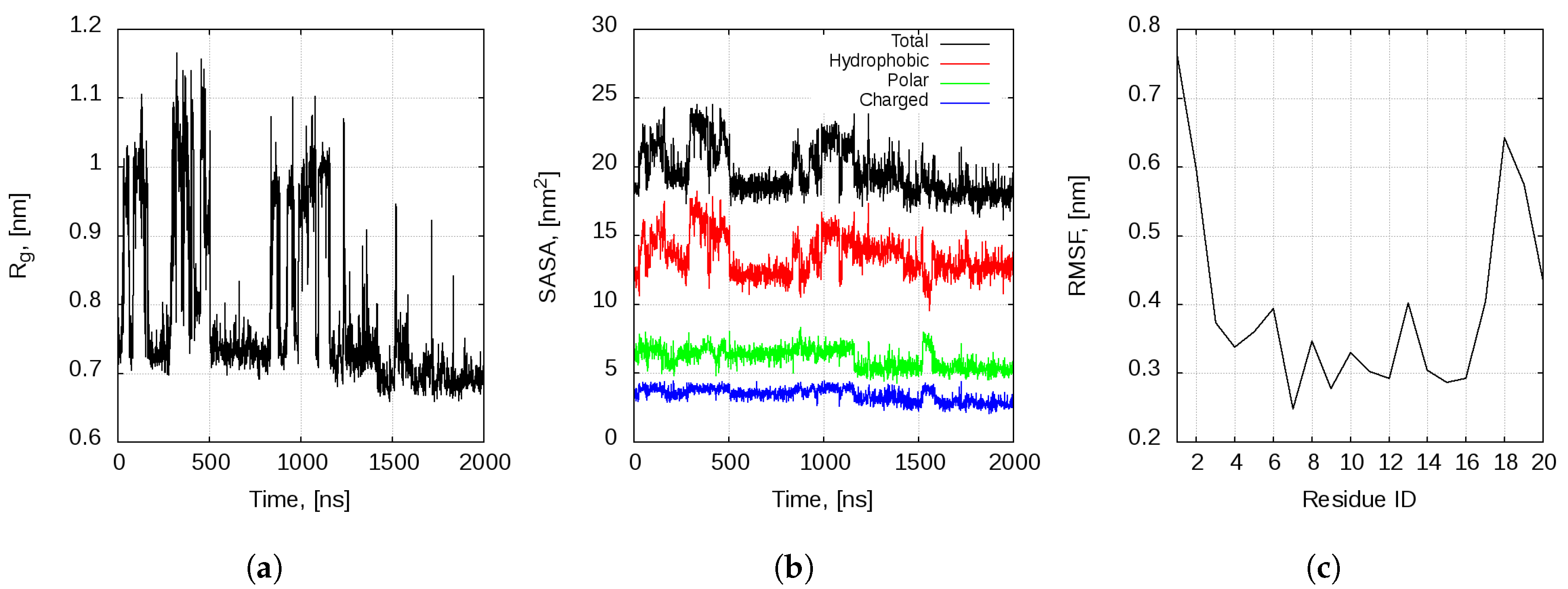
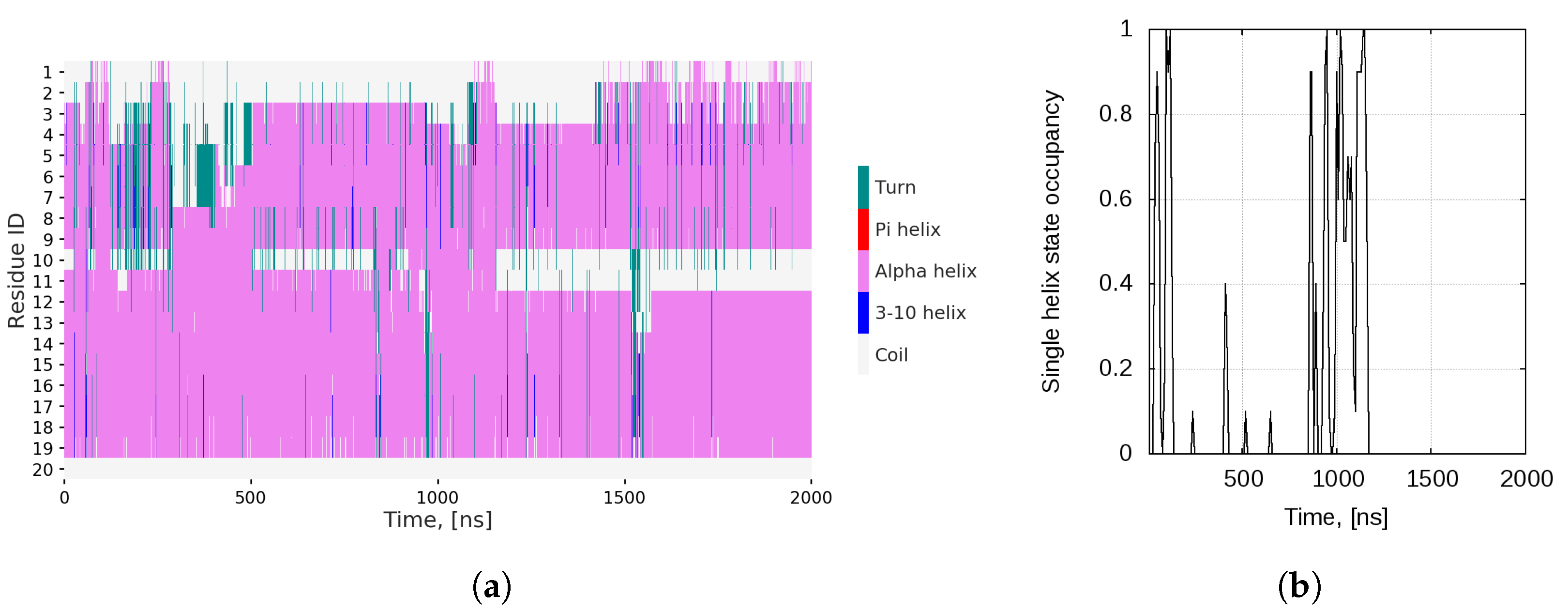
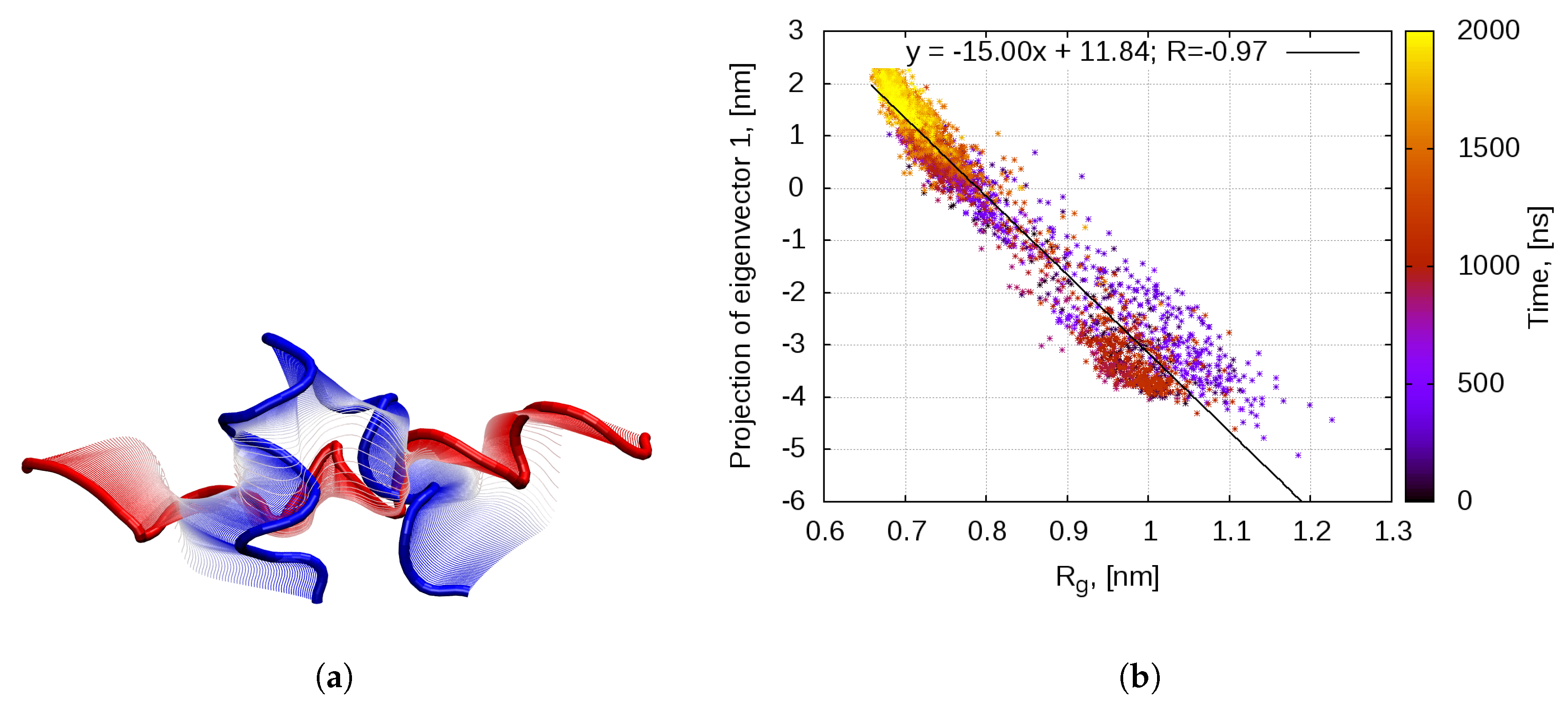
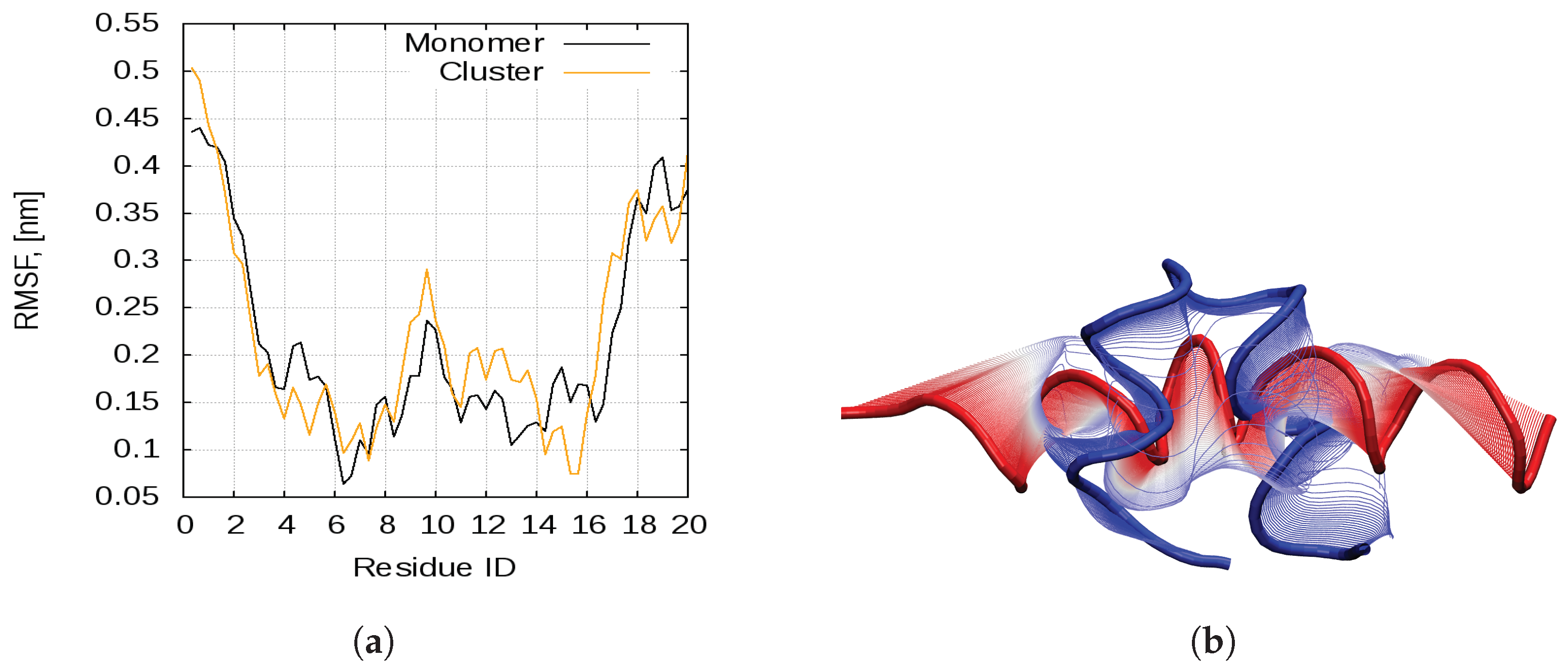
2.1. Dynamics of the Bombinin H2 Monomer in Solution
2.2. Peptide Self-Assembly in Water Solution
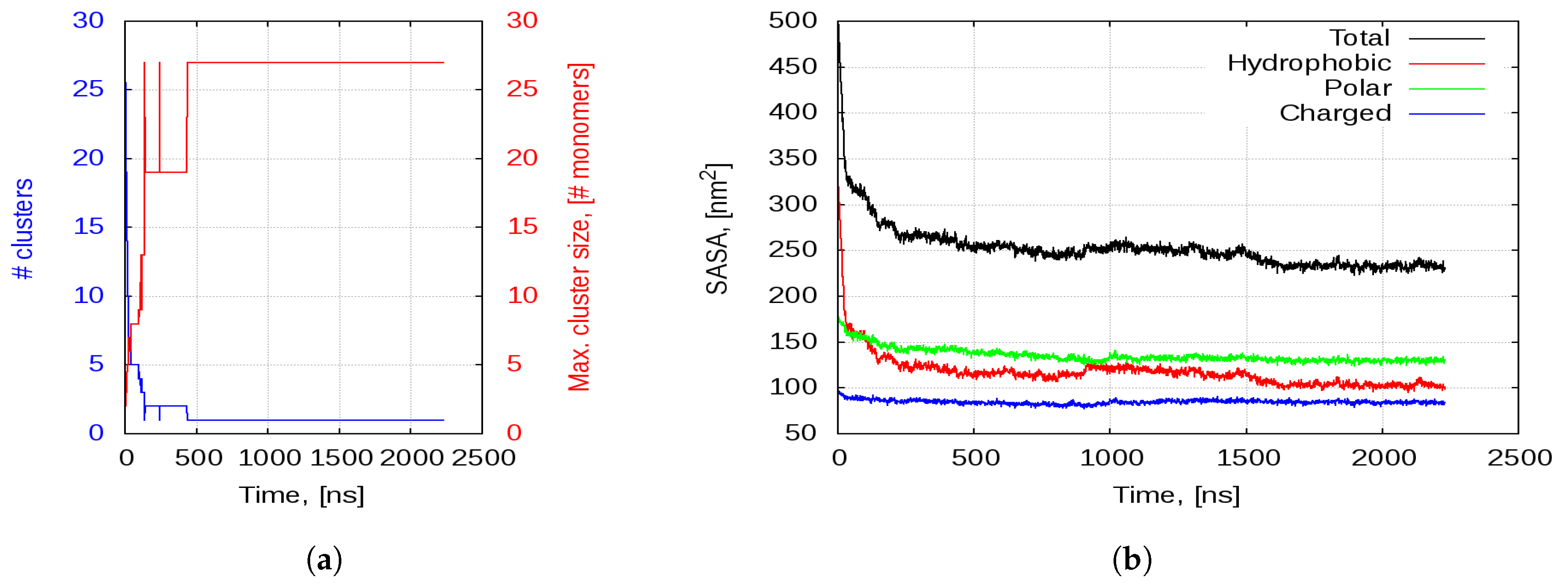
2.2.1. Aggregation
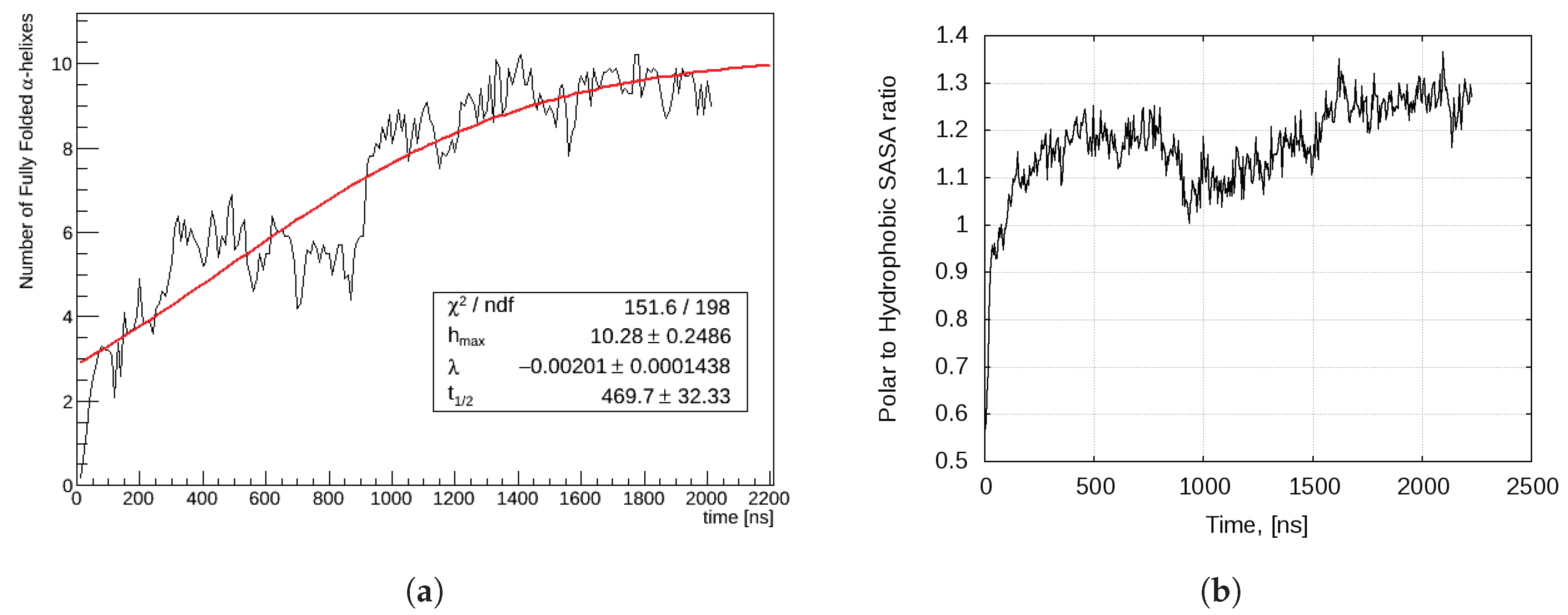
2.2.2. Aggregation-Driven Folding
3. Discussion
4. Materials and Methods
4.1. Input Structures
4.2. MD Simulation Protocol
4.3. Data Analysis
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ageitos, J.; Sánchez-Pérez, A.; Calo-Mata, P.; Villa, T. Antimicrobial peptides (AMPs): Ancient compounds that represent novel weapons in the fight against bacteria. Biochem. Pharmacol. 2017, 133, 117–138. [Google Scholar] [CrossRef]
- Yount, N.; Yeaman, M. Emerging themes and therapeutic prospects for anti-infective peptides. Annu. Rev. Pharmacol. Toxicol. 2012, 52, 337–360. [Google Scholar] [CrossRef]
- Hancock, R.E.W.; Sahl, H.G. Antimicrobial and host-defense peptides as new anti-infective therapeutic strategies. Nat. Biotechnol. 2006, 24, 1551–1557. [Google Scholar] [CrossRef]
- Boman, H.G. Peptide Antibiotics and Their Role in Innate Immunity. Annu. Rev. Immunol. 1995, 13, 61–92. [Google Scholar] [CrossRef]
- Fjell, C.D.; Hiss, J.A.; Hancock, R.E.W.; Schneider, G. Designing antimicrobial peptides: form follows function. Nat. Rev. Drug Discovery 2012, 11, 37–51. [Google Scholar] [CrossRef]
- Kang, H.K.; Kim, C.; Seo, C.H.; Park, Y. The therapeutic applications of antimicrobial peptides (AMPs): A patent review. J. Microbiol. 2017, 55, 1–12. [Google Scholar] [CrossRef]
- Stöckl, M.; Fischer, P.; Wanker, E.; Herrmann, A. Alpha-synuclein selectively binds to anionic phospholipids embedded in liquid-disordered domains. J. Mol. Biol. 2008, 375, 1394–1404. [Google Scholar] [CrossRef]
- Sato, H.; Feix, J.B. Peptide–membrane interactions and mechanisms of membrane destruction by amphipathic α-helical antimicrobial peptides. Biochim. Biophys. Acta (BBA) Biomembr. 2006, 1758, 1245–1256. [Google Scholar] [CrossRef] [PubMed]
- Bhargava, K.; Feix, J.B. Membrane binding, structure, and localization of cecropin-mellitin hybrid peptides: A site-directed spin-labeling study. Biophys. J. 2004, 86, 329–336. [Google Scholar] [CrossRef]
- Manzini, M.C.; Perez, K.R.; Riske, K.A.; Bozelli, J.C.; Santos, T.L.; da Silva, M.A.; Saraiva, G.K.; Politi, M.J.; Valente, A.P.; Almeida, F.C.; et al. Peptide:lipid ratio and membrane surface charge determine the mechanism of action of the antimicrobial peptide BP100. Conformational and functional studies. Biochim. Biophys. Acta (BBA) Biomembr. 2014, 1838, 1985–1999. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Schlamadinger, D.E.; Kim, J.E.; McCammon, J.A. Comparative molecular dynamics simulations of the antimicrobial peptide CM15 in model lipid bilayers. Biochim. Biophys. Acta (BBA) Biomembr. 2012, 1818, 1402–1409. [Google Scholar] [CrossRef] [PubMed]
- Domingues, T.M.; Perez, K.R.; Miranda, A.; Riske, K.A. Comparative study of the mechanism of action of the antimicrobial peptide gomesin and its linear analogue: The role of the β-hairpin structure. Biochim. Biophys. Acta (BBA) Biomembr. 2015, 1848, 2414–2421. [Google Scholar] [CrossRef] [PubMed]
- Perrin, B.; Scott, J.; Pastor, R.W. Simulations of Membrane-Disrupting Peptides I: Alamethicin Pore Stability and Spontaneous Insertion. Biophys. J. 2016, 111, 1248–1257. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.H.; Wiedman, G.; Khan, A.; Ulmschneider, M.B. Absorption and folding of melittin onto lipid bilayer membranes via unbiased atomic detail microsecond molecular dynamics simulation. Biochim. Biophys. Acta (BBA) Biomembr. 2014, 1838, 2243–2249. [Google Scholar] [CrossRef]
- Leontiadou, H.; Mark, A.E.; Marrink, S.J. Antimicrobial Peptides in Action. J. Am. Chem. Soc. 2006, 128, 12156–12161. [Google Scholar] [CrossRef]
- Huang, H.W. Molecular mechanism of antimicrobial peptides: The origin of cooperativity. Biochim. Biophys. Acta (BBA) Biomembr. 2006, 1758, 1292–1302. [Google Scholar] [CrossRef]
- Almeida, P.F.; Pokorny, A. Mechanisms of Antimicrobial, Cytolytic, and Cell-Penetrating Peptides: From Kinetics to Thermodynamics. Biochemistry 2009, 48, 8083–8093. [Google Scholar] [CrossRef]
- Wadhwani, P.; Strandberg, E.; Heidenreich, N.; Bürck, J.; Fanghänel, S.; Ulrich, A.S. Self-Assembly of Flexible β-Strands into Immobile Amyloid-Like β-Sheets in Membranes As Revealed by Solid-State 19F NMR. J. Am. Chem. Soc. 2012, 134, 6512–6515. [Google Scholar] [CrossRef]
- Lu, N.; Yang, K.; Yuan, B.; Ma, Y. Molecular Response and Cooperative Behavior during the Interactions of Melittin with a Membrane: Dissipative Quartz Crystal Microbalance Experiments and Simulations. J. Phys. Chem. B 2012, 116, 9432–9438. [Google Scholar] [CrossRef]
- Chen, C.; Pan, F.; Zhang, S.; Hu, J.; Cao, M.; Wang, J.; Xu, H.; Zhao, X.; Lu, J.R. Antibacterial Activities of Short Designer Peptides: A Link between Propensity for Nanostructuring and Capacity for Membrane Destabilization. Biomacromolecules 2010, 11, 402–411. [Google Scholar] [CrossRef]
- Buffy, J.J.; Waring, A.J.; Lehrer, R.I.; Hong, M. Immobilization and Aggregation of the Antimicrobial Peptide Protegrin-1 in Lipid Bilayers Investigated by Solid-State NMR. Biochemistry 2003, 42, 13725–13734. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Sani, M.A.; Jamasbi, E.; Otvos, L.; Hossain, M.A.; Wade, J.D.; Separovic, F. Membrane interactions of proline-rich antimicrobial peptide, Chex1-Arg20, multimers. Biochim. Biophys. Acta (BBA) Biomembr. 2016, 1858, 1236–1243. [Google Scholar] [CrossRef] [PubMed]
- Pino-Angeles, A.; Lazaridis, T. Effects of Peptide Charge, Orientation, and Concentration on Melittin Transmembrane Pores. Biophys. J. 2018, 114, 2865–2874. [Google Scholar] [CrossRef] [PubMed]
- Zou, R.; Zhu, X.; Tu, Y.; Wu, J.; Landry, M.P. Activity of Antimicrobial Peptide Aggregates Decreases with Increased Cell Membrane Embedding Free Energy Cost. Biochemistry 2018, 57, 2606–2610. [Google Scholar] [CrossRef]
- Pazderkova, M.; Malon, P.; Zima, V.; Hofbauerova, K.; Kocisova, E.; Pazderka, T.; Crovsky, V.; Bednarova, L. Interaction of Halictine-Related Antimicrobial Peptides with Membrane Models. Int. J. Mol. Sci. 2019, 20, 631. [Google Scholar] [CrossRef] [PubMed]
- Marinova, R.; Petkov, P.; Ilieva, N.; Lilkova, E.; Litov, L. Molecular Dynamics Study of the Solution Behaviour of Antimicrobial Peptide Indolicidin. Stud. Comput. Intell. 2019, 793, 257–265. [Google Scholar]
- Petkov, P.; Marinova, R.; Kochev, V.; Ilieva, N.; Lilkova, E.; Litov, L. Computational Study of Solution Behavior of Magainin 2 Monomers. J. Biomol. Struct. Dyn. 2019, 375, 1231–1240. [Google Scholar] [CrossRef]
- Mangoni, M.L.; Papo, N.; Saugar, J.M.; Barra, D.; Shai, Y.; Simmaco, M.; Rivas, L. Effect of Natural l- to d-Amino Acid Conversion on the Organization, Membrane Binding, and Biological Function of the Antimicrobial Peptides Bombinins H. Biochemistry 2006, 45, 4266–4276. [Google Scholar] [CrossRef]
- Zangger, K.; Gößler, R.; Khatai, L.; Lohner, K.; Jilek, A. Structures of the glycine-rich diastereomeric peptides bombinin H2 and H4. Toxicon 2008, 52, 246–254. [Google Scholar] [CrossRef]
- Kuroda, Y.; Suenaga, A.; Sato, Y.; Kosuda, S.; Taiji, M. All-atom molecular dynamics analysis of multi-peptide systems reproduces peptide solubility in line with experimental observations. Sci. Rep. 2016, 6, 19479. [Google Scholar] [CrossRef]
- Vanhoye, D.; Bruston, F.; Amri, S.E.; Ladram, A.; Amiche, M.; Nicolas, P. Membrane Association, Electrostatic Sequestration, and Cytotoxicity of Gly-Leu-Rich Peptide Orthologs with Differing Functions. Biochemistry 2004, 43, 8391–8409. [Google Scholar] [CrossRef] [PubMed]
- Park, Y.; Lee, D.G.; Jang, S.H.; Woo, E.R.; Jeong, H.G.; Choi, C.H.; Hahm, K.S. A Leu–Lys-rich antimicrobial peptide: Activity and mechanism. Biochim. Biophys. Acta 2003, 1645, 172–182. [Google Scholar] [CrossRef]
- Chen, F.Y.; Lee, M.T.; Huang, H.W. Sigmoidal Concentration Dependence of Antimicrobial Peptide Activity: A Case Study of Alamethicin. Biophys. J. 2002, 82, 908–914. [Google Scholar] [CrossRef]
- Sengupta, D.; Leontiadou, H.; Mark, A.E.; Marrink, S.J. Toroidal pores formed by antimicrobial peptides show significant disorder. Biochim. Biophys. Acta 2008, 1778, 2308–2317. [Google Scholar] [CrossRef] [PubMed]
- Laadhari, M.; Arnold, A.A.; Gravel, A.E.; Separovic, F.; Marcotte, I. Interaction of the antimicrobial peptides caerin 1.1 and aurein 1.2 with intact bacteria by 2H solid-state NMR. Biochim. Biophys. Acta 2016, 1858, 2959–2964. [Google Scholar] [CrossRef]
- Abraham, M.J.; Murtola, T.; Schulz, R.; Páll, S.; Smith, J.C.; Hess, B.; Lindahl, E. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 2015, 1–2, 19–25. [Google Scholar] [CrossRef]
- Mackerell, A.D., Jr.; Feig, M.; Brooks, C.L., III. Extending the treatment of backbone energetics in protein force fields: Limitations of gas-phase quantum mechanics in reproducing protein conformational distributions in molecular dynamics simulations. J. Comput. Chem. 2004, 25, 1400–1415. [Google Scholar] [CrossRef]
- MacKerell, A.D.; Bashford, D.; Bellott, M.; Dunbrack, R.L.; Evanseck, J.D.; Field, M.J.; Fischer, S.; Gao, J.; Guo, H.; Ha, S.; et al. All-Atom Empirical Potential for Molecular Modeling and Dynamics Studies of Proteins. J. Phys. Chem. B 1998, 102, 3586–3616. [Google Scholar] [CrossRef]
- Bussi, G.; Donadio, D.; Parrinello, M. Canonical sampling through velocity rescaling. J. Chem. Phys. 2007, 126, 014101. [Google Scholar] [CrossRef]
- Parrinello, M.; Rahman, A. Crystal Structure and Pair Potentials: A Molecular-Dynamics Study. Phys. Rev. Lett. 1980, 45, 1196. [Google Scholar] [CrossRef]
- Parrinello, M.; Rahman, A. Polymorphic transitions in single crystals: A new molecular dynamics method. J. Appl. Phys. 1981, 52, 7182. [Google Scholar] [CrossRef]
- Hockney, R.; Goel, S.; Eastwood, J. Quiet high-resolution computer models of a plasma. J. Comput. Phys. 1974, 14, 148–158. [Google Scholar] [CrossRef]
- Hess, B. P-LINCS: A Parallel Linear Constraint Solver for Molecular Simulation. J. Chem. Theory Comput. 2008, 4, 116–122. [Google Scholar] [CrossRef] [PubMed]
- Essmann, U.; Perera, L.; Berkowitz, M.L.; Darden, T.; Lee, H.; Pedersen, L.G. A smooth particle mesh Ewald method. J. Chem. Phys. 1995, 103, 8577–8593. [Google Scholar] [CrossRef]
- Frishman, D.; Argos, P. Knowledge-based secondary structure assignment. Proteins Struct. Funct. Genet. 1995, 23, 566–579. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD—Visual Molecular Dynamics. J. Mol. Graphics 1996, 14, 33–38. [Google Scholar] [CrossRef]

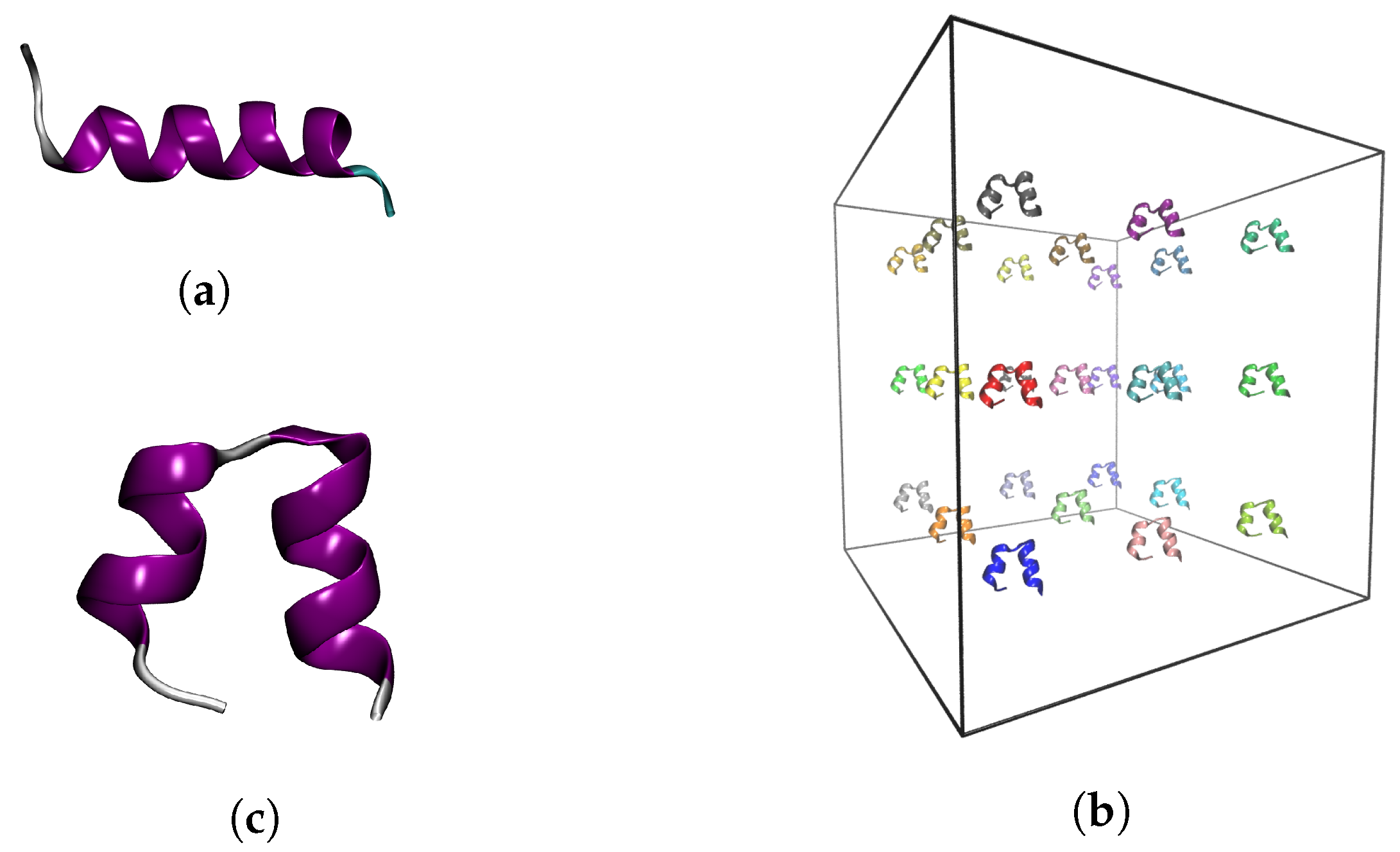
| Chain ID | Time [ns] | Neighbours | Aggregate |
|---|---|---|---|
| A | 903 | E, F, M, W, Y | 27-mer |
| B | 917 | G, H, K, N, P, S, Z | 27-mer |
| D | 931 | H, O, P | 27-mer |
| E | 735 | A, K, M, R, S, T | 27-mer |
| F | 404 | A, C, E, I, M, R, U, W, Y | 19-mer |
| J | 1516 | N, U, V, a | 27-mer |
| V | 25 | a | Dimer |
| W | 70 | A, F, Y | Tetramer |
| a | 22 | V | Dimer |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Petkov, P.; Lilkova, E.; Ilieva, N.; Litov, L. Self-Association of Antimicrobial Peptides: A Molecular Dynamics Simulation Study on Bombinin. Int. J. Mol. Sci. 2019, 20, 5450. https://doi.org/10.3390/ijms20215450
Petkov P, Lilkova E, Ilieva N, Litov L. Self-Association of Antimicrobial Peptides: A Molecular Dynamics Simulation Study on Bombinin. International Journal of Molecular Sciences. 2019; 20(21):5450. https://doi.org/10.3390/ijms20215450
Chicago/Turabian StylePetkov, Peicho, Elena Lilkova, Nevena Ilieva, and Leandar Litov. 2019. "Self-Association of Antimicrobial Peptides: A Molecular Dynamics Simulation Study on Bombinin" International Journal of Molecular Sciences 20, no. 21: 5450. https://doi.org/10.3390/ijms20215450
APA StylePetkov, P., Lilkova, E., Ilieva, N., & Litov, L. (2019). Self-Association of Antimicrobial Peptides: A Molecular Dynamics Simulation Study on Bombinin. International Journal of Molecular Sciences, 20(21), 5450. https://doi.org/10.3390/ijms20215450







