Next Article in Journal
Depression and Sleep
Next Article in Special Issue
Modulation of Disordered Proteins with a Focus on Neurodegenerative Diseases and Other Pathologies
Previous Article in Journal
Homeostatic Model Assessment of Insulin Resistance for Predicting the Recurrence of Hepatocellular Carcinoma after Curative Treatment
Previous Article in Special Issue
The Effect of FG-Nup Phosphorylation on NPC Selectivity: A One-Bead-Per-Amino-Acid Molecular Dynamics Study
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
IJMS
Volume 20
Issue 3
10.3390/ijms20030606
ijms-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Review

Modeling of Disordered Protein Structures Using Monte Carlo Simulations and Knowledge-Based Statistical Force Fields

by
Maciej Pawel Ciemny
1,2,
Aleksandra Elzbieta Badaczewska-Dawid
1,
Monika Pikuzinska
1,
Andrzej Kolinski
1 and
Sebastian Kmiecik
1,*
1
Faculty of Chemistry, Biological and Chemical Research Center, University of Warsaw, Pasteura 1, 02-093 Warsaw, Poland
2
Faculty of Physics, University of Warsaw, Pasteura 5, 02-093 Warsaw, Poland
*
Author to whom correspondence should be addressed.
Int. J. Mol. Sci. 2019, 20(3), 606; https://doi.org/10.3390/ijms20030606
Submission received: 13 December 2018 / Revised: 23 January 2019 / Accepted: 29 January 2019 / Published: 31 January 2019
(This article belongs to the Special Issue Functionally Relevant Macromolecular Interactions of Disordered Proteins)
Browse Figures
Versions Notes

Abstract

:
The description of protein disordered states is important for understanding protein folding mechanisms and their functions. In this short review, we briefly describe a simulation approach to modeling protein interactions, which involve disordered peptide partners or intrinsically disordered protein regions, and unfolded states of globular proteins. It is based on the CABS coarse-grained protein model that uses a Monte Carlo (MC) sampling scheme and a knowledge-based statistical force field. We review several case studies showing that description of protein disordered states resulting from CABS simulations is consistent with experimental data. The case studies comprise investigations of protein–peptide binding and protein folding processes. The CABS model has been recently made available as the simulation engine of multiscale modeling tools enabling studies of protein–peptide docking and protein flexibility. Those tools offer customization of the modeling process, driving the conformational search using distance restraints, reconstruction of selected models to all-atom resolution, and simulation of large protein systems in a reasonable computational time. Therefore, CABS can be combined in integrative modeling pipelines incorporating experimental data and other modeling tools of various resolution.

Graphical Abstract

1. Introduction

There is a growing body of evidence that some proteins act in multiple structural states [1]. It has been demonstrated that the ability of these proteins to switch between distinct structural states may be crucial for their function and regulation [1]. Additionally, a number of key biological functions have been proven to be performed by disordered or partially unstructured proteins [2]. Some proteins fold and obtain their structure only upon binding to their partners, while others form so called “fuzzy complexes” in which both proteins retain a certain degree of disorder [3]. These discoveries modified the core biochemistry principle of “structure determines function”. As for now, a consensus has been reached that protein function may be a result of an interplay between protein structure and its dynamics [4,5].
Internal protein motions may be studied both experimentally and with computational methods [6,7]. For example, nuclear magnetic resonance (NMR) spectroscopy is one of the richest sources of information on protein structure and dynamics, especially when accompanied with assisting methods that enhance resolution or provide an additional insight into the dynamics of structures [8]. This approach, however, results in an averaged image of the structural ensemble.
A variety of computational techniques have been developed to assist these challenging experimental studies [7,9]. In the last decades, molecular modeling was dominated by structure-based models or Go-like models (approaches that are biased toward known folded conformations [10,11]). These indeed lead to significant speedup of simulations but may result for example in an unrealistic picture of protein folding, which in reality may also depend on non-native interactions [12,13,14].
Recent works show that methods combining experimental data and computational approaches may produce the most promising pictures of protein equilibrium dynamics [15,16]. However, the development of these methods poses a number of challenges—both in terms of the validity of the approach and its computationally efficient implementation [17].
Molecular dynamics (MD) has been so far the most widespread computational method for the investigation of protein motions [18]. However, standard all-atom MD implementations are limited to sub-microsecond timescales and may suffer from limited sampling despite recent significant advances in code optimization and hardware [19]. To overcome this problem various MD extensions have been proposed. These extensions include for example replica-exchange MD, meta-dynamics, Markov state models and simulated annealing algorithms [6,20,21,22,23].
A number of non-MD sampling methods have also been developed to provide a comprehensive image of protein dynamics using limited computational resources. Of these, Monte Carlo (MC) is perhaps the most commonly used and generally applicable sampling method [11]. Monte Carlo randomly generates conformations and uses an energy-based acceptance criterion that promotes pseudo-trajectory convergence to an energetic minimum. On the expense of losing a direct image of the timescales or kinetics of the ensemble, MC manages to overcome some of the major limitations of MD [24].
Aside from the sampling method, a further extension of effective timescales is possible by using a simplified representation of protein structures to reduce the number of a system’s degrees of freedom. The accuracy of the available coarse-grained (CG) models may vary from detailed, almost atomistic representations (Primo [25], Rosetta [26]), medium resolution models (in which a single amino acid is represented by three to five beads: UNRES [27], CABS [28], AWSEM [29], MARTINI [30], PaLaCe [31]), and Scorpion [32]) to significantly simplified models like SURPASS [33,34]. Applications and implementations of these and other CG models are described in detail in a recent review [11].
In addition to the representation and sampling method, the choice of the force field to perform the simulation determines the success of modeling. Traditionally, force fields are divided into two main groups: physics-based, which involve (usually pairwise) interaction terms [35], and those employing a statistical approach; however, most of the successful approaches are usually a mixture of the two. A statistical force field is constructed using the probability of a chosen observable (or a set of observables) in a given ensemble of structures [36]. Early attempts focused on straightforward pairwise contacts [37]; however, with further development, more complex observables were analyzed. This resulted in a generation of knowledge-based force fields, or scores, for various representations, coarse-grained and all-atom: CABS [28], Rosetta [38], DOPE [39], GOAP [40], QUARK [41], Bcl::Score [42] or BACH [36]. Newly developed approaches go a step further and improve the results by combining these methods with experimental data [43,44]. An example of such approach is RosettaEPR [45], which includes distance data from site-directed spin labeling electron paramagnetic resonance experiments. It is generally agreed that statistical force fields frequently allow more accurate scoring than physics-based potentials [11]. The combination of knowledge-based force fields or scores with effective sampling schemes seems to be a promising approach to a number of problems [11], such as protein structure prediction [43,44,46,47], investigation of protein interactions [48] or studies of protein dynamics [17,49,50,51].
This review briefly describes one of these approaches: an MC-based and knowledge-based interaction scheme for modeling protein–peptide interactions and unfolded states of globular proteins using the CABS coarse-grained protein model. Firstly, the main features of the CABS method will be described, with a focus on their applicability for modeling disordered or unfolded proteins or their fragments. Subsequently, representative case studies will be discussed to provide detailed insights into the modeling results obtained for systems characterized by a varying level of disorder.

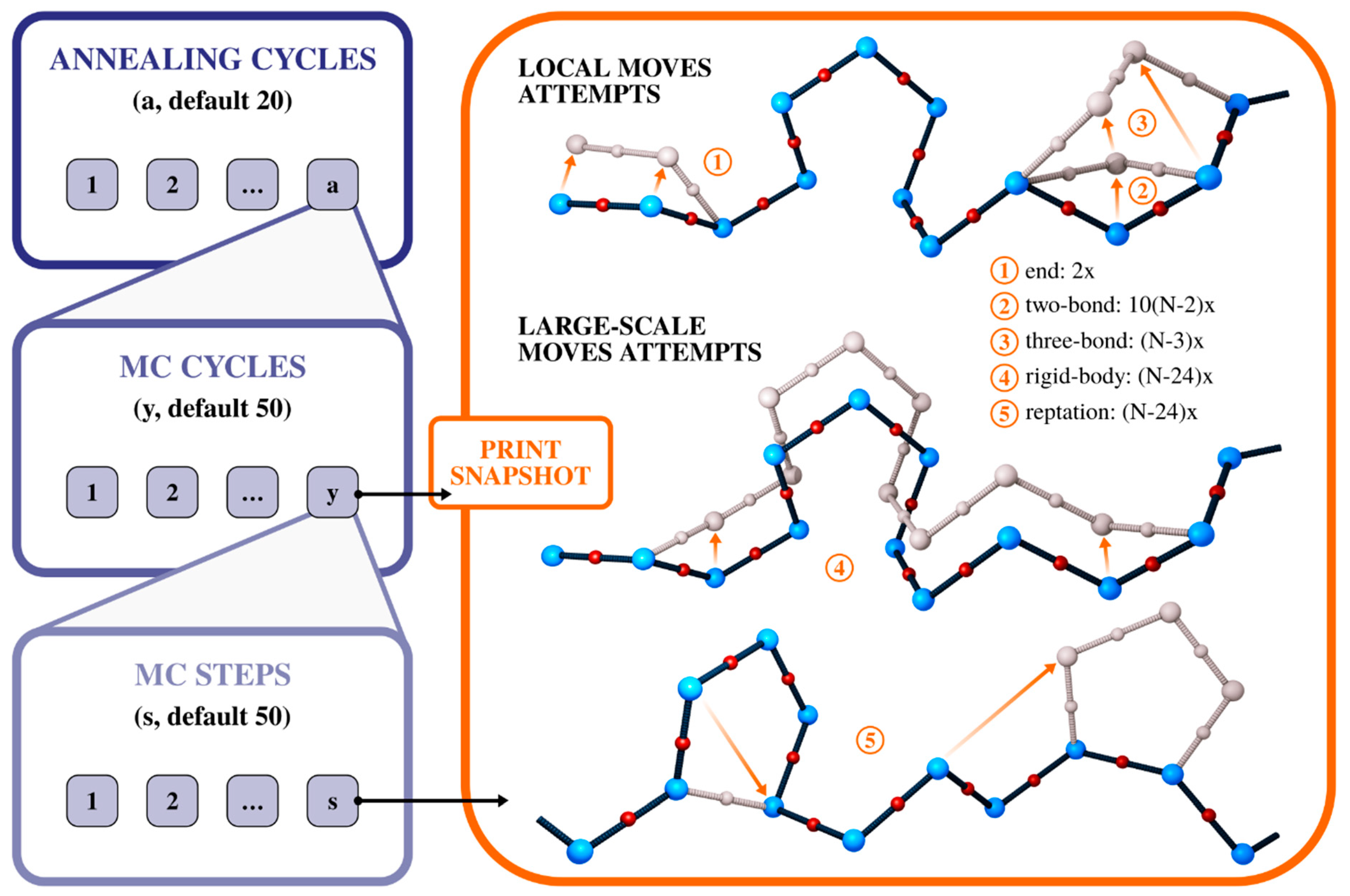
2. CABS Dynamics and Interaction Model

Since its development, the CABS model (C-alpha, C-beta and Side chain model) has been applied to a variety of modeling problems, such as protein folding mechanisms [49,50,52,53,54,55,56,57], protein structure prediction [58,59,60,61], protein–peptide docking including large-scale conformational flexibility [62,63,64,65,66,67,68] and simulations of near-native fluctuations of globular proteins [69,70,71,72,73]. When combined with careful bioinformatics selection of the generated models, CABS proved to be one of the two most accurate structure prediction tools evaluated in the CASP (Critical Assessment of protein Structure Prediction) experiment [60]. The CABS model uses up to four atoms or pseudo-atoms per residue (see the description below), but outputs protein systems in C-alpha representation only. Therefore, for practical applications, the obtained models need to be reconstructed to all-atom representation. In various multiscale modeling tools discussed below, CABS has been integrated with the MODELLER-based reconstruction procedure [74]. Other reconstruction scenarios are also possible to ensure the best possible quality of local protein structure. This can be realized by combination of different tools for protein backbone reconstruction from the C-alpha trace and side chain reconstruction, like BBQ [75] or SCWRL [76] for example, and optionally further refinement [77].
In this review, we discuss the applicability of the CABS CG model and its knowledge-based statistical force field [28] to the modeling of disordered or unfolded protein states. In the CABS model the polypeptide chain representation is reduced to up to four unified atoms per residue (see Figure 1). These interaction centers represent lattice-confined C-alpha atoms, C-beta atoms, the united side chain pseudo-atom, and additionally, pseudo-atoms representing geometrical centers of peptide bonds needed to define the hydrogen pseudo-bond. An example of a polypeptide chain in CABS representation is presented in Figure 1b. Even though the restriction of the C-alpha trace to the underlying low spacing (0.61 Å [28]) cubic lattice may appear to be a drastic simplification, it is not. Allowing small fluctuations of the C-alpha, C-alpha distance enables hundreds of possible orientations of this pseudo bond, and thereby the resulting model chains do not show any noticeable directional biases. Furthermore, the averaged resolution of the C-alpha traces is acceptable and below 0.5 Å [28]. Additionally, the lattice representation enables pre-calculation of local moves and corresponding changes of interactions, leading to a few times faster simulations in comparison with otherwise equivalent continuous space CG models [11].
The CABS model uses a knowledge-based statistical force field that consists of generic, sequence-independent interaction terms that favor protein-like conformations, and sequence-dependent interaction terms that determine some structural details [11,28,78]. The generic force field terms are derived from general features of polypeptide chains that result in protein-like behavior of the model chains. They account for properties of protein chains such as local stiffness, their biases toward secondary structures and packing compactness. The residue–residue interaction terms are derived from contact geometry statistics derived from folded globular proteins (illustrated in Figure 2a). Nevertheless, the local packing regularities in unfolded states appear to be very similar to that observed in native structures [11,28,33]. Thereby, CABS simulations provided correct pictures of protein folding [49,52,53,54,55,56,60] and flexibility of globular proteins [70,71].
The resulting force field takes a form of a precomputed matrix of contact pseudo-energies, presented schematically in Figure 2b. Additionally, to allow successful modeling of membrane proteins the CABS force field can be extended by introducing effective dielectric constant terms [79].
The main difference between CABS and other statistical force fields used in CG models of similar resolution [11] is the context and orientation dependence of side chain interaction pseudo-energy that encodes characteristic patterns observed in globular proteins. For instance, the oppositely charged side chains in single globules mostly contact in an almost parallel fashion (usually on the surface of a globule), while the antiparallel contacts (usually in the buried regions of the protein globule) are very rare. Therefore, in the context dependent force field these antiparallel contacts of oppositely charged residues are treated as repulsive. This way, the CABS force field implicitly incorporates information on the complicated interaction patterns with the solvent (via contact statistics) and its entropic contribution to system thermodynamics [11,28].
Using the mean-force force field derived from folded proteins to simulations of less-structured systems raises justified questions about the validity of this approach in studies of the disordered protein regions. The folding events observed in simulations performed using the CABS force field are consistent with both the experimental data and all-atom MD simulations [49,52,80,81]. Thus, it is hypothesized that unstructured (unfolded, partially unfolded or intrinsically disordered) proteins to a significant extent share similar stabilizing interaction patterns with the patterns observed for their well-structured counterparts [82,83].
The CABS method uses the MC asymmetric Metropolis sampling scheme that governs a set of local motions as well as multi-residue, small distance moves of the C-alpha atoms (see Figure 3). The method uses a replica exchange algorithm with simulated annealing to enhance the sampling of conformational states. The simulation is organized as a set of nested loops, in which the s number of MC steps are organized into the y number of MC cycles, and these in the a number of annealing cycles. Each of the MC steps consists of a per-set number of attempts to perform each of the five standard precomputed moves. The available motions and the details of implementation of the sampling scheme are presented in Figure 3.
The combination of the key features of CABS—its representation, force field and the scale of the movements used in the MC scheme—makes it suitable for the investigation of protein pseudo-dynamics. As mentioned above, the fine-grained lattice improves sampling efficiency, achieving effective timescales of milliseconds. As compared with MD, this is a considerably broader time range (in the study of flexibility of folded proteins [71] the CABS dynamics was estimated to be around 6 × 103 cheaper in terms of computational cost than the classical MD). The chosen micro-motions allow (via accumulation over simulation steps) cooperative, large-scale motions. The ensemble of structures produced by the CABS method resembles a dynamic ensemble averaged over the effective timescale. Due to the nature of the method, the picture of local dynamics is distorted (on the level of local moves); however, it may be argued (based on the works mentioned above that compared our simulations with experimental data) that the long-time pseudo-dynamics recovers the realistic picture of protein motions averaged over time.
The timescale of the CABS simulations is not a priori defined and depends on the CABS simulation temperature, due to hidden entropic contributions in the force field, accounting for implicit solvent effects and multi-body interactions encoded in the statistical force field. Nevertheless, the effective timescale of MC dynamics can be approximately identified by comparison with MD trajectories from sufficiently long simulations. This comparison was thoroughly discussed previously, and the results were compared to MD results [69] and NMR ensembles [71].
The CABS model is presently used as a simulation engine of a few multiscale modeling tools that merge CABS with models reconstruction to all-atom resolution. Those include the CABS-dock method for flexible protein-peptide docking (available as a web server [62] at http://biocomp.chem.uw.edu.pl/CABSdock and a standalone application [84] at https://bitbucket.org/lcbio/cabsdock/) (accessed on 30 January 2019). In comparison to other protein–peptide docking tools, reviewed recently [85], CABS-dock offers a unique opportunity for modeling large-scale rearrangements of protein receptor structure during on-the-fly docking of fully flexible peptides. Another CABS-based tool, CABS-flex, enables fast simulations of protein flexibility (available as a web server [73] at http://biocomp.chem.uw.edu.pl/CABSflex and a standalone application [72] at https://bitbucket.org/lcbio/cabsflex/, accessed on 30 January 2019). This approach has been also incorporated as the module in the Aggrescan3D method for prediction of protein aggregation properties (available as a web server [86] at http://biocomp.chem.uw.edu.pl/A3D and a standalone application at https://bitbucket.org/lcbio/aggrescan3D, accessed on 30 January 2019). By using CABS-flex predictions, Aggrescan3D enables predicting the impact of protein conformational fluctuations on aggregation properties. Finally, the CABS model is used in the CABS-fold method for protein structure prediction: in the de novo fashion (from an amino acid sequence only), guided by user-provided templates or user-provided distance restraints (available as a web server [58] at http://biocomp.chem.uw.edu.pl/CABSfold/, accessed on 30 January 2019). The access to CABS-based tools, together with the tools description, is also available from websites of the laboratories: http://biocomp.chem.uw.edu.pl/ and http://lcbio.pl/ (accessed on 30 January 2019).

3. CABS Applications to Simulation of Disordered or Unfolded Proteins

In this section, we review CABS applications to simulations of protein–peptide binding (Section 3.1) and folding of globular proteins (Section 3.2). We briefly discuss modeling results for the binding of three protein–peptide systems and protein folding of one protein system. Figure 4 shows native conformations of these systems determined by X-ray crystallography or NMR. In the figure, they are arranged according to the size of a fully flexible fragment of the modeled system, effective timescales required for a meaningful simulation of their motions, and thus the modeling difficulty: (1) modeling of FxxLF motif peptide docking to an androgen receptor (AR), (2) investigation of binding and folding of an unstructured pKID protein to KIX protein, (3) modeling of p53-derived peptide docking to the MDM2 protein receptor with partially unstructured regions, and (4) simulation of the de novo folding of barnase. The simulations were performed using the CABS-dock method for protein–peptide docking [62] and CABS-flex methodology [72,73] that enable running de novo folding simulations.

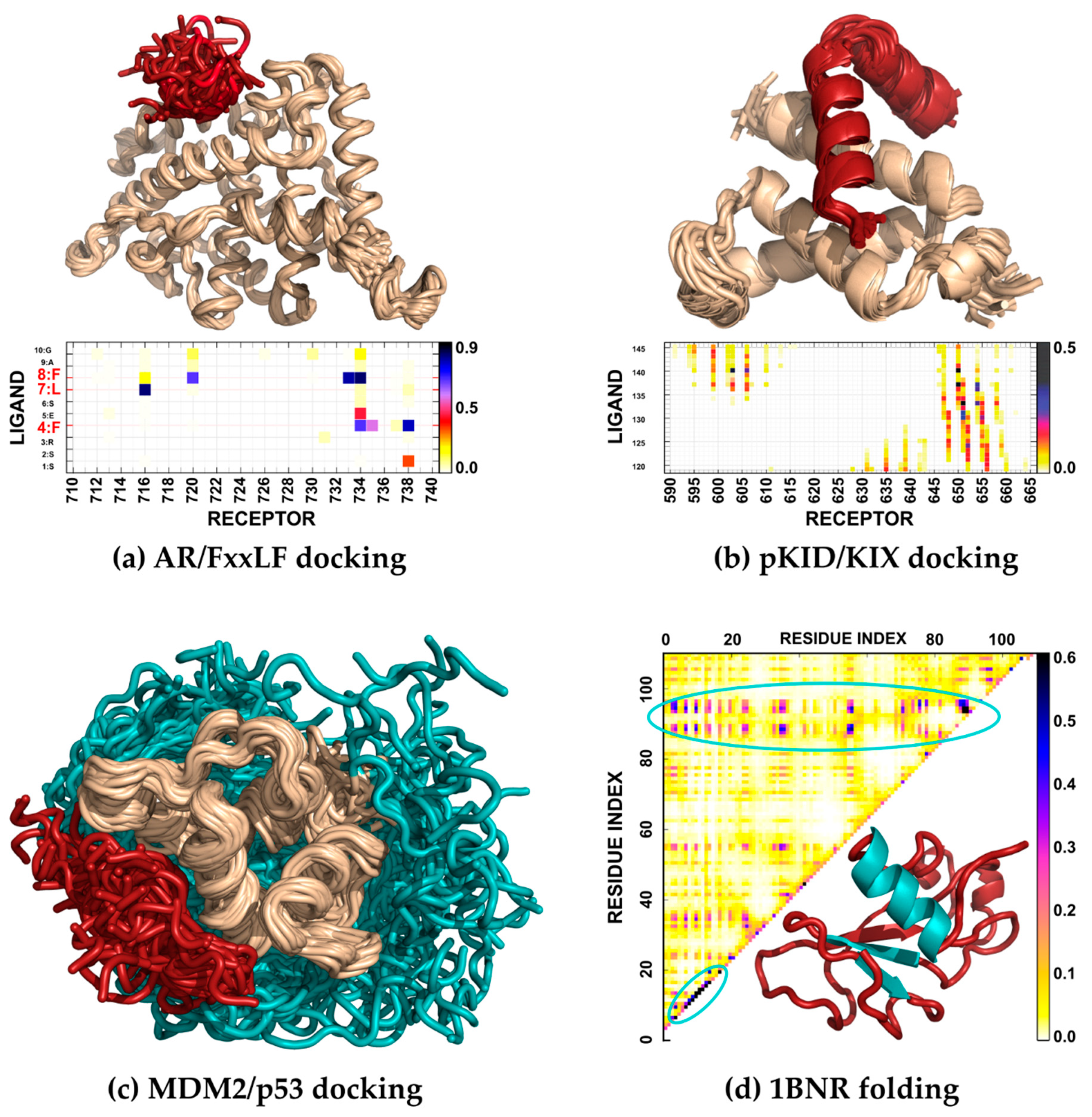
3.1. Protein–Peptide Binding

The CABS-dock method has been extensively tested using the PeptiDB benchmark set of protein–peptide complexes [62,65,87]. One of the benchmark cases is the androgen receptor ligand binding domain (AR) in complex with a peptide with the FxxLF motif [88] (PDB code: 1T7R). To further analyze the interaction details of this complex, we performed blind global docking (using no knowledge about the binding site and peptide conformation) using CABS-dock [62]. As the input we used information on peptide sequence (incorporating the FxxLF motif: SSRFESLFAGEKESR), peptide secondary structure information assigned by the DSSP method [89] and the structure of the AR protein receptor. In this docking study, the peptide structure was simulated as fully flexible, while fluctuations of the protein receptor were limited to small backbone movements around the input structure (around 1 Å). The docking simulation started from random peptide conformations placed in random positions around the receptor structure. During simulation, the peptide remained unstructured until it was bound to the receptor binding site (Figure 5a). The docking simulations provided a set of high-quality models—the best model was characterized by a peptide-RMSD (root-mean-square deviation) value of 1.97 Å—and contact maps in strong agreement with the experimental data. As expected from the experimentally obtained structures and sequence analysis [88] the FxxLF interaction motif residues were most frequently involved in stabilizing hydrophobic interactions with the receptor. These high-frequency contacts are clearly visible in Figure 5a.
The study of the pKID/KIX system [63] involved performing a folding simulation of an intrinsically disordered protein (pKID) and its binding to a well-structured KIX receptor (Figure 5b). According to the experimental studies, the pKID structure is disordered in its unbound form with a slight propensity toward a helix (for detailed description on how one-dimensional secondary structure information is used in the CABS model see [78]). In the complex with the KIX protein, pKID adopts a characteristic conformation of two perpendicular helices that wrap around the receptor. However, most simulation results for the coupled folding and binding of this system published prior to the CABS-based study used models which biased pKID toward its native conformation (see the discussion in [63]). Using our method for studying this system enabled fully flexible treatment of the pKID protein. The obtained results [63] suggested the binding mechanism that involve two encounter complexes and were in well agreement with the available NMR experimental data. The predicted models presented high fractions of native contacts and allowed identification of residues essential for the binding and stabilization of the complex.
In the simulation of MDM2/p53 binding [64], the most challenging task was to adequately model the flexibility of the relatively long, unstructured regions of the protein receptor in addition to the fully flexible peptide [64,90] (Figure 5c). To provide a detailed insight into MDM2/p53 binding, we performed CABS-dock simulations and captured system behavior in agreement with the experimental data [64]. During the simulation, the flexible N- and C- terminal MDM2 fragments remained significantly disordered. The best resulting model was characterized by a peptide-RMSD value of 2.76 Å and 54% of the native contacts while the top ranked model by 3.74 Å and 60%, respectively. During simulations, we observed ensembles of models in which the peptide adopted different conformations loosely bound to the binding site and models in which the N-terminal highly flexible MDM2 fragment was interacting with the binding site. These findings are in agreement with the experimental data suggesting that p53-MDM2 binding is affected by significant rearrangements of the N-terminal MDM2 fragment (see discussion in [64]).

3.2. Folding and Flexibility of Globular Proteins

The CABS model has been applied to de novo simulations of protein folding (using no knowledge about the protein structure) for several model systems that have been extensively studied by experiment and simulation tools. Those studies include barnase [50,52], chymotrypsin inhibitor [50,52], B1 domain of protein G [49,50], B domain of protein A [53], and others [50,54]. The CABS modeling protocol was also extended to enable studies of the chaperonin effect on the folding mechanism [55]. In these works, various parameters have been studied, including residue–residue contact frequency, radius of gyration, residual secondary structure and others. The obtained pictures, which covered protein dynamics from highly denatured states to ensembles close to the folded states, agreed well with available experimental data.
For example, simulation of barnase folding resulted in the adequate reproduction of the folding pathway in strong agreement with NMR data for denatured states and phi-value analysis [52]. The performed simulations show that barnase folding starts with developing a folding nucleation site that consists of protein fragments corresponding to two strands of a beta sheet and one of the helices in the folded structure (presented in Figure 5d). In addition, the characteristic patterns of hydrophobic interactions that are crucial for the initiation and sustenance of folding are in agreement with the experimental data (see discussion in Reference [52], the contact map resulting from these simulations is presented in Figure 5d).

4. Conclusions

The presented case studies review the applications of the CABS model in simulations of disordered or unfolded protein states. As discussed, the method succeeded in capturing the experimentally determined features of the investigated systems, such as binding site localization, key contacts, peptide hot-spot areas, distinctive conformational states of the system, transient encounter complexes and intermediate states in protein folding [49,52,63,64]. Additionally, CABS enables an investigation of fluctuations of globular proteins around the native (input) structure [69,70,71,72,73].
There is a number of tools commonly used for sampling of disordered protein states, which predictions agree with the experimental studies [91,92,93,94,95]. The CABS method is complementary to these and provides a unique approach allowing for effective modeling both ordered and disordered elements of the system. As observed in many previous studies, these features of CABS method allow for providing accurate pictures of folding pathways [49,52,53,54,55,56,60] and near-native dynamics [70,71]. Obviously, due to its coarse-graining, the geometric details are missed, and their reconstructions is approximate [11,28]. The main distinctive feature of CABS method as compared to the available tools is that the ensemble generation is (pseudo-)energy driven and thus may provide some information on the dynamics on the system. This is not the case in the above-mentioned examples of methods based on random-walk [91,92,95].
On the other hand, CABS force field side-chain interactions escape a clear interpretation, which may be a disadvantage compared to physics-based approaches that allow for straightforward and detailed description of each of the terms [93,94].
It is, however, noteworthy that statistical force fields suffer from inherent limitations, depending on the chosen method of derivation. The most commonly discussed challenges include the transferability, solvent interactions and integration of experimental data. Here, we briefly summarize these topics, a detailed discussion of the limitations of this approach, and possible workarounds may be found in review works [11,17]. The transferability of statistical force fields may be limited as they are applicable always to a certain subset of proteins. Therefore, the performance of knowledge-based approaches may be poor for rare or atypical structures, for which appropriate statistics of contact patterns could not be collected. It should also be noted that interactions with solvent are averaged and treated implicitly, which may lead to significant discrepancies if the method is applied to non-standard solvent conditions (such as extreme pH values). The CABS force field is derived assuming averaged effect solvent conditions for folded globular proteins. Therefore, a subtle effect of small molecules, such as pH, cannot be simulated in a strict fashion, although averaged effects (see modeling the chaperonin effect [55]) can be approximately taken into considerations.
One of the most challenging tasks in modeling protein systems is the effective incorporation of sparse experimental data to drive the modeling procedure. In the CABS model, the experimental data may be readily introduced into the simulation as geometry distance restraints and weighted according to their certainty. A thorough discussion of this possibility is presented in the documentation of CABS-based tools for the fast modeling of protein flexibility and protein–peptide docking [66,72,73]. On a similar basis, CABS simulations can be guided by computational predictions from other sources or integrated with other modeling tools of various resolution. Therefore, the CABS model can be incorporated into integrative modeling pipelines that would benefit from its effective sampling scheme. The recently published standalone application and web server tools are available for integration with external pipelines (access links are presented in the last paragraph of Section 2).

Author Contributions

S.K. and A.K. conceptualized this review. M.P. performed the simulations and analyzed the results for the AR/FxxLF system. The review was written by M.P.C., A.E.B-D., A.K. and S.K.

Funding

This research was funded by NCN Poland, grant number MAESTRO2014/14/A/ST6/00088.

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

CABSCα, Cβ, Side chain model
MCMonte Carlo
NMRnuclear magnetic resonance
MDmolecular dynamics
CGcoarse-grained
ARandrogen receptor
DSSPdictionary of protein secondary structure
RMSDroot-mean-square deviation of atomic positions
PDBProtein Data Bank
CASPCritical Assessment of protein Structure Prediction

References

  1. Dishman, A.F.; Volkman, B.F. Unfolding the Mysteries of Protein Metamorphosis. ACS Chem. Biol. 2018, 13, 1438–1446. [Google Scholar] [CrossRef] [PubMed]
  2. Uversky, V.N. Dancing protein clouds: The strange biology and chaotic physics of intrinsically disordered proteins. J. Biol. Chem. 2016, 291, 6681–6688. [Google Scholar] [CrossRef] [PubMed]
  3. Wright, P.E.; Dyson, H.J. Intrinsically disordered proteins in cellular signalling and regulation. Nat. Rev. Mol. Cell Biol. 2015, 16, 18–29. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  4. Henzler-Wildman, K.; Kern, D. Dynamic personalities of proteins. Nature 2007, 450, 964–972. [Google Scholar] [CrossRef] [PubMed]
  5. Vendruscolo, M.; Dobson, C.M. Dynamic visions of enzymatic reactions. Science 2006, 313, 1586–1587. [Google Scholar] [CrossRef] [PubMed]
  6. Wei, G.; Xi, W.; Nussinov, R.; Ma, B. Protein Ensembles: How Does Nature Harness Thermodynamic Fluctuations for Life? the Diverse Functional Roles of Conformational Ensembles in the Cell. Chem. Rev. 2016, 116, 6516–6551. [Google Scholar] [CrossRef]
  7. Best, R.B. Computational and theoretical advances in studies of intrinsically disordered proteins. Curr. Opin. Struct. Biol. 2017, 42, 147–154. [Google Scholar] [CrossRef]
  8. Kay, L.E. NMR studies of protein structure and dynamics. J. Magn. Reson. 2011, 213, 477–491. [Google Scholar] [CrossRef]
  9. Robustelli, P.; Piana, S.; Shaw, D.E. Developing a molecular dynamics force field for both folded and disordered protein states. Proc. Natl. Acad. Sci. USA 2018, 115, E4758–E4766. [Google Scholar] [CrossRef]
  10. Bowman, G.R.; Voelz, V.A.; Pande, V.S. Taming the complexity of protein folding. Curr. Opin. Struct. Biol. 2011, 21, 4–11. [Google Scholar] [CrossRef] [Green Version]
  11. Kmiecik, S.; Gront, D.; Kolinski, M.; Wieteska, L.; Dawid, A.E.; Kolinski, A. Coarse-Grained Protein Models and Their Applications. Chem. Rev. 2016, 116, 7898–7936. [Google Scholar] [CrossRef] [PubMed]
  12. Zhang, Z.; Chan, H.S. Competition between native topology and nonnative interactions in simple and complex folding kinetics of natural and designed proteins. Proc. Natl. Acad. Sci. USA 2010, 107, 2920–2925. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  13. Shan, B.; Eliezer, D.; Raleigh, D. The unfolded state of the C-terminal domain of the ribosomal protein L9 contains both native and non-native structure. Biochemistry 2009, 48, 4707–4719. [Google Scholar] [CrossRef] [PubMed]
  14. Rothwarf, D.M.; Scheraga, H.A. Role of non-native aromatic and hydrophobic interactions in the folding of hen egg white lysozyme. Biochemistry 1996, 35, 13797–13807. [Google Scholar] [CrossRef] [PubMed]
  15. Cavalli, A.; Montalvao, R.W.; Vendruscolo, M. Using chemical shifts to determine structural changes in proteins upon complex formation. J. Phys. Chem. B 2011, 115, 9491–9494. [Google Scholar] [CrossRef] [PubMed]
  16. Fu, B.; Kukic, P.; Camilloni, C.; Vendruscolo, M. MD Simulations of Intrinsically Disordered Proteins with Replica-Averaged Chemical Shift Restraints. Biophys. J. 2014, 106, 481a. [Google Scholar] [CrossRef] [Green Version]
  17. Kar, P.; Feig, M. Recent advances in transferable coarse-grained modeling of proteins. Adv. Protein Chem. Struct. Biol. 2014, 96, 143–180. [Google Scholar] [CrossRef]
  18. Greener, J.G.; Filippis, I.; Sternberg, M.J.E. Predicting Protein Dynamics and Allostery Using Multi-Protein Atomic Distance Constraints. Structure 2017, 25, 546–558. [Google Scholar] [CrossRef]
  19. Klepeis, J.L.; Lindorff-Larsen, K.; Dror, R.O.; Shaw, D.E. Long-timescale molecular dynamics simulations of protein structure and function. Curr. Opin. Struct. Biol. 2009, 19, 120–127. [Google Scholar] [CrossRef]
  20. Bernardi, R.C.; Melo, M.C.R.; Schulten, K. Enhanced sampling techniques in molecular dynamics simulations of biological systems. Biochim. Biophys. Acta - Gen. Subj. 2015, 1850, 872–877. [Google Scholar] [CrossRef] [Green Version]
  21. Shukla, D.; Hernández, C.X.; Weber, J.K.; Pande, V.S. Markov state models provide insights into dynamic modulation of protein function. Acc. Chem. Res. 2015, 48, 414–422. [Google Scholar] [CrossRef] [PubMed]
  22. Kolinski, A. Toward more efficient simulations of slow processes in large biomolecular systems: Comment on “Ligand diffusion in proteins via enhanced sampling in molecular dynamics” by Jakub Rydzewski and Wieslaw Nowak. Phys. Life Rev. 2017, 22–23, 75–76. [Google Scholar] [CrossRef] [PubMed]
  23. Rydzewski, J.; Nowak, W. Ligand diffusion in proteins via enhanced sampling in molecular dynamics. Phys. Life Rev. 2017, 22–23, 82–84. [Google Scholar] [CrossRef] [PubMed]
  24. Maximova, T.; Moffatt, R.; Ma, B.; Nussinov, R.; Shehu, A. Principles and Overview of Sampling Methods for Modeling Macromolecular Structure and Dynamics. PLoS Comput. Biol. 2016, 12, e1004619. [Google Scholar] [CrossRef] [PubMed]
  25. Hatherley, R.; Brown, D.K.; Glenister, M.; Bishop, Ö.T. PRIMO: An interactive homology modeling pipeline. PLoS ONE 2016, 11, e0166698. [Google Scholar] [CrossRef] [PubMed]
  26. Das, R.; Baker, D. Macromolecular Modeling with Rosetta. Annu. Rev. Biochem. 2008, 77, 363–382. [Google Scholar] [CrossRef] [PubMed]
  27. Czaplewski, C.; Karczyńska, A.; Sieradzan, A.K.; Liwo, A. UNRES server for physics-based coarse-grained simulations and prediction of protein structure, dynamics and thermodynamics. Nucleic Acids Res. 2018, 46, W304–W309. [Google Scholar] [CrossRef] [PubMed]
  28. Kolinski, A. Protein modeling and structure prediction with a reduced representation. Acta Biochim. Pol. 2004, 51, 349–371. [Google Scholar]
  29. Davtyan, A.; Schafer, N.P.; Zheng, W.; Clementi, C.; Wolynes, P.G.; Papoian, G.A. AWSEM-MD: Protein structure prediction using coarse-grained physical potentials and bioinformatically based local structure biasing. J. Phys. Chem. B 2012, 116, 8494–8503. [Google Scholar] [CrossRef]
  30. Marrink, S.J.; Tieleman, D.P. Perspective on the Martini model. Chem. Soc. Rev. 2013, 42, 6801. [Google Scholar] [CrossRef]
  31. Pasi, M.; Lavery, R.; Ceres, N. PaLaCe: A coarse-grain protein model for studying mechanical properties. J. Chem. Theory Comput. 2013, 9, 785–793. [Google Scholar] [CrossRef] [PubMed]
  32. Basdevant, N.; Borgis, D.; Ha-Duong, T. Modeling protein-protein recognition in solution using the coarse-grained force field SCORPION. J. Chem. Theory Comput. 2013, 9, 803–813. [Google Scholar] [CrossRef] [PubMed]
  33. Dawid, A.E.; Gront, D.; Kolinski, A. SURPASS Low-Resolution Coarse-Grained Protein Modeling. J. Chem. Theory Comput. 2017, 13, 5766–5779. [Google Scholar] [CrossRef] [PubMed]
  34. Dawid, A.E.; Gront, D.; Kolinski, A. Coarse-Grained Modeling of the Interplay between Secondary Structure Propensities and Protein Fold Assembly. J. Chem. Theory Comput. 2018, 14, 2277–2287. [Google Scholar] [CrossRef] [PubMed]
  35. Lopes, P.E.M.; Guvench, O.; MacKerell, A.D. Current Status of Protein Force Fields for Molecular Dynamics Simulations. In Molecular Modeling of Proteins; Humana Press: New York, NY, USA, 2015; pp. 47–71. [Google Scholar]
  36. Cossio, P.; Granata, D.; Laio, A.; Seno, F.; Trovato, A. A simple and efficient statistical potential for scoring ensembles of protein structures. Sci. Rep. 2012, 2, 351. [Google Scholar] [CrossRef]
  37. Tanaka, S.; Scheraga, H.A. Medium- and Long-Range Interaction Parameters between Amino Acids for Predicting Three-Dimensional Structures of Proteins. Macromolecules 1976, 9, 945–950. [Google Scholar] [CrossRef] [PubMed]
  38. Tsai, J.; Bonneau, R.; Morozov, A.V.; Kuhlman, B.; Rohl, C.A.; Baker, D. An improved protein decoy set for testing energy functions for protein structure prediction. Proteins Struct. Funct. Genet. 2003, 53, 76–87. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  39. Shen, M.; Sali, A. Statistical potential for assessment and prediction of protein structures. Protein Sci. 2006, 15, 2507–2524. [Google Scholar] [CrossRef] [Green Version]
  40. Zhou, H.; Skolnick, J. GOAP: A Generalized Orientation-Dependent, All-Atom Statistical Potential for Protein Structure Prediction. Biophys. J. 2011, 101, 2043–2052. [Google Scholar] [CrossRef] [Green Version]
  41. Xu, D.; Zhang, Y. Ab initio protein structure assembly using continuous structure fragments and optimized knowledge-based force field. Proteins Struct. Funct. Bioinforma. 2012, 80, 1715–1735. [Google Scholar] [CrossRef]
  42. Woetzel, N.; Karakaş, M.; Staritzbichler, R.; Müller, R.; Weiner, B.E.; Meiler, J. BCL::Score—Knowledge Based Energy Potentials for Ranking Protein Models Represented by Idealized Secondary Structure Elements. PLoS ONE 2012, 7, e49242. [Google Scholar] [CrossRef] [PubMed]
  43. Ovchinnikov, S.; Park, H.; Kim, D.E.; Liu, Y.; Wang, R.Y.-R.; Baker, D. Structure prediction using sparse simulated NOE restraints with Rosetta in CASP11. Proteins Struct. Funct. Bioinforma. 2016, 84, 181–188. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  44. Ovchinnikov, S.; Kim, D.E.; Wang, R.Y.-R.; Liu, Y.; DiMaio, F.; Baker, D. Improved de novo structure prediction in CASP11 by incorporating coevolution information into Rosetta. Proteins Struct. Funct. Bioinforma. 2016, 84, 67–75. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  45. Hirst, S.J.; Alexander, N.; Mchaourab, H.S.; Meiler, J. RosettaEPR: An integrated tool for protein structure determination from sparse EPR data. J. Struct. Biol. 2011, 173, 506–514. [Google Scholar] [CrossRef] [Green Version]
  46. Yang, J.; Zhang, W.; He, B.; Walker, S.E.; Zhang, H.; Govindarajoo, B.; Virtanen, J.; Xue, Z.; Shen, H.B.; Zhang, Y. Template-based protein structure prediction in CASP11 and retrospect of I-TASSER in the last decade. Proteins 2016, 84, 233–246. [Google Scholar] [CrossRef]
  47. Russel, D.; Lasker, K.; Webb, B.; Velázquez-Muriel, J.; Tjioe, E.; Schneidman-Duhovny, D.; Peterson, B.; Sali, A. Putting the Pieces Together: Integrative Modeling Platform Software for Structure Determination of Macromolecular Assemblies. PLoS Biol. 2012, 10, e1001244. [Google Scholar] [CrossRef]
  48. Rodrigues, J.P.G.L.M.; Bonvin, A.M.J.J. Integrative computational modeling of protein interactions. FEBS J. 2014, 281, 1988–2003. [Google Scholar] [CrossRef] [Green Version]
  49. Kmiecik, S.; Kolinski, A. Folding pathway of the B1 domain of protein G explored by multiscale modeling. Biophys. J. 2008, 94, 726–736. [Google Scholar] [CrossRef]
  50. Kolinski, A. Multiscale approaches to protein modeling: Structure prediction, dynamics, thermodynamics and macromolecular assemblies. In Multiscale Approaches to Protein Modeling: Structure Prediction, Dynamics, Thermodynamics and Macromolecular Assemblies; Kolinski, A., Ed.; Springer: New York, NY, USA, 2011; pp. 1–355. ISBN 9781441968890. [Google Scholar]
  51. Kmiecik, S.; Kouza, M.; Badaczewska-Dawid, A.E.; Kloczkowski, A.; Kolinski, A. Modeling of Protein Structural Flexibility and Large-Scale Dynamics: Coarse-Grained Simulations and Elastic Network Models. Int. J. Mol. Sci. 2018, 19, 3496. [Google Scholar] [CrossRef]
  52. Kmiecik, S.; Kolinski, A. Characterization of protein-folding pathways by reduced-space modeling. Proc. Natl. Acad. Sci. USA 2007, 104, 12330–12335. [Google Scholar] [CrossRef]
  53. Kmiecik, S.; Gront, D.; Kouza, M.; Kolinski, A. From coarse-grained to atomic-level characterization of protein dynamics: Transition state for the folding of B domain of protein A. J. Phys. Chem. B 2012, 116, 7026–7032. [Google Scholar] [CrossRef] [PubMed]
  54. Kmiecik, S.; Kurcinski, M.; Rutkowska, A.; Gront, D.; Kolinski, A. Denatured proteins and early folding intermediates simulated in a reduced conformational space. Acta Biochim. Pol. 2006, 53, 131–143. [Google Scholar] [CrossRef] [PubMed]
  55. Kmiecik, S.; Kolinski, A. Simulation of chaperonin effect on protein folding: A shift from nucleation - Condensation to framework mechanism. J. Am. Chem. Soc. 2011, 133, 10283–10289. [Google Scholar] [CrossRef] [PubMed]
  56. Jamroz, M.; Kolinski, A.; Kmiecik, S. Protocols for efficient simulations of long-time protein dynamics using coarse-grained CABS model. Methods Mol. Biol. 2014, 1137, 235–250. [Google Scholar] [CrossRef] [PubMed]
  57. Wabik, J.; Kmiecik, S.; Gront, D.; Kouza, M.; Koliński, A. Combining coarse-grained protein models with replica-exchange all-atom molecular dynamics. Int. J. Mol. Sci. 2013, 14, 9893–9905. [Google Scholar] [CrossRef] [PubMed]
  58. Blaszczyk, M.; Jamroz, M.; Kmiecik, S.; Kolinski, A. CABS-fold: Server for the de novo and consensus-based prediction of protein structure. Nucleic Acids Res. 2013, 41, W406–W411. [Google Scholar] [CrossRef] [PubMed]
  59. Kmiecik, S.; Jamroz, M.; Kolinski, M. Structure prediction of the second extracellular loop in G-protein-coupled receptors. Biophys. J. 2014, 106, 2408–2416. [Google Scholar] [CrossRef]
  60. Koliński, A.; Bujnicki, J.M. Generalized protein structure prediction based on combination of fold-recognition with de novo folding and evaluation of models. Proteins Struct. Funct. Genet. 2005, 61, 84–90. [Google Scholar] [CrossRef] [Green Version]
  61. Jamroz, M.; Kolinski, A. Modeling of loops in proteins: A multi-method approach. BMC Struct. Biol. 2010, 10. [Google Scholar] [CrossRef]
  62. Kurcinski, M.; Jamroz, M.; Blaszczyk, M.; Kolinski, A.; Kmiecik, S. CABS-dock web server for the flexible docking of peptides to proteins without prior knowledge of the binding site. Nucleic Acids Res. 2015, 43, W419–W424. [Google Scholar] [CrossRef]
  63. Kurcinski, M.; Kolinski, A.; Kmiecik, S. Mechanism of folding and binding of an intrinsically disordered protein as revealed by ab initio simulations. J. Chem. Theory Comput. 2014, 10, 2224–2231. [Google Scholar] [CrossRef] [PubMed]
  64. Ciemny, M.P.; Debinski, A.; Paczkowska, M.; Kolinski, A.; Kurcinski, M.; Kmiecik, S. Protein-peptide molecular docking with large-scale conformational changes: The p53-MDM2 interaction. Sci. Rep. 2016, 6. [Google Scholar] [CrossRef] [PubMed]
  65. Blaszczyk, M.; Kurcinski, M.; Kouza, M.; Wieteska, L.; Debinski, A.; Kolinski, A.; Kmiecik, S. Modeling of protein-peptide interactions using the CABS-dock web server for binding site search and flexible docking. Methods 2016, 93, 72–83. [Google Scholar] [CrossRef] [PubMed]
  66. Ciemny, M.; Kurcinski, M.; Kozak, K.; Kolinski, A.; Kmiecik, S. Highly flexible protein-peptide docking using cabs-dock. Methods Mol. Biol. 2017, 1561, 69–94. [Google Scholar] [CrossRef]
  67. Blaszczyk, M.; Ciemny, M.P.; Kolinski, A.; Kurcinski, M.; Kmiecik, S. Protein–peptide docking using CABS-dock and contact information. Brief. Bioinform. 2018, bby080. [Google Scholar] [CrossRef]
  68. Ciemny, M.P.; Kurcinski, M.; Blaszczyk, M.; Kolinski, A.; Kmiecik, S. Modeling EphB4-EphrinB2 protein-protein interaction using flexible docking of a short linear motif. Biomed. Eng. Online 2017, 16, 71. [Google Scholar] [CrossRef]
  69. Jamroz, M.; Orozco, M.; Kolinski, A.; Kmiecik, S. Consistent view of protein fluctuations from all-atom molecular dynamics and coarse-grained dynamics with knowledge-based force-field. J. Chem. Theory Comput. 2013, 9, 119–125. [Google Scholar] [CrossRef]
  70. Jamroz, M.; Kolinski, A.; Kmiecik, S. CABS-flex: Server for fast simulation of protein structure fluctuations. Nucleic Acids Res. 2013, 41, W427–W431. [Google Scholar] [CrossRef] [PubMed]
  71. Jamroz, M.; Kolinski, A.; Kmiecik, S. CABS-flex predictions of protein flexibility compared with NMR ensembles. Bioinformatics 2014, 30, 2150–2154. [Google Scholar] [CrossRef] [PubMed]
  72. Kurcinski, M.; Oleniecki, T.; Ciemny, P.M.; Kuriata, A.; Kolinski, A.; Kmiecik, S. CABS-flex standalone: A simulation environment for fast modeling of protein flexibility. Bioinformatics 2018, bty685. [Google Scholar] [CrossRef] [PubMed]
  73. Kuriata, A.; Gierut, A.M.; Oleniecki, T.; Ciemny, M.P.; Kolinski, A.; Kurcinski, M.; Kmiecik, S. CABS-flex 2.0: A web server for fast simulations of flexibility of protein structures. Nucleic Acids Res. 2018, 46, W338–W343. [Google Scholar] [CrossRef] [PubMed]
  74. Eswar, N.; John, B.; Mirkovic, N.; Fiser, A.; Ilyin, V.A.; Pieper, U.; Stuart, A.C.; Marti-Renom, M.A.; Madhusudhan, M.S.; Yerkovich, B.; Sali, A. Tools for comparative protein structure modeling and analysis. Nucleic Acids Res. 2003, 31, 3375–3380. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  75. Gront, D.; Kmiecik, S.; Kolinski, A. Backbone building from quadrilaterals: A fast and accurate algorithm for protein backbone reconstruction from alpha carbon coordinates. J. Comput. Chem. 2007, 28, 1593–1597. [Google Scholar] [CrossRef] [PubMed]
  76. Canutescu, A.A.; Shelenkov, A.A.; Dunbrack, R.L. A graph-theory algorithm for rapid protein side-chain prediction. Protein Sci. 2003, 12, 2001–2014. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  77. Gront, D.; Kmiecik, S.; Blaszczyk, M.; Ekonomiuk, D.; Koliński, A. Optimization of protein models. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2012, 2, 479–493. [Google Scholar] [CrossRef]
  78. Kmiecik, S.; Kolinski, A. One-dimensional structural properties of proteins in the coarse-grained cabs model. Methods Mol. Biol. 2017, 1484, 83–113. [Google Scholar] [CrossRef] [PubMed]
  79. Pulawski, W.; Jamroz, M.; Kolinski, M.; Kolinski, A.; Kmiecik, S. Coarse-grained simulations of membrane insertion and folding of small helical proteins using the CABS model. J. Chem. Inf. Model. 2016, 56, 2207–2215. [Google Scholar] [CrossRef]
  80. Adhikari, A.N.; Freed, K.F.; Sosnick, T.R. De novo prediction of protein folding pathways and structure using the principle of sequential stabilization. Proc. Natl. Acad. Sci. USA 2012, 109, 17442–17447. [Google Scholar] [CrossRef] [Green Version]
  81. Adhikari, A.N.; Freed, K.F.; Sosnick, T.R. Simplified protein models: Predicting folding pathways and structure using amino acid sequences. Phys. Rev. Lett. 2013, 111, 028103. [Google Scholar] [CrossRef]
  82. Konrat, R. NMR contributions to structural dynamics studies of intrinsically disordered proteins. J. Magn. Reson. 2014, 241, 74–85. [Google Scholar] [CrossRef] [Green Version]
  83. Kmiecik, S.; Wabik, J.; Kolinski, M.; Kouza, M.; Kolinski, A. Coarse-Grained Modeling of Protein Dynamics. In Computational Methods to Study the Structure and Dynamics of Biomolecules; Springer: Berlin/Heidelberg, Germany, 2014; Volume 1, pp. 55–79. ISBN 978-3-642-28553-0. [Google Scholar]
  84. Kurcinski, M.; Ciemny, M.P.; Oleniecki, T.; Kuriata, A.; Badaczewska-Dawid, A.E.; Kolinski, A.; Kmiecik, S. CABS-dock standalone: A toolbox for flexible protein-peptide docking. Bioinformatics 2019. submitted. [Google Scholar]
  85. Ciemny, M.; Kurcinski, M.; Kamel, K.; Kolinski, A.; Alam, N.; Schueler-Furman, O.; Kmiecik, S. Protein–peptide docking: Opportunities and challenges. Drug Discov. Today 2018, 23, 1530–1537. [Google Scholar] [CrossRef] [PubMed]
  86. Zambrano, R.; Jamroz, M.; Szczasiuk, A.; Pujols, J.; Kmiecik, S.; Ventura, S. AGGRESCAN3D (A3D): Server for prediction of aggregation properties of protein structures. Nucleic Acids Res. 2015, 43, W306–W313. [Google Scholar] [CrossRef]
  87. London, N.; Movshovitz-Attias, D.; Schueler-Furman, O. The Structural Basis of Peptide-Protein Binding Strategies. Structure 2010, 18, 188–199. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  88. Hur, E.; Pfaff, S.J.; Sturgis Payne, E.; Grøn, H.; Buehrer, B.M.; Fletterick, R.J. Recognition and accommodation at the androgen receptor coactivator binding interface. PLoS Biol. 2004, 2, E274. [Google Scholar] [CrossRef] [PubMed]
  89. Kabsch, W.; Sander, C. Dictionary of protein secondary structure: Pattern recognition of hydrogen-bonded and geometrical features. Biopolymers 1983, 22, 2577–2637. [Google Scholar] [CrossRef] [PubMed]
  90. Kussie, P.H.; Gorina, S.; Marechal, V.; Elenbaas, B.; Moreau, J.; Levine, A.J.; Pavletich, N.P. Structure of the MDM2 oncoprotein bound to the p53 tumor suppressor transactivation domain. Science 1996, 274, 948–953. [Google Scholar] [CrossRef] [PubMed]
  91. Ozenne, V.; Bauer, F.; Salmon, L.; Huang, J.R.; Jensen, M.R.; Segard, S.; Bernadó, P.; Charavay, C.; Blackledge, M. Flexible-meccano: A tool for the generation of explicit ensemble descriptions of intrinsically disordered proteins and their associated experimental observables. Bioinformatics 2012, 28, 1463–1470. [Google Scholar] [CrossRef] [PubMed]
  92. Feldman, H.J.; Hogue, C.W.V. Probabilistic sampling of protein conformations: New hope for brute force? Proteins Struct. Funct. Genet. 2002, 46, 8–23. [Google Scholar] [CrossRef] [PubMed]
  93. Vitalis, A.; Pappu, R.V. ABSINTH: A new continuum solvation model for simulations of polypeptides in aqueous solutions. J. Comput. Chem. 2009, 30, 673–699. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  94. Baul, U.; Chakraborty, D.; Mugnai, M.L.; Straub, J.E.; Thirumalai, D. Sequence effects on size, shape, and structural heterogeneity in Intrinsically Disordered Proteins. bioRxiv 2018, 427476. [Google Scholar] [CrossRef]
  95. Estaña, A.; Sibille, N.; Delaforge, E.; Vaisset, M.; Cortés, J.; Bernadó, P. Realistic Ensemble Models of Intrinsically Disordered Proteins Using a Structure-Encoding Coil Database. Structure 2018. [Google Scholar] [CrossRef] [PubMed]
Ijms 20 00606 g001 550
Figure 1. A three-residue protein fragment in: all-atom (a) and CABS model (b) representation. The spheres represent atoms: blue, C-alpha and C-beta atoms (the same in both representations); yellow, side chain atoms (one pseudo-atom in CABS); red, atoms involved in the peptide bond (one pseudo-atom in CABS placed in the geometric center of the peptide bond. A single slice (layer) of the lattice that confines the C-alpha trace in the CABS model is also presented.
Figure 1. A three-residue protein fragment in: all-atom (a) and CABS model (b) representation. The spheres represent atoms: blue, C-alpha and C-beta atoms (the same in both representations); yellow, side chain atoms (one pseudo-atom in CABS); red, atoms involved in the peptide bond (one pseudo-atom in CABS placed in the geometric center of the peptide bond. A single slice (layer) of the lattice that confines the C-alpha trace in the CABS model is also presented.
Ijms 20 00606 g001
Ijms 20 00606 g002a 550Ijms 20 00606 g002b 550
Figure 2. Key elements of a residue–residue interaction term in the CABS model force field. Panel (a) shows three examples of contact geometries in CABS representation: parallel (P), antiparallel (A), and intermediate (M), used to derive contact statistics from experimentally-derived structures of folded globular proteins. Panel (b) shows an example matrix of contact energies which depend on the geometry of the contacting pair, main chain geometry (compact (C) or extended (E)) for both amino acids (left part of the panel), and also on the amino acid identities (right part of the panel, the amino acids are represented using the one-letter code). The PCC matrix is presented which shows interaction energies between residues being in parallel orientation (P), where one residue belongs to a compact type of structure (C) and the second one as well (C).
Figure 2. Key elements of a residue–residue interaction term in the CABS model force field. Panel (a) shows three examples of contact geometries in CABS representation: parallel (P), antiparallel (A), and intermediate (M), used to derive contact statistics from experimentally-derived structures of folded globular proteins. Panel (b) shows an example matrix of contact energies which depend on the geometry of the contacting pair, main chain geometry (compact (C) or extended (E)) for both amino acids (left part of the panel), and also on the amino acid identities (right part of the panel, the amino acids are represented using the one-letter code). The PCC matrix is presented which shows interaction energies between residues being in parallel orientation (P), where one residue belongs to a compact type of structure (C) and the second one as well (C).
Ijms 20 00606 g002aIjms 20 00606 g002b
Ijms 20 00606 g003 550
Figure 3. Sampling scheme of the CABS model. Blue panels show implementation details of Monte Carlo (MC) iterations (loops). The orange panel shows all motions that may be performed in a single MC step. The simulation is organized as a set of nested loops, in which the s number of MC steps is organized into the y number of cycles, and these in a annealing cycles (number of a, y or s cycles can be controlled by the user in CABS-flex and CABS-dock standalone packages [72]). In the orange panel, numbers 1 to 5 denote the available moves, presented together with the number of attempts to perform a move in each of the MC steps. The resulting trajectory is comprised of simulation snapshots saved at the end of each MC cycle.
Figure 3. Sampling scheme of the CABS model. Blue panels show implementation details of Monte Carlo (MC) iterations (loops). The orange panel shows all motions that may be performed in a single MC step. The simulation is organized as a set of nested loops, in which the s number of MC steps is organized into the y number of cycles, and these in a annealing cycles (number of a, y or s cycles can be controlled by the user in CABS-flex and CABS-dock standalone packages [72]). In the orange panel, numbers 1 to 5 denote the available moves, presented together with the number of attempts to perform a move in each of the MC steps. The resulting trajectory is comprised of simulation snapshots saved at the end of each MC cycle.
Ijms 20 00606 g003
Ijms 20 00606 g004 550
Figure 4. Presentation of the modeling cases discussed in this work. The modeled systems are arranged according to the size of the fully flexible fragment of the modeled system and the effective timescales required to observe their motions. The regions of the systems that were modeled as fully flexible are marked with red, while the regions in which backbone fluctuations were limited to 1 Å RMSD with beige. The presented millisecond values are approximated up to the order of magnitude.
Figure 4. Presentation of the modeling cases discussed in this work. The modeled systems are arranged according to the size of the fully flexible fragment of the modeled system and the effective timescales required to observe their motions. The regions of the systems that were modeled as fully flexible are marked with red, while the regions in which backbone fluctuations were limited to 1 Å RMSD with beige. The presented millisecond values are approximated up to the order of magnitude.
Ijms 20 00606 g004
Ijms 20 00606 g005 550
Figure 5. Case studies of modeling disordered or unfolded structures of proteins with CABS-based tools. In the figures, red or cyan marks structure fragments simulated as fully flexible (cyan was used to mark regions of interest discussed in the text), while beige marks regions whose motions were confined to small backbone movements (around 1 Å from the input structure). (a) Modeling of the dynamics of a flexible peptide representing the FxxLF motif in the proximity of the binding site of AR protein together with an averaged contact map showing frequency of residue–residue contacts during the docking simulation. (b) Modeling of coupled folding and binding of the disordered pKID to the KIX domain [63]; the map presents the frequency of contacts of near-native conformations obtained in the simulation. (c) Modeling of p53 peptide binding to the MDM2 receptor [64], which includes fully-flexible regions of the protein receptor (shown in cyan) interacting with a fully-flexible peptide (shown in red). (d) Modeling of barnase folding [52] in the de novo fashion (using no knowledge about the structure); the map is a residue–residue contact map showing relative contact frequencies in denaturing conditions; the protein fragments that form the folding nucleation site are colored in cyan in the presented folded structure of barnase.
Figure 5. Case studies of modeling disordered or unfolded structures of proteins with CABS-based tools. In the figures, red or cyan marks structure fragments simulated as fully flexible (cyan was used to mark regions of interest discussed in the text), while beige marks regions whose motions were confined to small backbone movements (around 1 Å from the input structure). (a) Modeling of the dynamics of a flexible peptide representing the FxxLF motif in the proximity of the binding site of AR protein together with an averaged contact map showing frequency of residue–residue contacts during the docking simulation. (b) Modeling of coupled folding and binding of the disordered pKID to the KIX domain [63]; the map presents the frequency of contacts of near-native conformations obtained in the simulation. (c) Modeling of p53 peptide binding to the MDM2 receptor [64], which includes fully-flexible regions of the protein receptor (shown in cyan) interacting with a fully-flexible peptide (shown in red). (d) Modeling of barnase folding [52] in the de novo fashion (using no knowledge about the structure); the map is a residue–residue contact map showing relative contact frequencies in denaturing conditions; the protein fragments that form the folding nucleation site are colored in cyan in the presented folded structure of barnase.
Ijms 20 00606 g005

Share and Cite

MDPI and ACS Style

Ciemny, M.P.; Badaczewska-Dawid, A.E.; Pikuzinska, M.; Kolinski, A.; Kmiecik, S. Modeling of Disordered Protein Structures Using Monte Carlo Simulations and Knowledge-Based Statistical Force Fields. Int. J. Mol. Sci. 2019, 20, 606. https://doi.org/10.3390/ijms20030606

AMA Style

Ciemny MP, Badaczewska-Dawid AE, Pikuzinska M, Kolinski A, Kmiecik S. Modeling of Disordered Protein Structures Using Monte Carlo Simulations and Knowledge-Based Statistical Force Fields. International Journal of Molecular Sciences. 2019; 20(3):606. https://doi.org/10.3390/ijms20030606

Chicago/Turabian Style

Ciemny, Maciej Pawel, Aleksandra Elzbieta Badaczewska-Dawid, Monika Pikuzinska, Andrzej Kolinski, and Sebastian Kmiecik. 2019. "Modeling of Disordered Protein Structures Using Monte Carlo Simulations and Knowledge-Based Statistical Force Fields" International Journal of Molecular Sciences 20, no. 3: 606. https://doi.org/10.3390/ijms20030606

APA Style

Ciemny, M. P., Badaczewska-Dawid, A. E., Pikuzinska, M., Kolinski, A., & Kmiecik, S. (2019). Modeling of Disordered Protein Structures Using Monte Carlo Simulations and Knowledge-Based Statistical Force Fields. International Journal of Molecular Sciences, 20(3), 606. https://doi.org/10.3390/ijms20030606

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop