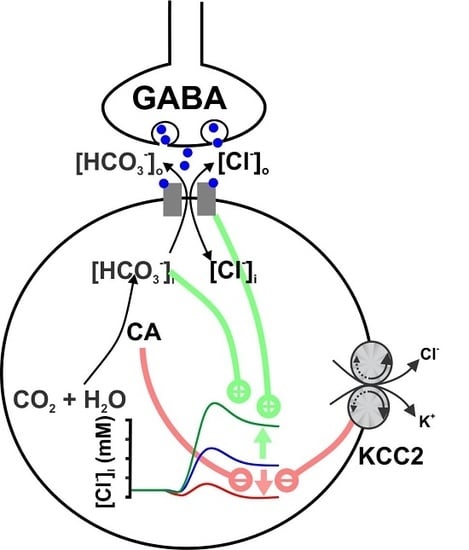
Interactions between Membrane Resistance, GABA-A Receptor Properties, Bicarbonate Dynamics and Cl⁻-Transport Shape Activity-Dependent Changes of Intracellular Cl⁻ Concentration

Abstract

The effects of ionotropic γ-aminobutyric acid receptor (GABA-A, GABA_A) activation depends critically on the Cl⁻-gradient across neuronal membranes. Previous studies demonstrated that the intracellular Cl⁻-concentration ([Cl⁻]_i) is not stable but shows a considerable amount of activity-dependent plasticity. To characterize how membrane properties and different molecules that are directly or indirectly involved in GABAergic synaptic transmission affect GABA-induced [Cl⁻]_i changes, we performed compartmental modeling in the NEURON environment. These simulations demonstrate that GABA-induced [Cl⁻]_i changes decrease at higher membrane resistance, revealing a sigmoidal dependency between both parameters. Increase in GABAergic conductivity enhances [Cl⁻]_i with a logarithmic dependency, while increasing the decay time of GABA_A receptors leads to a nearly linear enhancement of the [Cl⁻]_i changes. Implementing physiological levels of HCO₃⁻-conductivity to GABA_A receptors enhances the [Cl⁻]_i changes over a wide range of [Cl⁻]_i, but this effect depends on the stability of the HCO₃⁻ gradient and the intracellular pH. Finally, these simulations show that pure diffusional Cl⁻-elimination from dendrites is slow and that a high activity of Cl⁻-transport is required to improve the spatiotemporal restriction of GABA-induced [Cl⁻]_i changes. In summary, these simulations revealed a complex interplay between several key factors that influence GABA-induced [Cl]_i changes. The results suggest that some of these factors, including high resting [Cl⁻]_i, high input resistance, slow decay time of GABA_A receptors and dynamic HCO₃⁻ gradient, are specifically adapted in early postnatal neurons to facilitate limited activity-dependent [Cl⁻]_i decreases.

1. Introduction

GABA (γ-aminobutyric acid) is the main inhibitory neurotransmitter in the mature brain and acts via ionotropic GABA_A/GABA_C receptors and via metabotropic GABA_B receptors [1]. In the adult brain, GABA mediates its inhibitory effect by hyperpolarizing the membrane and by shunting excitatory inputs. GABA_A receptors are ligand-gated anion-channels with a high permeability for Cl⁻ ions and a considerable additional permeability for HCO₃⁻ ions [1]. In the mature brain the activity of a K⁺-Cl⁻-Cotransporter (KCC, mainly in its isoform KCC2) establishes a low intracellular Cl⁻ concentration ([Cl⁻]_i) [2,3], which accounts for a Cl⁻ influx and thus a membrane hyperpolarization upon activation of GABA_A receptors [1]. Due to this Cl⁻-flux, activation of GABA_A receptors can influence [Cl⁻]_i on a time scale of seconds to minutes [4,5,6,7,8,9], a process termed “ionic plasticity” [3,10,11]. The magnitude of activity-dependent [Cl⁻]_i-transients depends on the Cl⁻ influx, dendritic volume and morphology, as well as on the capacity of Cl⁻ extrusion systems [12,13,14,15,16,17]. In addition, the membrane potential and the HCO₃⁻ permeability of GABA_A receptors (P_HCO3) contribute to the size of [Cl⁻]_i changes [6,18,19,20]. Therefore recent concepts of inhibition considered neuronal [Cl⁻]_i as a state- and compartment-dependent parameter of individual cells [14,20]. Detectable activity-dependent [Cl⁻]_i changes can occur in the adult nervous system under massive GABAergic stimulation [12,21]. However, already small alterations in [Cl⁻]_i or in the dynamics of the [Cl⁻]_i homeostasis critically influence information processing in neurons [20,22]. As the proper function in the adult nervous system relies on adequate inhibition [1,23,24], these activity-dependent [Cl⁻]_i changes play important roles in physiological and pathophysiological processes [10,11,17].

In the immature nervous system GABA typically induces depolarizing membrane responses [25,26,27,28,29,30]. These depolarizing GABAergic responses are caused by an elevated intracellular Cl⁻ concentration ([Cl⁻]_i), which is maintained by a Cl⁻ accumulation via the isoform 1 of the Na⁺-dependent K⁺-Cl⁻-cotransporter (NKCC1) [3,29,31,32]. Recent studies suggest that at least in the postnatal neocortex, these depolarizing GABAergic responses mainly mediate inhibition [30,33], likely by increasing membrane shunting [1,34]. Several results indicate that depolarizing GABAergic neurotransmission is of specific relevance for immature spontaneous activity and for the maturation of the central nervous system [35,36,37]. Giant depolarizing potentials (GDPs) are a well-described network phenomenon in the immature hippocampus and the neocortex that represent spontaneous GABA-dependent activity [25,38,39]. In line with the high [Cl⁻]_i and the depolarizing responses, activation of GABA_A receptors causes a decline in [Cl⁻]_i of immature neurons [29,40,41,42]. This attenuation of the [Cl⁻] gradient reduces possible excitatory effects of GABA [29,42,43] and may serve to limit GABAergic excitation and/or to stabilize recurrent network events [10,13,40]. A recent study demonstrated that GDPs, which are associated with a high amount of GABAergic activity [25,44], induce long-lasting [Cl⁻]_i transients and influence the steady-state [Cl⁻]_i of CA3 pyramidal neurons in hippocampal slices from early postnatal mice neurons [45], making it a suitable model for ionic plasticity in the immature brain.

However, while the existence of ionic plasticity is well accepted and several factors influencing activity-dependent [Cl⁻]_i transients have been described, the role of biophysical membrane characteristics, molecular properties of GABA_A-receptors or Cl⁻-transporters, and the stability of HCO₃⁻ homeostasis on ionic plasticity has not yet been systematically investigated. Here we used a detailed biophysical compartmental model in the NEURON environment to demonstrate how cellular and molecular properties such as input resistance, pH, HCO₃⁻-selectivity, kinetics of GABA_A receptors, the kinetics of NKCC1 mediated Cl⁻ transmembrane transport, and the activity of carbonic anhydrases influence activity-dependent [Cl⁻]_i transients. While most modeling is performed in isolated dendritic compartments, here we also replicate the well-described GDP-induced [Cl⁻]_i transients of immature hippocampal CA3 neurons [45].

2. Results

In order to study the question how various membrane parameters and the properties of different molecules involved in GABAergic transmission influence activity-dependent [Cl⁻]_i transients, we first computed the GABA-induced [Cl⁻]_i changes in an isolated dendrite, which allows a better mechanistic understanding of the underlying processes. Subsequently we also used a model of a reconstructed CA3 pyramidal neuron [45] to compare the results of our computational models with the GDP-dependent [Cl⁻]_i transients recorded in immature hippocampal CA3 neurons [45]. For the latter model, we implemented experimentally derived parameters of GABAergic synapses and GDP-activity provided by Lombardi et al. [45].

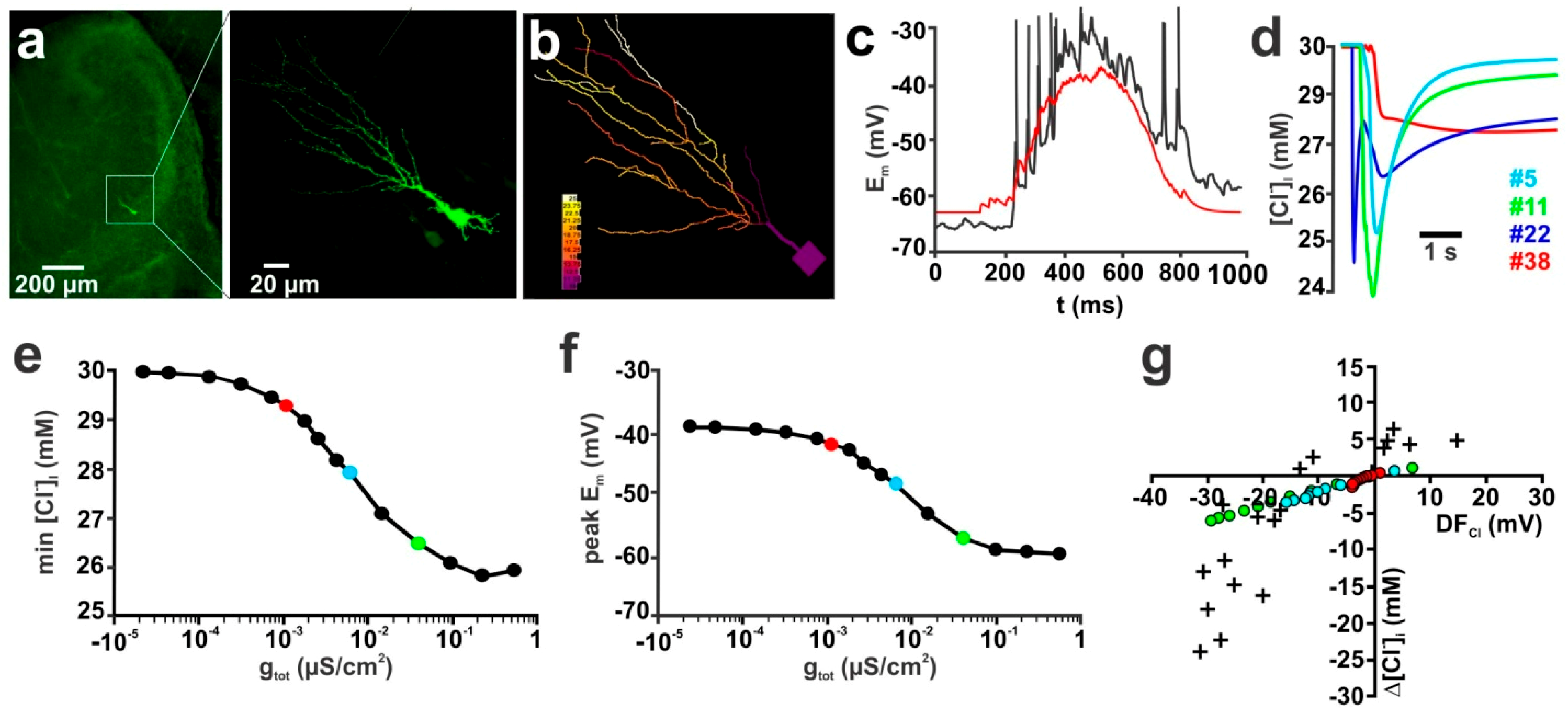
2.1. Influence of Membrane Conductance

First, we analyzed the influence of the membrane conductance on the [Cl⁻]_i changes induced by a single GABAergic input in an isolated dendrite. In this model, the experimentally determined conductance underlying single spontaneous GABAergic postsynaptic responses (g_GABA) was implemented in an isolated dendrite equipped with passive conductances (g_pas) varying between 10⁻⁶ S/cm² and 0.1 S/cm². These passive conductances correspond to input resistances (R_Input) between ca. 670 MΩ and 0.67 kΩ, respectively, when they were implemented in a reconstructed CA3 pyramidal neuron. The results of this experiment demonstrated that upon stimulation of a single GABAergic input (g_GABA = 0.789 nS, τ = 37 ms, P_HCO3 = 0, [Cl⁻]_i = 30 mM) not only the depolarization, but also the GABA-induced [Cl⁻]_i transient depended on the passive conductances. A detailed analysis revealed a strong, sigmoidal dependency between R_Input and peak [Cl⁻]_i changes (Figure 1a) or depolarization (Figure 1b) upon a single GABA stimulus. This effect of g_pas on the GABA-induced [Cl⁻]_i transients was caused by the fact that at lower g_pas the GABAergic currents induced a substantial depolarization, which attenuated the electromotive force on Cl⁻ ions (DF_Cl) during GABA stimulation (Figure 1c). At a low g_pas of 10⁻⁷ S/cm² (corresponding to a R_input of ca. 4 GΩ in the reconstructed neuron) the GABAergic depolarization reached E_Cl (Figure 1c, solid lines). Therefore, DF_Cl approximated 0 and no persistent Cl⁻ fluxes occurred. In contrast, at a g_pas of 0.018 S/cm² (corresponding to R_input of ca. 41 MΩ) E_m remained negative to E_Cl, thus enabling permanent Cl⁻ fluxes (Figure 1c, dashed lines).

Next we simulated how g_pas influences [Cl⁻]_i in a reconstructed neuron (Figure 2a,b), which receives complex GABAergic inputs that typically occur during GDP activity [45] (Figure 2c,d). For these experiments we initially equipped the dendrite with 101 GABAergic synapses (g = 0.789 nS, τ = 37 ms; all values from Lombardi et al. [45]), set P_HCO3 to 0 and used an initial [Cl⁻]_i to 30 mM. Each of these 101 GABAergic synapses was randomly distributed within the dendrites of the reconstructed neuron. The time points for the stimulation of every synapse follows a normal distribution (µ = 600ms, σ = 900 ms). These values were derived from in-vitro experiments and resemble the distribution of GABAergic inputs during a GDP [45] (Figure 2c). In order to reduce the complexity of the analysis and to mimic the procedures of [Cl⁻]_i estimation used by Lombardi et al. [45] (which estimated [Cl⁻]_i changes from changes in E_Rev determined by focal GABA application within the dendritic compartment) we use for all further analyses the average [Cl⁻]_i of all dendrites.

Using this model, we investigated how different g_pas between 10⁻⁶ S/cm² and 0.1 S/cm² affect the GDP-induced [Cl⁻]_i transients. This simulation demonstrated that also in a complex dendritic compartment g_pas critically influenced the amount of [Cl⁻]_i changes (Figure 2e). Also, under these conditions the GABAergic depolarization during a GDP approached E_Cl at low g_pas (Figure 2f), which minimized DF_Cl and the remaining Cl⁻ fluxes. One particular result of this computational study was that the GDP-induced [Cl⁻]_i transient amounts to less than 1 mM in a reconstructed CA3 pyramidal neuron equipped with the passive membrane conductance determined experimentally in these neurons (red symbols in Figure 2e–g), which is lower than the experimentally determined [Cl⁻]_i changes of 10.3 ± 3.3 mM (n = 4) in a real CA3 pyramidal neuron at comparable conditions [45]. To further specify the influence of g_pas on the GDP-induced [Cl⁻]_i transients, we simulated the peak dendritic [Cl⁻]_i change for different initial [Cl⁻]_i at three different g_pas. For this purpose we used values of 0.049 mS/cm² (corresponding to a R_Input of 901 MΩ, typical for immature hippocampal neurons [45]), 0.28 mS/cm² (189 MΩ, adult neuron in whole-cell patch-clamp configuration [46]), and 1.8 mS/cm² (41 MΩ, adult neuron with sharp electrode [47]). These simulations demonstrated that, if mature properties of g_pas were implemented in the simulated neuron, the GDP-induced [Cl⁻]_i changes were roughly comparable to the values observed in real CA3 pyramidal neurons (Figure 2g), while at g_pas typical for immature CA3 pyramidal neurons only marginal GDP-induced [Cl⁻]_i changes occurred.

In order to adapt the simulation of GDP-induced responses to the physiological properties of CA3 pyramidal neurons we incorporated an inward rectification in the background conductance (Supplementary Figure S1a,b). In addition, we had to increase the number of GABAergic synaptic inputs (n_GABA) to compensate the influence of massive space clamp problems on the experimental determination of this parameter (Supplementary Figure S1c–f). For all further simulations in the reconstructed neurons we used the inward rectifying background conductance and implemented 302, 395, and 523 GABAergic synapses for P_HCO3 values of 0.0, 0.18, and 0.44, respectively. However, even with the inward rectifying conductance and 302 synaptic inputs the GDP-induced [Cl⁻]_i changes were smaller than observed under in-vitro conditions (Supplementary Figure S1e).

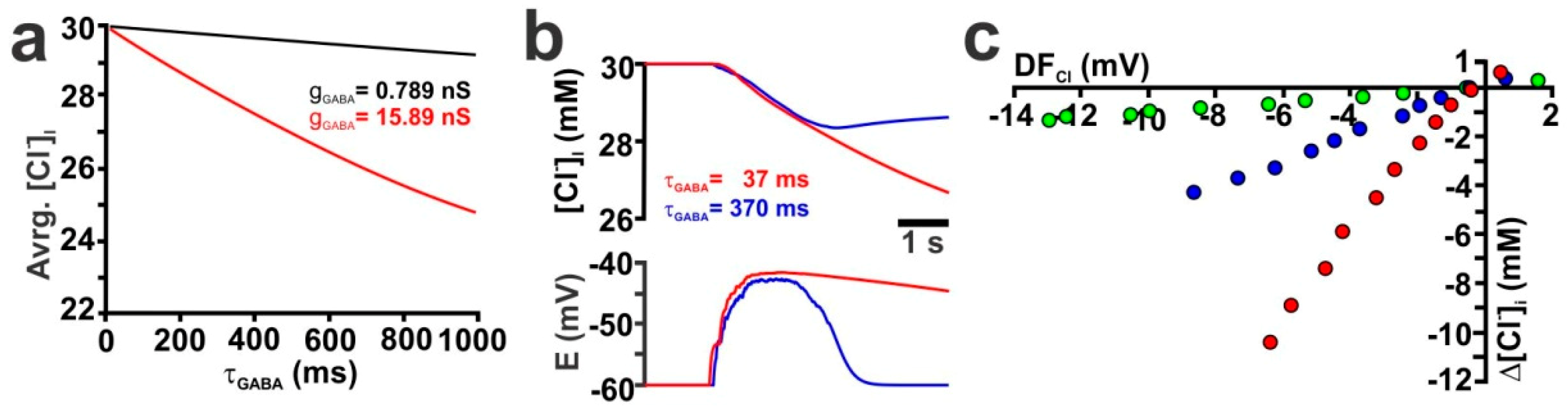
2.2. Influence of GABA Receptor Conductivity and Kinetics

Next we analyzed the influence of the GABAergic conductance (g_GABA) on [Cl⁻]_i transients. Initial experiments in an isolated dendrite showed that initially the [Cl⁻]_i transient was localized underneath the synapse, and within 3 s a diffusional equilibration throughout the dendrite occurred (Supplementary Figure S2a,b). Therefore, we estimated the total amount of GABA-evoked [Cl⁻]_i changes by averaging the [Cl⁻]_i over all nodes of the dendrite 3 s after the GABAergic stimulus. To analyze the relation between total g_GABA and the [Cl⁻]_i changes, we first systematically increase g_GABA from 0.789 nS to 78.9 nS (Figure 3a). These simulations demonstrated that the GABA-evoked [Cl⁻]_i changes rose with increasing g_GABA, but did not depend linearly on g_GABA (Figure 3b, black line). This nonlinear effect was due to the larger membrane depolarization upon stronger GABAergic stimulation, which reduced DF_Cl under this condition (data not shown). In an additional set of simulations, we enhanced the level of GABAergic stimulation by increasing the number of GABAergic synapses (n_GABA) from 1 to 100, with g_GABA of 0.789 nS for each synapse. The synapses were for each n_GABA evenly distributed across the isolated dendrite. These simulations revealed that this distributed stimulation led to a reduced relative [Cl⁻]_i decrease at higher n_GABA (Figure 3b, red line), as compared to the previous simulation paradigm (Figure 3b, black line). This observation is most probably due to the fact that with distributed synapses E_m reaches more depolarized values close to E_Cl (−56.9 mV at 1 × 78.9 nS vs. −40.7 mV at 100 × 0.789 nS, data not shown).

To investigate whether a similar dependency between the amount of GABAergic inputs and [Cl⁻]_i could also be observed during a simulated GDP in a CA3 pyramidal neuron we increased g_GABA from 0.789 nS (Figure 3c, blue line) to 7.89 nS (red line) at each of the 302 synapses used to simulate a GDP. This 10× increase in g_GABA augmented the maximal GDP-induced [Cl⁻]_i decrease from 4.3 mM to 6.8 mM (Figure 3d). This surprisingly small effect was due to the fact that the increased g_GABA also reduced the average DF_Cl from −8.6 mV to −5 mV (Figure 3d). When a similar increase in the amount of GABAergic stimulation was implemented by a 10× increase in n_GABA (from 301 to 3010) a slightly larger maximal [Cl⁻]_i decrease by 7.1 mM was observed (Figure 3c,d, green line/symbols). This result indicates that the GDP-induced [Cl⁻]_i changes were close to saturation values when realistic values for n_GABA, g_GABA and R_Input were implemented in a simulated CA3 pyramidal neuron.

In addition, we simulated how changes in the decay kinetics of GABA_A receptor-mediated currents (τ_GABA) influence the [Cl⁻]_i transients (Supplementary Figure S2c,d). Systematic variation of τ_GABA between 10 ms and 1000 ms for a single synapse (g_GABA = 0.789 nS) in an isolated dendrite revealed that the average [Cl⁻]_i showed a nearly linear dependency on τ_GABA (Figure 4a, black line). If g_GABA was increased by a factor of 20 (g_GABA = 15.78 nS) the average [Cl⁻]_i concentration still showed a nearly linear dependency on τ_GABA (Figure 4a, red line). Since these responses suggested a strong influence of τ_GABA on the GABA-induced Cl⁻ fluxes, we also varied τ_GABA of all GABAergic synapses that were implemented on the reconstructed CA3 pyramidal neurons. These simulations revealed that an increase in τ_GABA indeed increased the GDP-induced [Cl⁻]_i changes (Figure 4b). The maximal GDP-induced decline in [Cl⁻]_i increases from 1.3 mM to 4.3 mM and 10.4 mM for τ_GABA of 3.7 ms, 37 ms and 370 ms, respectively (Figure 4c).

2.3. Contribution of the HCO₃⁻ Conductance of GABA Receptors

In all previous experiments, we simulated GABA_A mediated responses under the simplified consideration that GABA_A receptors are ligand-gated Cl⁻ channels. However, GABA_A receptors are anion channels with a considerable HCO₃⁻ permeability [1]. The relative HCO₃⁻-permeability of GABA_A receptors (P_HCO3) ranges between 0.18 (determined in spinal cord neurons [48]) and 0.44 (determined in adult hippocampal neurons [49]), although also higher values have been suggested [1]. Therefore, we next simulated how P_HCO3 affects GABAergic E_m and [Cl⁻]_i responses upon stimulation of a single synapse in an isolated dendrite. Addition of a HCO₃⁻ conductance to GABAergic currents induce a depolarizing shift in the peak depolarizations induced by GABAergic stimulation (Supplementary Figure S3a,b). Since this additional depolarization affected the DF_Cl, the GABAergic [Cl⁻]_i changes were also influenced by P_HCO3. Under particular conditions, i.e. when E_m crossed E_Cl during synaptic responses, the GABAergic activation lead to biphasic [Cl⁻]_i changes (Figure 5a). For further analysis we plotted for such biphasic responses the maximal and minimal [Cl⁻]_i upon GABAergic stimulation (e.g. Figure 5b, blue lines). A systematic analysis of the effect of GABAergic inputs on the [Cl⁻]_i changes revealed that the [Cl⁻]_i changes were shifted towards more outward fluxes at higher P_HCO3 (Figure 5b), indicating that with increasing P_HCO3 a substantial [Cl⁻]_i increase is induced by GABAergic stimulation.

However, these initial assumptions neglect the fact that the HCO₃⁻ fluxes will also affect [HCO₃⁻]_i. Rapid regeneration of [HCO₃⁻]_i levels by carbonic anhydrases, which stabilize [HCO₃⁻]_i, is absent in immature neurons [50]. Therefore, we first simulated the GABA-induced E_m and [Cl⁻]_i changes under the assumption that HCO₃⁻ will not be replenished (by implementing a HCO₃⁻ relaxation time constant (τ_HCO3⁻) of 10 min) and is only redistributed by diffusion. These simulations revealed that the activation of GABA_A receptors induced a rapid decline in [HCO₃⁻]_i (Supplementary Figure S3c). The [HCO₃⁻]_i decline depended on both P_HCO3 and [Cl⁻]_i and was maximal at low [Cl⁻]_i with values of 1.8 mM and 2.3 mM for P_HCO3 of 0.18 and 0.44, respectively (Figure 5c). In line with this [HCO₃⁻]_i decline, the GABAergic depolarization was drastically decreased (Figure 5d) under dynamic [HCO₃⁻]_i conditions. The attenuation of activity-dependent [HCO₃⁻] gradients also reduced the size of associated [Cl⁻]_i changes (Figure 5e) and at intermediate [Cl⁻]_i even reversed the effect (Supplementary Figure S3d).

As suggested from the results in isolated dendrites, the GDP-induced depolarization simulated in the reconstructed neuron was augmented if P_HCO3 was increased from 0.0 to 0.18 and 0.44 under the assumption of stable [HCO₃⁻] gradients (Figure 6a,c, shaded symbols). And because under these conditions E_m could become positive to E_Cl, the Cl⁻ fluxes were enhanced and GDP-induced [Cl⁻]_i transients increased (Figure 6a,d, shaded symbols). Increasing P_HCO3 shifted the [Cl⁻]_i level at which GDP-induced [Cl⁻]_i transients change from influx to efflux, reflecting the impact of E_HCO3 on the DF_CL. The maximal influence of P_HCO3 on the [Cl⁻]_i changes was observed at low [Cl⁻]_i (Figure 6d, shaded symbols), because at these conditions, the depolarizing effect of HCO₃⁻ fluxes opposed the hyperpolarizing effects of E_Cl.

Implementation of a model that allowed dynamic [HCO₃⁻]_i changes (using a τ_HCO3 of 10 min) in the reconstructed CA3 pyramidal neuron showed that the GDP-induced GABAergic currents induced massive changes in [HCO₃⁻]_i, depending on P_HCO3 (Supplementary Figure S3e). This GDP-induced [HCO₃⁻]_i decrease during a GDP diminished the membrane depolarization (Figure 6b,c, plain lines/symbols), which in turn caused a drastic reduction in the GDP-induced [Cl⁻]_i transients (Figure 6b,d, plain lines/symbols). In summary, addition of P_HCO3 to GABAergic currents augmented the DF_Cl and thus the GDP-induced [Cl⁻]_i transients (Figure 6e). Using these parameters, the simulated GDP-induced [Cl⁻]_i transients resembled the size of [Cl⁻]_i transients observed in real cells, however, only in the quadrant with positive DF_Cl values (Figure 6e).

2.4. The Stability of HCO₃⁻ Gradients Influences Activity-Dependent [Cl⁻]_i Transients

The previous results clearly demonstrate that GABA_A receptor-mediated [HCO₃⁻]_i transients massively influence the E_m and [Cl⁻]_i changes under these conditions. However, the two conditions used in these experiments (stable [HCO₃⁻]_i or negligible [HCO₃⁻]_i regeneration at τ_HCO3 of 10 min) are obviously not physiological in immature neurons, which lack carbonic anhydrases, but in which spontaneous CO₂ hydration and/or transmembrane transport of HCO₃⁻ can occur [50]. Therefore, we next investigated how τ_HCO3 influences the stability of [HCO₃⁻] gradients and GABA induced [Cl⁻]_i transients. For that we systematically changed the decay-time of [HCO₃⁻]_i relaxation (τ_HCO3) implemented in the NEURON model (Supplementary Figure S4a,b). A systematic simulation in isolated dendrites revealed that [Cl⁻]_i changes remained rather constant at τ_HCO3 ≥ 90 ms (Figure 7a). The half-maximal [Cl⁻]_i changes occurred at a τ_HCO3 around 10 ms, which is substantially shorter than the τ_HCO3 of ca. 70 ms for half-maximal [HCO₃⁻]_i changes (Supplementary Figure S4b). More than 85% of the maximal [Cl⁻]_i changes took place at τ_HCO3 below 100 ms (Figure 7a). However, it must also be considered that a decreased temporal stability of the [HCO₃⁻] gradient will also influence the lateral diffusion of HCO₃⁻. Indeed, a systematic simulation of the spatial aspects of the activity-dependent [HCO₃⁻]_i transients revealed that the stability of HCO₃⁻ massively influenced the [HCO₃⁻] gradient along the isolated dendrite (Figure 7b), although the maximal [HCO₃⁻]_i change at the synaptic site was nearly saturated already at a τ_HCO3 ≥ 90 ms (Figure 7b). In accordance with the results obtained in isolated dendrites, also in the reconstructed CA3 pyramidal neuron τ_HCO3 had a large effect on the GDP-induced [HCO₃⁻]_i transients (Supplementary Figure S4c,d), but only a minor effect on the associated [Cl⁻]_i changes (Figure 7c). For τ_HCO3 ≥ 90 ms the GDP-induced [Cl⁻]_i changes were only marginally affected (Figure 7c, Supplementary Figure S4c) by changes in τ_HCO3. At τ_HCO3 of 1 ms, the maximal GDP-induced [Cl⁻]_i decrease amounted to 5.2 mM, while it was 4.6 mM, 4.5 mM and 4.4 mM for τ_HCO3 values of 90 ms, 518 ms and 3 s, respectively. This small effect was also reflected by the minimal changes in the relation between DF_Cl and GDP-induced [Cl⁻]_i transients (Figure 7d).

GABAergic [51] and glutamatergic [52,53] synaptic transmission is accompanied by substantial pH changes. These pH changes, however, indirectly affect GABAergic transmission, since they alter the [HCO₃⁻]_i. To estimate, how such pH changes influence activity-dependent [Cl⁻]_i transients, we first simulated the effect of such pH shifts by constantly altering the pH value from 7.2 to 7.0 or 7.4 in an isolated dendrite. According to the Henderson-Hasselbalch equation, these pH shifts alter [HCO₃⁻]_i from 14.1 mM to 9 mM or 22.7 mM, respectively. Because this pH-dependent differences in [HCO₃⁻]_i affect DF_GABA, the membrane depolarization upon GABA_A receptor activation was reduced at pH 7.0 and enhanced at a more alkaline pH of 7.4 (Figure 8a). In line with this altered GABAergic membrane depolarization, the DF_Cl during GABAergic stimulation was also affected, shifting the resulting Cl⁻ fluxes. This can be exemplified at intermediate [Cl⁻]_i, where the biphasic Cl⁻ fluxes at a normal pH of 7.2, were transformed to Cl⁻ efflux at a pH of 7.0 and to a Cl⁻ influx at a pH of 7.4 (Figure 8a). A systematic analysis of Cl⁻ fluxes at different initial [Cl⁻]_i demonstrated that, in comparison to pH 7.2, the Cl⁻ influx at low initial [Cl⁻]_i was decreased at pH 7.0, while it was enhanced at pH 7.4 (Figure 8b). In contrast, the Cl⁻ efflux at high [Cl⁻]_i was enhanced at pH 7.0 and reduced at pH 7.4 (Figure 8d). In consequence, intracellular acidification shifted the [Cl⁻]_i range at which Cl⁻ efflux occurs to lower initial [Cl⁻]_i, whereas intracellular alkalinization shifted this range to higher initial [Cl⁻]_i (Figure 8b).

Simulations in the reconstructed CA3 pyramidal neuron revealed that a lower pH of 7.0 led to smaller GDP-induced membrane depolarizations, as compared to the standard pH of 7.2 (Figure 8c, Supplementary Figure S4e, red line/symbols). This reduced depolarization resulted in a reduced GDP-associated Cl⁻ influx (4.6 mM vs. 7.6 mM) at low initial [Cl⁻]_i and in an increased Cl⁻ efflux (−6.1 mM vs. −4.3 mM) at high initial [Cl⁻]_i concentration (Figure 8d, red symbols). Conversely, at a higher pH of 7.4 the membrane responses during a GDP were more depolarized (Figure 8c, Supplementary Figure S4e green lines/symbols), which resulted in enhanced Cl⁻ influx of 11.2 mM at low initial [Cl⁻]_i and a decreased Cl⁻ efflux of −2.3 mM at low [Cl⁻]_i (Figure 8d, green symbols). In summary, these results demonstrate that the acidification associated with synaptic transmission reduced the activity-dependent [Cl⁻]_i transients at low [Cl⁻]_i, while the activity-dependent Cl⁻ efflux at high [Cl⁻]_i was enhanced by such acidic shifts.

2.5. Influence of Transmembrane Cl⁻ Transport

Finally, we analyzed how the kinetics of the [Cl⁻]_i homeostasis influenced the temporal and spatial constrains of the activity-dependent [Cl⁻]_i changes. For that we systematically changed the decay-time of the [Cl⁻]_i relaxation (τ_Cl) implemented in the NEURON model. Initial simulations in isolated and soma-attached dendrites revealed that for τ_Cl of ≥ 10 s the decay of [Cl⁻]_i response was dominated by diffusional exchange with the soma (Supplementary Figure S4f–h). At a τ_Cl of 321 s 99.2% of Cl⁻ fluxes were depleted by diffusional exchange with the soma, while at faster τ_Cl a substantial smaller fraction of only 83.5 % (τ_Cl = 10 s), 33.2 % (τ_Cl = 1 s) and 2.4% (τ_Cl = 100 ms) of the Cl⁻ fluxes was eliminated by diffusion from the dendrite to the soma. Analysis of the spatial distribution of [Cl⁻]_i along the dendrite revealed that τ_Cl also affects the size of activity-dependent [Cl⁻]_i changes at distant dendritic sites (Supplementary Figure S4i–k). The dominance of diffusional elimination of Cl⁻ was also reflected by the observation that at slow τ_Cl ≤ 10s the [Cl⁻]_i was substantial lower at the proximal than at the distal end of the dendrite (Supplementary Figure S4i–k).

To analyze the influence of τ_Cl on the spatial aspects of the [Cl⁻]_i transients we implemented two simultaneous GABAergic inputs that were located equidistant to the [Cl⁻]_i recording site at distances of 10 µm, 30 µm, 100 µm and 300 µm and systematically increased τ_Cl from 1 ms to 220 s (Figure 9a). These simulations revealed not only that the maximal [Cl⁻]_i depended on the distance between GABAergic stimulation sites and the node of [Cl⁻]_i determination, but also that τ_Cl critically influenced the [Cl⁻]_i change at a given distance to the stimulation sites (Figure 9a). This dependency between spatial restrictions of activity-dependent [Cl⁻]_i changes and τ_Cl was quantified by the τ_Cl at which half-maximal [Cl⁻]_i changes occur (τ^Cl₅₀). If the distance of the GABAergic synapses was 10 µm τ^Cl₅₀ amounted to 12 ms, and this τ^Cl₅₀ increased to 60.5 ms, 726 ms and 4.6 s at synaptic distances of 30 µm, 100 µm and 300 µm, respectively. To analyze the temporal aspects of [Cl⁻]_i summation we simulated five consecutive GABA stimulations at frequencies (f_GABA) of 0.3 Hz, 1 Hz, 3 Hz and 10 Hz and determine the [Cl⁻]_i at the stimulation site, while systematically varying τ_Cl (Figure 9b). These simulations revealed a sigmoidal dependency between τ_Cl and the temporal summation of [Cl⁻]_i. A larger amount of [Cl⁻]_i summation and a lower τ^Cl₅₀ was observed at higher frequencies. The τ^Cl₅₀ amounted to 1.9 s for f_GABA of 0.1 Hz, 931 ms for f_GABA of 1 Hz, 268 ms for f_GABA of 3 Hz, and 53 ms for f_GABA of 10 Hz. In summary, these results demonstrated that τ_Cl values of less than 1 s are required to prevent substantial activity-dependent [Cl⁻]_i changes in the spatial and/or temporal domain at f_GABA ≥ 1Hz and less than 100 µm distance between synaptic sites.

In accordance with these results in single dendrites, all previous simulations of GDP-induced [Cl⁻]_i transients in the reconstructed CA3 pyramidal cells revealed substantial [Cl⁻]_i changes, because in these simulations the experimentally determined τ_Cl of 174 s for NKCC1-mediated active Cl⁻ re-accumulation and of 321 s for passive Cl⁻ reduction were implemented and during a GDP stimulation a high frequency of GABAergic input was applied. In order to get more insights into how the capacity of [Cl⁻]_i regulation systems can influence activity-dependent [Cl⁻]_i transients within a realistic dendritic compartment, we finally simulated how different τ_Cl influenced the GDP-induced [Cl⁻]_i transients in the reconstructed CA3 neuron (Figure 9c,d). This simulation revealed that decreasing τ_Cl from the experimentally determined values >100 s to 10 s or 1 s had only a minimal impact of the GDP-induced [Cl⁻]_i transients (Figure 9c). The maximal GDP-induced [Cl⁻]_i change amounted to 4.41 mM at a τ_Cl of 10 s and to 4.21 mM at a τ_Cl of 1 s, but were reduced to 2.99 mM at a τ_Cl of 0.1 s and to 0.88 mM at a τ_Cl of 10 ms. These results demonstrate that fast and efficient [Cl⁻]_i homeostatic processes are required to limit GDP-induced [Cl⁻]_i transients. Accordingly, the Δ[Cl⁻]_i vs. DF_Cl plot also revealed comparable GDP-induced [Cl⁻]_i changes at τ_Cl of 10 s and 1 s, and smaller [Cl⁻]_i changes at a τ_Cl of 100 ms (Figure 9d). Only a further reduction in τ_Cl to 10 ms substantially suppressed GDP-induced [Cl⁻]_i changes. In summary, these results indicate that τ_Cl influences the temporal and spatial properties of activity-dependent [Cl⁻]_i changes, but that τ_Cl values that are substantially smaller than the experimentally determined values are required to suppress activity-dependent [Cl⁻]_i changes.

3. Discussion

In the present study we used a detailed biophysical compartmental modeling in the NEURON environment to systematically investigate how several cellular and molecular neuronal parameters influence the GABA_A receptor-mediated [Cl⁻]_i changes. The main observations of this study can be summarized as follows: (i) A high R_input reduces activity-dependent [Cl⁻]_i transients, while at low R_input considerable activity-dependent [Cl⁻]_i transients can be observed. (ii) The activity-dependent [Cl⁻]_i transients show a logarithmic impact of g_GABA, while τ_GABA has in a wide g_GABA range a nearly linear influence on [Cl⁻]_i. (iii) The P_HCO3 of GABA_A-receptors enhances activity-dependent [Cl⁻]_i transients, but with instable [HCO₃⁻] gradients this effect is largely diminished. (iv) Activity-dependent Cl⁻ fluxes where shifted toward efflux at acidic and towards influx at alkaline pH. (v) τ_Cl has a major impact on the spatiotemporal aspects of activity-dependent [Cl⁻]_i transients, but unrealistically fast τ_Cl values are required to prevent [Cl⁻]_i transients at physiologically-relevant activity levels.

By 1990, it was suggested by Qian and Sejnowski [54] that the Cl⁻ fluxes via activated GABA_A receptors will dissipate the Cl⁻ gradient in small compartments and thus mediate potentially instable inhibitory responses. This theoretical assumption was proven by experimental studies, which demonstrated that massive GABAergic activation can shift hyperpolarizing responses toward depolarization [12,21] and induce [Cl⁻]_i transients [55]. In the past the physiological and pathophysiological consequences of such activity-dependent [Cl⁻]_i changes have been investigated and discussed [13,17,20,36,56] and the basic principles of activity-dependent [Cl⁻]_i changes and their implications for neuronal information processing have been modeled [7,15,16,22,57,58]. However, the complex interplay and contribution of passive membrane leak, GABA_A conductance, Cl⁻ diffusion/ transport and stability of [HCO₃⁻] gradients to these activity-dependent [Cl⁻]_i changes have not yet been systematically investigated.

Our simulations revealed a strong dependence between R_Input and the GABA_A receptor induced [Cl⁻]_i transients. While at high R_Input GABA-induced [Cl⁻]_i changes were minimal, they increased in a nonlinear relation with decreasing R_Input (Figure 1c). This relation between R_Input and the [Cl⁻]_i changes is due to the fact that at high R_Input even small GABAergic currents bring E_m close to E_Cl, which minimizes DF_Cl and thus the Cl⁻ fluxes (Figure 1c). At low R_Input the passive membrane conductance stabilizes E_m and thus DF_Cl. In consequence, larger Cl⁻ fluxes can be expected. Accordingly, implementation of “adult like” membrane properties [47] in a reconstructed immature neuron massively enhanced activity-dependent [Cl⁻]_i changes (Figure 1c). In contrast, it seems obvious that immature neurons, with their high R_Input [59], are less susceptible to activity-dependent [Cl⁻]_i changes.

However, in this respect, it is important to consider that in immature neurons [Cl⁻]_i is high and GABAergic responses are depolarizing [30,60,61], therefore activity-dependent Cl⁻ fluxes are directed outward and are leading to [Cl⁻]_i decrease [42,44]. In addition, the HCO₃⁻-permeability of GABA_A receptors also needs to be considered. The high R_Input in immature neurons causes E_m to approach E_GABA, which normally is positive to E_Cl due to the HCO₃⁻-permeability of GABA_A-receptors [1,4]. Therefore, stable Cl⁻ influx would be expected under this condition and [Cl⁻]_i should ultimately approach the value defined by E_HCO3, which at steady-state HCO₃⁻ gradients ([HCO₃⁻]_i = 14.1 mM and [HCO₃⁻]_e = 26 mM) amounts to 72.4 mM. This estimation suggests that under certain conditions GABAergic activity can even increase [Cl⁻]_i from the already high [Cl⁻]_i-levels in immature neurons (see Supplementary Figure S3d). But further properties of activity-dependent [Cl⁻]_i changes observed in our simulations protect immature neurons from excessive [Cl⁻]_i increases. In particular, we found that the influence of P_HCO3 is relatively small at high [Cl⁻]_i (Figure 6d), due to the fact that under this condition the contribution of E_HCO3 to E_GABA is small (as described by the Goldman-Hodgkin-Katz-Equation [1]). In addition, in immature neurons the HCO₃⁻ gradient is instable because they lack carbonic anhydrases [50], which additionally attenuates the depolarizing effect of HCO₃⁻ on E_m and thus reduces DF_Cl.

Under the assumption of a stable HCO₃⁻ gradient, E_GABA is in a wide range positive to E_Cl, thereby permitting Cl⁻ influx during GABAergic stimulation, unless the thermodynamics equilibrium at 72.4 mM is reached. This is supported by the observation that no stable steady-state [Cl⁻]_i is reached with realistic P_HCO3⁻ values of 0.18 or 0.44 in our simulation (Supplementary Figure S3d, shaded lines). Experimental studies indeed demonstrated that massive GABAergic stimulation can shift E_GABA from hyperpolarizing towards depolarizing and even excitation [12,62,63,64]. On the other hand, if we implemented in our model that [HCO₃⁻]_i can be altered by GABA_A receptors, the activity-dependent [Cl⁻]_i changes were massively reduced (Figure 5e). Our simulations also demonstrate that the switch from static [HCO₃⁻] to dynamic [HCO₃⁻] condition shifts the [Cl⁻]_i setpoint at which activity-dependent Cl⁻ influx was replaced by Cl⁻ efflux to considerably lower values (Figure 5e). This observation is due to the fact that the depolarizing HCO₃⁻ fluxes through the GABA_A receptor are attenuated by the dissipating HCO₃⁻ gradient, which reduces E_GABA and thus DF_Cl. Similar conclusions were drawn from experiments in which a block of carbonic anhydrases with acetazolamide, which provides a pharmacological destabilization of [HCO₃⁻], also reduces E_GABA shifts ([18], but see [62]). We conclude from these observations that the lack of carbonic anhydrase VII in immature neurons [50,65] may serve to limit the activity-dependent [Cl⁻]_i changes in these neurons.

On the other hand, our simulations in a reconstructed CA3 pyramidal neuron revealed that although massive [HCO₃⁻]_i changes are induced under this condition, the total GDP-induced [Cl⁻]_i change was only marginally affected by variations in τ_HCO3 (Figure 7d). This lack of effect was most probably due to the fact that the activity-dependent [HCO₃⁻]_i change was already maximal at a τ_HCO3 of 90 ms at the synaptic site. This local saturated [HCO₃⁻]_i change at the subsynaptic site is the only determinant for the synaptic effects of the [HCO₃⁻]_i. Our simulations also suggest that for an effective, physiologically relevant control of [HCO₃⁻]_i during GABAergic activity τ_HCO3 should be less than 70 ms (Supplementary Figure S4b). This fast relaxation time requires fast molecular processes that allow effective elimination of HCO₃⁻. Indeed, carbonic anhydrases, the enzymes that mediate the degradation or regeneration of HCO₃⁻ into/from H₂O and CO₂, are among the fastest enzymes known. The k_cat of murine carbonic anhydrase VII for the hydration oh CO₂ is 4.5 × 10⁵ s⁻¹ at physiological pH [66]. From the assumption that the ca. 2mM [HCO₃⁻]_i change in the dendrite corresponds at a dendritic volume of 16 pL to ca. 0.3 fmol HCO₃⁻ ions, it can be estimated that about 4000 molecules of carbonic anhydrase VII are required to replenish the lost HCO₃⁻ within 100 ms. This estimation suggests that it is reasonable that sufficient carbonic anhydrase activity can be located in the dendritic compartment to reliably stabilize [HCO₃⁻]_i. However, as the reaction mediated by carbonic anhydrases includes H⁺ ions, the kinetics and thermodynamics of this process depends on the intracellular pH [67]. Thus dendritic H⁺-buffering and handling indirectly also affects activity-dependent [Cl⁻]_i changes [15]. The acidification associated with neuronal activity [52,53] will slow down the kinetics of carbonic anhydrases [66]. However, this effect is negligible in comparison to the effect of the intracellular pH on [HCO₃⁻]_i. The intracellular pH is an essential parameter that determines [HCO₃⁻]_i [67]. Thus the intracellular acidification observed upon activation of GABAergic and glutamatergic synapses [51,52,53] will alter [HCO₃⁻]_i and subsequently influence GABAergic transmission. Our simulation revealed that an intracellular acidification will reduce the activity-dependent [Cl⁻]_i changes at low [Cl⁻]_i. This result, which is in accordance with a previous simulation [15], indicate that in adult neurons a parallel acidification will limit Cl⁻ influx and thus stabilize inhibitory transmission In contrast, at a high [Cl⁻]_i typical for immature neuron the intracellular acidification enhanced the activity-dependent Cl⁻ efflux and may contribute to the loss of depolarizing drive and putative excitatory effects after strong GABAergic stimulation.

Another factor that has a stringent effect on activity-dependent [Cl⁻]_i changes in our simulations is τ_GABA. This confirmed and extended previous computational analyses (c.f. Figure 4d in [7]). It has been found that in general the decay kinetics of GABAergic transmission get faster during development [68]. Therefore the slow decay kinetics of GABAergic transmission in immature neurons [68,69] may be a factor that enables activity-dependent [Cl⁻]_i transients, while the faster GABAergic postsynaptic currents in mature neurons not only improve the temporal precision of GABAergic transmission [68], but also the stability of inhibition. While a stable inhibition is a prerequisite for the proper function of mature neuronal networks, dynamic changes in [Cl⁻]_i can be mandatory for physiological relevant functional features of the immature central nervous system. It has been suggested that activity-dependent changes in [Cl⁻]_i, and the resulting switch from GABAergic inhibition to excitation, can underlie oscillatory activity [13]. In addition, in the immature nervous system the resting [Cl⁻]_i is decreased by GABAergic activity, which will result in a diminished excitatory drive and/or a dominance of shunting inhibition and may thus serve to limit a possible excitatory effect of GABA [40]. Therefore, for immature neurons an unstable [Cl⁻]_i homeostasis may be functionally relevant, as it allows activity-dependent scaling of [Cl⁻]_i-dependent synaptic transmission [42,43].

In consequence, the molecular configuration of immature neurons (high [Cl⁻]_i, long τ_GABA and missing CA-VII) will generate conditions that allow limited activity-dependent [Cl⁻]_i decreases. This, in addition to the aforementioned effect of the high input resistance, may be an explanation why the [Cl⁻]_i homeostasis of immature neurons is maintained by a relatively ineffective transmembrane Cl⁻ transport [29]. In contrast, in mature neurons the situation is different. In the adult brain, the low [Cl⁻]_i is needed to maintain hyperpolarizing inhibition [1] and an activity-dependent [Cl⁻]_i increase will attenuate membrane hyperpolarization. While it is obvious that massive changes in [Cl⁻]_i will impair GABAergic inhibition and can lead to hyperexcitability [18], recent modeling experiments demonstrate that even minimal changes in the capacity of Cl⁻-extrusion can have strong effects on information processing and storage in neurons [22]. Although the low R_Input and the fast τ_GABA counteracts activity-dependent [Cl⁻]_i increase in adult neurons, their low [Cl⁻]_i and their effective carbonic anhydrases can lead to substantial [Cl⁻]_i changes in their dendrite. The adverse effect of such local activity-dependent [Cl⁻]_i increases is enhanced by the more elaborated dendritic compartment in mature neurons, which limits diffusional elimination of Cl⁻-ions [13].

Our simulations reveal that the connection of an isolated dendrite to the soma drastically reduces the equilibrium [Cl⁻]_i after synaptic stimulation (Supplementary Figure S4f–k), demonstrating the important role of diffusional Cl⁻ elimination under this condition. The large volume to surface ratio (and thus volume to conductance ratio) of the soma enables this compartment to serve as Cl⁻ sink in these in-silico experiments. Also in-vitro it has been demonstrated that activation of dendritic GABA_A receptors induced massive shifts in E_GABA, whereas only minimal changes were observed upon perisomatic stimulation [10,12,26]. The dominance of perisomatic GABAergic terminals [70] may be related to the requirement of stable [Cl⁻] gradients to maintain stable inhibition over a wide range of activity levels. However, the diffusion of [Cl⁻]_i through dendrite is a relatively slow and inefficient process, due to the small diameter in distal dendrites [7,55]. Addition of spines to dendrites drastically slow down diffusion along dendrites [16], suggesting that the complexity of the dendritic compartment (i.e. the number of arborizations that enhance tortuosity in the dendritic compartment) hinders Cl⁻-elimination by diffusion to the soma. Therefore, active elimination of Cl⁻ from the cytoplasm is required to prevent or minimize activity-dependent [Cl⁻]_i changes in the elaborated dendritic compartment of adult neurons.

The elementary role of transmembrane Cl⁻ transporters for neuronal [Cl⁻]_i homeostasis has been shown by a variety of studies [2,29,32,58,71]. Modeling studies revealed that slightly altered rates of transmembrane Cl⁻-transport, which does only marginally affect resting [Cl⁻]_i levels, have a strong effect on the spatiotemporal distribution of activity-dependent [Cl⁻]_i-transients in dendrites [15]. Therefore it is not surprising that the simulation of an enhanced capacity of transmembrane Cl⁻ transport by increasing τ_Cl attenuates activity-dependent [Cl⁻]_i transients. However, to minimize these [Cl⁻]_i transients a rather low τ_Cl of < 100 ms is required. These low τ_Cl values are several orders of magnitude below the experimentally determined kinetics of the NKCC1-mediated Cl⁻-accumulation (τ_Cl = 158 s) in immature neurons [29]. Because of this slow kinetic of transmembrane transport of Cl⁻ in immature neurons, we also consider that a Cl⁻/HCO₃⁻ exchange mediated by the anion exchanger in immature neurons [72] has only a marginal effect on both activity-dependent [Cl⁻]_i and [HCO₃⁻]_i transients in these neurons. In the mature situation (low [Cl⁻]_i and effective transmembrane [Cl⁻]_i transport), modeling studies suggest that an interference between [Cl⁻]_i and [HCO₃⁻]_i by this mechanism can reduce the activity-dependent [Cl⁻]_i changes [15].

While it is generally assumed that the neuron-specific Cl⁻-extruder KCC2 mediates more efficient Cl⁻ transport than NKCC1, only few experimental studies addressed the kinetics of KCC2-dependent Cl⁻-extrusion. Experiments in brain stem neurons demonstrated that KCC2 mediated Cl⁻-extrusion after [Cl⁻]_i increase by ca. 10 mM requires several minutes [73]. In contrast, in-vivo experiments revealed that the activity-dependent [Cl⁻]_i increase after an epileptic seizure recovered within less than 30 s [9] and in hippocampal slices GABA-induced [Cl⁻]_i transients recovered back to low steady-stale levels with a time constant of 3.3 s [12]. However, it is not clear how diffusional processes and/or the kinetics of the used Cl⁻ sensor contribute to these kinetic properties. Simulations suggest that with realistic KCC2 levels τ_Cl in the distal dendrites (≥ 200 µm from the soma) is between 100 ms and 200 ms [15], and thus probably lower than estimated from experimental data. Even this time constant is higher than the τ_Cl required in our simulations to prevent local activity-dependent [Cl⁻]_i changes, suggesting that considerable [Cl⁻]_i changes can occur at GABAergic synaptic sites. While our and other simulations [15] suggest these transients may be restricted to local dendritic domains, it must be emphasized that subtle changes in the efficacy of KCC2 mediated Cl⁻-transport can already enhance the excitability in single neurons because activity-dependent [Cl⁻]_i transients may superimpose these effects [22]. In consequence, impairments of KCC2 mediated Cl⁻ transport can led to a breakdown of sufficient inhibition in neuronal networks and contribute to hyperexcitability [15,17,20,56,74]. In this respect it is also relevant to consider that the activity of both NKCC1 and KCC2 are regulated by a variety of processes [75,76,77,78]. This indicates that the spatiotemporal [Cl⁻]_i dynamics in the dendritic compartment may be adapted to the functional states.

The limitation of our model to fully describe GDP-induced [Cl⁻]_i transients in CA3 pyramidal neurons is obvious from the fact, that we massively underestimate the [Cl⁻]_i decrease observed in real CA3 pyramidal neurons at high [Cl⁻]_i (e.g. Figure 6e). Therefore, additional factors must be proposed, which enhance the GABA_A-receptor-mediated Cl⁻ efflux. Possible mechanisms that improve Cl⁻ efflux are e.g. an inhomogeneous distribution of voltage-activated K⁺ channels in the dendritic compartment, an underestimation of n_GABA in our in-vitro experiments due to voltage-clamp errors in the elaborated dendrite [79], or the effect of glutamatergic transmission during a GDP [20,80]. In addition, we also found that τ_GABA has a major impact on the GDP-induced [Cl⁻]_i transients, and it might well be that the decay kinetics of spontaneous GABAergic PSCs of 37 ms [45] reflect the kinetic properties of a subpopulation of GABAergic inputs, that is less involved in the generation of GDPs. Finally, in our simulations the dendrite was implemented as a hollow tube with a diameter determined from the histological reconstruction. Under realistic assumptions the neuron is, however, filled with cytoplasm that contains large proteins, particles of different sizes and vesicles and tubes of intracellular organelles. Thus the free, “unexcluded” volume in the cytoplasm is restricted to an estimated fraction of ca. 60%, a principle termed cytoplasmic crowding [81]. This restricted free cytoplasmic water volume will increase the size of [Cl⁻]_i transients upon identical Cl⁻ fluxes.

4. Materials and Methods

Compartmental Modeling

The biophysically realistic compartmental modelling was performed using the NEURON environment (neuron.yale.edu). The source code of models and stimulation files used in the present paper can be found in ModelDB [82] at http://modeldb.yale.edu/253369 (access date 14 March 2019) and was included in the supplementary material of this publication. For compartmental modelling we used either a simple ball and stick model (soma with d = 20 µm, linear dendrite with l = 200 µm and 103 nodes) or a reconstructed CA3 pyramidal cell (from Lombardi et al. [45]). Except where noted the dendrite was detached from the soma to analyse dendritic [Cl⁻]_i transients. The reconstructed neuron resembled the somatodendritic morphology of a typical immature CA3 pyramidal neuron (see Figure 2a,b). For this purpose images of a biocytin-filled neuron [83,84] were taken with 60× oil-immersion objectives and the somatodendritic morphology was reconstructed using Fiji (www.fiji.sc). It contained a soma (d = 15 µm), a dendritic trunk (d = 2 µm, l = 32 µm, 9 segments) and 56 dendrites (d = 0.36 µm, 9 segments each). In all of these compartments a specific axial resistance (R_a) of 34.5 Ωcm and a specific membrane capacitance (C_m) of 1 µF cm⁻²; were implemented. The specific membrane conductance (g_pas) varied (see Figure 1a and Figure 2e) and in the majority of the experiments was modeled by a voltage dependent process given by a Boltzmann-like equation:

$${\mathrm{g}}_{\mathrm{pas}}={\mathrm{g}}_{\min }+\frac{{\mathrm{g}}_{\max }}{\left(1+\exp \left(\frac{\left({\mathrm{E}}_{\mathrm{m}}-{\mathrm{E}}_{50}\right)}{\mathrm{s}}\right)\right)}$$

(1)

with g_max = 0.002800 S/cm² (experimentally determined g_Input at depolarized potentials, see Supplementary Figure S1a), gmin = 0.000660 S/cm² (experimentally determined minimal g_Input at hyperpolarized potentials, see Figure 3a), e50 = −31 mV (half-maximal voltage), s = −6 (slope of the voltage-dependency). The reversal potential of this voltage-depended g_pas was set to −60 mV.

GABA_A synapses were simulated as a postsynaptic parallel Cl⁻ and HCO₃⁻ conductance with exponential rise and exponential decay [7]:

I_GABA = I_Cl + I_HCO3 = 1/(1+P) g_GABA (V–E_Cl) + P/(1+P) g_GABA (V–E_HCO3)

(2)

where P is a fractional ionic conductance that was used to split the GABA_A conductance (g_GABA) into Cl⁻ and HCO₃⁻ conductance. E_Cl and E_HCO3 were calculated from Nernst equation. The GABA_A conductance was modeled using a two-term exponential function, using separate values of rise time (0.5 ms) and decay time (variable, mostly 37 ms) [45]. Parameters used in our simulations were as follows: [Cl⁻]_o = 133.5 mM, [HCO₃⁻]_i = 14.1 mM, [HCO₃⁻]_o = 24 mM, temperature = 31 °C, P = 0.44 [49]. For the ball and stick model a single GABA_A synapse was placed in the middle of the dendrite, except where noted. For the simulation of a GDP in the reconstructed CA3 neuron 101–3020 GABAergic synapses were randomly distributed within the dendrites of the reconstructed neuron. GABA inputs were activated stochastically using a normal distribution (µ = 600ms, σ = 900 ms) that emulates the distribution of GABAergic PSCs during a GDP observed in immature hippocampal CA3 pyramidal neurons [45]. The properties of these synapses were always given in the results part and/or the corresponding figure legends.

From the quotient between the charge transfer of a GDP and of spontaneous GABAergic postsynaptic currents at a holding potential (V_Hold) of 0 mV it was estimated that 101 GABAergic inputs underlie a GDP [45]. To compensate for the space-clamp problems during a GDP, that were not considered by Lombardi et al. [45], we simulated the charge transfer during a GDP under their experimental conditions ([Cl⁻]_i = 10 mM, V_Hold = 0 mV) and determined that 302, 395, and 523 (for P_HCO3 values of 0.0, 0.18, and 0.44, respectively) GABAergic synapses are required to generate the observed GDP-induced charge transfer (Supplementary Figure S1c–f). For these experiments we implement the single-electrode voltage clamp procedure provided by NEURON, using an access resistance of 5 MΩ. The charge transfer was calculated from the integral of the holding currents (I_Hold) during the GDP.

For the modeling of the GABA_A receptor-induced [Cl⁻]_i and [HCO₃⁻]_i changes, we calculated ion diffusion and uptake by standard compartmental diffusion modeling [16,85,86,87]. To simulate intracellular Cl⁻ and HCO₃⁻ dynamics, we adapted our previously published model [7]. Longitudinal Cl⁻ and HCO₃⁻ diffusion along dendrites was modeled as the exchange of anions between adjacent compartments. For radial diffusion, the volume was discretized into a series of 4 concentric shells around a cylindrical core [85] and Cl⁻ or HCO₃⁻ was allowed to flow between adjacent shells [88]. The free diffusion coefficient of Cl⁻ inside neurons was set to 2 µm²/ms [55,89]. Since the cytoplasmatic diffusion constant for HCO₃⁻ is, to our knowledge, unknown, we also used a value of 2 µm²/ms. To simulate transmembrane transport of Cl⁻ and HCO₃⁻, we implemented an exponential relaxation process for [Cl⁻]_i and [HCO₃⁻]_i to resting levels [Cl⁻]_i^rest or [HCO₃⁻]_i^rest with a time constant τ_Ion.

$$\frac{\mathrm{d}{\left[{\mathrm{Ion}}^{-}\right]}_{\mathrm{i}}}{\mathrm{dt}}=\frac{{\left[{\mathrm{Ion}}^{-}\right]}_{\mathrm{i}}^{\mathrm{rest}}-\mathrm{e}{\left[{\mathrm{Ion}}^{-}\right]}_{\mathrm{i}}}{{\mathsf{\tau }}_{\mathrm{Ion}}}$$

(3)

Cl⁻ transport was in most experiments (if not otherwise noted) modeled as bimodal process, for [Cl⁻]_i < [Cl⁻]_i^rest τ_Ion was set to 174 s to emulate an NKCC1-like Cl⁻ transport mechanism. For [Cl⁻]_i > [Cl⁻]_i^rest τ_Ion was set to 321 s to emulate passive Cl⁻ efflux (both values obtained from unpublished experiments on immature rat CA3 hippocampal neurons).

The impact of GABAergic Cl⁻ currents on [Cl⁻]_i and [HCO₃⁻]_i was calculated as:

$$\frac{\mathrm{d}{\left[{\mathrm{Ion}}^{-}\right]}_{\mathrm{i}}}{\mathrm{dt}}=\frac{1}{\mathrm{F}}\frac{{\mathrm{I}}_{\mathrm{Ion}}}{\mathrm{volume}}$$

(4)

To simulate the GABAergic activity during a GDP, a unitary peak conductance of 0.789 nS and a decay of 37 ms were applied to each GABAergic synapse. These values resulted in a unitary currents of pA, which was in accordance with the mean amplitude of spontaneous GABAergic postsynaptic currents in CA3 paramidal neurons [45].

For the isolated neurons the [Cl⁻]_i and [HCO₃⁻]_i concentration was averaged over all segments of the dendrite, except where noted. For the simulated neurons we analyzed mean [Cl⁻]_i and [HCO₃⁻]_i of all dendrites:

$${\left[\mathrm{C}{\mathrm{l}}^{-}\right]}_{\mathrm{i}}=\frac{1}{n_{dend}}\times {\displaystyle \sum }_{j=1}^{n_{dend}}{\left[\mathrm{C}{\mathrm{l}}^{-}\right]}_{\mathrm{i}}^{Dend\left(j\right)@0.5oftotallength}$$

(5)

This procedure mimics the experimental procedure of Lombardi et al [45], who determined E_GABA by focal application in the dendritic compartment.

For the calculation of Δ[Cl⁻]_i the maximal deviation of [Cl⁻]_i upon a GABAergic stimulus ([Cl⁻]_i^S) was subtracted from the resting [Cl⁻]_i before the stimulus ([Cl⁻]_i^R). For biphasic responses both minimal and maximal [Cl⁻]_i^R were determined and Δ[Cl⁻]_i was calculated as:

$$\Delta {\left[\mathrm{C}{\mathrm{l}}^{-}\right]}_{\mathrm{i}}={\left[\mathrm{C}{\mathrm{l}}^{-}\right]}_{\mathrm{i}}^{\mathrm{S},\min }-{\left[\mathrm{C}{\mathrm{l}}^{-}\right]}_{\mathrm{i}}^{\mathrm{R}}\mathrm{i}\mathrm{f}abs\left({\left[\mathrm{C}{\mathrm{l}}^{-}\right]}_{\mathrm{i}}^{\mathrm{S},\min }\right)>abs\left({\left[\mathrm{C}{\mathrm{l}}^{-}\right]}_{\mathrm{i}}^{\mathrm{S},\max }\right)$$

(6)

$$\Delta {\left[\mathrm{C}{\mathrm{l}}^{-}\right]}_{\mathrm{i}}={\left[\mathrm{C}{\mathrm{l}}^{-}\right]}_{\mathrm{i}}^{\mathrm{S},\max }-{\left[\mathrm{C}{\mathrm{l}}^{-}\right]}_{\mathrm{i}}^{\mathrm{R}}\mathrm{i}\mathrm{f}abs\left({\left[\mathrm{C}{\mathrm{l}}^{-}\right]}_{\mathrm{i}}^{\mathrm{S},\min }\right)\le abs\left({\left[\mathrm{C}{\mathrm{l}}^{-}\right]}_{\mathrm{i}}^{\mathrm{S},\max }\right)$$

(7)

The driving-force of Cl⁻ (DF_Cl) was calculated from the difference between the average E_m during a GDP and E_Cl (DF_Cl = E_m – E_Cl). To calculate the ratio between transmembrane [Cl⁻]_i transport and diffusional [Cl⁻]_i depletion into the soma, we normalized the diffusional exchange between the last somatic node and the soma (as calculated from Fick’s law) to conditions were transmembrane [Cl⁻]_i loss was absent (τ_Cl = 10⁹ ms) and diffusional dendrite to soma transport was allowed to equilibrate for 2 min.

All electrophysiological data were taken from our previous publication [45]. However, for a comparison of these results with the simulations, we had to take different P_HCO3 into account. Therefore the GDP-induced [Cl⁻]_i changes were recalculated using P_HCO3 values of 0.0, 0.18 (determined in spinal cord neurons [48]) and 0.44 (determined in adult hippocampal neurons [49]). The [Cl⁻]_i was calculated from E_GABA with the Goldman-Hodgkin-Katz equation:

$${\mathrm{E}}_{\mathrm{GGABA}}=\frac{\mathrm{RT}}{\mathrm{ZF}}\times \ln \left(\frac{{\mathrm{P}}_{\mathrm{C}\mathrm{l}}{\left[\mathrm{C}{\mathrm{l}}^{-}\right]}_{\mathrm{e}}+{\mathrm{P}}_{{\mathrm{HCO}}_3}{\left[{\mathrm{HCO}}_3{}^{-}\right]}_{\mathrm{e}}}{{\mathrm{P}}_{\mathrm{C}\mathrm{l}}{\left[\mathrm{C}{\mathrm{l}}^{-}\right]}_{\mathrm{i}}+{\mathrm{P}}_{{\mathrm{HCO}}_3}{\left[{\mathrm{HCO}}_3{}^{-}\right]}_{\mathrm{i}}}\right)$$

(8)

For the calculation of [Cl⁻]_i from E_GABA we used a [Cl⁻]_e of 133.5 mM, an extracellular HCO₃⁻ concentration ([HCO₃⁻]_e) of 24 mM and assumed a constant [HCO₃⁻]_i of 14.1 mM (calculated from an intracellular pH of 7.2 [90], a CO₂ pressure (pCO₂) of 38 mmHg, a Henry coefficient (α) of 0.0318 mM/mmHg and a pKs of 6.128 [91] with the Henderson-Hasselbalch equation), if not otherwise mentioned.

$${\left[{\mathrm{HCO}}_3{}^{-}\right]}_{\mathrm{i}}={10}^{\left(\mathrm{pH}-\mathrm{pKs}+\log \left(\mathsf{\alpha }\times {\mathrm{pCO}}_2\right)\right)}$$

(9)

R_Input was calculated from the E_m response upon a simulated current injection (I_Inj) according to Ohms law:

$${\mathrm{R}}_{\mathrm{Input}}=\frac{{\mathrm{E}}_{\mathrm{m}}}{{\mathrm{I}}_{\mathrm{I}\mathrm{n}\mathrm{j}}}$$

(10)