Understanding the Binding Induced Folding of Intrinsically Disordered Proteins by Protein Engineering: Caveats and Pitfalls
Abstract
:1. Introduction
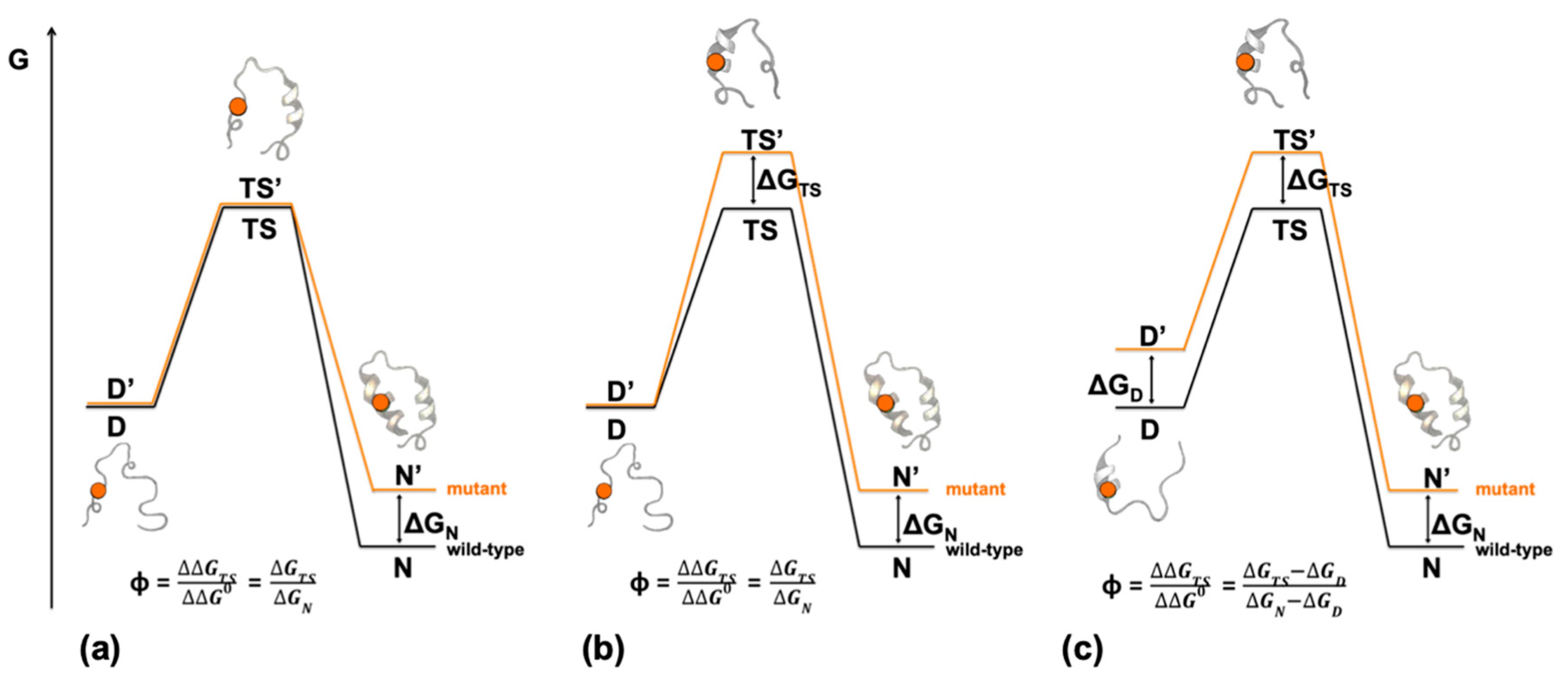
2. Depicting Reaction Mechanisms at Nearly Atomic Resolution—Design and Principles of Φ Value Analysis
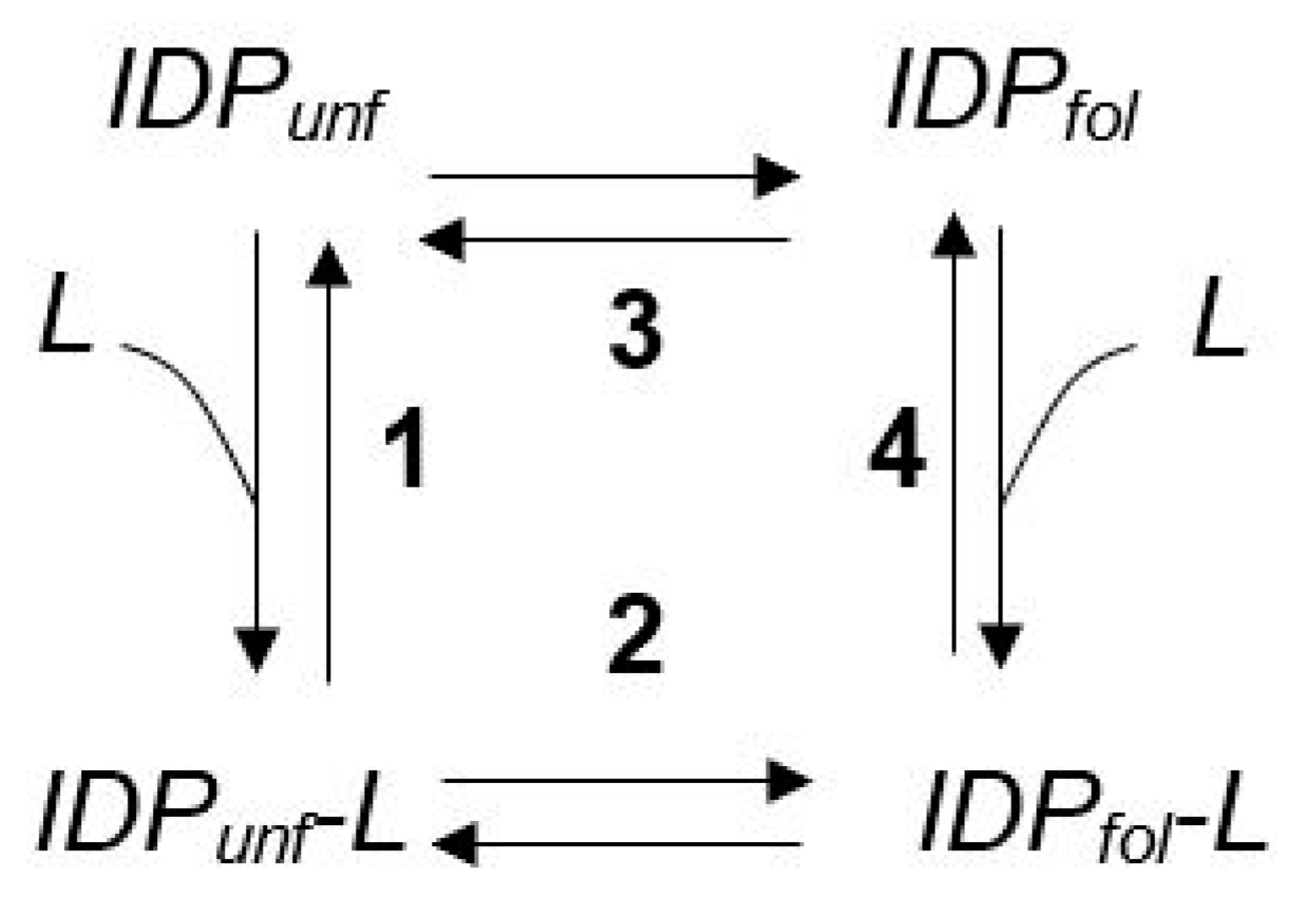
3. The Φ Value Analysis in IDPs
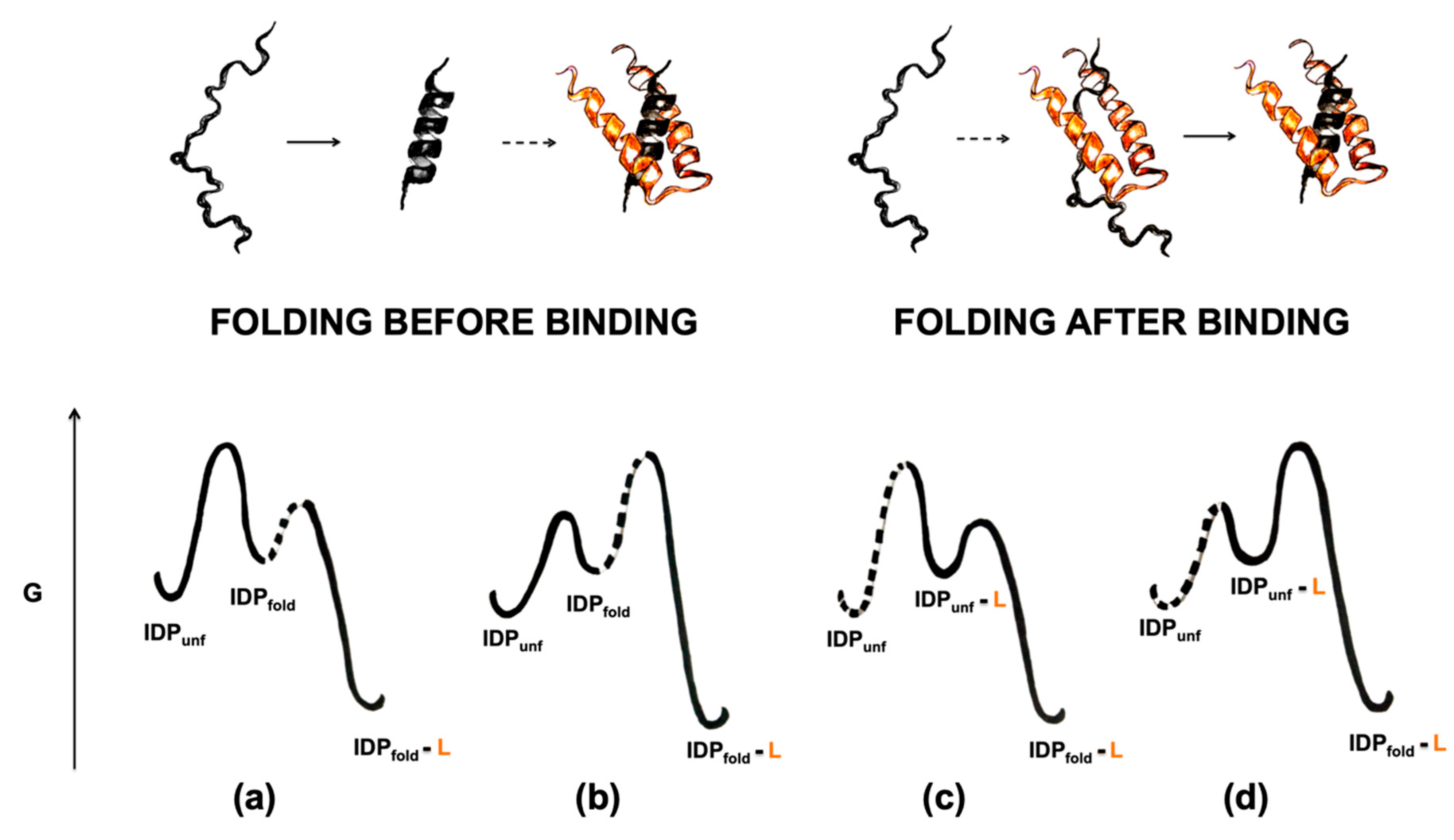
4. On the Cooperative Nature of Induced Folding and the Φ Value Analysis in IDPs
4.1. Folding before Binding
4.2. Folding after Binding
5. The Residual Structure of IDPs
6. Folding Pathway Malleability of IDPs
7. Additional Tests—Double Mutant Cycle and Φ−Φ Plots
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Uversky, V.N. Intrinsic disorder, protein–protein interactions, and disease. Adv. Protein Chem. Struct. Biol. 2018, 110, 85–121. [Google Scholar] [CrossRef]
- Schramm, A.; Bignon, C.; Brocca, S.; Grandori, R.; Santambrogio, C.; Longhi, S. An arsenal of methods for the experimental characterization of intrinsically disordered proteins—How to choose and combine them? Arch. Biochem. Biophys. 2019, 676, 108055. [Google Scholar] [CrossRef] [PubMed]
- Pauwels, K.; Lebrun, P.; Tompa, P. To be disordered or not to be disordered: Is that still a question for proteins in the cell? Cell. Mol. Life Sci. 2017, 74, 3185–3204. [Google Scholar] [CrossRef] [PubMed]
- Berlow, R.; Dyson, H.J.; Wright, P.E. Expanding the paradigm: Intrinsically disordered proteins and allosteric regulation. J. Mol. Biol. 2018, 430, 2309–2320. [Google Scholar] [CrossRef] [PubMed]
- Adamski, W.; Salvi, N.; Maurin, D.; Magnat, J.; Milles, S.; Jensen, M.R.; Abyzov, A.; Moreau, C.J.; Blackledge, M. A unified description of intrinsically disordered protein dynamics under physiological conditions using NMR spectroscopy. J. Am. Chem. Soc. 2019, 141, 17817–17829. [Google Scholar] [CrossRef]
- Dunker, A.K.; Silman, I.; Uversky, V.N.; Sussman, J.L. Function and structure of inherently disordered proteins. Curr. Opin. Struct. Biol. 2008, 18, 756–764. [Google Scholar] [CrossRef]
- Tantos, Á.; Han, K.-H.; Tompa, P. Intrinsic disorder in cell signaling and gene transcription. Mol. Cell. Endocrinol. 2012, 348, 457–465. [Google Scholar] [CrossRef] [PubMed]
- Tompa, P. Unstructural biology coming of age. Curr. Opin. Struct. Biol. 2011, 21, 419–425. [Google Scholar] [CrossRef]
- Berlow, R.; Dyson, H.J.; Wright, P.E. Functional advantages of dynamic protein disorder. FEBS Lett. 2015, 589, 2433–2440. [Google Scholar] [CrossRef] [Green Version]
- Bignon, C.; Troilo, F.; Gianni, S.; Longhi, S. Modulation of measles virus NTAIL interactions through fuzziness and sequence features of disordered binding sites. Biomolecules 2018, 9, 8. [Google Scholar] [CrossRef] [Green Version]
- Crabtree, M.D.; Mendonca, C.A.T.F.D.; Bubb, Q.; Clarke, J. Folding and binding pathways of BH3-only proteins are encoded within their intrinsically disordered sequence, not templated by partner proteins. J. Biol. Chem. 2018, 293, 9718–9723. [Google Scholar] [CrossRef] [Green Version]
- Dogan, J.; Gianni, S.; Jemth, P. The binding mechanisms of intrinsically disordered proteins. Phys. Chem. Chem. Phys. 2014, 16, 6323–6331. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dosnon, M.; Bonetti, D.; Morrone, A.; Erales, J.; Di Silvio, E.; Longhi, S.; Gianni, S. Demonstration of a folding after binding mechanism in the recognition between the measles virus NTAIL and X domains. ACS Chem. Biol. 2015, 10, 795–802. [Google Scholar] [CrossRef] [PubMed]
- Gianni, S.; Dogan, J.; Jemth, P. Coupled binding and folding of intrinsically disordered proteins: What can we learn from kinetics? Curr. Opin. Struct. Biol. 2016, 36, 18–24. [Google Scholar] [CrossRef]
- Shammas, S.; Crabtree, M.D.; Dahal, L.; Wicky, B.I.M.; Clarke, J. Insights into coupled folding and binding mechanisms from kinetic studies. J. Biol. Chem. 2016, 291, 6689–6695. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dahal, L.; Kwan, T.O.; Shammas, S.L.; Clarke, J. pKID binds to KIX via an unstructured transition state with nonnative interactions. Biophys. J. 2017, 113, 2713–2722. [Google Scholar] [CrossRef] [Green Version]
- Borgia, A.; Borgia, M.B.; Bugge, K.; Kissling, V.M.; Heidarsson, P.O.; Fernandes, C.B.; Sottini, A.; Soranno, A.; Buholzer, K.; Nettels, D.; et al. Extreme disorder in an ultrahigh-affinity protein complex. Nature 2018, 555, 61–66. [Google Scholar] [CrossRef] [Green Version]
- Tuttle, L.M.; Pacheco, D.; Warfield, L.; Luo, J.; Ranish, J.; Hahn, S.; Klevit, R.E. Gcn4-mediator specificity is mediated by a large and dynamic fuzzy protein-protein complex. Cell Rep. 2018, 22, 3251–3264. [Google Scholar] [CrossRef] [Green Version]
- Fuxreiter, M. Fold or not to fold upon binding—Does it really matter? Curr. Opin. Struct. Biol. 2019, 54, 19–25. [Google Scholar] [CrossRef]
- Miskei, M.; Horváth, A.; Vendruscolo, M.; Fuxreiter, M. Sequence-based determinants and prediction of fuzzy interactions in protein complexes. J. Mol. Biol. 2020, 432, 2289–2303. [Google Scholar] [CrossRef]
- Olsen, J.G.; Teilum, K.; Kragelund, B.B. Behaviour of intrinsically disordered proteins in protein–protein complexes with an emphasis on fuzziness. Cell. Mol. Life Sci. 2017, 74, 3175–3183. [Google Scholar] [CrossRef] [PubMed]
- Toto, A.; Malagrinò, F.; Visconti, L.; Troilo, F.; Pagano, L.; Brunori, M.; Jemth, P.; Gianni, S. Templated folding of intrinsically disordered proteins. J. Biol. Chem. 2020, 295, 6586–6593. [Google Scholar] [CrossRef] [Green Version]
- Fersht, A.R.; Sato, S. Phi-value analysis and the nature of protein-folding transition states. Proc. Natl. Acad. Sci. USA 2004, 101, 7976–7981. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bonetti, D.; Troilo, F.; Brunori, M.; Longhi, S.; Gianni, S. How robust is the mechanism of folding-upon-binding for an intrinsically disordered protein? Biophys. J. 2018, 114, 1889–1894. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bonetti, D.; Troilo, F.; Toto, A.; Brunori, M.; Longhi, S.; Gianni, S. Analyzing the folding and binding steps of an intrinsically disordered protein by protein engineering. Biochemistry 2017, 56, 3780–3786. [Google Scholar] [CrossRef] [PubMed]
- Crabtree, M.D.; Borcherds, W.; Poosapati, A.; Shammas, S.L.; Daughdrill, G.W.; Clarke, J. Conserved helix-flanking prolines modulate intrinsically disordered protein:target affinity by altering the lifetime of the bound complex. Biochemistry 2017, 56, 2379–2384. [Google Scholar] [CrossRef]
- Dogan, J.; Mu, X.; Engström, Å.; Jemth, P. The transition state structure for coupled binding and folding of disordered protein domains. Sci. Rep. 2013, 3, 2076. [Google Scholar] [CrossRef] [Green Version]
- Giri, R.; Morrone, A.; Toto, A.; Brunori, M.; Gianni, S. Structure of the transition state for the binding of c-Myb and KIX highlights an unexpected order for a disordered system. Proc. Natl. Acad. Sci. USA 2013, 110, 14942–14947. [Google Scholar] [CrossRef] [Green Version]
- Iesmantavicius, V.; Dogan, J.; Jemth, P.; Teilum, K.; Kjaergaard, M. Helical propensity in an intrinsically disordered protein accelerates ligand binding. Angew. Chem. Int. Ed. 2014, 53, 1548–1551. [Google Scholar] [CrossRef] [Green Version]
- Karlsson, E.; Andersson, E.; Dogan, J.; Gianni, S.; Jemth, P.; Camilloni, C. A structurally heterogeneous transition state underlies coupled binding and folding of disordered proteins. J. Biol. Chem. 2019, 294, 1230–1239. [Google Scholar] [CrossRef] [Green Version]
- Karlsson, O.A.; Chi, C.N.; Engström, Å.; Jemth, P. The transition state of coupled folding and binding for a flexible β-finger. J. Mol. Biol. 2012, 417, 253–261. [Google Scholar] [CrossRef] [PubMed]
- Rogers, J.M.; Oleinikovas, V.; Shammas, S.L.; Wong, C.T.; De Sancho, D.; Baker, C.M.; Clarke, J. Interplay between partner and ligand facilitates the folding and binding of an intrinsically disordered protein. Proc. Natl. Acad. Sci. USA 2014, 111, 15420–15425. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rogers, J.M.; Wong, C.T.; Clarke, J. Coupled folding and binding of the disordered protein PUMA does not require particular residual structure. J. Am. Chem. Soc. 2013, 136, 5197–5200. [Google Scholar] [CrossRef] [PubMed]
- Toto, A.; Gianni, S. Mutational analysis of the binding-induced folding reaction of the mixed-lineage leukemia protein to the KIX domain. Biochemistry 2016, 55, 3957–3962. [Google Scholar] [CrossRef]
- Toto, A.; Giri, R.; Brunori, M.; Gianni, S. The mechanism of binding of the KIX domain to the mixed lineage leukemia protein and its allosteric role in the recognition of c-Myb. Protein Sci. 2014, 23, 962–969. [Google Scholar] [CrossRef] [Green Version]
- Jackson, S.E.; Fersht, A.R. Folding of chymotrypsin inhibitor 2. 1. Evidence for a two-state transition. Biochemistry 1991, 30, 10428–10435. [Google Scholar] [CrossRef]
- Gianni, S.; Ivarsson, Y.; Jemth, P.; Brunori, M.; Travaglini-Allocatelli, C. Identification and characterization of protein folding intermediates. Biophys. Chem. 2007, 128, 105–113. [Google Scholar] [CrossRef] [Green Version]
- Matouschek, A.; Kellis, J.T.; Serrano, L.; Bycroft, M.; Fersht, A.R. Transient folding intermediates characterized by protein engineering. Nature 1990, 346, 440–445. [Google Scholar] [CrossRef]
- Eyring, H. The activated complex in chemical reactions. J. Chem. Phys. 1935, 3, 107. [Google Scholar] [CrossRef]
- Meng, F.; Uversky, V.N.; Kurgan, L. Comprehensive review of methods for prediction of intrinsic disorder and its molecular functions. Cell. Mol. Life Sci. 2017, 74, 3069–3090. [Google Scholar] [CrossRef]
- Daggett, V.; Fersht, A.R. Is there a unifying mechanism for protein folding? Trends Biochem. Sci. 2003, 28, 18–25. [Google Scholar] [CrossRef]
- Troilo, F.; Bonetti, D.; Bignon, C.; Longhi, S.; Gianni, S. Understanding intramolecular crosstalk in an intrinsically disordered protein. ACS Chem. Biol. 2019, 14, 337–341. [Google Scholar] [CrossRef] [PubMed]
- Koshland, D.E.; Nemethy, G.; Filmer, D. Comparison of experimental binding data and theoretical models in proteins containing subunits. Biochemistry 1966, 5, 365–385. [Google Scholar] [CrossRef]
- Monod, J.; Wyman, J.; Changeux, J.-P. On the nature of allosteric transitions: A plausible model. J. Mol. Biol. 1965, 12, 88–118. [Google Scholar] [CrossRef]
- Sen, S.; Udgaonkar, J.B. Binding-induced folding under unfolding conditions: Switching between induced fit and conformational selection mechanisms. J. Biol. Chem. 2019, 294, 16942–16952. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Gao, M.; Xiong, J.; Su, Z.; Huang, Y. Features of molecular recognition of intrinsically disordered proteins via coupled folding and binding. Protein Sci. 2019, 28, 1952–1965. [Google Scholar] [CrossRef]
- Collins, A.P.; Anderson, P.C. Complete coupled binding–folding pathway of the intrinsically disordered transcription factor protein brinker revealed by molecular dynamics simulations and markov state modeling. Biochemistry 2018, 57, 4404–4420. [Google Scholar] [CrossRef]
- Lindström, I.; Dogan, J. Native hydrophobic binding interactions at the transition state for association between the TAZ1 domain of CBP and the disordered TAD-STAT2 are not a requirement. Biochemistry 2017, 56, 4145–4153. [Google Scholar] [CrossRef]
- Cho, J.-H.; Raleigh, D.P. Denatured state effects and the origin of nonclassical φ values in protein folding. J. Am. Chem. Soc. 2006, 128, 16492–16493. [Google Scholar] [CrossRef]
- Fuxreiter, M.; Simon, I.; Friedrich, P.; Tompa, P. Preformed structural elements feature in partner recognition by intrinsically unstructured proteins. J. Mol. Biol. 2004, 338, 1015–1026. [Google Scholar] [CrossRef]
- Tompa, P. The interplay between structure and function in intrinsically unstructured proteins. FEBS Lett. 2005, 579, 3346–3354. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kim, D.-H.; Han, K.-H. Transient secondary structures as general target-binding motifs in intrinsically disordered proteins. Int. J. Mol. Sci. 2018, 19, 3614. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nwanochie, E.; Uversky, V.N. Structure determination by single-particle cryo-electron microscopy: Only the sky (and intrinsic disorder) is the limit. Int. J. Mol. Sci. 2019, 20, 4186. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kragelj, J.; Blackledge, M.; Jensen, M.R. Ensemble calculation for intrinsically disordered proteins using NMR parameters. Adv. Exp. Med. Biol. 2015, 870, 123–147. [Google Scholar] [CrossRef] [PubMed]
- Sibille, N.; Bernadó, P. Structural characterization of intrinsically disordered proteins by the combined use of NMR and SAXS. Biochem. Soc. Trans. 2012, 40, 955–962. [Google Scholar] [CrossRef] [Green Version]
- Fuertes, G.; Banterle, N.; Ruff, K.M.; Chowdhury, A.; Mercadante, D.; Koehler, C.; Kachala, M.; Girona, G.E.; Milles, S.; Mishra, A.; et al. Decoupling of size and shape fluctuations in heteropolymeric sequences reconciles discrepancies in SAXS vs. FRET measurements. Proc. Natl. Acad. Sci. USA 2017, 114, E6342–E6351. [Google Scholar] [CrossRef] [Green Version]
- Fersht, A.R. Structure and Mechanism in Protein Science; Freeman: New York, NY, USA, 1999. [Google Scholar]
- Leffler, J.E. Parameters for the description of transition states. Science 1953, 117, 340–341. [Google Scholar] [CrossRef]
- Toto, A.; Camilloni, C.; Giri, R.; Brunori, M.; Vendruscolo, M.; Gianni, S. Molecular recognition by templated folding of an intrinsically disordered protein. Sci. Rep. 2016, 6, 21994–22000. [Google Scholar] [CrossRef]
- Horovitz, A.; Fleisher, R.C.; Mondal, T. Double-mutant cycles: New directions and applications. Curr. Opin. Struct. Biol. 2019, 58, 10–17. [Google Scholar] [CrossRef]
- Calosci, N.; Chi, C.N.; Richter, B.; Camilloni, C.; Engström, Å.; Eklund, L.; Travaglini-Allocatelli, C.; Gianni, S.; Vendruscolo, M.; Jemth, P. Comparison of successive transition states for folding reveals alternative early folding pathways of two homologous proteins. Proc. Natl. Acad. Sci. USA 2008, 105, 19241–19246. [Google Scholar] [CrossRef] [Green Version]
- Gianni, S.; Jemth, P. Conserved nucleation sites reinforce the significance of Phi value analysis in protein-folding studies. IUBMB Life 2014, 66, 449–452. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Di Silvio, E.; Brunori, M.; Gianni, S. Frustration sculpts the early stages of protein folding. Angew. Chem. Int. Ed. Engl. 2015, 54. [Google Scholar] [CrossRef] [PubMed]
- Ivarsson, Y.; Travaglini-Allocatelli, C.; Brunori, M.; Gianni, S. Engineered symmetric connectivity of secondary structure elements highlights malleability of protein folding pathways. J. Am. Chem. Soc. 2009, 131, 11727–11733. [Google Scholar] [CrossRef] [PubMed]
- Longhi, S. Structural disorder within paramyxoviral nucleoproteins. FEBS Lett. 2015, 589, 2649–2659. [Google Scholar] [CrossRef] [PubMed]


© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Malagrinò, F.; Visconti, L.; Pagano, L.; Toto, A.; Troilo, F.; Gianni, S. Understanding the Binding Induced Folding of Intrinsically Disordered Proteins by Protein Engineering: Caveats and Pitfalls. Int. J. Mol. Sci. 2020, 21, 3484. https://doi.org/10.3390/ijms21103484
Malagrinò F, Visconti L, Pagano L, Toto A, Troilo F, Gianni S. Understanding the Binding Induced Folding of Intrinsically Disordered Proteins by Protein Engineering: Caveats and Pitfalls. International Journal of Molecular Sciences. 2020; 21(10):3484. https://doi.org/10.3390/ijms21103484
Chicago/Turabian StyleMalagrinò, Francesca, Lorenzo Visconti, Livia Pagano, Angelo Toto, Francesca Troilo, and Stefano Gianni. 2020. "Understanding the Binding Induced Folding of Intrinsically Disordered Proteins by Protein Engineering: Caveats and Pitfalls" International Journal of Molecular Sciences 21, no. 10: 3484. https://doi.org/10.3390/ijms21103484
APA StyleMalagrinò, F., Visconti, L., Pagano, L., Toto, A., Troilo, F., & Gianni, S. (2020). Understanding the Binding Induced Folding of Intrinsically Disordered Proteins by Protein Engineering: Caveats and Pitfalls. International Journal of Molecular Sciences, 21(10), 3484. https://doi.org/10.3390/ijms21103484





