PremPRI: Predicting the Effects of Missense Mutations on Protein–RNA Interactions
Abstract
:1. Introduction
2. Results and Discussion
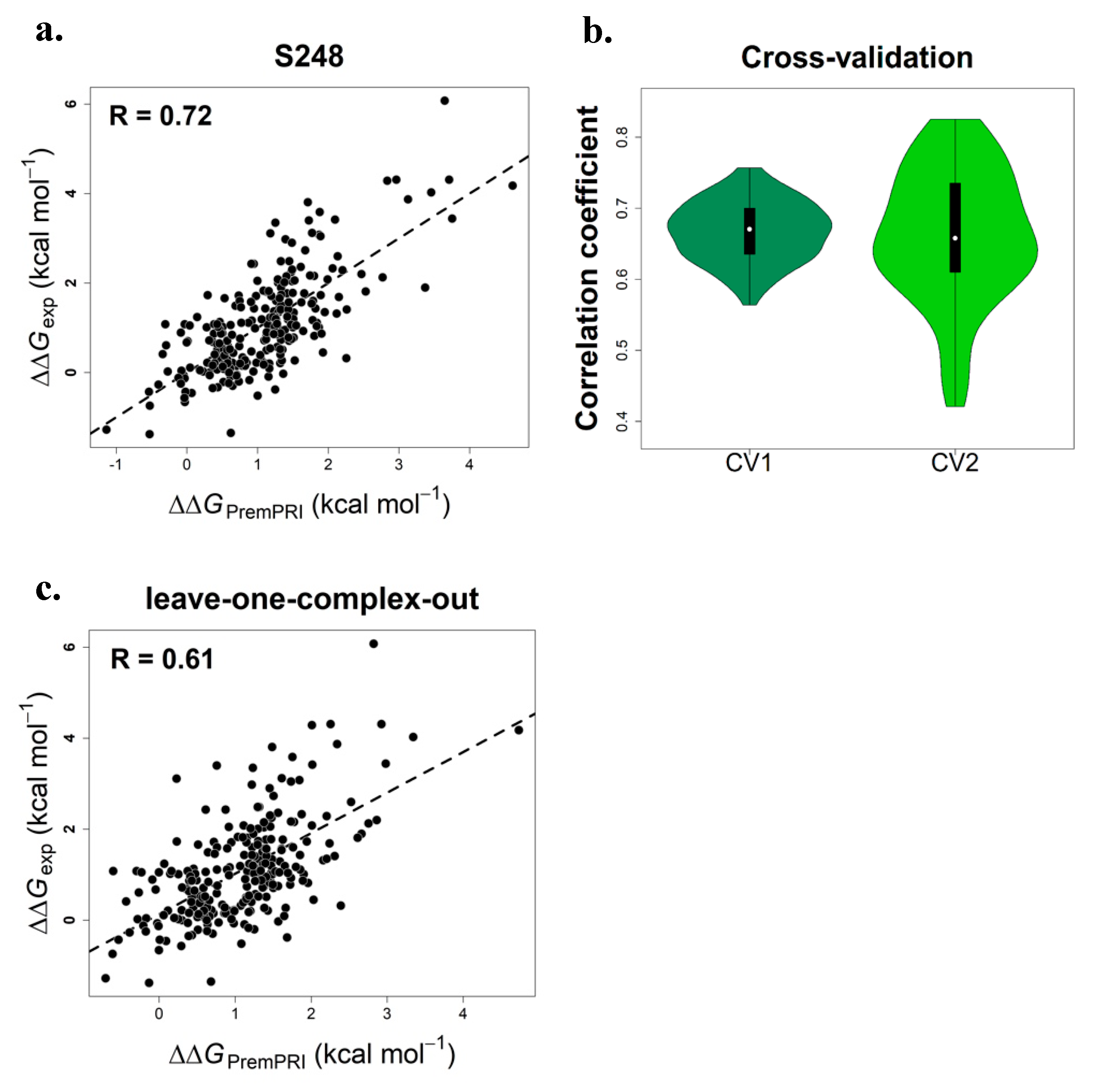
2.1. Multiple Linear Regression Model of PremPRI
2.2. Performance on Three Types of Cross-Validation
2.3. Comparison with Other Methods
2.4. Online Webserver
2.4.1. Input
2.4.2. Output
3. Methods
3.1. Experimental Datasets Used for Training
3.2. Structural Optimization Protocol
3.3. The PremPRI Model
- is the difference of van der Waals interaction energies between mutant and wild type (). is the difference of van der Waals energies between a protein–RNA complex and each binding partner (Partner 1: protein; Partner 2: RNA), which is calculated using the ENERGY module of the CHARMM program [50].
- is the difference of van der Waals repulsive energies between mutant and wild type. Here, the van der Waals repulsive energy only counts the repulsion between the residue at the mutated site and the nucleotides.
- is the difference of electrostatic interaction energies between mutant and wild type ( = is the electrostatic interaction energy between the residue at the mutated site and its contact residues/nucleotides. If any side-chain atom/base of a residue/nucleotide is located within 10 Å from any side-chain atom of the mutated site, we defined it as a contact residue/nucleotide. The calculation is carried out using the ENERGY module of the CHARMM program.
- is the number of amino acids at the protein–RNA binding interface. If the solvent-accessible surface area of a residue in the protein is more than that in the complex, we define it as the interface residue. The SASA module of CHARMM is used to calculate the solvent-accessible surface area.
- is the ratio of protein length and its surface area. and SASA is the total number of residues and the solvent-accessible surface area of unbound protein, respectively. The structure of the unbound protein is extracted from the minimized wild-type complex structure.
- Closeness of the node of the mutated site in the residue interaction network. It is defined as:where is the shortest-path distance between the node u of the mutated site and any node . V is the set of all nodes and n is the number of nodes in the residue interaction network. The shortest-path distance between two nodes refers to the minimum number of nodes that reach from one node to the other [51]. The Cα atom of a residue is considered as a node. If the distance between two Cα atoms is <6 Å, we define them as having a direct interaction. Closeness is calculated using the Python package NetworkX [52].
- is the difference of solvent accessible surface areas between mutant and wild type ( = . is the solvent accessible surface area of the residue at the mutated site in the unbound protein that is extracted from the minimized complex structure.
- , and are the number of exposed residues in the coil conformation and all residues in the mutated protein chain, respectively. Secondary structure elements other than α-helices and β-strands are defined as coil, which are assigned by the DSSP program [53]. If the ratio of the solvent-accessible surface area of a residue in the complex and in solvent is more than 0.25 [54], we defined it as the exposed residue.
- is the difference of hydrophobicity scale between mutant and wild-type residue types. The hydrophobicity scale (OMH) for each type of amino acid was derived by considering the observed frequency of amino acid replacements among thousands of related structures, which was taken from the study of [55] directly.
- and = , = , and . , , and are the number of aromatic (F, W and Y), positively charged (K and R), negatively charged (D and E) and all amino acids in the mutated protein chain, respectively.
3.4. Statistical Analysis and Evaluation of Performance
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Gerstberger, S.; Hafner, M.; Tuschl, T. A census of human RNA-binding proteins. Nat. Rev. Genet. 2014, 15, 829–845. [Google Scholar] [CrossRef] [PubMed]
- Mitchell, S.F.; Parker, R. Principles and Properties of Eukaryotic mRNPs. Mol. Cell 2014, 54, 547–558. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fabian, M.R.; Sonenberg, N.; Filipowicz, W. Regulation of mRNA Translation and Stability by microRNAs. Annu. Rev. Biochem. 2010, 79, 351–379. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Licatalosi, D.D.; Darnell, R.B. RNA processing and its regulation: Global insights into biological networks. Nat. Rev. Genet. 2010, 11, 75–87. [Google Scholar] [CrossRef] [PubMed]
- Mittal, N.; Roy, N.; Babu, M.M.; Janga, S.C. Dissecting the expression dynamics of RNA-binding proteins in posttranscriptional regulatory networks. Proc. Natl. Acad. Sci. USA 2009, 106, 2030–20305. [Google Scholar] [CrossRef] [Green Version]
- Hogan, D.J.; Riordan, D.P.; Gerber, A.P.; Herschlag, D.; Brown, P.O. Diverse RNA-binding proteins interact with functionally related sets of RNAs, suggesting an extensive regulatory system. PLoS Boil. 2008, 6, e255. [Google Scholar] [CrossRef] [Green Version]
- Kechavarzi, B.; Janga, S.C. Dissecting the expression landscape of RNA-binding proteins in human cancers. Genome Boil. 2014, 15, R14. [Google Scholar] [CrossRef] [Green Version]
- Lukong, K.E.; Chang, K.-W.; Khandjian, E.W.; Richard, S. RNA-binding proteins in human genetic disease. Trends Genet. 2008, 24, 416–425. [Google Scholar] [CrossRef]
- Teng, S.; Madej, T.; Panchenko, A.; Alexov, E. Modeling Effects of Human Single Nucleotide Polymorphisms on Protein-Protein Interactions. Biophys. J. 2009, 96, 2178–2188. [Google Scholar] [CrossRef] [Green Version]
- Nishi, H.; Tyagi, M.; Teng, S.; Shoemaker, B.A.; Hashimoto, K.; Alexov, E.; Wuchty, S.; Panchenko, A.R. Cancer Missense Mutations Alter Binding Properties of Proteins and Their Interaction Networks. PLoS ONE 2013, 8, e66273. [Google Scholar] [CrossRef] [Green Version]
- Sahni, N.; Yi, S.; Taipale, M.; Bass, J.I.F.; Coulombe-Huntington, J.; Yang, F.; Peng, J.; Weile, J.; Karras, G.I.; Wang, Y.; et al. Widespread Macromolecular Interaction Perturbations in Human Genetic Disorders. Cell 2015, 161, 647–660. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wang, X.; Wei, X.; Thijssen, B.; Das, J.; Lipkin, S.M.; Yu, H. Three-dimensional reconstruction of protein networks provides insight into human genetic disease. Nat. Biotechnol. 2012, 30, 159–164. [Google Scholar] [CrossRef] [Green Version]
- Ozdemir, E.S.; Gursoy, A.; Keskin, O. Analysis of single amino acid variations in singlet hot spots of protein–protein interfaces. Bioinformatics 2018, 34, i795–i801. [Google Scholar] [CrossRef] [PubMed]
- Jubb, H.; Pandurangan, A.P.; Turner, M.A.; Ochoa-Montaño, B.; Blundell, T.L.; Ascher, D.B. Mutations at protein-protein interfaces: Small changes over big surfaces have large impacts on human health. Prog. Biophys. Mol. Boil. 2017, 128, 3–13. [Google Scholar] [CrossRef] [PubMed]
- Kobren, S.N.; Singh, M. Systematic domain-based aggregation of protein structures highlights DNA-, RNA- and other ligand-binding positions. Nucleic Acids Res. 2018, 47, 582–593. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Porta-Pardo, E.; Garcia-Alonso, L.; Hrabe, T.; Dopazo, J.; Godzik, A. A Pan-Cancer Catalogue of Cancer Driver Protein Interaction Interfaces. PLoS Comput. Boil. 2015, 11, e1004518. [Google Scholar]
- Teh, H.F.; Peh, W.Y.X.; Su, X.; Thomsen, J.S. Characterization of Protein−DNA Interactions Using Surface Plasmon Resonance Spectroscopy with Various Assay Schemes. Biochemistry 2007, 46, 2127–2135. [Google Scholar] [CrossRef]
- Velázquez-Campoy, A.; Ohtaka, H.; Nezami, A.; Muzammil, S.; Freire, E. Isothermal Titration Calorimetry. Curr. Protoc. Cell Boil. 2004, 23, 17–18. [Google Scholar] [CrossRef]
- Buenrostro, J.D.; Araya, C.L.; Chircus, L.; Layton, C.J.; Chang, H.Y.; Snyder, M.P.; Greenleaf, W.J. Quantitative analysis of RNA-protein interactions on a massively parallel array reveals biophysical and evolutionary landscapes. Nat. Biotechnol. 2014, 32, 562–568. [Google Scholar] [CrossRef]
- Lambert, N.; Robertson, A.; Jangi, M.; McGeary, S.; Sharp, P.A.; Burge, C.B. RNA Bind-n-Seq: Quantitative Assessment of the Sequence and Structural Binding Specificity of RNA Binding Proteins. Mol. Cell 2014, 54, 887–900. [Google Scholar] [CrossRef] [Green Version]
- Tome, J.M.; Özer, A.; Pagano, J.M.; Gheba, D.; Schroth, G.P.; Lis, J.T. Comprehensive analysis of RNA-protein interactions by high-throughput sequencing–RNA affinity profiling. Nat. Methods 2014, 11, 683–688. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jain, N.; Lin, H.-C.; Morgan, C.E.; E Harris, M.; Tolbert, B.S. Rules of RNA specificity of hnRNP A1 revealed by global and quantitative analysis of its affinity distribution. Proc. Natl. Acad. Sci. USA 2017, 114, 2206–2211. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Getov, I.; Petukh, M.; Alexov, E. SAAFEC: Predicting the Effect of Single Point Mutations on Protein Folding Free Energy Using a Knowledge-Modified MM/PBSA Approach. Int. J. Mol. Sci. 2016, 17, 512. [Google Scholar] [CrossRef] [PubMed]
- Guerois, R.; Nielsen, J.E.; Serrano, L. Predicting Changes in the Stability of Proteins and Protein Complexes: A Study of More Than 1000 Mutations. J. Mol. Boil. 2002, 320, 369–387. [Google Scholar] [CrossRef]
- Dehouck, Y.; Kwasigroch, J.M.; Gilis, D.; Rooman, M. PoPMuSiC 2.1: A web server for the estimation of protein stability changes upon mutation and sequence optimality. BMC Bioinform. 2011, 12, 151. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Simonetti, F.L.; Goncearenco, A.; Panchenko, A.R. MutaBind estimates and interprets the effects of sequence variants on protein–protein interactions. Nucleic Acids Res. 2016, 44, W494–W501. [Google Scholar] [CrossRef] [Green Version]
- Dehouck, Y.; Kwasigroch, J.M.; Rooman, M.; Gilis, D. BeAtMuSiC: Prediction of changes in protein–protein binding affinity on mutations. Nucleic Acids Res. 2013, 41, W333–W339. [Google Scholar] [CrossRef] [Green Version]
- Rodrigues, C.H.M.; Myung, Y.; Pires, D.E.V.; Ascher, D.B. mCSM-PPI2: Predicting the effects of mutations on protein–protein interactions. Nucleic Acids Res. 2019, 47, W338–W344. [Google Scholar] [CrossRef] [Green Version]
- Petukh, M.; Dai, L.; Alexov, E. SAAMBE: Webserver to Predict the Charge of Binding Free Energy Caused by Amino Acids Mutations. Int. J. Mol. Sci. 2016, 17, 547. [Google Scholar] [CrossRef] [Green Version]
- Li, M.; Petukh, M.; Alexov, E.; Panchenko, A.R. Predicting the Impact of Missense Mutations on Protein–Protein Binding Affinity. J. Chem. Theory Comput. 2014, 10, 1770–1780. [Google Scholar] [CrossRef]
- Pahari, S.; Li, G.; Murthy, A.K.; Liang, S.; Fragoza, R.; Yu, H.; Alexov, E. SAAMBE-3D: Predicting Effect of Mutations on Protein–Protein Interactions. Int. J. Mol. Sci. 2020, 21, 2563. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, N.; Chen, Y.; Lu, H.; Zhao, F.; Alvarez, R.V.; Goncearenco, A.; Panchenko, A.R.; Li, M. MutaBind2: Predicting the Impacts of Single and Multiple Mutations on Protein-Protein Interactions. Iscience 2020, 23, 100939. [Google Scholar] [CrossRef] [Green Version]
- Pires, D.E.V.; Ascher, D.B. mCSM-NA: Predicting the effects of mutations on protein-nucleic acids interactions. Nucleic Acids Res. 2017, 45, W241–W246. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, N.; Chen, Y.; Zhao, F.; Yang, Q.; Simonetti, F.L.; Li, M. PremPDI estimates and interprets the effects of missense mutations on protein-DNA interactions. PLoS Comput. Boil. 2018, 14, e1006615. [Google Scholar] [CrossRef] [PubMed]
- Peng, Y.; Sun, L.; Jia, Z.; Li, L.; Alexov, E. Predicting protein–DNA binding free energy change upon missense mutations using modified MM/PBSA approach: SAMPDI webserver. Bioinformatics 2017, 34, 779–786. [Google Scholar] [CrossRef] [PubMed]
- Pan, Y.; Wang, Z.; Zhan, W.; Deng, L. Computational identification of binding energy hot spots in protein–RNA complexes using an ensemble approach. Bioinformatics 2017, 34, 1473–1480. [Google Scholar] [CrossRef]
- Krüger, D.M.; Neubacher, S.; Grossmann, T.N. Protein–RNA interactions: Structural characteristics and hotspot amino acids. RNA 2018, 24, 1457–1465. [Google Scholar] [CrossRef]
- Jones, S. Protein-RNA interactions: A structural analysis. Nucleic Acids Res. 2001, 29, 943–954. [Google Scholar] [CrossRef]
- Barik, A.; Nithin, C.; Karampudi, N.B.R.; Mukherjee, S.; Bahadur, R.P. Probing binding hot spots at protein-RNA recognition sites. Nucleic Acids Res. 2015, 44, e9. [Google Scholar] [CrossRef] [Green Version]
- Delgado, J.; Radusky, L.G.; Cianferoni, D.; Serrano, L. FoldX 5.0: Working with RNA, small molecules and a new graphical interface. Bioinformatics 2019, 35, 4168–4169. [Google Scholar] [CrossRef] [Green Version]
- Tishchenko, S.; Kostareva, O.; Gabdulkhakov, A.; Mikhaylina, A.O.; Nikonova, E.; Nevskaya, N.; Sarskikh, A.; Piendl, W.; Garber, M.; Nikonov, S. Protein–RNA affinity of ribosomal protein L1 mutants does not correlate with the number of intermolecular interactions. Acta Crystallogr. Sect. D Boil. Crystallogr. 2015, 71, 376–386. [Google Scholar] [CrossRef] [PubMed]
- Jubb, H.; Higueruelo, A.; Ochoa-Montaño, B.; Pitt, W.R.; Ascher, D.B.; Blundell, T. Arpeggio: A Web Server for Calculating and Visualising Interatomic Interactions in Protein Structures. J. Mol. Boil. 2016, 429, 365–371. [Google Scholar] [CrossRef] [PubMed]
- Kumar, M.D.S. ProTherm and ProNIT: Thermodynamic databases for proteins and protein-nucleic acid interactions. Nucleic Acids Res. 2006, 34, D204–D206. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, L.; Xiong, Y.; Gao, H.; Wei, D.-Q.; Mitchell, J.C.; Zhu, X. dbAMEPNI: A database of alanine mutagenic effects for protein-nucleic acid interactions. Database 2018, 2018. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Berman, H.M.; Westbrook, J.; Feng, Z.; Gilliland, G.; Bhat, T.N.; Weissig, H.; Shindyalov, I.N.; Bourne, P.E. The Protein Data Bank. Nucleic Acids Res. 2000, 28, 235–242. [Google Scholar] [CrossRef] [Green Version]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- MacKerell, A.D.; Bashford, D.; Bellott, M.; Dunbrack, R.L.; Evanseck, J.D.; Field, M.J.; Fischer, S.; Gao, J.; Guo, H.; Ha, S.; et al. All-Atom Empirical Potential for Molecular Modeling and Dynamics Studies of Proteins†. J. Phys. Chem. B 1998, 102, 3586–3616. [Google Scholar] [CrossRef]
- Phillips, J.C.; Braun, R.; Wang, W.; Gumbart, J.; Tajkhorshid, E.; Villa, E.; Chipot, C.; Skeel, R.D.; Kale, L.; Schulten, K. Scalable molecular dynamics with NAMD. J. Comput. Chem. 2005, 26, 1781–1802. [Google Scholar] [CrossRef] [Green Version]
- Hoover, W.G. Canonical dynamics: Equilibrium phase-space distributions. Phys. Rev. A 1985, 31, 1695–1697. [Google Scholar] [CrossRef] [Green Version]
- Brooks, B.R.; Bruccoleri, R.E.; Olafson, B.D.; States, D.J.; Swaminathan, S.; Karplus, M. CHARMM: A program for macromolecular energy, minimization, and dynamics calculations. J. Comput. Chem. 1983, 4, 187–217. [Google Scholar] [CrossRef]
- Chakrabarty, B.; Parekh, N. NAPS: Network Analysis of Protein Structures. Nucleic Acids Res. 2016, 44, W375–W382. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hagberg, P.S.A.; Schult, D. Exploring network structure, dynamics, and function using NetworkX. In Proceedings of the 7th Python in Science Conference (SciPy2008), Pasadena, CA, USA, 19–24 August 2008; pp. 11–15. [Google Scholar]
- Joosten, R.P.; Beek, T.A.H.T.; Krieger, E.; Hekkelman, M.L.; Hooft, R.W.W.; Schneider, R.; Sander, C.; Vriend, G. A series of PDB related databases for everyday needs. Nucleic Acids Res. 2010, 39, D411–D419. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Brender, J.R.; Zhang, Y. Predicting the Effect of Mutations on Protein-Protein Binding Interactions through Structure-Based Interface Profiles. PLoS Comput. Boil. 2015, 11, e1004494. [Google Scholar] [CrossRef]
- Sweet, R.M.; Eisenberg, D. Correlation of sequence hydrophobicities measures similarity in three-dimensional protein structure. J. Mol. Boil. 1983, 171, 479–488. [Google Scholar] [CrossRef]
- Hittner, J.B.; May, K.; Silver, N.C. A Monte Carlo Evaluation of Tests for Comparing Dependent Correlations. J. Gen. Psychol. 2003, 130, 149–168. [Google Scholar] [CrossRef]
- Diedenhofen, B.; Musch, J. cocor: A Comprehensive Solution for the Statistical Comparison of Correlations. PLoS ONE 2015, 10, e0121945. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Delong, E.R.; Delong, D.M.; Clarke-Pearson, D.L. Comparing the Areas under Two or More Correlated Receiver Operating Characteristic Curves: A Nonparametric Approach. Biometrics 1988, 44, 837. [Google Scholar] [CrossRef]


| Method | R | RMSE | Slope |
|---|---|---|---|
| PremPRI | 0.72 | 0.76 | 1.00 |
| PremPRI (CV1) | 0.68 | 0.80 | 0.94 |
| PremPRI (CV2) | 0.68 | 0.80 | 0.95 |
| PremPRI (CV3) | 0.61 | 0.87 | 0.89 |
| Method | R | RMSE | AUC-ROC | AUC-PR | MCC |
|---|---|---|---|---|---|
| PremPRI (CV3) | 0.61 | 0.87 | 0.76 | 0.76 | 0.45 |
| mCSM-NA | 0.24 * | 5.41 | 0.56 * | 0.60 | 0.22 |
| FoldX | 0.20 * | 1.57 | 0.53 * | 0.59 | 0.24 |
| PrabHot | - | - | 0.58 * | 0.61 | 0.26 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, N.; Lu, H.; Chen, Y.; Zhu, Z.; Yang, Q.; Wang, S.; Li, M. PremPRI: Predicting the Effects of Missense Mutations on Protein–RNA Interactions. Int. J. Mol. Sci. 2020, 21, 5560. https://doi.org/10.3390/ijms21155560
Zhang N, Lu H, Chen Y, Zhu Z, Yang Q, Wang S, Li M. PremPRI: Predicting the Effects of Missense Mutations on Protein–RNA Interactions. International Journal of Molecular Sciences. 2020; 21(15):5560. https://doi.org/10.3390/ijms21155560
Chicago/Turabian StyleZhang, Ning, Haoyu Lu, Yuting Chen, Zefeng Zhu, Qing Yang, Shuqin Wang, and Minghui Li. 2020. "PremPRI: Predicting the Effects of Missense Mutations on Protein–RNA Interactions" International Journal of Molecular Sciences 21, no. 15: 5560. https://doi.org/10.3390/ijms21155560
APA StyleZhang, N., Lu, H., Chen, Y., Zhu, Z., Yang, Q., Wang, S., & Li, M. (2020). PremPRI: Predicting the Effects of Missense Mutations on Protein–RNA Interactions. International Journal of Molecular Sciences, 21(15), 5560. https://doi.org/10.3390/ijms21155560





