Next Article in Journal
Role of Regular Physical Activity in Neuroprotection against Acute Ischemia
Previous Article in Journal
TGF-β Induced CTGF Expression in Human Lung Epithelial Cells through ERK, ADAM17, RSK1, and C/EBPβ Pathways
Previous Article in Special Issue
Evaluating the Performance of a Non-Bonded Cu2+ Model Including Jahn−Teller Effect into the Binding of Tyrosinase Inhibitors
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
IJMS
Volume 21
Issue 23
10.3390/ijms21239085
ijms-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

DFT Quantum-Chemical Modeling Molecular Structures of Cobalt Macrocyclic Complexes with Porphyrazine or Its Benzo-Derivatives and Two Oxygen Acido Ligands

by
Oleg V. Mikhailov
1,* and
Denis V. Chachkov
2
1
Kazan National Research Technological University, K. Marx Street 68, 420015 Kazan, Russia
2
Kazan Department of Joint Supercomputer Center of Russian Academy of Sciences—Branch of Federal Scientific Center “Scientific Research Institute for System Analysis of the RAS”, Lobachevskii Street 2/31, 420111 Kazan, Russia
*
Author to whom correspondence should be addressed.
Int. J. Mol. Sci. 2020, 21(23), 9085; https://doi.org/10.3390/ijms21239085
Submission received: 7 October 2020 / Revised: 25 November 2020 / Accepted: 27 November 2020 / Published: 29 November 2020
(This article belongs to the Special Issue Quantum-Chemical Modeling and Design of Chelate and Macrocyclic Metal Complexes)
Browse Figures
Versions Notes

Abstract

:
Based on the results of a quantum chemical calculation using the DFT method with the OPBE/TZVP and B3PW91/TZVP levels, the possibility of the existence of three cobalt heteroligand complexes containing in the inner coordination sphere porphyrazine, di[benzo]- and tetra[benzo]porphyrazine, and two oxygen (O2−) ions with probable oxidation state VI of Co, which is unknown for this element at the present time, was shown. Data on the structural parameters are presented. It was shown that CoN4 chelate nodes as well as all metal-chelate and non-chelate cycles in each of these complexes, were strictly planar. Besides, the bond angles formed by two donor nitrogen atoms and a Co atom were close or equal to 90°, while the bond angles formed by donor atoms N, Co, and O, in most cases, albeit insignificantly, differed from this value. Good agreement between the calculated data obtained using the above two versions of the DFT method was found. Standard thermodynamic parameters of formation (standard enthalpy ΔH0f, 298, entropy S0f, 298 and Gibbs’s energy ΔG0f, 298) for the indicated complexes were presented too.

1. Introduction

As is known, cobalt in its currently known chemical compounds can be in oxidation states from 0 up to V, wherein its highest oxidation state, namely IV and V, are uncharacteristic for the given element [1,2,3]. In particular, such compounds as CoO2 dioxide and cesium hexafluorocobaltate(IV) Cs2CoF6 [4,5], have been known for Co(IV) for a long time and for Co(V), sodium tetraoxocobaltates(V) Na3CoO4 and potassium K3CoO4 [6,7], and also a number of organometallic complexes [3,8,9,10]. An availability of Co(VI) was supposed in the matrix of cesium tetraoxoferrate(VI) (Cs2FeO4) as isomorphically replacing Fe(VI), and its identification was carried out by Mössbauer spectroscopy [11]; however, any compound with a stoichiometric chemical composition for a given oxidation state of cobalt was described neither in this work nor in other publications. By taking into account the theoretical considerations expressed in the introduction to the articles [12,13] devoted to Cu(IV) and Zn(IV) complexes with porphyrazine and its benzo-derivatives (in particular, trans-di[benzo]porphyrazine and tetra[benzo]porphyrazine) and one oxo ligand, we have every reason to believe that the given macrocyclic ligands in combination with two oxo ligands will also be able to form complexes with structural formulas [CoL1(O)2] (I), [CoL2(O)2] (II) and [CoL3(O)2] (III) (where L12−, L22− and L32− are double deprotonated forms of porphyrazine H2L1, trans-di[benzo]porphyrazine H2L2 and tetra[benzo]porphyrazine H2L3). These complexes are interesting in that, as it is easy to see from these formulas, in any of these complexes the cobalt atom is bonded to other atoms by eight chemical bonds, six of which are formed by the exchange mechanism (namely, two with each of two oxygen atoms and one with the each of two nitrogen atoms), and according to the generally accepted definition, the concept of “oxidation state”, the value of this parameter for a given atom of a 3d-element should be accepted equal to (+6). It should be specially noted that no mention of complexes of type I–III in the special literature devoted to (NNNN)-donor atomic macrocyclic ligands—porphyrins, porphyrazines and their derivatives [14,15,16,17,18,19,20,21,22], or anywhere else, could not be found. In this connection, the given article will be devoted to a theoretical analysis regarding the possibility of the existence in principle of such complexes with the use of modern methods of quantum chemistry, namely, the density functional theory (DFT) method. Ijms 21 09085 i001

2. Results

The chemical bond lengths between atoms and bond angles for the [CoL1(O)2] (I), [CoL2(O)2] (II) and [CoL3(O)2] (III) metal complexes calculated by the DFT OPBE/TZVP and DFT B3PW91/TZVP methods, are presented in the Table 1. The images of molecular structures of the given complexes obtained by the DFT B3PW91/TZVP method are shown in Figure 1, Figure 2 and Figure 3. The images of molecular structures of complexes under consideration obtained with the DFT OPBE/TZVP method are generally similar to those obtained with using the DFT B3PW91/TZVP method.
The values of the dipole electric moments for this complex, calculated using the OPBE/TZVP method, are 0.02 ([CoL1(O)2]), 0.01 ([CoL2(O)2]), and 0.00 ([CoL3(O)2]) Debye units; using the B3PW91/TZVP method, they are 0.27, 0.00 and 0.67 Debye units, respectively.
The most important data of NBO analysis, and namely the values of effective charges on Co, donor N and O atoms for heteroligand macrocyclic cobalt complexes under consideration obtained by the DFT OPBE/TZVP method, are presented in Table 2. For complete NBO analysis data, see Supplementary Materials, too.
The pictures of spin density distribution in the complexes under study are shown in Figure 4.
Standard thermodynamic parameters of formation (ΔH0f, 298, S0f, 298 and ΔG0f, 298) for [CoL1(O)2], [CoL2(O)2], and [CoL3(O)2] complexes are presented in Table 3. As may be seen, all these parameters are positive for each of the complexes under consideration.

3. Discussion

As can be seen from the data presented in Table 1, both versions of DFT methods used by us, on the whole, give similar values of key parameters of molecular structures for the chemical compounds under study. According to these data, all four 5-membered and 6-membered metal chelate rings as well as chelate nodes CoN4 and N4 groupings in them, are a strong plane or, at least, are practically plane because the sum of the bond angles in each of these structural fragments are exactly 540.0°, 720.0°, 360.0°, and 360.0°, respectively, or very close to these values (deviation from planarity is not more than 0.2°). Besides, all chelate and non-chelate rings are completely identical to each other in the sum of bond angles in them, but are slightly different between themselves in the lengths of bonds between the corresponding atoms and in the assortment of bond angles in them. In [CoL1(O)2] and [CoL2(O)2] complexes, however, both 5-membered and 6-membered rings are identical only in pairs because the assortment of bond angles in these pairs differ among themselves. This difference becomes quite understandable if we take into account only the pairwise equality of (NCoN) bond angles formed by the central metal atom Co with neighboring donor nitrogen atoms (Table 1). Unlike [CoL1(O)2] and [CoL2(O)2], in the [CoL3(O)2] complex, all these rings are fully identical between themselves (Table 1). According to DFT B3PW91/TZVP method data, all three complexes are characterized by a tetragonal-bipyramidal orientation of the donor nitrogen atoms relative to the 3d-element central atom whereas according to DFT OPBE/TZVP method data, this takes place only in the [CoL3(O)2] complex. Nevertheless, as a rule, the bond angles in the CoN4 chelate node between the nitrogen and cobalt atoms in the complexes under study are equal to each other and to 90°, or differ from this value by only 0.1°. The deviations (NCoO) in bond angles formed by nitrogen atoms in the chelate node, Co and oxygen atoms from 90° are more significant, sometimes reaching 5° (Table 1).
The bond lengths and bond angles listed above in [CoL1(O)2], [CoL2(O)2], and [CoL3(O)2] are quite typical for coordination compounds of 3d-elements containing L12−, L22−, and L32− as ligands (see, e.g., Supplementary Materials). It should be noted in this connection that within the framework of any of these structures, there are bonds between cobalt and oxygen atoms, the lengths of which (169–179 pm) correspond to double Co=O bonds, and bonds between cobalt and nitrogen atoms, the lengths of which (192–196 pm) correspond to a single Co–N bond. Note in this regard that the lengths of cobalt–nitrogen, carbon–nitrogen, and carbon–carbon bonds, as well as bond angles in the CoN4 chelate node and in metal chelate rings in the most bulky structures of these three complexes, namely [CoL3(O)2], are very close to the experimental values of the corresponding parameters for the complex of cobalt(II) with tetra [benzo]porphyrazine (phthalocyanine) [CoL3] found in [23,24].
As mentioned above, both the independent DFT methods used by us give rather close values of the key structural parameters for these complexes, but there are very significant differences on two points. On the one hand, according to the DFT OPBE/TZVP data, the bond angles formed by two oxygen and cobalt atoms (O1Co1O2) differ quite noticeably from 180°, while according to the DFT B3PW91/TZVP data, on the contrary, they are exactly 180°. On the other hand, that is interestingly the Co–O interatomic distances according to the OPBE/TZVP method, which are equal in each of the three complexes, while according to the DFT B3PW91/TZVP method, this equality occurs only in the case of [CoL2(O)2]. By taking into account this circumstance, one would expect that the electric moment of a dipole for [CoL1(O)2] and [CoL2(O)2], calculated using the DFT OPBE/TZVP method would be more significant than the electric moment of a dipole calculated using the DFT B3PW91/TZVP method. However, in fact, the opposite state of affairs takes place, because the values of the electric moment of a dipole for these complexes calculated by DFT OPBE/TZVP and DFT B3PW91/TZVP methods, are respectively 0.02 and 0.27 ([CoL1(O)2]), 0.01 and 0.00 ([CoL2(O)2]) Debye units. The reasons for this phenomenon remain yet unclear (be that as it may, none of them has a center of symmetry), but perhaps we are dealing here with an artifact or some calculation errors. However, in the case of [CoL3(O)2], where, according to the DFT OPBE/TZVP method data, the cobalt–oxygen bond lengths are the same (175.4 pm each), and according to the DFT B3PW91/TZVP method, they are significantly different (171.5 and 179.0 pm), one should expect a higher value of the dipole moment in the framework of the second of these methods, and it really turns out to be so (0.00 and 0.67 Debye units, respectively).
Earlier in the work [25], the molecular structure of the Co(IV) complex with porphyrazine and one axially oriented oxo-ligand of the formula [CoL1(O)] was calculated by the DFT OPBE/TZVP method; in this connection, it is possible to compare the key structural parameters of the [CoL1(O)] and [CoL1(O)2] complexes, calculated by this method. To begin with, according to [25], the CoN4 chelate node in the [CoL1(O)] complex, as well as in the [CoL1(O)2] complex, has a strictly planar structure, and the sets of (NCoN) bond angles in them is exactly the same; the groupings of donor nitrogen atoms N4 in both of these complexes are also strictly planar. The 5-membered chelate rings in both of these complexes are also strictly planar, while the 6-membered rings in them differ slightly from each other (in [CoL1(O)2], they are strictly flat, in [CoL1(O)], they have a small (1.2°) deviation from coplanarity [25]). The Co–N bond lengths in [CoL1(O)] are the same (190.4 pm each) and are somewhat shorter here than in [CoL1(O)2], whereas for the cobalt–oxygen bond lengths (170.1 pm and 168.9 pm, respectively) the opposite is true (Table 1). Since the [CoL1(O)] complex, as follows from the data [25], has a square-pyramidal structure, and the [CoL1(O)2] complex has an octahedral structure, then theoretically, the greatest difference between them should be expected for the bond angles formed of oxygen, cobalt, and donor nitrogen atoms, and this is indeed the case (these angles in the case of [CoL1(O)] are 96.5° and 95.3° [25], in the case of [CoL1(O)2], 85.1°, 90.0° and 94.9° (Table 1)). As can be seen from above, the key parameters of the molecular structures of heteroligand cobalt complexes containing porphyrazine and oxo ligands in the inner coordination sphere, but differing in the oxidation degree of the central atom (+4 in [CoL1(O)] and +6 in [CoL1(O)2]) are very similar to each other. Unfortunately, structural data on the [CoL2(O)] and [CoL3(O)] complexes obtained by quantum-chemical calculations by the DFT OPBE/TZVP method (as well as by any other calculation method) are still lacking in the literature, and, hence, a comparison between them and the [CoL2(O)2] and [CoL3(O)2] complexes under examination, respectively, does not seem possible.
As may be seen from Table 2, values of effective charges on Co atoms are considerably less than +6.000 ē which would be the case if all chemical bonds between Co, N, and O atoms would be ionic; the similar situation occurs for N donor atoms and O atoms, the values of charges on which are very different from −3.000 and −2.000 ē, respectively, too. This is evidence that a very high degree of electron density delocalization takes place in the each of the given coordination compounds.
According to the data of our calculations, the ground state of the [CoL1(O)2] and [CoL2(O)2] heteroligand complexes under study in the framework of the DFT OPBE/TZVP method is a spin doublet whereas the ground state of the [CoL3(O)2] one is a spin quartet. Besides, according to the data of this method, the nearest excited state (quartet in the case [CoL1(O)2] and [CoL2(O)2] and doublet in the case [CoL3(O)2]) has much higher energy (64.2, 33.8 and 39.9 kJ/mol, respectively). DFT B3PW91/TZVP give other data: the ground state of the [CoL1(O)2] and [CoL3(O)2] is a spin doublet, of the [CoL2(O)2] one is spin quartet; the nearest excited state is located higher than ground one, on 17.6, 48.3 and 55.9 kJ/mol, respectively. The difference in the values of the “energetic distances” in the ground and the nearest excited states given by these methods turns out to be very significant, but in any case, in our opinion, they allow us to make a conclusion that a spin crossover for such complexes should not have occurred. By taking into consideration the important fact that, as will be indicated further (see Section 4), the DFT OPBE/TZVP method in the case of 3d elements more adequately predicts the relative energy stabilities of high-spin and low-spin states than the DFT B3PW91/TZVP one, we consider it more correct to conclude that the ground state of [CoL1(O)2] and [CoL2(O)2] is namely a spin doublet, the ground state of [CoL3(O)2] is namely a spin quartet. An additional argument in favor of this conclusion is the values of <S**2> for these complexes (Table 2), each of which corresponds to the presence of precisely either one (in the case of [CoL1(O)2] and [CoL2(O)2]) or three (in the case of [CoL3(O)2]) unpaired electrons in the ground state and, therefore, MS= 2 and MS= 4, respectively. On the other hand, testing the wave functions of the ground state for stability within of this method using the STABLE = OPT procedure showed that, in all cases, the wave function did not show any attributes of instability.

4. Materials and Methods

As in our articles [12,13], and also in earlier ones, in particular [26,27,28,29,30], quantum-chemical calculations were performed by the DFT method with OPBE/TZVP level combining the common TZVP extended triple zeta split-valence basis set [31,32] and the OPBE non-hybrid functional [33,34]. As shown in [34,35,36,37,38], 3d elements more adequately predict the relative energy stabilities of high-spin and low-spin states, and reliably characterize the key geometric parameters of corresponding molecular structures. Moreover, for comparison, the other variant of the DFT method, namely with the B3PW91/TZVP level, which combining the TZVP and B3PW91 functional [39,40], was used in the given work; according to data [41], this has a minimal value of so-called “normal error” in comparison with other variants of the DFT method. This conclusion is in full harmony with the data of structural parameters of macrocyclic complexes of various 3d-elements with phthalocyanine obtained as a result of various DFT quantum-chemical calculations and in experiment (see Supplementary Materials). For comparison, the Supplementary Materials also presents the calculation data for the known complex of cobalt with phthalocyanine [CoL3], carried out using the DFTD wB97XD/TZVP method described in [42] and taking into account dispersion (Van der Waals) interactions; as it turned out, this method gives structural data close to those obtained by the DFT OPBE/TZVP and DFT B3PW91/TZVP methods. However, in comparison with them, it is much more costly in terms of the calculation time. That is why, [CoL1(O)2], [CoL2(O)2] and [CoL3(O)2] complexes under examination, were not calculated using the DFTD wB97XD/TZVP method.
Calculations were performed with the Gaussian09 program package [43]. The correspondence of the found stationary points to energy minima was proved in all cases by the calculation of second derivatives of energy with respect to atom coordinates; all equilibrium structures corresponding to minima of the potential energy surfaces had only real positive frequency values. When carrying out calculations within the framework of any of the above two variants of the DFT method (OPBE/TZVP as well as D3PW91/TZVP), we did not impose any symmetry restrictions; the structure with the C1 symmetry group was initially specified. Theoretically, Co(VI) must have 3d3 electronic configuration, and spin multiplicities 2 and 4 were considered for it. Among the structures optimized at these multiplicities, the lowest-lying structure was selected. Parameters of molecular structures with the given multiplicities were always calculated by unrestricted methods (UOPBE and UB3PW91, correspondingly). In addition, in all cases, the wave functions at the minimum point were checked for stability according to procedure STABLE = OPT in Gaussian. The standard thermodynamic parameters of formation (ΔH0f, 298, S0f, 298 and ΔG0f, 298) for the given macrocyclic metal chelates under examination were calculated using the method described in [44].

5. Conclusions

The data obtained using two various DFT methods, namely with OPBE/TZVP and B3PW91/TZVP levels and presented above in the given paper, unambiguously predicted the possibility of the existence of three novel cobalt complexes having [CoL1(O)2], [CoL2(O)2], and [CoL3(O)2] compositions where L12−, L22−, and L32− is a double deprotonated form of porphyrazine, trans-di[benzo]porphyrazine and tetra[benzo]porphyrazine, respectively. In each of them, there are six bonds formed by cobalt atoms with atoms having greater electronegativity in comparison with it, according to the exchange mechanism—two chemical bonds with nitrogen atoms, and four with oxygen atoms. The generally accepted definition of the term “oxidation degree” is as follows: “the oxidation degree is the charge in units of electron charge that would occur on the atom of a given element in a given chemical compound under the assumption that within the framework of each of the conditionally existing in this compound two-center two-electron chemical bonds formed by the exchange mechanism, there would be a complete transfer of electrons from the atom with less electronegativity to the atom with more electronegativity”. The oxidation degree of the each of central atoms in the metal complexes (i.e., Co) may be postulated equal to + 6. But since the oxidation state of any chemical element with a positive oxidation degree is determined as the modulus of oxidation degree and is displayed by the corresponding Roman numeral, in each of these compounds, the oxidation state of cobalt may be considered equal to VI. Naturally, the real charge on the Co atoms in the complexes under consideration differ significantly from the value of +6.00 ē, but given that the parameter is not connected with the above definition, in principle it cannot be used as a definition of the oxidation state [2]. Be that as it may, the results of our quantum-chemical calculation completely fit into the idea of a fairly high stability of those chemical compounds with a high oxidation state of the central atom, where the coordination polyhedron is formed from the most durable and difficult-to-oxidize acid ligands having atoms with the highest electronegativity (in our case, O2−). Note in this regard that, upon the introduction of the second oxo ligand into the inner coordination sphere of the square pyramidal complex [CoL1(O)] described in [25], the molecular structure of the resulting complex [CoL1(O)2] remains practically unchanged in comparison with that for [CoL1(O)2], both qualitatively and quantitatively.
As can be seen from the data presented in Table 3, the values of standard thermodynamic parameters of formation ΔH0f, 298, S0f, 298 and ΔG0f, 298 for the cobalt complexes of types I–III are positive and this is an indirect indication of their relatively low stability. This circumstance, however, is in no way a contraindication to attempts to obtain them, since it is known that there are a number of chemical compounds for which there is a similar situation with respect to standard thermodynamic characteristics, but which, nevertheless, were obtained experimentally in one way or another (f.e., boranes having general formula BnHn+2, dicarbon dinitride (cyanogen) C2N2 et al.) Moreover, according to the above data of a quantum-chemical calculation by the two independent DFT methods indicated above, the molecular structures of these complexes presented in Figure 1, Figure 2 and Figure 3 are quite stable). As for the possible synthesis of these chemical compounds, then, in principle, any of them could be obtained by exposure to very strong oxidizing agents, for example F2, KrF2, or of such an exotic oxidizer as difluoride dioxygen O2F2, on cobalt(II) complexes with the macrocyclic ligands L1, L2 and L3. In particular, in the case of [CoL3(O)2], such a synthesis may be realized according to the general schemes (1–3).
[CoL3] + 2F2 + 4KOH → [CoL3(O)2] + 2H2O + 4KF
[CoL3] + 2KrF2 + 4KOH → [CoL3(O)2] + 2Kr + 2H2O + 4KF
[CoL3] + O2F2 + 2KOH →[CoL3(O)2] + 2H2O + 2KF
It can be assumed that these macrocyclic compounds, if they will be obtained in experiment, will gain not only purely academic, but also very substantial practical interest and may be promising in a number of industry areas, in particular in catalysis, photonic, electronic, and electrochemical technologies. On the other hand, the complexes under study may be used as “precursors” in the various reactions of synthesis coordination compounds and, also, in the reactions of coordinated ligands owing to which, in principle, novel macrocyclic compounds may be obtained.

Supplementary Materials

Supplementary Materials can be found at https://www.mdpi.com/1422-0067/21/23/9085/s1.

Author Contributions

Conceptualization, O.V.M.; Methodology, O.V.M. and D.V.C.; Software, D.V.C.; Validation, O.V.M. and D.V.C.; Formal Analysis, O.V.M. and D.V.C.; Investigation, O.V.M. and D.V.C.; Resources, D.V.C.; Data Curation, D.V.C.; Writing—Original Draft Preparation, O.V.M. and D.V.C.; Writing—Review and Editing, O.V.M.; Visualization, O.V.M. and D.V.C.; Supervision, O.V.M.; Project Administration, O.V.M.; Funding Acquisition, D.V.C. All authors have read and agreed to the published version of the manuscript.

Funding

Contribution of author Chachkov D.V. was funded by the state assignment to the Federal State Institution “Scientific Research Institute for System Analysis of the Russian Academy of Sciences” for scientific research (http://www.jscc.ru).

Acknowledgments

All quantum-chemical calculations were performed at the Kazan Department of Joint Supercomputer Center of Russian Academy of Sciences—Branch of Federal Scientific Center “Scientific Research Institute for System Analysis of the RAS” that is acknowledgement for technical support.

Conflicts of Interest

The authors declare that they have no conflict of interest, financial or otherwise.

References

  1. Weller, M.; Overton, T.; Rourke, J.; Armstrong, F. Inorganic Chemistry, 6th ed.; OUP: Oxford, UK, 2014. [Google Scholar]
  2. Kiselev, Y.M.; Tretiyakov, Y.D. The Problem of Oxidation State Stabilization and Some Regularities of a Periodic System of the Elements. Russ. Chem. Rev. 1999, 68, 365–379. [Google Scholar] [CrossRef]
  3. Riedel, S.; Kaupp, M. The highest oxidation states of the transition metal elements. Coord. Chem. Rev. 2009, 253, 606–624. [Google Scholar] [CrossRef]
  4. Quail, J.W.; Rivett, G.A. Complex Fluorides of Tetravalent Cobalt. Can. J. Chem. 1972, 50, 2447–2450. [Google Scholar] [CrossRef]
  5. Allen, G.C.; Warren, K.D. Electronic spectrum of the hexafluorocobaltate(IV) anion. Inorg. Chem. 1969, 8, 1902–1904. [Google Scholar] [CrossRef]
  6. Brendel, C.; Klemm, W. Weitere Versuche zur Darstellung von Kaliumcobaltat (V). Z. Anorg. Allgem. Chem. 1963, 320, 59–63. [Google Scholar] [CrossRef]
  7. Nicholls, D. The Chemistry of Iron, Cobalt and Nickel: Comprehensive Inorganic Chemistry; Elsevier Science: Amsterdam, The Netherlands, 2013. [Google Scholar]
  8. Byrne, E.K.; Theopold, K.H. Redox chemistry of tetrakis(1-norbornyl)cobalt. Synthesis and characterization of a cobalt(V) alkyl and self-exchange rate of a Co(III)/Co(IV) couple. J. Am. Chem. Soc. 1987, 109, 1282–1283. [Google Scholar] [CrossRef]
  9. Brookhart, M.; Grant, B.E.; Lenges, C.P.; Prosenc, M.H.; White, P.S. High Oxidation State Organocobalt Complexes: Synthesis and Characterization of Dihydridodisilyl Cobalt(V) Species. Angew. Chem. Int. Ed. 2000, 39, 1676–1679. [Google Scholar] [CrossRef]
  10. Ingleson, M.; Fan, H.; Pink, M.; Tomaszewski, J.; Caulton, K.G. Three-Coordinate Co(I) Provides Access to Unsaturated Dihydrido-Co(III) and Seven-Coordinate Co(V). J. Am. Chem. Soc. 2006, 128, 1804–1805. [Google Scholar] [CrossRef]
  11. Kopelev, N.; Kulikov, L.; Peréliev, Y. Mössbauer effect study of Cs2Fe(57Co)O4. Hyperfine Interact. 1994, 90, 377–381. [Google Scholar] [CrossRef]
  12. Mikhailov, O.V.; Chachkov, D.V. About of Possibility of Existence of Zn(IV) Oxidation State in Heteroligand Complexes with Porphyrazine, trans-Di[benzo]porphyrazine, Phthalocyanine, and Oxo Ligands: Quantum-Chemical Review. Comm. Inorg. Chem. 2020, 40, 107–115. [Google Scholar] [CrossRef]
  13. Mikhailov, O.V.; Chachkov, D.V. Copper (IV) Stabilization in Macrocyclic Complexes with 3,7,11,15-Tetraazaporphine, Its Di[benzo]- or Tetra[benzo] Derivatives and Oxide Anion: Quantum-Chemical Research. Materials 2020, 13, 3162. [Google Scholar] [CrossRef] [PubMed]
  14. Kasuda, K.; Tsutsui, M. Some new developments in the chemistry of metallophthalocyanines. Coord. Chem. Rev. 1980, 32, 67–95. [Google Scholar] [CrossRef] [Green Version]
  15. Thomas, A.L. Phthalocyanines. Research & Applications; CRC Press: Boca Raton, FL, USA, 1990. [Google Scholar]
  16. Sliva, W.; Mianovska, B. Metalloporphyrin arrays. Transit. Met. Chem. 2000, 25, 491–504. [Google Scholar] [CrossRef]
  17. Mamardashvili, G.M.; Mamardashvili, N.Z.; Koifman, O.I. Self-assembling systems based on porphyrins. Russ. Chem. Rev. 2008, 77, 59–75. [Google Scholar] [CrossRef]
  18. Donzello, M.P.; Ercolani, C.; Novakova, V.; Zimcik, P.; Stuzhin, P.A. tetrapyrazinoporphyrazines and their metal derivatives. Part I: Synthesis and basic structural information. Coord. Chem. Rev. 2016, 309, 107–179. [Google Scholar] [CrossRef]
  19. Lomova, T.N. Axial Coordinated Metal Porphyrins in Science and Practice; URSS: Moscow, Russia, 2018. [Google Scholar]
  20. Khelevina, O.G.; Malyasova, A.S. 40 years with porphyrazines. J. Porphyr. Phthalocyanines 2019, 23, 1251–1264. [Google Scholar] [CrossRef]
  21. Calborean, A.; Morari, C.; Maldivi, P. Combined molecular and periodic DFT analysis of the adsorption of co macrocycles on graphene. J. Comput. Chem. 2018, 39, 130–138. [Google Scholar] [CrossRef]
  22. Patel, A.; Abozeid, S.M.; Cullen, P.A.; Morrow, J.R. Co(II) Macrocyclic Complexes Appended with Fluorophores as paraCEST and cellCEST Agents. Inorg. Chem. 2020, 59, 16531–16544. [Google Scholar] [CrossRef]
  23. Reynolds, P.A.; Figgis, B.N.; Kucharski, E.S.; Mason, S.A. Neutron diffraction at 115 K to 1.09 Å-1 from cobalt phthalocyanine. Acta Cryst. B 1991, 47, 899–904. [Google Scholar] [CrossRef]
  24. Ballirano, P.; Caminiti, R.; Ercolani, C.; Maras, A.; Orru, M.A. X-ray Powder Diffraction Structure Reinvestigation of the α and β Forms of Cobalt Phthalocyanine and Kinetics of the α→β Phase Transition. J. Am. Chem. Soc. 1998, 120, 12798–12807. [Google Scholar] [CrossRef]
  25. Chachkov, D.V.; Mikhailov, O.V. Density Functional Theory Modeling of Molecular Structures of Heteroligand 3d M(IV) Complexes with Porphyrazine and Oxo Anion. Russ. J. Inorg. Chem. 2020, 65, 1019–1024. [Google Scholar] [CrossRef]
  26. Chachkov, D.V.; Mikhailov, O.V. Quantum-chemical calculation of molecular structures of (5656)macrotetracyclic 3d-metal complexes “self-assembled” in quaternary systems M(II) ion-ethanedithioamide- formaldehyde- ammonia by the density functional theory method. Russ. J. Inorg. Chem. 2014, 59, 218–223. [Google Scholar] [CrossRef]
  27. Mikhailov, O.V. Synthesis of 3d-element metalmacrocyclic chelates into polypeptide biopolymer medium and their molecular structures. Inorg. Chim. Acta 2013, 394, 664–684. [Google Scholar] [CrossRef]
  28. Chachkov, D.V.; Mikhailov, O.V. Structure of (5656)macrotetracyclic chelates in the ternary systems M(II)-ethanedithioamide-acetone (M = Mn, Fe, Co, Ni, Cu, Zn) according to DFT calculations. Russ. J. Inorg. Chem. 2013, 58, 1073–1078. [Google Scholar] [CrossRef]
  29. Mikhailov, O.V.; Chachkov, D.V. Novel oxidation state—Zinc(III) in chelate with 3,7,11,15-tetraazaporphine and one fluorine ligand: Quantum-chemical modeling. J. Porphyr. Phthalocyanines 2019, 23, 685–689. [Google Scholar] [CrossRef]
  30. Mikhailov, O.V.; Chachkov, D.V. M(VI) Oxidation State Stabilization in Iron, Cobalt and Nickel Heteroligand Metal Chelates Containing 3,7,11,15-Tetraazaporphine and Two Axial Oxo Ligands: Quantum-Chemical Simulation. Int. J. Mol. Sci. 2020, 21, 1494. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  31. Schaefer, A.; Horn, H.; Ahlrichs, R. Fully optimized contracted Gaussian basis sets for atoms Li to Kr. J. Chem. Phys. 1992, 97, 2571–2577. [Google Scholar] [CrossRef]
  32. Schaefer, A.; Huber, C.; Ahlrichs, R. Fully optimized contracted Gaussian basis sets of triple zeta valence quality for atoms Li to Kr. J. Chem. Phys. 1994, 100, 5829–5835. [Google Scholar] [CrossRef]
  33. Hoe, W.M.; Cohen, A.; Handy, N.C. Assessment of a new local exchange functional OPTX. Chem. Phys. Lett. 2001, 341, 319–328. [Google Scholar] [CrossRef]
  34. Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1997, 78, 1396. [Google Scholar] [CrossRef] [Green Version]
  35. Paulsen, H.; Duelund, L.; Winkler, H.; Toftlund, H.; Trautwein, A.X. Free Energy of Spin-Crossover Complexes Calculated with Density Functional Methods. Inorg. Chem. 2001, 40, 2201–2203. [Google Scholar] [CrossRef] [PubMed]
  36. Swart, M.; Groenhof, A.R.; Ehlers, A.W.; Lammertsma, K. Validation of Exchange−Correlation Functionals for Spin States of Iron Complexes. J. Phys. Chem. A 2004, 108, 5479–5483. [Google Scholar] [CrossRef]
  37. Swart, M.; Ehlers, A.W.; Lammertsma, K. Performance of the OPBE exchange-correlation functional. Mol. Phys. 2004, 102, 2467–2474. [Google Scholar] [CrossRef]
  38. Swart, M. Metal–ligand bonding in metallocenes: Differentiation between spin state, electrostatic and covalent bonding. Inorg. Chim. Acta 2007, 360, 179–189. [Google Scholar] [CrossRef]
  39. Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef]
  40. Perdew, J.P.; Burke, K.; Wang, Y. Generalized gradient approximation for the exchange-correlation hole of a many-electron system. Phys. Rev. B 1996, 54, 16533–16539. [Google Scholar] [CrossRef] [Green Version]
  41. Medvedev, M.G.; Bushmarinov, I.S.; Sun, J.; Perdew, J.P.; Lyssenko, K.A. Density functional theory is straying from the path toward the exact functional. Science 2017, 355, 49–52. [Google Scholar] [CrossRef]
  42. Chai, J.-D.; Head-Gordon, M. Long-range corrected hybrid density functionals with damped atom-atom dispersion corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. [Google Scholar] [CrossRef] [Green Version]
  43. Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V. Gaussian 09; Revision A.01; Gaussian, Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
  44. Ochterski, J.W. Thermochemistry in Gaussian; Gaussian, Inc.: Wallingford, CT, USA, 2000. [Google Scholar]
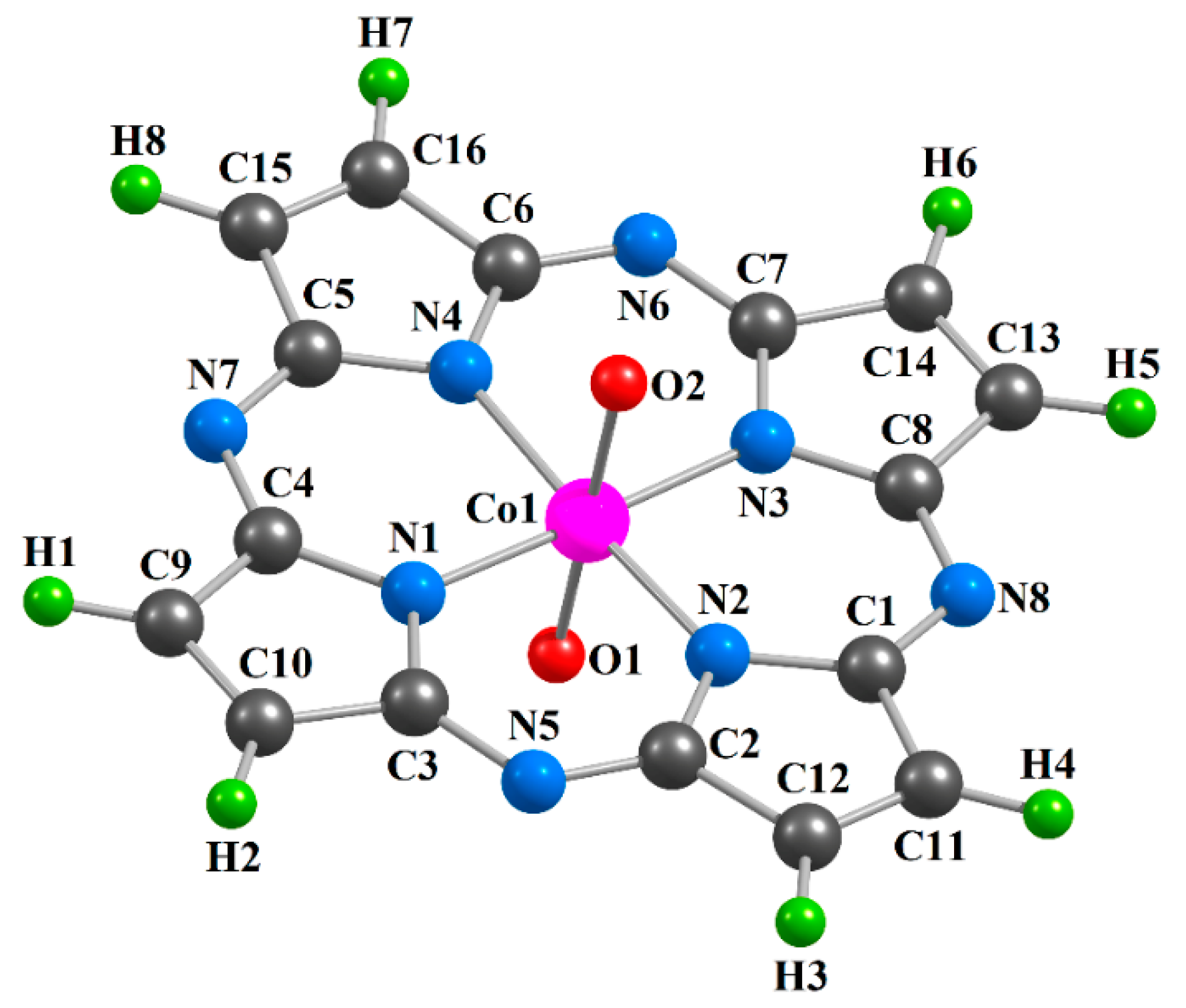
Ijms 21 09085 g001 550
Figure 1. Molecular structure of the [CoL1(O)2] complex obtained as a result of DFT B3PW91/TZVP quantum-chemical calculation.
Figure 1. Molecular structure of the [CoL1(O)2] complex obtained as a result of DFT B3PW91/TZVP quantum-chemical calculation.
Ijms 21 09085 g001
Ijms 21 09085 g002 550
Figure 2. Molecular structure of the [CoL2(O)2] complex obtained as a result of DFT B3PW91/TZVP quantum-chemical calculation.
Figure 2. Molecular structure of the [CoL2(O)2] complex obtained as a result of DFT B3PW91/TZVP quantum-chemical calculation.
Ijms 21 09085 g002
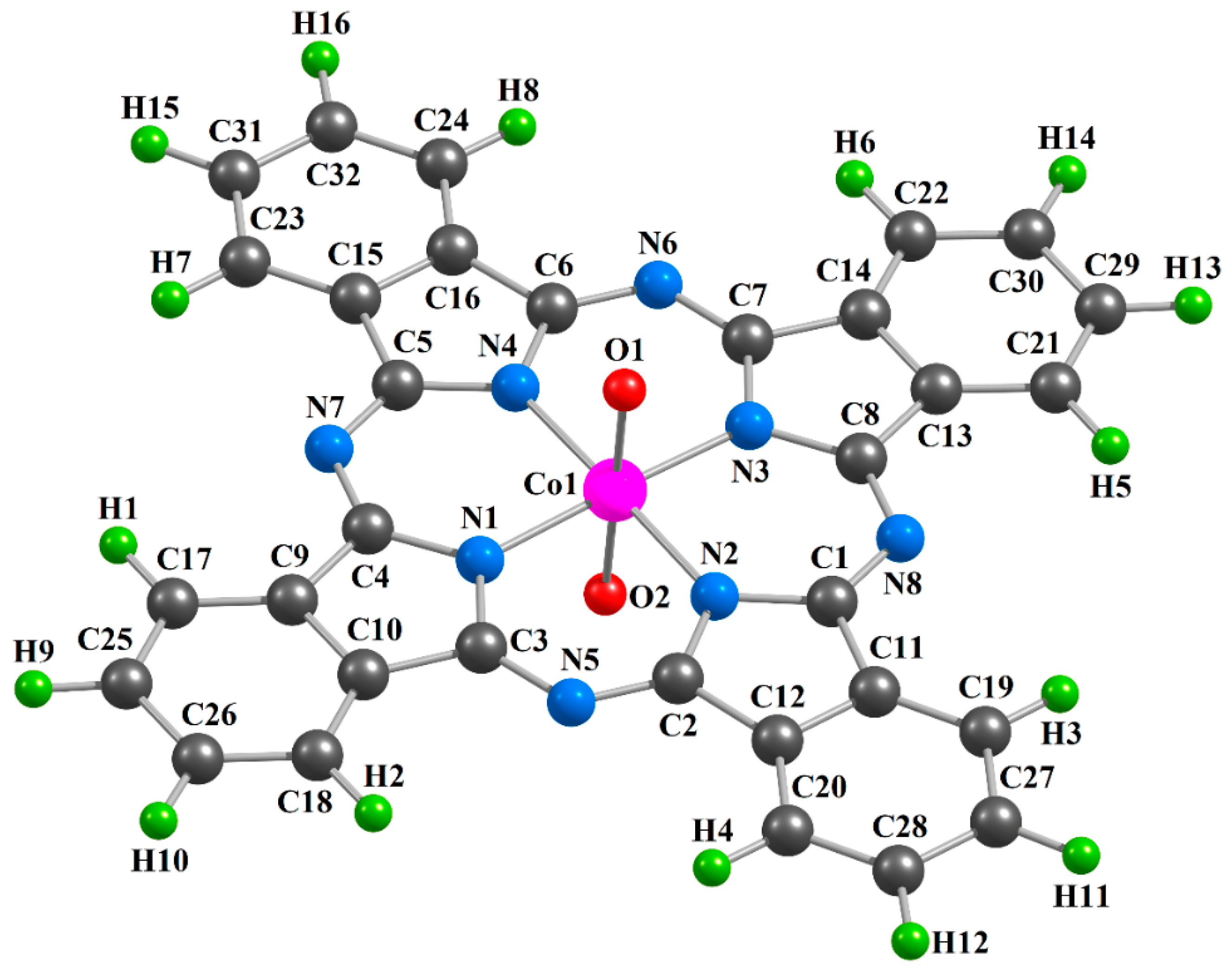
Ijms 21 09085 g003 550
Figure 3. Molecular structure of the [CoL3(O)2] complex obtained as a result of DFT B3PW91/TZVP quantum-chemical calculation.
Figure 3. Molecular structure of the [CoL3(O)2] complex obtained as a result of DFT B3PW91/TZVP quantum-chemical calculation.
Ijms 21 09085 g003
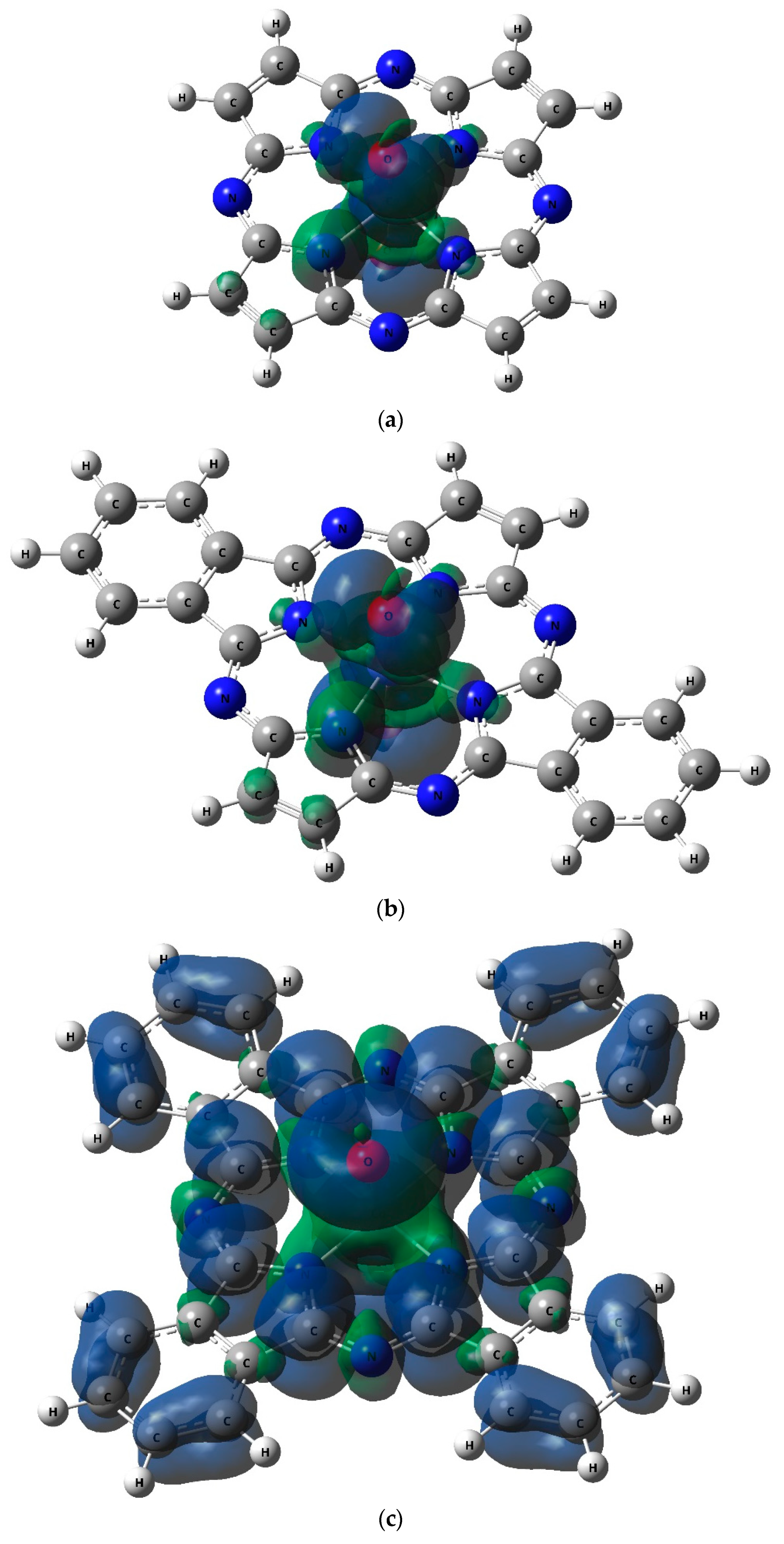
Ijms 21 09085 g004 550
Figure 4. The pictures of spin density distribution in the [CoL1(O)2] (a), [CoL2(O)2] (b), and [CoL3(O)2] (c) complexes obtained by using the DFT OPBE/TZVP method.
Figure 4. The pictures of spin density distribution in the [CoL1(O)2] (a), [CoL2(O)2] (b), and [CoL3(O)2] (c) complexes obtained by using the DFT OPBE/TZVP method.
Ijms 21 09085 g004
Table
Table 1. Bond lengths and bond angles in the nickel complexes of types I, II, and III calculated by OPBE/TZVP and B3PW91/TZVP methods.
Table 1. Bond lengths and bond angles in the nickel complexes of types I, II, and III calculated by OPBE/TZVP and B3PW91/TZVP methods.
Complex[CoL1(O)2][CoL2(O)2][CoL3(O)2]
Structural parameterCalculated by DFTCalculated by DFTCalculated by DFT
OPBE/TZVPB3PW91/TZVPOPBE/TZVPB3PW91/TZVPOPBE/TZVPB3PW91/TZVP
Co–N bond lengths in chelate node MN4, pm
Co1N1192.2192.2195.2193.2193.6194.0
Co1N2193.2191.5194.8192.4193.6195.3
Co1N3194.2192.2195.2193.2193.6194.0
Co1N4193.2191.5192.8192.4193.6195.3
Co–O bond lengths, pm
Co1O1168.9173.1168.7174.5175.4171.5
Co1O2168.9176.7168.7174.5175.4179.0
C–N bond lengths in 6-numbered chelate rings, pm
N1C3136.4135.4136.7135.7136.2136.8
N1C4136.4135.4136.6135.7136.2136.8
N2C1136.3135.7136.7135.1136.2136.3
N2C2136.2135.7136.7135.1136.2136.3
N3C7136.7135.4136.6135.7136.2136.8
N3C8136.7135.4136.7135.7136.2136.8
N4C5136.2135.7136.4135.1136.2136.3
N4C6136.3135.7136.4135.1136.2136.3
N5C2132.4131.3132.3131.8132.0131.3
N5C3132.4132.7131.9131.8132.0131.3
N6C6132.4131.3132.4131.8132.0131.3
N6C7132.3132.7131.9131.8132.0131.3
N7C4132.4132.7131.9131.8132.0131.3
N7C5132.4131.3132.4131.8132.0131.3
N8C1132.4131.3132.3131.8132.0131.3
N8C8132.3132.7131.9131.8132.0131.3
C–C bond lengths in 5-numbered chelate ring (N1C4C9C10C3), pm
C4C9145.2146.2145.8146.4146.4145.0
C9C10135.7134.4140.2139.4139.9139.7
C10C3145.2146.2145.8146.4146.4145.0
Bond angles in chelate node CoN4, deg
(N1Co1N2)90.190.089.990.090.090.0
(N2Co1N3)89.989.989.990.090.090.0
(N3Co1N4)89.990.090.190.090.090.0
(N4Co1N1)90.189.990.190.090.090.0
Bond angles sum (BAS), deg360.0359.8360.0360.0360.0360.0
Non-bond angles between N atoms in N4 grouping, deg
(N1N2N3)90.090.290.290.290.089.6
(N2N3N4)89.889.789.689.890.090.4
(N3N4N1)90.090.290.690.290.089.6
(N4N1N2)90.289.789.689.890.090.4
Non-bond angles sum (NBAS), deg360.0359.8360.0360.0360.0360.0
Bond angles in 6-numbered chelate ring (Co1N1C4N7C5N4), deg
(Co1N1C4)126.1126.3125.3125.6125.8125.5
(N1C4N7)128.3127.9128.4128.4128.5128.3
(C4N7C5)121.4121.1121.7121.7121.4122.6
(N7C5N4)128.1128.4128.3128.0128.5128.1
(C5N4Co1)126.1126.3126.2126.3125.8125.5
(N4Co1N1)90.089.990.190.090.090.0
Bond angles sum (BAS61), deg720.0719.9720.0720.0720.0720.0
Bond angles in 6-numbered chelate ring (Co1N4C6N6C7N3), deg
(Co1N4C6)126.1126.3126.2126.3125.8125.6
(N4C6N6)128.5128.4128.3128.0128.5128.0
(C6N6C7)121.4121.1121.7121.7121.4122.6
(N6C7N3)128.2127.9128.4128.4128.5128.2
(C7N3Co1)125.9126.3125.3125.6125.8125.6
(N3Co1N4)89.989.990.190.090.090.0
Bond angles sum (BAS62), deg720.0719.9720.0720.0720.0720.0
Bond angles in 5-numbered ring (C3N1C4C9C10), deg
(C3N1C4)107.8107.3109.3108.8108.4108.9
(N1C4C9)109.1109.7108.9109.5109.7109.0
(C4C9C10)107.0106.6106.4106.1106.1106.6
(C9C10C3)107.0106.6106.5106.1106.1106.6
(C10C3N1)109.1109.7108.9109.5109.7108.9
Bond angles sum (BAS51), deg540.0539.9540.0540.0540.0540.0
Bond angles in 5-numbered ring (C1N2C2C12C11), deg
(C1N2C2)107.8107.5108.0107.4108.4108.9
(N2C2C12)109.2109.4108.9109.8109.7109.1
(C2C12C11)106.9106.8107.1106.5106.1106.4
(C12C11C1)107.0106.8107.1106.5106.1106.4
(C11C1N2)109.1109.4108.9109.8109.7109.1
Bond angles sum (BAS52), deg540.0539.9540.0540.0540.0540.0
Bond angles between O, Co and N atoms, deg
O1Co1N194.991.190.090.090.091.5
O1Co1N290.092.785.090.090.091.0
O1Co1N385.191.190.090.090.091.5
O1Co1N490.092.795.090.090.091.0
O2Co1N194.988.990.090.090.088.5
O2Co1N290.087.385.090.090.089.0
O2Co1N385.188.990.090.090.088.5
O2Co1N490.087.385.090.090.089.0
Bond angles between Co and two O atoms, deg
O1Co1O2170.1180.0169.9180.0180.0180.0
Table
Table 2. NBO analysis data for the cobalt complexes of types I, II, and III.
Table 2. NBO analysis data for the cobalt complexes of types I, II, and III.
ComplexEffective Charge of Atom, in Units of Electron Charge (ē)<S**2>
Co1N1 (N3)N2 (N4)O1 (O2)
[CoL1(O)2]+0.0647−0.2989 (−0.2938)−0.2905 (−0.2905)−0.0895 (−0.0895)0.7609
[CoL2(O)2]+0.0859−0.2699 (−0.2699)−0.2982 (−0.3065)−0.1673 (−0.1673)0.7627
[CoL3(O)2]+0.0881−0.2669 (−02669)−0.2669 (−02669)−0.4071 (−0.4071)3.7715
Table
Table 3. Standard thermodynamic parameters of formation (ΔH0f, 298, S0f, 298 and ΔG0f, 298) for the cobalt complexes of types I–III.
Table 3. Standard thermodynamic parameters of formation (ΔH0f, 298, S0f, 298 and ΔG0f, 298) for the cobalt complexes of types I–III.
ComplexΔH0f, 298, kJ/moleS0f, 298, J/mole ∙KΔG0f, 298, kJ/mole
[CoL1(O)2]616.3759.8842.1
[CoL2(O)2]567.7949.8814.5
[CoL3(O)2]530.11168.9789.3
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Mikhailov, O.V.; Chachkov, D.V. DFT Quantum-Chemical Modeling Molecular Structures of Cobalt Macrocyclic Complexes with Porphyrazine or Its Benzo-Derivatives and Two Oxygen Acido Ligands. Int. J. Mol. Sci. 2020, 21, 9085. https://doi.org/10.3390/ijms21239085

AMA Style

Mikhailov OV, Chachkov DV. DFT Quantum-Chemical Modeling Molecular Structures of Cobalt Macrocyclic Complexes with Porphyrazine or Its Benzo-Derivatives and Two Oxygen Acido Ligands. International Journal of Molecular Sciences. 2020; 21(23):9085. https://doi.org/10.3390/ijms21239085

Chicago/Turabian Style

Mikhailov, Oleg V., and Denis V. Chachkov. 2020. "DFT Quantum-Chemical Modeling Molecular Structures of Cobalt Macrocyclic Complexes with Porphyrazine or Its Benzo-Derivatives and Two Oxygen Acido Ligands" International Journal of Molecular Sciences 21, no. 23: 9085. https://doi.org/10.3390/ijms21239085

APA Style

Mikhailov, O. V., & Chachkov, D. V. (2020). DFT Quantum-Chemical Modeling Molecular Structures of Cobalt Macrocyclic Complexes with Porphyrazine or Its Benzo-Derivatives and Two Oxygen Acido Ligands. International Journal of Molecular Sciences, 21(23), 9085. https://doi.org/10.3390/ijms21239085

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop