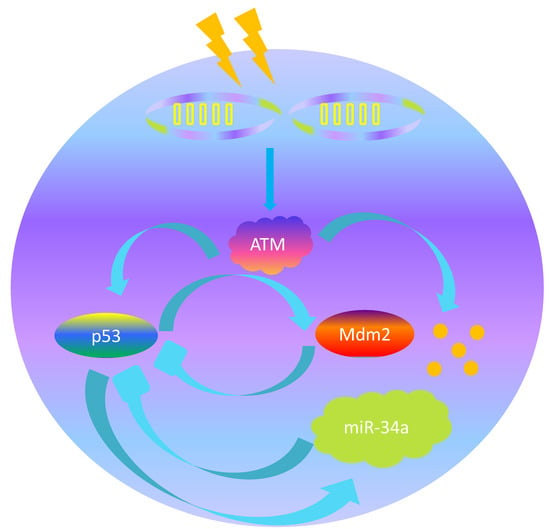
Dynamic Behavior of p53 Driven by Delay and a Microrna-34a-Mediated Feedback Loop
Abstract
:1. Introduction
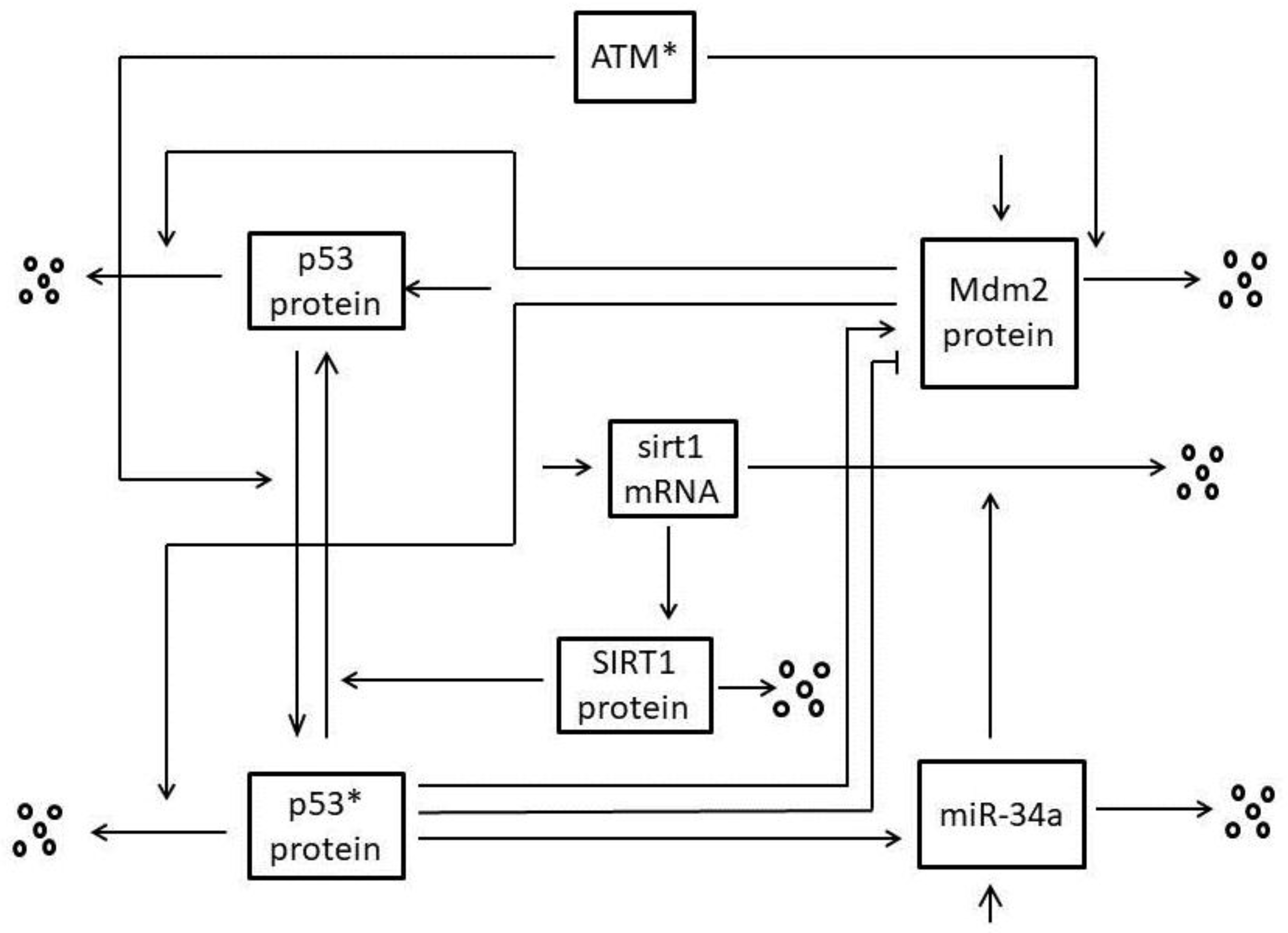
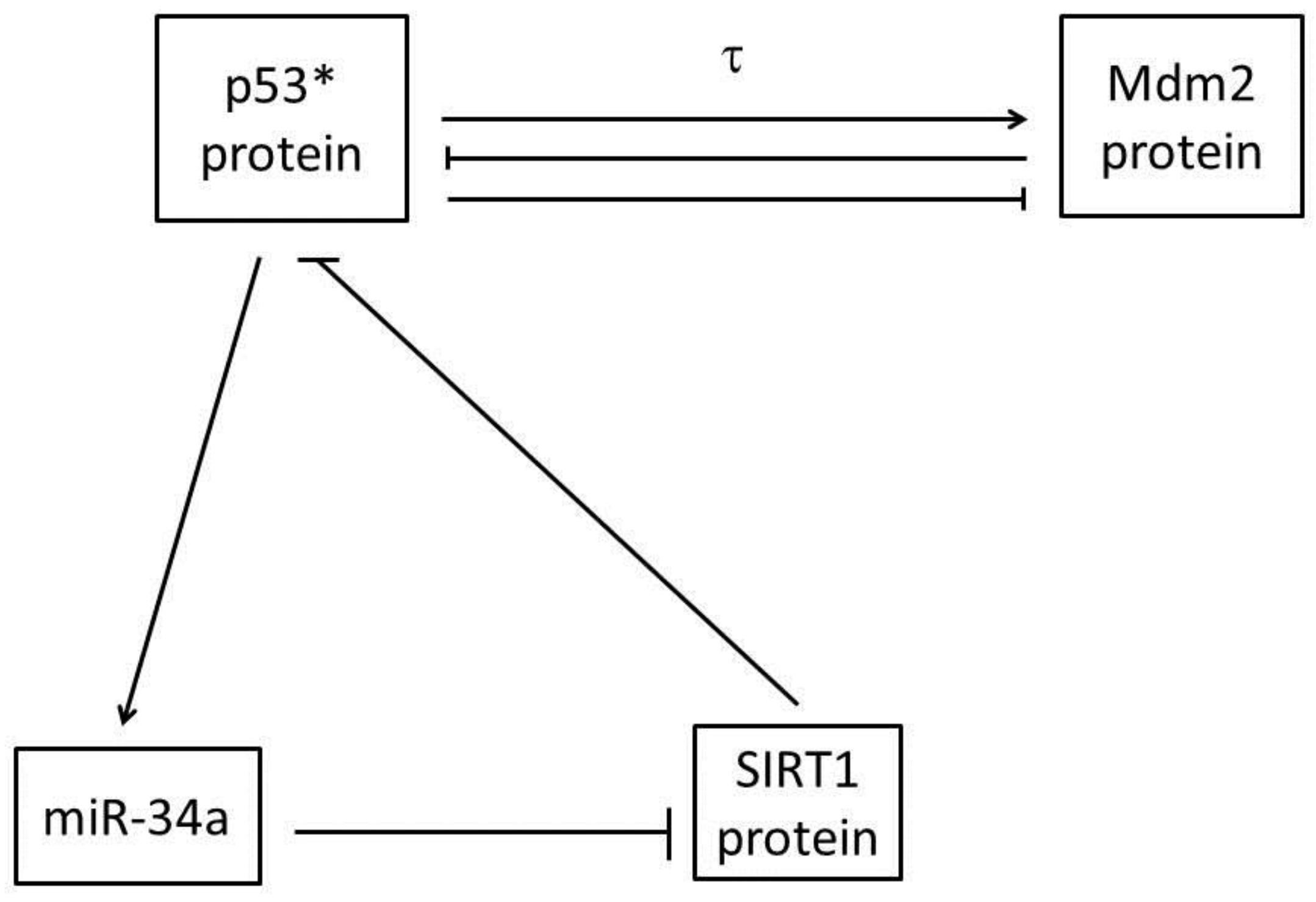
2. Mathematical Model
3. Results
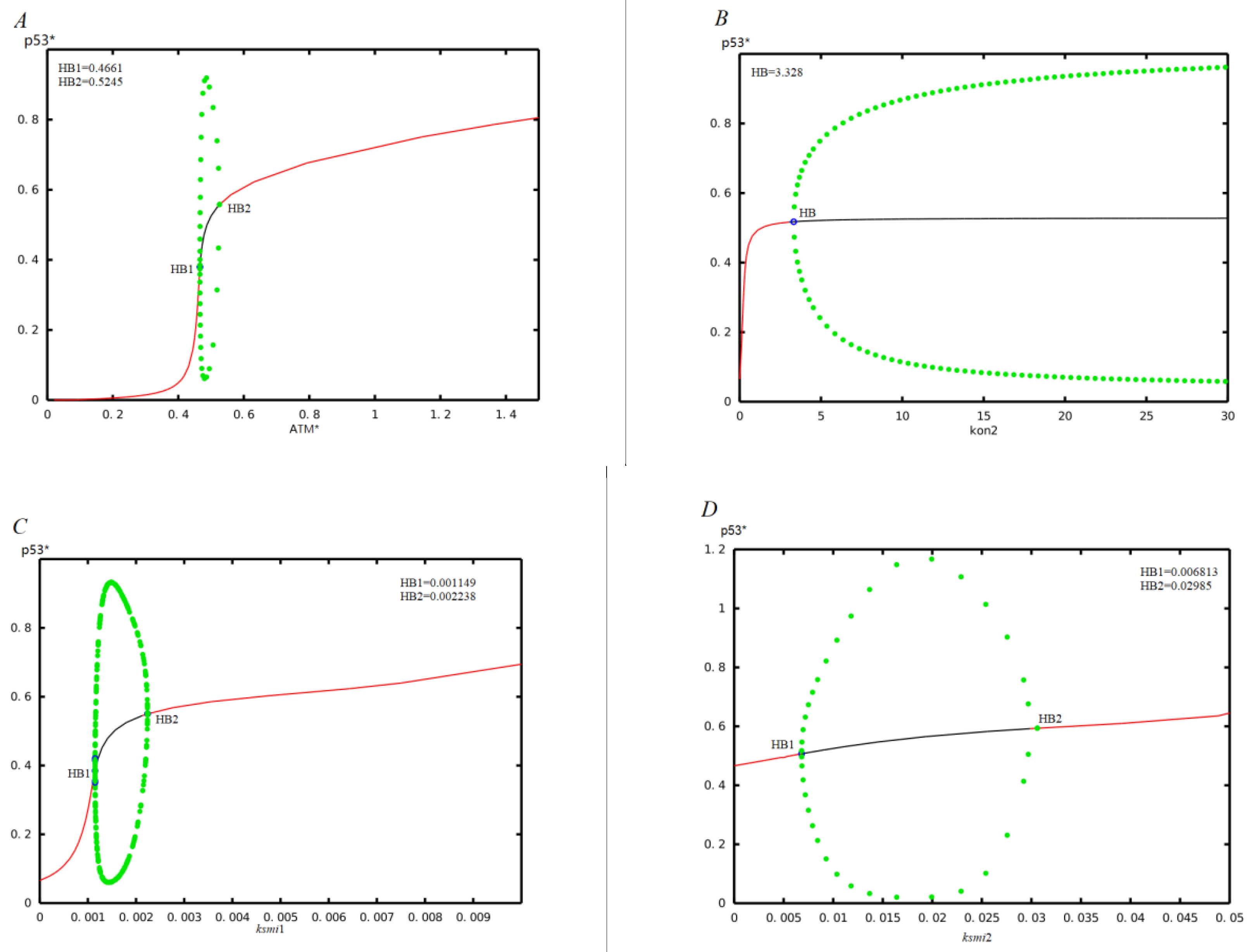
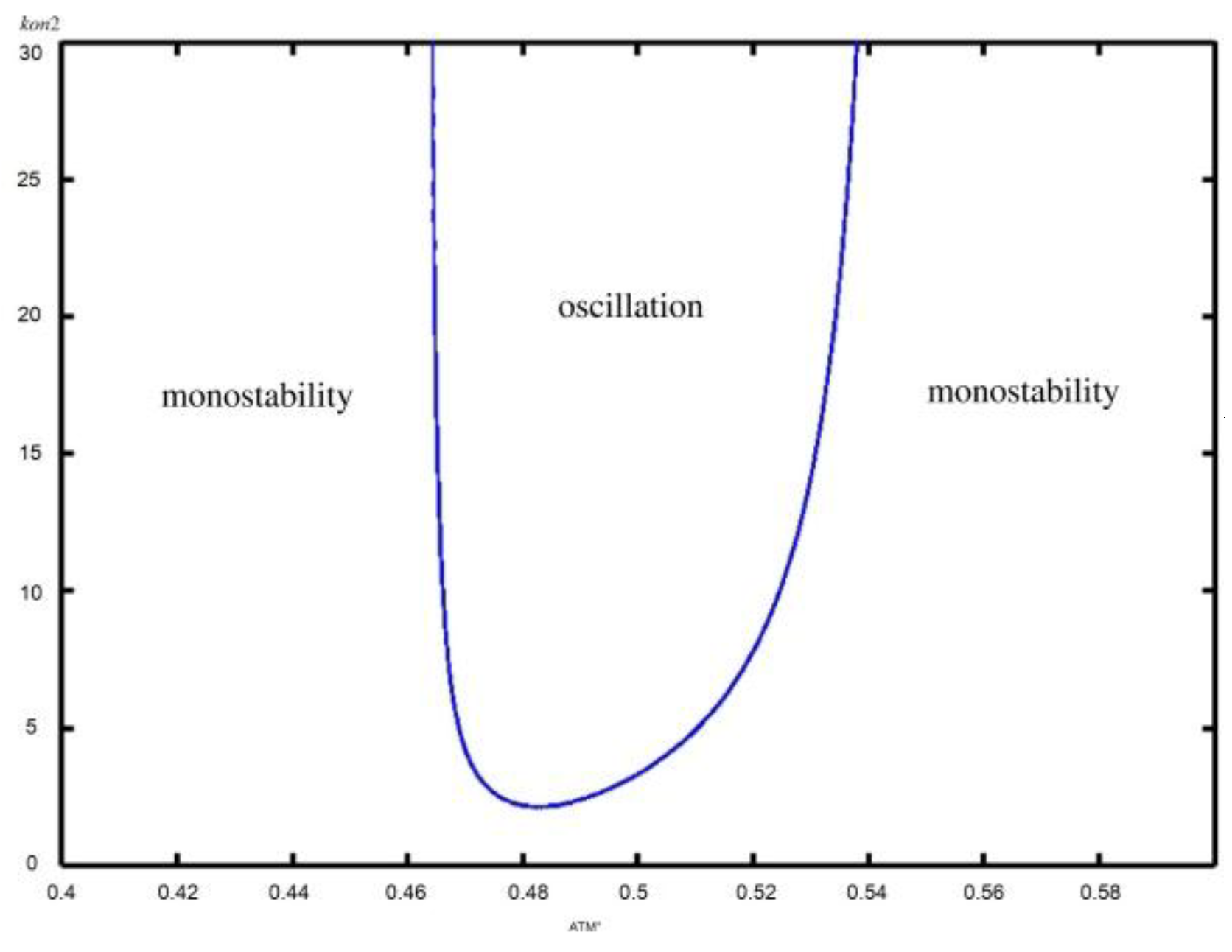
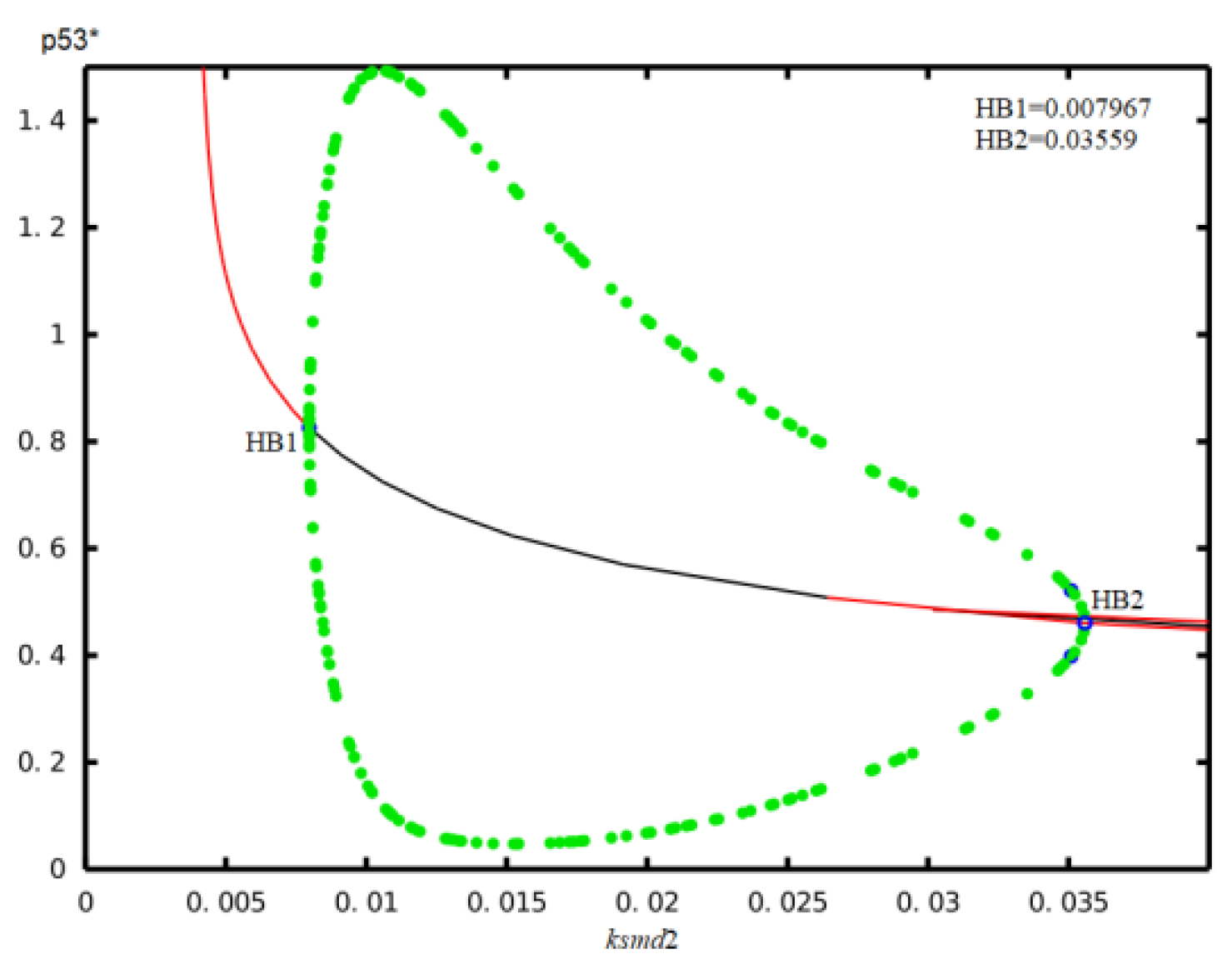
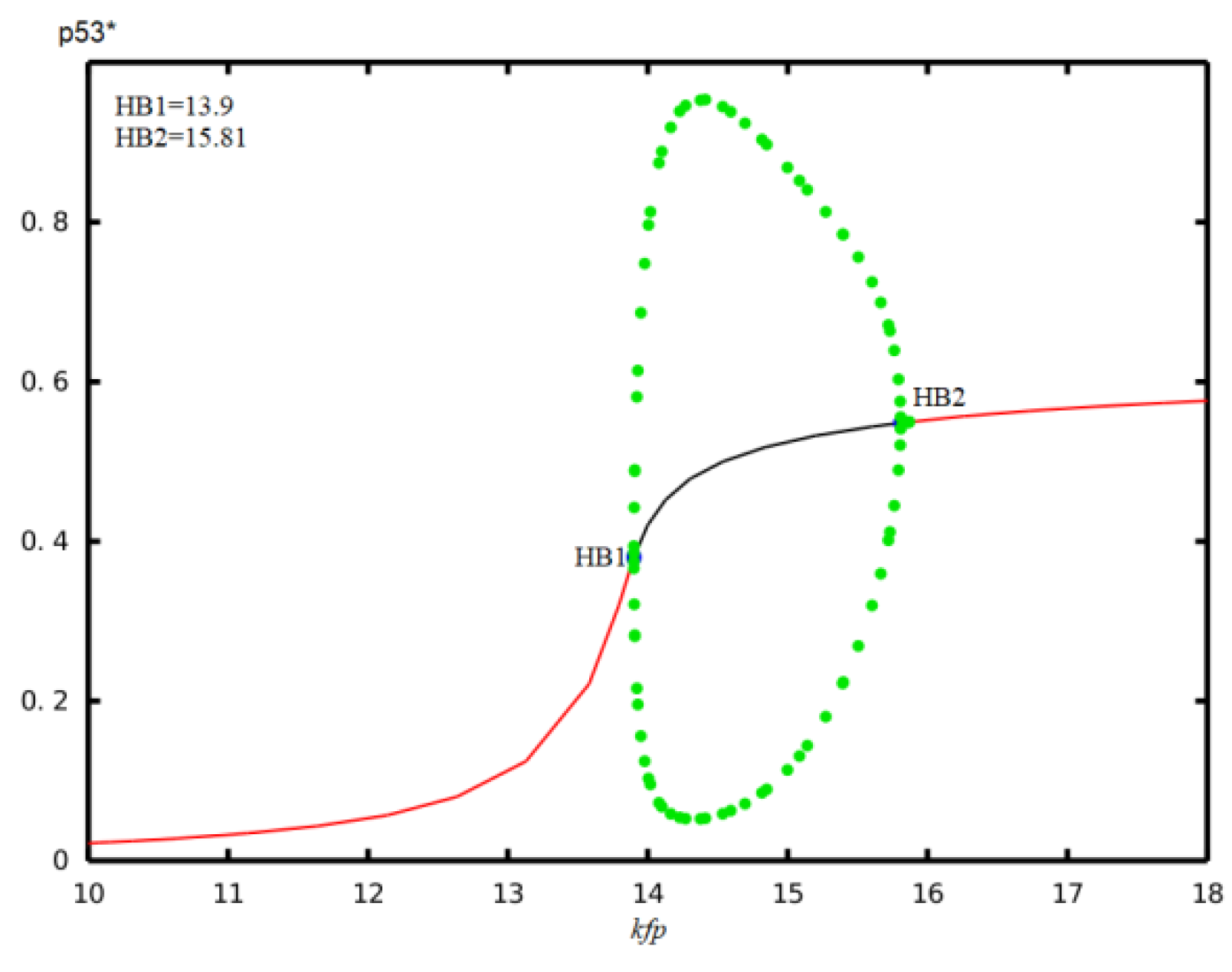
3.1. The Effect of Mir-34a on p53 Oscillations without Time Delay
3.2. The Effect of Time Delay on the p53-mdm2 Network without MiR-34a
3.3. Co-Regulation of the p53 Oscillatios by Time Delay and Mir-34a
4. Discussion
5. Materials and Methods
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hollstein, M.; Sidransky, D.; Vogelstein, B.; Harris, C. p53 mutations in human cancers. Science 1991, 253, 49–53. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vogelstein, B.; Lane, D.; Levine, A. Surfing the p53 network. Nature 2000, 408, 307–310. [Google Scholar] [CrossRef] [PubMed]
- Levine, A.J.; Hu, W.; Feng, A. The p53 pathway: what questions remain to be explored? Cell Death Differ. 2006, 13, 1027–1036. [Google Scholar] [CrossRef] [PubMed]
- Fiona, M.Z.; Slee, E.A.; Xin, L. A complex barcode underlies the heterogeneous response of p53 to stress. Nat. Rev. Mol. Cell Biol. 2008, 9, 702. [Google Scholar]
- Yael, A.; Moshe, O. Living with p53, dying of p53. Cell 2007, 130, 597–600. [Google Scholar]
- Ko, L.; Prives, C. p53: puzzle and paradigm. Genes Dev. 1996, 10, 1054. [Google Scholar] [CrossRef] [Green Version]
- Purvis, J.E.; Karhohs, K.W.; Caroline, M.; Eric, B.; Alexander, L.; Galit, L. p53 dynamics control cell fate. Science 2012, 336, 1440–1444. [Google Scholar] [CrossRef] [Green Version]
- Béla, N.; Tyson, J.J. Design principles of biochemical oscillators. Nat. Rev. Mol. Cell Biol. 2008, 9, 981–991. [Google Scholar]
- Lahav, G. Oscillations by the p53-mdm2 feedback loop. Adv. Exp. Med. Biol. 2008, 641, 28–38. [Google Scholar]
- Monk, N. Oscillatory expression of hes1, p53, and nf-kappab driven by transcriptional time delays. Curr. Biol. 2003, 13, 1409–1413. [Google Scholar] [CrossRef] [Green Version]
- Ma, L.; Wagner, J.; Rice, J.; Hu, W.; Levine, A.; Stolovitzky, G. A plausible model for the digital response of p53 to DNA damage. Proc. Natl. Acad. Sci. USA 2005, 102, 14266–14271. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wagner, J.; Ma, L.; Rice, J.; Hu, W. p53-mdm2 loop controlled by a balance of its feedback strength and effective dampening using atm and delayed feedback. Syst. Biol. 2005, 152, 109. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Geva-Zatorsky, N.; Rosenfeld, N.; Itzkovitz, S.; Milo, R.; Sigal, A.; Dekel, E.; Yarnitzky, T.; Liron, Y.; Polak, P.; Lahav, G. Oscillations and variability in the p53 system. Mol. Syst. Biol. 2006, 2, 2006.0033. [Google Scholar] [CrossRef] [PubMed]
- Lujambio, A.; Lowe, S.W. The microcosmos of cancer. Nature 2012, 482, 347–355. [Google Scholar] [CrossRef]
- Esquelakerscher, A.; Slack, F.J. Oncomirs-micrornas with a role in cancer. Nat. Rev. Cancer 2006, 6, 259–269. [Google Scholar] [CrossRef] [PubMed]
- Michael, T.J.; Martin, N.; Parker, J.S.; Morin-Kensicki, E.M.; Tricia, W.; Hammond, S.M. Extensive post-transcriptional regulation of micrornas and its implications for cancer. Genes Dev. 2006, 20, 2202–2207. [Google Scholar]
- Welch, C.; Chen, Y.; Stallings, R.L. Microrna-34a functions as a potential tumor suppressor by inducing apoptosis in neuroblastoma cells. Oncogene 2007, 26, 5017–5022. [Google Scholar] [CrossRef] [Green Version]
- Bommer, G.T.; Gerin, I.; Feng, Y.; Kaczorowski, A.J.; Kuick, R.; Love, R.E.; Zhai, Y.; Giordano, T.J.; Qin, Z.S.; Moore, B.B. p53-mediated activation of mirna34 candidate tumor-suppressor genes. Curr. Biol. 2007, 17, 1298. [Google Scholar] [CrossRef] [Green Version]
- Zhaohui, F.; Cen, Z.; Rui, W.; Wenwei, H. Tumor suppressor p53 meets micrornas. J. Mol. Cell Biol. 2011, 3, 44–50. [Google Scholar]
- Chang, T.C.; Wentzel, E.A.; Kent, O.A.; Ramachandran, K.; Mullendore, M.; Lee, K.H.; Feldmann, G.; Yamakuchi, M.; Ferlito, M.; Lowenstein, C.J. Transactivation of mir-34a by p53 broadlyinfluences gene expression andpromotesapoptosis. Mol. Cell 2007, 26, 745–752. [Google Scholar] [CrossRef] [Green Version]
- Lin, H.; Xingyue, H.; Lim, L.P.; Elisa, D.S.; Zhenyu, X.; Yu, L.; Wen, X.; Lars, Z.; Jill, M.; Dana, R. A microrna component of the p53 tumour suppressor network. Nature 2007, 447, 1130–1134. [Google Scholar]
- Ciliberto, A.; Novak, B.; Tyson, J.J. Steady states and oscillations in the p53/mdm2 network. Cell Cycle 2005, 4, 488–493. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, X.; Liu, F.; Cheng, Z.; Wang, W. Cell fate decision mediated by p53 pulses. Proc. Natl. Acad. Sci. USA 2009, 106, 12245–12250. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wee, K.; Aguda, B. Akt versus p53 in a network of oncogenes and tumor suppressor genes regulating cell survival and death. Biophys. J. 2006, 91, 857. [Google Scholar] [CrossRef] [Green Version]
- Lev, B.; Maya, R.; Segel, L.; Alon, U.; Levine, A.; Oren, M. Generation of oscillations by the p53-mdm2 feedback loop: a theoretical and experimental study. Proc. Natl. Acad. Sci. USA 2000, 97, 11250–11255. [Google Scholar]
- Pandita, T.K.; Lieberman, H.B.; Lim, D.S.; Dhar, S.; Zheng, W.; Taya, Y.; Kastan, M. Ionizing radiation activates the atm kinase throughout the cell cycle. Oncogene 2000, 19, 1386–1391. [Google Scholar] [CrossRef] [Green Version]
- John, R.; Jackson, S.P. Interfaces between the detection, signaling, and repair of DNA damage. Science 2002, 297, 547–551. [Google Scholar]
- Stommel, J.; Wahl, G. Accelerated mdm2 auto-degradation induced by DNA damage kinases is required for p53 activation. EMBO J. 2014, 23, 1547–1556. [Google Scholar] [CrossRef] [Green Version]
- Yin, Y.; Stephen, C.; Luciani, M.; Haeus, R.F. p53 stability and activity is regulated by mdm2-mediated induction of alternative p53 translation products. Nat. Cell Biol. 2002, 4, 462–467. [Google Scholar] [CrossRef]
- Lewin, B. Genes VIII; Prentice Hall: New York, NY, USA, 2004. [Google Scholar]
- Audibert, A.; Weil, D.; Dautry, F. In vivo kinetics of mrna splicing and transport in mammalian cells. Mol. Cell. Biol. 2002, 22, 6706–6718. [Google Scholar] [CrossRef] [Green Version]
- Vivanco, I.; Sawyers, C. The phosphatidylinositol 3-kinase akt pathway in human cancer. Nat. Rev. Cancer 2002, 2, 489–501. [Google Scholar] [CrossRef] [PubMed]
- Tarasov, V.; Jung, P.; Verdoodt, B.; Lodygin, D.; Epanchintsev, A.; Menssen, A.; Meister, G.; Hermeking, H. Differential regulation of micrornas by p53 revealed by massively parallel sequencing: mir-34a is a p53 target that induces apoptosis and g1-arrest. Cell Cycle 2007, 6, 1586–1593. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- He, L.; He, X.; Lim, L.P.; Stanchina, E.D.; Xuan, Z.; Liang, Y.; Xue, W.; Zender, L.; Magnus, J.; Ridzon, D. A microrna component of the p53 tumour suppressor network. Nature 2007, 447, 1130–1134. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tazawa, H.; Tsuchiya, N.; Izumiya, M.; Nakagama, H. Tumor-suppressive mir-34 induces senescence-like growth arrest through modulation of the e2f pathway in human colon cancer cells. Proc. Natl. Acad. Sci. USA 2007, 104, 15472–15477. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ravershapira, N.; Marciano, E.; Meiri, E.; Spector, Y.; Rosenfeld, N.; Moskovits, N.; Bentwich, Z.; Oren, M. Transcriptional activation of mir-34a contributes to p53-mediated apoptosis. Mol. Cell 2007, 26, 731–743. [Google Scholar] [CrossRef]
- Yamakuchi, M.; Ferlito, M.; Lowenstein, C.J. mir-34a repression of sirt1 regulates apoptosis. Proc. Natl. Acad. Sci. USA 2008, 105, 13421–13426. [Google Scholar] [CrossRef] [Green Version]
- Eaton, E.N. hsir2(sirt1) functions as an nad-dependent p53 deacetylase. Cell 2001, 107, 149–159. [Google Scholar]
- Lai, X.; Wolkenhauer, O.; Vera, J. Modeling mirna regulation in cancer signaling systems: mir-34a regulation of the p53/sirt1 signaling module. Methods Mol. Biol. 2012, 880, 87. [Google Scholar]
- Zhang, X.; Liu, F.; Wang, W. Two-phase dynamics of p53 in the DNA damage response. Proc. Natl. Acad. Sci. USA 2011, 108, 8990. [Google Scholar] [CrossRef] [Green Version]
- Richard, M.; Kiang, O.H.; Kang, T.; Leonidas, B.; Lan, M. Mir-192-mediated positive feedback loop controls the robustness of stress-induced p53 oscillations in breast cancer cells. PloS Comput. Biol. 2015, 11, e1004653. [Google Scholar]
- Yan, F.; Liu, H.; Liu, Z. Dynamic analysis of the combinatorial regulation involving transcription factors and micrornas in cell fate decisions. Biochim. Biophys. Acta 2014, 1844, 248–257. [Google Scholar] [CrossRef] [PubMed]
- Bakkenist, C.J.; Kastan, M.B. DNA damage activates ATM intermolecular autophosphorylation and dimer dissociation. Nature 2003, 421, 499–506. [Google Scholar] [CrossRef] [PubMed]
- Banin, S.; Moyal, L.; Taya, Y.; Anderson, C.; Chessa, L.; Smorodinsky, N.; Prives, C.; Reiss, Y.; Shiloh, Y.; Ziv, Y. Enhanced phosphorylation of p53 by atm in response to DNA damage. Science 1998, 281, 1674–1677. [Google Scholar] [CrossRef] [PubMed]
- Pomerening, J.R.; Kim, S.Y.; Ferrell, J.E. Systems-level dissection of the cell-cycle oscillator: bypassing positive feedback produces damped oscillations. Cell 2005, 122, 565–578. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Su, W.; Fang, J.; Cheng, F.; Liu, C.; Zhou, F.; Zhang, J. Rnf2/ring1b negatively regulates p53 expression in selective cancer cell types to promote tumor development. Proc. Natl. Acad. Sci. USA 2013, 110, 1720–1725. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Levine, A.; Oren, M. The first 30 years of p53: growing ever more complex. Nat. Rev. Cancer 2009, 9, 749–758. [Google Scholar] [CrossRef] [Green Version]
- Meek, D.W. The p53 response to DNA damage. DNA Repair 2004, 3, 1049–1056. [Google Scholar] [CrossRef]
- Zhang, T.; Brazhnik, P.; Tyson, J.J. Exploring mechanisms of the DNA-damage response: p53 pulses and their possible relevance to apoptosis. Cell Cycle 2007, 6, 85–94. [Google Scholar] [CrossRef] [Green Version]
- Vousden, K.; Lu, X. Live or let die: the cell’s response to p53. Nat. Rev. Cancer 2002, 2, 594–604. [Google Scholar] [CrossRef] [Green Version]
- Vousden, K.; Lane, D. p53 in health and disease. Nature Reviews Mol. Cell Biol. 2007, 8, 275. [Google Scholar] [CrossRef]
- Calin, G.A.; Amelia, C.; Muller, F.; Manuela, F.; Wojcik, S.E.; Masayoshi, S.; Cristian, T.; Nicola, Z.; Ramiro, G.; Aqeilan, R.I. Mir-15a and mir-16-1 cluster functions in human leukemia. Proc. Natl. Acad. Sci. USA 2008, 105, 5166–5171. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Muller, F.; Ramiro, G.; Amelia, C.; Zhongfa, L.; Nicola, Z.; Elisa, C.; Shujun, L.; Hansjuerg, A.; Stefan, C.; Cecilia, F.C. MicroRNA-29 family reverts aberrant methylation in lung cancer by targeting DNA methyltransferases 3A and 3B. Proc. Natl. Acad. Sci. USA 2007, 104, 15805–15810. [Google Scholar]



| Parameter | Description | Value | Reference |
|---|---|---|---|
| ksp53 | Production rate of p53 | 0.2 | [40] |
| kda1 | Deactivation rate of p53* by SIRT1 | 3.3 | [41] |
| k0 | Michaelis constant of SIRT1-dependent p53 deactivation | 0.0087 | [41] |
| kdp531 | Basal degradation rate of p53 | 0.02 | [11] |
| kdp532 | Mdm2-dependent degradation rate of p53 | 0.7 | [40] |
| kd1 | Threshold conc. for Mdm2-dependent p53 degradation | 0.03 | [11] |
| kd2 | Threshold conc. for Mdm2-dependent p53* degradation | 0.3 | [11] |
| kfp | The post-translational modifications rate including phosphorylation, methylation, acetylation, etc. on multiple different sites of p53 | 15 | [41] |
| kp | Michaelis constant of ATM*-dependent p53 phosphorylation | 0.87 | [41] |
| A | ATM* concentration | 0~10 | [12] |
| krp | Dephosphorylation rate of p53* | 0.2 | [11] |
| kdp53s | Mdm2-dependent degradation rate of p53* | 0.14 | [40] |
| ksmd1 | Basal production rate of Mdm2 | 0.002 | [41] |
| ksmd2 | P53-dependent synthetic rate of Mdm2 | 0.024 | [41] |
| k | Michaelis constant of p53-dependent Mdm2 production | 1 | [11] |
| kdmdm20 | Basal degradation rate of Mdm2 | 0.003 | [40] |
| kdmdm21 | ATM*-dependent degradation rate of Mdm2 | 0.05 | [40] |
| ksmi1 | Basal induction rate of miR-34a | 0.0018 | [39] |
| ksmi2 | P53*-induced transcription rate of miR-34a | 0.01 | [39] |
| j1 | Michaelis constant of p53*-dependent miR-34a transcription | 1 | Estimate |
| kdmi | Degradation rate of miR-34a | 0.0078 | [41] |
| kon2 | Association rate between sirt1 mRNA and miR-34a | 10 | [41] |
| koff2 | Dissociation rate of sirt1-miR-34a complex | 0.13 | [41] |
| ksmir | Degradation rate of sirt1-miR-34a complex | 0.062 | [41] |
| kss | Basal induction rate of sirt1 mRNA | 0.01 | [42] |
| kssi | Degradation rate of sirt1 mRNA | 0.062 | [41] |
| rsirt1 | Translation rate of SIRT1 protein | 0.42 | [41] |
| ksirt1 | Degradation rate of SIRT1 protein | 0.03 | [41] |
| τ | Transcriptional and translation time delays | 0∼30min | Estimate |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, C.; Liu, H.; Yan, F. Dynamic Behavior of p53 Driven by Delay and a Microrna-34a-Mediated Feedback Loop. Int. J. Mol. Sci. 2020, 21, 1271. https://doi.org/10.3390/ijms21041271
Gao C, Liu H, Yan F. Dynamic Behavior of p53 Driven by Delay and a Microrna-34a-Mediated Feedback Loop. International Journal of Molecular Sciences. 2020; 21(4):1271. https://doi.org/10.3390/ijms21041271
Chicago/Turabian StyleGao, Chunyan, Haihong Liu, and Fang Yan. 2020. "Dynamic Behavior of p53 Driven by Delay and a Microrna-34a-Mediated Feedback Loop" International Journal of Molecular Sciences 21, no. 4: 1271. https://doi.org/10.3390/ijms21041271
APA StyleGao, C., Liu, H., & Yan, F. (2020). Dynamic Behavior of p53 Driven by Delay and a Microrna-34a-Mediated Feedback Loop. International Journal of Molecular Sciences, 21(4), 1271. https://doi.org/10.3390/ijms21041271