Unraveling a Force-Generating Allosteric Pathway of Actomyosin Communication Associated with ADP and Pi Release
Abstract
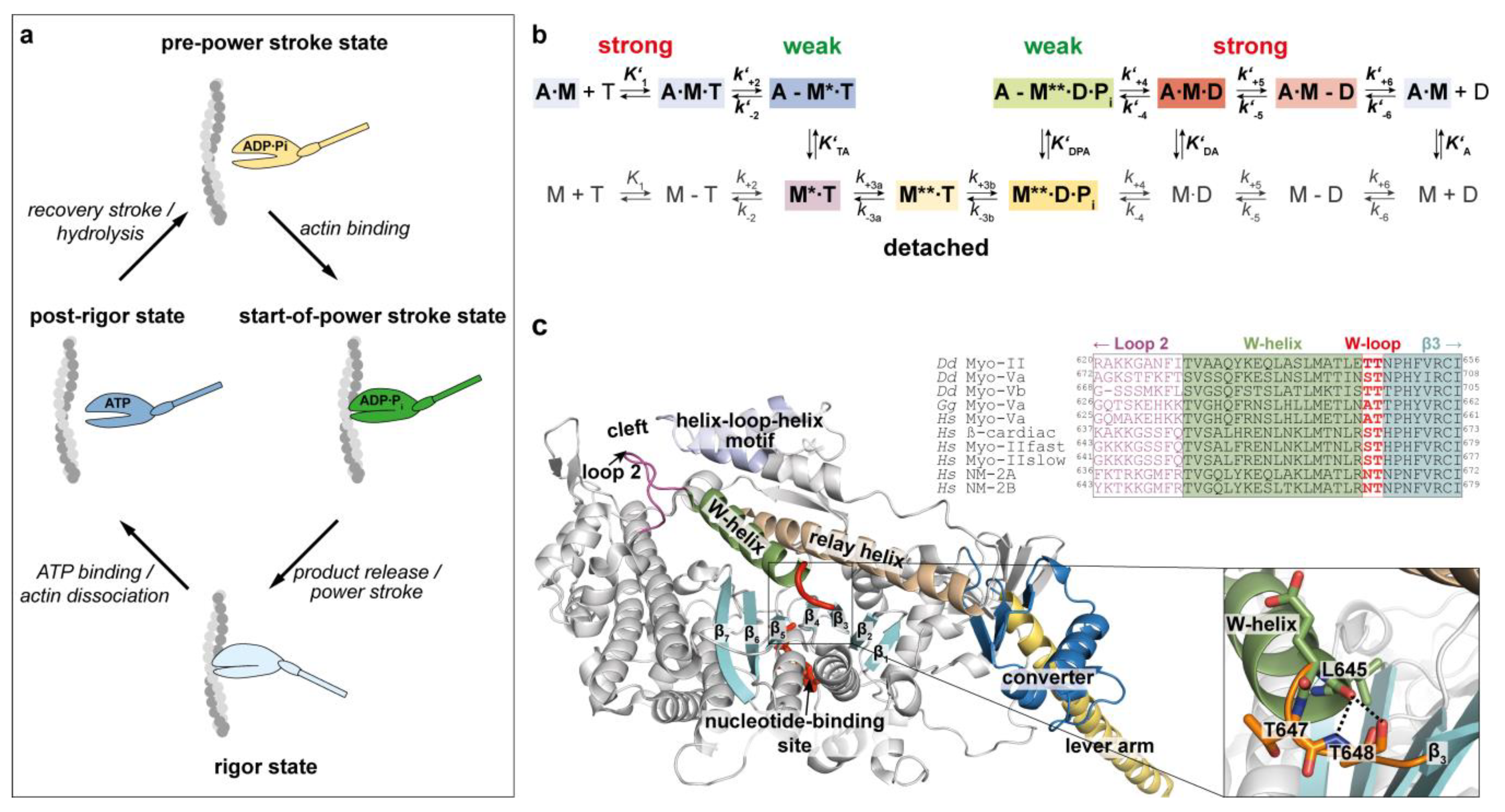
1. Introduction
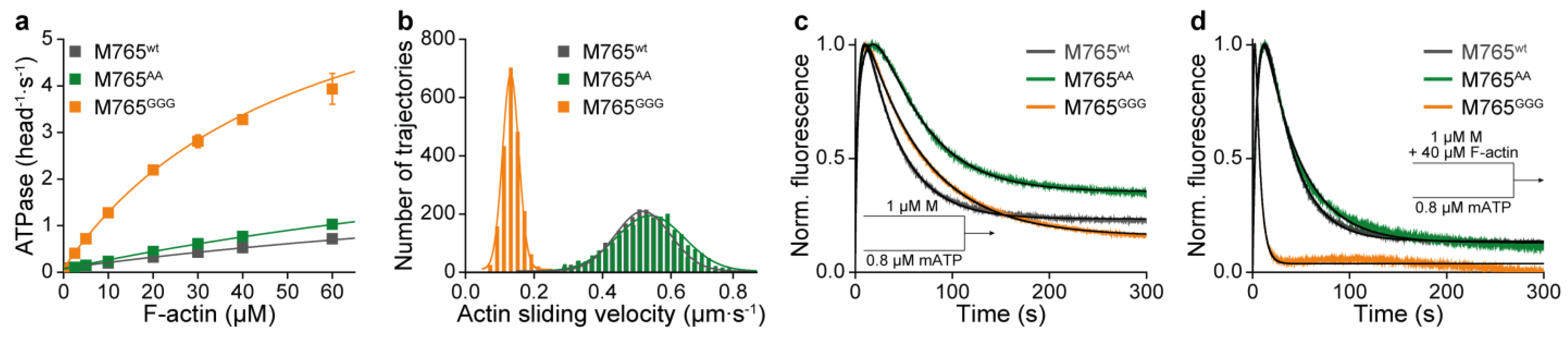
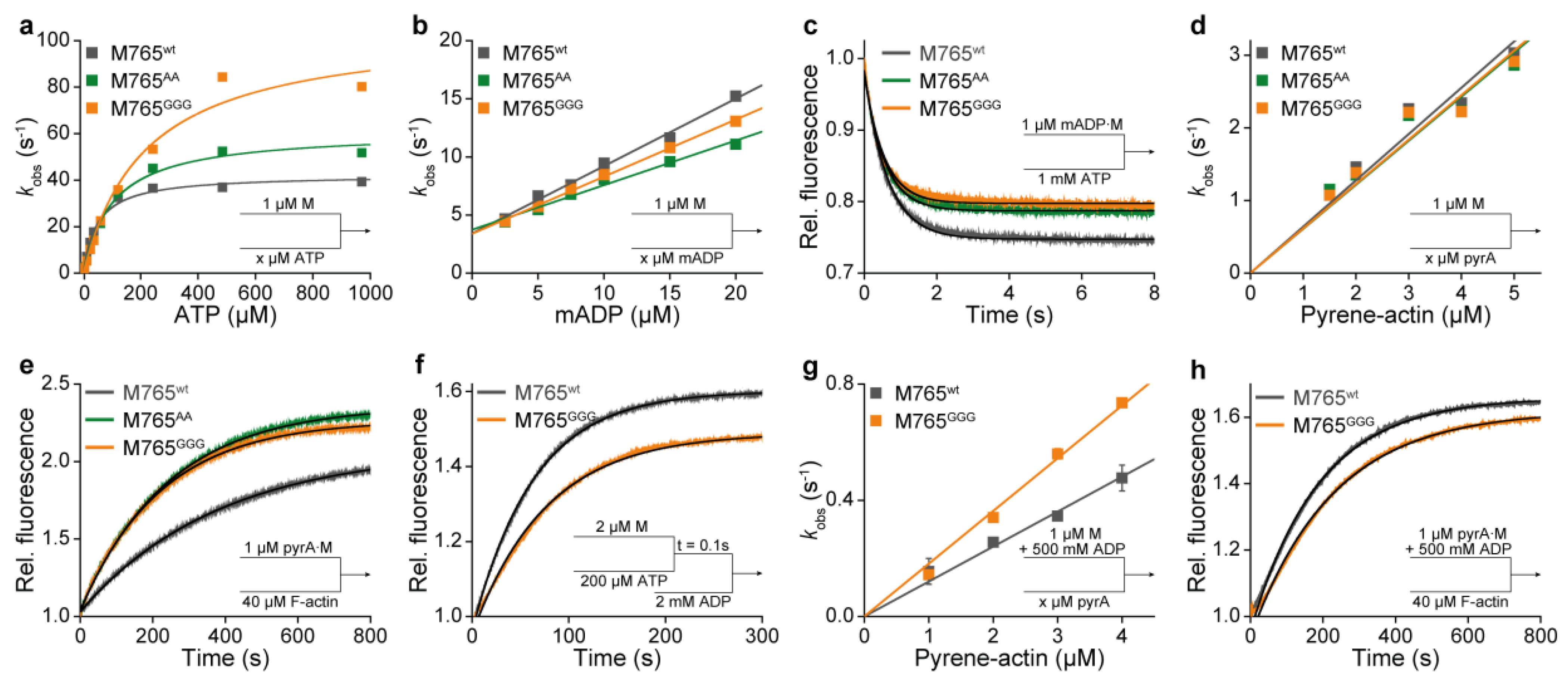
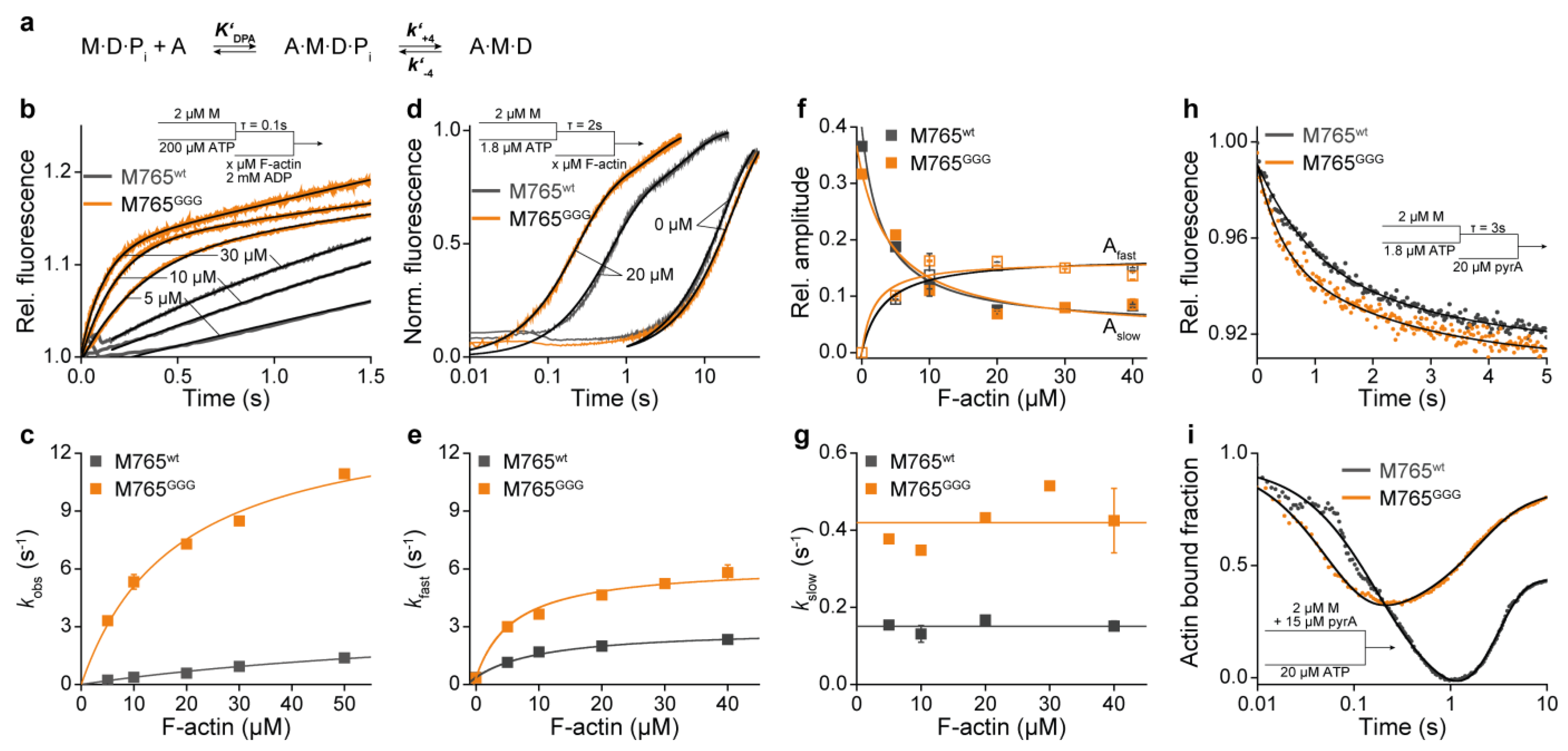
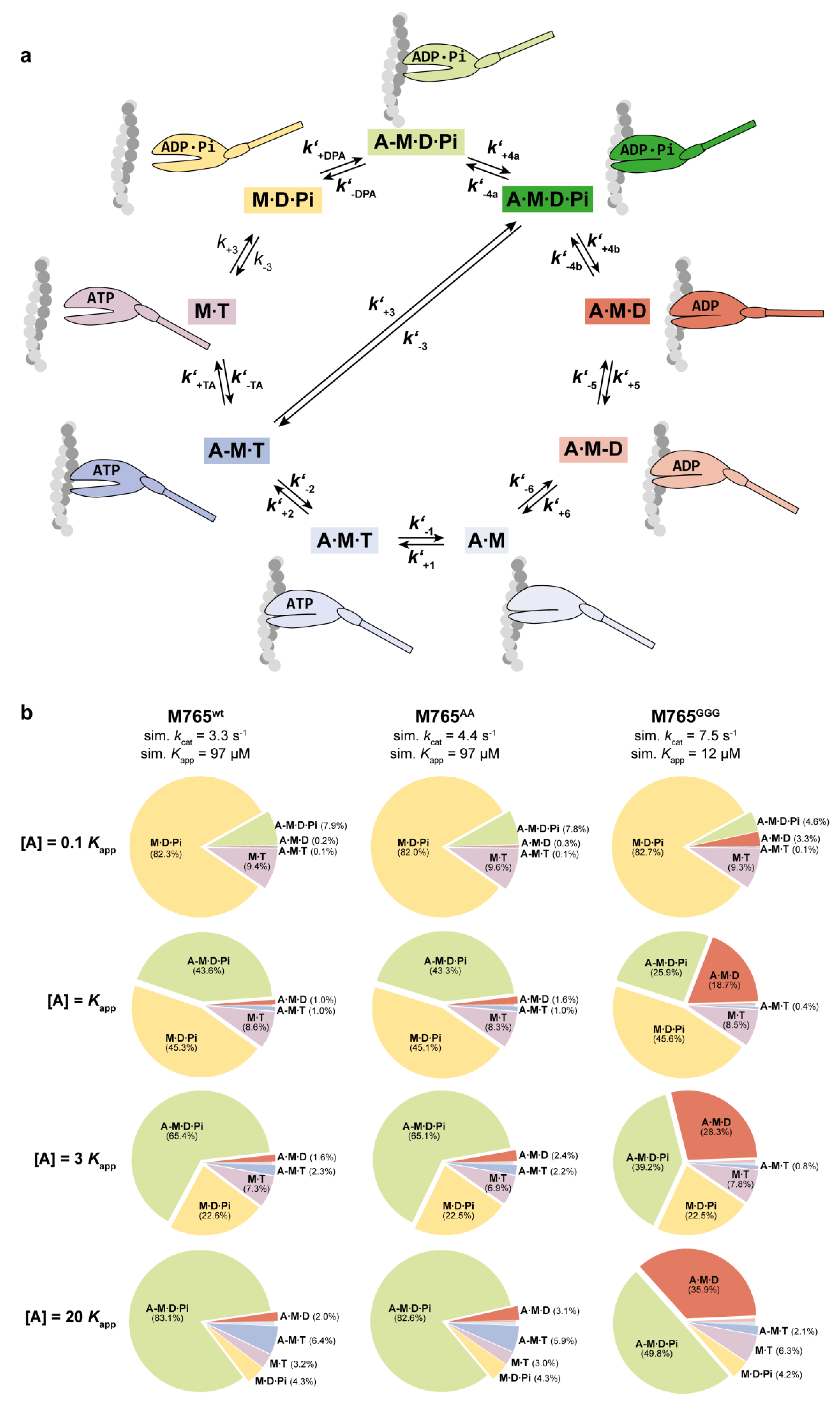
2. Results and Discussion
3. Conclusions
4. Materials and Methods
4.1. Plasmid Construction and Protein Purification
4.2. X-ray Crystallographic Analysis
4.3. Kinetic Experiments, Simulations, and In Vitro Motility Assays
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ADP, D | Adenosine diphosphate |
| ATP, T | Adenosine triphosphate |
| mATP | (2′-(or-3′-O-(N-Methylanthraniloyl) Adenosine 5′-Triphosphate |
| mADP | (2′-(or-3′)-O-(N-Methylanthraniloyl) Adenosine 5′-Diphosphate |
| Pi | Inorganic phosphate |
| A | Actin |
| M | Myosin |
| MDCC-PBP | 7-Diethylamino-3-((((2-Maleimidyl)ethyl)amino)carbonyl)coumarin-labeled Phosphate Binding Protein |
| pyrA | Pyrene-labeled F-actin |
| Rel. | Relative |
| Norm. | Normalized |
| TMD | Targeted Molecular Dynamics |
References
- Houdusse, A.; Sweeney, H.L. How Myosin Generates Force on Actin Filaments. Trends Biochem. Sci. 2016, 41, 989–997. [Google Scholar] [CrossRef] [PubMed]
- Månsson, A.; Rassier, D.; Tsiavaliaris, G. Poorly Understood Aspects of Striated Muscle Contraction. BioMed Res. Int. 2015. [Google Scholar] [CrossRef]
- Lymn, R.W.; Taylor, E.W. Mechanism of Adenosine Triphosphate Hydrolysis by Actomyosin. Biochemistry 1971, 10, 4617–4624. [Google Scholar] [CrossRef] [PubMed]
- Geeves, M.A.; Jeffries, T.E. The effect of nucleotide upon a specific isomerization of actomyosin subfragment 1. Biochem. J. 1988, 256, 41–46. [Google Scholar] [CrossRef] [PubMed]
- Bauer, C.B.; Holden, H.M.; Thoden, J.B.; Smith, R.; Rayment, I. X-ray Structures of the Apo and MgATP-Bound States of Dictyostelium discoideum Myosin Motor Domain. J. Biol. Chem. 2000, 275, 38494–38499. [Google Scholar] [CrossRef]
- Gulick, A.M.; Bauer, C.B.; Thoden, J.B.; Pate, E.; Yount, R.G.; Rayment, I. X-ray Structures of the Dictyostelium Discoideum Myosin Motor Domain with Six non-Nucleotide Analogs. J. Biol. Chem. 2000. [Google Scholar] [CrossRef] [PubMed]
- Preller, M.; Bauer, S.; Adamek, N.; Fujita-Becker, S.; Fedorov, R.; Geeves, M.A.; Manstein, D.J. Structural Basis for the Allosteric Interference of Myosin Function by Reactive Thiol Region Mutations G680A and G680V. J. Biol. Chem. 2011. [Google Scholar] [CrossRef]
- Smith, C.A.; Rayment, I. X-ray Structure of the Magnesium(II)·ADP·Vanadate Complex of the Dictyostelium discoideum Myosin Motor Domain to 1.9 Å Resolution. Biochemistry 1996, 35, 5404–5417. [Google Scholar] [CrossRef] [PubMed]
- Ménétrey, J.; Llinas, P.; Mukherjea, M.; Sweeney, H.L.; Houdusse, A. The Structural Basis for the Large Powerstroke of Myosin VI. Cell 2007. [Google Scholar] [CrossRef][Green Version]
- Ménétrey, J.; Isabet, T.; Ropars, V.; Mukherjea, M.; Pylypenko, O.; Liu, X.; Perez, J.; Vachette, P.; Sweeney, H.L.; Houdusse, A.M. Processive Steps in the Reverse Direction Require Uncoupling of the Lead Head Lever Arm of Myosin VI. Mol. Cell 2012. [Google Scholar] [CrossRef]
- Preller, M.; Holmes, K.C. The Myosin Start-of-Power Stroke State and How Actin Binding Drives the Power Stroke. Cytoskeleton 2013. [Google Scholar] [CrossRef] [PubMed]
- Varkuti, B.; Yang, Z.; Kintses, B.; Erdelyi, P.; Vellai, T.; Kellermayer, M.; Malnasi-Csizmadia, A. A Novel Actin Binding Site of Myosin is Responsible for Effective Muscle Contraction. Biophys. J. 2011. [Google Scholar] [CrossRef][Green Version]
- Takács, B.; Billington, N.; Gyimesi, M.; Kintses, B.; Málnási-Csizmadia, A.; Knight, P.J.; Kovács, M. Myosin Complexed with ADP and Blebbistatin Reversibly Adopts a Conformation Resembling the Start Point of the Working Stroke. Proc. Natl. Acad. Sci. USA 2010. [Google Scholar] [CrossRef] [PubMed]
- Trivedi, D.V.; Muretta, J.M.; Swenson, A.M.; Davis, J.P.; Thomas, D.D.; Yengo, C.M. Direct Measurements of the Coordination of Lever Arm Swing and the Catalytic Cycle in Myosin V. Proc. Natl. Acad. Sci. USA 2015. [Google Scholar] [CrossRef] [PubMed]
- Wulf, S.F.; Ropars, V.; Fujita-Becker, S.; Oster, M.; Hofhaus, G.; Trabuco, L.G.; Pylypenko, O.; Sweeney, H.L.; Houdusse, A.M.; Schröder, R.R.; et al. Force-Producing ADP State of Myosin Bound to Actin. Proc. Natl. Acad. Sci. USA 2016. [Google Scholar] [CrossRef]
- Reubold, T.F.; Eschenburg, S.; Becker, A.; Kull, F.J.; Manstein, D.J. A Structural Model for Actin-Induced Nucleotide Release in Myosin. Nat. Struct. Biol. 2003. [Google Scholar] [CrossRef]
- Muretta, J.M.; Petersen, K.J.; Thomas, D.D. Direct Real-Time Detection of the Actin-Activated Power Stroke within the Myosin Catalytic Domain. Proc. Natl. Acad. Sci. USA 2013. [Google Scholar] [CrossRef]
- Fischer, S.; Windshügel, B.; Horak, D.; Holmes, K.C.; Smith, J.C. Structural Mechanism of the Recovery Stroke in the Myosin Molecular Motor. Proc. Natl. Acad. Sci. USA 2005. [Google Scholar] [CrossRef]
- Sweeney, H.L.; Houdusse, A. Structural and Functional Insights into the Myosin Motor Mechanism. Annu. Rev. Biophys. 2010. [Google Scholar] [CrossRef]
- Málnási-Csizmadia, A.; Kovács, M. Emerging Complex Pathways of the Actomyosin Powerstroke. Trends Biochem. Sci. 2010. [Google Scholar] [CrossRef]
- Brune, M.; Hunter, J.L.; Corrie, J.E.T.; Webb, M.R. Direct, Real-Time Measurement of Rapid Inorganic Phosphate Release Using a Novel Fluorescent Probe and Its Application to Actomyosin Subfragment 1 ATPase. Biochemistry 1994. [Google Scholar] [CrossRef] [PubMed]
- Llinas, P.; Isabet, T.; Song, L.; Ropars, V.; Zong, B.; Benisty, H.; Sirigu, S.; Morris, C.; Kikuti, C.; Safer, D.; et al. How Actin Initiates the Motor Activity of Myosin. Dev. Cell 2015. [Google Scholar] [CrossRef] [PubMed]
- Smith, C.A.; Rayment, I. X-ray Structure of the Magnesium(II)-Pyrophosphate Complex of the Truncated Head of Dictyostelium discoideum Myosin to 2.7 Å Resolution. Biochemistry 1995. [Google Scholar] [CrossRef] [PubMed]
- Bauer, C.B.; Kuhlman, P.A.; Bagshaw, C.R.; Rayment, I. X-ray Crystal Structure and Solution Fluorescence Characterization of Mg 2′(3′)-O-(N-methylanthraniloyl) Nucleotides Bound to the Dictyostelium discoideum Myosin Motor Domain. J. Mol. Biol. 1997. [Google Scholar] [CrossRef] [PubMed]
- Holmes, K.C.; Schröder, R.R.; Sweeney, H.L.; Houdusse, A. The Structure of the Rigor Complex and Its Implications for the Power Stroke. Philos. Trans. R. Soc. B Biol. Sci. 2004. [Google Scholar] [CrossRef]
- Behrmann, E.; Müller, M.; Penczek, P.A.; Mannherz, H.G.; Manstein, D.J.; Raunser, S. Structure of the Rigor Actin-Tropomyosin-Myosin Complex. Cell 2012. [Google Scholar] [CrossRef]
- Von Der Ecken, J.; Heissler, S.M.; Pathan-Chhatbar, S.; Manstein, D.J.; Raunser, S. Cryo-EM Structure of a Human Cytoplasmic Actomyosin Complex at Near-Atomic Resolution. Nature 2016. [Google Scholar] [CrossRef]
- Málnási-Csizmadia, A.; Dickens, J.L.; Zeng, W.; Bagshaw, C.R. Switch Movements and the Myosin Crossbridge Stroke. J. Muscle Res. Cell Motil. 2005. [Google Scholar] [CrossRef]
- Coureux, P.D.; Sweeney, H.L.; Houdusse, A. Three Myosin V Structures Delineate Essential Features of Chemo-Mechanical Transduction. EMBO J. 2004. [Google Scholar] [CrossRef]
- Reubold, T.F.; Eschenburg, S.; Becker, A.; Leonard, M.; Schmid, S.L.; Vallee, R.B.; Kull, F.J.; Manstein, D.J. Crystal Structure of the GTPase Domain of Rat Dynamin 1. Proc. Natl. Acad. Sci. USA 2005. [Google Scholar] [CrossRef]
- Blanc, F.; Isabet, T.; Benisty, H.; Sweeney, H.L.; Cecchini, M.; Houdusse, A. An Intermediate along the Recovery Stroke of Myosin VI Revealed by X-ray Crystallography and Molecular Dynamics. Proc. Natl. Acad. Sci. USA 2018. [Google Scholar] [CrossRef] [PubMed]
- Málnási-Csizmadia, A.; Tóth, J.; Pearson, D.S.; Hetényi, C.; Nyitray, L.; Geeves, M.A.; Bagshaw, C.R.; Kovács, M. Selective Perturbation of the Myosin Recovery Stroke by Point Mutations at the Base of the Lever arm Affects ATP Hydrolysis and Phosphate Release. J. Biol. Chem. 2007. [Google Scholar] [CrossRef] [PubMed]
- Smith, D.A.; Sleep, J. Mechanokinetics of Rapid Tension Recovery in Muscle: The Myosin Working Stroke Is Followed by a Slower Release of Phosphate. Biophys. J. 2004. [Google Scholar] [CrossRef]
- Yu, H.; Ma, L.; Yang, Y.; Cui, Q. Mechanochemical Coupling in the Myosin Motor Domain. II. Analysis of Critical Residues. PLoS Comput. Biol. 2007. [Google Scholar] [CrossRef] [PubMed]
- Mesentean, S.; Koppole, S.; Smith, J.C.; Fischer, S. The Principal Motions Involved in the Coupling Mechanism of the Recovery Stroke of the Myosin Motor. J. Mol. Biol. 2007. [Google Scholar] [CrossRef]
- Gyimesi, M.; Kintses, B.; Bodor, A.; Perczel, A.; Fischer, S.; Bagshaw, C.R.; Málnási-Csizmadia, A. The Mechanism of the Reverse Recovery Step, Phosphate Release, and Actin Activation of Dictyostelium Myosin II. J. Biol. Chem. 2008. [Google Scholar] [CrossRef]
- Ewert, W.; Franz, P.; Tsiavaliaris, G.; Preller, M. Structural and Computational Insights Into a Blebbistatin-Bound Myosin adp Complex with Characteristics of an adp-Release Conformation along the Two-Step Myosin Power Stoke. Int. J. Mol. Sci. 2020, 21, 7417. [Google Scholar] [CrossRef]
- Cecchini, M.; Houdusse, A.; Karplus, M. Allosteric Communication in Myosin V: From Small Conformational Changes to Large Directed Movements. PLoS Comput. Biol. 2008. [Google Scholar] [CrossRef]
- Robert-Paganin, J.; Pylypenko, O.; Kikuti, C.; Sweeney, H.L.; Houdusse, A. Force Generation by Myosin Motors: A Structural Perspective. Chem. Rev. 2020. [Google Scholar] [CrossRef]
- Sweeney, H.L.; Houdusse, A.; Robert-Paganin, J. Myosin Structures. In Advances in Experimental Medicine and Biology; Springer Science and Business Media: Berlin, Germany, 2020. [Google Scholar]
- Zhang, X.C.; Feng, W. Thermodynamic Aspects of ATP Hydrolysis of Actomyosin Complex. Biophys. Rep. 2016. [Google Scholar] [CrossRef][Green Version]
- Yang, Y.; Gourinath, S.; Kovács, M.; Nyitray, L.; Reutzel, R.; Himmel, D.M.; O’Neall-Hennessey, E.; Reshetnikova, L.; Szent-Györgyi, A.G.; Brown, J.H.; et al. Rigor-Like Structures from Muscle Myosins Reveal Key Mechanical Elements in the Transduction Pathways of This Allosteric Motor. Structure 2007. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Yu, H.; Cui, Q. Extensive Conformational Transitions Are Required to Turn On ATP Hydrolysis in Myosin. J. Mol. Biol. 2008. [Google Scholar] [CrossRef]
- Moore, J.R.; Leinwand, L.; Warshaw, D.M. Understanding Cardiomyopathy Phenotypes Based on the Functional Impact of Mutations in the Myosin Motor. Circ. Res. 2012. [Google Scholar] [CrossRef]
- Anson, M.; Geeves, M.A.; Kurzawa, S.E.; Manstein, D.J. Myosin Motors with Artificial Lever Arms. EMBO J. 1996. [Google Scholar] [CrossRef]
- Nayak, A.; Wang, T.; Franz, P.; Steffen, W.; Chizhov, I.; Tsiavaliaris, G.; Amrute-Nayak, M. Single-Molecule Analysis Reveals that Regulatory Light Chains Fine-Tune Skeletal Myosin II Function. J. Biol. Chem. 2020. [Google Scholar] [CrossRef] [PubMed]
- Warshaw, D.M. The In Vitro Motility Assay: A Window into the Myosin Molecular Motor. News Physiol. Sci. 1996. [Google Scholar] [CrossRef]
- Tsiavaliaris, G.; Fujita-Becker, S.; Batra, R.; Levitsky, D.I.; Kill, F.J.; Geeves, M.A.; Manstein, D.J. Mutations in the Relay Loop Region Result in Dominant-Negative Inhibition of Myosin II Function in Dictyostelium. EMBO Rep. 2002. [Google Scholar] [CrossRef]
- Hannemann, D.E.; Cao, W.; Olivares, A.O.; Robblee, J.P.; De La Cruz, E.M. Magnesium, ADP, and Actin Binding Linkage of Myosin V: Evidence for Multiple Myosin V-ADP and Actomyosin V-ADP States. Biochemistry 2005. [Google Scholar] [CrossRef]
- Brito, C.; Sousa, S. Non-Muscle Myosin 2A (NM2A): Structure, Regulation and Function. Cells 2020, 9, 1590. [Google Scholar] [CrossRef]
- Chinthalapudi, K.; Heissler, S.M.; Preller, M.; Sellers, J.R.; Manstein, D.J. Mechanistic Insights Into the Active Site and Allosteric Communication Pathways in Human Nonmuscle Myosin-2C. eLife 2017. [Google Scholar] [CrossRef]
- Heissler, S.M.; Manstein, D.J. Nonmuscle Myosin-2: Mix and Match. Cell. Mol. Life Sci. 2013. [Google Scholar] [CrossRef] [PubMed]
- Kurzawa, S.E.; Manstein, D.J.; Geeves, M.A. Dictyostelium discoideum Myosin II: Characterization of Functional Myosin Motor Fragments. Biochemistry 1997. [Google Scholar] [CrossRef] [PubMed]
- Henn, A.; De La Cruz, E.M. Vertebrate Myosin VIIb Is a High Duty Ratio Motor Adapted for Generating and Maintaining Tension. J. Biol. Chem. 2005. [Google Scholar] [CrossRef] [PubMed]
- Taft, M.H.; Hartmann, F.K.; Rump, A.; Keller, H.; Chizhov, I.; Manstein, D.J.; Tsiavaliaris, G. Dictyostelium Myosin-5b Is a Conditional Processive Motor. J. Biol. Chem. 2008. [Google Scholar] [CrossRef]
- Chizhov, I.; Hartmann, F.K.; Hundt, N.; Tsiavaliaris, G. Global Fit Analysis of Myosin-5b Motility Reveals Thermodynamics of Mg2+-Sensitive Acto-Myosin-ADP States. PLoS ONE 2013. [Google Scholar] [CrossRef]
- Rosenfeld, S.S.; Houdusse, A.; Sweeney, H.L. Magnesium Regulates ADP Dissociation from Myosin V. J. Biol. Chem. 2005. [Google Scholar] [CrossRef]
- Criddle, A.H.; Geeves, M.A.; Jeffries, T. The Use of Actin Labelled with N-(1-pyrenyl)iodoacetamide to Study the Interaction of Actin with Myosin Subfragments and Troponin/Tropomyosin. Biochem. J. 1985, 232, 343–349. [Google Scholar] [CrossRef]
- Mijailovich, S.M.; Nedic, D.; Svicevic, M.; Stojanovic, B.; Walklate, J.; Ujfalusi, Z.; Geeves, M.A. Modeling the Actin. Myosin ATPase Cross-Bridge Cycle for Skeletal and Cardiac Muscle Myosin Isoforms. Biophys. J. 2017. [Google Scholar] [CrossRef]
- Sun, M.; Rose, M.B.; Ananthanarayanan, S.K.; Jacobs, D.J.; Yengo, C.M. Characterization of the Pre-force-generation State in the Actomyosin Cross-bridge Cycle. Proc. Natl. Acad. Sci. USA 2008. [Google Scholar] [CrossRef]
- Gunther, L.K.; Rohde, J.A.; Tang, W.; Cirilo, J.A.; Marang, C.P.; Scott, B.D.; Thomas, D.D.; Debold, E.P.; Yengo, C.M. FRET and Optical Trapping Reveal Mechanisms of Actin-Activation of the Power Stroke and Phosphate-Release in Myosin V. J. Biol. Chem. 2020. [Google Scholar] [CrossRef]
- Sweeney, H.L.; Rosenfeld, S.S.; Brown, F.; Faust, L.; Smith, J.; Xing, J.; Stein, L.A.; Sellers, J.R. Kinetic Tuning of Myosin via a Flexible Loop Adjacent to the Nucleotide Binding Pocket. J. Biol. Chem. 1998. [Google Scholar] [CrossRef]
- Diensthuber, R.P.; Tominaga, M.; Preller, M.; Hartmann, F.K.; Orii, H.; Chizhov, I.; Oiwa, K.; Tsiavaliaris, G. Kinetic Mechanism of Nicotiana tabacum Myosin-11 Defines a New Type of a Processive Motor. FASEB J. 2015. [Google Scholar] [CrossRef] [PubMed]
- Pardee, J.D.; Aspudich, J. Purification of Muscle Actin. Methods Enzymol. 1982. [Google Scholar] [CrossRef]
- Franz, P.; Gassl, V.; Topf, A.; Eckelmann, L.; Iorga, B.; Tsiavaliaris, G. A Thermophoresis-Based Biosensor for Real-Time Detection of Inorganic Phosphate during Enzymatic Reactions. Biosens. Bioelectron. 2020, 169, 112616. [Google Scholar] [CrossRef] [PubMed]
- Kabsch, W. XDS. Acta Crystallogr. Sect. D 2010, 66, 125–132. [Google Scholar] [CrossRef]
- Evans, P.R.; Murshudov, G.N. How good are my data and what is the resolution? Acta Crystallogr. Sect. D Biol. Crystallogr. 2013. [Google Scholar] [CrossRef]
- Winn, M.D.; Ballard, C.C.; Cowtan, K.D.; Dodson, E.J.; Emsley, P.; Evans, P.R.; Keegan, R.M.; Krissinel, E.B.; Leslie, A.G.W.; McCoy, A.; et al. Overview of the CCP4 suite and current developments. Acta Crystallogr. Sect. D Biol. Crystallogr. 2011, 67, 235–242. [Google Scholar] [CrossRef]
- McCoy, A.J.; Grosse-Kunstleve, R.W.; Adams, P.D.; Winn, M.D.; Storoni, L.C.; Read, R.J. Phaser crystallographic software. J. Appl. Crystallogr. 2007. [Google Scholar] [CrossRef]
- Emsley, P.; Lohkamp, B.; Scott, W.G.; Cowtan, K. Features and development of Coot. Acta Crystallogr. Sect. D Biol. Crystallogr. 2010. [Google Scholar] [CrossRef]
- Afonine, P.V.; Poon, B.K.; Read, R.J.; Sobolev, O.V.; Terwilliger, T.C.; Urzhumtsev, A.; Adams, P.D. Real-space refinement in PHENIX for cryo-EM and crystallography. Acta Crystallogr. Sect. D Struct. Biol. 2018. [Google Scholar] [CrossRef]
- Berman, H.M.; Westbrook, J.; Feng, Z.; Gilliland, G.; Bhat, T.N.; Weissig, H.; Shindyalov, I.N.; Bourne, P.E. The Protein Data Bank. Nucleic Acids Res. 2000, 28, 235–242. [Google Scholar] [CrossRef] [PubMed]


| M765AA | M765GGG | |
|---|---|---|
| Data collection | ||
| Space group | C2221 | C2221 |
| Cell dimensions | ||
| a, b, c (Å) | 89.76, 146.47, 154.85 | 89.19, 149.03, 153.93 |
| α, β, γ (°) | 90.00, 90.00, 90.00 | 90.00, 90.00, 90.00 |
| Resolution (Å) | 43.11–2.60 (2.69–2.60) | 43.40–2.55 (2.64–2.55) |
| Rmerge [%] | 0.037 (0.355) | 0.055 (0.361) |
| I / σI | 13.68 (1.96) | 9.77 (2.09) |
| CC1/2 | 0.999 (0.747) | 0.997 (0.844) |
| Completeness (%) | 99.77 (99.84) | 99.55 (99.85) |
| Redundancy | 2.0 | 2.0 |
| Refinement | ||
| Resolution (Å) | 43.11–2.60 | 43.40–2.55 |
| No. reflections | 31661 (3109) | 33626 (3315) |
| Rwork/Rfree | 20.94/26.26 | 20.64/25.21 |
| No. atoms | 5958 | 6129 |
| Protein | 5788 | 5906 |
| Ligand/ion | 74 | 129 |
| Water | 96 | 94 |
| B-factors | ||
| Protein | 63.27 | 56.10 |
| Ligand/ion | 68.30 | 66.39 |
| Water | 45.87 | 41.83 |
| R.m.s. deviations | ||
| Bond lengths (Å) | 0.007 | 0.006 |
| Bond angles (°) | 0.79 | 0.87 |
| Unit | M765wt | M765AA | M765GGG | |
|---|---|---|---|---|
| ATPase activity 1 | ||||
| kbasal | (s−1) | 0.09 ± 0.02 | 0.07 ± 0.01 | 0.08 ± 0.01 |
| kcat | (s−1) | 2.6 ± 0.5 | 4.1 ± 0.5 | 7.8 ± 0.5 |
| Kapp | (µM) | >100 | >100 | 54 ± 5 |
| kcat/Kapp | (µM−1s−1) | <0.03 | <0.03 | 0.14 ± 0.01 |
| In vitro actin filament sliding velocities 1 | ||||
| vavg | (µms−1) | 0.52 ± 0.02 | 0.54 ± 0.01 | 0.13 ± 0.01 |
| Single ATP turnover kinetics and coupling ratios 1 | ||||
| kon | (s−1) | 0.24 ± 0.01 | 0.070 ± 0.01 | 0.27 ± 0.01 |
| koff | (s−1) | 0.03 ± 0.01 | 0.02 ± 0.01 | 0.02 ± 0.01 |
| k’on 2 | (s−1) | 0.16 ± 0.01 | 0.23 ± 0.01 | 0.83 ± 0.02 |
| k’off 2 | (s−1) | 0.04 ± 0.01 | 0.03 ± 0.01 | 0.20 ± 0.01 |
| k’on/kon | - | 0.7 ± 0.1 | 3.3 ± 0.1 | 3.1 ± 0.1 |
| k’off/koff | - | 1.3 ± 0.1 | 1.5 ± 0.1 | 10 ± 0.1 |
| Unit | M765wt | M765AA | M765GGG | |
|---|---|---|---|---|
| ATP binding to myosin 1 | ||||
| K1k+2 | (µM−1s−1) | 0.48 ± 0.01 | 0.38 ± 0.01 | 0.38 ± 0.01 |
| k−2 | (s−1) | 0.79 ± 0.49 | 0.54 ± 0.24 | 0.43 ± 0.25 |
| k+3+k−3 | (s−1) | 42 ± 1 | 61 ± 2 | 106 ± 8 |
| ADP binding to myosin 1 | ||||
| k−5K6 | (µM−1s−1) | 0.58 ± 0.02 | 0.38 ± 0.02 | 0.49 ± 0.01 |
| k+5 | (s−1) | 1.6 ± 0.1 | 1.8 ± 0.1 | 1.9 ± 0.1 |
| 1/(K5K6) | (µM) | 2.8 ± 0.2 | 4.7 ± 0.4 | 3.9 ± 0.2 |
| Rate of Pi release 1 | ||||
| k+4 | (s−1) | 0.02 ± 0.01 | n.d. | 0.02 ± 0.01 |
| Unit | M765wt | M765AA | M765GGG | |
|---|---|---|---|---|
| Actomyosin interactions in the absence and presence of ADP | ||||
| k’+A | (µM−1s−1) | 0.64 ± 0.03 | 0.61 ± 0.03 | 0.61 ± 0.03 |
| k’−A | (s−1) | 0.003 | 0.004 | 0.005 |
| 1/K’A 1 | (µM) | 0.0057 ± 0.0005 | 0.010 ± 0.009 | 0.011 ± 0.009 |
| k’+DA | (µM−1s−1) | 0.12 ± 0.01 | n.d. | 0.18 ± 0.01 |
| k’−DA | (s−1) | 0.006 ± 0.001 | n.d. | 0.005 ± 0.001 |
| 1/K’DA 2 | (µM) | 0.063 ± 0.002 | n.d. | 0.024 ± 0.001 |
| ATP interactions of actomyosin | ||||
| K’1k’+2 | (µM−1s−1) | 0.24 ± 0.01 | 0.32 ± 0.01 | 0.92 ± 0.01 |
| k’+2 | (s−1) | 719 ± 22 | 871 ± 80 | 923 ± 19 |
| k’−2 | (s−1) | 0.08 ± 0.05 | 0.62 ± 0.05 | 1.48 ± 0.13 |
| 1/K’1 | (µM) | 3200 ± 130 | 2702 ± 279 | 883 ± 30 |
| ADP interactions of actomyosin | ||||
| k’−5K’6 3 | (µM−1s−1) | >1.0/>0.74 | >1.47/>2.94 | 4.7 ± 1/3.6 ± 1 4 |
| 1/(K’5K’6) | (µM) | 135 ± 10 5 | 34 ± 4 5 | 3.4 ± 1 6 |
| k’+5 | (s−1) | >100 7 | >100 7 | 16 ± 1 8 |
| Pi kinetics of actomyosin | ||||
| k’+4 | (s−1) | 3.8 ± 1.1 | n.d. | 14.4 ± 1.0 |
| k’+4K’DPA | (µM−1s−1) | 0.04 ± 0.01 | n.d. | 0.79 ± 0.08 |
| 1/K’DPA | (µM) | 94 ± 32 | n.d. | 18 ± 3 |
| Weak-to-strong transition | ||||
| k’weak-strong | (s−1) | 1.0 ± 0.01 | n.d. | 2.6 ± 0.04 |
| Duty ratio | ||||
| tstrong/ttotal | % | 3 ± 1 | <4 ± 1 | 49 ± 4 |
| Experimental | % | <1 | n.d. | 35 |
| Unit | M765wt | M765AA | M765GGG | |
|---|---|---|---|---|
| Equilibrium constants | ||||
| K’DPA | (µM−1) | 0.01 | 0.01 | 0.05 |
| K’4 | (µM−1) | 0.00001 | 0.00001 | 0.00001 |
| K’5 | - | 0.5 | 0.74 | 7.14 |
| K’6 | (µM−1) | 0.02 | 0.02 | 0.02 |
| K’1 | (µM−1) | 0.0003 | 0.004 | 0.001 |
| K’2 | - | 8988 | 1405 | 624 |
| K’TA | (µM−1) | 0.001 | 0.001 | 0.001 |
| K3 | - | 9.5 | 9.2 | 9.6 |
| K’3 | - | 95 | 92 | 96 |
| Rate constants of forward reactions | ||||
| k’+DPA | (µM−1s−1) | 10 | 10 | 50 |
| k’+4 | (s−1) | 3.8 | 5.0 | 14.4 |
| k’+5 | (s−1) | 235 | 160 | 20 |
| k’+6 | (s−1) | 1000 | 1000 | 1000 |
| k’+1 | (µM−1s−1) | 100 | 100 | 100 |
| k’+2 | (s−1) | 719 | 871 | 923 |
| k’+TA | (s−1) | 1000 | 1000 | 1000 |
| k+3 | (s−1) | 38 | 55 | 96 |
| k’+3 | (s−1) | 38 | 55 | 96 |
| Rate constants of backwards reactions | ||||
| k’−DPA | (s−1) | 1000 | 1000 | 1000 |
| k’−4 | (µM−1s−1) | 0.000038 | 0.00005 | 0.000144 |
| k’−5 | (s−1) | 470 | 216 | 2.8 |
| k’−6 | (µM−1s−1) | 20 | 20 | 20 |
| k’−1 | (s−1) | 333,300 | 250,000 | 88,500 |
| k’−2 | (s−1) | 0.08 | 0.62 | 1.48 |
| k’−TA | (µM−1s−1) | 1 | 1 | 1 |
| k−3 | (s−1) | 4 | 6 | 10 |
| k’−3 | (s−1) | 0.4 | 0.6 | 1 |
| Actin (µM) | ATPase (s−1) | Detached 1 | Weak 2 | Strong 3 | Motility (µms−1) | ||
|---|---|---|---|---|---|---|---|
| M765wt | 0.1Kapp: | 9.7 | 0.30 | 0.92 | 0.08 | 0.003 | 0.52 |
| 1Kapp: | 97 | 1.67 | 0.54 | 0.44 | 0.020 | ||
| 3Kapp: | 291 | 2.49 | 0.30 | 0.68 | 0.020 | ||
| 20Kapp: | 1940 | 3.16 | 0.08 | 0.89 | 0.030 | ||
| M765AA | 0.1Kapp: | 9.7 | 0.39 | 0.92 | 0.08 | 0.004 | 0.48 |
| 1Kapp: | 97 | 2.17 | 0.53 | 0.45 | 0.020 | ||
| 3Kapp: | 291 | 3.25 | 0.29 | 0.68 | 0.030 | ||
| 20Kapp: | 1940 | 4.17 | 0.07 | 0.89 | 0.040 | ||
| M765GGG | 0.1Kapp: | 1.2 | 0.66 | 0.92 | 0.05 | 0.030 | 0.10 |
| 1Kapp: | 12 | 3.73 | 0.54 | 0.26 | 0.200 | ||
| 3Kapp: | 36 | 5.64 | 0.30 | 0.40 | 0.300 | ||
| 20Kapp: | 240 | 7.17 | 0.11 | 0.52 | 0.390 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Franz, P.; Ewert, W.; Preller, M.; Tsiavaliaris, G. Unraveling a Force-Generating Allosteric Pathway of Actomyosin Communication Associated with ADP and Pi Release. Int. J. Mol. Sci. 2021, 22, 104. https://doi.org/10.3390/ijms22010104
Franz P, Ewert W, Preller M, Tsiavaliaris G. Unraveling a Force-Generating Allosteric Pathway of Actomyosin Communication Associated with ADP and Pi Release. International Journal of Molecular Sciences. 2021; 22(1):104. https://doi.org/10.3390/ijms22010104
Chicago/Turabian StyleFranz, Peter, Wiebke Ewert, Matthias Preller, and Georgios Tsiavaliaris. 2021. "Unraveling a Force-Generating Allosteric Pathway of Actomyosin Communication Associated with ADP and Pi Release" International Journal of Molecular Sciences 22, no. 1: 104. https://doi.org/10.3390/ijms22010104
APA StyleFranz, P., Ewert, W., Preller, M., & Tsiavaliaris, G. (2021). Unraveling a Force-Generating Allosteric Pathway of Actomyosin Communication Associated with ADP and Pi Release. International Journal of Molecular Sciences, 22(1), 104. https://doi.org/10.3390/ijms22010104





