Biomolecular Simulations with the Three-Dimensional Reference Interaction Site Model with the Kovalenko-Hirata Closure Molecular Solvation Theory
Abstract
1. Introduction
2. Theoretical Background
3. Biomolecular Simulations with the 3D-RISM-KH Molecular Solvation Theory
4. Binding Site Mapping
5. Protein-Ligand Binding Energy
6. Molecular Solvation Energy Calculations
7. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Alder, B.J.; Wainwright, T.E. Studies in Molecular Dynamics. I. General Method. J. Chem. Phys. 1959, 31, 459–466. [Google Scholar] [CrossRef]
- Schlick, T. Molecular Modeling and Simulation: An Interdisciplinary Guide, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Tuckerman, M. Statistical Mechanics: Theory and Molecular Simulation; Oxford University Press: Oxford, UK, 2010. [Google Scholar]
- Frenkel, D.; Smit, B. Understanding Molecular Simulation: From Algorithms to Applications, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2002. [Google Scholar]
- Harrison, J.A.; Schall, J.D.; Maskey, S.; Mikulski, P.T.; Knippenberg, M.T.; Morrow, B.H. Review of force fields and intermolecular potentials used in atomistic computational materials research. Appl. Phys. Rev. 2018, 5, 031104. [Google Scholar] [CrossRef]
- Lopes, P.E.M.; Guvench, O.; MacKerell, A.D., Jr. Current Status of Protein Force Fields for Molecular Dynamics. Methods Mol. Biol. 2015, 1215, 47–71. [Google Scholar] [PubMed]
- Martín-García, F.; Papaleo, E.; Gomez-Puertas, P.; Boomsma, W.; Lindorff-Larsen, K. Comparing Molecular Dynamics Force Fields in the Essential Subspace. PLoS ONE 2015, 10, e0121114. [Google Scholar] [CrossRef] [PubMed]
- Ploetz, E.A.; Karunaweera, S.; Bentenitis, N.; Chen, F.; Dai, S.; Gee, M.B.; Jiao, Y.; Kang, M.; Kariyawasam, N.L.; Naleem, N.; et al. Kirkwood–Buff-Derived Force Field for Peptides and Proteins: Philosophy and Development of KBFF20. J. Chem. Theory Comput. 2021. [Google Scholar] [CrossRef]
- Ploetz, E.A.; Smith, P.E. A Kirkwood–Buff force field for the aromatic amino acids. Phys. Chem. Chem. Phys. 2011, 13, 18154–18167. [Google Scholar] [CrossRef] [PubMed]
- Weerasinghe, S.; Smith, P.E. A Kirkwood-Buff derived force field for the simulation of aqueous guanidinium chloride solutions. J. Chem. Phys. 2004, 121, 2180–2186. [Google Scholar] [CrossRef] [PubMed]
- Bernardi, R.C.; Melo, M.C.R.; Schulten, K. Enhanced sampling techniques in molecular dynamics simulations of biological systems. Biochim. Biophys. Acta 2015, 1850, 872–877. [Google Scholar] [CrossRef]
- Liao, A.; Parrinello, M. Escaping free-energy minima. Proc. Natl. Acad. Sci. USA 2002, 99, 12562–12566. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Schheraga, H. Monte Carlo-minimization approach to the multiple-minima problem in protein folding. Proc. Natl. Acad. Sci. USA 1987, 84, 6611–6615. [Google Scholar] [CrossRef]
- Sicher, M.; Mohr, S.; Goedecker, S. Efficient moves for global geometry optimization methods and their application to binary systems. J. Chem. Phys. 2011, 134, 044106. [Google Scholar] [CrossRef]
- Chmiela, S.; Sauceda, H.E.; Müller, K.-R.; Takatchenko, A. Towards exact molecular dynamics simulations with machine-learned force fields. Nat. Commun. 2018, 9, 3887. [Google Scholar] [CrossRef] [PubMed]
- Ramabhadran, R.O.; Raghavachari, K. Extrapolation to the Gold-Standard in Quantum Chemistry: Computationally Efficient and Accurate CCSD(T) Energies for Large Molecules Using an Automated Thermochemical Hierarchy. J. Chem. Theory Comput. 2013, 9, 3986–3994. [Google Scholar] [CrossRef] [PubMed]
- Bartlett, R.J. How and Why Coupled-Cluster Theory Became the Pre-eminent Method in ab initio Quantum Chemistry. In Theory and Applications of Computational Chemistry: The First Fifty Years; Dykstra, C.E., Frenking, G., Kim, K.S., Scuseria, G.E., Eds.; Elsevier: Amsterdam, The Netherlands, 2005; pp. 1191–1221. [Google Scholar]
- Smith, J.S.; Nabgen, B.T.; Zubatyuk, R.; Lubbers, N.; Devereux, C.; Barros, K.; Tretiak, S.; Isayev, O.; Roitberg, A.E. Approaching coupled cluster accuracy with a general-purpose neural network potential through transfer learning. Nat. Commun. 2019, 10, 2903. [Google Scholar] [CrossRef] [PubMed]
- Bartlett, R.J.; Lotrich, V.F.; Schweigert, I.V. Ab initio density functional theory: The best of both worlds? J. Chem. Phys. 2005, 123, 062205. [Google Scholar] [CrossRef] [PubMed]
- Cossi, M.; Barone, V.; Cammi, R.; Tomasi, J. Ab initio study of solvated molecules: A new implementation of the polarizable continuum model. Chem. Phys. Lett. 1996, 255, 327–335. [Google Scholar] [CrossRef]
- Mennucci, B.; Tomasi, J. Continuum solvation models: A new approach to the problem of solute’s charge distribution and cavity boundaries. J. Chem. Phys. 1997, 106, 5151–5158. [Google Scholar] [CrossRef]
- Tomasi, J.; Mennucci, B.; Cammi, R. Quantum mechanical continuum solvation models. Chem. Rev. 2005, 105, 2999–3093. [Google Scholar] [CrossRef]
- Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Universal solvation model based on solute electron density and a continuum model of the solvent defined by the bulk dielectric constant and atomic surface tensions. J. Phys. Chem. B 2009, 113, 6378–6396. [Google Scholar] [CrossRef]
- Klamt, A. The COSMO and COSMO-RS solvation models. WIREs Comput. Mol. Sci. 2011, 1, 699–709. [Google Scholar] [CrossRef]
- Svensson, M.; Humbel, S.; Froese Robert, D.J.; Matsubara, T.; Sieber, S.; Morokuma, K. ONIOM: A Multilayered Integrated MO + MM Method for Geometry Optimizations and Single Point Energy Predictions. A Test for Diels−Alder Reactions and Pt(P(t-Bu)3)2+ H2Oxidative Addition. J. Phys. Chem. 1996, 100, 19357. [Google Scholar] [CrossRef]
- Senn, H.; Thiel, W. QM/MM studies of enzymes. Curr. Opin. Chem. Biol. 2007, 11, 182–187. [Google Scholar] [CrossRef]
- Vreven, T.; Byun, K.S.; Komáromi, I.; Dapprich, S.; Montgomery, J.A., Jr.; Morokuma, K.; Frisch, M.J. Combining quantum mechanics methods with molecular mechanics methods in ONIOM. J. Chem. Theory Comput. 2006, 2, 815–826. [Google Scholar] [CrossRef] [PubMed]
- Ahmadi, S.; Herrera, L.B.; Chehelamirani, M.; Hostaš, J.; Jalife, S.; Salahub, D.R. Multiscale modeling of enzymes: QM-cluster, QM/MM, and QM/MM/MD: A tutorial review. Int. J. Quant. Chem. 2018, 118, e25558. [Google Scholar] [CrossRef]
- Hansen, J.-P.; McDonald, I.R. Chapter 11—Molecular Liquids. In Theory of Simple Liquids, 4th ed.; Hansen, J.-P., McDonald, I.R., Eds.; Academic Press: Oxford, UK, 2013; pp. 455–510. [Google Scholar]
- Kovalenko, A. Molecular Theory of Solvation; Chapter 4; Hirata, F., Ed.; Kluwer Academic Publishers: New York, NY, USA, 2003; Volume 24, pp. 169–276. [Google Scholar]
- Ratkova, E.L.; Palmer, D.S.; Fedorov, M.V. Solvation Thermodynamics of Organic Molecules by the Molecular Integral Equation Theory: Approaching Chemical Accuracy. Chem. Rev. 2015, 115, 6312. [Google Scholar] [CrossRef]
- Luchko, T.; Gusarov, S.; Roe, D.R.; Simmerling, C.; Case, D.A.; Tuszynski, J.; Kovalenko, A. Three-Dimensional Molecular Theory of Solvation Coupled with Molecular Dynamics in Amber. J. Chem. Theory Comput. 2010, 6, 607. [Google Scholar] [CrossRef] [PubMed]
- Gusarov, S.; Ziegler, T.; Kovalenko, A. Self-Consistent Combination of the Three-Dimensional RISM Theory of Molecular Solvation with Analytical Gradients and the Amsterdam Density Functional Package. J. Phys. Chem. A 2006, 110, 6083. [Google Scholar] [CrossRef]
- Casanova, D.; Gusarov, S.; Kovalenko, A.; Ziegler, T. Evaluation of the SCF Combination of KS-DFT and 3D-RISM-KH; Solvation Effect on Conformational Equilibria, Tautomerization Energies, and Activation Barriers. J. Chem. Theory Comput. 2007, 3, 458. [Google Scholar] [CrossRef]
- Aono, S.; Mori, T.; Sakaki, S. 3D-RISM-MP2 Approach to Hydration Structure of Pt(II) and Pd(II) Complexes: Unusual H-Ahead Mode vs Usual O-Ahead One. J. Chem. Theory Comput. 2016, 12, 1189–1206. [Google Scholar] [CrossRef]
- Sosnis, S.; Misin, M.; Palmer, D.S.; Fedorov, M.V. 3D matters! 3D-RISM and 3D convolutional neural network for accurate bioaccumulation prediction. J. Phys. Condens. Matter 2018, 30, 32LT03. [Google Scholar] [CrossRef]
- Roy, D.; Kovalenko, A. Performance of 3D-RISM-KH in Predicting Hydration Free Energy: Effect of Solute Parameters. J. Phys. Chem. A 2019, 123, 4087–4093. [Google Scholar] [CrossRef]
- Nikolić, D.; Blinov, N.; Wishart, D.; Kovalenko, A. 3D-RISM-Dock: A New Fragment-Based Drug Design Protocol. J. Chem. Theory Comput. 2012, 8, 3356–3372. [Google Scholar] [CrossRef] [PubMed]
- Kiyota, Y.; Yoshida, N.; Hirata, F. A New Approach for Investigating the Molecular Recognition of Protein: Toward Structure-Based Drug Design Based on the 3D-RISM Theory. J. Chem. Theory Comput. 2011, 7, 3803–3815. [Google Scholar] [CrossRef]
- Palmer, D.S.; Mišin, M.; Fedorov, M.V.; Llinas, A. Fast and General Method To Predict the Physicochemical Properties of Druglike Molecules Using the Integral Equation Theory of Molecular Liquids. Mol. Pharm. 2015, 12, 3420–3432. [Google Scholar] [CrossRef] [PubMed]
- Roy, D.; Hinge, V.K.; Kovalenko, A. To Pass or Not To Pass: Predicting the Blood–Brain Barrier Permeability with the 3D-RISM-KH Molecular Solvation Theory. ACS Omega 2019, 4, 16774–16780. [Google Scholar] [CrossRef]
- Roy, D.; Kovalenko, A. Application of the Approximate 3D-Reference Interaction Site Model (RISM) Molecular Solvation Theory to Acetonitrile as Solvent. J. Phys. Chem. B 2020, 124, 4590–4597. [Google Scholar] [CrossRef] [PubMed]
- Subramanian, V.; Ratkova, E.; Palmer, D.; Engkvist, E.; Fedorov, M.; Llinas, A. Multisolvent Models for Solvation Free Energy Predictions Using 3D-RISM Hydration Thermodynamic Descriptors. J. Chem. Inf. Model. 2020, 60, 2977–2988. [Google Scholar] [CrossRef] [PubMed]
- Roy, D.; Dutta, D.; Wishsart, D.S.; Kovalenko, A. Predicting PAMPA permeability using the 3D-RISM-KH theory: Are we there yet? J. Comput. Aided Mol. Des. 2021, 35, 261–269. [Google Scholar] [CrossRef]
- Hinge, V.K.; Roy, D.; Kovalenko, A. Predicting skin permeability using the 3D-RISM-KH theory based solvation energy descriptors for a diverse class of compounds. J. Comput. Aided Mol. Des. 2019, 33, 605–611. [Google Scholar] [CrossRef]
- Hinge, V.K.; Roy, D.; Kovalenko, A. Prediction of P-glycoprotein inhibitors with machine learning classification models and 3D-RISM-KH theory based solvation energy descriptors. J. Comput. Aided Mol. Des. 2019, 33, 965–971. [Google Scholar] [CrossRef]
- Huang, W.J.; Blinov, N.; Kovalenko, A. Octanol-Water Partition Coefficient from 3D-RISM-KH Molecular Theory of Solvation with Partial Molar Volume Correction. J. Phys. Chem. B 2015, 119, 5588–5597. [Google Scholar] [CrossRef] [PubMed]
- Luchko, T.; Blinov, N.; Limon, G.C.; Joyce, K.P.; Kovalenko, A. SAMPL5: 3D-RISM partition coefficient calculations with partial molar volume corrections and solute conformational sampling. J. Comput. Aided Mol. Des. 2016, 30, 1115–1127. [Google Scholar] [CrossRef]
- Chandler, D. Equilibrium structure and molecular motion in liquids. Acc. Chem. Res. 1974, 7, 246. [Google Scholar] [CrossRef]
- Lowden, L.J.; Chandler, D. Solution of a new integral equation for pair correlation functions in molecular liquids. J. Chem. Phys. 1973, 59, 6587. [Google Scholar] [CrossRef]
- Lowden, L.J.; Chandler, D. Theory of intermolecular pair correlations for molecular liquids. Applications to the liquids carbon tetrachloride, carbon disulfide, carbon diselenide, and benzene. J. Chem. Phys. 1974, 61, 5228. [Google Scholar] [CrossRef]
- Chandler, D. Derivation of an integral equation for pair correlation functions in molecular fluids. J. Chem. Phys. 1973, 59, 2742. [Google Scholar] [CrossRef]
- Chandler, D.; Hsu, C.S.; Street, W.B. Comparisons of Monte Carlo and RISM calculations of pair correlation functions. J. Chem. Phys. 1977, 66, 5231. [Google Scholar] [CrossRef]
- Singer, S.J.; Chandler, D. Free energy functions in the extended RISM approximation. Mol. Phys. 1985, 55, 621. [Google Scholar] [CrossRef]
- Chandler, D.; Silbey, R.; Ladanyi, B.M. New and proper integral equations for site-site equilibrium correlations in molecular fluids. Mol. Phys. 1982, 46, 1335. [Google Scholar] [CrossRef]
- Richardson, D.M.; Chandler, D. Calculation of orientational pair correlation factors with the interaction site formalism. J. Chem. Phys. 1984, 80, 4484. [Google Scholar] [CrossRef]
- Perkyns, J.; Pettitt, B.M. A site–site theory for finite concentration saline solutions. J. Chem. Phys. 1992, 97, 7656. [Google Scholar] [CrossRef]
- Kovalenko, A.; Hirata, F. Potentials of mean force of simple ions in ambient aqueous solution. I. Three-dimensional reference interaction site model approach. J. Chem. Phys. 2000, 112, 10391. [Google Scholar] [CrossRef]
- Kovalenko, A. Multiscale modeling of solvation in chemical and biological nanosystems and in nanoporous materials. Pure Appl. Chem. 2013, 85, 159–199. [Google Scholar] [CrossRef]
- Sergiievskyi, V.; Jeanmairet, G.; Levesque, M.; Borgis, D. Solvation free-energy pressure corrections in the three dimensional reference interaction site model. J. Chem. Phys. 2015, 143, 184116. [Google Scholar] [CrossRef] [PubMed]
- Misin, M.; Vainikka, P.A.; Fedorov, M.V.; Palmer, D.S. Salting-out effects by pressure-corrected 3D-RISM. J. Chem. Phys. 2016, 145, 194501. [Google Scholar] [CrossRef]
- Pettitt, B.M.; Rossky, P.J. Integral equation predictions of liquid state structure for waterlike intermolecular potentials. J. Chem. Phys. 1982, 77, 1451–1457. [Google Scholar] [CrossRef]
- Hirata, F.; Levy, R.M. A new RISM integral equation for solvated polymers. Chem. Phys. Lett. 1987, 136, 267–273. [Google Scholar] [CrossRef]
- Noé, F. Beating the Millisecond Barrier in Molecular Dynamics Simulations. Biophys. J. 2015, 108, 228. [Google Scholar] [CrossRef][Green Version]
- Shaw, D.E. Millisecond-long molecular dynamics simulations of proteins on a special-purpose machine. Biophys. J. 2013, 104, 45A. [Google Scholar] [CrossRef]
- Voelz, V.A.; Bowman, G.R.; Beauchamp, K.; Pande, V.S. Molecular Simulation of ab Initio Protein Folding for a Millisecond Folder NTL9(1−39). J. Am. Chem. Soc. 2010, 132, 1526. [Google Scholar] [CrossRef]
- Miyata, T.; Hirata, F. Combination of molecular dynamics method and 3D-RISM theory for conformational sampling of large flexible molecules in solution. J. Comput. Chem. 2008, 29, 871–882. [Google Scholar] [CrossRef]
- Omelyan, I.; Kovalenko, A. MTS-MD of Biomolecules Steered with 3D-RISM-KH Mean Solvation Forces Accelerated with Generalized Solvation Force Extrapolation. J. Chem. Theory Comput. 2015, 11, 1875–1895. [Google Scholar] [CrossRef]
- Omelyan, I.; Kovalenko, A. Enhanced solvation force extrapolation for speeding up molecular dynamics simulations of complex biochemical liquids. J. Chem. Phys. 2019, 151, 214102. [Google Scholar] [CrossRef]
- Murray, C.W.; Rees, D.C. The rise of fragment-based drug discovery. Nat. Chem. 2009, 1, 187–192. [Google Scholar] [CrossRef]
- Tounge, B.A.; Parker, M.H. Chapter one—Designing a Diverse High-Quality Library for Crystallography-Based FBDD Screening. Methods Enzymol. 2011, 493, 3–20. [Google Scholar]
- Imai, T.; Oda, K.; Kovalenko, A.; Hirata, F.; Kidera, A. Ligand Mapping on Protein Surfaces by the 3D-RISM Theory: Toward Computational Fragment-Based Drug Design. J. Am. Chem. Soc. 2009, 131, 12430. [Google Scholar] [CrossRef]
- Sugita, M.; Hamano, M.; Kasahara, K.; Kikuchi, T.; Hirata, F. New Protocol for Predicting the Ligand-Binding Site and Mode Based on the 3D-RISM/KH Theory. J. Chem. Theory Comput. 2020, 16, 2864. [Google Scholar] [CrossRef] [PubMed]
- Imai, T. A Novel Ligand-Mapping Method Based on Molecular Liquid Theory. Curr. Pharm. Des. 2011, 17, 1685–1694. [Google Scholar] [CrossRef] [PubMed]
- Lemmon, G.; Meiler, J. Towards Ligand Docking Including Explicit Interface Water Molecules. PLoS ONE 2013, 8, e67536. [Google Scholar] [CrossRef] [PubMed]
- Ross, G.A.; Morris, G.M.; Biggin, P.C. Rapid and Accurate Prediction and Scoring of Water Molecules in Protein Binding Sites. PLoS ONE 2012, 7, e32036. [Google Scholar] [CrossRef]
- Rudling, A.; Orro, A.; Carlsson, J. Prediction of Ordered Water Molecules in Protein Binding Sites from Molecular Dynamics Simulations: The Impact of Ligand Binding on Hydration Networks. J. Chem. Inf. Model. 2018, 58, 350–361. [Google Scholar] [CrossRef]
- Imai, T.; Hiraoka, R.; Kovalenko, A.; Hirta, F. Water Molecules in a Protein Cavity Detected by a Statistical−Mechanical Theory. J. Am. Chem. Soc. 2005, 127, 15334. [Google Scholar] [CrossRef] [PubMed]
- Sindhikara, D.J.; Yoshida, N.; Hirata, F. Placevent: An algorithm for prediction of explicit solvent atom distribution-application to HIV-1 protease and F-ATP synthase. J. Comput. Chem. 2012, 33, 1536. [Google Scholar] [CrossRef] [PubMed]
- Hinge, V.K.; Blinov, N.; Roy, D.; Wishart, D.S.; Kovalenko, A. The role of hydration effects in 5-fluorouridine binding to SOD1: Insight from a new 3D-RISM-KH based protocol for including structural water in docking simulations. J. Comput. Aided Mol. Des. 2019, 33, 913. [Google Scholar] [CrossRef]
- Molecular Operating Environment (MOE), 2019.01; Chemical Computing Group ULC: Montreal, QC, Canada, 2021.
- Nukaga, M.; Yoon, M.J.; Taracilia, M.A.; Hoshino, T.; Becka, S.A.; Zeiser, E.T.; Johnson, J.R.; Papp-Wallace, K.M. Assessing the Potency of β-Lactamase Inhibitors with Diverse Inactivation Mechanisms against the PenA1 Carbapenemase from Burkholderia multivorans. ACS Infect. Dis. 2021, 7, 826–837. [Google Scholar] [CrossRef]
- Hüfner-Wulsdorf, T.; Klebe, G. Mapping Water Thermodynamics on Drug Candidates via Molecular Building Blocks: A Strategy to Improve Ligand Design and Rationalize SAR. J. Med. Chem. 2021. [Google Scholar] [CrossRef]
- Aggarwal, L.; Biswas, P. Hydration Thermodynamics of Familial Parkinson’s Disease-Linked Mutants of α-Synuclein. J. Chem. Inf. Model. 2021. [Google Scholar] [CrossRef]
- Nguyen, C.; Yamazaki, T.; Kovalenko, A.; Case, D.A.; Gilson, M.K.; Kurtzman, T.; Luchko, T. A molecular reconstruction approach to site-based 3D-RISM and comparison to GIST hydration thermodynamic maps in an enzyme active site. PLoS ONE 2019, 14, e0219473. [Google Scholar] [CrossRef]
- Blinov, N.; Wishart, D.S.; Kovalenko, A. Solvent Composition Effects on the Structural Properties of the Aβ42 Monomer from the 3D-RISM-KH Molecular Theory of Solvation. J. Phys. Chem. B 2019, 123, 2491–2506. [Google Scholar] [CrossRef] [PubMed]
- Ariz-Extreme, I.; Hub, J.S. Potential of Mean Force Calculations of Solute Permeation across UT-B and AQP1: A Comparison between Molecular Dynamics and 3D-RISM. J. Phys. Chem. B 2017, 121, 1506–1519. [Google Scholar] [CrossRef] [PubMed]
- Lee, F.S.; Chu, Z.-T.; Bolger, M.B.; Warshel, A. Calculations of antibody-antigen interactions: Microscopic and semi-microscopic evaluation of the free energies of binding of phosphorylcholine analogs to McPC603. Protein Eng. 1992, 5, 215–228. [Google Scholar] [CrossRef]
- Sham, Y.Y.; Chu, Z.T.; Tao, H.; Warshel, A. Examining methods for calculations of binding free energies: LRA, LIE, PDLD-LRA, and PDLD/S-LRA calculations of ligands binding to an HIV protease. Proteins: Struct. Funct. Genet. 2000, 39, 393–407. [Google Scholar] [CrossRef]
- Warshel, A.; Sharma, P.K.; Kato, M.; Parson, W.W. Modeling electrostatic effects in proteins. Biochim. Biophys. Acta 2006, 1764, 1647–1676. [Google Scholar] [CrossRef]
- Åqvist, J.; Medina, C.; Samuelsson, J.E. A new method for predicting binding affinity in computer-aided drug design. Protein Eng. 1994, 7, 385–391. [Google Scholar] [CrossRef]
- Hansson, T.; Marelius, J.; Åqvist, J. Ligand binding affinity prediction by linear interaction energy methods. J. Comput. Aided Mol. Des. 1998, 12, 27–35. [Google Scholar] [CrossRef]
- Kollman, P.A.; Massova, I.; Reyes, C.; Kuhn, B.; Huo, S.; Chong, L.; Lee, M.; Lee, T.; Duan, Y.; Wang, W.; et al. Calculating Structures and Free Energies of Complex Molecules: Combining Molecular Mechanics and Continuum Models. Acc. Chem. Res. 2000, 33, 889–897. [Google Scholar] [CrossRef] [PubMed]
- Genheden, S.; Luchko, T.; Gusarov, S.; Kovalenko, A.; Ryde, U. An MM/3D-RISM Approach for Ligand Binding Affinities. J. Phys. Chem. B 2010, 114, 8505–8516. [Google Scholar] [CrossRef] [PubMed]
- Sugita, M.; Kuwano, I.; Higashi, T.; Motoyama, K.; Arima, H.; Hirata, F. Computational Screening of a Functional Cyclodextrin Derivative for Suppressing a Side Effect of Doxorubicin. J. Phys. Chem. B 2021, 125, 2308–2316. [Google Scholar] [CrossRef]
- Suárez, D.; Díaz, N. Affinity Calculations of Cyclodextrin Host–Guest Complexes: Assessment of Strengths and Weaknesses of End-Point Free Energy Methods. J. Chem. Inf. Model. 2019, 59, 421–440. [Google Scholar] [CrossRef]
- Miller, B.R., III; McGee, T.D., Jr.; Swails, J.M.; Homeyer, N.; Gohlke, H.; Roitberg, A.E. MMPBSA.py: An Efficient Program for End-State Free Energy Calculations. J. Chem. Theory Comput. 2012, 8, 3314–3321. [Google Scholar] [CrossRef] [PubMed]
- Palmer, D.S.; Frolov, A.I.; Ratkova, E.L.; Fedorov, M.V. Towards a universal method for calculating hydration free energies: A 3D reference interaction site model with partial molar volume correction. J. Phys. Condens. Matter 2010, 22, 492101. [Google Scholar] [CrossRef]
- Mobley, D.L.; Guthrie, J.P. FreeSolv: A database of experimental and calculated hydration free energies, with input files. J. Comput. Aided Mol. Des. 2014, 28, 711–720. [Google Scholar] [CrossRef] [PubMed]
- Truchon, J.-F.; Pettit, B.M.; Labute, O. A Cavity Corrected 3D-RISM Functional for Accurate Solvation Free Energies. J. Chem. Theory Comput. 2014, 10, 934. [Google Scholar] [CrossRef]
- Roy, D.; Hinge, V.K.; Kovalenko, A. Predicting Blood–Brain Partitioning of Small Molecules Using a Novel Minimalistic Descriptor-Based Approach via the 3D-RISM-KH Molecular Solvation Theory. ACS Omega 2019, 4, 3055–3060. [Google Scholar] [CrossRef]
- Roy, D.; Blinov, N.; Kovalenko, A. Predicting Accurate Solvation Free Energy in n-Octanol Using 3D-RISM-KH Molecular Theory of Solvation: Making Right Choices. J. Phys. Chem. B 2017, 121, 9268–9273. [Google Scholar] [CrossRef] [PubMed]
- Roy, D.; Kovalenko, A. Application of the 3D-RISM-KH molecular solvation theory for DMSO as solvent. J. Comput. Aided Mol. Des. 2019, 33, 905–912. [Google Scholar] [CrossRef] [PubMed]
- Roy, D.; Kovalenko, A. A 3D-RISM-KH study of liquid nitromethane, nitroethane, and nitrobenzene as solvents. J. Mol. Liq. 2021, 332, 115857. [Google Scholar] [CrossRef]
- Marenich, A.V.; Kelly, C.P.; Thompson, J.D.; Hawkins, G.D.; Chambers, C.C.; Giesen, D.J.; Winget, P.; Cramer, C.J.; Truhlar, D.G. Minnesota Solvation Database—Version 2012; University of Minnesota: Minneapolis, MN, USA, 2012. [Google Scholar]
- Maruyama, Y.; Yoshida, N.; Tadano, H.; Takahashi, D.; Sato, M.; Hirata, F. Massively parallel implementation of 3D-RISM calculation with volumetric 3D-FFT. J. Comput. Chem. 2014, 35, 1347–1355. [Google Scholar] [CrossRef]
- Maruyama, Y.; Hirata, F. Modified Anderson Method for Accelerating 3D-RISM Calculations Using Graphics Processing Unit. J. Chem. Theory Comput. 2012, 8, 3015–3021. [Google Scholar] [CrossRef] [PubMed]
- Onishi, I.; Tsuji, H.; Irisa, M. A tool written in Scala for preparation and analysis in MD simulation and 3D-RISM calculation of biomolecules. Biophys. Physicobiol. 2019, 16, 485–489. [Google Scholar] [CrossRef]
- Reimann, M.; Kaupp, M. Evaluation of an Efficient 3D-RISM-SCF Implementation as a Tool for Computational Spectroscopy in Solution. J. Phys. Chem. A 2020, 124, 7439–7452. [Google Scholar] [CrossRef] [PubMed]

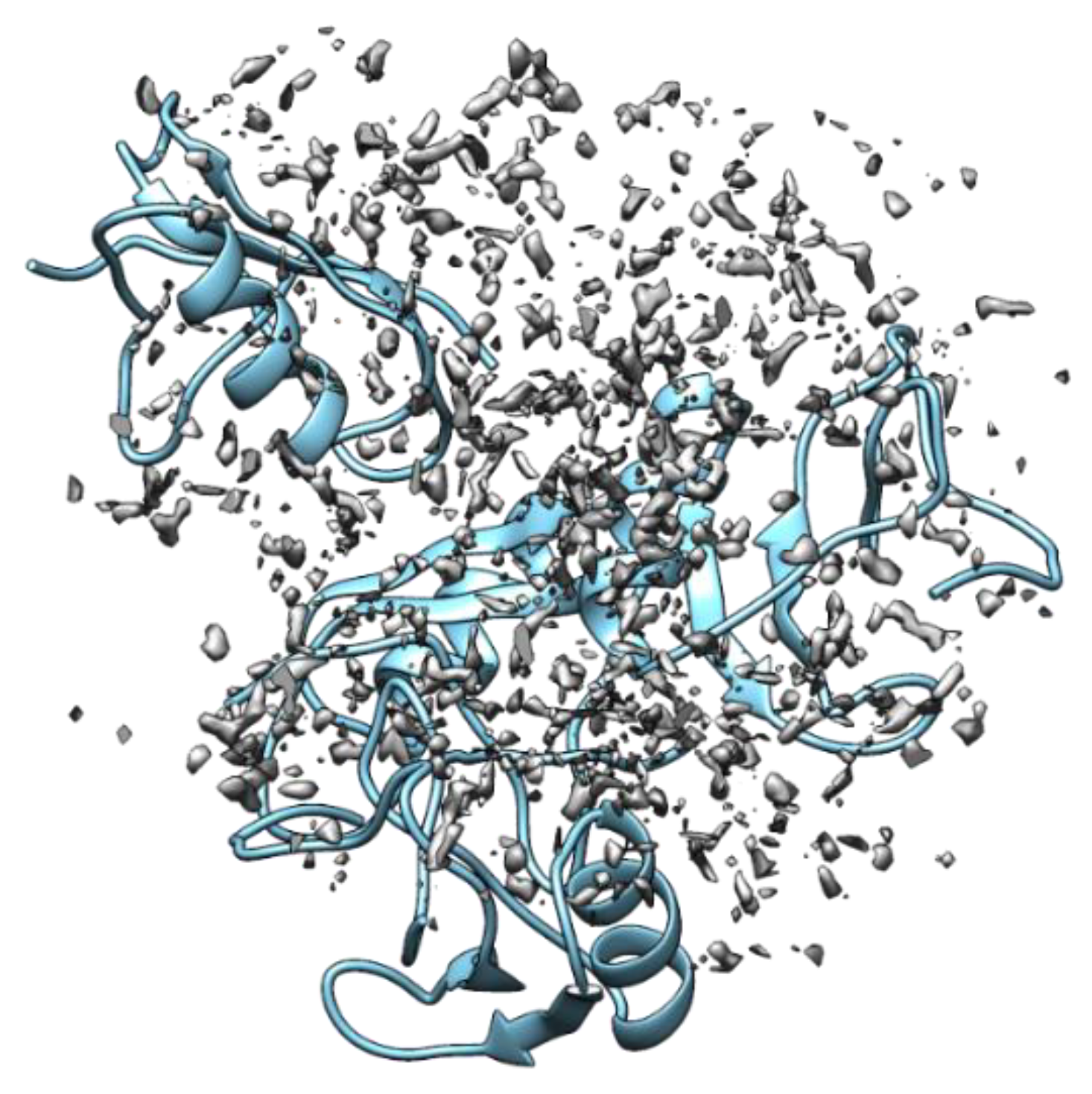
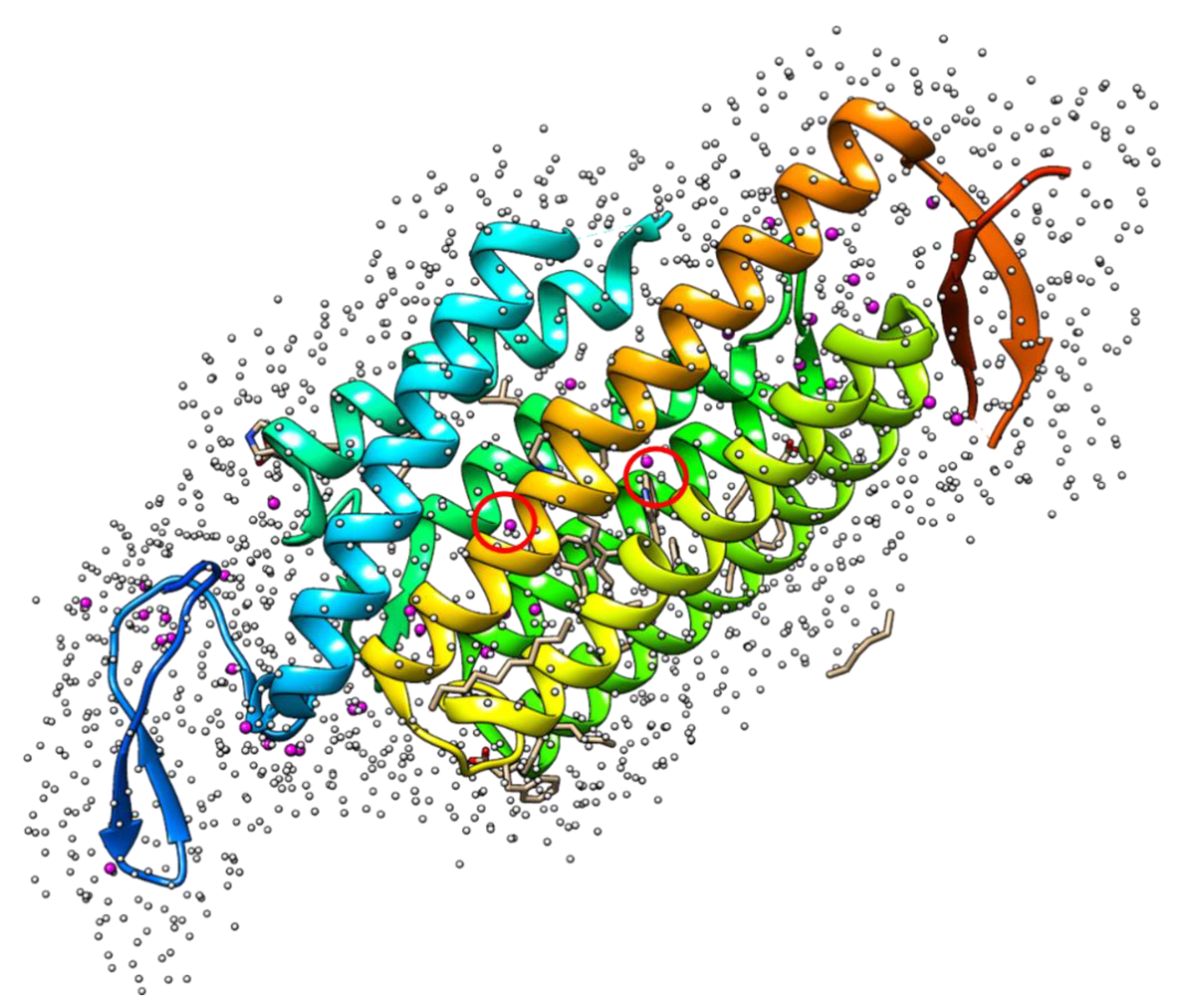
| Solvent | Dielectric Constant | No. of Solutes | Accuracy (Kcal/Mol) | Reference |
|---|---|---|---|---|
| Water | 78.5 | 504 | 0.91–0.95 a (1.51) c | [99] |
| 0.89 a | [100] | |||
| n-Octanol | 9.86 | 205 | 0.94 b | [41] |
| 158 | 1.03 b | [102] | ||
| Cyclohexane | 2.0165 | 91 | 1.12 a | [37,101] |
| Hexadecane | 2.0402 | 189 | 0.88 a | [37,101] |
| Chloroform | 4.7113 | 105 | 0.75 a | [37,101] |
| Acetonitrile | 35.688 | 7 | 2.2 a (1.9) d | [47] |
| Nitromethane | 36.562 | 7 | 1.32 a (1.83) d | [103] |
| Nitroethane | 28.29 | 7 | 0.38 a (2.00) d | [103] |
| Nitrobenzene | 34.809 | 15 | 0.88 a (2.91) d | [103] |
| DMSO | 46.826 | 8 | 2.09 a | [42] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Roy, D.; Kovalenko, A. Biomolecular Simulations with the Three-Dimensional Reference Interaction Site Model with the Kovalenko-Hirata Closure Molecular Solvation Theory. Int. J. Mol. Sci. 2021, 22, 5061. https://doi.org/10.3390/ijms22105061
Roy D, Kovalenko A. Biomolecular Simulations with the Three-Dimensional Reference Interaction Site Model with the Kovalenko-Hirata Closure Molecular Solvation Theory. International Journal of Molecular Sciences. 2021; 22(10):5061. https://doi.org/10.3390/ijms22105061
Chicago/Turabian StyleRoy, Dipankar, and Andriy Kovalenko. 2021. "Biomolecular Simulations with the Three-Dimensional Reference Interaction Site Model with the Kovalenko-Hirata Closure Molecular Solvation Theory" International Journal of Molecular Sciences 22, no. 10: 5061. https://doi.org/10.3390/ijms22105061
APA StyleRoy, D., & Kovalenko, A. (2021). Biomolecular Simulations with the Three-Dimensional Reference Interaction Site Model with the Kovalenko-Hirata Closure Molecular Solvation Theory. International Journal of Molecular Sciences, 22(10), 5061. https://doi.org/10.3390/ijms22105061






