Impact of the Spectral Composition of Kilovoltage X-rays on High-Z Nanoparticle-Assisted Dose Enhancement
Abstract
:1. Introduction
2. Results and Discussion
3. Materials and Methods
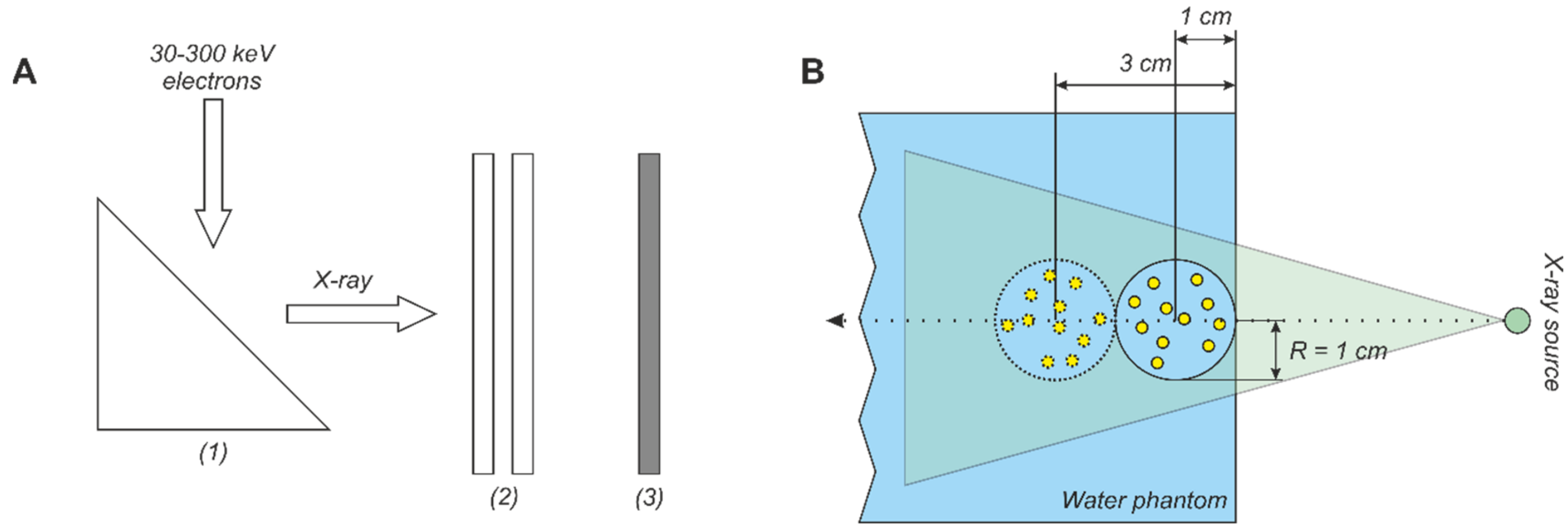
3.1. Analytical Calculation of Dose Enhancement Factor
3.2. Monte-Carlo Simulation of X-ray Spectra
3.3. Model Tumor Simulation
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, L.; Yuan, H.; Inscoe, C.; Chtcheprov, P.; Hadsell, M.; Lee, Y.; Lu, J.; Chang, S.; Zhou, O. Nanotube x-ray for cancer therapy: A compact microbeam radiation therapy system for brain tumor treatment. Expert Rev. Anticancer. Ther. 2014, 14, 1411–1418. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Palade, C.; Slav, A.; Lepadatu, A.-M.; Stavarache, I.; Dascalescu, I.; Maraloiu, V.-A.; Negrila, C.; Logofatu, C.; Stoica, T.; Teodorescu, V.S.; et al. Orthorhombic HfO2 with embedded Ge nanoparticles in nonvolatile memories used for the detection of ionizing radiation. Nanotechnology 2019, 30, 445501. [Google Scholar] [CrossRef] [PubMed]
- Petriev, V.M.; Tischenko, V.K.; Mikhailovskaya, A.A.; Popov, A.A.; Tselikov, G.; Zelepukin, I.; Deyev, S.M.; Kaprin, A.D.; Ivanov, S.; Timoshenko, V.Y.; et al. Nuclear nanomedicine using Si nanoparticles as safe and effective carriers of 188Re radionuclide for cancer therapy. Sci. Rep. 2019, 9, 1–10. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Thomas, G.; Boudon, J.; Maurizi, L.; Moreau, M.; Walker, P.; Severin, I.; Oudot, A.; Goze, C.; Poty, S.; Vrigneaud, J.-M.; et al. Innovative Magnetic Nanoparticles for PET/MRI Bimodal Imaging. ACS Omega 2019, 4, 2637–2648. [Google Scholar] [CrossRef]
- Abbasi, A.Z.; Gordijo, C.R.; Amini, M.A.; Maeda, A.; Rauth, A.M.; Dacosta, R.S.; Wu, X.Y. Hybrid Manganese Dioxide Nanoparticles Potentiate Radiation Therapy by Modulating Tumor Hypoxia. Cancer Res. 2016, 76, 6643–6656. [Google Scholar] [CrossRef] [Green Version]
- Guo, Z.; Zhu, S.; Yong, Y.; Zhang, X.; Dong, X.; Du, J.; Xie, J.; Wang, Q.; Gu, Z.; Zhao, Y. Synthesis of BSA-Coated BiOI@Bi2S3 Semiconductor Heterojunction Nanoparticles and Their Applications for Radio/Photodynamic/Photothermal Synergistic Therapy of Tumor. Adv. Mater. 2017, 29, 1704136. [Google Scholar] [CrossRef]
- Kim, S.-R.; Kim, E.-H. Gold nanoparticles as dose-enhancement agent for kilovoltage X-ray therapy of melanoma. Int. J. Radiat. Biol. 2017, 93, 517–526. [Google Scholar] [CrossRef]
- Du, J.; Wang, X.; Dong, X.; Zhang, C.; Mei, L.; Zang, Y.; Yan, L.; Zhang, H.; Gu, Z. Enhanced radiosensitization of ternary Cu3BiSe3 nanoparticles by photo-induced hyperthermia in the second near-infrared biological window. Nanoscale 2019, 11, 7157–7165. [Google Scholar] [CrossRef]
- Xie, J.; Gong, L.; Zhu, S.; Yong, Y.; Gu, Z.; Zhao, Y. Emerging Strategies of Nanomaterial-Mediated Tumor Radiosensitization. Adv. Mater. 2019, 31, e1802244. [Google Scholar] [CrossRef]
- Hainfeld, J.F.; Slatkin, D.N.; Smilowitz, H.M. The use of gold nanoparticles to enhance radiotherapy in mice. Phys. Med. Biol. 2004, 49, N309–N315. [Google Scholar] [CrossRef]
- Sun, H.; Wang, X.; Zhai, S. The Rational Design and Biological Mechanisms of Nanoradiosensitizers. Nanomaterials 2020, 10, 504. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Yang, J.; Fu, S.; Wu, J. Gold Nanoparticles as Radiosensitizers in Cancer Radiotherapy. Int. J. Nanomed. 2020, ume 15, 9407–9430. [Google Scholar] [CrossRef]
- Howard, D.; Sebastian, S.; Le, Q.V.-C.; Thierry, B.; Kempson, I. Chemical Mechanisms of Nanoparticle Radiosensitization and Radioprotection: A Review of Structure-Function Relationships Influencing Reactive Oxygen Species. Int. J. Mol. Sci. 2020, 21, 579. [Google Scholar] [CrossRef] [Green Version]
- Choi, J.; Kim, G.; Bin Cho, S.; Im, H.-J. Radiosensitizing high-Z metal nanoparticles for enhanced radiotherapy of glioblastoma multiforme. J. Nanobiotechnology 2020, 18, 1–23. [Google Scholar] [CrossRef]
- Moradi, F.; Saraee, K.R.E.; Sani, S.A.; Bradley, D. Metallic nanoparticle radiosensitization: The role of Monte Carlo simulations towards progress. Radiat. Phys. Chem. 2021, 180, 109294. [Google Scholar] [CrossRef]
- Bonvalot, S.; Rutkowski, P.L.; Thariat, J.; Carrère, S.; Ducassou, A.; Sunyach, M.-P.; Agoston, P.; Hong, A.; Mervoyer, A.; Rastrelli, M.; et al. NBTXR3, a first-in-class radioenhancer hafnium oxide nanoparticle, plus radiotherapy versus radiotherapy alone in patients with locally advanced soft-tissue sarcoma (Act.In.Sarc): A multicentre, phase 2–3, randomised, controlled trial. Lancet Oncol. 2019, 20, 1148–1159. [Google Scholar] [CrossRef]
- Verry, C.; Sancey, L.; Dufort, S.; Le Duc, G.; Mendoza, C.; Lux, F.; Grand, S.; Arnaud, J.; Quesada, J.L.; Villa, J.; et al. Treatment of multiple brain metastases using gadolinium nanoparticles and radiotherapy: NANO-RAD, a phase I study protocol. BMJ Open 2019, 9, e023591. [Google Scholar] [CrossRef]
- Rong, Y.; Zuo, L.; Shang, L.; Bazan, J.G. Radiotherapy treatment for nonmelanoma skin cancer. Expert Rev. Anticancer. Ther. 2015, 15, 765–776. [Google Scholar] [CrossRef]
- Eaton, D.J. Electronic brachytherapy—Current status and future directions. Br. J. Radiol. 2015, 88, 20150002. [Google Scholar] [CrossRef] [Green Version]
- Veness, M.; Delishaj, D.; Barnes, E.; Безуглый, А.; Rembielak, A. Current Role of Radiotherapy in Non-melanoma Skin Cancer. Clin. Oncol. 2019, 31, 749–758. [Google Scholar] [CrossRef]
- Kong, T.; Zeng, J.; Wang, X.; Yang, X.; Yang, J.; McQuarrie, S.; McEwan, A.; Roa, W.; Chen, J.; Xing, J.Z. Enhancement of Radiation Cytotoxicity in Breast-Cancer Cells by Localized Attachment of Gold Nanoparticles. Small 2008, 4, 1537–1543. [Google Scholar] [CrossRef]
- Jain, S.; Coulter, J.A.; Hounsell, A.R.; Butterworth, K.T.; McMahon, S.J.; Hyland, W.B.; Muir, M.F.; Dickson, G.R.; Prise, K.M.; Currell, F.J.; et al. Cell-Specific Radiosensitization by Gold Nanoparticles at Megavoltage Radiation Energies. Int. J. Radiat. Oncol. 2011, 79, 531–539. [Google Scholar] [CrossRef] [Green Version]
- Briggs, A.; Corde, S.; Oktaria, S.; Brown, R.; Rosenfeld, A.; Lerch, M.; Konstantinov, K.; Tehei, M. Cerium oxide nanoparticles: Influence of the high-Z component revealed on radioresistant 9L cell survival under X-ray irradiation. Nanomed. Nanotechnol. Biol. Med. 2013, 9, 1098–1105. [Google Scholar] [CrossRef] [Green Version]
- Her, S.; Jaffray, D.A.; Allen, C. Gold nanoparticles for applications in cancer radiotherapy: Mechanisms and recent advancements. Adv. Drug Deliv. Rev. 2017, 109, 84–101. [Google Scholar] [CrossRef]
- Rahman, W.N.; Bishara, N.; Ackerly, T.; He, C.F.; Jackson, P.; Wong, C.; Davidson, R.; Geso, M. Enhancement of radiation effects by gold nanoparticles for superficial radiation therapy. Nanomed. Nanotechnol. Biol. Med. 2009, 5, 136–142. [Google Scholar] [CrossRef]
- Morozov, V.N.; Belousov, A.V.; Zverev, V.I.; Shtil, A.A.; Kolyvanova, M.A.; Krivoshapkin, P.V. The Prospects of Metal Oxide Nanoradiosensitizers: The Effect of the Elemental Composition of Particles and Characteristics of Radiation Sources on Enhancement of the Adsorbed Dose. Biophysics 2020, 65, 533–540. [Google Scholar] [CrossRef]
- Popov, A.L.; Zaichkina, S.I.; Popova, N.R.; Rozanova, O.M.; Romanchenko, S.P.; Ivanova, O.S.; Smirnov, A.A.; Mironova, E.V.; Selezneva, I.I.; Ivanov, V.K. Radioprotective effects of ultra-small citrate-stabilized cerium oxide nanoparticles in vitro and in vivo. RSC Adv. 2016, 6, 106141–106149. [Google Scholar] [CrossRef]
- Popova, N.R.; Popov, A.L.; Ermakov, A.M.; Reukov, V.V.; Ivanov, V.K. Ceria-Containing Hybrid Multilayered Microcapsules for Enhanced Cellular Internalisation with High Radioprotection Efficiency. Molecules 2020, 25, 2957. [Google Scholar] [CrossRef]
- Roeske, J.C.; Nunez, L.; Hoggarth, M.; Labay, E.; Weichselbaum, R.R. Characterization of the theoretical radiation dose enhancement from nanoparticles. Technol. Cancer Res. Treat. 2007, 6, 395–401. [Google Scholar] [CrossRef]
- Brun, E.; Sanche, L.; Sicard-Roselli, C. Parameters governing gold nanoparticle X-ray radiosensitization of DNA in solution. Colloids Surf. B Biointerfaces 2009, 72, 128–134. [Google Scholar] [CrossRef]
- Hossain, M.; Su, M. Nanoparticle Location and Material-Dependent Dose Enhancement in X-ray Radiation Therapy. J. Phys. Chem. C 2012, 116, 23047–23052. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Koger, B.; Kirkby, C. Optimization of photon beam energies in gold nanoparticle enhanced arc radiation therapy using Monte Carlo methods. Phys. Med. Biol. 2016, 61, 8839–8853. [Google Scholar] [CrossRef] [PubMed]
- Rabus, H.; Gargioni, E.; Li, W.B.; Nettelbeck, H.; Villagrasa, C. Determining dose enhancement factors of high-Z nanoparticles from simulations where lateral secondary particle disequilibrium exists. Phys. Med. Biol. 2019, 64, 155016. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Morozov, K.V.; Kolyvanova, M.A.; Kartseva, M.E.; Shishmakova, E.M.; Dement’Eva, O.V.; Isagulieva, A.K.; Salpagarov, M.H.; Belousov, A.V.; Rudoy, V.M.; Shtil, A.A.; et al. Radiosensitization by Gold Nanoparticles: Impact of the Size, Dose Rate, and Photon Energy. Nanomaterials 2020, 10, 952. [Google Scholar] [CrossRef] [PubMed]
- Brown, R.; Tehei, M.; Oktaria, S.; Briggs, A.; Stewart, C.; Konstantinov, K.; Rosenfeld, A.B.; Corde, S.; Lerch, M. High-Z Nanostructured Ceramics in Radiotherapy: First Evidence of Ta2O5-Induced Dose Enhancement on Radioresistant Cancer Cells in an MV Photon Field. Part. Part. Syst. Charact. 2014, 31, 500–505. [Google Scholar] [CrossRef]
- Engels, E.; Westlake, M.; Li, N.; Vogel, S.; Gobert, Q.; Thorpe, N.; Rosenfeld, A.; Lerch, M.L.F.; Corde, S.; Tehei, M. Thulium Oxide Nanoparticles: A new candidate for image-guided radiotherapy. Biomed. Phys. Eng. Express 2018, 4, 044001. [Google Scholar] [CrossRef] [Green Version]
- Shiryaeva, E.S.; Baranova, I.A.; Kiselev, G.O.; Morozov, V.N.; Belousov, A.V.; Sherstiuk, A.A.; Kolyvanova, M.A.; Krivoshapkin, P.V.; Feldman, V.I. Hafnium Oxide as a Nanoradiosensitizer under X-ray Irradiation of Aqueous Organic Systems: A Model Study Using the Spin-Trapping Technique and Monte Carlo Simulations. J. Phys. Chem. C 2019, 123, 27375–27384. [Google Scholar] [CrossRef]
- Guerreiro, A.; Chatterton, N.; Crabb, E.M.; Golding, J.P. A comparison of the radiosensitisation ability of 22 different element metal oxide nanoparticles using clinical megavoltage X-rays. Cancer Nanotechnol. 2019, 10, 1–20. [Google Scholar] [CrossRef]
- Zhao, J.; Liu, P.; Ma, J.; Li, D.; Yang, H.; Chen, W.; Jiang, Y. Enhancement of Radiosensitization by Silver Nanoparticles Functionalized with Polyethylene Glycol and Aptamer As1411 for Glioma Irradiation Therapy. Int. J. Nanomed. 2019, 14, 9483–9496. [Google Scholar] [CrossRef] [Green Version]
- Sisin, N.N.T.; Razak, K.A.; Abidin, S.Z.; Mat, N.F.C.; Abdullah, R.; Ab Rashid, R.; Anuar, M.A.K.; Zainudin, N.H.M.; Tagiling, N.; Nawi, N.M.; et al. Radiosensitization Effects by Bismuth Oxide Nanoparticles in Combination with Cisplatin for High Dose Rate Brachytherapy. Int. J. Nanomed. 2019, 14, 9941–9954. [Google Scholar] [CrossRef] [Green Version]
- Davydov, A.S.; Belousov, A.V.; Krusanov, G.A.; Kolyvanova, M.A.; Kovalev, B.B.; Komlev, A.S.; Krivoshapkin, P.V.; Morozov, V.N.; Zverev, V.I. Promising magnetic nanoradiosensitizers for combination of tumor hyperthermia and x-ray therapy: Theoretical calculation. J. Appl. Phys. 2021, 129, 033902. [Google Scholar] [CrossRef]
- Seegenschmiedt, M.H.; Micke, O.; Muecke, R.; The German Cooperative Group on Radiotherapy for Non-malignant Diseases (GCG-BD). Radiotherapy for non-malignant disorders: State of the art and update of the evidence-based practice guidelines. Br. J. Radiol. 2015, 88, 20150080. [Google Scholar] [CrossRef]
- Khoshgard, K.; Hashemi, B.; Arbabi, A.; Rasaee, M.J.; Soleimani, M. Radiosensitization effect of folate-conjugated gold nanoparticles on HeLa cancer cells under orthovoltage superficial radiotherapy techniques. Phys. Med. Biol. 2014, 59, 2249–2263. [Google Scholar] [CrossRef]
- Enferadi, M.; Fu, S.-Y.; Hong, J.-H.; Tung, C.-J.; Chao, T.-C.; Wey, S.-P.; Chiu, C.-H.; Wang, C.-C.; Sadeghi, M. Radiosensitization of ultrasmall GNP–PEG–cRGDfK in ALTS1C1 exposed to therapeutic protons and kilovoltage and megavoltage photons. Int. J. Radiat. Biol. 2018, 94, 124–136. [Google Scholar] [CrossRef]
- Chithrani, D.B.; Jelveh, S.; Jalali, F.; Van Prooijen, M.; Allen, C.; Bristow, R.G.; Hill, R.P.; Jaffray, D.A. Gold Nanoparticles as Radiation Sensitizers in Cancer Therapy. Radiat. Res. 2010, 173, 719–728. [Google Scholar] [CrossRef]
- Yogo, K.; Misawa, M.; Shimizu, M.; Shimizu, H.; Kitagawa, T.; Hirayama, R.; Ishiyama, H.; Furukawa, T.; Yasuda, H. Effect of Gold Nanoparticle Radiosensitization on Plasmid DNA Damage Induced by High-Dose-Rate Brachytherapy. Int. J. Nanomed. 2021, 16, 359–370. [Google Scholar] [CrossRef]
- McMahon, S.J.; Mendenhall, M.; Jain, S.; Currell, F. Radiotherapy in the presence of contrast agents: A general figure of merit and its application to gold nanoparticles. Phys. Med. Biol. 2008, 53, 5635–5651. [Google Scholar] [CrossRef]
- Martelli, S.; Chow, J.C.L. Dose Enhancement for the Flattening-Filter-Free and Flattening-Filter Photon Beams in Nanoparticle-Enhanced Radiotherapy: A Monte Carlo Phantom Study. Nanomaterials 2020, 10, 637. [Google Scholar] [CrossRef] [Green Version]
- Bobyk, L.; Edouard, M.; Deman, P.; Vautrin, M.; Pernet-Gallay, K.; Delaroche, J.; Adam, J.-F.; Estève, F.; Ravanat, J.-L.; Elleaume, H. Photoactivation of gold nanoparticles for glioma treatment. Nanomed. Nanotechnol. Biol. Med. 2013, 9, 1089–1097. [Google Scholar] [CrossRef]
- XMuDat: Photon Attenuation Data on, PC. Available online: https://www-nds.iaea.org/publications/iaea-nds/iaea-nds-0195.htm (accessed on 18 February 2021).
- Hubbell, J.H.; Seltzer, S.M. Tables of X-Ray Mass Attenuation Coefficients and Mass Energy-Absorption Coefficients 1 keV to 20 MeV for Elements Z= 1 to 92 and 48 Additional Substances of Dosimetric Interest. Available online: https://www.nist.gov/pml/x-ray-mass-attenuation-coefficients (accessed on 19 August 2020).
- Allison, J.; Amako, K.; Apostolakis, J.; Arce, P.; Asai, M.; Aso, T.; Bagli, E.; Bagulya, A.; Banerjee, S.; Barrand, G.; et al. Recent developments in Geant4. Nucl. Instrum. Methods Phys. Res. 2016, 835, 186–225. [Google Scholar] [CrossRef]
- Xstrahl®: Superficial and Orthovoltage X-Ray Systems. Available online: https://xstrahl.com/medical-home/ (accessed on 18 February 2021).

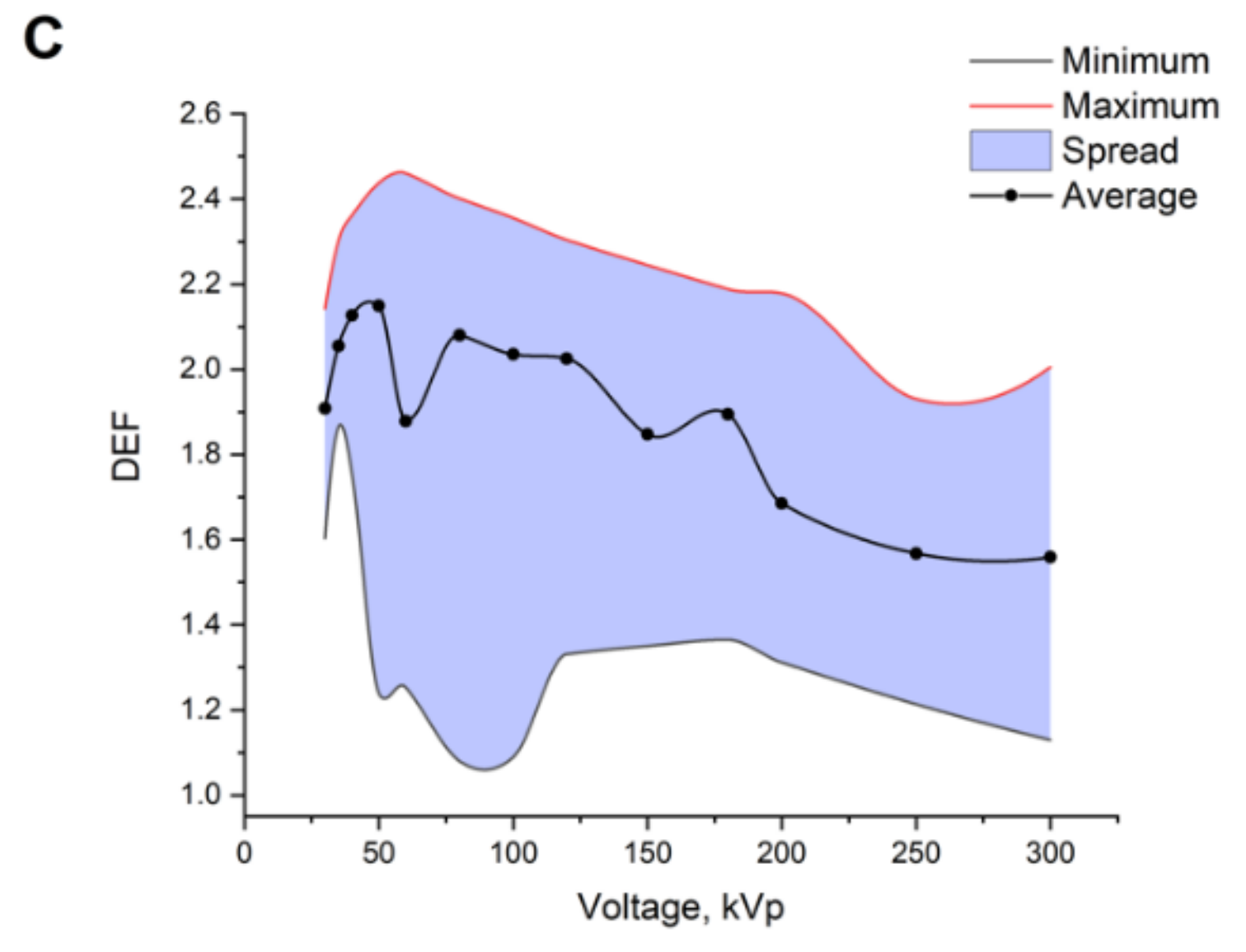
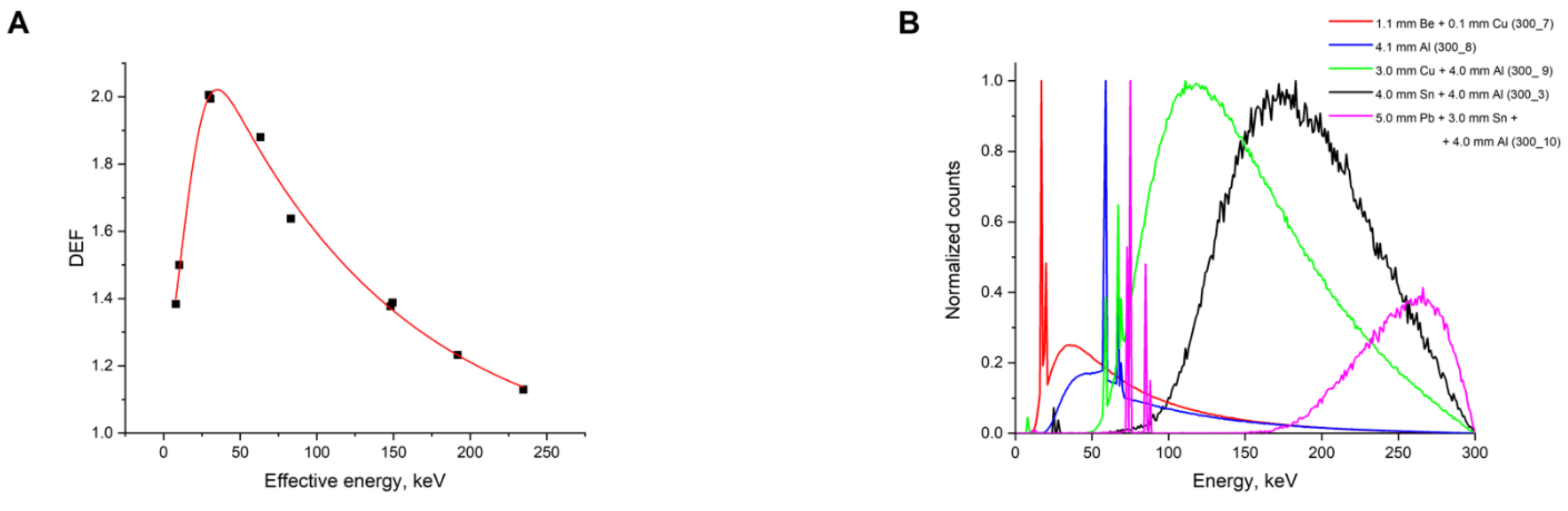
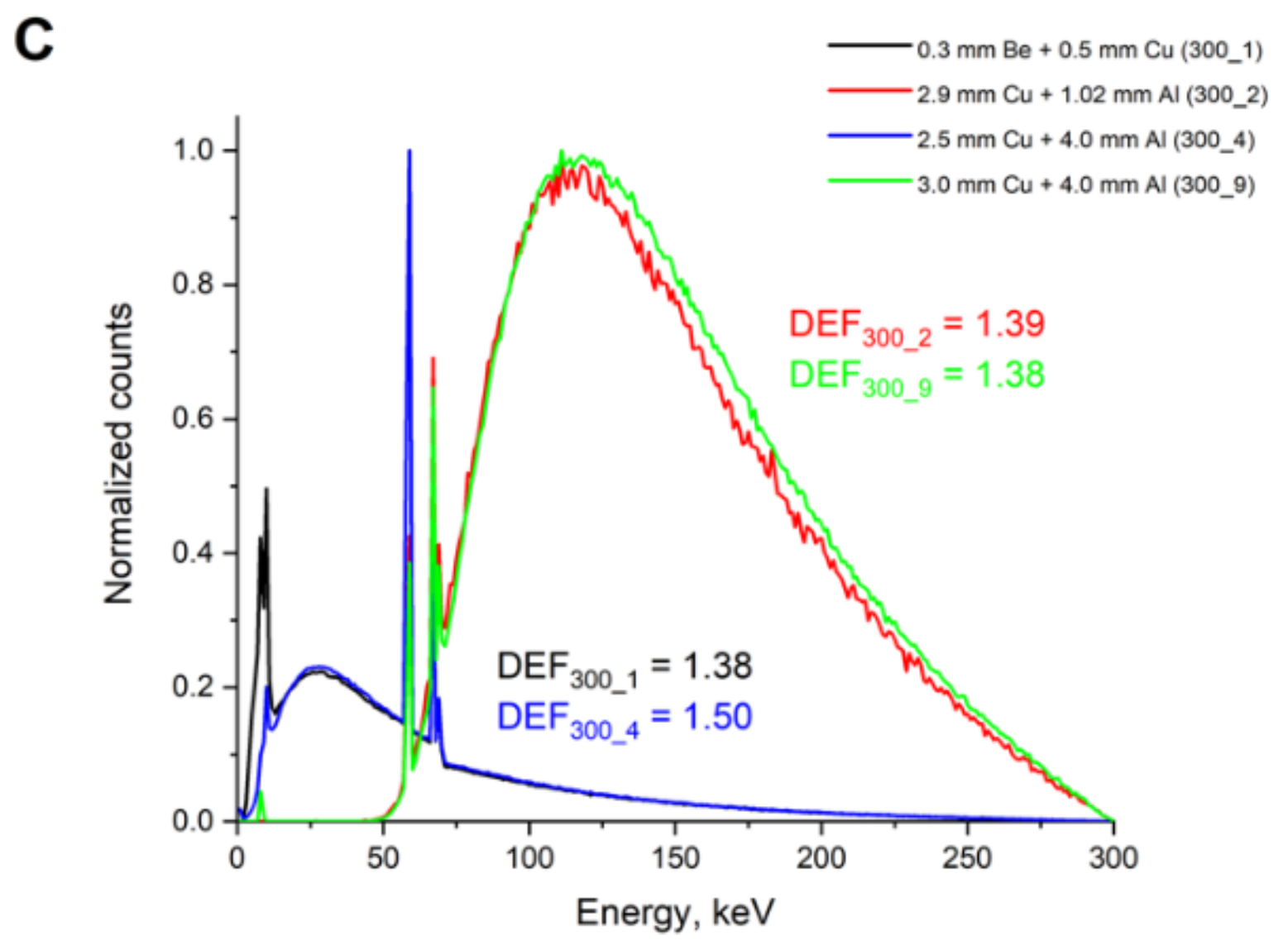



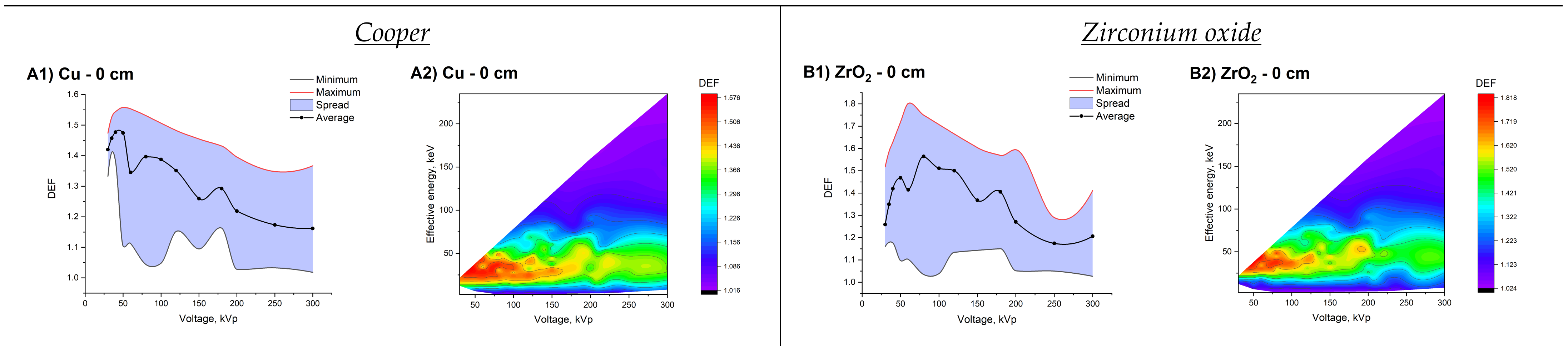



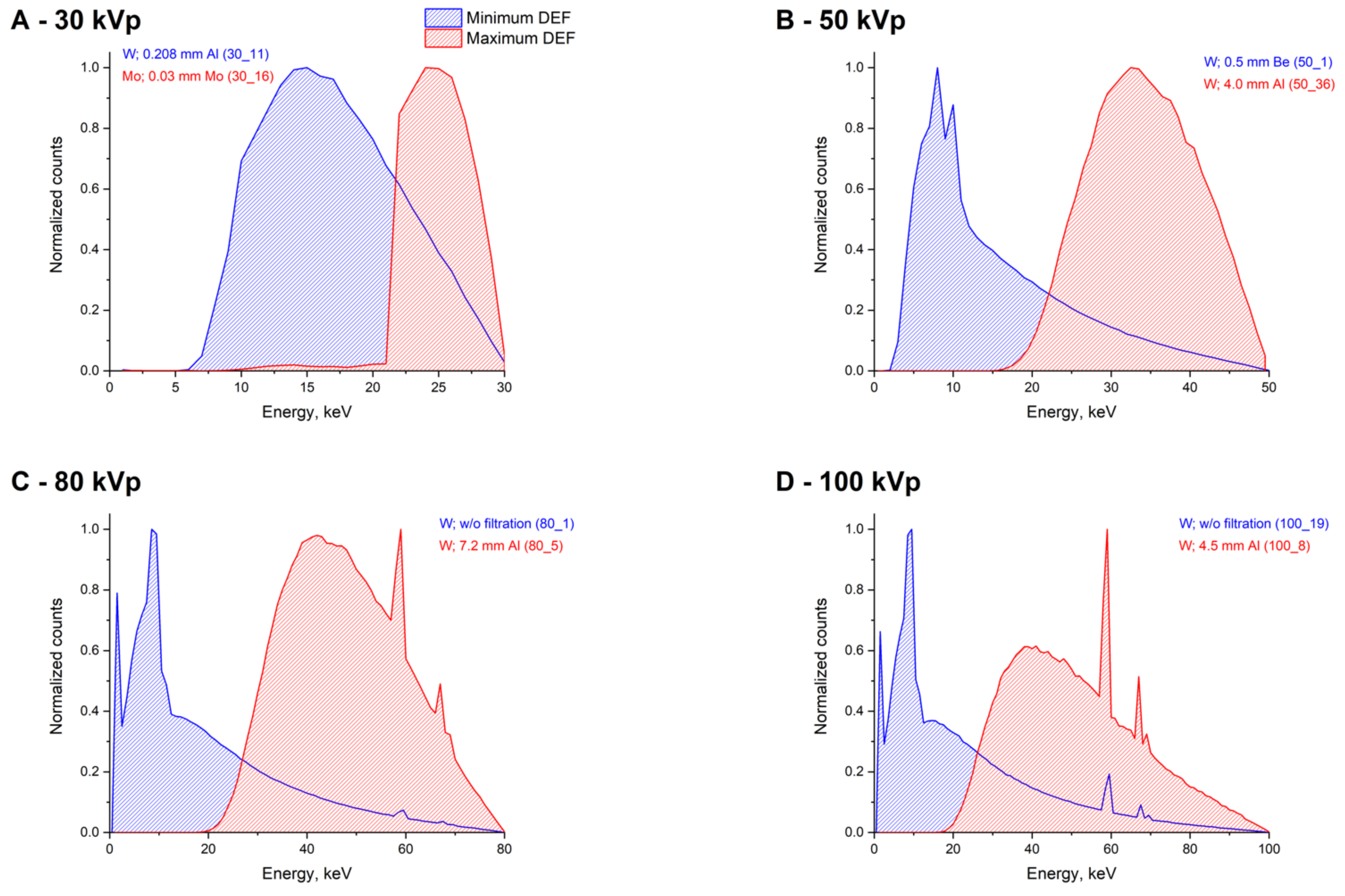
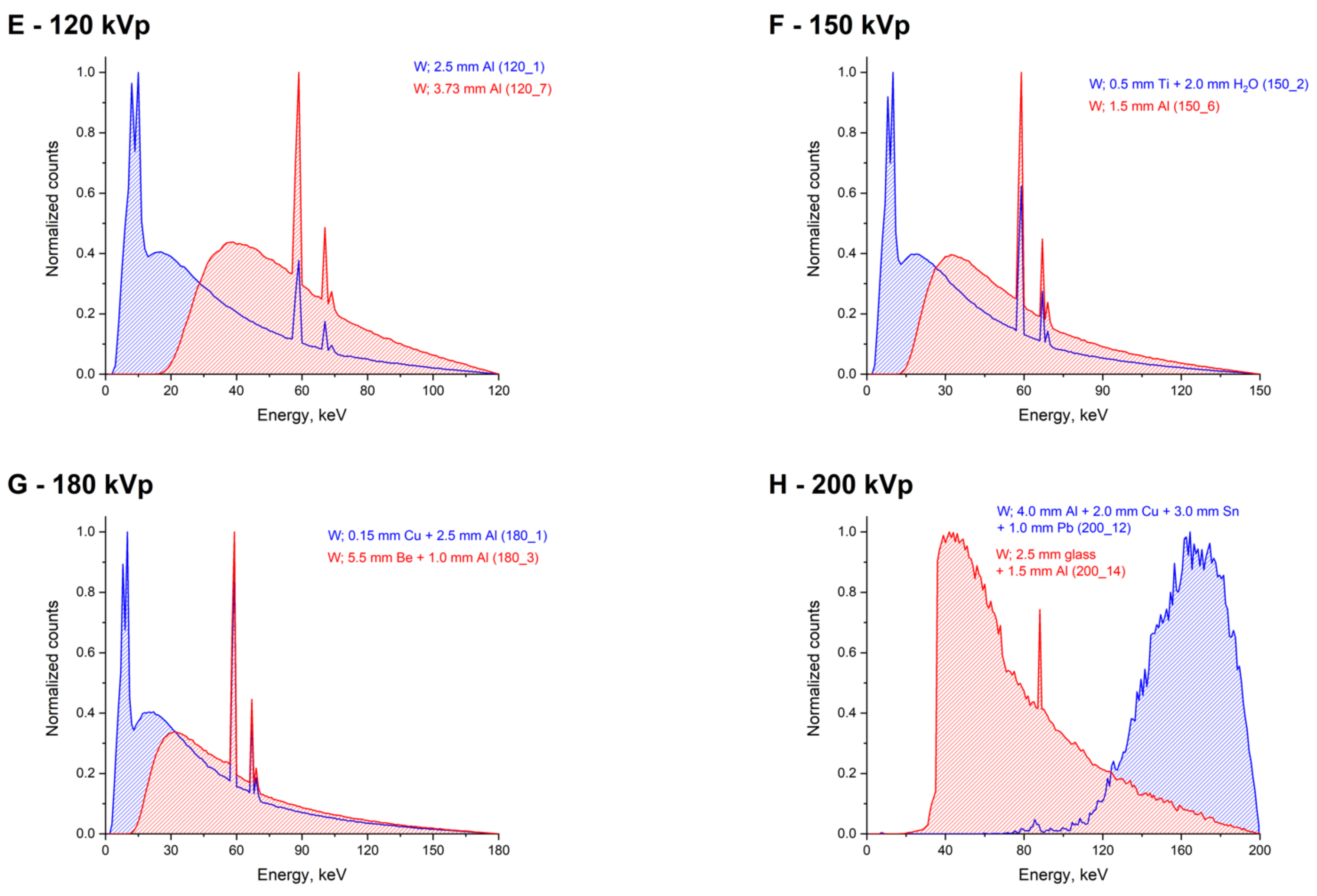
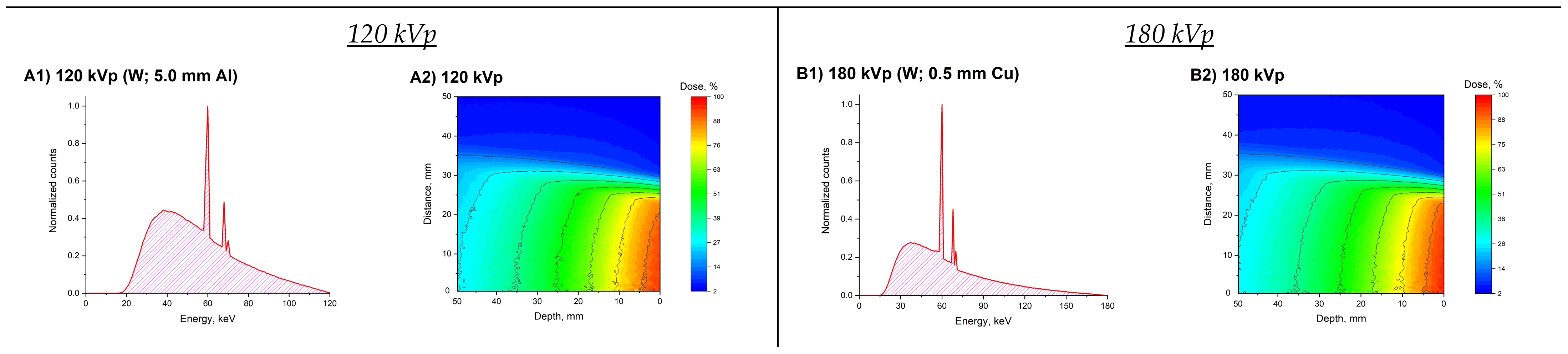
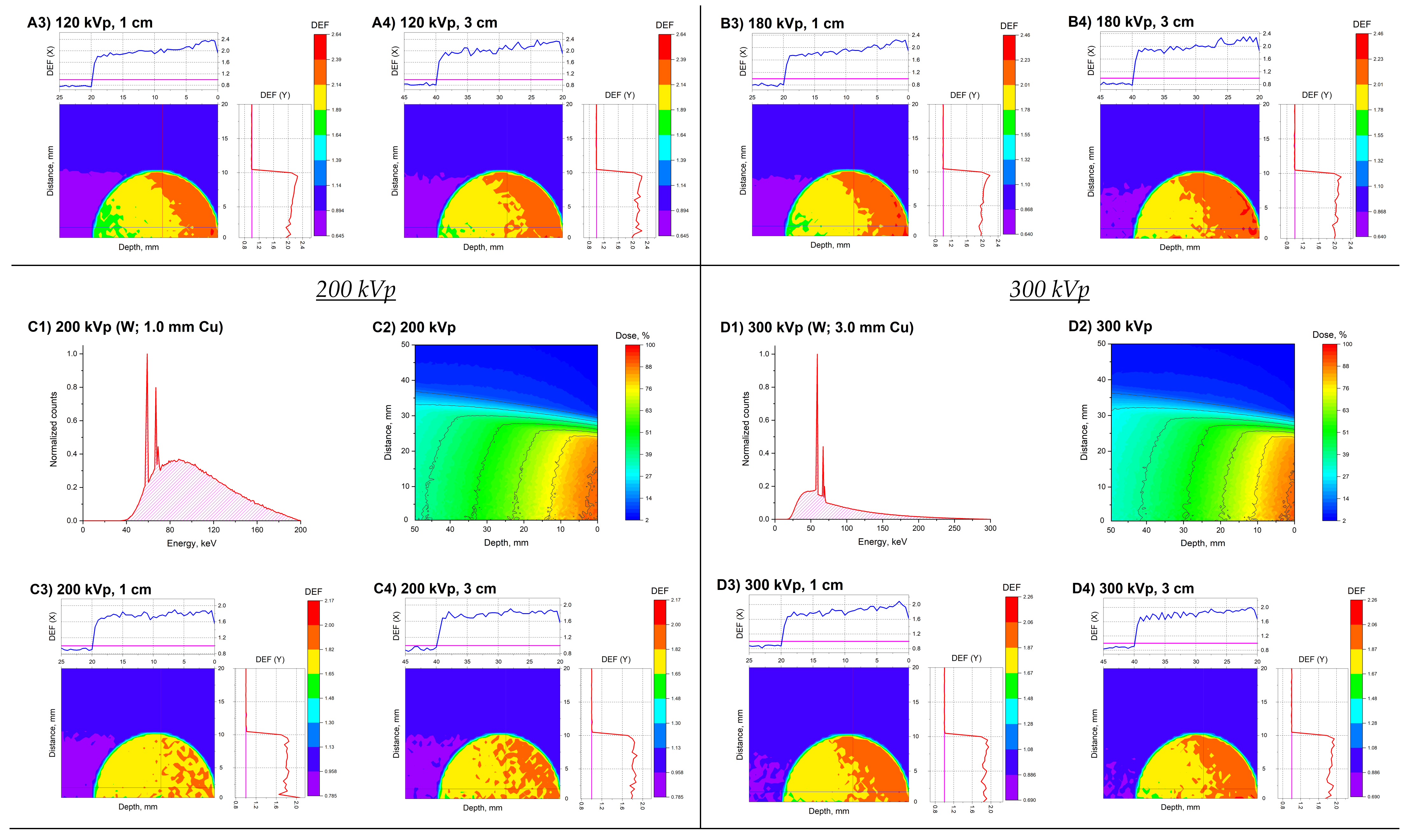
| Spectrum Number | Anode Material | Filtration System | Average Energy, keV | Effective Energy, keV | DEF |
|---|---|---|---|---|---|
| 300_1 (5) | W | 0.3 mm Be + 0.5 mm Cu | 62.24 | 7.98 | 1.38 |
| 300_2 (73) | W | 2.9 mm Cu + 1.02 mm Al | 144.93 | 149.34 | 1.39 |
| 300_3 (74) | W | 4.0 mm Sn + 4.0 mm Al | 186.84 | 191.80 | 1.23 |
| 300_4 (119) | W | 2.5 mm Cu + 4.0 mm Al | 66.94 | 10.25 | 1.50 |
| 300_5 (122) | W | 6.5 mm Sn + 4.0 mm Al | 75.09 | 30.59 | 1.99 |
| 300_6 (124) | W | 4.1 mm Be + 0.4 mm Cu | 102.77 | 83.06 | 1.64 |
| 300_7 (126) | W | 1.1 mm Be + 0.1 mm Cu | 72.25 | 29.56 | 2.01 |
| 300_8 (129) | W | 4.1 mm Al | 85.79 | 63.21 | 1.88 |
| 300_9 (254) | W | 3.0 mm Cu + 4.0 mm Al | 147.06 | 148.12 | 1.38 |
| 300_10 (260) | W | 5.0 mm Pb + 3.0 mm Sn + 4.0 mm Al | 235.62 | 234.76 | 1.13 |
| Cu | ZrO2 | Ag | CeO2 | Gd2O3 | Tm2O3 | HfO2 | Bi2O3 | Au | |
|---|---|---|---|---|---|---|---|---|---|
| At the surface | |||||||||
| DEFmin | 1.02 | 1.03 | 1.05 | 1.06 | 1.07 | 1.07 | 1.06 | 1.08 | 1.08 |
| DEFav | 1.36 | 1.39 | 1.56 | 1.51 | 1.61 | 1.68 | 1.69 | 1.91 | 1.95 |
| DEFmax | 1.56 | 1.80 | 2.38 | 2.07 | 2.06 | 1.95 | 1.96 | 2.49 | 2.46 |
| At 0.4 cm depth | |||||||||
| DEFmin | 1.02 | 1.03 | 1.05 | 1.06 | 1.08 | 1.10 | 1.10 | 1.13 | 1.13 |
| DEFav | 1.42 | 1.46 | 1.64 | 1.57 | 1.68 | 1.77 | 1.79 | 2.05 | 2.09 |
| DEFmax | 1.57 | 1.82 | 2.40 | 2.20 | 2.17 | 2.06 | 1.98 | 2.53 | 2.50 |
| At 1.0 cm depth | |||||||||
| DEFmin | 1.02 | 1.03 | 1.05 | 1.06 | 1.08 | 1.09 | 1.10 | 1.12 | 1.13 |
| DEFav | 1.43 | 1.49 | 1.69 | 1.60 | 1.70 | 1.79 | 1.82 | 2.11 | 2.14 |
| DEFmax | 1.57 | 1.82 | 2.40 | 2.21 | 2.18 | 2.06 | 1.98 | 2.53 | 2.51 |
| At 2.0 cm depth | |||||||||
| DEFmin | 1.02 | 1.03 | 1.05 | 1.06 | 1.08 | 1.09 | 1.10 | 1.12 | 1.13 |
| DEFav | 1.43 | 1.53 | 1.74 | 1.62 | 1.72 | 1.81 | 1.83 | 2.15 | 2.17 |
| DEFmax | 1.58 | 1.82 | 2.40 | 2.21 | 2.18 | 2.06 | 1.99 | 2.53 | 2.50 |
| Cu | ZrO2 | Ag | CeO2 | Gd2O3 | Tm2O3 | HfO2 | Bi2O3 | Au | |
|---|---|---|---|---|---|---|---|---|---|
| At the surface | |||||||||
| <1.2 | 53 | 50 | 18 | 15 | 8 | 12 | 13 | 4 | 4 |
| 1.2–1.4 | 55 | 71 | 75 | 48 | 32 | 28 | 27 | 35 | 34 |
| 1.4–1.6 | 129 | 73 | 48 | 98 | 60 | 10 | 11 | 4 | 3 |
| 1.6–1.8 | - | 42 | 37 | 46 | 98 | 110 | 104 | 33 | 18 |
| 1.8–2.0 | - | 1 | 30 | 25 | 37 | 77 | 82 | 58 | 54 |
| 2.0–2.2 | - | - | 24 | 5 | 2 | - | - | 45 | 65 |
| >2.2 | - | - | 5 | - | - | - | - | 58 | 59 |
| At 0.4 cm depth | |||||||||
| <1.2 | 21 | 13 | 8 | 4 | 4 | 3 | 3 | 1 | 1 |
| 1.2–1.4 | 45 | 82 | 44 | 11 | 5 | 6 | 6 | 7 | 6 |
| 1.4–1.6 | 171 | 83 | 77 | 146 | 52 | 4 | 6 | 3 | 3 |
| 1.6–1.8 | - | 55 | 41 | 38 | 128 | 123 | 101 | 18 | 9 |
| 1.8–2.0 | - | 4 | 29 | 31 | 43 | 99 | 121 | 77 | 66 |
| 2.0–2.2 | - | - | 29 | 7 | 5 | 2 | - | 57 | 68 |
| >2.2 | - | - | 9 | - | - | - | - | 74 | 84 |
| At 1.0 cm depth | |||||||||
| <1.2 | 21 | 12 | 8 | 4 | 4 | 3 | 3 | 1 | 1 |
| 1.2–1.4 | 46 | 47 | 32 | 7 | 5 | 6 | 6 | 7 | 6 |
| 1.4–1.6 | 170 | 113 | 58 | 130 | 23 | 4 | 6 | 3 | 3 |
| 1.6–1.8 | - | 61 | 67 | 54 | 154 | 95 | 58 | 12 | 9 |
| 1.8–2.0 | - | 4 | 31 | 35 | 46 | 127 | 164 | 38 | 28 |
| 2.0–2.2 | - | - | 32 | 7 | 5 | 2 | - | 84 | 80 |
| >2.2 | - | - | 9 | - | - | - | - | 92 | 110 |
| At 2.0 cm depth | |||||||||
| <1.2 | 21 | 12 | 8 | 4 | 4 | 3 | 3 | 1 | 1 |
| 1.2–1.4 | 50 | 35 | 27 | 7 | 5 | 6 | 6 | 7 | 7 |
| 1.4–1.6 | 166 | 105 | 38 | 112 | 13 | 4 | 6 | 5 | 2 |
| 1.6–1.8 | - | 81 | 62 | 70 | 159 | 67 | 46 | 11 | 9 |
| 1.8–2.0 | - | 4 | 57 | 35 | 51 | 155 | 176 | 27 | 30 |
| 2.0–2.2 | - | - | 36 | 9 | 5 | 2 | - | 55 | 46 |
| >2.2 | - | - | 9 | - | - | - | - | 131 | 142 |
| Cu | ZrO2 | Ag | CeO2 | Gd2O3 | Tm2O3 | HfO2 | Bi2O3 | Au | |
|---|---|---|---|---|---|---|---|---|---|
| Cu | 55–87% | 72–85% | 61–67% | 100% | 100% | 100% | 100% | 100% | |
| ZrO2 | 13–45% | 85–91% | 63–82% | 96–99% | 100% | 100% | 100% | 100% | |
| Ag | 15–28% | 9–15% | 23–47% | 46–70% | 67–76% | 68–74% | 99% | 99% | |
| CeO2 | 33–39% | 18–37% | 53–73% | 95% | 93–94% | 74–78% | 98% | 99% | |
| Gd2O3 | 0% | 1–4% | 30–54% | 5% | 73–87% | 72–85% | 94% | 98% | |
| Tm2O3 | 0% | 0% | 24–33% | 6–7% | 13–27% | 64–78% | 95–96% | 98% | |
| HfO2 | 0% | 0% | 26–32% | 12–16% | 15–28% | 22–36% | 97–98% | 100% | |
| Bi2O3 | 0% | 0% | 1% | 2% | 6% | 4–5% | 2–3% | 81–87% | |
| Au | 0% | 0% | 1% | 1% | 2% | 2% | 0% | 13–19% |
| Number | Formula | Mass Composition | Atomic Number (Z) | Effective Atomic Number (Z) |
|---|---|---|---|---|
| 1 | Cu | Cu: 100% | ZCu = 29 | 29 |
| 2 | ZrO2 | Zr: 74% O: 26% | ZZr = 40 ZO = 8 | 36.34 |
| 3 | Ag | Ag: 100% | ZAg = 47 | 47 |
| 4 | CeO2 | Ce: 81.4% O: 18.6% | ZCe = 58 ZO = 8 | 59.64 |
| 5 | Gd2O3 | Gd: 86.8% O: 13.2% | ZGd = 64 ZO = 8 | 62.28 |
| 6 | Tm2O3 | Tm: 87.6% O: 12.4% | ZTm = 69 ZO = 8 | 67.28 |
| 7 | HfO2 | Hf: 84.8% O: 15.2% | ZHf = 72 ZO = 8 | 67.99 |
| 8 | Ta2O5 | Ta: 81.9% O: 18.1% | ZTa = 73 ZO = 8 | 68.12 |
| 9 | Bi2O3 | Bi: 89.7% O: 10.3% | ZBi = 83 ZO = 8 | 81.26 |
| 10 | Pt | Pt: 100% | ZPt = 78 | 78 |
| 11 | Au | Au: 100% | ZAu = 79 | 79 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kolyvanova, M.A.; Belousov, A.V.; Krusanov, G.A.; Isagulieva, A.K.; Morozov, K.V.; Kartseva, M.E.; Salpagarov, M.H.; Krivoshapkin, P.V.; Dement’eva, O.V.; Rudoy, V.M.; et al. Impact of the Spectral Composition of Kilovoltage X-rays on High-Z Nanoparticle-Assisted Dose Enhancement. Int. J. Mol. Sci. 2021, 22, 6030. https://doi.org/10.3390/ijms22116030
Kolyvanova MA, Belousov AV, Krusanov GA, Isagulieva AK, Morozov KV, Kartseva ME, Salpagarov MH, Krivoshapkin PV, Dement’eva OV, Rudoy VM, et al. Impact of the Spectral Composition of Kilovoltage X-rays on High-Z Nanoparticle-Assisted Dose Enhancement. International Journal of Molecular Sciences. 2021; 22(11):6030. https://doi.org/10.3390/ijms22116030
Chicago/Turabian StyleKolyvanova, Maria A., Alexandr V. Belousov, Grigorii A. Krusanov, Alexandra K. Isagulieva, Kirill V. Morozov, Maria E. Kartseva, Magomet H. Salpagarov, Pavel V. Krivoshapkin, Olga V. Dement’eva, Victor M. Rudoy, and et al. 2021. "Impact of the Spectral Composition of Kilovoltage X-rays on High-Z Nanoparticle-Assisted Dose Enhancement" International Journal of Molecular Sciences 22, no. 11: 6030. https://doi.org/10.3390/ijms22116030
APA StyleKolyvanova, M. A., Belousov, A. V., Krusanov, G. A., Isagulieva, A. K., Morozov, K. V., Kartseva, M. E., Salpagarov, M. H., Krivoshapkin, P. V., Dement’eva, O. V., Rudoy, V. M., & Morozov, V. N. (2021). Impact of the Spectral Composition of Kilovoltage X-rays on High-Z Nanoparticle-Assisted Dose Enhancement. International Journal of Molecular Sciences, 22(11), 6030. https://doi.org/10.3390/ijms22116030






