Pattern Formation upon Evaporation of Sessile Droplets of Polyelectrolyte/Surfactant Mixtures on Silicon Wafers
Abstract
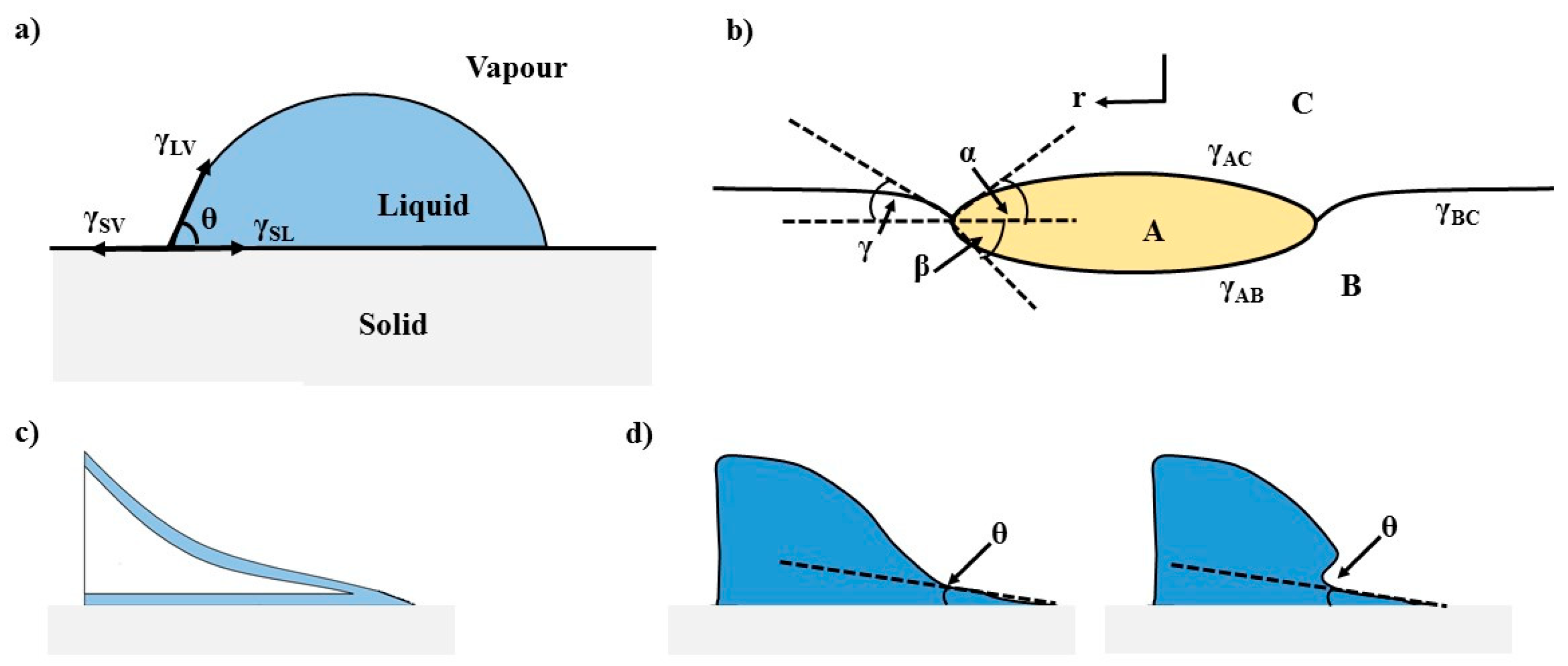
1. Introduction
2. Results
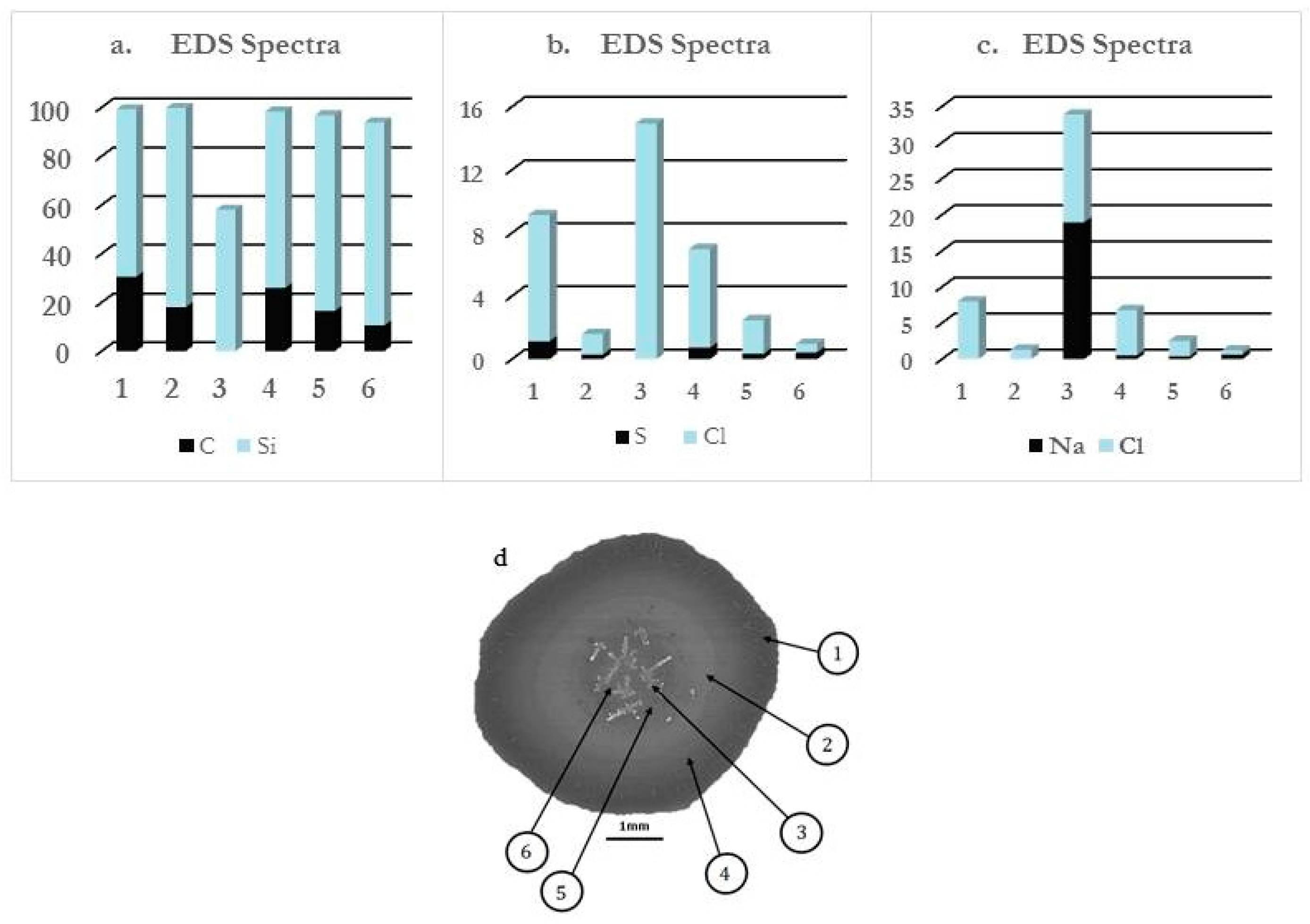
2.1. SImages
- Region 1 is the perimeter of the pattern, i.e., the coffee ring which appears in all of the deposits, in agreement with those reported for dried droplets of other complex mixtures [43,44]. The obtained results suggest that the thickness of the ring is independent of the surfactant concentration, which might be ascribed to the similar composition of the ring in all cases. This may be understood considering that the formation of the ring is associated with the presence of PDADMAC in the mixture which presents a constant concentration (5 g/L). In addition, cracks, associated with the release of internal stresses which accumulate during the drying process, are observed in the ring areas which are more obvious when PDADMAC–SLMT deposits are considered.
- Region 2 is the secondary area of the deposits which is made up of crystal-like structures distributed uniformly within the droplet. These structures are NaCl crystals formed as a result of the release of counterions during the binding of the anionic surfactant to the polycation. The formation of this salt crystals agrees with the picture expected from the binding isotherm reported in our previous publication [40], with their deposition and growth being probably related to an anisotropy of surface tension between the substrate and the droplet mixture [45]. This may lead to a concentration gradient that favors the growth of the salt crystals, with such growth being commonly oriented towards the external polymeric ring. The results show that the salt crystals start to be formed from the edge of the pattern, appearing uniformly distributed close to the center of the droplets. It should be stressed the studied mixtures do not contain inorganic electrolytes, and hence the salt crystals can be only ascribed to the release of counterions occurring during the association between the PDADMAC and the surfactant. This contrasts with the salt crystal found in deposits obtained upon evaporation of other complex mixtures in which inorganic electrolytes were initially added [45,46].
- Region 3 is located at the center of the obtained deposits, emerging as an accumulation of crystal structures.
2.2. Governing Mechanism for Crystal Formation and Crystal Size Variation with Surfactant Concentration
3. Materials and Methods
3.1. Chemicals
3.2. Preparation of the Polyelectrolyte–Surfactant Solutions
3.3. Preparation of the Silicon Wafer Surface
3.4. Scanning Electron Microscope
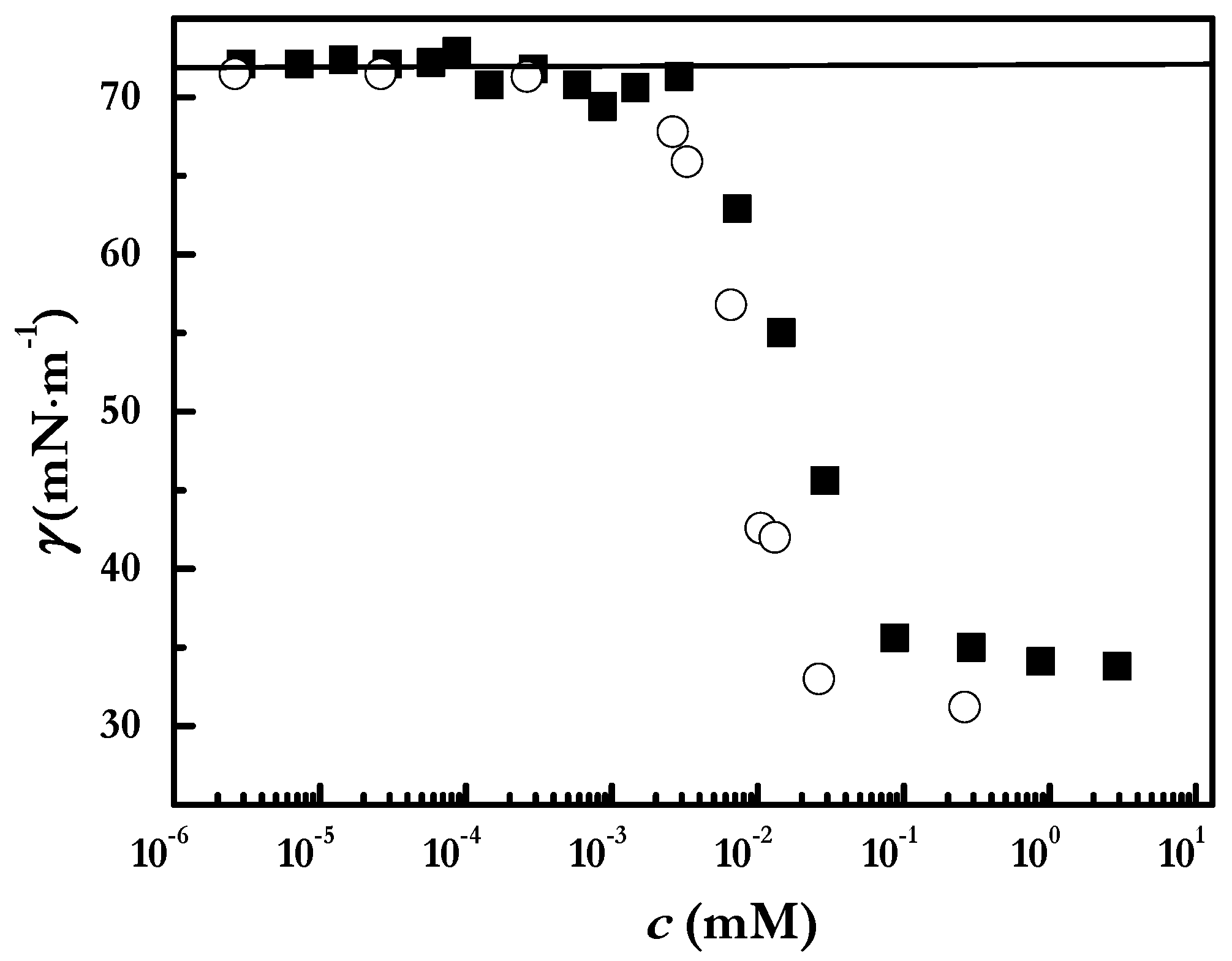
3.5. Surface Tension Measurements
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Γ | equilibrium interfacial tension |
| γ0 | surface tension of the water |
| γsv | interfacial tension of the solid/vapor interface |
| γsl | interfacial tension of the solid/liquid interface |
| γlv | interfacial tension of the liquid/vapor interface |
| Θ | equilibrium contact angle |
| θa | advancing contact angle |
| θr | receding contact angle |
| Δθ | contact angle hysteresis |
| C | surfactant concentration |
| EDS | energy-dispersive X-ray spectrometer |
| Mw | weight average molecular mass |
| PDADMAC | poly(diallyldimethylammonium chloride) |
| SEM | scanning electron microscopy |
| SLES | sodium laureth sulfate |
| SLMT | sodium N-lauroyl-N-methyltaurate |
| T | time |
| TPCL | three-phase contact line |
| V | instantaneous volume of the droplet |
| V0 | initial volume of the droplet |
References
- Starov, V.M.; Velarde, M.G. Wetting and Spreading Dynamics; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- Butt, H.-J.; Kappl, M. Surface and Interfacial Forces; Wiley-VCH: Berlin, Germany, 2010. [Google Scholar]
- Lyklema, J. (Ed.) Fundamentals of Interface and Colloid Science: Solid-Liquid Interfaces; Academic Press: San Diego, CA, USA, 1995; Volume 2. [Google Scholar]
- Semenov, S.; Trybala, A.; Rubio, R.G.; Kovalchuk, N.; Starov, V.; Velarde, M.G. Simultaneous spreading and evaporation: Recent developments. Adv. Colloid Interface Sci. 2014, 206, 382–398. [Google Scholar] [CrossRef]
- Huang, Q.; Zhang, Z.; Liu, Z.; Zhang, F.; Cheng, G.; Ding, J. Pinning effect in droplet self-driving and its reduction mechanism by monolayer graphene. Appl. Surf. Sci. 2021, 542, 148666. [Google Scholar] [CrossRef]
- Akanno, A.; Perrin, L.; Guzmán, E.; Llamas, S.; Starov, V.M.; Ortega, F.; Rubio, R.G.; Velarde, M.G. Evaporation of Sessile Droplets of Polyelectrolyte/Surfactant Mixtures on Silicon Wafers. Colloids Interfaces 2021, 5, 12. [Google Scholar] [CrossRef]
- Pham, T.; Kumar, S. Drying of Droplets of Colloidal Suspensions on Rough Substrates. Langmuir 2017, 33, 10061–10076. [Google Scholar] [CrossRef]
- Larson, R.G. Transport and deposition patterns in drying sessile droplets. AIChE J. 2014, 60, 1538–1571. [Google Scholar] [CrossRef]
- Parsa, M.; Harmand, S.; Sefiane, K. Mechanisms of pattern formation from dried sessile drops. Adv. Colloid Interface Sci. 2018, 254, 22–47. [Google Scholar] [CrossRef] [PubMed]
- Still, T.; Yunker, P.J.; Yodh, A.G. Surfactant-Induced Marangoni Eddies Alter the Coffee-Rings of Evaporating Colloidal Drops. Langmuir 2012, 28, 4984–4988. [Google Scholar] [CrossRef]
- Al-Milaji, K.N.; Zhao, H. New Perspective of Mitigating the Coffee-Ring Effect: Interfacial Assembly. J. Phys. Chem. C 2019, 123, 12029–12041. [Google Scholar] [CrossRef]
- Mampallil, D.; Eral, H.B. A review on suppression and utilization of the coffee-ring effect. Adv. Colloid Interface Sci. 2018, 252, 38–54. [Google Scholar] [CrossRef]
- Guo, H.; Fuchs, P.; Casdorff, K.; Michen, B.; Chanana, M.; Hagendorfer, H.; Romanyuk, Y.E.; Burgert, I. Bio-Inspired Superhydrophobic and Omniphobic Wood Surfaces. Adv. Mat. Interfaces 2017, 4, 1600289. [Google Scholar] [CrossRef]
- Mondal, R.; Basavaraj, M.G. Influence of the drying configuration on the patterning of ellipsoids—Concentric rings and concentric cracks. Phys. Chem. Chem. Phys. 2019, 21, 20045–20054. [Google Scholar] [CrossRef] [PubMed]
- Willmer, D.; Baldwin, K.A.; Kwartnik, C.; Fairhurst, D.J. Growth of solid conical structures during multistage drying of sessile poly(ethylene oxide) droplets. Phys. Chem. Chem. Phys. 2010, 12, 3998–4004. [Google Scholar] [CrossRef]
- Maheshwari, S.; Zhang, L.; Zhu, Y.; Chang, H.-C. Coupling between Precipitation and Contact-Line Dynamics: Multiring Stains and Stick-Slip Motion. Phys. Rev. Lett. 2008, 100, 044503. [Google Scholar] [CrossRef]
- Baldwin, K.A.; Roest, S.; Fairhurst, D.J.; Sefiane, K.; Shanahan, M.E.R. Monolith formation and ring-stain suppression in low-pressure evaporation of poly(ethylene oxide) droplets. J. Fluid Mech. 2012, 695, 321–329. [Google Scholar] [CrossRef]
- Orejon, D.; Sefiane, K.; Shanahan, M.E.R. Stick–Slip of Evaporating Droplets: Substrate Hydrophobicity and Nanoparticle Concentration. Langmuir 2011, 27, 12834–12843. [Google Scholar] [CrossRef]
- Bhardwaj, R.; Fang, X.; Attinger, D. Pattern formation during the evaporation of a colloidal nanoliter drop: A numerical and experimental study. New J. Phys. 2009, 11, 075020. [Google Scholar] [CrossRef]
- Keseroğlu, K.; Çulha, M. Assembly of nanoparticles at the contact line of a drying droplet under the influence of a dipped tip. J. Colloid Interface Sci. 2011, 360, 8–14. [Google Scholar] [CrossRef]
- Maillard, M.; Motte, L.; Pileni, M.-P. Rings and Hexagons Made of Nanocrystals. Adv. Mat. 2001, 13, 200–204. [Google Scholar] [CrossRef]
- Majumder, M.; Rendall, C.; Li, M.; Behabtu, N.; Eukel, J.A.; Hauge, R.H.; Schmidt, H.K.; Pasquali, M. Insights into the physics of spray coating of SWNT films. Chem. Eng. Sci. 2010, 65, 2000–2008. [Google Scholar] [CrossRef]
- Chung, S.; Ul Karim, M.A.; Spencer, M.; Kwon, H.-J.; Grigoropoulos, C.P.; Alon, E.; Subramanian, V. Exploitation of the coffee-ring effect to realize mechanically enhanced inkjet-printed microelectromechanical relays with U-bar-shaped cantilevers. Appl. Phys. Lett. 2014, 105, 261901. [Google Scholar] [CrossRef]
- Sefiane, K. On the Formation of Regular Patterns from Drying Droplets and Their Potential Use for Bio-Medical Applications. J. Bionic Eng. 2010, 7, S82–S93. [Google Scholar] [CrossRef]
- Wen, J.T.; Ho, C.-M.; Lillehoj, P.B. Coffee Ring Aptasensor for Rapid Protein Detection. Langmuir 2013, 29, 8440–8446. [Google Scholar] [CrossRef]
- Kong, Y.L.; Tamargo, I.A.; Kim, H.; Johnson, B.N.; Gupta, M.K.; Koh, T.-W.; Chin, H.-A.; Steingart, D.A.; Rand, B.P.; McAlpine, M.C. 3D Printed Quantum Dot Light-Emitting Diodes. Nano Lett. 2014, 14, 7017–7023. [Google Scholar] [CrossRef]
- Wu, J.; Wang, R.; Yu, H.; Li, G.; Xu, K.; Tien, N.C.; Roberts, R.C.; Li, D. Inkjet-printed microelectrodes on PDMS as biosensors for functionalized microfluidic systems. Lab Chip 2015, 15, 690–695. [Google Scholar] [CrossRef]
- Fang, X.; Li, B.; Petersen, E.; Seo, Y.-S.; Samuilov, V.A.; Chen, Y.; Sokolov, J.C.; Shew, C.-Y.; Rafailovich, M.H. Drying of DNA Droplets. Langmuir 2006, 22, 6308–6312. [Google Scholar] [CrossRef]
- Jin, H.; Qian, J.; Zhou, L.; Yuan, J.; Huang, H.; Wang, Y.; Tang, W.M.; Chan, H.L.W. Suppressing the Coffee-Ring Effect in Semitransparent MnO2 Film for a High-Performance Solar-Powered Energy Storage Window. ACS Appl. Mat. Interfaces 2016, 8, 9088–9096. [Google Scholar] [CrossRef]
- Carreón, Y.J.P.; Ríos-Ramírez, M.; Moctezuma, R.E.; González-Gutiérrez, J. Texture analysis of protein deposits produced by droplet evaporation. Sci. Rep. 2018, 8, 9580. [Google Scholar] [CrossRef]
- Yakhno, T.A.; Yakhno, V.G.; Sanin, A.G.; Sanina, O.A.; Pelyushenko, A.S.; Egorova, N.A.; Terentiev, I.G.; Smetanina, S.V.; Korochkina, O.V.; Yashukova, E.V. The informative-capacity phenomenon of drying drops. IEEE Eng. Med. Biol. Mag. 2005, 24, 96–104. [Google Scholar] [CrossRef]
- Rapis, E. A change in the physical state of a nonequilibrium blood plasma protein film in patients with carcinoma. Tech. Phys. 2002, 47, 510–512. [Google Scholar] [CrossRef]
- Layani, M.; Gruchko, M.; Milo, O.; Balberg, I.; Azulay, D.; Magdassi, S. Transparent Conductive Coatings by Printing Coffee Ring Arrays Obtained at Room Temperature. ACS Nano 2009, 3, 3537–3542. [Google Scholar] [CrossRef]
- Marsico, A.L.M.; Duncan, B.; Landis, R.F.; Tonga, G.Y.; Rotello, V.M.; Vachet, R.W. Enhanced Laser Desorption/Ionization Mass Spectrometric Detection of Biomolecules Using Gold Nanoparticles, Matrix, and the Coffee Ring Effect. Anal. Chem. 2017, 89, 3009–3014. [Google Scholar] [CrossRef]
- Llamas, S.; Guzmán, E.; Ortega, F.; Baghdadli, N.; Cazeneuve, C.; Rubio, R.G.; Luengo, G.S. Adsorption of polyelectrolytes and polyelectrolytes-surfactant mixtures at surfaces: A physico-chemical approach to a cosmetic challenge. Adv. Colloid Interface Sci. 2015, 222, 461–487. [Google Scholar] [CrossRef] [PubMed]
- Fernández-Peña, L.; Guzmán, E.; Leonforte, F.; Serrano-Pueyo, A.; Regulski, K.; Tournier-Couturier, L.; Ortega, F.; Rubio, R.G.; Luengo, G.S. Effect of molecular structure of eco-friendly glycolipid biosurfactants on the adsorption of hair-care conditioning polymers. Colloids Surf. B 2020, 185, 110578. [Google Scholar] [CrossRef]
- Lindman, B.; Antunes, F.; Aidarova, S.; Miguel, M.; Nylander, T. Polyelectrolyte-surfactant association—From fundamentals to applications. Colloid J. 2014, 76, 585–594. [Google Scholar] [CrossRef]
- Fernández-Peña, L.; Guzmán, E. Physicochemical Aspects of the Performance of Hair-Conditioning Formulations. Cosmetics 2020, 7, 26. [Google Scholar] [CrossRef]
- Llamas, S.; Fernández-Peña, L.; Akanno, A.; Guzmán, E.; Ortega, V.; Ortega, F.; Csaky, A.G.; Campbell, R.A.; Rubio, R.G. Towards understanding the behavior of polyelectrolyte–surfactant mixtures at the water/vapor interface closer to technologically-relevant conditions. Phys. Chem. Chem. Phys. 2018, 20, 1395–1407. [Google Scholar] [CrossRef]
- Guzmán, E.; Fernández-Peña, L.; Akanno, A.; Llamas, S.; Ortega, F.; Rubio, G.R. Two Different Scenarios for the Equilibration of Polycation—Anionic Solutions at Water–Vapor Interfaces. Coatings 2019, 9, 438. [Google Scholar] [CrossRef]
- Llamas, S.; Guzmán, E.; Baghdadli, N.; Ortega, F.; Cazeneuve, C.; Rubio, R.G.; Luengo, G.S. Adsorption of poly(diallyldimethylammonium chloride)—Sodium methyl-cocoyl-taurate complexes onto solid surfaces. Colloids Surf. A 2016, 505, 150–157. [Google Scholar] [CrossRef]
- Senses, E.; Black, M.; Cunningham, T.; Sukhishvili, S.A.; Akcora, P. Spatial ordering of colloids in a drying aqueous polymer droplet. Langmuir 2013, 29, 2588–2594. [Google Scholar] [CrossRef]
- Tarasevich, Y.Y.; Pravoslavnova, D. Drying of a multicomponent solution drop on a solid substrate: Qualitative analysis. Tech. Phys. 2007, 52, 159–163. [Google Scholar] [CrossRef]
- Gorr, H.M.; Zueger, J.M.; McAdams, D.R.; Barnard, J.A. Salt-induced pattern formation in evaporating droplets of lysozyme solutions. Colloids Surf. B 2013, 103, 59–66. [Google Scholar] [CrossRef] [PubMed]
- Kaya, D.; Belyi, V.; Muthukumar, M. Pattern formation in drying droplets of polyelectrolyte and salt. J. Chem. Phys. 2010, 133, 114905. [Google Scholar] [CrossRef]
- Chen, G.; Mohamed, J.G. Complex protein patterns formation via salt-induced self-assembly and droplet evaporation. Eur. Phys. J. E 2010, 33, 19–26. [Google Scholar] [CrossRef]
- Choudhury, M.D.; Jana, S.; Dutta, S.; Tarafdar, S. Pattern formation in a drying drop of starch gel with sodium chloride. Colloids Surf. A 2013, 432, 110–118. [Google Scholar] [CrossRef]
- Poulard, C.; Damman, P. Control of spreading and drying of a polymer solution from Marangoni flows. Eur. Phys. Lett. 2007, 80, 64001. [Google Scholar] [CrossRef]
- Hu, H.; Larson, R.G. Marangoni Effect Reverses Coffee-Ring Depositions. J. Phys. Chem. B 2006, 110, 7090–7094. [Google Scholar] [CrossRef] [PubMed]
- Efstratiou, M.; Christy, J.; Sefiane, K. Crystallization-Driven Flows within Evaporating Aqueous Saline Droplets. Langmuir 2020, 36, 4995–5002. [Google Scholar] [CrossRef]
- Koga, Y. Solution Thermodynamics and Its Application to Aqueous Solutions; Elsevier: Amsterdam, The Netherlands, 2017. [Google Scholar]
- Weon, B.M.; Je, J.H. Capillary force repels coffee-ring effect. Phys. Rev. E 2010, 82, 015305. [Google Scholar] [CrossRef] [PubMed]
- Arangalage, M.; Li, X.; Lequeux, F.; Talini, L. Dual Marangoni effects and detection of traces of surfactants. Soft Matter 2018, 14, 3378–3386. [Google Scholar] [CrossRef] [PubMed]
- Langer, J.S. Instabilities and pattern formation in crystal growth. Rev. Mod. Phys. 1980, 52, 1–28. [Google Scholar] [CrossRef]
- Mullins, W.W.; Sekerka, R.F. Morphological stability of a particle growing by diffusion or heat flow. J. Appl. Phys. 1963, 34, 323–329. [Google Scholar] [CrossRef]
- Fteiti, M.; Alaidrous, A. Latent Heat Storage during Melting and Solidification of a Phase Change Material (PCM) Embedded with a Porous Matrix of High Thermal Conductivity. Int. J. Energy Eng. 2020, 10, 1–9. [Google Scholar] [CrossRef]
- Guzmán, E.; Ritacco, H.; Rubio, J.E.; Rubio, R.G.; Ortega, F. Salt-induced changes in the growth of polyelectrolyte layers of poly (diallyl-dimethylammonium chloride) and poly (4-styrene sulfonate of sodium). Soft Matter 2009, 5, 2130–2142. [Google Scholar] [CrossRef]
- Pinho, S.P.; Macedo, E.A. Solubility of NaCl, NaBr, and KCl in Water, Methanol, Ethanol, and Their Mixed Solvents. J. Chem. Eng. Data 2005, 50, 29–32. [Google Scholar] [CrossRef]
- Coriell, S.R.; Sekerka, R.F. The effect of the anisotropy of surface tension and interface kinetics on morphological stability. J. Cryst. Growth 1976, 34, 157–163. [Google Scholar] [CrossRef]
- Friedrich, L.C.; Silva, V.O.; Moreira, P.F., Jr.; Tcacenco, C.M.; Quina, F.H. Time-resolved fluorescence quenching studies of sodium lauryl ether sulfate micelles. J. Braz. Chem. Soc. 2013, 24, 241–245. [Google Scholar] [CrossRef]
- Gavazzoni Dias, M.F. Hair cosmetics: An overview. Int. J. Tribol. 2015, 7, 2–15. [Google Scholar] [CrossRef]
- Wege, H.; Holgado-Terriza, J.A.; Cabrerizo-Vílchez, M. Development of a constant surface pressure penetration Langmuir balance based on axisymmetric drop shape analysis. J. Colloid Interface Sci. 2002, 249, 263–273. [Google Scholar] [CrossRef][Green Version]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Perrin, L.; Akanno, A.; Guzman, E.; Ortega, F.; Rubio, R.G. Pattern Formation upon Evaporation of Sessile Droplets of Polyelectrolyte/Surfactant Mixtures on Silicon Wafers. Int. J. Mol. Sci. 2021, 22, 7953. https://doi.org/10.3390/ijms22157953
Perrin L, Akanno A, Guzman E, Ortega F, Rubio RG. Pattern Formation upon Evaporation of Sessile Droplets of Polyelectrolyte/Surfactant Mixtures on Silicon Wafers. International Journal of Molecular Sciences. 2021; 22(15):7953. https://doi.org/10.3390/ijms22157953
Chicago/Turabian StylePerrin, Lionel, Andrew Akanno, Eduardo Guzman, Francisco Ortega, and Ramon G. Rubio. 2021. "Pattern Formation upon Evaporation of Sessile Droplets of Polyelectrolyte/Surfactant Mixtures on Silicon Wafers" International Journal of Molecular Sciences 22, no. 15: 7953. https://doi.org/10.3390/ijms22157953
APA StylePerrin, L., Akanno, A., Guzman, E., Ortega, F., & Rubio, R. G. (2021). Pattern Formation upon Evaporation of Sessile Droplets of Polyelectrolyte/Surfactant Mixtures on Silicon Wafers. International Journal of Molecular Sciences, 22(15), 7953. https://doi.org/10.3390/ijms22157953









