Possible Steps of the Carboxylation of Ribulose-1,5-biphosphate from Intermediates: 2,3-Enediol versus 1,2-Enol
Abstract
:1. Introduction
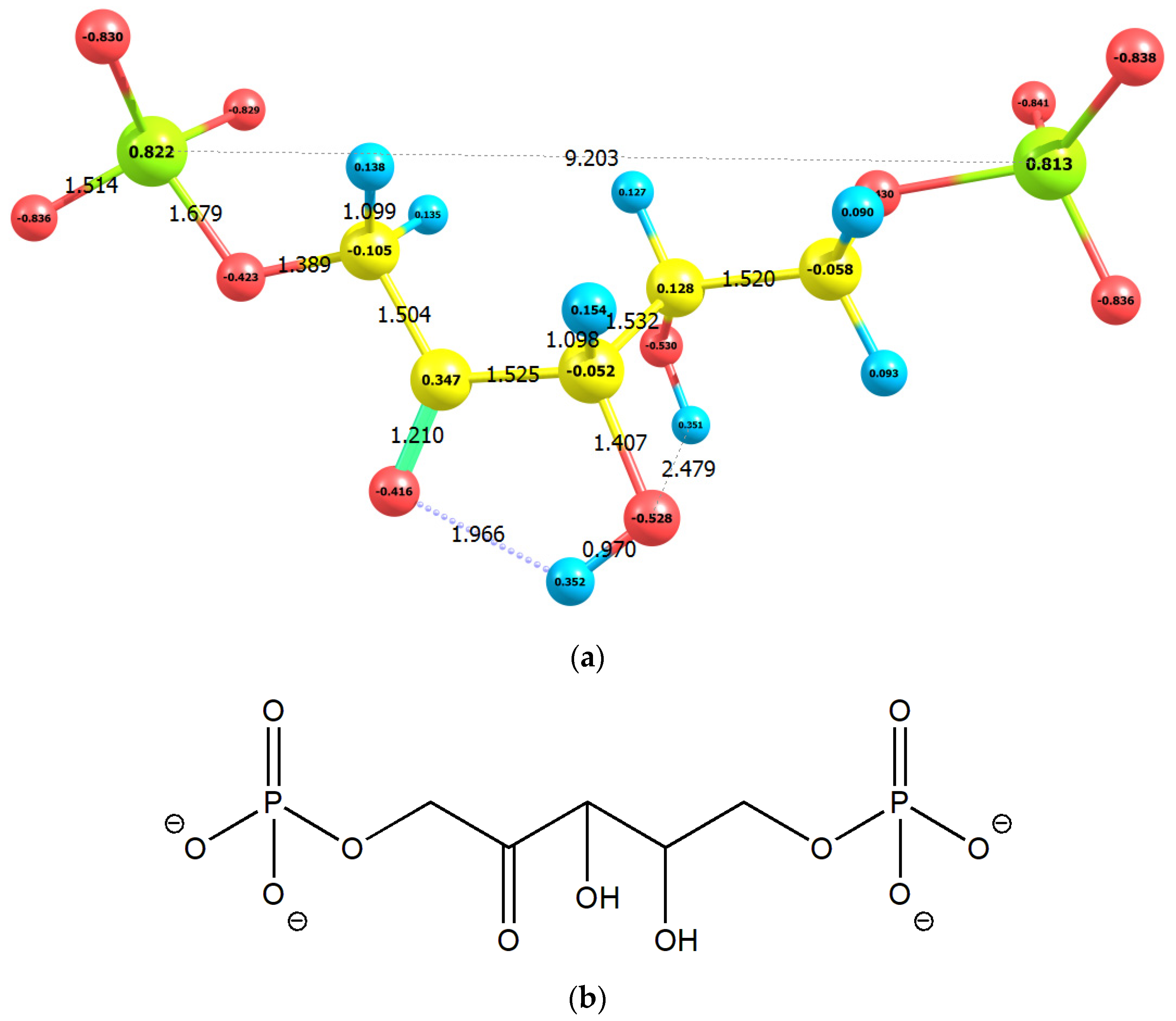
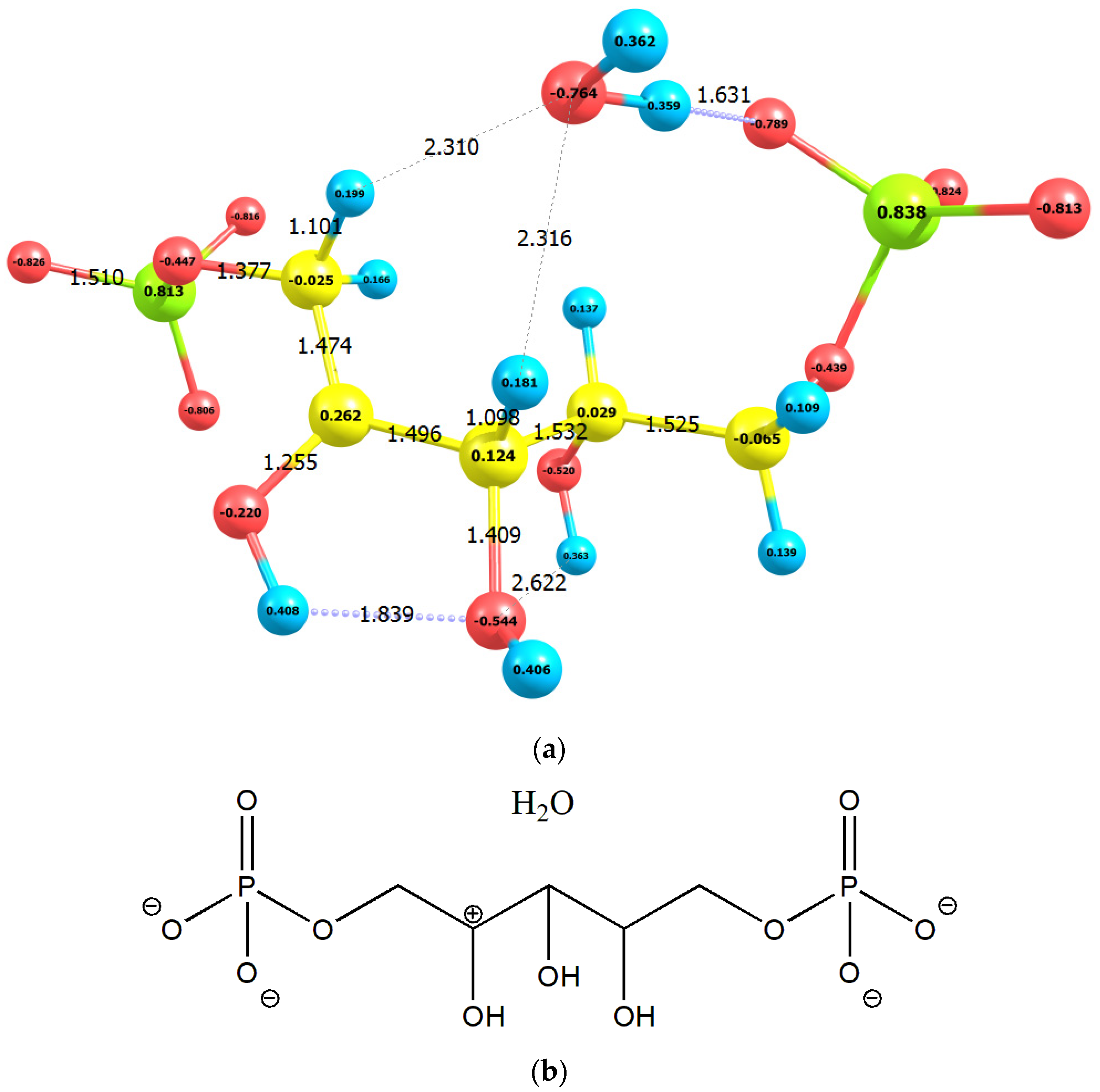
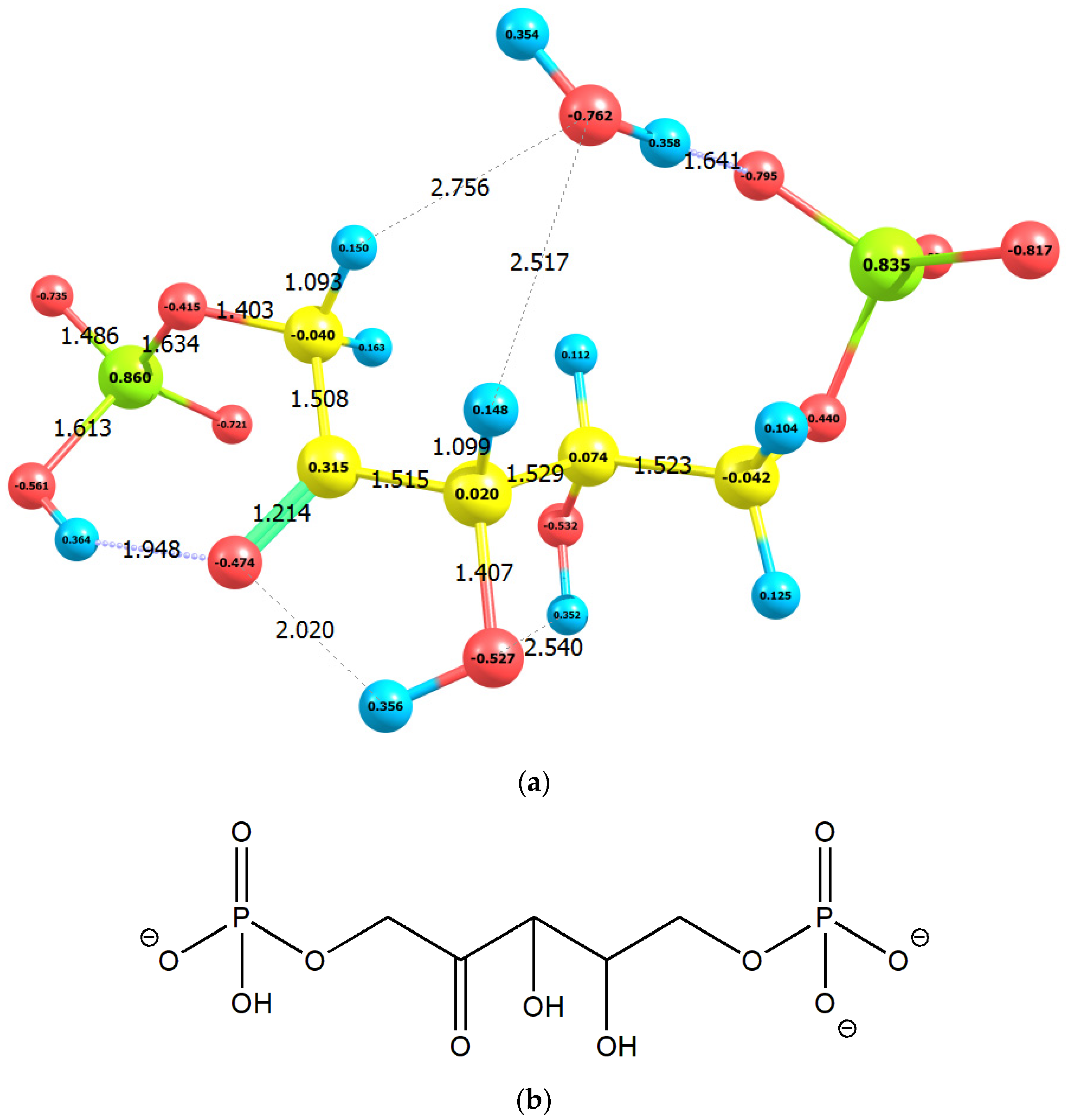
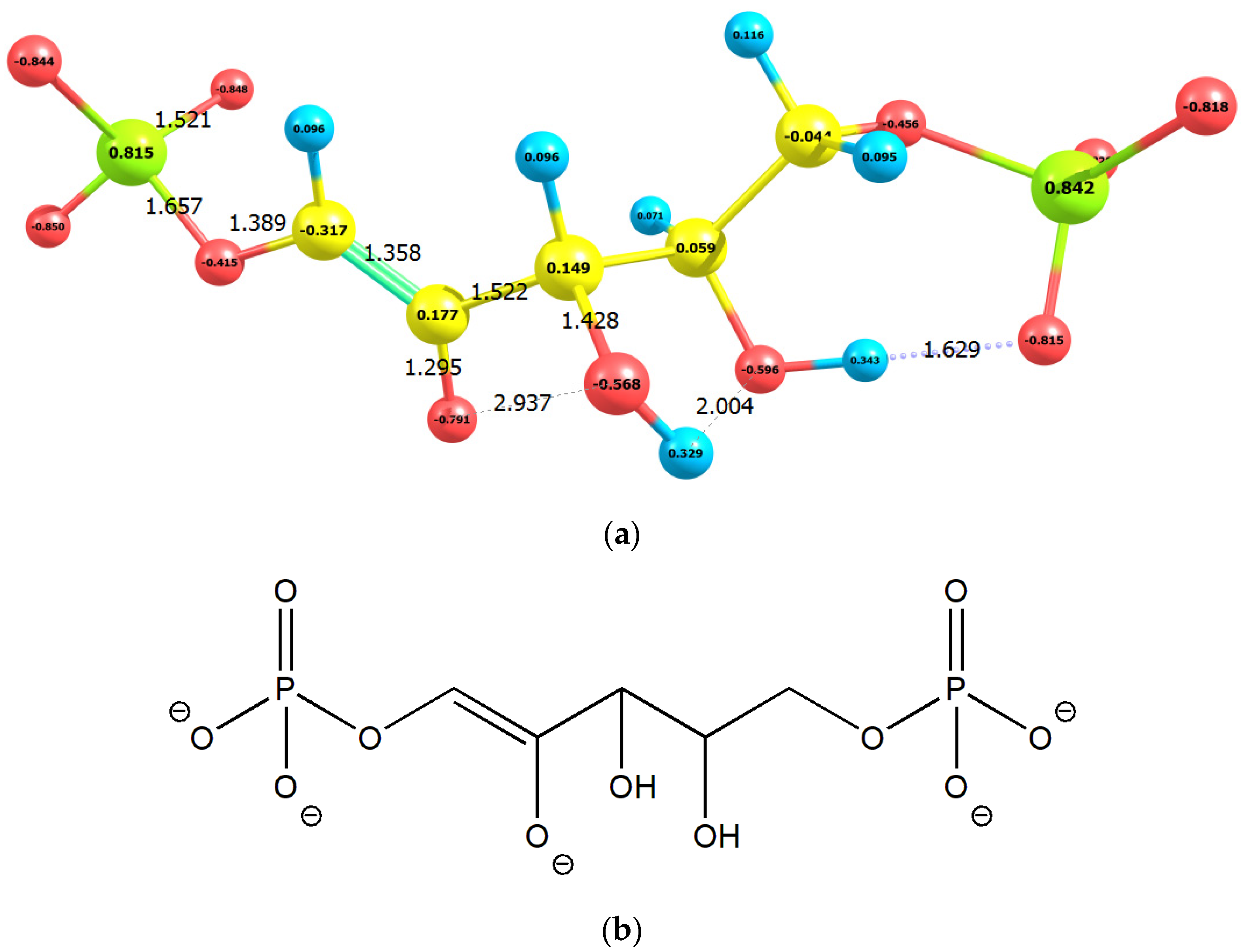
2. Results
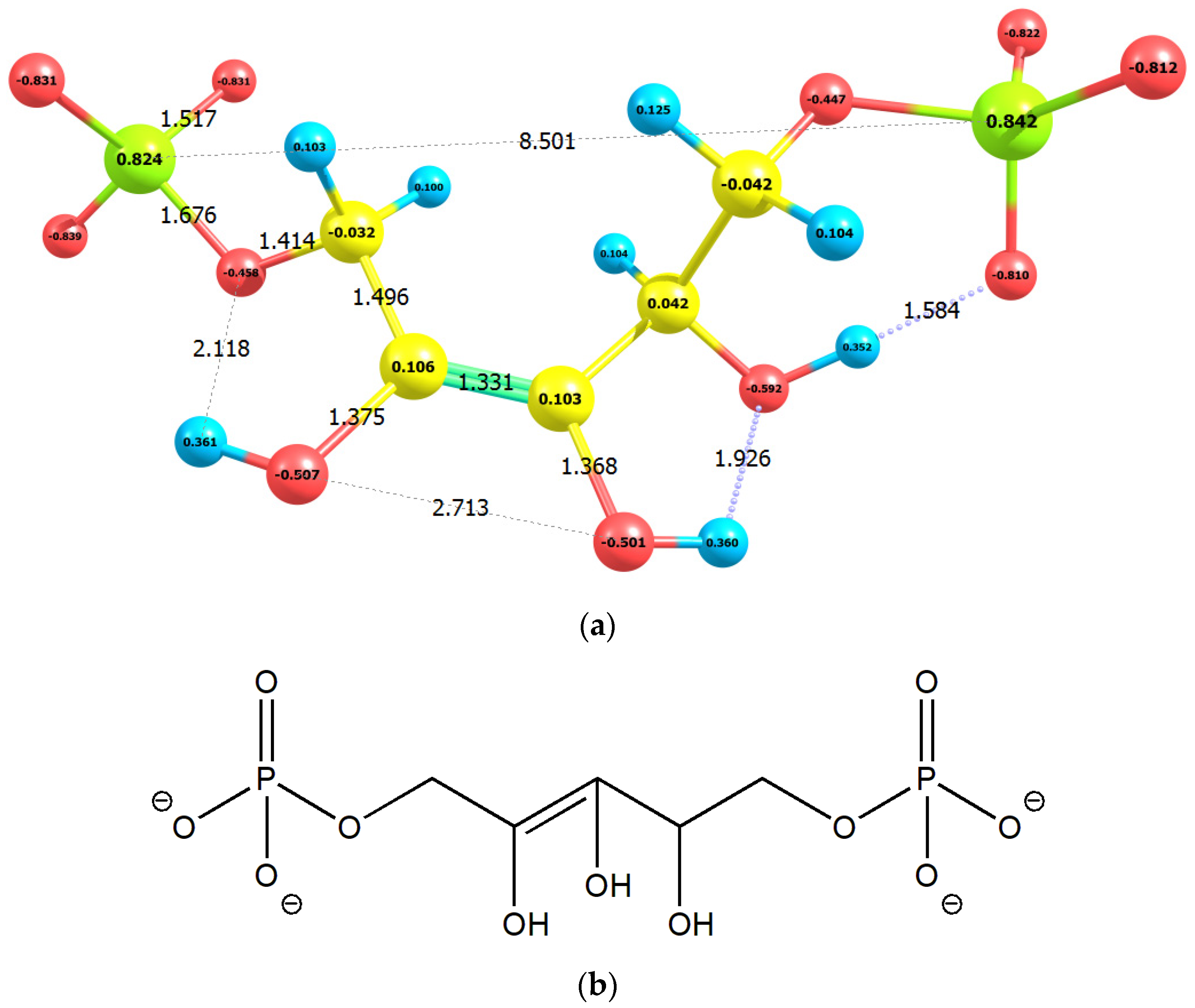
2.1. Enolization
2.2. CO2 Fixation
3. Discussion
4. Materials and Methods
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A










References
- Sage, R.F.; Sage, T.L. C4 Plants. In Encyclopedia of Biodiversity, 2nd ed.; Levin, S.A., Ed.; Academic Press: Pachuca, México, 2013; Volume 2, pp. 361–381. [Google Scholar]
- Zhu, X.G.; Long, S.P. Improving Photosynthetic Efficiency for Greater Yield. Annu. Rev. Plant Biol. 2010, 61, 235–261. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Weber, A.P.M.; Bar-Even, A. Update: Improving the Efficiency of Photosynthetic Carbon Reactions. Plant Physiol. 2019, 179, 803–812. [Google Scholar] [CrossRef] [Green Version]
- Miller, T.E.; Beneyton, T.; Schwander, T.; Diehl, C.; Girault, M.; McLean, R.; Chotel, T.; Claus, P.; Socorro Cortina, N.; Baret, J.-C.; et al. Light-powered CO2 fixation in a chloroplast mimic with natural and synthetic parts. Science 2020, 368, 649–654. [Google Scholar] [CrossRef] [PubMed]
- Bar-Even, A.; Noor, E.; Lewis, N.E.; Milo, R. Design and analysis of synthetic carbon fixation pathways. PNAS 2010, 107, 8889–8894. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sokolov, V.A. On a Possible Way to Increase the Efficiency of Photosynthesis. Dokl. Biochem. Biophys. 2020, 491, 98–100. [Google Scholar] [CrossRef]
- Kannappan, B.; Gready, J.E. Redefinition of Rubisco Carboxylase Reaction Reveals Origin of Water for Hydration and New Roles for Active-Site Residues. J. Am. Chem. Soc. 2008, 130, 15063–15080. [Google Scholar] [CrossRef]
- Götze, J.P.; Saalfrank, P. Quantum chemical modeling of the kinetic isotope effect of the carboxylation step in RuBisCO. J. Mol. Model. 2012, 18, 1877–1883. [Google Scholar] [CrossRef] [PubMed]
- Cummins, P.L.; Gready, J.E. Kohn−Sham Density Functional Calculations Reveal Proton Wires in the Enolization and Carboxylase Reactions Catalyzed by Rubisco. J. Phys. Chem. B 2020, 124, 3015–3026. [Google Scholar] [CrossRef] [PubMed]
- El-Hendawy, M.M.; English, N.J.; Mooney, D.A. Comparative studies for evaluation of CO2 fixation in the cavity of the Rubisco enzyme using QM, QM/MM and linear-scaling DFT methods. J. Mol. Model. 2013, 19, 2329–2334. [Google Scholar] [CrossRef] [Green Version]
- King, W.A.; Gready, J.E.; Andrews, T.J. Quantum Chemical Analysis of the Enolization of Ribulose Bisphosphate: The First Hurdle in the Fixation of CO2 by Rubisco. Biochemistry 1998, 37, 15414–15422. [Google Scholar] [CrossRef]
- El-Hendawy, M.M.; Garate, J.-A.; English, N.J.; O’Reilly, S.; Mooney, D.A. Diffusion and interactions of carbon dioxide and oxygen in the vicinity of the active site of Rubisco: Molecular dynamics and quantum chemical studies. J. Chem. Phys. 2012, 137, 145103. [Google Scholar] [CrossRef] [PubMed]
- Cummins, P.L.; Kannappan, B.; Gready, J.E. Revised mechanism of carboxylation of ribulose-1,5-biphosphate by rubisco from large scale quantum chemical calculations. J. Comput. Chem. 2018, 39, 1656–1665. [Google Scholar] [CrossRef]
- Cummins, P.L.; Kannappan, B.; Gready, J.E. Ab Initio Molecular Dynamics Simulation and Energetics of the Ribulose-1,5-biphosphate Carboxylation Reaction Catalyzed by Rubisco: Toward Elucidating the Stereospecific Protonation Mechanism. J. Phys. Chem. B 2019, 123, 2679–2686. [Google Scholar] [CrossRef]
- Chai, J.-D.; Head-Gordon, M. Systematic optimization of long-range corrected hybrid density functional. J. Chem. Phys. 2008, 128, 084106. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.-S.; Li, G.-D.; Mao, S.-P.; Chai, J.-D. Long-Range Corrected Hybrid Density Functionals with Improved Dispersion Corrections. J. Chem. Theory Comput. 2013, 9, 263–272. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Neese, F.; Wennmohs, F.; Hansen, A.; Becker, U. Efficient, approximate and parallel Hartree–Fock and hybrid DFT calculations. A ‘chain-of-spheres’ algorithm for the Hartree–Fock exchange. Chem. Phys. 2009, 356, 98–109. [Google Scholar] [CrossRef]
- Weigend, F. Accurate Coulomb-fitting basis sets for H to Rn. Phys. Chem. Chem. Phys. 2006, 8, 1057. [Google Scholar] [CrossRef] [PubMed]
- Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297. [Google Scholar] [CrossRef] [PubMed]
- Barone, V.; Cossi, M.; Tomasi, J. A New Definition of Cavities for the Computation of Solvation Free Energies by the Polarizable Continuum Model. J. Chem. Phys. 1997, 107, 3210. [Google Scholar] [CrossRef]
- Cossi, M.; Scalmani, G.; Rega, N.; Barone, V. New Developments in the Polarizable Continuum Model for Quantum Mechanical and Classical Calculations on Molecules in Solution. J. Chem. Phys. 2002, 117, 43. [Google Scholar] [CrossRef]
- Tomasi, J.; Mennucci, B.; Cammi, R. Quantum Mechanical Continuum Solvation Models. Chem. Rev. 2005, 105, 2999–3094. [Google Scholar] [CrossRef] [PubMed]
- Neese, F. Software update: The ORCA program system, version 4.0. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2018, 8, e1327. [Google Scholar] [CrossRef]
- Chemcraft-Graphical Software for Visualization of Quantum Chemistry Computations. Available online: https://www.chemcraftprog.com (accessed on 1 January 2021).





| No | Molecule | Q | M | qC1 | qC2 | qC3 | E0 | G0 | EHOMO | ELUMO |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | RuBP | −4 | 1 | −0.105 | 0.347 | −0.052 | −46,437.91 | −46,434.57 | −8.08 | 1.55 |
| 2 | RuBP1+⋅H2O | −3 | 1 | −0.025 | 0.262 | 0.124 | −48,530.12 | −48,525.85 | −8.27 | −0.16 |
| 3 | RuBP2+⋅H2O | −3 | 1 | −0.040 | 0.315 | 0.020 | −48,531.77 | −48,527.58 | −8.31 | 1.28 |
| 4 | 1,2-enol | −4 | 1 | −0.060 | 0.073 | 0.129 | −46,437.76 | −46,434.44 | −7.64 | 3.43 |
| 5 | 1,2-enolate | −5 | 1 | −0.317 | 0.177 | 0.149 | −46,424.13 | −46,421.11 | −6.14 | 3.88 |
| 6 | 2,3-enediol | −4 | 1 | −0.032 | 0.106 | 0.103 | −46,437.75 | −46,434.39 | −7.65 | 3.32 |
| 7 | 2,3-enediolate | −5 | 1 | 0.048 | −0.012 | 0.106 | −46,424.27 | −46,421.25 | −5.97 | 4.14 |
| 8 | BPGA | −4 | 1 | 0.002 | 0.068 | 0.075 | −51,603.38 | −51,599.04 | −6.55 | 2.20 |
| 9 | CABP | −4 | 1 | −0.094 | 0.296 | 0.006 | −51,603.53 | −51,599.18 | −8.09 | 2.45 |
| 10 | 3kCABP | −4 | 1 | −0.122 | 0.254 | 0.339 | −51,570.72 | −51,567.08 | −8.35 | 1.24 |
| 11 | H2O | 0 | 1 | - | - | - | −2080.34 | −2080.25 | −11.36 | 3.50 |
| 12 | H3O+ | 1 | 1 | - | - | - | −2091.54 | −2091.10 | −15.95 | 2.38 |
| 13 | CO2 | 0 | 1 | 0.474 | - | - | −5132.52 | −5132.76 | −12.80 | 3.23 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fedunov, R.G.; Sokolov, V.A. Possible Steps of the Carboxylation of Ribulose-1,5-biphosphate from Intermediates: 2,3-Enediol versus 1,2-Enol. Int. J. Mol. Sci. 2021, 22, 9749. https://doi.org/10.3390/ijms22189749
Fedunov RG, Sokolov VA. Possible Steps of the Carboxylation of Ribulose-1,5-biphosphate from Intermediates: 2,3-Enediol versus 1,2-Enol. International Journal of Molecular Sciences. 2021; 22(18):9749. https://doi.org/10.3390/ijms22189749
Chicago/Turabian StyleFedunov, Roman G., and Victor A. Sokolov. 2021. "Possible Steps of the Carboxylation of Ribulose-1,5-biphosphate from Intermediates: 2,3-Enediol versus 1,2-Enol" International Journal of Molecular Sciences 22, no. 18: 9749. https://doi.org/10.3390/ijms22189749
APA StyleFedunov, R. G., & Sokolov, V. A. (2021). Possible Steps of the Carboxylation of Ribulose-1,5-biphosphate from Intermediates: 2,3-Enediol versus 1,2-Enol. International Journal of Molecular Sciences, 22(18), 9749. https://doi.org/10.3390/ijms22189749






