The Anomalous Behavior of Thermodynamic Parameters in the Three Widom Deltas of Carbon Dioxide-Ethanol Mixture
Abstract
:1. Introduction
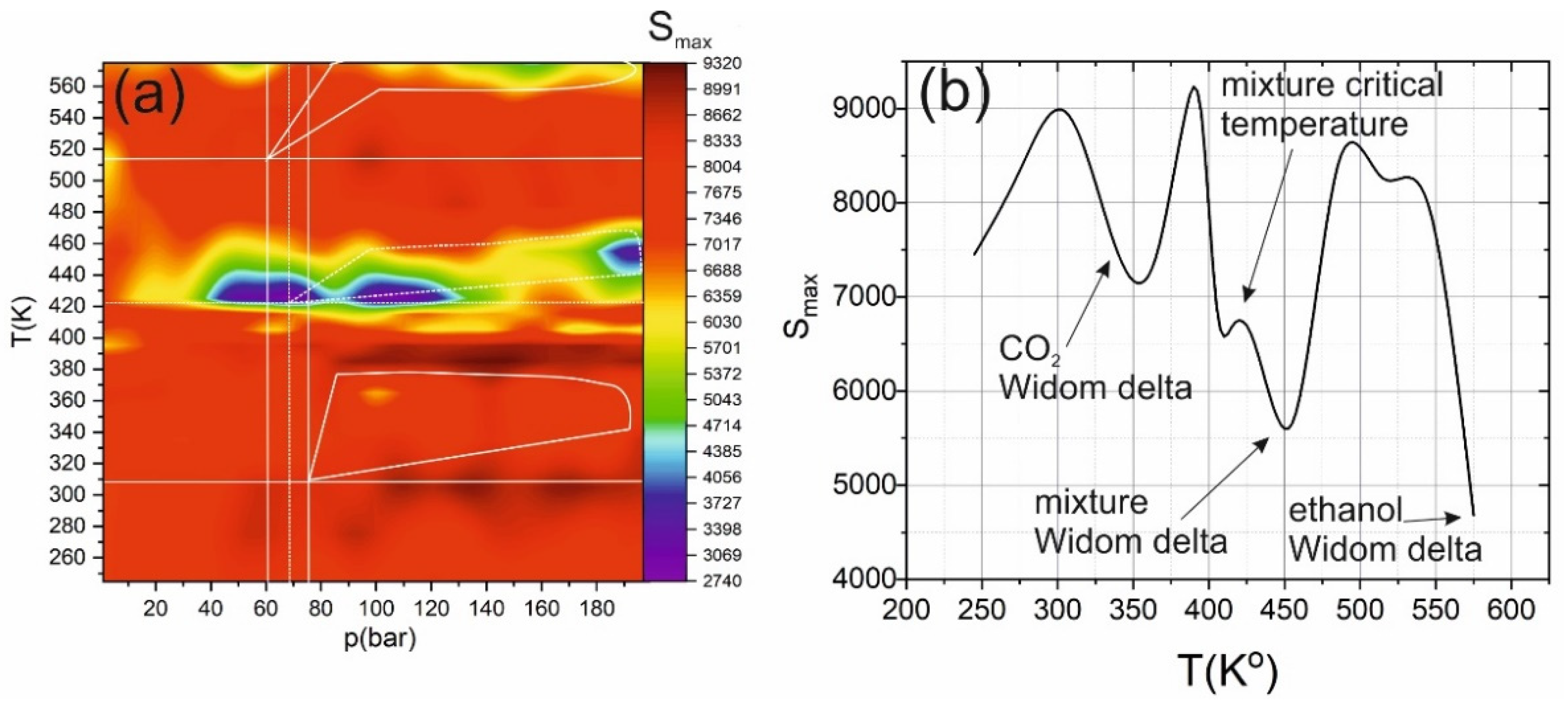
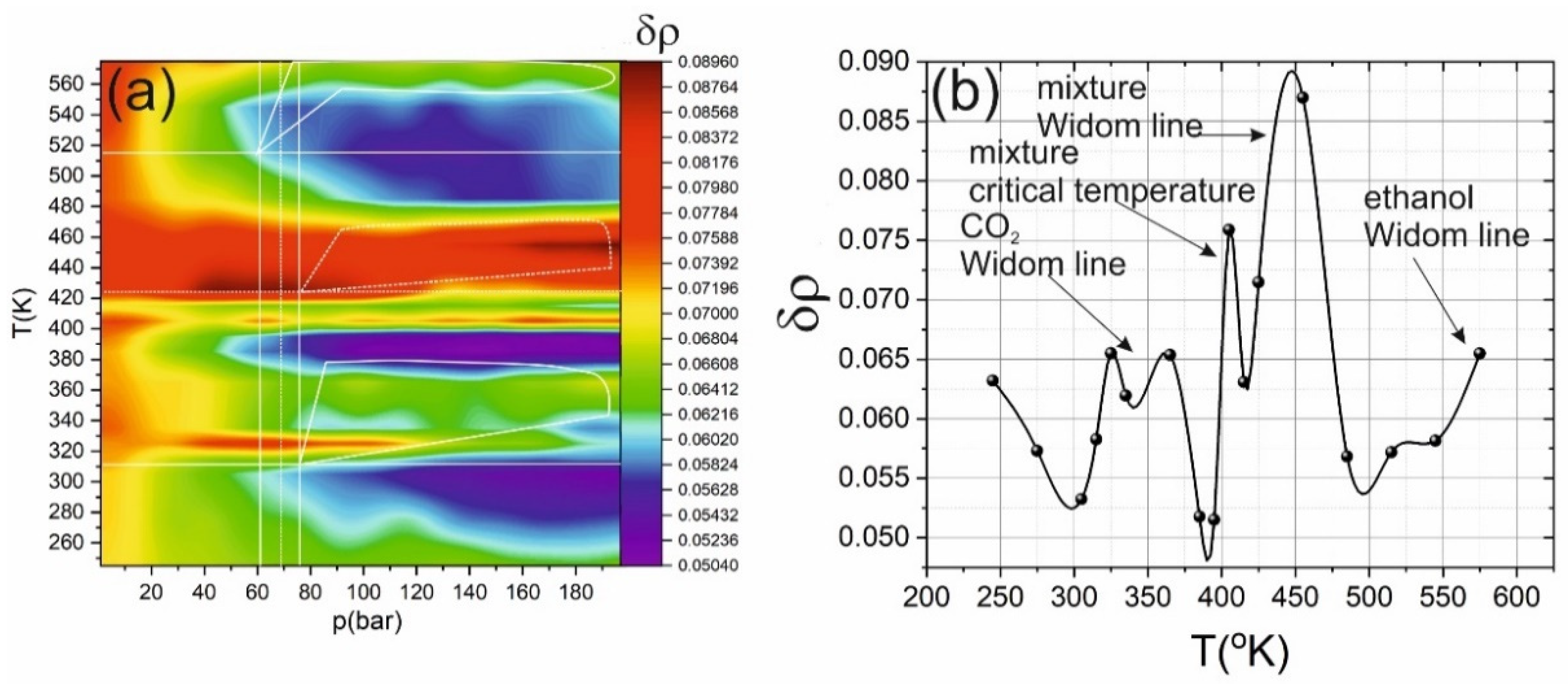
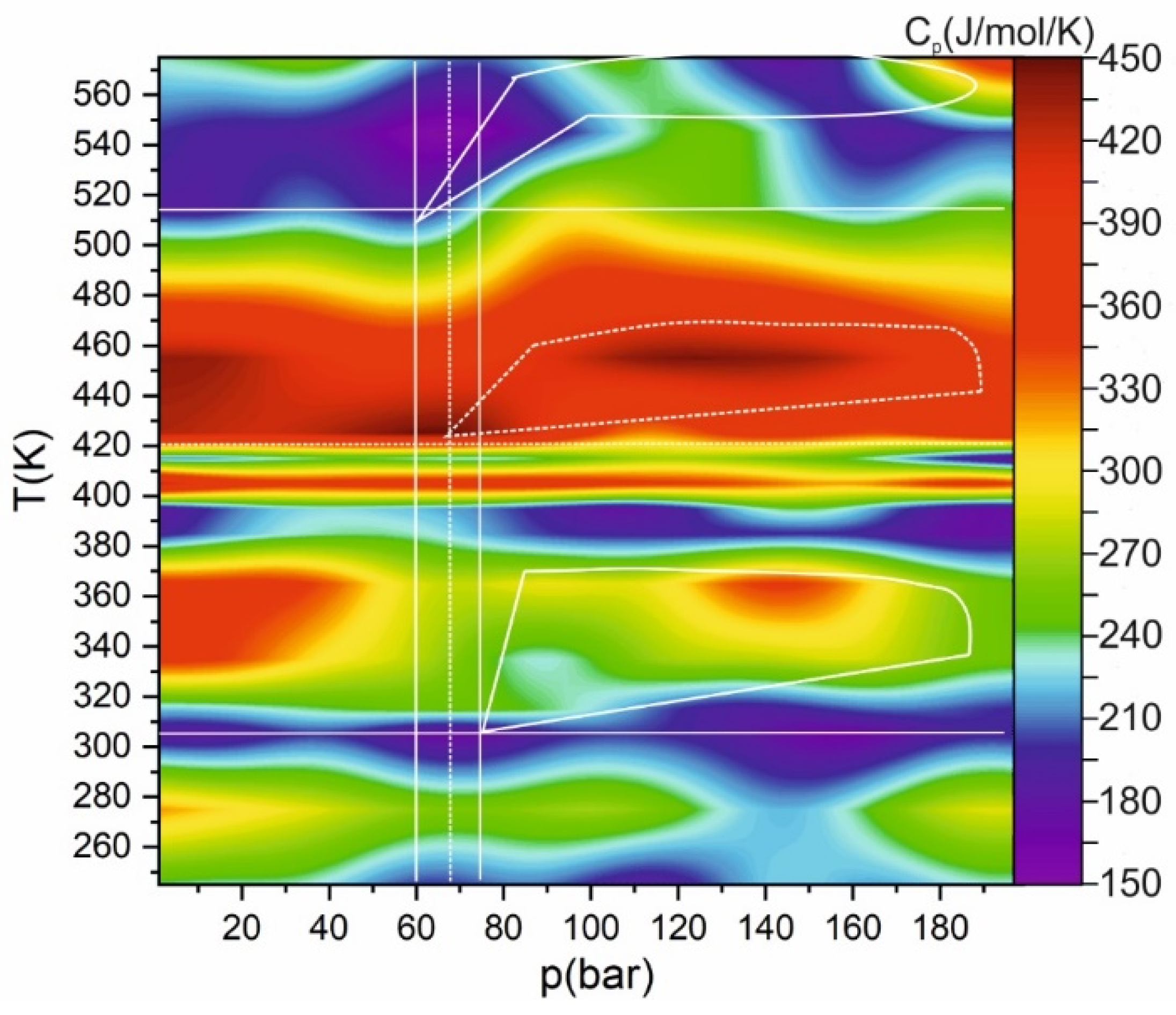
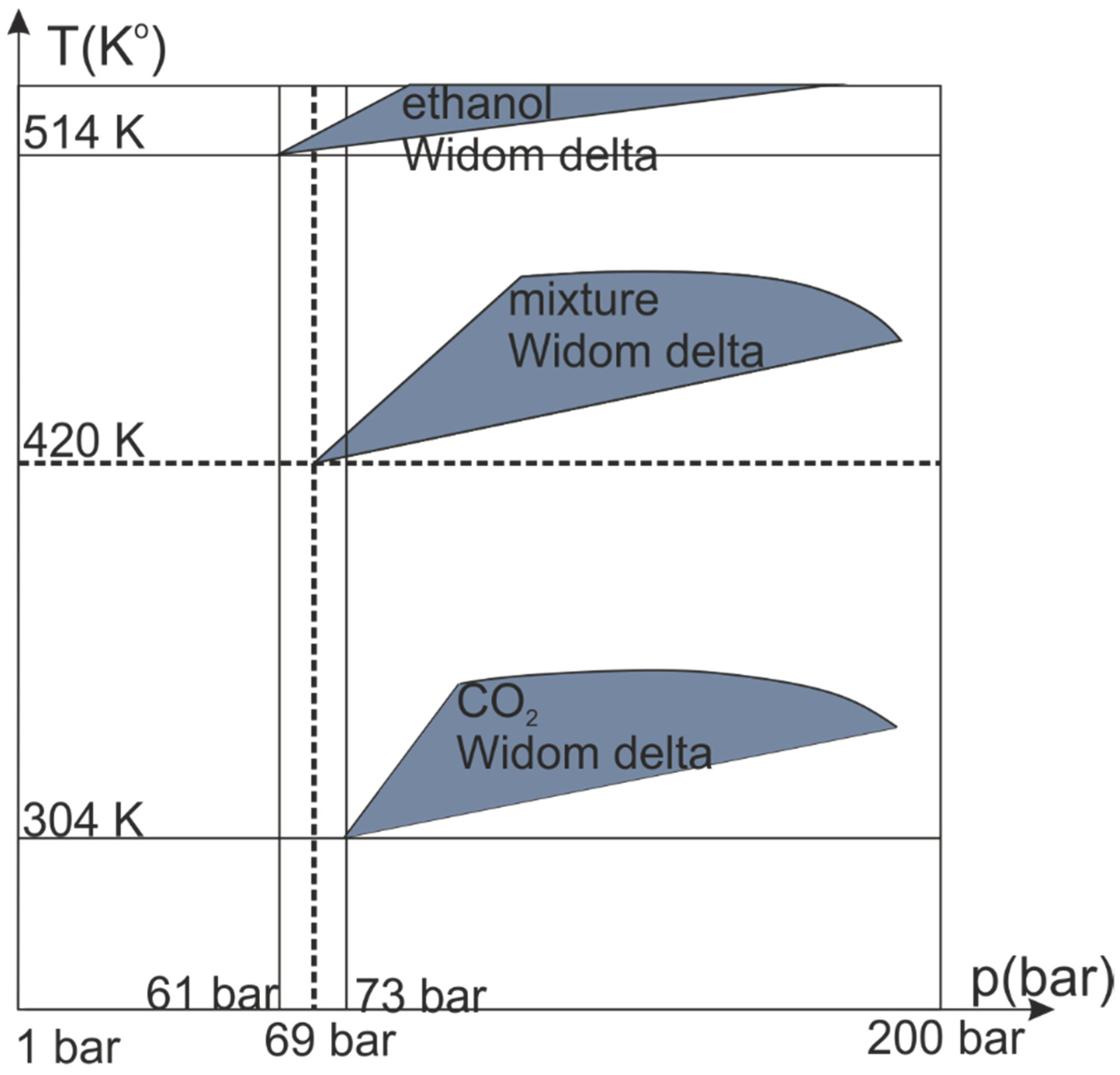
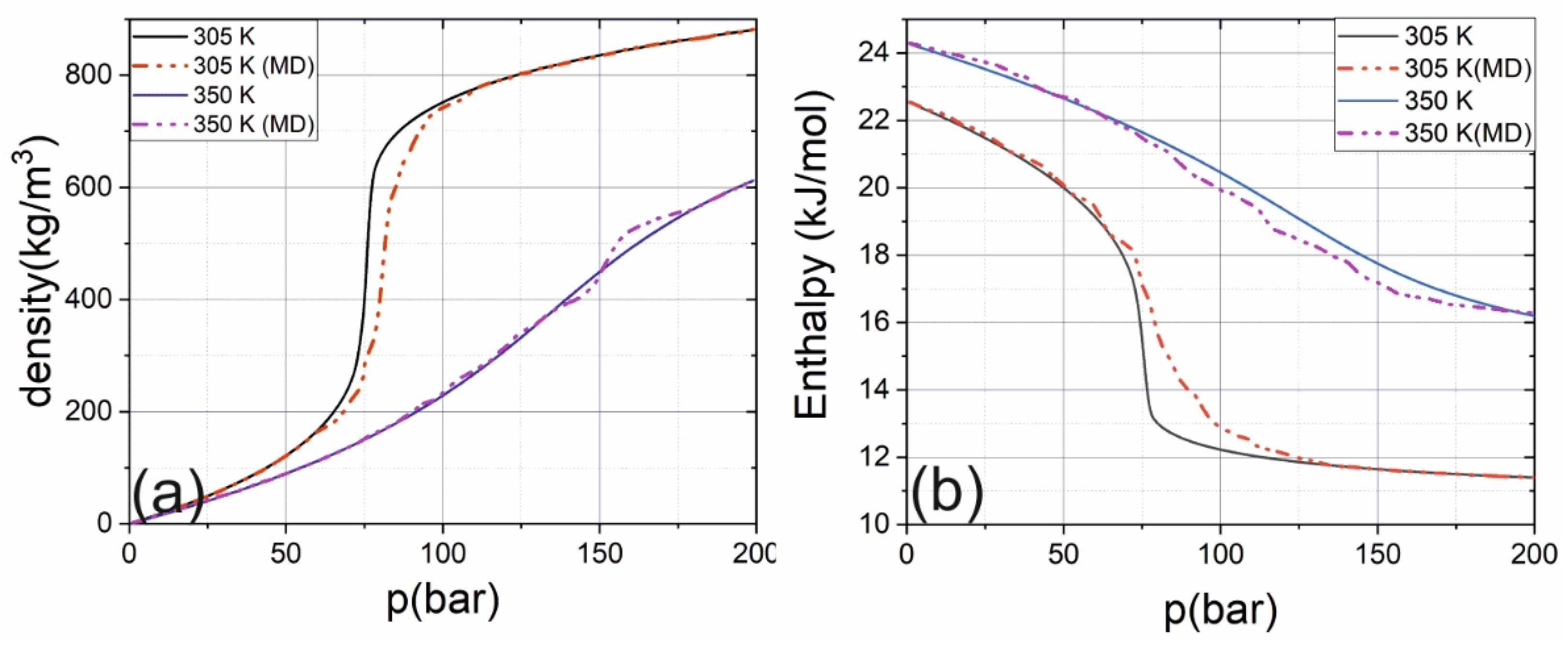
2. Results and Discussion
3. Methods
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Brunner, G. Applications of Supercritical Fluids. Annu. Rev. Chem. Biomol. Eng. 2010, 1, 321–342. [Google Scholar] [CrossRef] [PubMed]
- Bellan, J. Supercritical (and subcritical) fluid behavior and modeling: Drops, streams, shear and mixing layers, jets and sprays. Prog. Energy Combust. Sci. 2000, 26, 329–366. [Google Scholar] [CrossRef] [Green Version]
- MacHmudah, S.; Wahyudiono; Kuwahara, Y.; Sasaki, M.; Goto, M. Nano-structured particles production using pulsed laser ablation of gold plate in supercritical CO2. J. Supercrit. Fluids 2011, 60, 63–68. [Google Scholar] [CrossRef]
- Byrappa, K.; Ohara, S.; Adschiri, T. Nanoparticles synthesis using supercritical fluid technology—Towards biomedical applications. Adv. Drug Deliv. Rev. 2008, 60, 299–327. [Google Scholar] [CrossRef] [PubMed]
- Taylor, L.T. Supercritical fluid chromatography. Anal. Chem. 2010, 82, 4925–4935. [Google Scholar] [CrossRef]
- Gorelli, F.A.; Bryk, T.; Krisch, M.; Ruocco, G.; Santoro, M.; Scopigno, T. Dynamics and Thermodynamics beyond the critical point. Sci. Rep. 2013, 3, 1203. [Google Scholar] [CrossRef] [PubMed]
- Simeoni, G.G.; Bryk, T.; Gorelli, F.A.; Krisch, M.; Ruocco, G.; Santoro, M.; Scopigno, T. The Widom line as the crossover between liquid-like and gas-like behaviour in supercritical fluids. Nat. Phys. 2010, 6, 503–507. [Google Scholar] [CrossRef]
- Whitesides, G.M. The origins and the future of microfluidics. Nature 2006, 442, 368–373. [Google Scholar] [CrossRef]
- McMillan, P.F.; Stanley, H.E. Fluid phases: Going supercritical. Nat. Phys. 2010, 6, 479–480. [Google Scholar] [CrossRef]
- Nishikawa, K.; Tanaka, I. Correlation lengths and density fluctuations in supercritical states of carbon dioxide. Chem. Phys. Lett. 1995, 244, 149–152. [Google Scholar] [CrossRef]
- Brazhkin, V.V.; Lyapin, A.G.; Ryzhov, V.N.; Trachenko, K.; Fomin, Y.D.; Tsiok, E.N. Where is the supercritical fluid on the phase diagram? Physics-Uspekhi 2012, 55, 1061–1079. [Google Scholar] [CrossRef] [Green Version]
- Sedunov, B. The Analysis of the Equilibrium Cluster Structure in Supercritical Carbon Dioxide. Am. J. Anal. Chem. 2012, 3, 899–904. [Google Scholar] [CrossRef] [Green Version]
- Gorelli, F.; Santoro, M.; Scopigno, T.; Krisch, M.; Ruocco, G. Liquidlike behavior of supercritical fluids. Phys. Rev. Lett. 2006, 97, 15–18. [Google Scholar] [CrossRef] [Green Version]
- Ha, M.Y.; Yoon, T.J.; Tlusty, T.; Jho, Y.; Lee, W.B. Widom Delta of Supercritical Gas-Liquid Coexistence. J. Phys. Chem. Lett. 2018, 9, 1734–1738. [Google Scholar] [CrossRef] [Green Version]
- Sciortino, F.; Poole, P.H.; Essmann, U.; Stanley, H.E. Line of compressibility maxima in the phase diagram of supercooled water. Phys. Rev. E-Stat. Phys. Plasmas Fluids Relat. Interdiscip. Top. 1997, 55, 727–737. [Google Scholar] [CrossRef] [Green Version]
- May, H.O.; Mausbach, P. Riemannian geometry study of vapor-liquid phase equilibria and supercritical behavior of the Lennard-Jones fluid. Phys. Rev. E-Stat. Nonlinear Soft Matter Phys. 2012, 85, 1–9. [Google Scholar] [CrossRef]
- Liu, L.; Chen, S.H.; Faraone, A.; Yen, C.W.; Mou, C.Y. Pressure dependence of fragile-to-strong transition and a possible second critical point in supercooled confined water. Phys. Rev. Lett. 2005, 95, 1–4. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Santoro, M.; Gorelli, F.A. Structural changes in supercritical fluids at high pressures. Phys. Rev. B-Condens. Matter Mater. Phys. 2008, 77, 1–4. [Google Scholar] [CrossRef]
- Banuti, D.T. Crossing the Widom-line—Supercritical pseudo-boiling. J. Supercrit. Fluids 2015, 98, 12–16. [Google Scholar] [CrossRef]
- Ruppeiner, G.; Sahay, A.; Sarkar, T.; Sengupta, G. Thermodynamic geometry, phase transitions, and the Widom line. Phys. Rev. E-Stat. Nonlinear Soft Matter Phys. 2012, 86, 3–6. [Google Scholar] [CrossRef] [Green Version]
- Raju, M.; Banuti, D.T.; Ma, P.C.; Ihme, M. Widom lines in binary mixtures of supercritical fluids. Sci. Rep. 2017, 7, 3027. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Imre, A.R.; Ramboz, C.; Deiters, U.K.; Kraska, T. Anomalous fluid properties of carbon dioxide in the supercritical region: Application to geological CO2 storage and related hazards. Environ. Earth Sci. 2015, 73, 4373–4384. [Google Scholar] [CrossRef] [Green Version]
- Imre, A.R.; Házi, G.; Horváth, Á.; Maráczy, C.; Mazur, V.; Artemenko, S. The effect of low-concentration inorganic materials on the behaviour of supercritical water. Nucl. Eng. Des. 2011, 241, 296–300. [Google Scholar] [CrossRef]
- Nishikawa, K.; Morita, T. Inhomogeneity of molecular distribution in supercritical fluids Inhomogeneity of molecular distribution in supercritical fluids. Chem. Phys. Lett. 2000, 316, 238–242. [Google Scholar] [CrossRef]
- Mareev, E.; Aleshkevich, V.; Potemkin, F.; Bagratashvili, V.; Minaev, N.; Gordienko, V. Anomalous behavior of nonlinear refractive indexes of CO2 and Xe in supercritical states. Opt. Express 2018, 26, 13229–13238. [Google Scholar] [CrossRef] [PubMed]
- Mareev, E.I.; Aleshkevich, V.A.; Potemkin, F.V.; Minaev, N.V.; Gordienko, V.M. Molecular Refraction and Nonlinear Refractive Index of Supercritical Carbon Dioxide under Clustering Conditions. Russ. J. Phys. Chem. B 2019, 13, 1–6. [Google Scholar] [CrossRef]
- Bolmatov, D.; Zav’Yalov, D.; Gao, M.; Zhernenkov, M. Structural evolution of supercritical CO2 across the Frenkel line. J. Phys. Chem. Lett. 2014, 5, 2785–2790. [Google Scholar] [CrossRef] [Green Version]
- Fomin, D.; Ryzhov, V.N.; Tsiok, E.N.; Brazhkin, V.V.; Trachenko, K. Thermodynamics and Widom lines in supercritical carbon dioxide. Phys. Rev. E 2015, 91, 022111. [Google Scholar] [CrossRef]
- Brazhkin, V.V.; Fomin, Y.D.; Ryzhov, V.N.; Tareyeva, E.E.; Tsiok, E.N. True Widom line for a square-well system. Phys. Rev. E-Stat. Nonlinear Soft Matter Phys. 2014, 89, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Brazhkin, V.V.; Fomin, Y.D.; Lyapin, A.G.; Ryzhov, V.N.; Trachenko, K. Two liquid states of matter: A dynamic line on a phase diagram. Phys. Rev. E-Stat. Nonlinear Soft Matter Phys. 2012, 85, 1–12. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Imre, A.R.; Deiters, U.K.; Kraska, T.; Tiselj, I. The pseudocritical regions for supercritical water. Nucl. Eng. Des. 2012, 252, 179–183. [Google Scholar] [CrossRef]
- Mareev, E.; Semenov, T.; Lazarev, A.; Minaev, N.; Sviridov, A.; Potemkin, F.; Gordienko, V. Optical Diagnostics of Supercritical CO2 and CO2-Ethanol Mixture in the Widom Delta. Molecules 2020, 25, 5424. [Google Scholar] [CrossRef] [PubMed]
- Grijó, D.R.; Vieitez Osorio, I.A.; Cardozo-Filho, L. Supercritical extraction strategies using CO2 and ethanol to obtain cannabinoid compounds from Cannabis hybrid flowers. J. CO2 Util. 2018, 28, 174–180. [Google Scholar] [CrossRef]
- Sarker, M.Z.I.; Selamat, J.; Habib, A.S.M.A.; Ferdosh, S.; Akanda, M.J.H.; Jaffri, J.M. Optimization of supercritical CO2 extraction of fish oil from viscera of African Catfish (Clarias gariepinus). Int. J. Mol. Sci. 2012, 13, 11312–11322. [Google Scholar] [CrossRef] [Green Version]
- McHugh, M.A.; Krukonis, V.J. Supercritical Fluid Extraction: Principles and Practice; Butterworth-Heinemann: Oxford, UK, 1994; ISBN 9780080518176. [Google Scholar]
- Reddy, V.; Saharay, M. Solubility of Caffeine in Supercritical CO2: A Molecular Dynamics Simulation Study. J. Phys. Chem. B 2019, 123, 9685–9691. [Google Scholar] [CrossRef]
- Woźniak, L.; Marszalek, K.; Skapska, S.; Jedrzejczak, R. The application of supercritical carbon dioxide and ethanol for the extraction of phenolic compounds from chokeberry pomace. Appl. Sci. 2017, 7, 322. [Google Scholar] [CrossRef] [Green Version]
- Artemenko, S.; Krijgsman, P.; Mazur, V. The Widom line for supercritical fluids. J. Mol. Liq. 2017, 238, 122–128. [Google Scholar] [CrossRef]
- Braeuer, A.; Dowy, S.; Leipertz, A.; Schatz, R.; Schluecker, E. Injection of ethanol into supercritical CO2: Determination of mole fraction and phase state using linear Raman scattering. Opt. Express 2007, 15, 8377. [Google Scholar] [CrossRef]
- Lalanne, P.; Tassaing, T.; Danten, Y.; Cansell, F.; Tucker, S.C.; Besnard, M. CO2-Ethanol Interaction Studied by Vibrational Spectroscopy in Supercritical CO2. J. Phys. Chem. A 2004, 108, 2617–2624. [Google Scholar] [CrossRef]
- Cordray, D.R.; Izatt, R.M.; Christensen, J.J.; Oscarson, J.L. Dortmund Data Bank. Available online: http://www.ddbst.com/en/EED/HE/HE Ethanol%3BCarbon dioxide.php (accessed on 7 December 2020).
- Day, C.Y.; Chang, C.J.; Chen, C.Y. Phase equilibrium of ethanol + CO2 and acetone + CO2 at elevated pressures. J. Chem. Eng. Data 1996, 41, 839–843. [Google Scholar] [CrossRef]
- Span, R.; Wagner, W. NIST Database. Available online: http://webbook.nist.gov/ (accessed on 9 September 2021).
- Yoon, T.J.; Ha, M.Y.; Lee, W.B.; Lee, Y.W. A corresponding-state framework for the structural transition of supercritical fluids across the Widom delta. J. Chem. Phys. 2019, 150, 154503. [Google Scholar] [CrossRef]
- Rycroft, C.H. VORO++: A three-dimensional Voronoi cell library in C++. Chaos 2009, 19, 41111. [Google Scholar] [CrossRef] [Green Version]
- Gorbaty, Y.; Bondarenko, G.V. Transition of liquid water to the supercritical state. J. Mol. Liq. 2017, 239, 5–9. [Google Scholar] [CrossRef]
- Nishikawa, K.; Tanaka, I.; Amemiya, Y. Small-Angle X-ray Scattering Study of Supercritical Carbon Dioxide. J. Phys. Chem. 1996, 100, 418–421. [Google Scholar] [CrossRef]
- Arakcheev, V.G.; Bagratashvili, V.N.; Valeev, A.A.B.; Gordienko, V.M.; Kireev, V.V.; Morozov, V.B.; Olenin, A.N.; Popov, V.K.; Tunkin, V.G.E.; Yakovlev, D.V. CARS spectroscopy of carbon dioxide in the critical point vicinity. Quantum Electron. 2007, 34, 86–90. [Google Scholar] [CrossRef]
- Morita, T.; Nishikawa, K.; Takematsu, M.; Iida, H.; Furutaka, S. Structure study of supercritical CO2 near high-order phase transition line by X-ray diffraction. J. Phys. Chem. B 1997, 101, 7158–7162. [Google Scholar] [CrossRef]
- Subramanlamr, B.; McHugh, M.A. Reactions in Supercritical Fluids—A Review. Ind. Eng. Chem. Process Des. Dev. 1986, 25, 1–12. [Google Scholar] [CrossRef]
- Oparin, R.D.; Krestyaninov, M.A.; Vorobyev, E.A.; Pokrovskiy, O.I.; Parenago, O.O.; Kiselev, M.G. An insight into possibility of chemical reaction between dense carbon dioxide and methanol. J. Mol. Liq. 2017, 239, 83–91. [Google Scholar] [CrossRef]
- Lazarev, A.V.; Tatarenko, K.A. Gas dynamic model of the expansion of a supercritical carbon dioxide pulse jet: A self-similar solution. Russ. J. Phys. Chem. B 2016, 10, 1248–1255. [Google Scholar] [CrossRef]
- Strong, S.E.; Shi, L.; Skinner, J.L. Percolation in supercritical water: Do the Widom and percolation lines coincide? J. Chem. Phys. 2018, 149, 084504. [Google Scholar] [CrossRef]
- Guevara-Carrion, G.; Ancherbak, S.; Mialdun, A.; Vrabec, J.; Shevtsova, V. Diffusion of methane in supercritical carbon dioxide across the Widom line. Sci. Rep. 2019, 9, 8466. [Google Scholar] [CrossRef]
- Bolmatov, D.; Zhernenkov, M.; Zav’yalov, D.; Tkachev, S.N.; Cunsolo, A.; Cai, Y.Q. The Frenkel Line: A direct experimental evidence for the new thermodynamic boundary. Sci. Rep. 2015, 5, 15850. [Google Scholar] [CrossRef] [Green Version]
- Plimpton, S. Fast Parallel Algorithms for Short–Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–42. [Google Scholar] [CrossRef] [Green Version]
- COMPASS. Force Field Manual; COMPASS: Calgary, AB, Canada, 1998; pp. 1–48. [Google Scholar]
- Jewett, A.I.; Stelter, D.; Lambert, J.; Saladi, S.M.; Roscioni, O.M.; Ricci, M.; Autin, L.; Maritan, M.; Bashusqeh, S.M.; Keyes, T.; et al. Moltemplate: A Tool for Coarse-Grained Modeling of Complex Biological Matter and Soft Condensed Matter Physics. J. Mol. Biol. 2021, 433, 166841. [Google Scholar] [CrossRef]
- Jewettaji, A. Ethanol Molecule. Available online: https://github.com/jewettaij/moltemplate/blob/master/examples/all_atom/force_field_OPLSAA/waterTIP5P+ethanol/moltemplate_files/ethanol.lt (accessed on 9 September 2021).
- Kohlmeyer, A. CO2 Molecule. Available online: https://github.com/lammps/lammps/blob/master/examples/gcmc/in.gcmc.co2 (accessed on 9 September 2021).
- Rigby, D. Fluid density predictions using the COMPASS force field. Fluid Phase Equilib. 2004, 217, 77–87. [Google Scholar] [CrossRef]
- Schneider, T.; Stoll, E. Molecular-dynamics study of a three-dimensional one-component model for distortive phase transitions. Phys. Rev. B 1978, 17, 1302–1322. [Google Scholar] [CrossRef]
- Berendsen, H.J.C.; Postma, J.P.M.; Van Gunsteren, W.F.; Dinola, A.; Haak, J.R. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 1984, 81, 3684–3690. [Google Scholar] [CrossRef] [Green Version]
- Goos, E.; Riedel, U.; Zhao, L.; Blum, L. Phase diagrams of CO2 and CO2-N2 gas mixtures and their application in compression processes. Energy Procedia 2011, 4, 3778–3785. [Google Scholar] [CrossRef] [Green Version]
- Marcus, Y. Extraction by subcritical and supercriticalwater, methanol, ethanol and their mixtures. Separations 2018, 5, 4. [Google Scholar] [CrossRef] [Green Version]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mareev, E.I.; Sviridov, A.P.; Gordienko, V.M. The Anomalous Behavior of Thermodynamic Parameters in the Three Widom Deltas of Carbon Dioxide-Ethanol Mixture. Int. J. Mol. Sci. 2021, 22, 9813. https://doi.org/10.3390/ijms22189813
Mareev EI, Sviridov AP, Gordienko VM. The Anomalous Behavior of Thermodynamic Parameters in the Three Widom Deltas of Carbon Dioxide-Ethanol Mixture. International Journal of Molecular Sciences. 2021; 22(18):9813. https://doi.org/10.3390/ijms22189813
Chicago/Turabian StyleMareev, Evgenii Igorevich, Alexander Petrovich Sviridov, and Vyacheslav Mihailovich Gordienko. 2021. "The Anomalous Behavior of Thermodynamic Parameters in the Three Widom Deltas of Carbon Dioxide-Ethanol Mixture" International Journal of Molecular Sciences 22, no. 18: 9813. https://doi.org/10.3390/ijms22189813
APA StyleMareev, E. I., Sviridov, A. P., & Gordienko, V. M. (2021). The Anomalous Behavior of Thermodynamic Parameters in the Three Widom Deltas of Carbon Dioxide-Ethanol Mixture. International Journal of Molecular Sciences, 22(18), 9813. https://doi.org/10.3390/ijms22189813





