Dimensional Changes in Lipid Rafts from Human Brain Cortex Associated to Development of Alzheimer’s Disease. Predictions from an Agent-Based Mathematical Model
Abstract
1. Introduction
2. Results
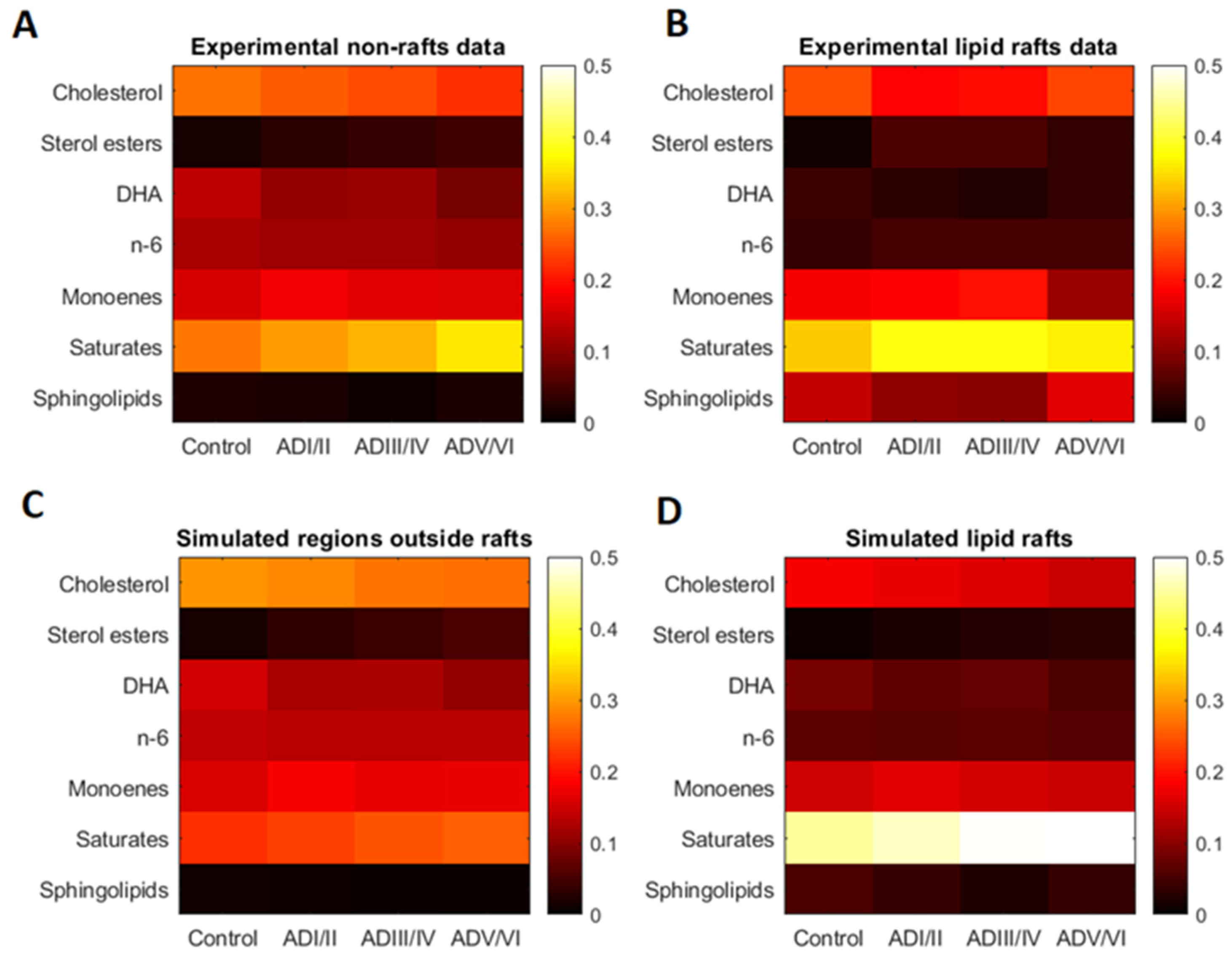
2.1. Lipid Classes Composition of Cell Membranes and Lipid Rafts in Human Frontal Cortex
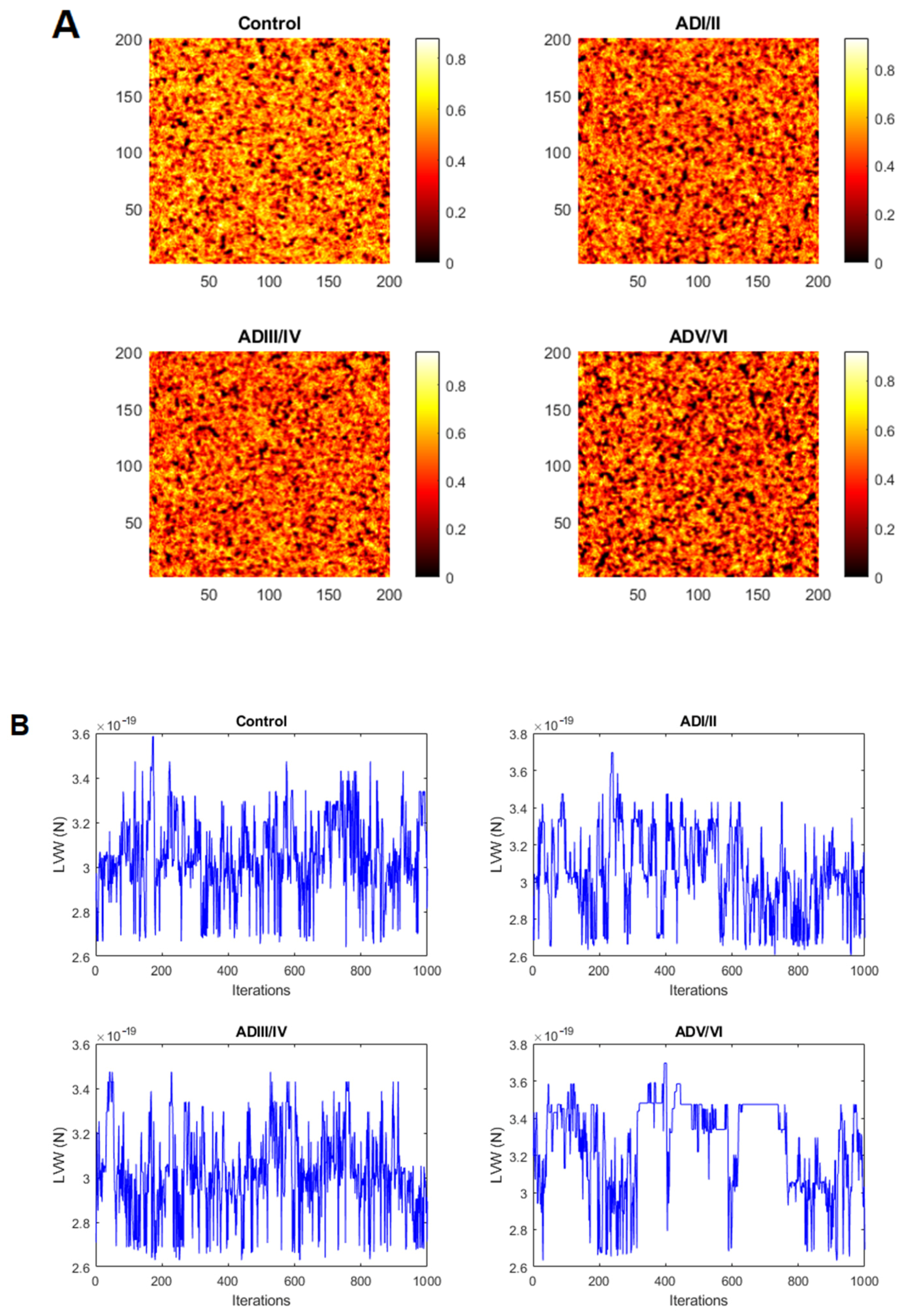
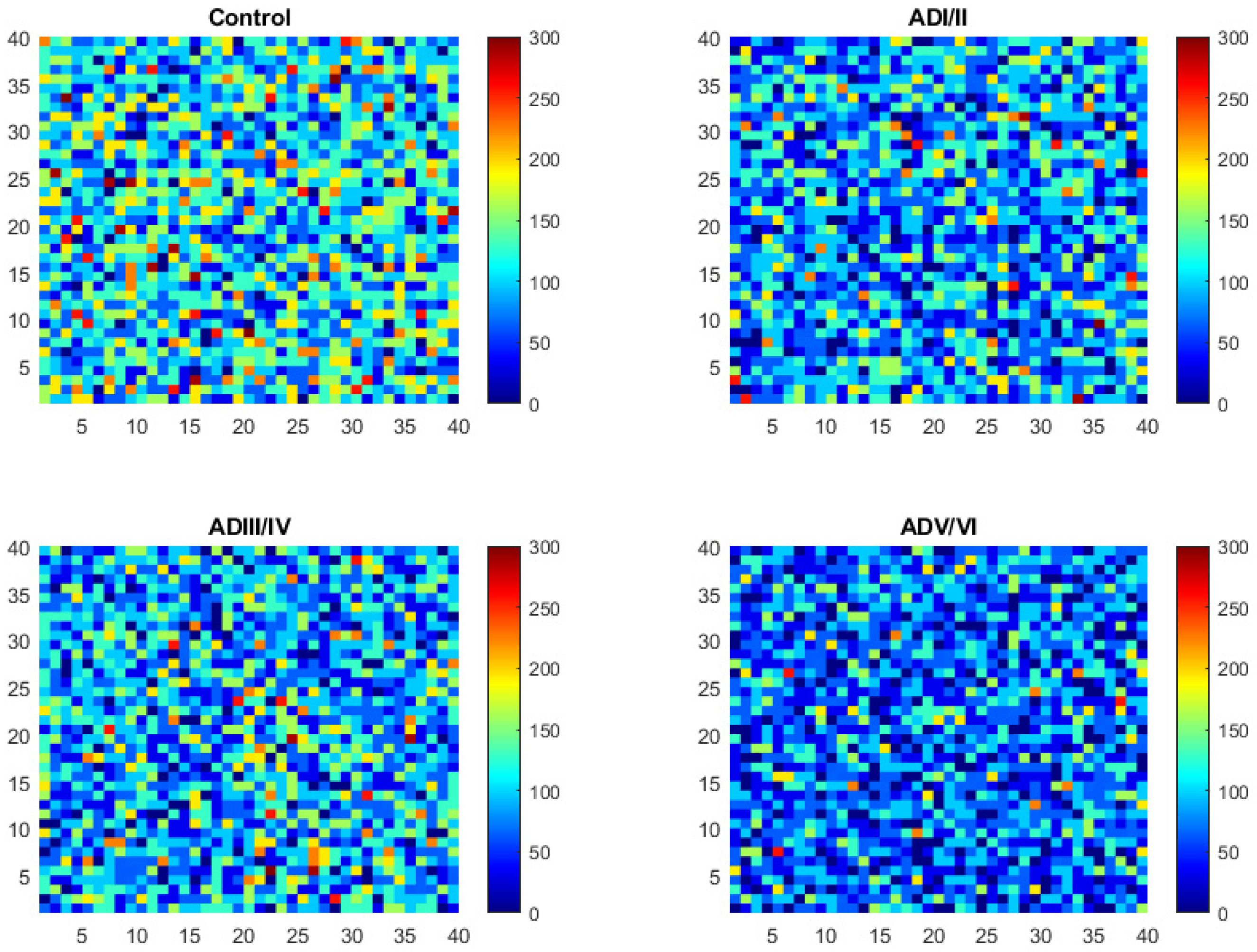
2.2. Simulation of Cell Membrane Domains during the Evolution of AD
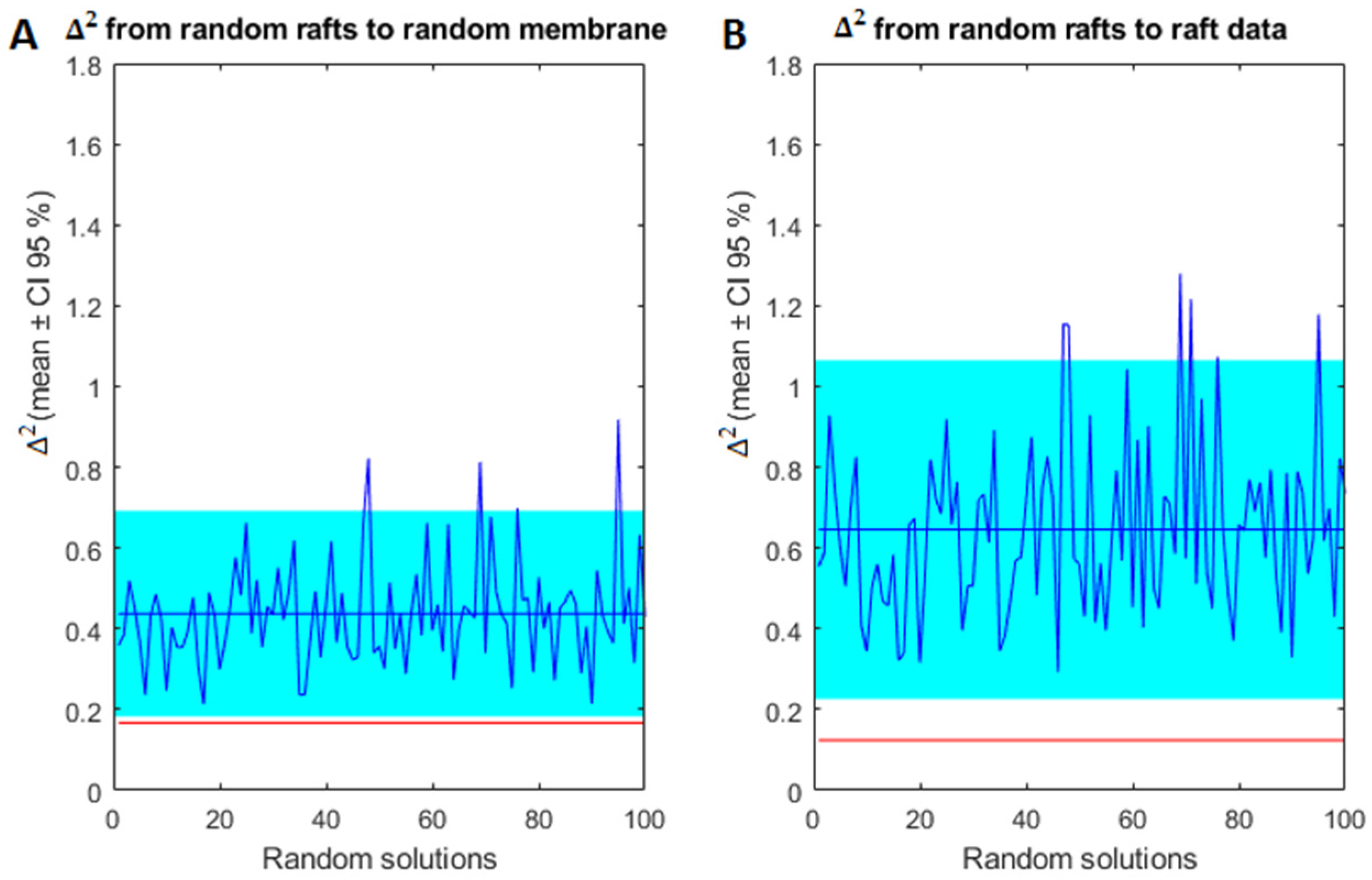
2.3. Model Validation of Frontal Cortex Lipid Raft Composition
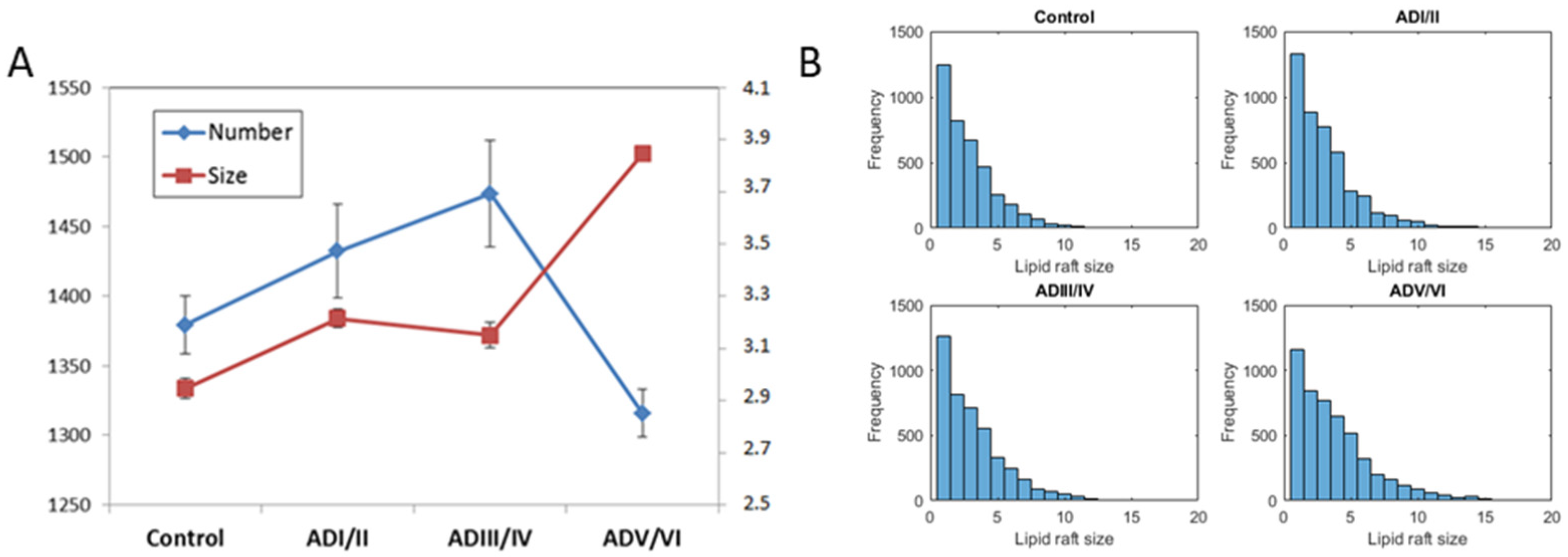
2.4. Prediction of the Number and Size of Lipid Rafts along Stages
2.5. Prediction of Membrane Peroxidability during the Evolution of AD
3. Discussion
4. Materials and Methods
4.1. Experimental Data
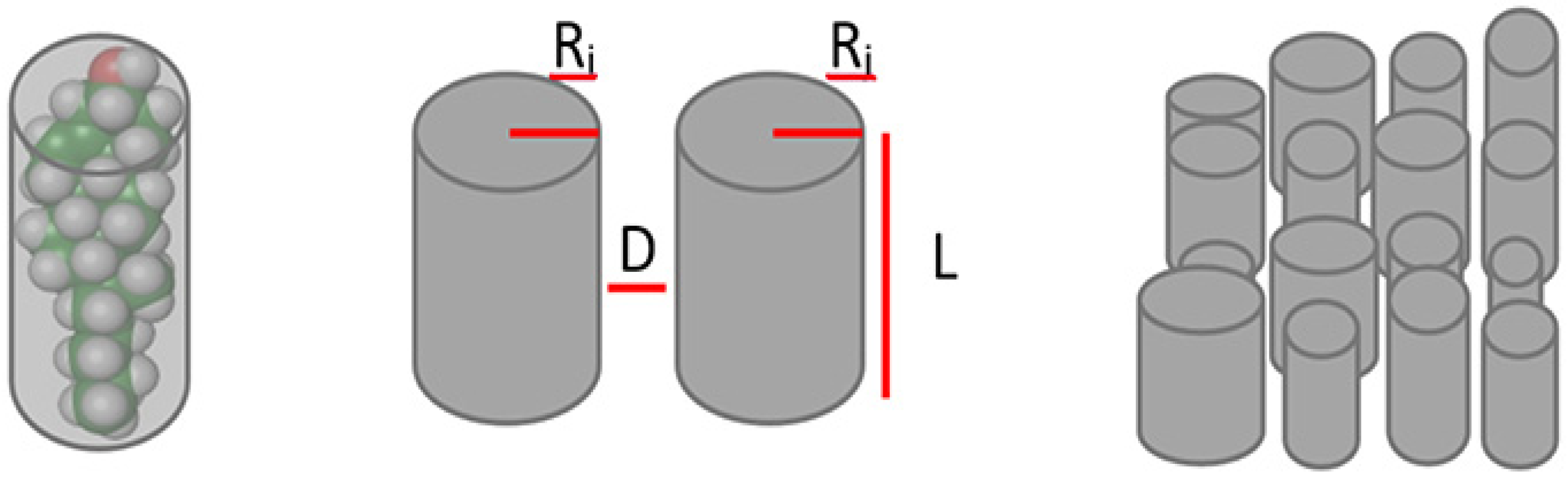
4.2. Mathematical Model
4.3. Simulations
4.4. Analysis of Results
4.5. Estimation of Lipid Rafts Number, Lipid Rafts Sizes and Membrane Peroxidability
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Ferri, C.P.; Prince, M.; Brayne, C.; Brodaty, H.; Fratiglioni, L.; Ganguli, M.; Hall, K.; Hasegawa, K.; Hendrie, H.; Huang, Y.; et al. Global prevalence of dementia: A Delphi consensus study. Lancet 2005, 366, 2112–2117. [Google Scholar] [CrossRef]
- Nehls, M. Unified theory of Alzheimer’s disease (UTAD): Implications for prevention and curative therapy. J. Mol. Psychiatry 2016, 4, 3. [Google Scholar] [CrossRef] [PubMed]
- Hampel, H.; Hardy, J.; Blennow, K.; Chen, C.; Perry, G.; Kim, S.H.; Villemagne, V.L.; Aisen, P.; Vendruscolo, M.; Iwatsubo, T.; et al. The Amyloid-β Pathway in Alzheimer’s Disease. Mol. Psychiatry 2021, 21, 1249. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.; Huang, X.; Yan, L.; Zhou, L.; Yan, C.; Wu, J.; Su, Z.; Huang, Y. The Structure Biology of Tau and Clue for Aggregation Inhibitor Design. Protein J. 2021, 40, 656–668. [Google Scholar] [CrossRef] [PubMed]
- Díaz, M.; Marin, R. Lipid rafts and development of Alzheimer’s disease. In Cerebral and Cerebellar Cortex–Interaction and Dynamics in Health and Disease; InTechOpen: London, UK, 2021; ISBN 978-1-83968-093-9. [Google Scholar]
- Allen, J.A.; Halverson-Tamboli, R.A.; Rasenick, M.M. Lipid raft microdomains and neurotransmitter signalling. Nat. Rev. Neurosci. 2006, 8, 128–140. [Google Scholar] [CrossRef] [PubMed]
- Tsui-Pierchala, B.A.; Encinas, M.; Milbrandt, J.; Johnson, E.M. Lipid rafts in neuronal signaling and function. Trends Neurosci. 2002, 25, 412–417. [Google Scholar] [CrossRef]
- Cheng, H.; Vetrivel, K.S.; Gong, P.; Meckler, X.; Parent, A.; Thinakaran, G. Mechanisms of Disease: New therapeutic strategies for Alzheimer’s disease—Targeting APP processing in lipid rafts. Nat. Clin. Pract. Neurol. 2007, 3, 374–382. [Google Scholar] [CrossRef]
- Hicks, D.A.; Nalivaeva, N.N.; Turner, A.J. Lipid Rafts and Alzheimer’s Disease: Protein-Lipid Interactions and Perturbation of Signaling. Front. Physiol. 2012, 3, 189. [Google Scholar] [CrossRef]
- Cordy, J.M.; Hooper, N.; Turner, A.J. The involvement of lipid rafts in Alzheimer’s disease (Review). Mol. Membr. Biol. 2006, 23, 111–122. [Google Scholar] [CrossRef]
- Díaz, M.; Fabelo, N.; Martín, V.; Ferrer, I.; Gómez, T.; Marín, R. Biophysical Alterations in Lipid Rafts from Human Cerebral Cortex Associate with Increased BACE1/AβPP Interaction in Early Stages of Alzheimer’s Disease. J. Alzheimer’s Dis. 2014, 43, 1185–1198. [Google Scholar] [CrossRef]
- Diaz, M.L.; Fabelo, N.; Marín, R. Genotype-induced changes in biophysical properties of frontal cortex lipid raft from APP/PS1 transgenic mice. Front. Physiol. 2012, 3, 454. [Google Scholar] [CrossRef]
- Fabelo, N.; Martín, M.V.; Marín, R.; Santpere, G.; Aso, E.; Ferrer, I.; Díaz, M. Evidence for Premature Lipid Raft Aging in APP/PS1 Double-Transgenic Mice, a Model of Familial Alzheimer Disease. J. Neuropathol. Exp. Neurol. 2012, 71, 868–881. [Google Scholar] [CrossRef]
- Fabelo, N.; Martín, V.; Marín, R.; Moreno, D.; Ferrer, I.; Díaz, M. Altered lipid composition in cortical lipid rafts occurs at early stages of sporadic Alzheimer’s disease and facilitates APP/BACE1 interactions. Neurobiol. Aging 2014, 35, 1801–1812. [Google Scholar] [CrossRef]
- Martín, V.; Fabelo, N.; Santpere, G.; Puig, B.; Marín, R.; Ferrer, I.; Díaz, M. Lipid Alterations in Lipid Rafts from Alzheimer’s Disease Human Brain Cortex. J. Alzheimer’s Dis. 2010, 19, 489–502. [Google Scholar] [CrossRef] [PubMed]
- Casañas-Sánchez, V.; Pérez, J.A.; Fabelo, N.; Alemany, D.Q.; Díaz, M.L. Docosahexaenoic (DHA) modulates phospholipid-hydroperoxide glutathione peroxidase (Gpx4) gene expression to ensure self-protection from oxidative damage in hippocampal cells. Front. Physiol. 2015, 6, 203. [Google Scholar] [CrossRef] [PubMed]
- Patrick, R.P. Role of phosphatidylcholine-DHA in preventing APOE4-associated Alzheimer’s disease. FASEB J. 2019, 33, 1554–1564. [Google Scholar] [CrossRef] [PubMed]
- Yuki, D.; Sugiura, Y.; Zaima, N.; Akatsu, H.; Takei, S.; Yao, I.; Maesako, M.; Kinoshita, A.; Yamamoto, T.; Kon, R.; et al. DHA-PC and PSD-95 decrease after loss of synaptophysin and before neuronal loss in patients with Alzheimer’s disease. Sci. Rep. 2014, 4, 7130. [Google Scholar] [CrossRef]
- Hartmann, T.; Kuchenbecker, J.; Grimm, M. Alzheimer’s disease: The lipid connection. J. Neurochem. 2007, 103, 159–170. [Google Scholar] [CrossRef]
- Huang, T.L. Omega-3 Fatty Acids, Cognitive Decline, and Alzheimer’s Disease: A Critical Review and Evaluation of the Literature. J. Alzheimer’s Dis. 2010, 21, 673–690. [Google Scholar] [CrossRef]
- Oster, T.; Pillot, T. Docosahexaenoic acid and synaptic protection in Alzheimer’s disease mice. Biochim. Biophys. Acta (BBA)-Mol. Cell Biol. Lipids 2010, 1801, 791–798. [Google Scholar] [CrossRef]
- Stillwell, W.; Wassall, S.R. Docosahexaenoic acid: Membrane properties of a unique fatty acid. Chem. Phys. Lipids 2003, 126, 1–27. [Google Scholar] [CrossRef]
- Aso, E.; Lomoio, S.; Gonzalez, M.D.; Joda, L.; Carmona, M.; Fernández-Yagüe, N.; Jiménez-Moreno, J.; José, A.; Juvés, S.; Pujol, A.; et al. Amyloid Generation and Dysfunctional Immunoproteasome Activation with Disease Progression in Animal Model of Familial Alzheimer’s Disease. Brain Pathol. 2011, 22, 636–653. [Google Scholar] [CrossRef] [PubMed]
- Santos, G.; Díaz, M.; Torres, N.V. Lipid Raft Size and Lipid Mobility in Non-raft Domains Increase during Aging and Are Exacerbated in APP/PS1 Mice Model of Alzheimer’s Disease. Predictions from an Agent-Based Mathematical Model. Front. Physiol. 2016, 7, 90. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Risselada, H.J.; Marrink, S.J. The Molecular Face of Lipid Rafts in Model Membranes. Proc. Natl. Acad. Sci. USA 2008, 105, 17367–17372. [Google Scholar] [CrossRef]
- Marrink, S.J.; de Vries, A.H.; Harroun, T.A.; Katsaras, J.; Wassall, S.R. Cholesterol Shows Preference for the Interior of Polyunsaturated Lipid Membranes. J. Am. Chem. Soc. 2008, 130, 10–11. [Google Scholar] [CrossRef] [PubMed]
- Perlmutter, J.D.; Sachs, J.N. Interleaflet Interaction and Asymmetry in Phase Separated Lipid Bilayers: Molecular Dynamics Simulations. J. Am. Chem. Soc. 2011, 133, 6563–6577. [Google Scholar] [CrossRef]
- Kučerka, N.; Marquardt, D.; Harroun, T.A.; Nieh, M.-P.; Wassall, S.R.; de Jong, D.H.; Schäfer, L.V.; Marrink, S.J.; Katsaras, J. Cholesterol in Bilayers with PUFA Chains: Doping with DMPC or POPC Results in Sterol Reorientation and Membrane-Domain Formation. Biochemistry 2010, 49, 7485–7493. [Google Scholar] [CrossRef]
- Fischer, T.; Risselada, H.J.; Vink, R.L.C. Membrane Lateral Structure: The Influence of Immobilized Particles on Domain Size. Phys. Chem. Chem. Phys. 2012, 14, 14500–14508. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Wurthner, J.U.; Mukhopadhyay, A.K.; Peimann, C.J. A Cellular Automaton Model of Cellular Signal Transduction. Comput. Biol. Med. 2000, 30, 1–21. [Google Scholar] [CrossRef]
- Braak, H.; Braak, E. Evolution of neuronal changes in the course of Alzheimer’s disease. J. Neural Transm. Suppl. 1998, 53, 127–140. [Google Scholar] [CrossRef]
- Catalá, A.; Díaz, M. Editorial: Impact of Lipid Peroxidation on the Physiology and Pathophysiology of Cell Membranes. Front. Physiol. 2016, 7, 423. [Google Scholar] [CrossRef] [PubMed]
- Cosgrove, J.P.; Church, D.F.; Pryor, W.A. The Kinetics of the Autoxidation of Polyunsaturated Fatty Acids. Lipids 1987, 22, 299–304. [Google Scholar] [CrossRef] [PubMed]
- Hamaker, H.C. The London—Van der Waals attraction between spherical particles. Physica 1937, 4, 1058–1072. [Google Scholar] [CrossRef]
- Duyckaerts, C.; Dickson, D. Neuropathology of Alzheimer’s disease and its variants. In Neurodegeneration: The Molecular Pathology of Dementia and Movement Disorders, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2011; pp. 62–91. ISBN 978-1-4443-4125-6. [Google Scholar]
- Pimenova, A.; Raj, T.; Goate, A.M. Untangling Genetic Risk for Alzheimer’s Disease. Biol. Psychiatry 2018, 83, 300–310. [Google Scholar] [CrossRef] [PubMed]
- Hal, D.R.; Rüb, U.; Orantes, M.; Braak, H. Phases of Aβ-deposition in the human brain and its relevance for the development of AD. Neurology 2002, 58, 1791–1800. [Google Scholar] [CrossRef]
- Marin, R.; Diaz, M. Estrogen Interactions with Lipid Rafts Related to Neuroprotection. Impact of Brain Ageing and Menopause. Front. Neurosci. 2018, 12, 128. [Google Scholar] [CrossRef] [PubMed]
- Niemelä, P.S.; Hyvönen, M.T.; Vattulainen, I. Atom-scale molecular interactions in lipid raft mixtures. Biochim. Biophys. Acta (BBA)-Biomembr. 2009, 1788, 122–135. [Google Scholar] [CrossRef][Green Version]
- De Strooper, B.; Vassar, R.; Golde, T. The secretases: Enzymes with therapeutic potential in Alzheimer disease. Nat. Rev. Neurol. 2010, 6, 99–107. [Google Scholar] [CrossRef]
- Selkoe, D.J.; Hardy, J. The amyloid hypothesis of Alzheimer’s disease at 25 years. EMBO Mol. Med. 2016, 8, 595–608. [Google Scholar] [CrossRef]
- Das, U.; Scott, D.A.; Ganguly, A.; Koo, E.H.; Tang, Y.; Roy, S. Activity-Induced Convergence of APP and BACE-1 in Acidic Microdomains via an Endocytosis-Dependent Pathway. Neuron 2013, 79, 447–460. [Google Scholar] [CrossRef]
- Müller, W.E.; Kirsch, C.; Eckert, G.P. Membrane-Disordering Effects of Beta-Amyloid Peptides. Biochem. Soc. Trans. 2001, 29, 617–623. [Google Scholar] [CrossRef]
- Wood, W.; Schroeder, F.; Igbavboa, U.; Avdulov, N.A.; Chochina, S.V.; Avdulov, N. Brain membrane cholesterol domains, aging and amyloid beta-peptides. Neurobiol. Aging 2002, 23, 685–694. [Google Scholar] [CrossRef]
- Buccellato, F.R.; D’Anca, M.; Fenoglio, C.; Scarpini, E.; Galimberti, D. Role of Oxidative Damage in Alzheimer’s Disease and Neurodegeneration: From Pathogenic Mechanisms to Biomarker Discovery. Antioxidants 2021, 10, 1353. [Google Scholar] [CrossRef] [PubMed]
- Collin, F. Chemical Basis of Reactive Oxygen Species Reactivity and Involvement in Neurodegenerative Diseases. Int. J. Mol. Sci. 2019, 20, 2407. [Google Scholar] [CrossRef]
- Lei, P.; Ayton, S.; Bush, A.I. The essential elements of Alzheimer’s disease. J. Biol. Chem. 2021, 296, 100105. [Google Scholar] [CrossRef] [PubMed]
- Zhang, G.; Zhang, Y.; Shen, Y.; Wang, Y.; Zhao, M.; Sun, L. The Potential Role of Ferroptosis in Alzheimer’s Disease. J. Alzheimer’s Dis. 2021, 80, 907–925. [Google Scholar] [CrossRef]
- Catalá, A. Lipid peroxidation of membrane phospholipids generates hydroxy-alkenals and oxidized phospholipids active in physiological and/or pathological conditions. Chem. Phys. Lipids 2009, 157, 1–11. [Google Scholar] [CrossRef]
- Díaz, M.; Mesa-Herrera, F.; Marín, R. DHA and Its Elaborated Modulation of Antioxidant Defenses of the Brain: Implications in Aging and AD Neurodegeneration. Antioxidants 2021, 10, 907. [Google Scholar] [CrossRef]
- Ferrer, I. Altered mitochondria, energy metabolism, voltage-dependent anion channel, and lipid rafts converge to exhaust neurons in Alzheimer’s disease. J. Bioenerg. Biomembr. 2009, 41, 425–431. [Google Scholar] [CrossRef]
- Israelachvili, J.N. Intermolecular and Surface Forces, 3rd ed.; Academic Press: Cambridge, MA, USA, 2011; ISBN 978-0-12-391927-4. [Google Scholar]

| (A) Frontal Cortex Lipid Rafts | (B) Frontal Cortex Cell Membrane | |||||||
|---|---|---|---|---|---|---|---|---|
| Control | ADI/II | ADIII/IV | ADV/VI | Control | ADI/II | ADIII/IV | ADV/VI | |
| Cholesterol | 24.57 | 18.87 | 19.40 | 23.78 | 27.06 | 25.24 | 24.05 | 22.20 |
| Sterol esters | 1.20 | 5.57 | 5.33 | 3.69 | 1.58 | 2.96 | 3.81 | 4.51 |
| DHA | 4.28 | 3.16 | 2.42 | 3.66 | 13.73 | 10.66 | 11.16 | 8.68 |
| n-6 LCPUFA | 3.95 | 4.95 | 4.90 | 4.89 | 12.19 | 11.41 | 11.49 | 10.69 |
| Monoenes | 18.01 | 18.71 | 19.81 | 11.31 | 15.71 | 17.72 | 16.53 | 16.29 |
| Saturates | 33.54 | 38.26 | 38.03 | 36.18 | 27.47 | 30.10 | 31.90 | 35.67 |
| Sphingolipids | 14.45 | 10.49 | 10.10 | 16.49 | 2.26 | 1.92 | 1.06 | 1.97 |
| Width (Radius Å) | Length (Å) | |
|---|---|---|
| Cholesterol | 5.94 | 19.99 |
| Sterol esters | 5.94 | 19.99 |
| DHA | 6.74 | 19.01 |
| n-6 LCPUFA | 5.84 | 19.70 |
| Monoenoic fatty acids | 5.30 | 22.59 |
| Saturated fatty acids | 6.14 | 22.44 |
| Sphingolipids | 6.18 | 22.44 |
| Intermolecular distance (Å) | 1.50 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Santos, G.; Díaz, M. Dimensional Changes in Lipid Rafts from Human Brain Cortex Associated to Development of Alzheimer’s Disease. Predictions from an Agent-Based Mathematical Model. Int. J. Mol. Sci. 2021, 22, 12181. https://doi.org/10.3390/ijms222212181
Santos G, Díaz M. Dimensional Changes in Lipid Rafts from Human Brain Cortex Associated to Development of Alzheimer’s Disease. Predictions from an Agent-Based Mathematical Model. International Journal of Molecular Sciences. 2021; 22(22):12181. https://doi.org/10.3390/ijms222212181
Chicago/Turabian StyleSantos, Guido, and Mario Díaz. 2021. "Dimensional Changes in Lipid Rafts from Human Brain Cortex Associated to Development of Alzheimer’s Disease. Predictions from an Agent-Based Mathematical Model" International Journal of Molecular Sciences 22, no. 22: 12181. https://doi.org/10.3390/ijms222212181
APA StyleSantos, G., & Díaz, M. (2021). Dimensional Changes in Lipid Rafts from Human Brain Cortex Associated to Development of Alzheimer’s Disease. Predictions from an Agent-Based Mathematical Model. International Journal of Molecular Sciences, 22(22), 12181. https://doi.org/10.3390/ijms222212181







