Electron-Induced Repair of 2′-Deoxyribose Sugar Radicals in DNA: A Density Functional Theory (DFT) Study
Abstract
:1. Introduction
2. Methods of Calculation
3. Results and Discussion
3.1. Structures and Populations
3.1.1. Sugar Radicals
3.1.2. One-Electron Reduced Sugar Radicals (Anions)
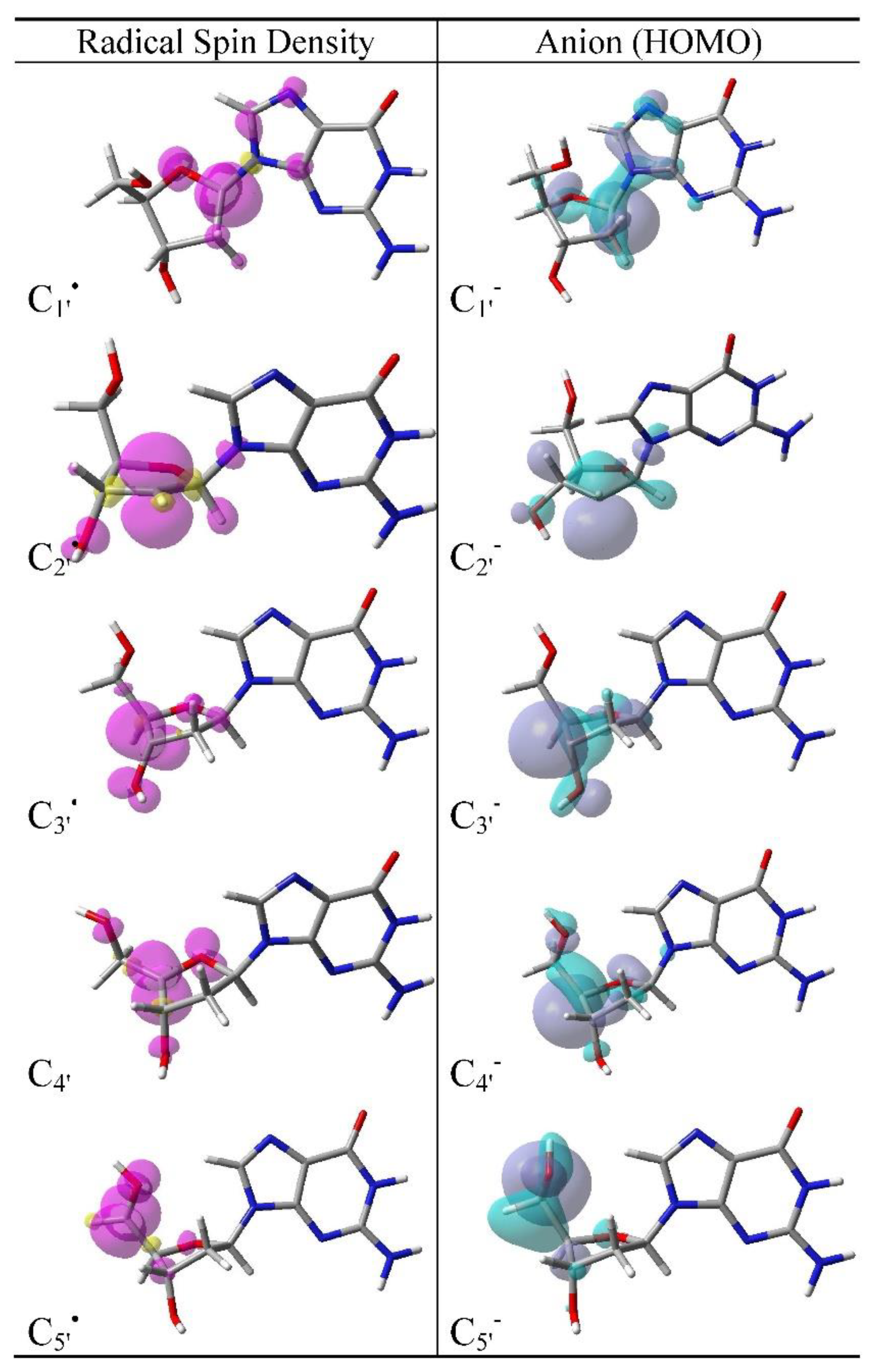
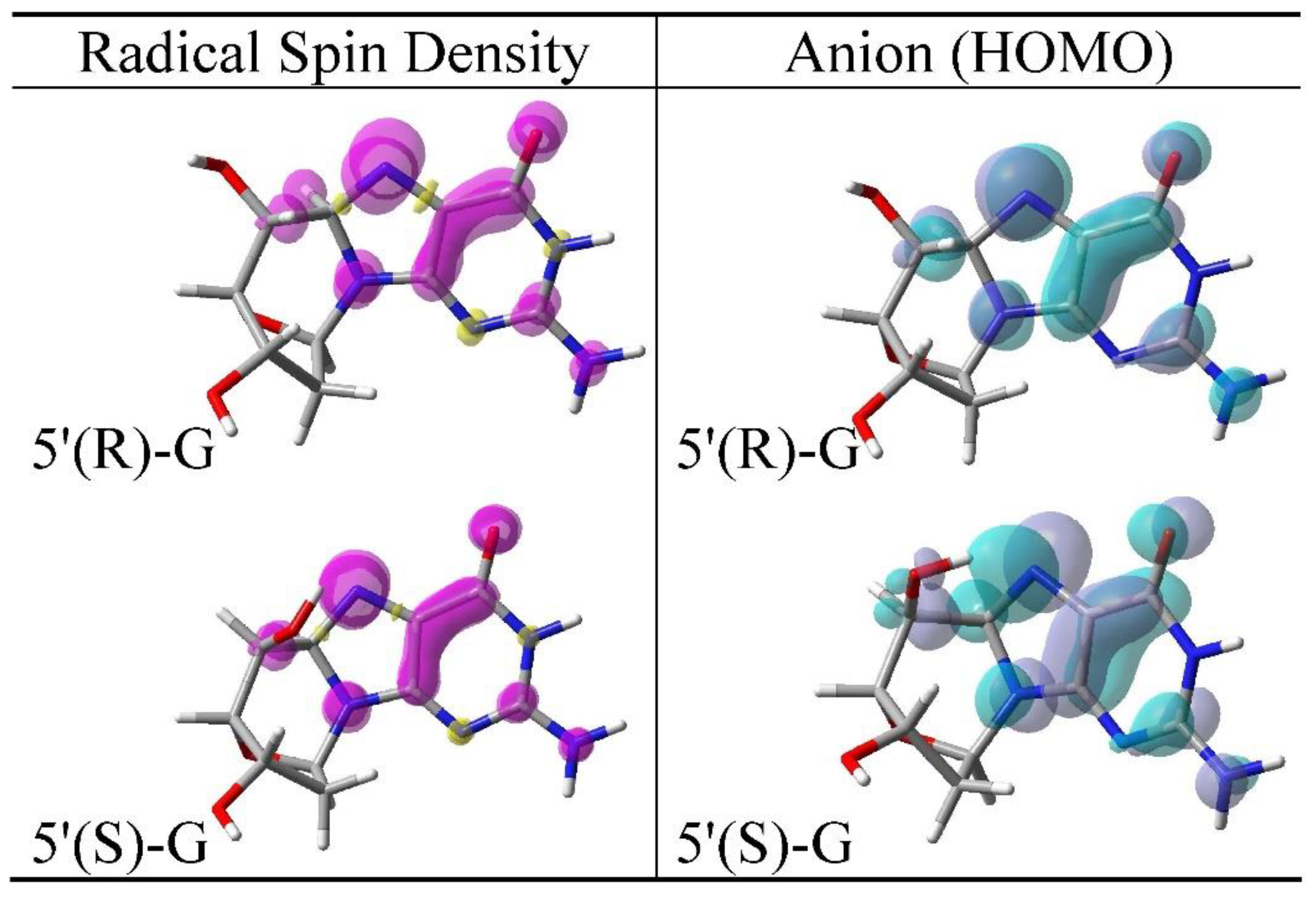
3.2. Spin Density Distributions of Sugar Radicals and HOMO of Their Anions
3.3. Electron Affinity and Reduction Potential (E°) of Sugar Radicals
3.4. Cyclization of C5′• and C8 of Guanine
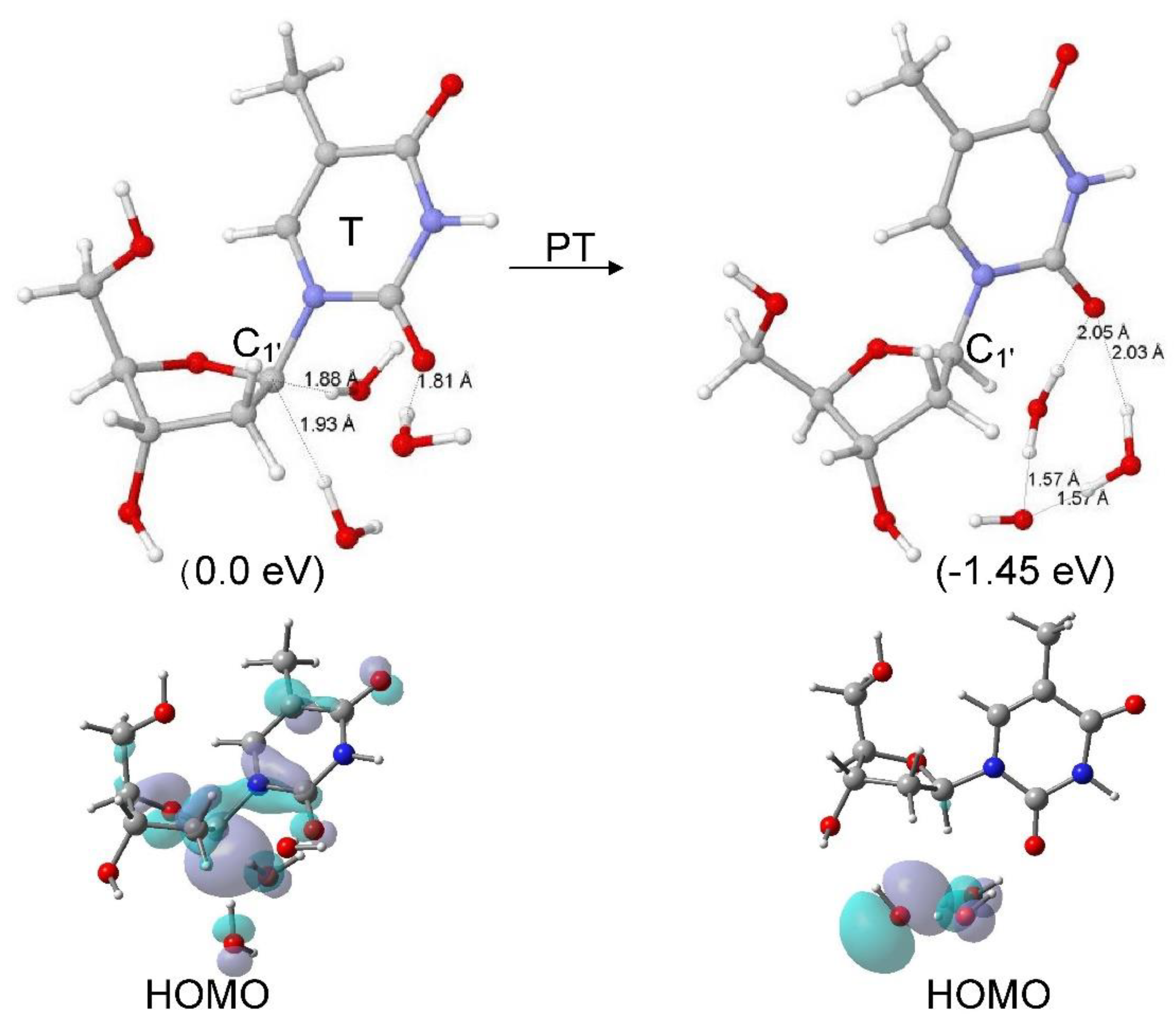
4. Protonation of Reduced Sugar Radicals from Water
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- von Sonntag, C. Free-Radical-Induced DNA Damage and Its Repair: A Chemical Perspective; Springer: Berlin, Germany, 2006; ISBN 978-3-540-26120-9. [Google Scholar]
- Kumar, A.; Sevilla, M.D. Proton-coupled electron transfer in DNA on formation of radiation-produced ion radicals. Chem. Rev. 2010, 110, 7002–7023. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Sevilla, M.D. DFT treatment of radiation produced radicals in DNA model systems. In Advances in Quantum Chemistry; Sabin, J.R., Brändas, E., Eds.; Academic Press: Cambridge, MA, USA, 2007; Volume 52, pp. 59–87. [Google Scholar]
- Sevilla, M.D.; Becker, D.; Yan, M.; Summerfield, S.R. Relative abundances of primary ion radicals in γ-irradiated DNA: Cytosine vs. thymine anions and guanine vs. adenine cations. J. Phys. Chem. 1991, 95, 3409–3415. [Google Scholar] [CrossRef]
- Yan, M.; Becker, D.; Summerfield, S.; Renke, P.; Sevilla, M.D. Relative abundance and reactivity of primary ion radicals in Gamma.-irradiated DNA at low temperatures. 2. Single-vs double-stranded DNA. J. Phys. Chem. 1992, 96, 1983–1989. [Google Scholar] [CrossRef]
- Kumar, A.; Sevilla, M.D. Theoretical Modeling of Radiation-Induced DNA Damage. In Radical and Radical Ion Reactivity in Nucleic Acid Chemistry; Greenberg, M.M., Ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2009; pp. 1–40. ISBN 978-0-470-52627-9. [Google Scholar]
- Kumar, A.; Sevilla, M.D. Radiation effects on DNA: Theoretical investigations of electron, hole and excitation pathways to DNA damage. In Radiation Induced Molecular Phenomena in Nucleic Acids; Shukla, M.K., Leszczynski, J., Eds.; Challenges and Advances in Computational Chemistry and Physics; Springer: Amsterdam, The Netherlands, 2008; pp. 577–617. ISBN 978-1-4020-8183-5. [Google Scholar]
- Kumar, A.; Becker, D.; Adhikary, A.; Sevilla, M.D. Reaction of electrons with DNA: Radiation damage to radiosensitization. Int. J. Mol. Sci. 2019, 20, 3998. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Swiderek, P. Fundamental processes in radiation damage of DNA. Angew. Chem. Int. Ed. 2006, 45, 4056–4059. [Google Scholar] [CrossRef]
- Becker, D.; Sevilla, M.D. The chemical consequences of radiation damage to DNA. In Advances in Radiation Biology; Elsevier: Amsterdam, The Netherlands, 1993; Volume 17, pp. 121–180. ISBN 978-0-12-035417-7. [Google Scholar]
- Becker, D.; Kumar, A.; Adhikary, A.; Sevilla, M.D. Gamma- and Ion-beam DNA radiation damage: Theory and experiment. In DNA Damage, DNA Repair and Disease; Dizdaroglu, M., Lloyd, R.S., Eds.; Royal Society of Chemistry: Croydon, UK, 2020; Volume 2, ISBN 978-1-83916-251-0. [Google Scholar]
- Kuznetsova, A.A.; Knorre, D.G.; Fedorova, O.S. Oxidation of DNA and its components with reactive oxygen species. Russ. Chem. Rev. 2009, 78, 659–678. [Google Scholar] [CrossRef]
- Patel, R.P.; McAndrew, J.; Sellak, H.; White, C.R.; Jo, H.; Freeman, B.A.; Darley-Usmar, V.M. Biological aspects of reactive nitrogen species. Biochim. Biophys. Acta BBA Bioenerg. 1999, 1411, 385–400. [Google Scholar] [CrossRef] [Green Version]
- Becker, D.; Bryant-Friedrich, A.; Trzasko, C.; Sevilla, M.D. Electron spin resonance study of DNA irradiated with an argon-ion beam: Evidence for formation of sugar phosphate backbone radicals. Radiat. Res. 2003, 160, 174–185. [Google Scholar] [CrossRef]
- Becker, D.; Razskazovskii, Y.; Callaghan, M.U.; Sevilla, M.D. Electron spin resonance of DNA irradiated with a heavy-ion beam (16O8+): Evidence for damage to the deoxyribose phosphate backbone. Radiat. Res. 1996, 146, 361–368. [Google Scholar] [CrossRef] [PubMed]
- Shukla, L.I.; Pazdro, R.; Huang, J.; DeVreugd, C.; Becker, D.; Sevilla, M.D. The formation of DNA sugar radicals from photoexcitation of guanine cation radicals. Radiat. Res. 2004, 161, 582–590. [Google Scholar] [CrossRef]
- Shukla, L.I.; Pazdro, R.; Becker, D.; Sevilla, M.D. Sugar radicals in DNA: Isolation of neutral radicals in gamma-irradiated DNA by hole and electron scavenging. Radiat. Res. 2005, 163, 591–602. [Google Scholar] [CrossRef]
- Adhikary, A.; Kumar, A.; Sevilla, M.D. Photo-induced hole transfer from base to sugar in DNA: Relationship to primary radiation damage. Radiat. Res. 2006, 165, 479–484. [Google Scholar] [CrossRef]
- Adhikary, A.; Collins, S.; Khanduri, D.; Sevilla, M.D. Sugar radicals formed by photoexcitation of guanine cation radical in oligonucleotides. J. Phys. Chem. B 2007, 111, 7415–7421. [Google Scholar] [CrossRef] [Green Version]
- Adhikary, A.; Khanduri, D.; Kumar, A.; Sevilla, M.D. Photoexcitation of adenine cation radical [A+] in the near UV−vis region produces sugar radicals in adenosine and in its nucleotides. J. Phys. Chem. B 2008, 112, 15844–15855. [Google Scholar] [CrossRef] [Green Version]
- Khanduri, D.; Collins, S.; Kumar, A.; Adhikary, A.; Sevilla, M.D. Formation of sugar radicals in RNA model systems and oligomers via excitation of guanine cation radical. J. Phys. Chem. B 2008, 112, 2168–2178. [Google Scholar] [CrossRef]
- Adhikary, A.; Malkhasian, A.Y.S.; Collins, S.; Koppen, J.; David, D.; Sevilla, M.D. UVA-visible photo-excitation of guanine radical cations produces sugar radicals in DNA and model structures. Nucleic Acids Res. 2005, 33, 5553–5564. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Adhikary, A.; Becker, D.; Collins, S.; Koppen, J.; Sevilla, M.D. C5’- and C3’-sugar radicals produced via photo-excitation of one-electron oxidized adenine in 2’-deoxyadenosine and its derivatives. Nucleic Acids Res. 2006, 34, 1501–1511. [Google Scholar] [CrossRef] [Green Version]
- Kumar, A.; Sevilla, M.D. Photoexcitation of dinucleoside radical cations: A time-dependent density functional study. J. Phys. Chem. B 2006, 110, 24181–24188. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bernhard, W.A. Radical reaction pathways initiated by direct energy deposition in DNA by ionizing radiation. In Radical and Radical Ion Reactivity in Nucleic Acid Chemistry; Greenberg, M.M., Ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2009; pp. 41–68. ISBN 978-0-470-52627-9. [Google Scholar]
- Close, D.M. Where are the sugar radicals in irradiated DNA? Radiat. Res. 1997, 147, 663–673. [Google Scholar] [CrossRef] [PubMed]
- Kumar, A.; Sevilla, M.D. Sugar radical formation by a proton coupled hole transfer in 2′-deoxyguanosine radical cation (2′-DG+): A theoretical treatment. J. Phys. Chem. B 2009, 113, 13374–13380. [Google Scholar] [CrossRef] [Green Version]
- Swarts, S.G.; Sevilla, M.D.; Becker, D.; Tokar, C.J.; Wheeler, K.T. Radiation-induced DNA damage as a function of hydration: I. release of unaltered bases. Radiat. Res. 1992, 129, 333–344. [Google Scholar] [CrossRef]
- Breen, A.P.; Murphy, J.A. Reactions of oxyl radicals with DNA. Free Radic. Biol. Med. 1995, 18, 1033–1077. [Google Scholar] [CrossRef]
- Chatgilialoglu, C. Reactivity of nucleic acid sugar radicals. In Radical and Radical Ion Reactivity in Nucleic Acid Chemistry; Greenberg, M.M., Ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2009; pp. 99–133. ISBN 978-0-470-52627-9. [Google Scholar]
- Greenberg, M.M. Pyrimidine nucleobase radical reactivity. In Radical and Radical Ion Reactivity in Nucleic Acid Chemistry; Greenberg, M.M., Ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2009; pp. 135–162. ISBN 978-0-470-52627-9. [Google Scholar]
- Steenken, S. Purine bases, nucleosides, and nucleotides: Aqueous solution redox chemistry and transformation reactions of their radical cations And e- and OH adducts. Chem. Rev. 1989, 89, 503–520. [Google Scholar] [CrossRef]
- Kumar, A.; Pottiboyina, V.; Sevilla, M.D. Hydroxyl radical (OH) reaction with guanine in an aqueous environment: A DFT study. J. Phys. Chem. B 2011, 115, 15129–15137. [Google Scholar] [CrossRef] [Green Version]
- Phadatare, S.D.; Sharma, K.K.K.; Rao, B.S.M.; Naumov, S.; Sharma, G.K. Spectral characterization of guanine C4-OH adduct: A radiation and quantum chemical study. J. Phys. Chem. B 2011, 115, 13650–13658. [Google Scholar] [CrossRef] [PubMed]
- Chatgilialoglu, C.; D’Angelantonio, M.; Guerra, M.; Kaloudis, P.; Mulazzani, Q.G. A reevaluation of the ambident reactivity of the guanine moiety towards hydroxyl radicals. Angew. Chem. Int. Ed. 2009, 48, 2214–2217. [Google Scholar] [CrossRef] [PubMed]
- Gervasio, F.L.; Laio, A.; Iannuzzi, M.; Parrinello, M. Influence of DNA structure on the reactivity of the guanine radical cation. Chem. Eur. J. 2004, 10, 4846–4852. [Google Scholar] [CrossRef] [PubMed]
- Adhikary, A.; Kumar, A.; Heizer, A.N.; Palmer, B.J.; Pottiboyina, V.; Liang, Y.; Wnuk, S.F.; Sevilla, M.D. Hydroxyl ion addition to one-electron oxidized thymine: Unimolecular interconversion of C5 to C6 OH-adducts. J. Am. Chem. Soc. 2013, 135, 3121–3135. [Google Scholar] [CrossRef] [Green Version]
- Balasubramanian, B.; Pogozelski, W.K.; Tullius, T.D. DNA strand breaking by the hydroxyl radical is governed by the accessible surface areas of the hydrogen atoms of the DNA backbone. Proc. Natl. Acad. Sci. USA 1998, 95, 9738–9743. [Google Scholar] [CrossRef] [Green Version]
- Pogozelski, W.K.; Tullius, T.D. Oxidative strand scission of nucleic acids: Routes initiated by hydrogen abstraction from the sugar moiety. Chem. Rev. 1998, 98, 1089–1108. [Google Scholar] [CrossRef]
- Pratviel, G.; Bernadou, J.; Meunier, B. Carbon—Hydrogen bonds of DNA sugar units as targets for chemical nucleases and drugs. Angew. Chem. Int. Ed. Engl. 1995, 34, 746–769. [Google Scholar] [CrossRef]
- Dedon, P.C. The chemical toxicology of 2-deoxyribose oxidation in DNA. Chem. Res. Toxicol. 2008, 21, 206–219. [Google Scholar] [CrossRef]
- Chen, B.; Zhou, X.; Taghizadeh, K.; Chen, J.; Stubbe, J.; Dedon, P.C. GC/MS methods to quantify the 2-deoxypentos-4-ulose and 3’-phosphoglycolate pathways of 4’ oxidation of 2-deoxyribose in DNA: Application to DNA damage produced by γ radiation and bleomycin. Chem. Res. Toxicol. 2007, 20, 1701–1708. [Google Scholar] [CrossRef] [Green Version]
- Roginskaya, M.; Bernhard, W.A.; Marion, R.T.; Razskazovskiy, Y. The release of 5-methylene-2-furanone from irradiated DNA catalyzed by cationic polyamines and divalent metal cations. Radiat. Res. 2005, 163, 85–89. [Google Scholar] [CrossRef] [Green Version]
- Roginskaya, M.; Razskazovskiy, Y.; Bernhard, W.A. 2-deoxyribonolactone lesions in X-ray-irradiated DNA: Quantitative determination by catalytic 5-methylene-2-Furanone release. Angew. Chem. Int. Ed. 2005, 44, 6210–6213. [Google Scholar] [CrossRef] [PubMed]
- Xue, L.; Greenberg, M.M. Use of fluorescence sensors to determine that 2-deoxyribonolactone is the major alkali-Labile deoxyribose lesion produced in oxidatively damaged DNA. Angew. Chem. Int. Ed. 2007, 46, 561–564. [Google Scholar] [CrossRef] [PubMed]
- Sato, K.; Greenberg, M.M. Selective detection of 2-deoxyribonolactone in DNA. J. Am. Chem. Soc. 2005, 127, 2806–2807. [Google Scholar] [CrossRef] [PubMed]
- Jacobs, A.C.; Resendiz, M.J.E.; Greenberg, M.M. Product and mechanistic analysis of the reactivity of a C6-pyrimidine radical in RNA. J. Am. Chem. Soc. 2011, 133, 5152–5159. [Google Scholar] [CrossRef] [Green Version]
- Resendiz, M.J.E.; Pottiboyina, V.; Sevilla, M.D.; Greenberg, M.M. Direct strand scission in double stranded RNA via a C5-pyrimidine radical. J. Am. Chem. Soc. 2012, 134, 3917–3924. [Google Scholar] [CrossRef] [Green Version]
- Melvin, T.; Botchway, S.W.; Parker, A.W.; O’Neill, P. Induction of strand breaks in single-stranded polyribonucleotides and DNA by photoionization: One electron oxidized nucleobase radicals as precursors. J. Am. Chem. Soc. 1996, 118, 10031–10036. [Google Scholar] [CrossRef]
- Sugiyama, H.; Fujimoto, K.; Saito, I. Stereospecific 1,2-hydride shift in ribonolactone formation in the photoreaction of 2’-iododeoxyuridine. J. Am. Chem. Soc. 1995, 117, 2945–2946. [Google Scholar] [CrossRef]
- Romieu, A.; Gasparutto, D.; Cadet, J. Synthesis and characterization of oligonucleotides containing 5‘,8-cyclopurine 2‘-deoxyribonucleosides: (5‘R)-5‘,8-cyclo-2‘-deoxyadenosine, (5‘S)-5‘,8-cyclo-2‘-deoxyguanosine, and (5‘R)-5‘,8-cyclo-2‘-deoxyguanosine. Chem. Res. Toxicol. 1999, 12, 412–421. [Google Scholar] [CrossRef] [PubMed]
- Chatgilialoglu, C.; Bazzanini, R.; Jimenez, L.B.; Miranda, M.A. (5’S)- and (5’R)-5′,8-Cyclo-2′-Deoxyguanosine: Mechanistic insights on the 2′-deoxyguanosin-5′-Yl radical cyclization. Chem. Res. Toxicol. 2007, 20, 1820–1824. [Google Scholar] [CrossRef]
- Flyunt, R.; Bazzanini, R.; Chatgilialoglu, C.; Mulazzani, Q.G. Fate of the 2‘-deoxyadenosin-5‘-Yl radical under anaerobic conditions. J. Am. Chem. Soc. 2000, 122, 4225–4226. [Google Scholar] [CrossRef]
- Chatgilialoglu, C.; Guerra, M.; Mulazzani, Q.G. Model studies of DNA C5‘ radicals. Selective generation and reactivity of 2‘-deoxyadenosin-5‘-yl radical. J. Am. Chem. Soc. 2003, 125, 3839–3848. [Google Scholar] [CrossRef] [PubMed]
- Kroeger, K.M.; Jiang, Y.L.; Kow, Y.W.; Goodman, M.F.; Greenberg, M.M. Mutagenic effects of 2-deoxyribonolactone in Escherichia coli. An abasic lesion that disobeys the A-rule. Biochemistry 2004, 43, 6723–6733. [Google Scholar] [CrossRef]
- Faure, V. 2’-deoxyribonolactone lesion produces G->A transitions in E. coli. Nucleic Acids Res. 2004, 32, 2937–2946. [Google Scholar] [CrossRef] [Green Version]
- Pitié, M.; Pratviel, G. Activation of DNA carbon−hydrogen bonds by metal complexes. Chem. Rev. 2010, 110, 1018–1059. [Google Scholar] [CrossRef]
- Kumar, A.; Pottiboyina, V.; Sevilla, M.D. One-electron oxidation of neutral sugar radicals of 2′-deoxyguanosine and 2′-deoxythymidine: A density functional theory (DFT) study. J. Phys. Chem. B 2012, 116, 9409–9416. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Razskazovskii, Y.; Roginskaya, M.; Sevilla, M.D. Modification of the reductive pathway in gamma-irradiated DNA by electron scavengers: Targeting the sugar-phosphate backbone. Radiat. Res. 1998, 149, 422–432. [Google Scholar] [CrossRef]
- Colson, A.-O.; Sevilla, M.D. Ab initio molecular orbital calculations of radicals formed by H• and •OH addition to the DNA bases: Electron affinities and ionization potentials. J. Phys. Chem. 1995, 99, 13033–13037. [Google Scholar] [CrossRef]
- Kumar, A.; Adhikary, A.; Shamoun, L.; Sevilla, M.D. Do solvated electrons (Eaq–) reduce DNA bases? A gaussian 4 and density functional theory-molecular dynamics study. J. Phys. Chem. B 2016, 120, 2115–2123. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Seidel, C.A.; Schulz, A.; Sauer, M.H. Nucleobase-specific quenching of fluorescent dyes. 1. Nucleobase one-electron redox potentials and their correlation with static and dynamic quenching efficiencies. J. Phys. Chem. 1996, 100, 5541–5553. [Google Scholar] [CrossRef]
- Huang, H.; Das, R.S.; Basu, A.K.; Stone, M.P. Structure of (5′ S)-8,5′-cyclo-2′-deoxyguanosine in DNA. J. Am. Chem. Soc. 2011, 133, 20357–20368. [Google Scholar] [CrossRef] [Green Version]
- Jaruga, P.; Dizdaroglu, M. 8,5′-cyclopurine-2′-deoxynucleosides in DNA: Mechanisms of formation, measurement, repair and biological effects. DNA Repair 2008, 7, 1413–1425. [Google Scholar] [CrossRef] [PubMed]
- Jaruga, P.; Birincioglu, M.; Rodriguez, H.; Dizdaroglu, M. Mass spectrometric assays for the tandem lesion 8,5‘-cyclo-2‘-deoxyguanosine in Mammalian DNA. Biochemistry 2002, 41, 3703–3711. [Google Scholar] [CrossRef] [PubMed]
- Chai, J.-D.; Head-Gordon, M. Systematic optimization of Long-range corrected hybrid density functionals. J. Chem. Phys. 2008, 128, 084106. [Google Scholar] [CrossRef]
- Chai, J.-D.; Head-Gordon, M. Long-range corrected hybrid density functionals with damped atom–atom dispersion corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kumar, A.; Sevilla, M.D. Proton transfer induced SOMO-to-homo level switching in one-electron oxidized A-T and G-C base pairs: A density functional theory study. J. Phys. Chem. B 2014, 118, 5453–5458. [Google Scholar] [CrossRef]
- Kumar, A.; Walker, J.A.; Bartels, D.M.; Sevilla, M.D. A simple Ab initio model for the hydrated electron that matches experiment. J. Phys. Chem. A 2015, 119, 9148–9159. [Google Scholar] [CrossRef] [Green Version]
- Kumar, A.; Sevilla, M.D. Cytosine iminyl radical (CytN•) formation via electron-induced debromination of 5-bromocytosine: A DFT and gaussian 4 study. J. Phys. Chem. A 2017, 121, 4825–4829. [Google Scholar] [CrossRef]
- Kumar, A.; Sevilla, M.D. Excited states of one-electron oxidized guanine-cytosine base pair radicals: A time dependent density functional theory study. J. Phys. Chem. A 2019, 123, 3098–3108. [Google Scholar] [CrossRef]
- Ma, J.; Kumar, A.; Muroya, Y.; Yamashita, S.; Sakurai, T.; Denisov, S.A.; Sevilla, M.D.; Adhikary, A.; Seki, S.; Mostafavi, M. Observation of dissociative quasi-free electron attachment to nucleoside via excited anion radical in solution. Nat. Commun. 2019, 10, 102. [Google Scholar] [CrossRef] [PubMed]
- Kumar, A.; Adhikary, A.; Sevilla, M.D.; Close, D.M. One-electron oxidation of ds(5′-GGG-3′) and ds(5′-G(8OG)G-3′) and the nature of hole distribution: A density functional theory (DFT) study. Phys. Chem. Chem. Phys. 2020, 22, 5078–5089. [Google Scholar] [CrossRef] [PubMed]
- Bravaya, K.B.; Epifanovsky, E.; Krylov, A.I. Four bases score a run: Ab initio calculations quantify a cooperative effect of H-bonding and π-stacking on the ionization energy of adenine in the AATT tetramer. J. Phys. Chem. Lett. 2012, 3, 2726–2732. [Google Scholar] [CrossRef]
- Zuluaga, C.; Spata, V.A.; Matsika, S. Benchmarking quantum mechanical methods for the description of charge-transfer states in π-stacked nucleobases. J. Chem. Theory Comput. 2020, 17, 376–387. [Google Scholar] [CrossRef]
- Marenich, A.V.; Ho, J.; Coote, M.L.; Cramer, C.J.; Truhlar, D.G. Computational electrochemistry: Prediction of liquid-phase reduction potentials. Phys. Chem. Chem. Phys. 2014, 16, 15068. [Google Scholar] [CrossRef] [PubMed]
- Trasatti, S. The absolute electrode potential: An explanatory note. Pure Appl. Chem. 1986, 58, 955–966. [Google Scholar] [CrossRef]
- Ho, J. Are thermodynamic cycles necessary for continuum solvent calculation of pKas and reduction potentials? Phys. Chem. Chem. Phys. 2015, 17, 2859–2868. [Google Scholar] [CrossRef] [PubMed]
- Bartmess, J.E. Thermodynamics of the electron and the proton. J. Phys. Chem. 1994, 98, 6420–6424. [Google Scholar] [CrossRef]
- Tomasi, J.; Mennucci, B.; Cammi, R. Quantum mechanical continuum solvation models. Chem. Rev. 2005, 105, 2999–3094. [Google Scholar] [CrossRef] [PubMed]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision, A.03, Gaussian.Com; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Nielsen, A.B.; Holder, A.J. GaussView, Version 5; Gaussian Inc.: Pittsburgh, PA, USA, 2009. [Google Scholar]
- Jmol: An Open-Source Browser-Based HTML5 Viewer and Stand-Alone Java Viewer for Chemical Structures in 3D. Available online: http://jmol.sourceforge.net/ (accessed on 2 October 2018).
- Li, M.-J.; Liu, L.; Fu, Y.; Guo, Q.-X. Development of an ONIOM-G3B3 method to accurately predict C−H and N−H bond dissociation enthalpies of ribonucleosides and deoxyribonucleosides. J. Phys. Chem. B 2005, 109, 13818–13826. [Google Scholar] [CrossRef]
- Miaskiewicz, K.; Osman, R. Theoretical study on the deoxyribose radicals formed by hydrogen abstraction. J. Am. Chem. Soc. 1994, 116, 232–238. [Google Scholar] [CrossRef]
- Colson, A.-O.; Sevilla, M.D. Structure and relative stability of deoxyribose radicals in a model DNA backbone: Ab initio molecular orbital calculations. J. Phys. Chem. 1995, 99, 3867–3874. [Google Scholar] [CrossRef]
- Li, M.-J.; Liu, L.; Wei, K.; Fu, Y.; Guo, Q.-X. Significant effects of phosphorylation on relative stabilities of DNA and RNA sugar radicals: Remarkably high susceptibility of H-2’ abstraction in RNA. J. Phys. Chem. B 2006, 110, 13582–13589. [Google Scholar] [CrossRef] [PubMed]
- Kumar, A.; Sevilla, M.D. π- vs σ-radical states of one-electron-oxidized DNA/RNA bases: A density functional theory study. J. Phys. Chem. B 2013, 117, 11623–11632. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gu, J.; Leszczynski, J.; Schaefer, H.F. Interactions of electrons with bare and hydrated biomolecules: From nucleic acid bases to DNA segments. Chem. Rev. 2012, 112, 5603–5640. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Cai, Z.; Sevilla, M.D. DFT calculations of the electron affinities of nucleic acid bases: Dealing with negative electron affinities. J. Phys. Chem. A 2002, 106, 1596–1603. [Google Scholar] [CrossRef]
- Kumar, A.; Sevilla, M.D. Low-energy electron attachment to 5‘-thymidine monophosphate: Modeling single strand breaks through dissociative electron attachment. J. Phys. Chem. B 2007, 111, 5464–5474. [Google Scholar] [CrossRef]
- Kumar, A.; Sevilla, M.D.; Suhai, S. Microhydration of the Guanine−Cytosine (GC) base pair in the neutral and anionic radical states: A density functional study. J. Phys. Chem. B 2008, 112, 5189–5198. [Google Scholar] [CrossRef]
- Schwarz, H.A. Free radicals generated by radiolysis of aqueous solutions. J. Chem. Educ. 1981, 58, 101. [Google Scholar] [CrossRef] [Green Version]
- Wardman, P. Reduction potentials of one-electron couples involving free radicals in aqueous solution. J. Phys. Chem. Ref. Data 1989, 18, 1637–1755. [Google Scholar] [CrossRef] [Green Version]
- Karwowski, B. The difference in stability between 5′R and 5′S diastereomers of 5′,8-cyclopurine-2′-deoxynucleosides. DFT study in gaseous and aqueous phase. Cent. Eur. J. Chem. 2010, 8, 134–141. [Google Scholar] [CrossRef]
- Karwowski, B.T. 5′,8-cyclopurine-2′-deoxynucleosides: Molecular structure and charge distribution–DFT study in gaseous and aqueous phase. J. Mol. Struct. Theochem. 2009, 915, 73–78. [Google Scholar] [CrossRef]
- Adriaanse, C.; Sulpizi, M.; VandeVondele, J.; Sprik, M. The electron attachment energy of the aqueous hydroxyl radical predicted from the detachment energy of the aqueous hydroxide anion. J. Am. Chem. Soc. 2009, 131, 6046–6047. [Google Scholar] [CrossRef]
- Slavíček, P.; Winter, B.; Faubel, M.; Bradforth, S.E.; Jungwirth, P. Ionization energies of aqueous nucleic acids: Photoelectron spectroscopy of pyrimidine nucleosides and Ab initio calculations. J. Am. Chem. Soc. 2009, 131, 6460–6467. [Google Scholar] [CrossRef]
- Manetto, A.; Georganakis, D.; Leondiadis, L.; Gimisis, T.; Mayer, P.; Carell, T.; Chatgilialoglu, C. Independent generation of C5‘-nucleosidyl radicals in thymidine and 2‘-deoxyguanosine. J. Org. Chem. 2007, 72, 3659–3666. [Google Scholar] [CrossRef]
- Chatgilialoglu, C.; Ferreri, C.; Geacintov, N.E.; Krokidis, M.G.; Liu, Y.; Masi, A.; Shafirovich, V.; Terzidis, M.A.; Tsegay, P.S. 5′,8-cyclopurine lesions in DNA damage: Chemical, analytical, biological, and diagnostic significance. Cells 2019, 8, 513. [Google Scholar] [CrossRef] [Green Version]

| 2′-Deoxyguanosine a ωB97XD-PCM/6-31++G** | ||||||
|---|---|---|---|---|---|---|
| Radical | ΔG (kJ/mol) | Population (%) at 298 K | Electron Affinity (eV) | E° vs. SHE (Volt) | ||
| Vertical b Adiabatic c | ||||||
| C1′ | 0.88 | 38.6 | 1.91 | 2.64 | −1.84 d | −1.50 e |
| C2′ | 28.96 | 0.0 | 2.72 | 3.26 | −1.22 d | −1.79 e |
| C3′ | 14.87 | 0.14 | 1.66 | 2.76 | −1.72 d | −1.65 e |
| C4′ | 0.00 | 55.2 | 1.93 | 2.72 | −1.76 d | −1.49 e |
| C5′ | 7.21 | 6.0 | 1.80 | 2.61 | −1.87 d | −1.57 e |
| 2′-Deoxythymidine a ωB97XD-PCM/6-31++G** | ||||||
|---|---|---|---|---|---|---|
| Radical | ΔG (kJ/mol) | Population (%) at 298 K | Electron Affinity (eV) | E° vs. SHE (Volt) | ||
| Vertical b Adiabatic c | ||||||
| C1′ | 1.45 | 29.3 | 1.78 | 2.65 | −1.83 d | −1.55 e |
| C2′ | 23.59 | 0.0 | 2.79 | 3.21 | −1.27 d | −1.78 e |
| C3′ | 8.33 | 1.83 | 1.60 | 2.75 | −1.73 d | −1.62 e |
| C4′ | 0.00 | 52.6 | 2.07 | 2.80 | −1.68 d | −1.53 e |
| C5′ | 4.65 | 16.1 | 1.92 | 2.77 | −1.71 d | −1.58 e |
| Radical | Average Boltzman Population a | DNA Relative Yields γ-Radiation b | Relative Yields by OH• Attack on DNA c | |
|---|---|---|---|---|
| Exp | Solvent Access | |||
| C1′ | 34 | 12.5 | 11 | 1 |
| C2′ | 0 | - | 13 | 11 |
| C3′ | 1 | 25 | 17 | 14 |
| C4′ | 54 | - | 22 | 28 |
| C5′ | 11 | 62.5 | 57 | 46 |
| 5′,8-Cyclo-2′-dG ωB97XD-PCM/6-31++G** | |||||
|---|---|---|---|---|---|
| Radical | ΔG (kJ/mol) | Population (%) at 298 K | Electron Affinity (eV) | E° vs. SHE (Volt) | |
| Vertical c Adiabatic d | |||||
| 5′(R) a | 0.00 | 64.1 | 2.59 | 2.85 | −1.63 |
| 5′(S) b | 1.44 | 35.9 | 2.71 | 3.11 | −1.37 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bell, M.; Kumar, A.; Sevilla, M.D. Electron-Induced Repair of 2′-Deoxyribose Sugar Radicals in DNA: A Density Functional Theory (DFT) Study. Int. J. Mol. Sci. 2021, 22, 1736. https://doi.org/10.3390/ijms22041736
Bell M, Kumar A, Sevilla MD. Electron-Induced Repair of 2′-Deoxyribose Sugar Radicals in DNA: A Density Functional Theory (DFT) Study. International Journal of Molecular Sciences. 2021; 22(4):1736. https://doi.org/10.3390/ijms22041736
Chicago/Turabian StyleBell, Michael, Anil Kumar, and Michael D. Sevilla. 2021. "Electron-Induced Repair of 2′-Deoxyribose Sugar Radicals in DNA: A Density Functional Theory (DFT) Study" International Journal of Molecular Sciences 22, no. 4: 1736. https://doi.org/10.3390/ijms22041736
APA StyleBell, M., Kumar, A., & Sevilla, M. D. (2021). Electron-Induced Repair of 2′-Deoxyribose Sugar Radicals in DNA: A Density Functional Theory (DFT) Study. International Journal of Molecular Sciences, 22(4), 1736. https://doi.org/10.3390/ijms22041736







