A Volumetric Analysis of the 1H NMR Chemical Shielding in Supramolecular Systems
Abstract
1. Introduction
2. Results
2.1. Selection of the Computational Approach
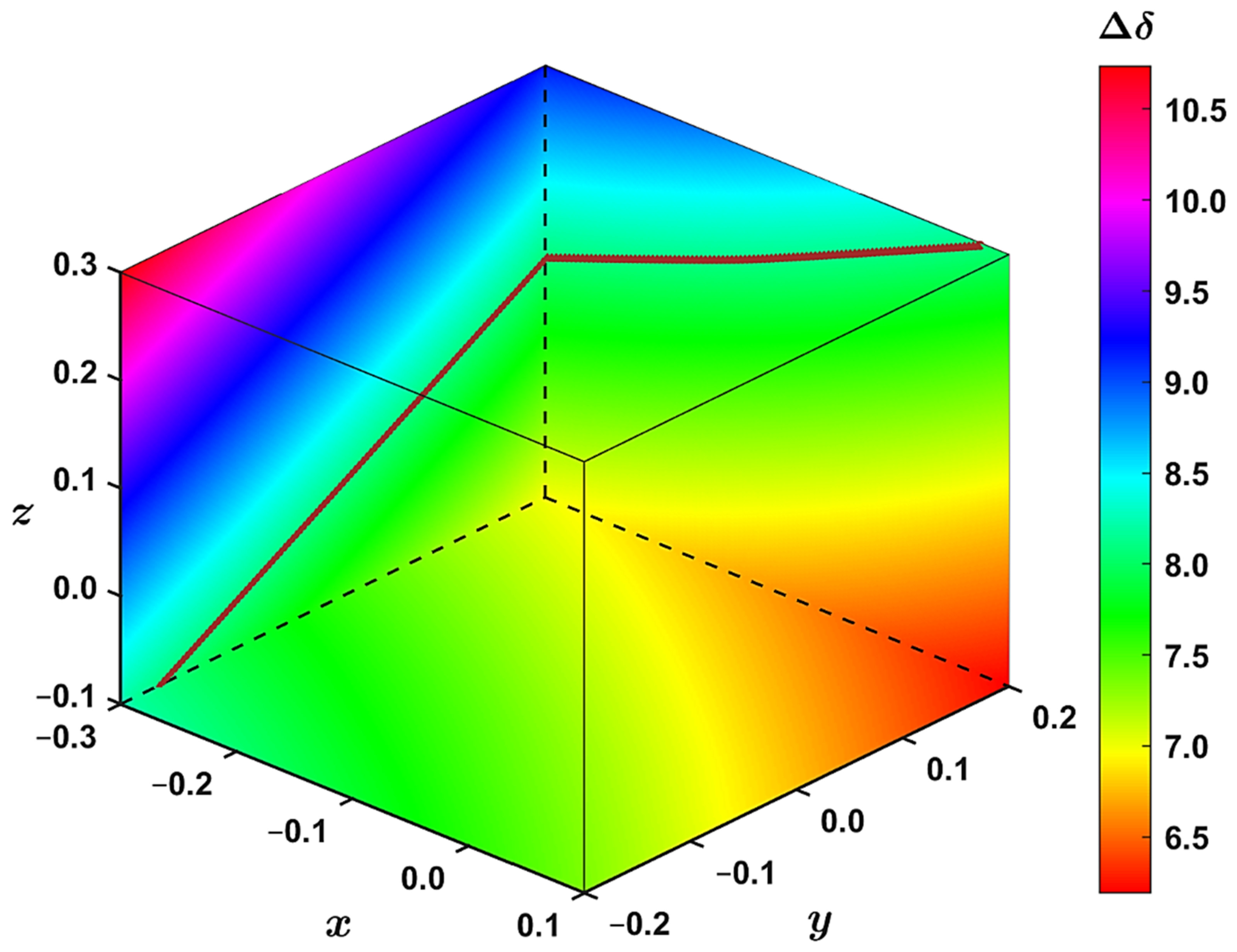
2.2. The 1H CS in Aromatic and Antiaromatic Systems
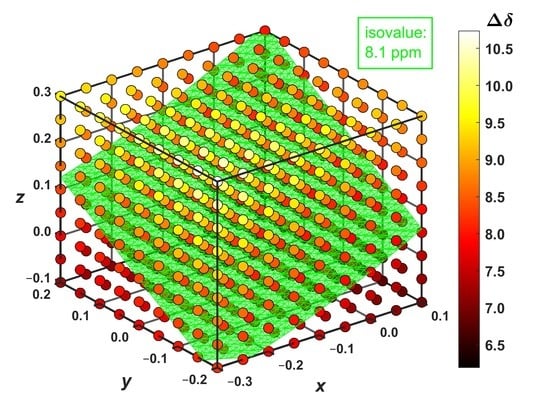
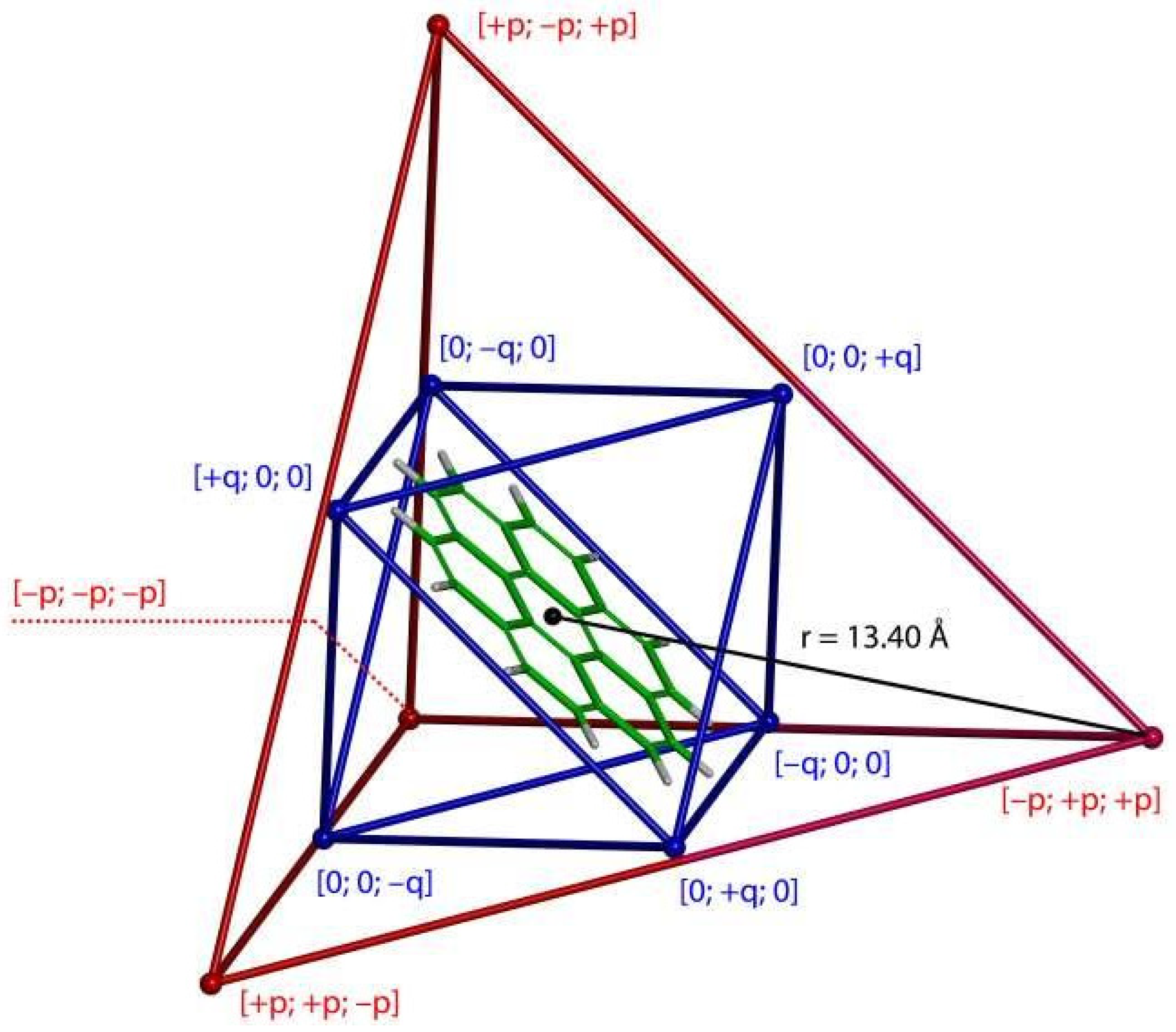
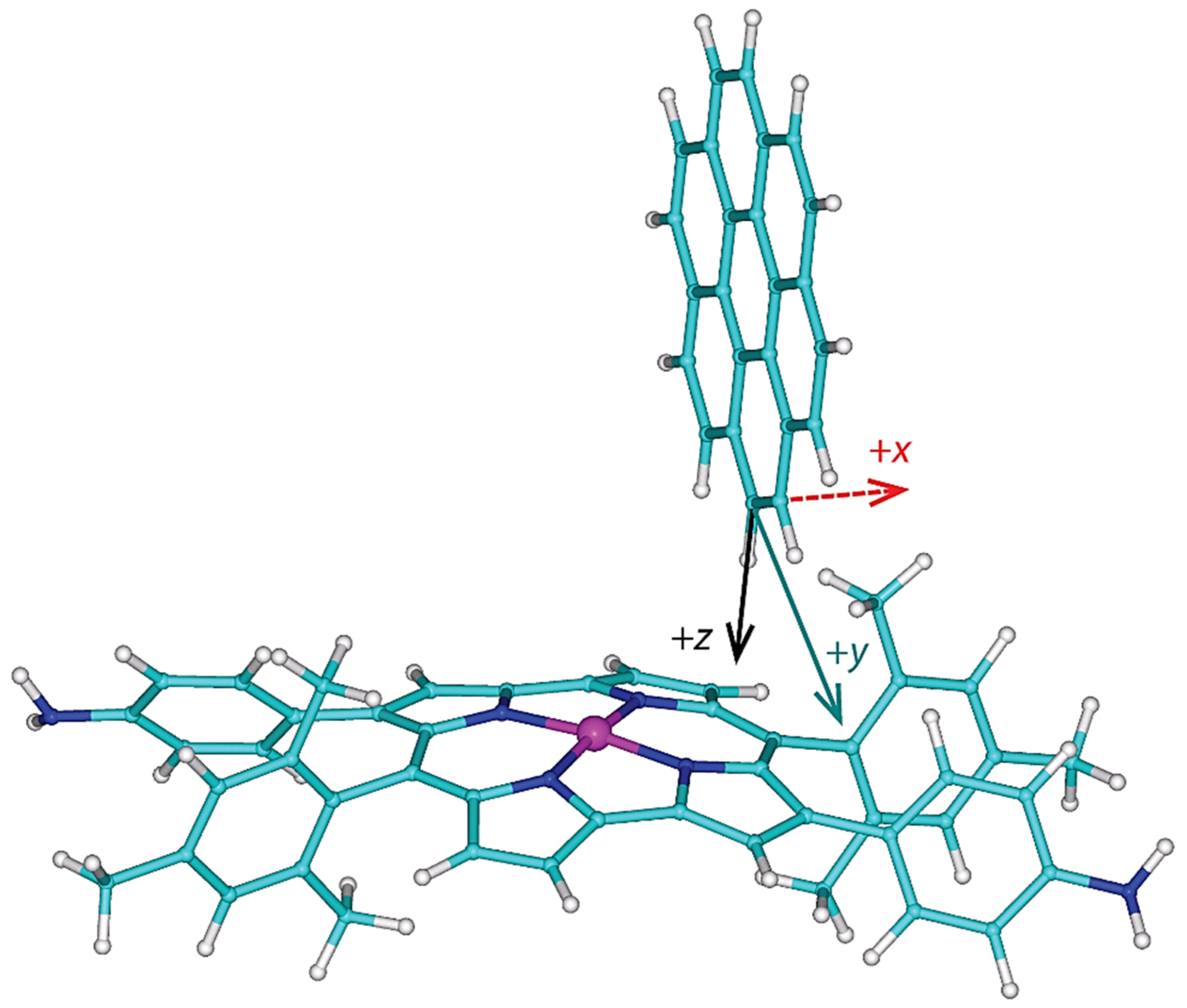
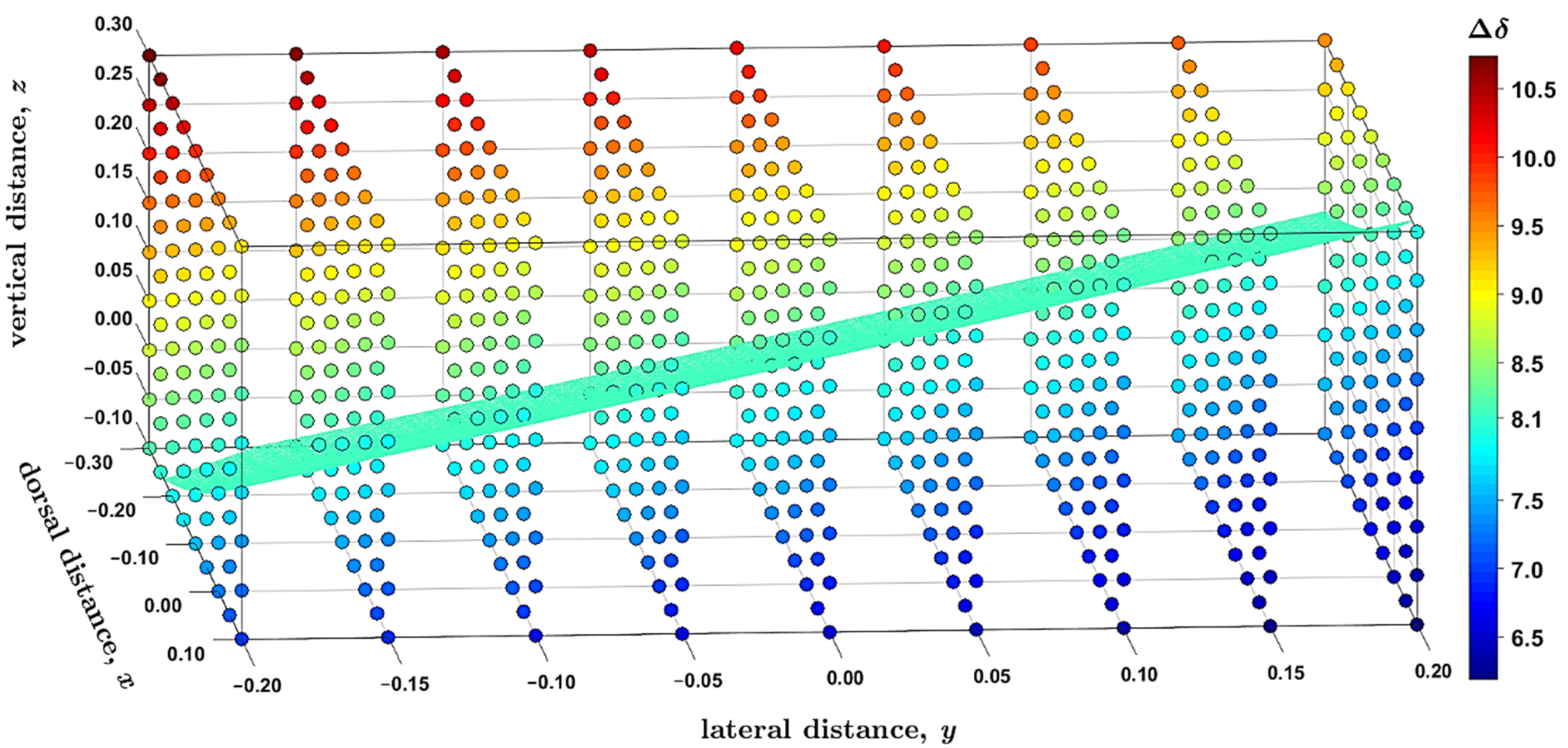
2.3. Modeling the Coronene Complex
3. Discussion
4. Materials and Methods
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Gao, W.-X.; Feng, H.-J.; Guo, B.-B.; Lu, Y.; Jin, G.-X. Coordination-Directed Construction of Molecular Links. Chem. Rev. 2020, 120, 6288–6325. [Google Scholar] [CrossRef]
- Percástegui, E.G.; Ronson, T.K.; Nitschke, J.R. Design and Applications of Water-Soluble Coordination Cages. Chem. Rev. 2020, 120, 13480–13544. [Google Scholar] [CrossRef]
- Hardy, M.; Lützen, A. Better Together: Functional Heterobimetallic Macrocyclic and Cage-like Assemblies. Chem. A Eur. J. 2020, 26, 13332–13346. [Google Scholar] [CrossRef] [PubMed]
- Ling, Q.-H.; Zhu, J.-L.; Qin, Y.; Xu, L. Naphthalene diimide- and perylene diimide-based supramolecular cages. Mater. Chem. Front. 2020, 4, 3176–3189. [Google Scholar] [CrossRef]
- Bao, S.-J.; Xu, Z.-M.; Ju, Y.; Song, Y.-L.; Wang, H.; Niu, Z.; Li, X.; Braunstein, P.; Lang, J.-P. The Covalent and Coordination Co-Driven Assembly of Supramolecular Octahedral Cages with Controllable Degree of Distortion. J. Am. Chem. Soc. 2020, 142, 13356–13361. [Google Scholar] [CrossRef] [PubMed]
- Zhang, D.; Ronson, T.K.; Greenfield, J.L.; Brotin, T.; Berthault, P.; Léonce, E.; Zhu, J.-L.; Xu, L.; Nitschke, J.R. Enantiopure [Cs+/Xe⊂Cryptophane]⊂FeII4L4 Hierarchical Superstructures. J. Am. Chem. Soc. 2019, 141, 8339–8345. [Google Scholar] [CrossRef]
- Shi, Q.; Zhou, X.; Yuan, W.; Su, X.; Neniškis, A.; Wei, X.; Taujenis, L.; Snarskis, G.; Ward, J.S.; Rissanen, K.; et al. Selective Formation of S4- and T-Symmetric Supramolecular Tetrahedral Cages and Helicates in Polar Media Assembled via Cooperative Action of Coordination and Hydrogen Bonds. J. Am. Chem. Soc. 2020, 142, 3658–3670. [Google Scholar] [CrossRef]
- Shan, Z.; Wu, X.; Xu, B.; Hong, Y.-L.; Wu, M.; Wang, Y.; Nishiyama, Y.; Zhu, J.; Horike, S.; Kitagawa, S.; et al. Dynamic Transformation between Covalent Organic Frameworks and Discrete Organic Cages. J. Am. Chem. Soc. 2020, 142, 21279–21284. [Google Scholar] [CrossRef]
- Pilgrim, B.S.; Champness, N.R. Metal-Organic Frameworks and Metal-Organic Cages—A Perspective. ChemPlusChem 2020, 85, 1842–1856. [Google Scholar] [CrossRef]
- Jiao, J.; Li, Z.; Qiao, Z.; Li, X.; Liu, Y.; Dong, J.; Jiang, J.; Cui, Y. Design and self-assembly of hexahedral coordination cages for cascade reactions. Nat. Commun. 2018, 9, 1–8. [Google Scholar] [CrossRef]
- Acharyya, K.; Mukherjee, P.S. Organic Imine Cages: Molecular Marriage and Applications. Angew. Chem. Int. Ed. 2019, 58, 8640–8653. [Google Scholar] [CrossRef] [PubMed]
- Marcarino, M.O.; Zanardi, M.M.; Cicetti, S.; Sarotti, A.M. NMR Calculations with Quantum Methods: Development of New Tools for Structural Elucidation and Beyond. Acc. Chem. Res. 2020, 53, 1922–1932. [Google Scholar] [CrossRef] [PubMed]
- Ito, T.; Hayashi, Y.; Shimizu, S.; Shin, J.-Y.; Kobayashi, N.; Shinokubo, H. Gram-Scale Synthesis of Nickel(II) Norcorrole: The Smallest Antiaromatic Porphyrinoid. Angew. Chem. Int. Ed. 2012, 51, 8542–8545. [Google Scholar] [CrossRef] [PubMed]
- Yamashina, M.; Tanaka, Y.; Lavendomme, R.; Ronson, T.K.; Pittelkow, M.; Nitschke, J.R. An antiaromatic-walled nanospace. Nat. Cell Biol. 2019, 574, 511–515. [Google Scholar] [CrossRef]
- Zhang, D.; Ronson, T.K.; Zou, Y.-Q.; Nitschke, J.R. Metal–organic cages for molecular separations. Nat. Rev. Chem. 2021, 5, 168–182. [Google Scholar] [CrossRef]
- Dračínský, M.; Hurtado, C.S.; Masson, E.; Kaleta, J. Stuffed pumpkins: Mechanochemical synthesis of host–guest complexes with cucurbit[7]uril. Chem. Commun. 2021, 57, 2132–2135. [Google Scholar] [CrossRef] [PubMed]
- Czernek, J.; Brus, J. Theoretical predictions of the two-dimensional solid-state NMR spectra: A case study of the 13C–1H correlations in metergoline. Chem. Phys. Lett. 2013, 586, 56–60. [Google Scholar] [CrossRef]
- Czernek, J.; Brus, J. The covariance of the differences between experimental and theoretical chemical shifts as an aid for assigning two-dimensional heteronuclear correlation solid-state NMR spectra. Chem. Phys. Lett. 2014, 608, 334–339. [Google Scholar] [CrossRef]
- Hodgkinson, P. NMR crystallography of molecular organics. Prog. Nucl. Magn. Reson. Spectrosc. 2020, 118–119, 10–53. [Google Scholar] [CrossRef]
- Brus, J.; Czernek, J.; Kobera, L.; Urbanova, M.; Abbrent, S.; Husak, M. Predicting the Crystal Structure of Decitabine by Powder NMR Crystallography: Influence of Long-Range Molecular Packing Symmetry on NMR Parameters. Cryst. Growth Des. 2016, 16, 7102–7111. [Google Scholar] [CrossRef]
- Takao, K.; Kai, H.; Yamada, A.; Fukushima, Y.; Komatsu, D.; Ogura, A.; Yoshida, K. Total Syntheses of (+)-Aquatolide and Related Humulanolides. Angew. Chem. Int. Ed. 2019, 58, 9851–9855. [Google Scholar] [CrossRef]
- Buevich, A.V.; Elyashberg, M.E. Synergistic Combination of CASE Algorithms and DFT Chemical Shift Predictions: A Powerful Approach for Structure Elucidation, Verification, and Revision. J. Nat. Prod. 2016, 79, 3105–3116. [Google Scholar] [CrossRef] [PubMed]
- Pauli, G.F.; Niemitz, M.; Bisson, J.; Lodewyk, M.W.; Soldi, C.; Shaw, J.T.; Tantillo, D.J.; Saya, J.M.; Vos, K.; Kleinnijenhuis, R.A.; et al. Toward Structural Correctness: Aquatolide and the Importance of 1D Proton NMR FID Archiving. J. Org. Chem. 2015, 81, 878–889. [Google Scholar] [CrossRef]
- Liu, Y.; Saurí, J.; Mevers, E.; Peczuh, M.W.; Hiemstra, H.; Clardy, J.; Martin, G.E.; Williamson, R.T. Unequivocal determination of complex molecular structures using anisotropic NMR measurements. Science 2017, 356, eaam5349. [Google Scholar] [CrossRef] [PubMed]
- Rickhaus, M.; Jirasek, M.; Tejerina, L.; Gotfredsen, H.; Peeks, M.D.; Haver, R.; Jiang, H.-W.; Claridge, T.D.W.; Anderson, H.L. Global aromaticity at the nanoscale. Nat. Chem. 2020, 12, 236–241. [Google Scholar] [CrossRef]
- Kudisch, B.; Maiuri, M.; Moretti, L.; Oviedo, M.B.; Wang, L.; Oblinsky, D.G.; Prud’Homme, R.K.; Wong, B.M.; McGill, S.A.; Scholes, G.D. Ring currents modulate optoelectronic properties of aromatic chromophores at 25 T. Proc. Natl. Acad. Sci. USA 2020, 117, 11289–11298. [Google Scholar] [CrossRef]
- Lampkin, B.J.; Karadakov, P.B.; VanVeller, B. Detailed Visualization of Aromaticity Using Isotropic Magnetic Shielding. Angew. Chem. Int. Ed. 2020, 59, 19275–19281. [Google Scholar] [CrossRef]
- Conradie, J.; Foroutan-Nejad, C.; Ghosh, A. Norcorrole as a Delocalized, Antiaromatic System. Sci. Rep. 2019, 9, 4852. [Google Scholar] [CrossRef]
- Karadakov, P.B. Norcorrole: Aromaticity and Antiaromaticity in Contest. Org. Lett. 2020, 22, 8676–8680. [Google Scholar] [CrossRef]
- Zhang, D.; Ronson, T.K.; Nitschke, J.R. Functional Capsules via Subcomponent Self-Assembly. Acc. Chem. Res. 2018, 51, 2423–2436. [Google Scholar] [CrossRef] [PubMed]
- Alvarez, S. Polyhedra in (inorganic) chemistry. Dalton Trans. 2005, 2209–2233. [Google Scholar] [CrossRef]
- Czernek, J.; Brus, J. On the predictions of the 11B solid state NMR parameters. Chem. Phys. Lett. 2016, 655–656, 66–70. [Google Scholar] [CrossRef]
- Czernek, J.; Brus, J. Parametrizing the Spatial Dependence of 1H NMR Chemical Shifts in π-Stacked Molecular Fragments. Int. J. Mol. Sci. 2020, 21, 7908. [Google Scholar] [CrossRef] [PubMed]
- Harvard Dataverse, V1; isosurface.txt [fileName]. Available online: https://doi.org/10.7910/DVN/JVVS2J (accessed on 24 March 2021).
- Hoffmann, C.M. Geometric and Solid Modeling, 1st ed.; Morgan Kaufmann Publishers: San Francisco, CA, USA, 1989. [Google Scholar]
- Platzer, G.; Mayer, M.; Beier, A.; Brüschweiler, S.; Fuchs, J.E.; Engelhardt, H.; Geist, L.; Bader, G.; Schörghuber, J.; Lichtenecker, R.; et al. PI by NMR: Probing CH–π Interactions in Protein–Ligand Complexes by NMR Spectroscopy. Angew. Chem. 2020, 132, 14861–14868. [Google Scholar] [CrossRef] [PubMed]
- Cai, X.; Kataria, R.; Gibb, B.C. Intrinsic and Extrinsic Control of the pKa of Thiol Guests inside Yoctoliter Containers. J. Am. Chem. Soc. 2020, 142, 8291–8298. [Google Scholar] [CrossRef] [PubMed]
- Ditchfield, R. Self-consistent perturbation theory of diamagnetism. Mol. Phys. 1974, 27, 789–807. [Google Scholar] [CrossRef]
- Wolinski, K.; Hinton, J.F.; Pulay, P. Efficient implementation of the gauge-independent atomic orbital method for NMR chemical shift calculations. J. Am. Chem. Soc. 1990, 112, 8251–8260. [Google Scholar] [CrossRef]
- Frish, M.J.; Trucks, J.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16; Revision C.01; Gaussian, Inc.: Wallingford, CT, USA, 2019. [Google Scholar]


| Parameter | Compound | |
|---|---|---|
| Aquatolide | The Diamine from Reference [14] | |
| number of 13C–1H pairs | 12 | 8 |
| calibration for carbons | = −0.92285 × + 168.15 ppm | = −0.96517 × + 176.04 ppm |
| standard deviation | 1.37 ppm | 0.990 ppm |
| calibration for protons | = −0.95874 × + 30.484 ppm | = −0.94376 × + 29.951 ppm |
| standard deviation | 0.145 ppm | 0.075 ppm |
| covariance | 0.013 (ppm)2 | 0.009 (ppm)2 |
| norm | 4.55 ppm | 2.62 ppm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Czernek, J.; Brus, J. A Volumetric Analysis of the 1H NMR Chemical Shielding in Supramolecular Systems. Int. J. Mol. Sci. 2021, 22, 3333. https://doi.org/10.3390/ijms22073333
Czernek J, Brus J. A Volumetric Analysis of the 1H NMR Chemical Shielding in Supramolecular Systems. International Journal of Molecular Sciences. 2021; 22(7):3333. https://doi.org/10.3390/ijms22073333
Chicago/Turabian StyleCzernek, Jiří, and Jiří Brus. 2021. "A Volumetric Analysis of the 1H NMR Chemical Shielding in Supramolecular Systems" International Journal of Molecular Sciences 22, no. 7: 3333. https://doi.org/10.3390/ijms22073333
APA StyleCzernek, J., & Brus, J. (2021). A Volumetric Analysis of the 1H NMR Chemical Shielding in Supramolecular Systems. International Journal of Molecular Sciences, 22(7), 3333. https://doi.org/10.3390/ijms22073333