Configurational Entropy of Folded Proteins and Its Importance for Intrinsically Disordered Proteins
Abstract
:1. Introduction
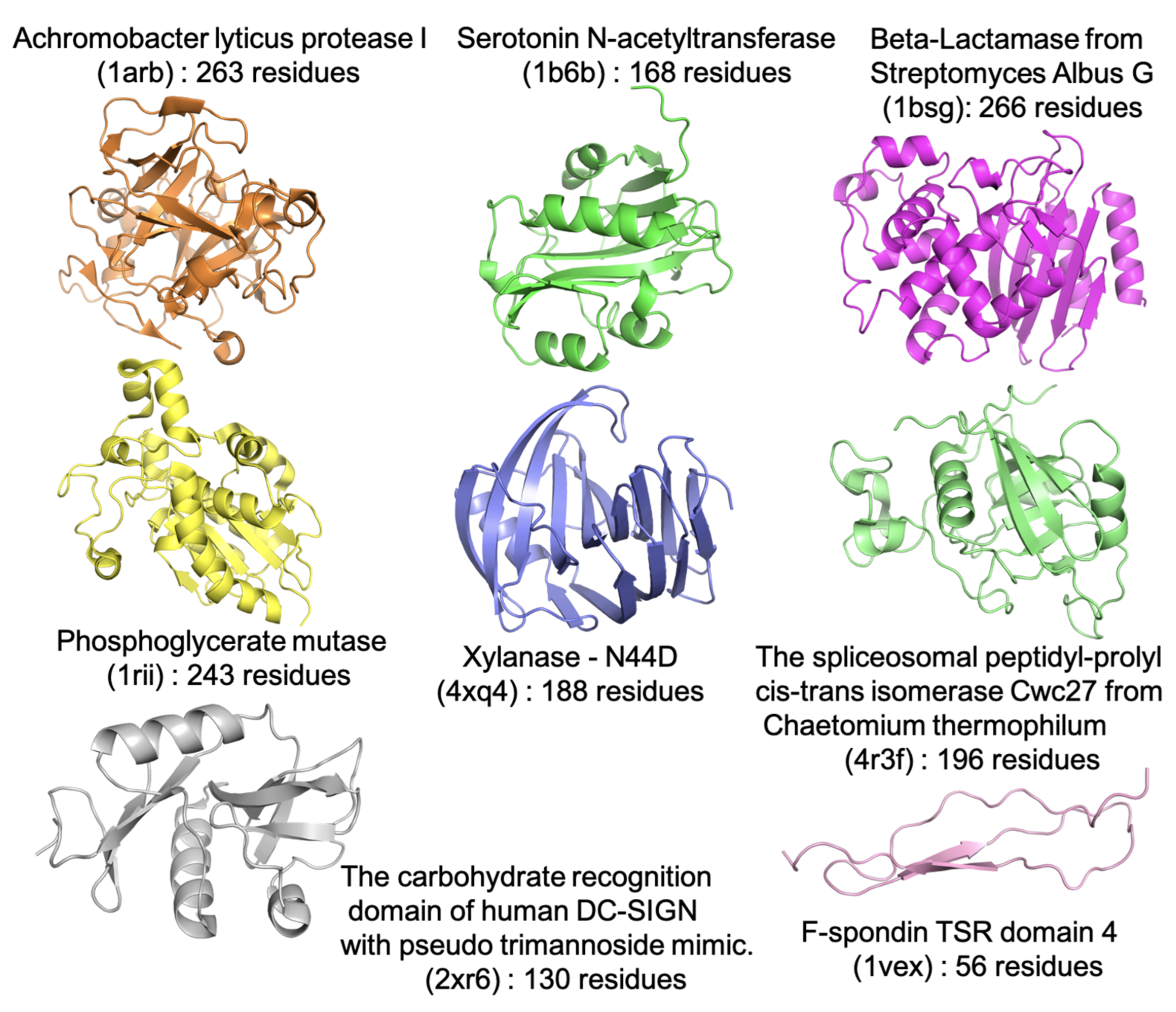
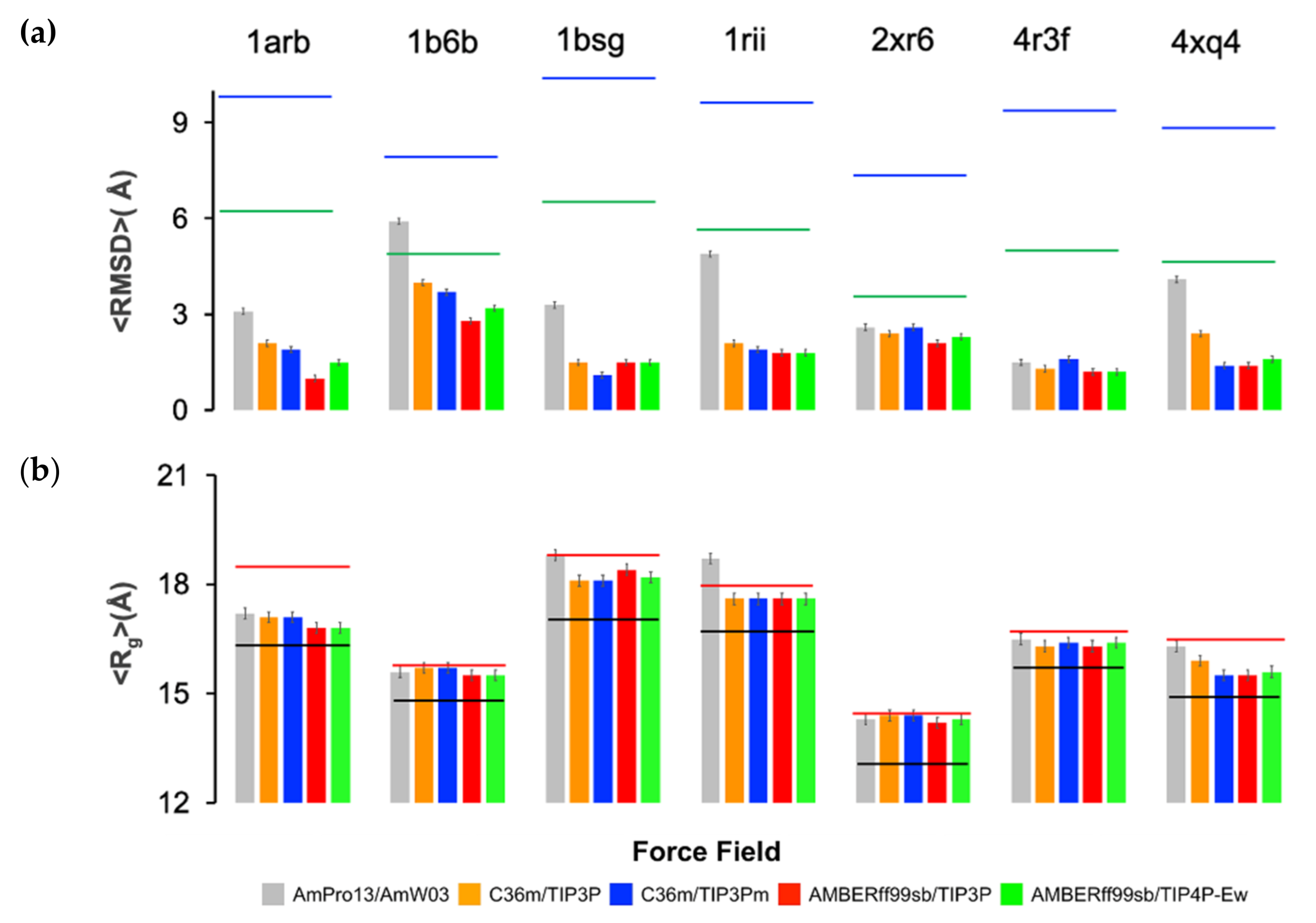
2. Results
3. Discussion
4. Materials and Methods
4.1. System and Simulation Preparation
4.2. Production Simulation Details and Analysis
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wright, P.E.; Dyson, H.J. Intrinsically disordered proteins in cellular signalling and regulation. Nat. Rev. Mol. Cell Biol. 2015, 16, 18–29. [Google Scholar] [CrossRef] [PubMed]
- Fawzi, N.L.; Phillips, A.H.; Ruscio, J.Z.; Doucleff, M.; Wemmer, D.E.; Head-Gordon, T. Structure and dynamics of the Aβ(21–30) peptide from the interplay of NMR experiments and molecular simulations. J. Am. Chem. Soc. 2008, 130, 6145–6158. [Google Scholar] [CrossRef] [Green Version]
- Gomes, G.-N.W.; Krzeminski, M.; Namini, A.; Martin, E.W.; Mittag, T.; Head-Gordon, T.; Forman-Kay, J.D.; Gradinaru, C.C. Conformational Ensembles of an Intrinsically Disordered Protein Consistent with NMR, SAXS, and Single-Molecule FRET. J. Am. Chem. Soc. 2020, 142, 15697–15710. [Google Scholar] [CrossRef]
- Svergun, D.; Barberato, C.; Koch, M.H.J. CRYSOL—A Program to Evaluate X-ray Solution Scattering of Biological Macromolecules from Atomic Coordinates. J. Appl. Crystallogr. 1995, 28, 768–773. [Google Scholar] [CrossRef]
- Bhowmick, A.; Brookes, D.H.; Yost, S.R.; Dyson, H.J.; Forman-Kay, J.D.; Gunter, D.; Head-Gordon, M.; Hura, G.L.; Pande, V.S.; Wemmer, D.E.; et al. Finding Our Way in the Dark Proteome. J. Am. Chem. Soc. 2016, 138, 9730–9742. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ozenne, V.; Bauer, F.; Salmon, L.; Huang, J.-R.; Jensen, M.R.; Segard, S.; Bernadó, P.; Charavay, C.; Blackledge, M. Flexible-meccano: A tool for the generation of explicit ensemble descriptions of intrinsically disordered proteins and their associated experimental observables. Bioinformatics 2012, 28, 1463–1470. [Google Scholar] [CrossRef]
- Krzeminski, M.; Marsh, J.A.; Neale, C.; Choy, W.Y.; Forman-Kay, J.D. Characterization of disordered proteins with ENSEMBLE. Bioinformatics 2013, 29, 398–399. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ball, K.A.; Wemmer, D.E.; Head-Gordon, T. Comparison of structure determination methods for intrinsically disordered amyloid-beta peptides. J. Phys. Chem. B 2014, 118, 6405–6416. [Google Scholar] [CrossRef]
- Brookes, D.H.; Head-Gordon, T. Experimental Inferential Structure Determination of Ensembles for Intrinsically Disordered Proteins. J. Am. Chem. Soc. 2016, 138, 4530–4538. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Köfinger, J.; Stelzl, L.S.; Reuter, K.; Allande, C.; Reichel, K.; Hummer, G. Efficient Ensemble Refinement by Reweighting. J. Chem. Theory Comput. 2019, 15, 3390–3401. [Google Scholar] [CrossRef]
- Lincoff, J.; Haghighatlari, M.; Krzeminski, M.; Teixeira, J.M.C.; Gomes, G.-N.W.; Gradinaru, C.C.; Forman-Kay, J.D.; Head-Gordon, T. Extended experimental inferential structure determination method in determining the structural ensembles of disordered protein states. Commun. Chem. 2020, 3, 74. [Google Scholar] [CrossRef] [PubMed]
- Nerenberg, P.S.; Head-Gordon, T. New developments in force fields for biomolecular simulations. Curr. Opin. Struct. Biol. 2018, 49, 129–138. [Google Scholar] [CrossRef] [Green Version]
- Nerenberg, P.S.; Head-Gordon, T. Optimizing protein-solvent force fields to reproduce intrinsic conformational preferences of model peptides. J. Chem. Theory Comput. 2011, 7, 1220–1230. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chong, S.-H.; Chatterjee, P.; Ham, S. Computer Simulations of Intrinsically Disordered Proteins. Annu. Rev. Phys. Chem. 2017, 68, 117–134. [Google Scholar] [CrossRef]
- Henriques, J.; Cragnell, C.; Skepö, M. Molecular dynamics simulations of intrinsically disordered proteins: Force field evaluation and comparison with experiment. J. Chem. Theory Comput. 2015, 11, 3420–3431. [Google Scholar] [CrossRef]
- Siwy, C.M.; Lockhart, C.; Klimov, D.K. Is the Conformational Ensemble of Alzheimer’s Aβ10-40 Peptide Force Field Dependent? PLoS Comput. Biol. 2017, 13, e1005314. [Google Scholar] [CrossRef]
- Wickstrom, L.; Okur, A.; Simmerling, C. Evaluating the performance of the ff99SB force field based on NMR scalar coupling data. Biophys. J. 2009, 97, 853–856. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zaslavsky, B.Y.; Uversky, V.N. In Aqua Veritas: The Indispensable yet Mostly Ignored Role of Water in Phase Separation and Membrane-Less Organelles. Biochemistry 2018, 57, 2437–2451. [Google Scholar] [CrossRef]
- Lindorff-Larsen, K.; Piana, S.; Palmo, K.; Maragakis, P.; Klepeis, J.L.; Dror, R.O.; Shaw, D.E. Improved side-chain torsion potentials for the Amber ff99SB protein force field. Proteins Struct. Funct. Bioinform. 2010, 78, 1950–1958. [Google Scholar] [CrossRef] [Green Version]
- Robustelli, P.; Piana, S.; Shaw, D.E. Developing a molecular dynamics force field for both folded and disordered protein states. Proc. Natl. Acad. Sci. USA 2018, 115, E4758–E4766. [Google Scholar] [CrossRef] [Green Version]
- Lincoff, J.; Sasmal, S.; Head-Gordon, T. The combined force field-sampling problem in simulations of disordered amyloid-beta peptides. J. Chem. Phys. 2019, 150, 104108. [Google Scholar] [CrossRef]
- Piana, S.; Donchev, A.G.; Robustelli, P.; Shaw, D.E. Water dispersion interactions strongly influence simulated structural properties of disordered protein states. J. Phys. Chem. B 2015, 119, 5113–5123. [Google Scholar] [CrossRef] [PubMed]
- Best, R.B.; Zheng, W.; Mittal, J. Balanced Protein-Water Interactions Improve Properties of Disordered Proteins and Non-Specific Protein Association. J. Chem. Theory Comput. 2014, 10, 5113–5124. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Abascal, J.L.F.; Vega, C. A general purpose model for the condensed phases of water: TIP4P/2005. J. Chem. Phys. 2005, 123, 234505. [Google Scholar] [CrossRef] [PubMed]
- Fluitt, A.M.; de Pablo, J.J. An Analysis of Biomolecular Force Fields for Simulations of Polyglutamine in Solution. Biophys. J. 2015, 109, 1009–1018. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Chu, X.; Longhi, S.; Roche, P.; Han, W.; Wang, E.; Wang, J. Multiscaled exploration of coupled folding and binding of an intrinsically disordered molecular recognition element in measles virus nucleoprotein. Proc. Natl. Acad. Sci. USA 2013, 110, E3743–E3752. [Google Scholar] [CrossRef] [Green Version]
- Moritsugu, K.; Terada, T.; Kidera, A. Disorder-to-order transition of an intrinsically disordered region of sortase revealed by multiscale enhanced sampling. J. Am. Chem. Soc. 2012, 134, 7094–7101. [Google Scholar] [CrossRef]
- Wells, M.; Tidow, H.; Rutherford, T.J.; Markwick, P.; Jensen, M.R.; Mylonas, E.; Svergun, D.I.; Blackledge, M.; Fersht, A.R. Structure of tumor suppressor p53 and its intrinsically disordered N-terminal transactivation domain. Proc. Natl. Acad. Sci. USA 2008, 105, 5762–5767. [Google Scholar] [CrossRef] [Green Version]
- Rauscher, S.; Pomès, R. The liquid structure of elastin. eLife 2017, 6, e26526. [Google Scholar] [CrossRef]
- Huang, J.; Rauscher, S.; Nawrocki, G.; Ran, T.; Feig, M.; de Groot, B.L.; Grubmuller, H.; MacKerell, A.D., Jr. CHARMM36m: An improved force field for folded and intrinsically disordered proteins. Nat. Methods 2017, 14, 71–73. [Google Scholar] [CrossRef] [Green Version]
- Ponder, J.W.; Wu, C.; Ren, P.; Pande, V.S.; Chodera, J.D.; Schnieders, M.J.; Haque, I.; Mobley, D.L.; Lambrecht, D.S.; DiStasio, R.A., Jr. Current status of the AMOEBA polarizable force field. J. Phys. Chem. B 2010, 114, 2549. [Google Scholar] [CrossRef] [Green Version]
- Demerdash, O.; Wang, L.-P.; Head-Gordon, T. Advanced models for water simulations. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2018, 8, e1355. [Google Scholar] [CrossRef] [Green Version]
- Shi, Y.; Xia, Z.; Zhang, J.; Best, R.; Wu, C.; Ponder, J.W.; Ren, P. The Polarizable Atomic Multipole-based AMOEBA Force Field for Proteins. J. Chem. Theory Comput. 2013, 9, 4046–4063. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ren, P.; Ponder, J.W. Polarizable atomic multipole water model for molecular mechanics simulation. J. Phys. Chem. B 2003, 107, 5933–5947. [Google Scholar] [CrossRef] [Green Version]
- Cragnell, C.; Durand, D.; Cabane, B.; Skepö, M. Coarse-grained modelling of the intrinsically disordered protein Histatin 5 in solution. Monte Carlo simulations in combination with SAXS. Proteins Struct. Func. Bioinform. 2016, 84, 777–791. [Google Scholar] [CrossRef]
- Lifson, S.; Warshel, A. Consistent Force Field for Calculations of Conformations, Vibrational Spectra, and Enthalpies of Cycloalkane and N-Alkane Molecules. J. Chem. Phys. 1968, 49, 5116–5129. [Google Scholar] [CrossRef] [Green Version]
- Hickman, A.B.; Klein, D.C.; Dyda, F. Melatonin Biosynthesis: The Structure of Serotonin N-Acetyltransferase at 2.5Å Resolution Suggests a Catalytic Mechanism. Mol. Cell 1999, 3, 23–32. [Google Scholar] [CrossRef]
- Tsunasawa, S.; Masaki, T.; Hirose, M.; Soejima, M.; Sakiyama, F. The primary structure and structural characteristics of Achromobacter lyticus protease I, a lysine-specific serine protease. J. Biol. Chem. 1989, 264, 3832–3839. [Google Scholar] [CrossRef]
- Dideberg, O.; Charlier, P.; Wéry, J.P.; Dehottay, P.; Dusart, J.; Erpicum, T.; Frère, J.M.; Ghuysen, J.M. The crystal structure of the β-lactamase of Streptomyces albus G at 0.3 nm resolution. Biochem. J. 1987, 245, 911–913. [Google Scholar] [CrossRef]
- Muller, P.; Sawaya, M.R.; Pashkov, I.; Chan, S.; Nguyen, C.; Wu, Y.; Perry, L.J.; Eisenberg, D. The 1.70 angstroms X-ray crystal structure of Mycobacterium tuberculosis phosphoglycerate mutase. Acta Crystallogr. D Biol. Crystallogr. 2005, 61 Pt 3, 309–315. [Google Scholar] [CrossRef] [PubMed]
- Sutkeviciute, I.; Thepaut, M.; Sattin, S.; Berzi, A.; McGeagh, J.; Grudinin, S.; Weiser, J.; Le Roy, A.; Reina, J.J.; Rojo, J.; et al. Unique DC-SIGN clustering activity of a small glycomimetic: A lesson for ligand design. ACS Chem. Biol. 2014, 9, 1377–1385. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ulrich, A.; Wahl, M.C. Structure and evolution of the spliceosomal peptidyl-prolyl cis-trans isomerase Cwc27. Acta Crystallogr. D Biol. Crystallogr. 2014, 70 Pt 12, 3110–3123. [Google Scholar] [CrossRef]
- Wan, Q.; Parks, J.M.; Hanson, B.L.; Fisher, S.Z.; Ostermann, A.; Schrader, T.E.; Graham, D.E.; Coates, L.; Langan, P.; Kovalevsky, A. Direct determination of protonation states and visualization of hydrogen bonding in a glycoside hydrolase with neutron crystallography. Proc. Natl. Acad. Sci. USA 2015, 112, 12384–12389. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Paakkonen, K.; Tossavainen, H.; Permi, P.; Rakkolainen, H.; Rauvala, H.; Raulo, E.; Kilpelainen, I.; Guntert, P. Solution structures of the first and fourth TSR domains of F-spondin. Proteins 2006, 64, 665–672. [Google Scholar] [CrossRef]
- Maiorov, V.N.; Crippen, G.M. Significance of Root-Mean-Square Deviation in Comparing Three-Dimensional Structures of Globular Proteins. J. Mol. Biol. 1994, 235, 625–634. [Google Scholar] [CrossRef] [Green Version]
- Kolinski, A.; Godzik, A.; Skolnick, J. A general method for the prediction of the three dimensional structure and folding pathway of globular proteins: Application to designed helical proteins. J. Chem. Phys. 1993, 98, 7420–7433. [Google Scholar] [CrossRef] [Green Version]
- Dima, R.I.; Thirumalai, D. Asymmetry in the Shapes of Folded and Denatured States of Proteins. J. Phys. Chem. B 2004, 108, 6564–6570. [Google Scholar] [CrossRef] [Green Version]
- Yang, L.-W.; Eyal, E.; Chennubhotla, C.; Jee, J.; Gronenborn, A.M.; Bahar, I. Insights into equilibrium dynamics of proteins from comparison of NMR and X-ray data with computational predictions. Structure 2007, 15, 741–749. [Google Scholar] [CrossRef] [Green Version]
- Andrec, M.; Snyder, D.A.; Zhou, Z.; Young, J.; Montelione, G.T.; Levy, R.M. A large data set comparison of protein structures determined by crystallography and NMR: Statistical test for structural differences and the effect of crystal packing. Proteins Struct. Funct. Bioinform. 2007, 69, 449–465. [Google Scholar] [CrossRef]
- Hura, G.L.; Hodge, C.D.; Rosenberg, D.; Guzenko, D.; Duarte, J.M.; Monastyrskyy, B.; Grudinin, S.; Kryshtafovych, A.; Tainer, J.A.; Fidelis, K.; et al. Small angle X-ray scattering-assisted protein structure prediction in CASP13 and emergence of solution structure differences. Proteins Struct. Funct. Bioinform. 2019, 87, 1298–1314. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pitera, J.W. Expected Distributions of Root-Mean-Square Positional Deviations in Proteins. J. Phys. Chem. B 2014, 118, 6526–6530. [Google Scholar] [CrossRef]
- Lindemann, F. The calculation of molecular vibration frequencies. Z. Phys. 1910, 11, 609–612. [Google Scholar]
- Zhou, Y.; Vitkup, D.; Karplus, M. Native proteins are surface-molten solids: Application of the lindemann criterion for the solid versus liquid state. J. Mol. Biol. 1999, 285, 1371–1375. [Google Scholar] [CrossRef] [Green Version]
- Katava, M.; Stirnemann, G.; Zanatta, M.; Capaccioli, S.; Pachetti, M.; Ngai, K.L.; Sterpone, F.; Paciaroni, A. Critical structural fluctuations of proteins upon thermal unfolding challenge the Lindemann criterion. Proc. Natl. Acad. Sci. USA 2017, 114, 9361. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhou, Y.; Karplus, M. Folding thermodynamics of a model three-helix-bundle protein. Proc. Natl. Acad. Sci. USA 1997, 94, 14429–14432. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Freddolino, P.L.; Harrison, C.B.; Liu, Y.; Schulten, K. Challenges in protein-folding simulations. Nat. Phys. 2010, 6, 751–758. [Google Scholar] [CrossRef] [Green Version]
- Sosnick, T.R.; Hinshaw, J.R. How Proteins Fold. Science 2011, 334, 464. [Google Scholar] [CrossRef] [PubMed]
- Piana, S.; Lindorff-Larsen, K.; Shaw, D.E. How Robust Are Protein Folding Simulations with Respect to Force Field Parameterization? Biophys. J. 2011, 100, L47–L49. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Alowolodu, O.; Johnson, G.; Alashwal, L.; Addou, I.; Zhdanova, I.V.; Uversky, V.N. Intrinsic disorder in spondins and some of their interacting partners. Intrinsically Disord. Proteins 2016, 4, e1255295. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Brewer, D.; Hunter, H.; Lajoie, G. NMR studies of the antimicrobial salivary peptides histatin 3 and histatin 5 in aqueous and nonaqueous solutions. Biochem. Cell Biol. 1998, 76, 247–256. [Google Scholar] [CrossRef] [PubMed]
- Raj, P.A.; Marcus, E.; Sukumaran, D.K. Structure of human salivary histatin 5 in aqueous and nonaqueous solutions. Biopolymers 1998, 45, 51–67. [Google Scholar] [CrossRef]
- Shalongo, W.; Dugad, L.; Stellwagen, E. Distribution of Helicity within the Model Peptide Acetyl(AAQAA)3amide. J. Am. Chem. Soc. 1994, 116, 8288–8293. [Google Scholar] [CrossRef]
- Shirley, W.A.; Brooks, C.L., III. Curious structure in “canonical” alanine-based peptides. Proteins Struct. Funct. Bioinform. 1997, 28, 59–71. [Google Scholar] [CrossRef]
- Huang, J.; MacKerell, A.D., Jr. Induction of peptide bond dipoles drives cooperative helix formation in the (AAQAA)3 peptide. Biophys. J. 2014, 107, 991–997. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mayo, A.; Yap, K. Empirical Analysis of Backbone Chemical Shifts in Proteins; Ikura Laboratory, Department of Medical Biophysics, University of Toronto, Division of Molecular and Structural Biology, Ontario Cancer Institute: Toronto, ON, Canada, 2001. [Google Scholar]
- Best, R.B.; Hummer, G. Optimized molecular dynamics force fields applied to the helix-coil transition of polypeptides. J. Phys. Chem. B 2009, 113, 9004–9015. [Google Scholar] [CrossRef] [Green Version]
- Boonstra, S.; Onck, P.R.; van der Giessen, E. CHARMM TIP3P Water Model Suppresses Peptide Folding by Solvating the Unfolded State. J. Phys. Chem. B 2016, 120, 3692–3698. [Google Scholar] [CrossRef] [PubMed]
- Marsh, J.A.; Singh, V.K.; Jia, Z.; Forman-Kay, J.D. Sensitivity of secondary structure propensities to sequence differences between α- and γ-synuclein: Implications for fibrillation. Protein Sci. 2006, 15, 2795–2804. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Camilloni, C.; De Simone, A.; Vranken, W.F.; Vendruscolo, M. Determination of Secondary Structure Populations in Disordered States of Proteins Using Nuclear Magnetic Resonance Chemical Shifts. Biochemistry 2012, 51, 2224–2231. [Google Scholar] [CrossRef]
- Hornak, V.; Abel, R.; Okur, A.; Strockbine, B.; Roitberg, A.; Simmerling, C. Comparison of multiple Amber force fields and development of improved protein backbone parameters. Proteins 2006, 65, 712–725. [Google Scholar] [CrossRef] [Green Version]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Horn, H.W.; Swope, W.C.; Pitera, J.W.; Madura, J.D.; Dick, T.J.; Hura, G.L.; Head-Gordon, T. Development of an improved four-site water model for biomolecular simulations: TIP4P-Ew. J. Chem. Phys. 2004, 120, 9665–9678. [Google Scholar] [CrossRef]
- Eastman, P.; Friedrichs, M.S.; Chodera, J.D.; Radmer, R.J.; Bruns, C.M.; Ku, J.P.; Beauchamp, K.A.; Lane, T.J.; Wang, L.-P.; Shukla, D. OpenMM 4: A reusable, extensible, hardware independent library for high performance molecular simulation. J. Chem. Theory Comput. 2013, 9, 461. [Google Scholar] [CrossRef]
- Harger, M.; Li, D.; Wang, Z.; Dalby, K.; Lagardere, L.; Piquemal, J.P.; Ponder, J.; Ren, P. Tinker-OpenMM: Absolute and relative alchemical free energies using AMOEBA on GPUs. J. Comput. Chem. 2017, 38, 2047–2055. [Google Scholar] [CrossRef] [PubMed]
- Brown, S.; Head-Gordon, T. Cool walking: A new Markov chain Monte Carlo sampling method. J. Comput. Chem. 2003, 24, 68–76. [Google Scholar] [CrossRef]
- Lincoff, J.; Sasmal, S.; Head-Gordon, T. Comparing generalized ensemble methods for sampling of systems with many degrees of freedom. J. Chem. Phys. 2016, 145, 174107. [Google Scholar] [CrossRef] [PubMed]
- Roe, D.R.; Cheatham, T.E., 3rd. PTRAJ and CPPTRAJ: Software for Processing and Analysis of Molecular Dynamics Trajectory Data. J. Chem. Theory Comput. 2013, 9, 3084–3095. [Google Scholar] [CrossRef] [PubMed]
- Jo, S.; Lim, J.B.; Klauda, J.B.; Im, W. CHARMM-GUI Membrane Builder for mixed bilayers and its application to yeast membranes. Biophys. J. 2009, 97, 50–58. [Google Scholar] [CrossRef] [Green Version]
- Rackers, J.A.; Wang, Z.; Lu, C.; Laury, M.L.; Lagardere, L.; Schnieders, M.J.; Piquemal, J.P.; Ren, P.; Ponder, J.W. Tinker 8: Software Tools for Molecular Design. J. Chem. Theory Comput. 2018, 14, 5273–5289. [Google Scholar] [CrossRef]



| Force Field/Proteine | Ave. | |||||||
|---|---|---|---|---|---|---|---|---|
| 1arb | 1b6b | 1bsg | 1rii | 2xr6 | 4r3f | 4xq4 | ||
| ff99sb/TIP3P | 0.10 | 0.14 | 0.14 | 0.13 | 0.11 | 0.11 | 0.12 | 0.12 |
| ff99sb/TIP4P-Ew | 0.10 | 0.13 | 0.12 | 0.12 | 0.11 | 0.12 | 0.10 | 0.11 |
| C36m/TIP3P | 0.11 | 0.14 | 0.11 | 0.12 | 0.11 | 0.12 | 0.14 | 0.12 |
| C36m/TIP3Pm | 0.12 | 0.18 | 0.11 | 0.13 | 0.14 | 0.12 | 0.12 | 0.13 |
| AmPro13/AmW03 | 0.13 | 0.16 | 0.18 | 0.22 | 0.13 | 0.16 | 0.17 | 0.16 |
| Force Field | ||||
|---|---|---|---|---|
| ff99sb/TIP3P | 3.8 | 0.16 | 0.18 | 0.17 |
| ff99sb/TIP4P-Ew | 3.5 | 0.16 | 0.20 | 0.18 |
| C36m/TIP3P | 3.1 | 0.17 | 0.23 | 0.20 |
| C36m/TIP3Pm | 3.0 | 0.18 | 0.24 | 0.21 |
| AmPro13/AmW03 | 5.5 | 0.20 | 0.29 | 0.25 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, M.; Das, A.K.; Lincoff, J.; Sasmal, S.; Cheng, S.Y.; Vernon, R.M.; Forman-Kay, J.D.; Head-Gordon, T. Configurational Entropy of Folded Proteins and Its Importance for Intrinsically Disordered Proteins. Int. J. Mol. Sci. 2021, 22, 3420. https://doi.org/10.3390/ijms22073420
Liu M, Das AK, Lincoff J, Sasmal S, Cheng SY, Vernon RM, Forman-Kay JD, Head-Gordon T. Configurational Entropy of Folded Proteins and Its Importance for Intrinsically Disordered Proteins. International Journal of Molecular Sciences. 2021; 22(7):3420. https://doi.org/10.3390/ijms22073420
Chicago/Turabian StyleLiu, Meili, Akshaya K. Das, James Lincoff, Sukanya Sasmal, Sara Y. Cheng, Robert M. Vernon, Julie D. Forman-Kay, and Teresa Head-Gordon. 2021. "Configurational Entropy of Folded Proteins and Its Importance for Intrinsically Disordered Proteins" International Journal of Molecular Sciences 22, no. 7: 3420. https://doi.org/10.3390/ijms22073420
APA StyleLiu, M., Das, A. K., Lincoff, J., Sasmal, S., Cheng, S. Y., Vernon, R. M., Forman-Kay, J. D., & Head-Gordon, T. (2021). Configurational Entropy of Folded Proteins and Its Importance for Intrinsically Disordered Proteins. International Journal of Molecular Sciences, 22(7), 3420. https://doi.org/10.3390/ijms22073420






