Experimental and Computational Studies on Structure and Energetic Properties of Halogen Derivatives of 2-Deoxy-D-Glucose
Abstract
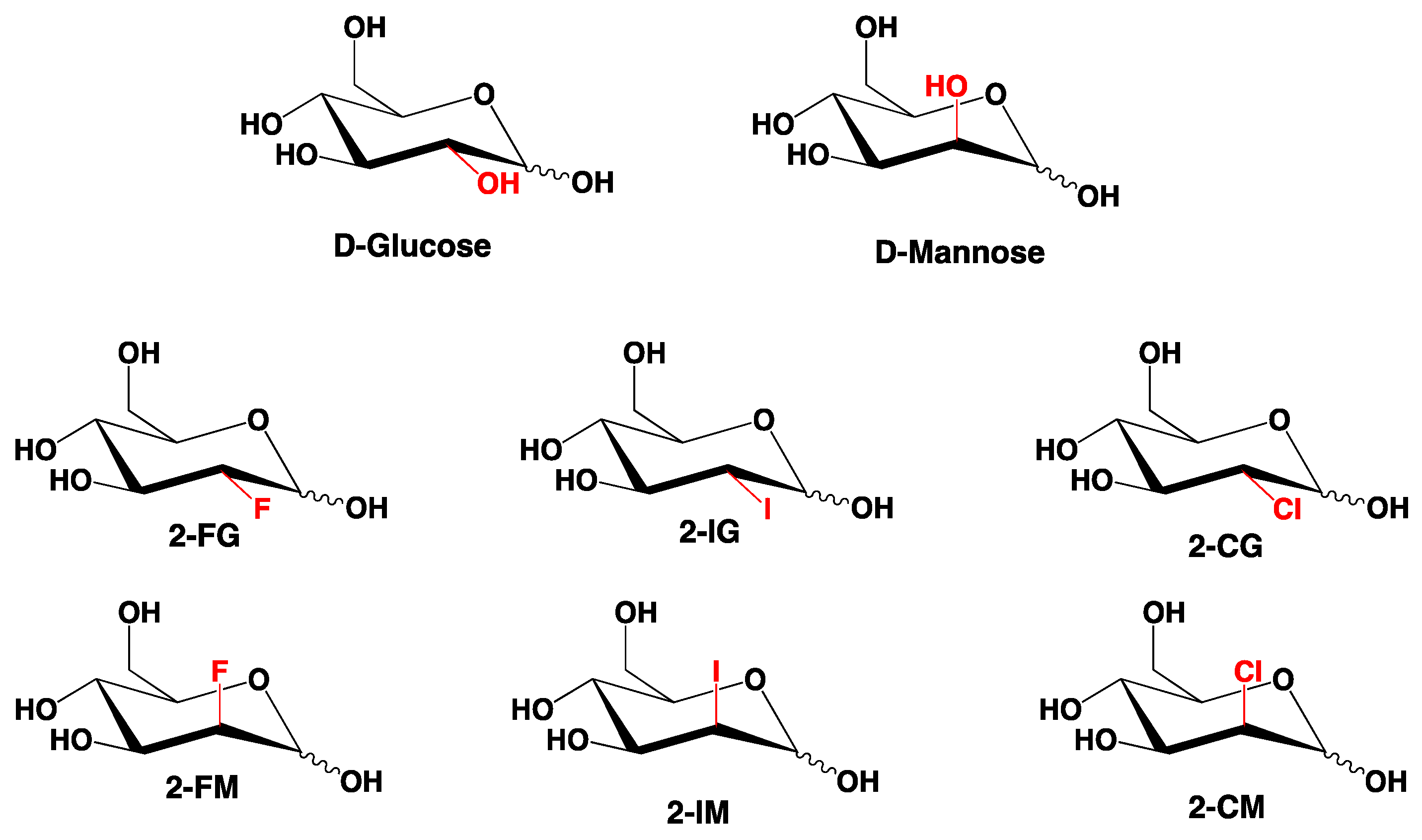
1. Introduction
2. Results and Discussion
2.1. Crystallization and Crystal Morphology
2.2. X-ray Diffraction Studies
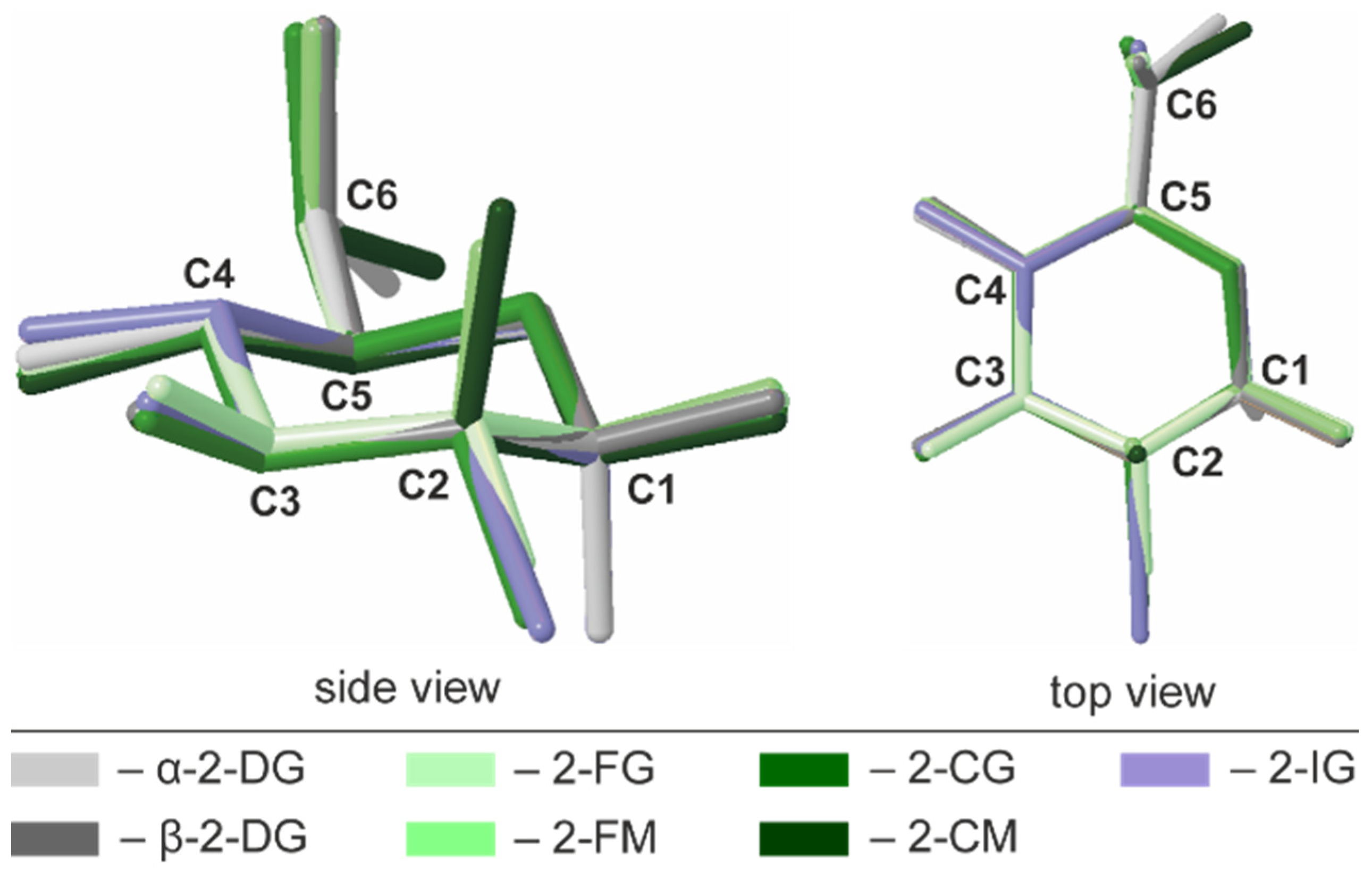
2.3. Conformational Analysis of the Pyranose Ring
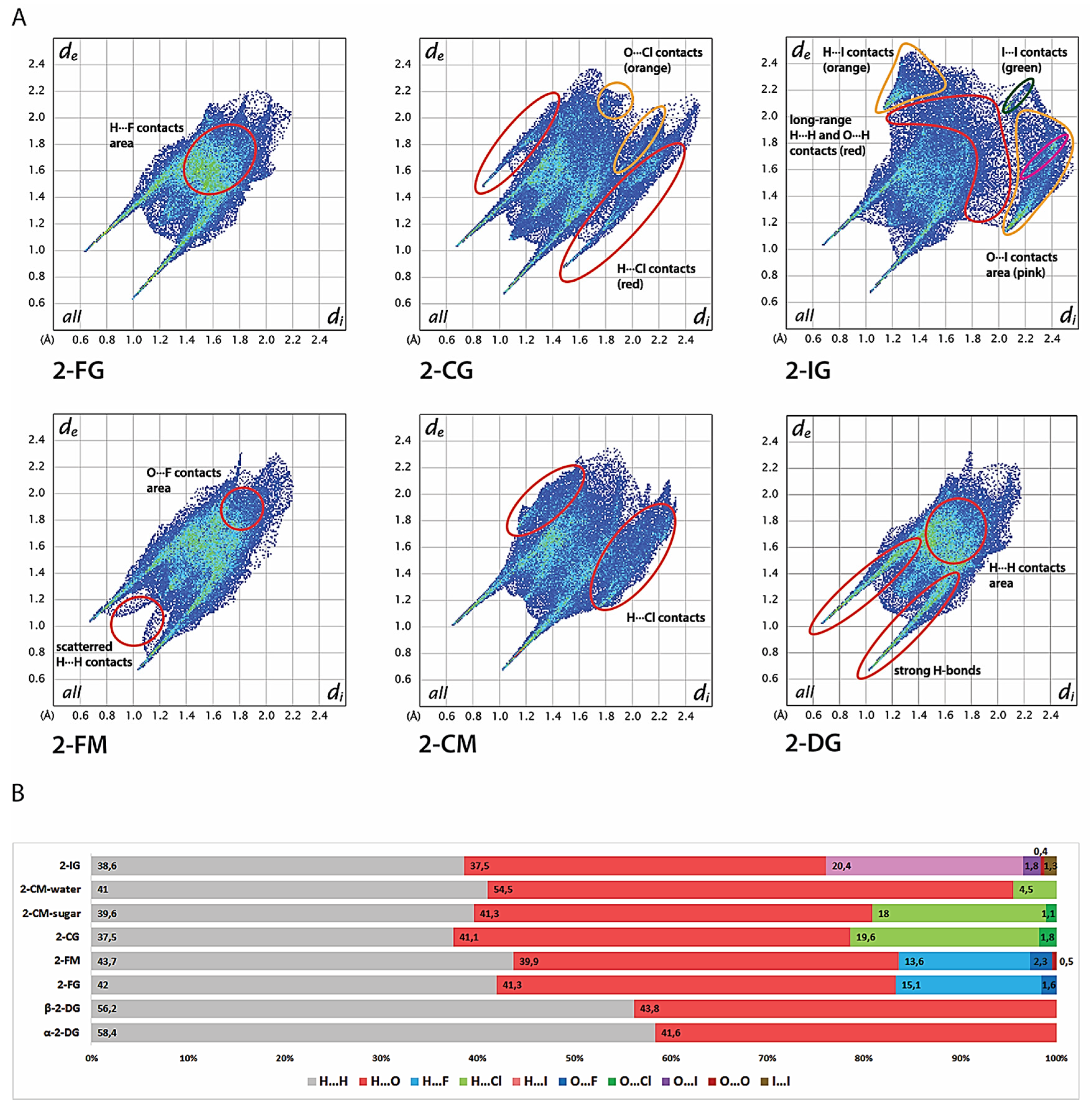
2.4. Intermolecular Interactions
2.5. Hirshfeld Surface Analysis
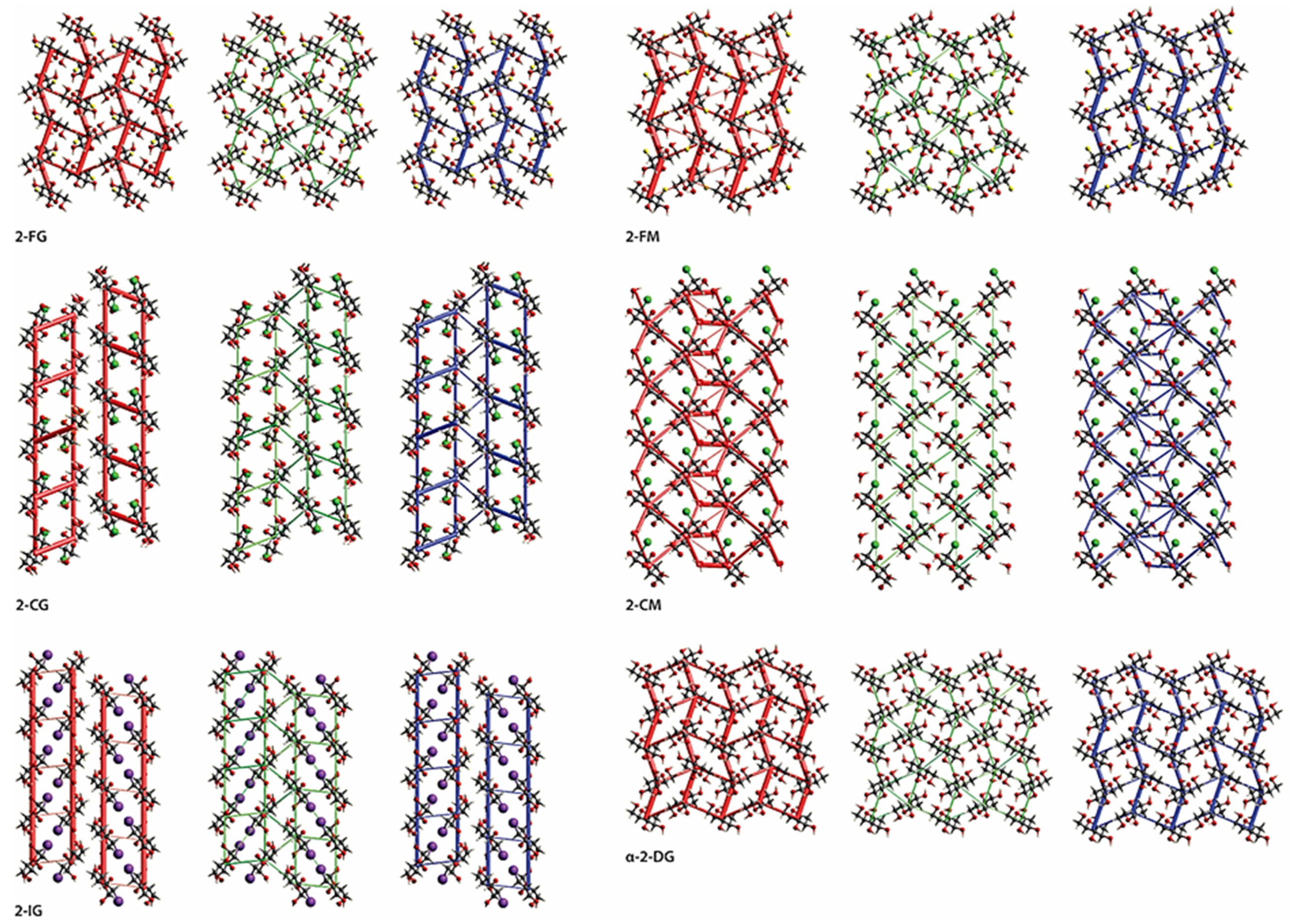
2.6. Cohesive Energies and Energy Frameworks
2.7. Structure in Aqueous Solution
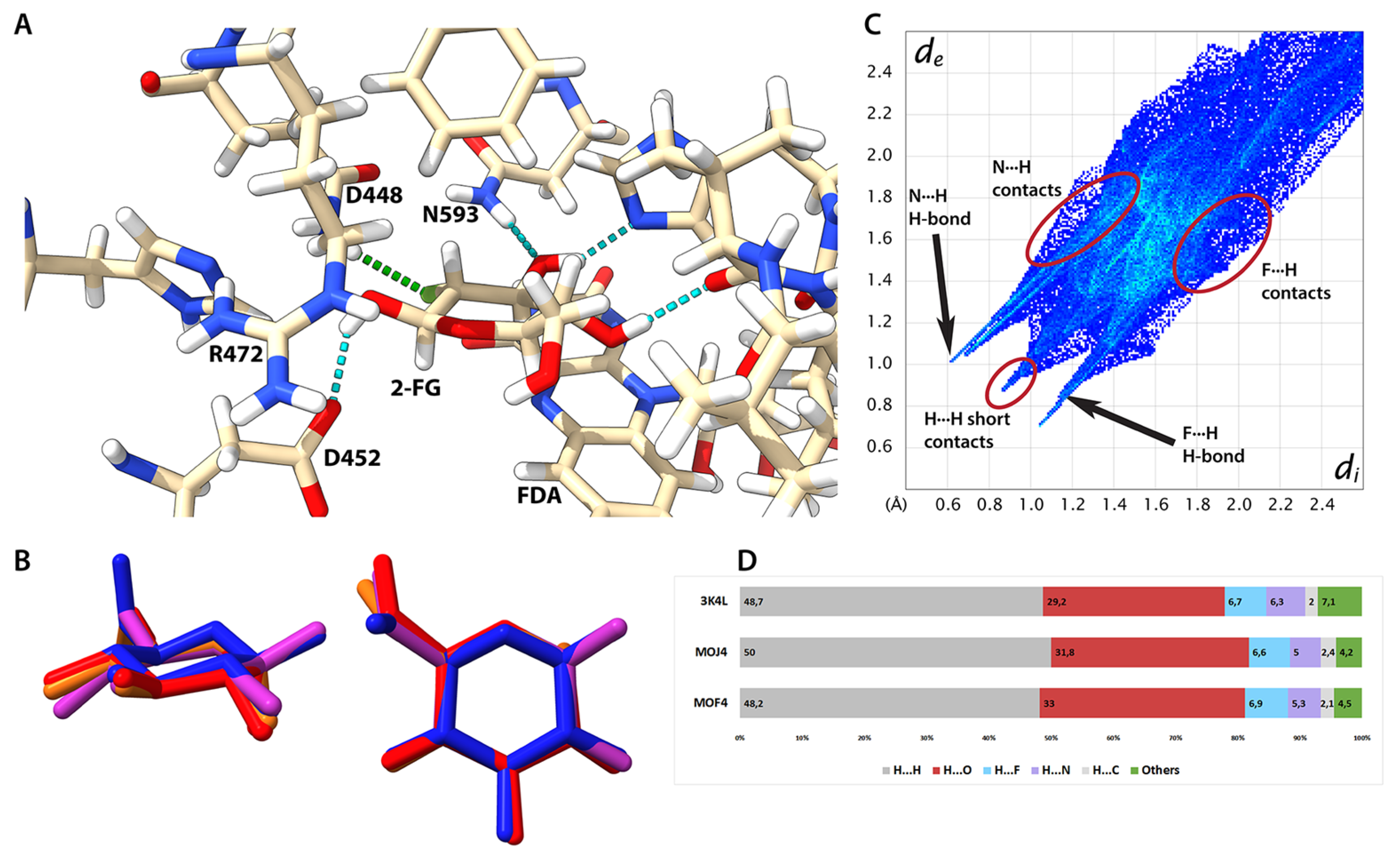
2.8. Protein-Ligand Interaction
3. Materials and Methods
3.1. X-ray Data Collection and Structure Refinement
3.2. Hirshfeld Analysis and Crystal Lattice Energy
3.3. Electrostatic Calculations (Ligand-Protein Complexes)
3.3.1. Preparation of the Protein Structures
3.3.2. Electrostatic Interaction Energy between Ligand and Protein
3.3.3. Geometry of Ligand Binding and Molecular Visualisation
3.4. NMR Spectroscopy
3.4.1. Data Collection and Processing
3.4.2. Conformational Analysis
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pajak, B.; Siwiak, E.; Sołtyka, M.; Priebe, A.; Zieliński, I.R.; Fokt, I.; Ziemniak, M.; Jaśkiewicz, A.; Borowski, R.; Domoradzki, T.; et al. 2-Deoxy-D-glucose and its analogs: From diagnostic to therapeutic agents. Int. J. Mol. Sci. 2019, 21, 234. [Google Scholar] [CrossRef] [PubMed]
- Phelps, M.E. PET: Molecular Imaging and its Biological Applications; Springer: New York, NY, USA, 2004. [Google Scholar]
- Fonti, R.; Conson, M.; Del Vecchio, S. PET/CT in radiation oncology. Semin. Oncol. 2019, 46, 202–209. [Google Scholar] [CrossRef] [PubMed]
- De Castro, M.; Marzabadi, C.H. Preparation and reactions of iodo sugars. Tetrahedron 2010, 66, 3395–3404. [Google Scholar] [CrossRef]
- Fokt, I.; Szymański, S.; Skóra, S.; Cybulski, M.; Madden, T.; Priebe, W. D-Glucose and D-mannose-based antimetabolites. Part 2. Facile synthesis of 2-deoxy-2-halo-D-glucoses and -D-mannoses. Carbohydr. Res. 2009, 344, 1464–1473. [Google Scholar] [CrossRef]
- Lampidis, T.J.; Kurtoglu, M.; Maher, J.C.; Liu, H.; Krishan, A.; Sheft, V.; Szymanski, S.; Fokt, I.; Rudnicki, W.R.; Ginalski, K.; et al. Efficacy of 2-halogen substituted D-glucose analogs in blocking glycolysis and killing “hypoxic tumor cells”. Cancer Chemother. Pharmacol. 2006, 58, 725–734. [Google Scholar] [CrossRef]
- Batra, S.; Adekola, K.U.A.; Rosen, S.T.; Shanmugam, M. Cancer metabolism as a therapeutic target. Oncology 2013, 27, 460–467. [Google Scholar]
- Oliveira, G.L.; Coelho, A.R.; Marques, R.; Oliveira, P.J. Cancer cell metabolism: Rewiring the mitochondrial hub. Biochim. Biophys. Acta 2021, 1867, 166016. [Google Scholar] [CrossRef]
- Laussel, C.; Léon, S. Cellular toxicity of the metabolic inhibitor 2-deoxyglucose and associated resistance mechanisms. Biochem. Pharmacol. 2020, 182, 114213. [Google Scholar] [CrossRef]
- Liu, C.C.; Jiang, C.J.; Lavis, A.; Croft, L.; Dong, H.Y.; Tseng, F.; Yang, K.; Tay, H.; Hersey, P.; Zhang, X.D. 2-deoxy-D-glucose enhances TRAIL-induced apoptosis in human melanoma cells through XBP-1-mediated upregulation of TRAIL-R2. Mol. Cancer 2009, 8, 122. [Google Scholar] [CrossRef]
- Sottnik, J.L.; Lori, J.C.; Rose, B.J.; Thamm, D.H. Glycolysis inhibition by 2-deoxy-D-glucose reverts the metastatic phenotype in vitro and in vivo. Clin. Exp. Metastasis 2011, 28, 865–875. [Google Scholar] [CrossRef]
- Parris, G. 2-deoxy-D-glucose as a potential drug against fusogenic viruses including HIV. Med. Hypotheses 2008, 70, 776–782. [Google Scholar] [CrossRef] [PubMed]
- Bojkova, D.; Klann, K.; Koch, B.; Widera, M.; Krause, D.; Ciesek, S.; Cinatl, J.; Munch, C. Proteomics of SARS-CoV-2-infected host cells reveals therapy targets. Nature 2020, 583, 469–472. [Google Scholar] [CrossRef]
- Balkrishna, A.; Thakur, P.; Singh, S.; Dev, S.; Jain, V.; Varshney, A.; Sharma, R. Computional screening approaches for investigating potential activity of phytoligands against SARS-CoV-2. Res. Square 2021. [Google Scholar] [CrossRef]
- Niccoli, S.; Boreham, D.R.; Phenix, C.P.; Lees, S.J. Non-radioactive 2-deoxy-2-fluoro-D-glucose inhibits glucose uptake in xenograft tumours and sensitizes HeLa cells to doxorubicin in vitro. PLoS ONE 2017, 12, e0187584. [Google Scholar] [CrossRef] [PubMed]
- Piña, Y.; Decatur, C.; Murray, T.G.; Houston, S.K.; Lopez-Cavalcante, M.; Hernandez, E.; Celdran, M.; Shah, N.; Feuer, W.; Lampidis, T. Retinoblastoma treatment: Utilization of the glycolytic inhibitor, 2-deoxy-2-fluoro-D-glucose (2-FG), to target the chemoresistant hypoxic regions in LH9BETA)T(AG) retinal tumors. Investig. Ophthalmol. Vis. Sci. 2012, 53, 996–1002. [Google Scholar] [CrossRef][Green Version]
- Zhang, W.; Oliver, A.G.; Serianni, A.S. Co-crystals of 3-deoxy-3-fluoro-α-D-glucopyranose and 3-deoxy-β-D-glucopyranose. Acta Crystallogr. C Cryst. Struct. Commun. 2010, 66, o496–o498. [Google Scholar] [CrossRef]
- Denavit, V.; Lainé, D.; St-Gelais, J.; Johnson, P.A.; Giguère, D. A Chiron approach towards the stereoselective synthesis of polyfluorinated carbohydrates. Nat. Commun. 2018, 9, 4721. [Google Scholar] [CrossRef]
- Linclau, B.; Golten, S.; Light, M.; Sebban, M.; Oulyadi, H. The conformation of tetrafluorinated methyl galactoside anomers: Crystallographic and NMR studies. Carbohydrate Res. 2011, 346, 1129–1139. [Google Scholar] [CrossRef]
- St-Gelais, J.; Côté, E.; Lainé, D.; Johnson, P.A.; Giguère, D. Addressing the structural complexity of fluorinated glucose analogues: Insight into lipophilicities and solvation effects. Chem. Eur. J. 2020, 26, 13499–13506. [Google Scholar] [CrossRef]
- Snider, D.A.; Addicks, W.; Owens, W. Polymorphism in generic drug product development. Adv. Drug Deliv. Rev. 2004, 56, 391–395. [Google Scholar] [CrossRef]
- Censi, R.; Di Martino, P. Polymorph impact on the bioavailability and stability of poorly soluble drugs. Molecules 2015, 20, 18759–18776. [Google Scholar] [CrossRef] [PubMed]
- Turner, M.J.; Thomas, S.P.; Shi, M.W.; Jayatilaka, D.; Spackman, M.A. Energy frameworks: Insights into interaction anisotropy and the mechanical properties of molecular crystals. Chem. Commun. 2015, 51, 3735–3738. [Google Scholar] [CrossRef] [PubMed]
- Koritsanszky, T.S.; Coppens, P. Chemical applications of the X-ray charge-density analysis. Chem. Rev. 2001, 101, 1583–1628. [Google Scholar] [CrossRef] [PubMed]
- Pawlędzio, S.; Makal, A.; Trzybiński, D.; Woźniak, K. Crystal structure, interaction energies and experimental electron density of the popular drug ketoprofen. IUCrJ 2018, 1, 1150–1156. [Google Scholar]
- Krawczuk, A.; Macchi, P. Charge density analysis for crystal engineering. Chem. Cent. J. 2014, 8, 68. [Google Scholar] [CrossRef]
- Macchi, P. Modern charge density studies: The entanglement of experimental and theory. Crystallogr. Rev. 2013, 19, 58–101. [Google Scholar] [CrossRef]
- Bieszczad, B.; Pawlędzio, S.; Polak, K.; Antonowicz, J.; Mieczkowski, A.; Trzybinski, A. Influence of halogen size on the supramolecular and energy landscape of the THF solvates of the halogen derivatives of dianthranilide. CrystEngComm 2020, 22, 5389–5399. [Google Scholar] [CrossRef]
- Cremer, D.; Pople, J.A. A general definition of ring puckering coordinates. J. Am. Chem. Soc. 1975, 97, 1354–1358. [Google Scholar] [CrossRef]
- Maluszynska, H.; Ruble, J.R.; Jeffrey, G.A. The crystal structure of 2-deoxy-D-arabino-hexopyranose at -150°. Carbohydrate Res. 1981, 97, 199–204. [Google Scholar] [CrossRef]
- O’Hagan, D. Understanding organofluorine chemistry. An introduction to the C-F bond. Chem. Soc. Rev. 2008, 37, 308–319. [Google Scholar] [CrossRef]
- Meanwell, N.A. Fluorine and fluorinated motifs in the design and application of bioisosteres for drug design. J. Med. Chem. 2018, 61, 5822–5880. [Google Scholar] [CrossRef]
- Hess, D.; Klüfers, P. 2-deoxy-D-arabino-hexopyranose. Acta Crystallogr. Sect. E Struct. Rep. Online 2011, 67, o2615. [Google Scholar] [CrossRef]
- Widmalm, G. Perspective on the primary and three-dimensional structures of carbohydrates. Carbohydr. Res. 2013, 378, 123–132. [Google Scholar] [CrossRef] [PubMed]
- Kirby, A.J. The Anomeric Effect and Related Stereoelectronic Effects at Oxygen; Springer: Berlin/Heidelberg, Germany, 1983. [Google Scholar]
- Miljkovic, M. Carbohydrates; Springer: New York, NY, USA, 2009. [Google Scholar]
- Perrin, C.L.; Armstrong, K.B.; Fabian, M.A. The origin of the anomeric effect: Conformational analysis of 2-methoxy-1,3-dimethylhexahydropyrimidine. J. Am. Chem. Soc. 1994, 116, 715–722. [Google Scholar] [CrossRef]
- Reeves, R.E. The shape of pyranoside rings. J. Am. Chem. Soc. 1950, 72, 1499–1506. [Google Scholar] [CrossRef]
- Horton, D.; Turner, W.N. Conformational and configurational studies on some acetylated aldopyranosyl halides. J. Org. Chem. 1965, 30, 3387–3394. [Google Scholar] [CrossRef]
- Donders, L.A.; De Leeuw, F.A.A.M.; Altona, C. Relationship between proton-proton NMP coupling constants and subsituent electronegativities. IV—An extended Karplus equation accounting for interactions between substituents and its application to coupling constant data calculated by the Extended Huckel method. Magn. Reson. Chem. 1989, 27, 556–563. [Google Scholar]
- Blakeley, M.P.; Hasnain, S.S.; Antonyuk, S.V. Sub-atomic resolution X-ray crystallography and neutron crystallography: Promise, challenges and potential. IUCrJ 2015, 2, 464–474. [Google Scholar] [CrossRef]
- Stenutz, R.; Carmichael, I.; Widmalm, G.; Serianni, A.S. Hydroxymethyl group conformation in saccharides: Structural dependencies of 2JHH, 3JHH, and 1JCH spin-spin coupling constants. J. Org. Chem. 2002, 67, 949–958. [Google Scholar] [CrossRef]
- ten Have, R.; Teunissen, P.J. Oxidative mechanisms involved in lignin degradation by white-rot fungi. Chem. Rev. 2001, 101, 3397–3413. [Google Scholar] [CrossRef]
- Leitner, C.; Volc, J.; Haltrich, D. Purification and characterization of pyranose oxidase from white rot fungus Trametes multicolor. Appl. Environ. Microbiol. 2001, 67, 3636–3644. [Google Scholar] [CrossRef]
- Kujawa, M.; Ebner, H.; Leitner, C.; Hallberg, B.M.; Prongjit, M.; Sucharitakul, J.; Ludwig, R.; Rudsander, U.; Peterbauer, C.; Chaiyen, P.; et al. Structural basis for substrate binding and regioselective oxidation of monosac-charides at C3 by pyranose 2-oxidase. J. Biol. Chem. 2006, 281, 35104–35115. [Google Scholar] [CrossRef] [PubMed]
- Spadiut, O.; Tan, T.-C.; Pisanelli, I.; Haltrich, D.; Divne, C. Importance of the gating segment in the substrate-recognition loop of pyranose 2-oxidase. FEBS J. 2010, 277, 2892–2909. [Google Scholar] [CrossRef] [PubMed]
- Tan, T.C.; Spadiut, O.; Gandini, R.; Haltrich, D.; Divne, C. Structural basis for binding of fluorinated glucose and galactose to Trametes multicolor pyranose 2-oxidase variants with improved galactose conversion. PLoS ONE 2014, 9, e86736. [Google Scholar] [CrossRef] [PubMed]
- Clark, R.C.; Reid, J.S. The analytical calculation of absorption in multifaceted crystals. Acta Crystallogr. A 1995, 51, 887–897. [Google Scholar] [CrossRef]
- Sheldrick, G.M. Crystal structure refinement with SHELXL. Acta Crystallogr. A 2008, 64, 112–122. [Google Scholar] [CrossRef] [PubMed]
- Spek, A.L. Structure validation in chemical crystallography. Acta Crystallogr. D Biol Crystallogr. 2009, 65, 148–155. [Google Scholar] [CrossRef]
- Dolomanov, O.V.; Bourhis, L.J.; Gildea, R.J.; Howard, J.A.K.; Puschmann, H. OLEX2: A complete structure solution, refinement and analysis program. J. Appl. Crystallogr. 2009, 42, 339–341. [Google Scholar] [CrossRef]
- Macrae, C.F.; Bruno, I.J.; Chisholm, J.A.; Edgington, P.R.; McCabe, P.; Pidcock, E.; Rodriguez-Monge, L.; Taylor, R.; van de Streek, J.; Wood, P.A. New features for the visualization and investigation of crystal structures. J. Appl. Crystallogr. 2008, 41, 466–470. [Google Scholar] [CrossRef]
- Dovesi, R.; Orlando, R.; Erba, A.; Civalleri, B.; Roetti, C.; Saunders, V.R.; Zicovich-Wilson, C.M. CRYSTAL14: A program for the ab initio investigation of crystalline solids. Int. J. Quantum Chem. 2014, 114, 1287–1317. [Google Scholar] [CrossRef]
- Gatti, C.; Cargnoni, F.; Bertini, L. Chemical information from the source function. J. Comput. Chem. 2003, 24, 422–436. [Google Scholar] [CrossRef] [PubMed]
- Peintinger, M.F.; Oliveira, D.V.; Bredow, T. Consistent gaussian basis sets of Triple-Zeta valence with polarization quality for solid-state calculations. J. Comput. Chem. 2013, 34, 451–459. [Google Scholar] [CrossRef]
- Laun, J.; Vilela Oliveira, D.; Bredow, T. Consistent gaussian basis sets of double- and triple-zeta valence with polarization quality of the fifth period for solid-state calculations. J. Comput. Chem. 2018, 39, 1285–1290. [Google Scholar] [CrossRef]
- Grimme, S. Accurate description of van der Waals complexes by density functional theory including empirical corrections. J. Comput. Chem. 2004, 25, 1463–1473. [Google Scholar] [CrossRef]
- Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef] [PubMed]
- Boys, S.F.; Bernardi, F. The calculation of small molecular interactions by the differences of separate total energies. Mol. Phys. 1970, 19, 553–566. [Google Scholar] [CrossRef]
- Spackman, M.A.; Jayatilaka, D. Hishfeld surface analysis. Cryst. Eng. Comm. 2009, 11, 19–32. [Google Scholar] [CrossRef]
- McKinnon, J.J.; Spackman, M.A.; Mitchell, A.S. Novel tools for visualizing and exploring intermolecular interactions in molecular crystals. Acta Crystallogr. 2004, 60, 627–668. [Google Scholar] [CrossRef] [PubMed]
- Jelsch, C.; Ejsmont, K.; Huder, L. The enrichment ration of atomic contacts in crystals, an indicator derived the Hirshfeld surface analysis. IUCrJ 2014, 1, 119–128. [Google Scholar] [CrossRef]
- Jarzembska, K.N.; Dominiak, P.M. New version of the theoretical databank of transferable aspherical pseudoatoms, UBDB2011—Towards nucleic acid modelling. Acta Crystallogr. Sect. A 2012, 68, 139–147. [Google Scholar] [CrossRef]
- Berman, H.M.; Westbrook, J.; Feng, Z.; Gilliland, G.; Bhat, T.N.; Weissig, H.; Shindyalov, I.N.; Bourne, P.E. The protein data bank. Nucleic Acids Res. 2000, 28, 235–242. [Google Scholar] [CrossRef] [PubMed]
- Volkov, A.; Koritsanszky, T.; Coppens, P. Combination of the exact potential and multipole methods (EP/MM) for evaluation of intermolecular electrostatic interaction energies with pseudoatom representation of molecular electron densities. Chem. Phys. Lett. 2004, 391, 170–175. [Google Scholar] [CrossRef]
- Hansen, N.K.; Coppens, P. Testing aspherical atom refinements on small-molecule data sets. Acta Crystallogr. Sect. A 1978, 34, 909–921. [Google Scholar] [CrossRef]
- Volkov, A.; Macchi, P.; Farrugia, L.J.; Gatti, C.; Mallinson, P.; Richter, T.; Koritsanszky, T. XD2016—A Computer Program Package for Multipole Refinement, Topological Analysis of Charge Densities and Evaluation of Intermolecular Energies from Experimental and Theoretical Structure Factors; University at Buffalo—The State University of New York: New York, NY, USA, 2006. [Google Scholar]
- Goddard, T.D.; Huang, C.C.; Meng, E.C.; Pettersen, E.F.; Couch, G.S.; Morris, J.H.; Ferrin, T.E. UCSF ChimeraX: Meeting modern challenges in visualization and analysis. Protein Sci. 2018, 27, 14–25. [Google Scholar] [CrossRef]
- Goddard, T.D.; Kneller, D.G. SPARKY 3; University of California: San Francisco, CA, USA, 2008. [Google Scholar]
- Altona, C.; Francke, R.; de Haan, R.; Ippel, J.H.; Daalmans, G.J.; Hoekzema, A.J.A.W.; van Wijk, J. Empirical group electronegativities for vicinal NMR proton—Proton couplings along a C-C bond: Solvent effects and reparameterization of the Haasnoot equation. Magn. Reson. Chem. 1994, 32, 670–678. [Google Scholar] [CrossRef]
- Altona, C.; Ippel, J.H.; Hoekzema, A.J.A.W.; Erkelens, C.; Groesbeek, M.; Donders, L.A. Relationship between proton-proton NMR coupling constants and substituent electronegativities. V†—Empirical substituent constants deduced from ethanes and propane. Magn. Reson. Chem. 1989, 27, 564–576. [Google Scholar] [CrossRef]
- Pettersen, E.F.; Goddard, T.D.; Huang, C.C.; Couch, G.S.; Greenblatt, D.M.; Meng, E.C.; Ferrin, T.E. UCSF Chimera—A visualization system for exploratory research and analysis. J. Comput. Chem. 2004, 25, 1605–1612. [Google Scholar] [CrossRef]


| Compound | Total Energy (kJ mol−1) |
|---|---|
| α-2-DG | −197.10 |
| β-2-DG | −215.00 |
| β-2-FG | −217.56 |
| β-2-FM | −240.25 |
| β-2-CG | −208.16 |
| β-2-CM | −295.89 |
| α-2-IG | −199.70 |
| Residue Type | Number | Interaction Energy [kJ mol−1] | ||
|---|---|---|---|---|
| 3K4L (F454N) | 4MOF (H450G) | 4MOJ (H450G/V456C) | ||
| T | 169 | −56.0 | −144.3 | −140.3 |
| A | 171 | −22.5 | −22.3 | −24.9 |
| L | 361 | −26.7 | −27.9 | −30.8 |
| Q | 448 | −73.4 | −47.6 | −55.9 |
| H a | 450 | +11.5 | −3.4 | −3.2 |
| D | 452 | +419.1 | +431.7 | +494.5 |
| R | 472 | +449.2 | −440.6 | −497.2 |
| F | 474 | −53.1 | +86.0 | −59.4 |
| L | 545 | +48.7 | +34.0 | +53.0 |
| V b | 546 | −19.3 | −38.7 | −32.7 |
| H | 548 | −35.3 | −5.6 | −24.1 |
| N | 593 | −160.3 | −131.2 | −155.3 |
| FDA c | 801 | −103.5 | −188.9 | −163.7 |
| SUM | −512.3 | −490.0 | −635.1 | |
| Parameter a | 3K4L | 4MOF | 4MOJ |
|---|---|---|---|
| Total Eel [kJ mol−1] | −512.3 | −490.0 | −635.1 |
| Michaelis constant (Km) [mM] | 1.5 ± 0.1 | 0.939 ± 0.04 | 2.43 ± 0.27 |
| Turnover number (kcat) [s−1] | 12.0 ± 0.0 | 12.5 ± 0.2 | 16.8 ± 0.27 |
| Specificity constant (Km/kcat) [mM s−1] | 8.2 | 12.7 | 13.5 |
| Parameter | COSY | 13C-HSQC | HMBC | NOESY | 1H | 13C-HSQC-AP |
|---|---|---|---|---|---|---|
| Relaxation delay [s] | 1 | 1.5 | 1 | 6 | 1 | 1.5 |
| Number of transients | 4 | 2 | 4 | 4 | 8 | 8 |
| Acquisition time [s] | 0.15 | 0.15 | 0.15 | 0.15 | 1.7 | 1.2 |
| Number of increments | 200 | 300 | 200 | 200 | n.a. | 400 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ziemniak, M.; Zawadzka-Kazimierczuk, A.; Pawlędzio, S.; Malinska, M.; Sołtyka, M.; Trzybiński, D.; Koźmiński, W.; Skora, S.; Zieliński, R.; Fokt, I.; et al. Experimental and Computational Studies on Structure and Energetic Properties of Halogen Derivatives of 2-Deoxy-D-Glucose. Int. J. Mol. Sci. 2021, 22, 3720. https://doi.org/10.3390/ijms22073720
Ziemniak M, Zawadzka-Kazimierczuk A, Pawlędzio S, Malinska M, Sołtyka M, Trzybiński D, Koźmiński W, Skora S, Zieliński R, Fokt I, et al. Experimental and Computational Studies on Structure and Energetic Properties of Halogen Derivatives of 2-Deoxy-D-Glucose. International Journal of Molecular Sciences. 2021; 22(7):3720. https://doi.org/10.3390/ijms22073720
Chicago/Turabian StyleZiemniak, Marcin, Anna Zawadzka-Kazimierczuk, Sylwia Pawlędzio, Maura Malinska, Maja Sołtyka, Damian Trzybiński, Wiktor Koźmiński, Stanisław Skora, Rafał Zieliński, Izabela Fokt, and et al. 2021. "Experimental and Computational Studies on Structure and Energetic Properties of Halogen Derivatives of 2-Deoxy-D-Glucose" International Journal of Molecular Sciences 22, no. 7: 3720. https://doi.org/10.3390/ijms22073720
APA StyleZiemniak, M., Zawadzka-Kazimierczuk, A., Pawlędzio, S., Malinska, M., Sołtyka, M., Trzybiński, D., Koźmiński, W., Skora, S., Zieliński, R., Fokt, I., Priebe, W., Woźniak, K., & Pająk, B. (2021). Experimental and Computational Studies on Structure and Energetic Properties of Halogen Derivatives of 2-Deoxy-D-Glucose. International Journal of Molecular Sciences, 22(7), 3720. https://doi.org/10.3390/ijms22073720







