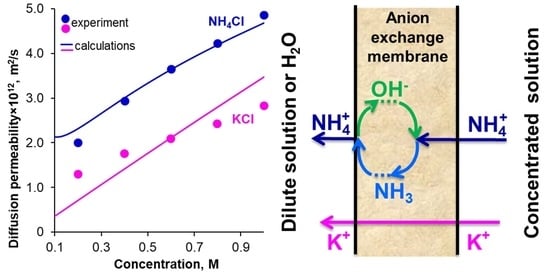
High Diffusion Permeability of Anion-Exchange Membranes for Ammonium Chloride: Experiment and Modeling
Abstract
:1. Introduction
2. Results and Discussions
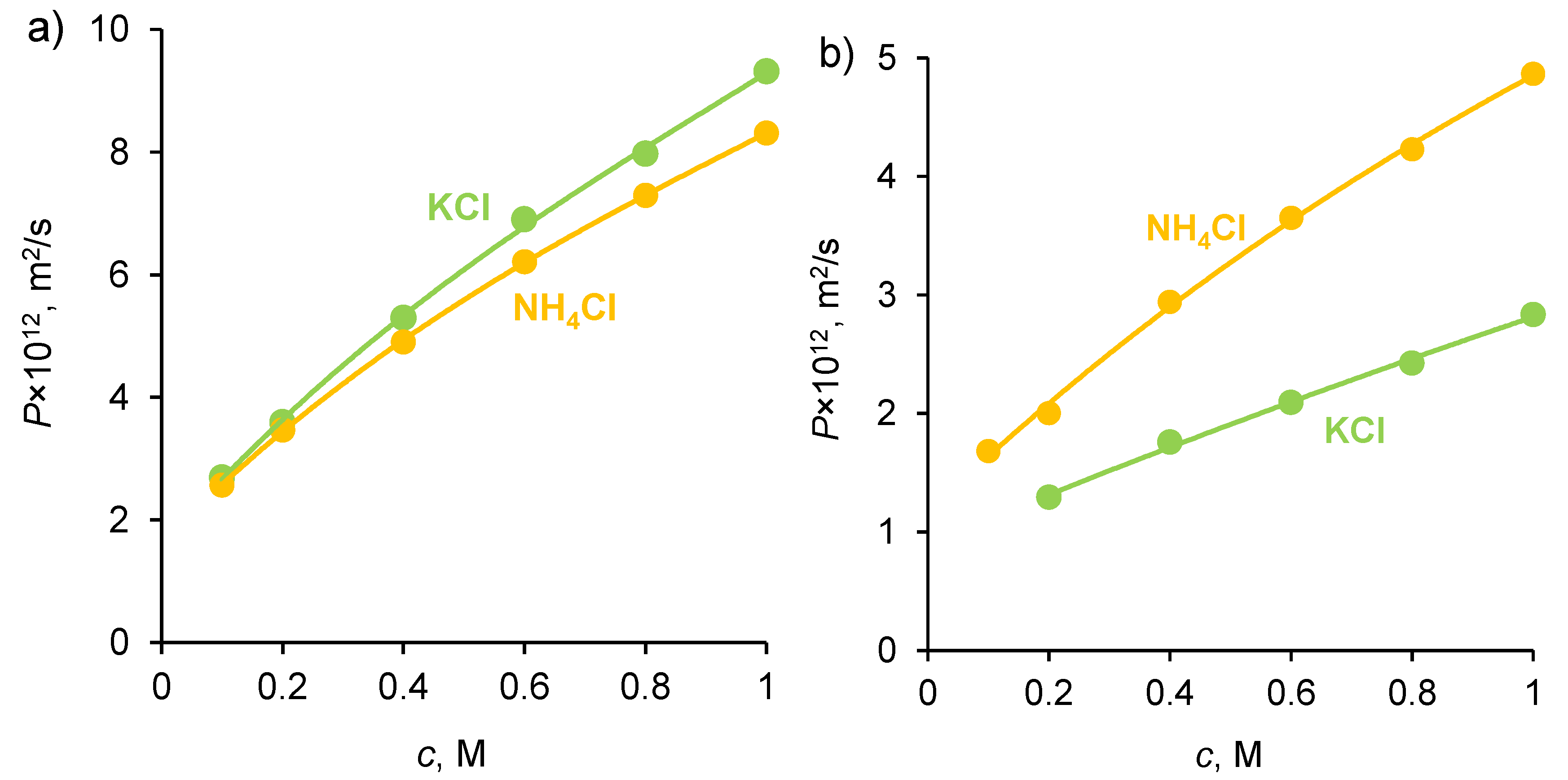
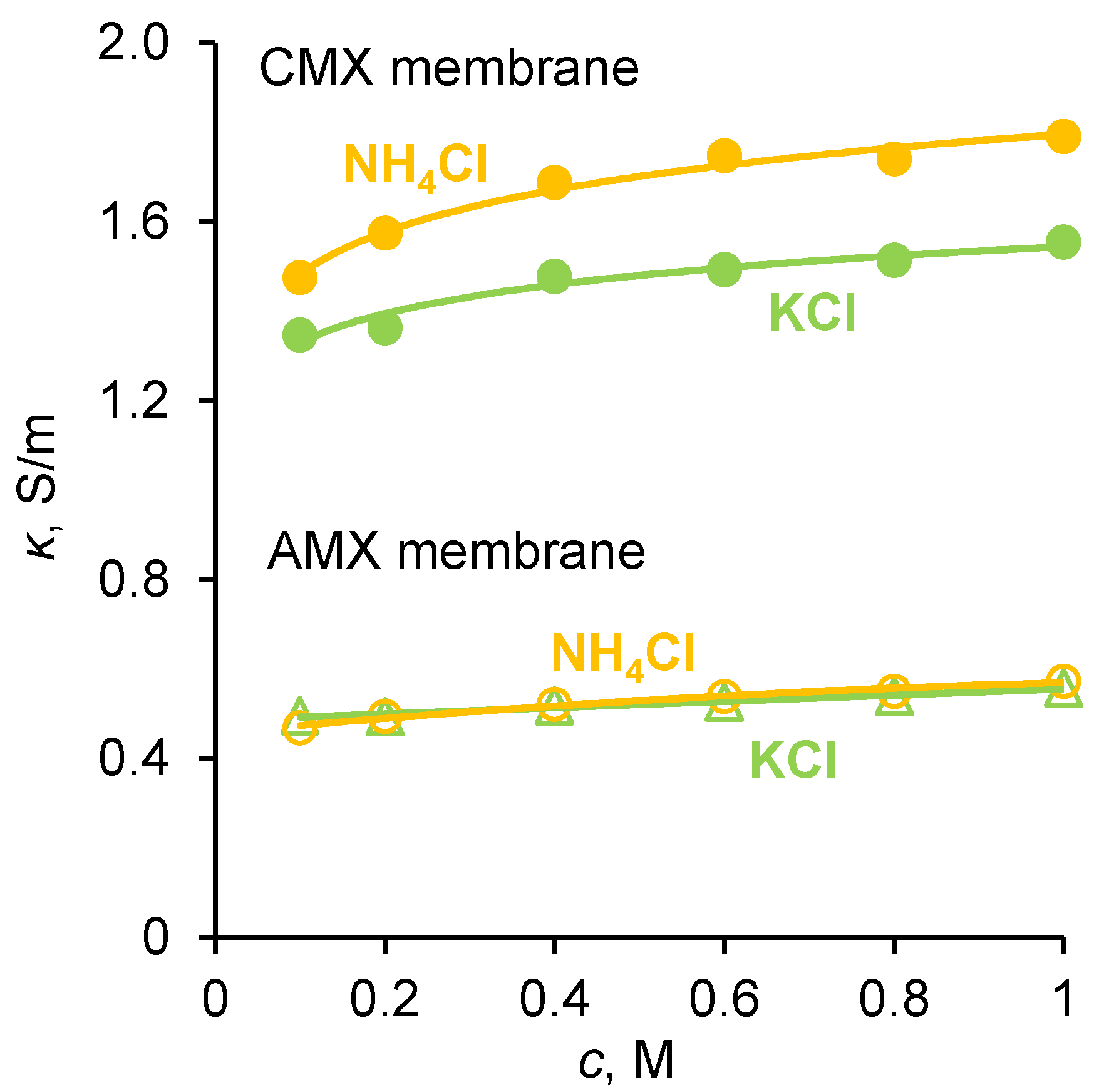
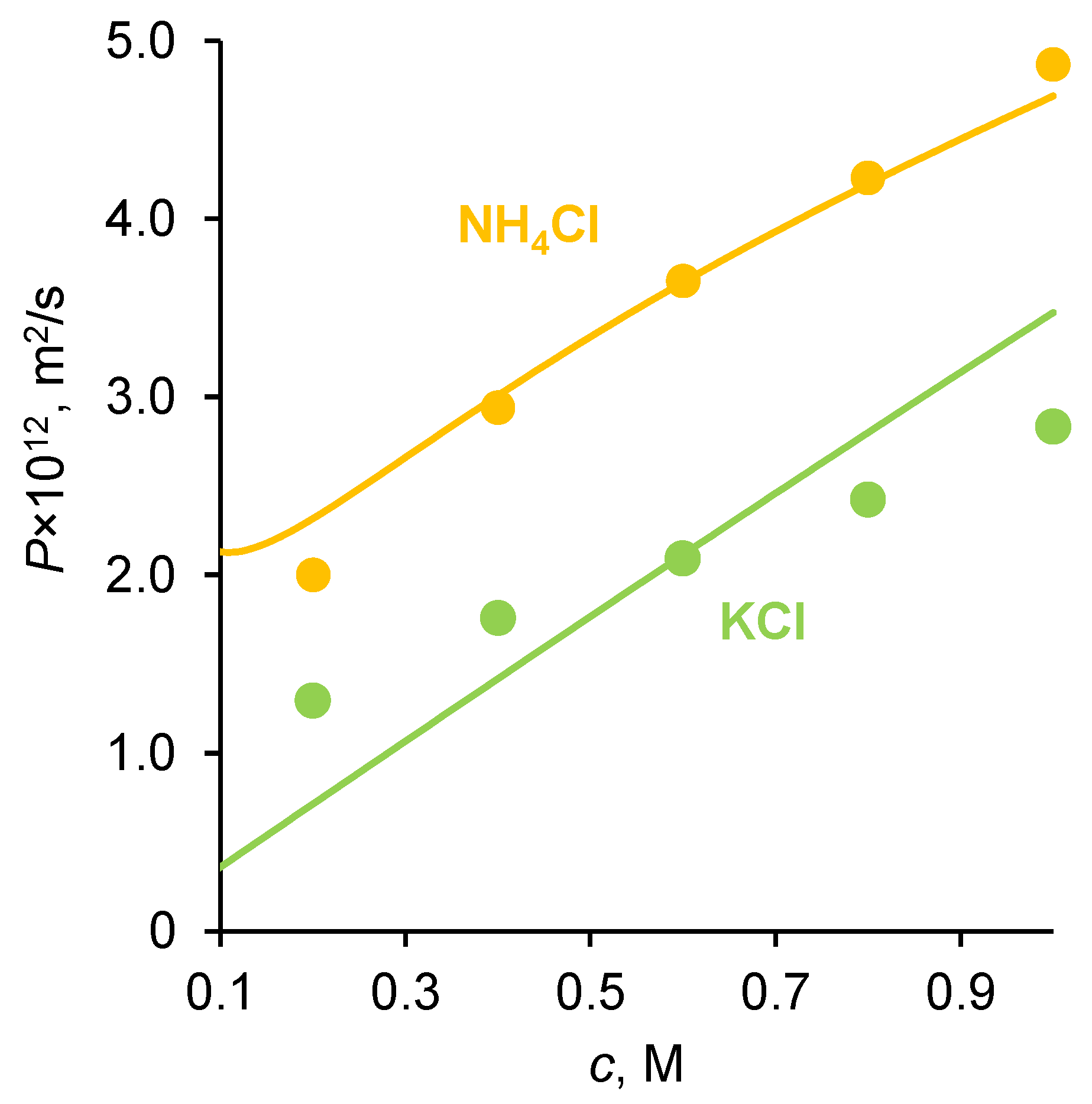
2.1. Diffusion Permeability and Conductivity of IEMs
2.2. Mathematical Modeling of Diffusion Permeability of the AMX Membrane
2.3. Determination of the Input Parameters
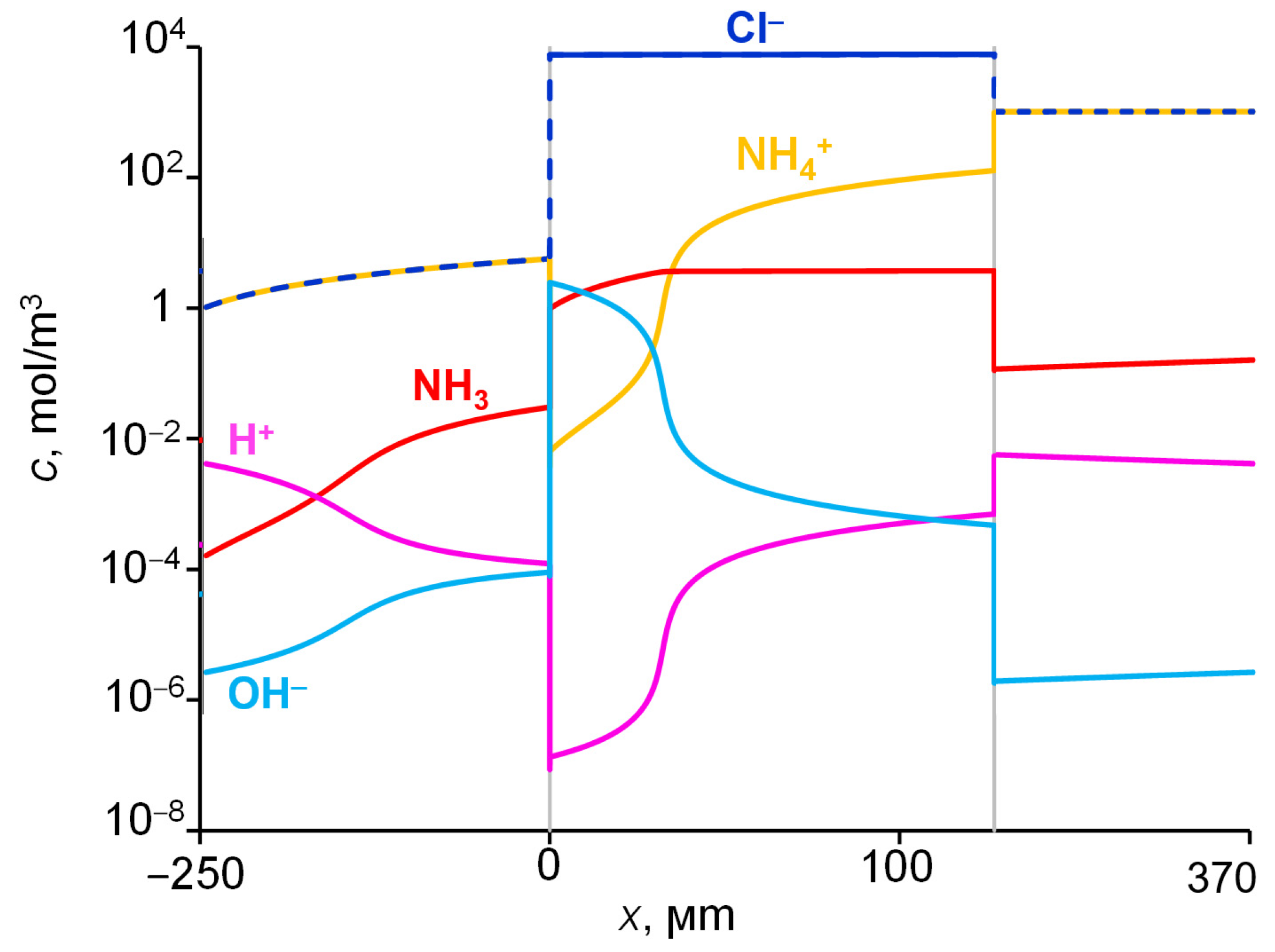
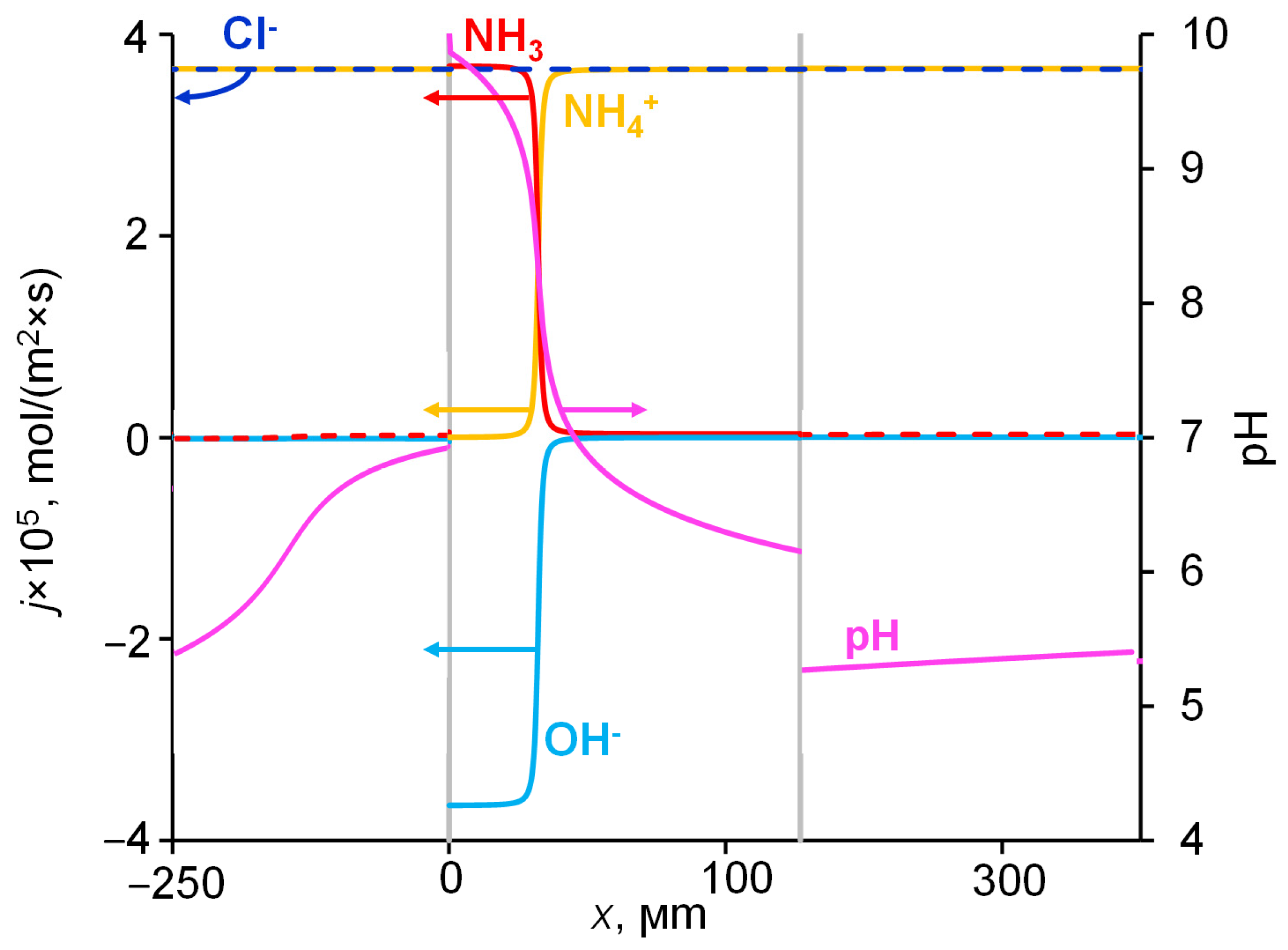
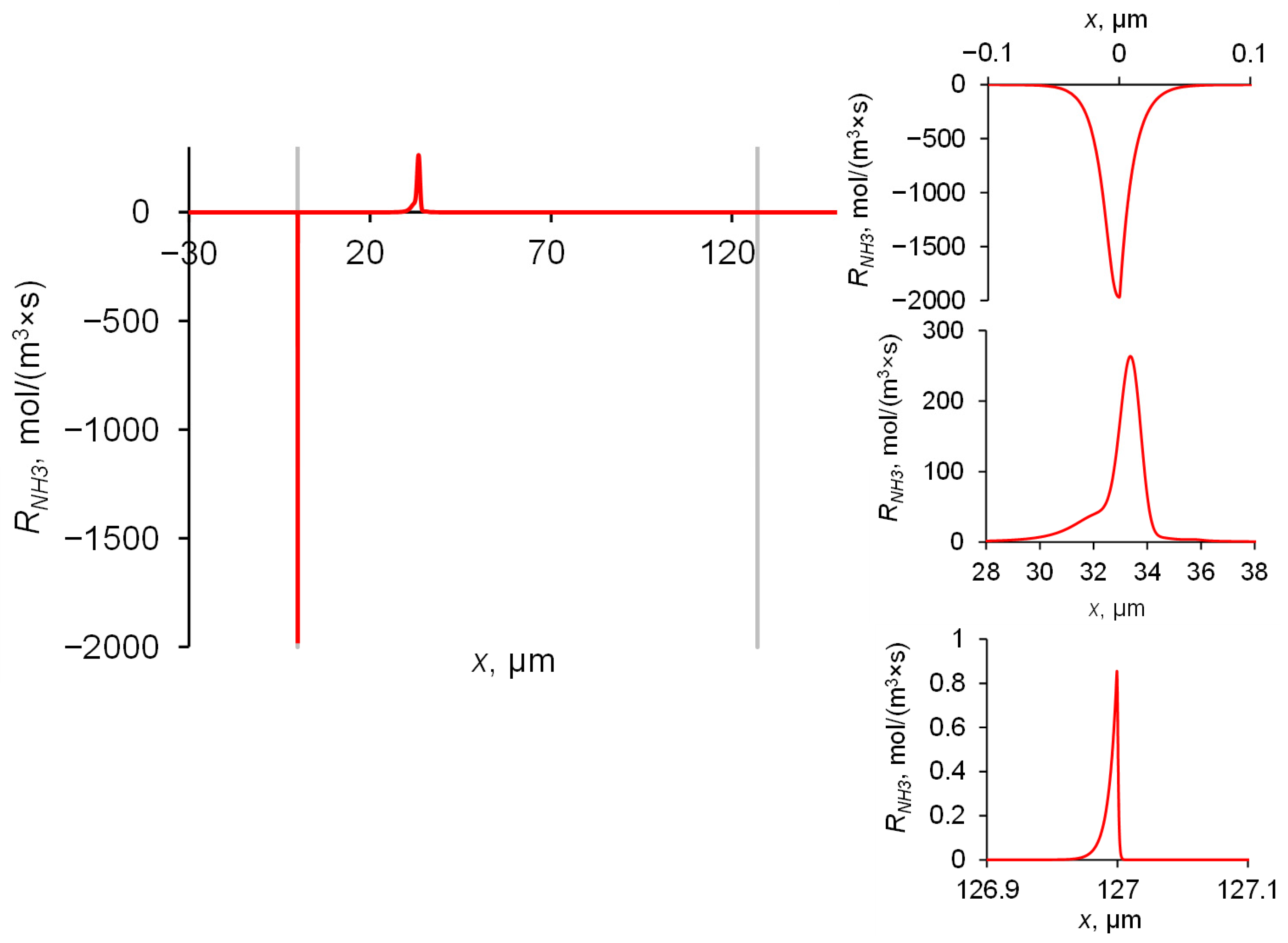
2.4. Concentrations and Fluxes in the Case of NH4Cl
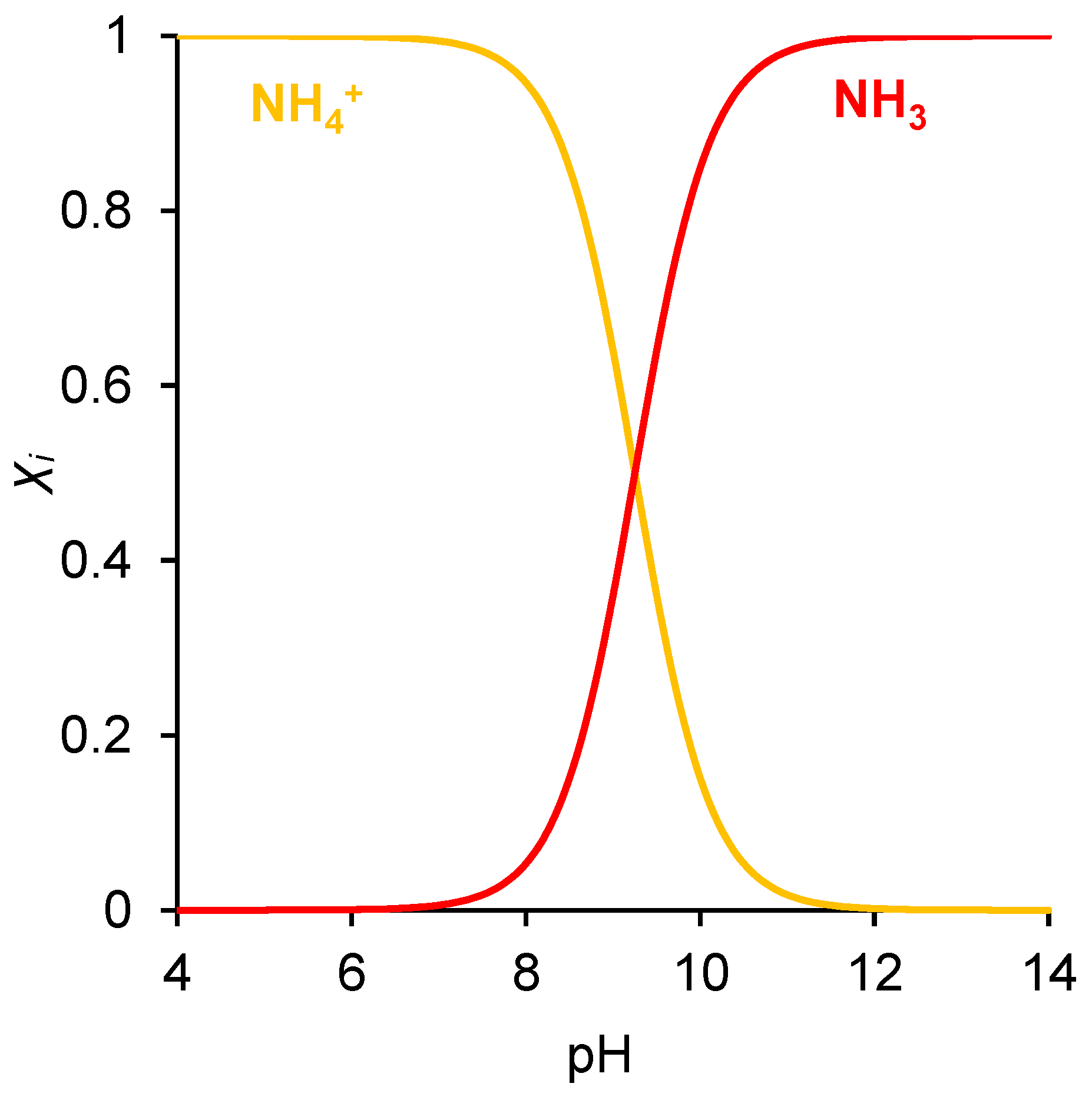
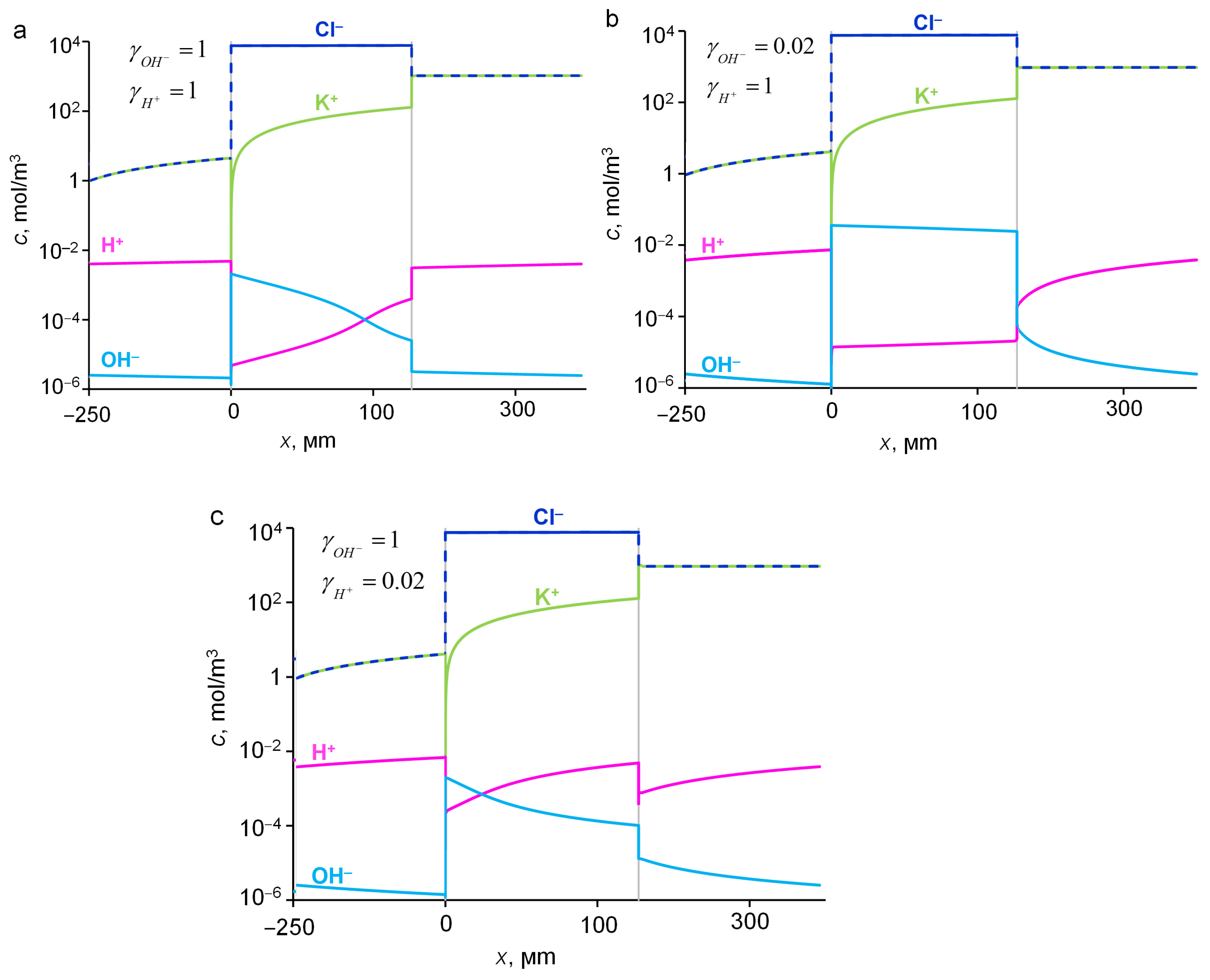
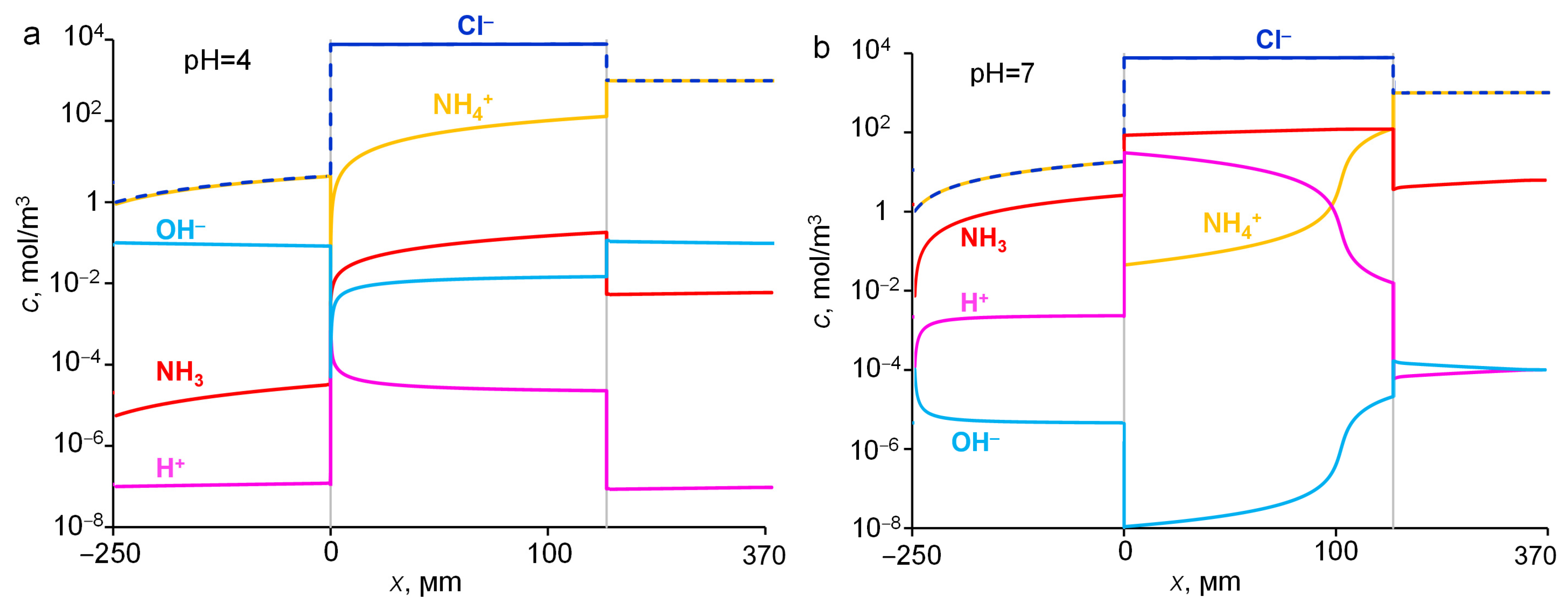
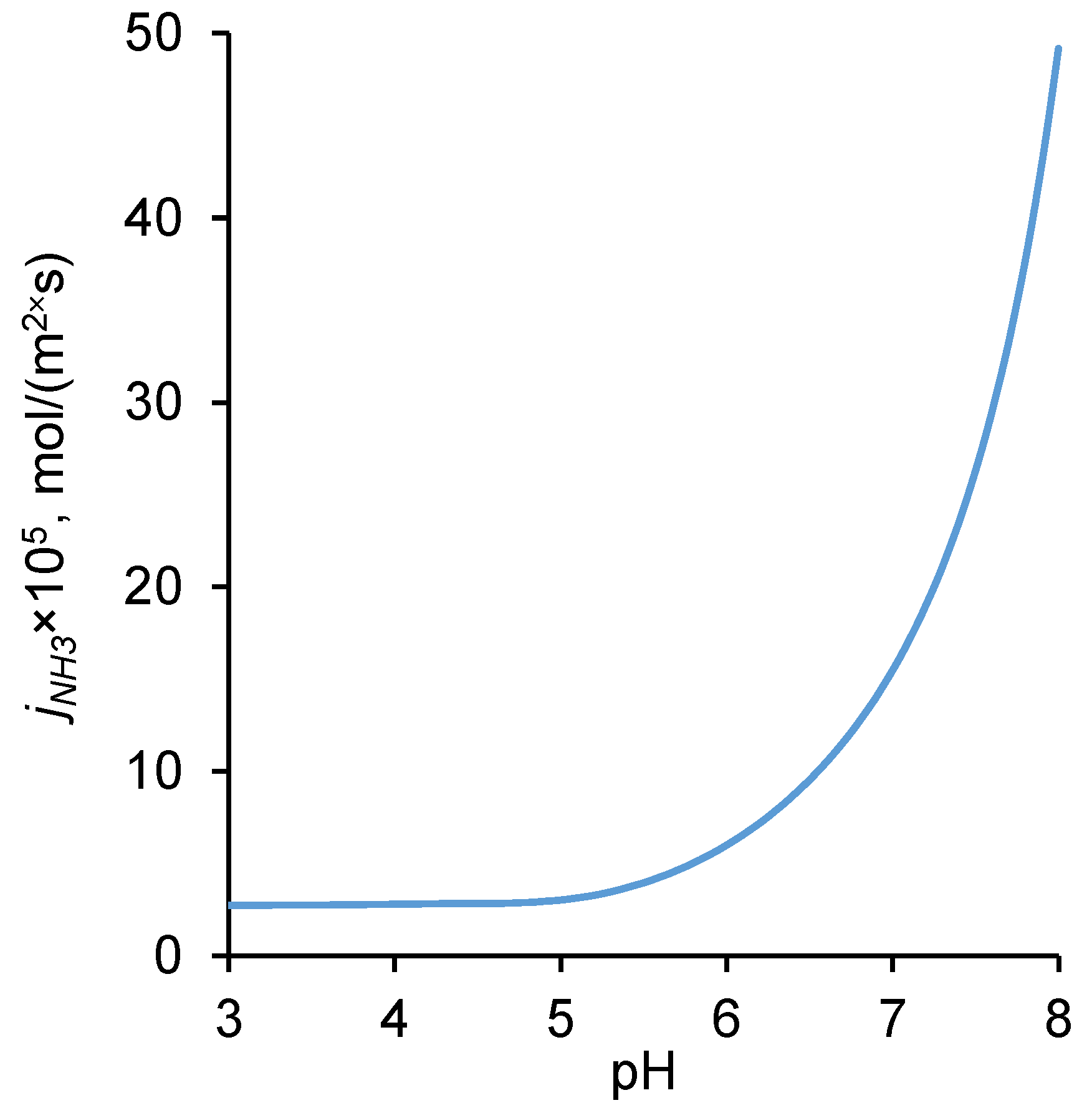
2.5. Influence of pH of External Solution
2.6. Discussion
3. Experimental Part
3.1. Membranes and Solutions
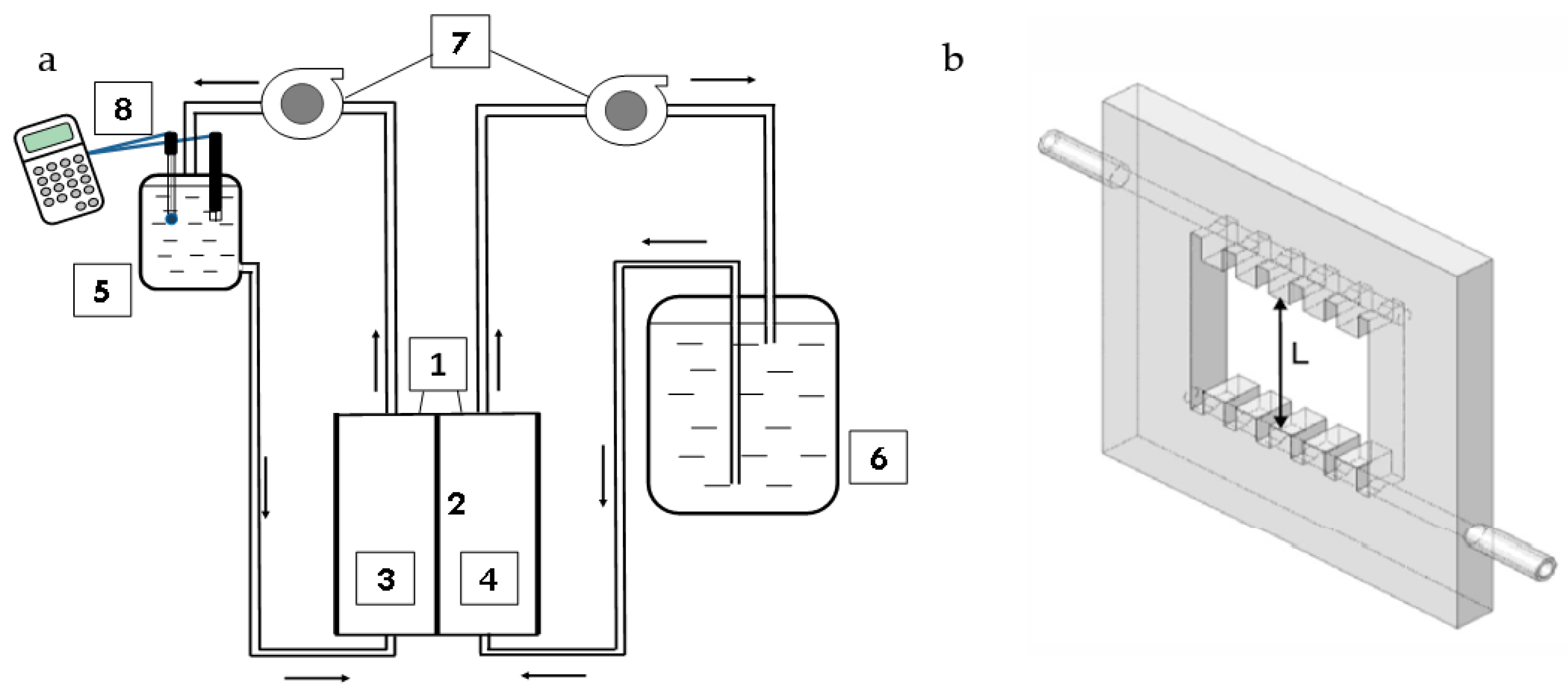
3.2. Diffusion Permeability
3.3. Conductivity of IEM
4. Mathematical Model
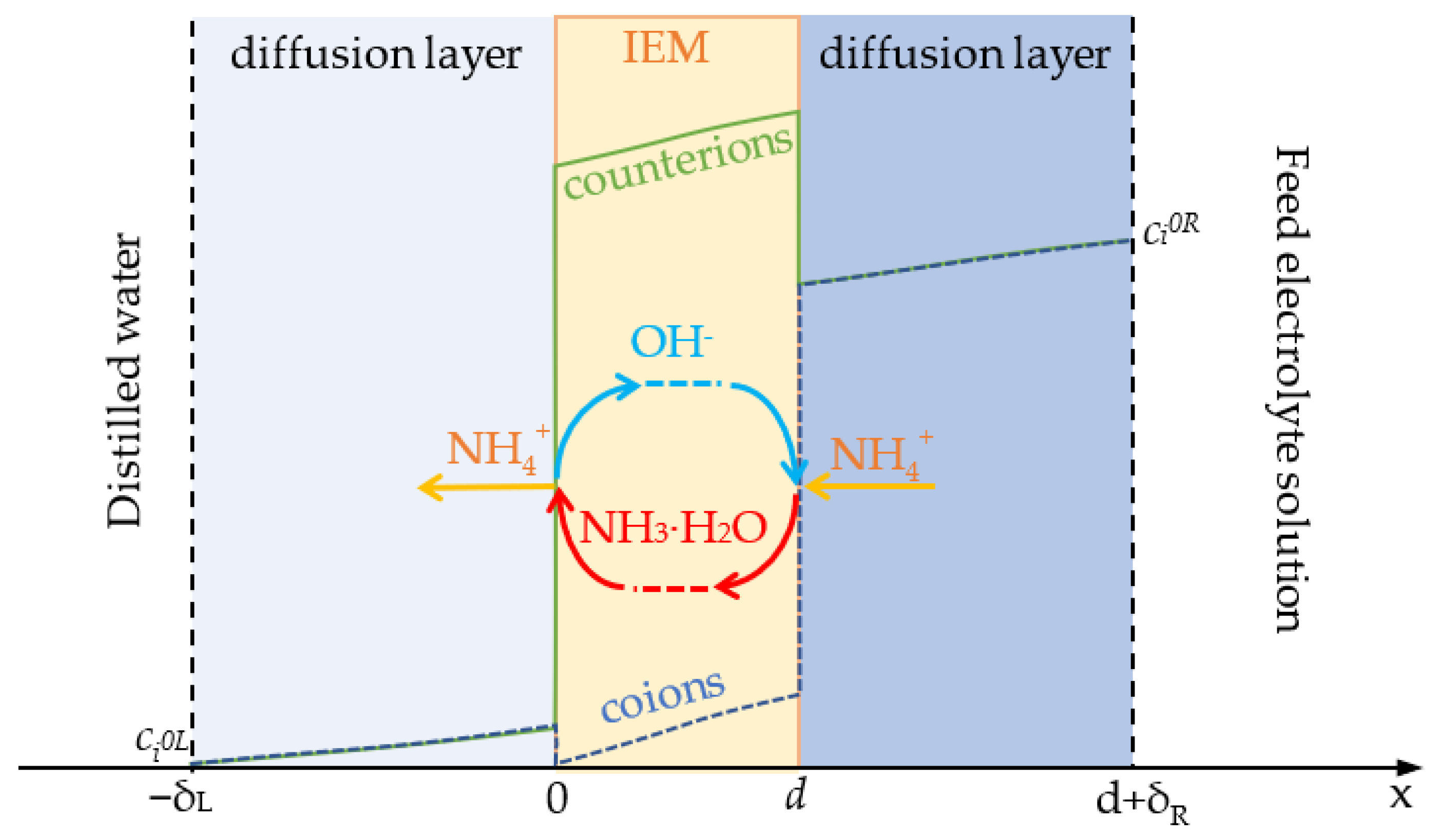
4.1. Model Formulation
4.2. Boundary Conditions
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- USEPA. Preventing Eutrophication: Scientific Support for Dual Nutrient Criteria; United States Environment Protaction Agency: Washington, DC, USA, 2015.
- Ravishankara, A.R.; Daniel, J.S.; Portmann, R.W. Nitrous oxide (N2O): The dominant ozone-depleting substance emitted in the 21st century. Science 2009, 326, 123–125. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Canfield, D.E.; Glazer, A.N.; Falkowski, P.G. The evolution and future of earth’s nitrogen cycle. Science 2010, 330, 192–196. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Anderson, D.M.; Burkholder, J.M.; Cochlan, W.P.; Glibert, P.M.; Gobler, C.J.; Heil, C.A.; Kudela, R.M.; Parsons, M.L.; Rensel, J.E.J.; Townsend, D.W.; et al. Harmful algal blooms and eutrophication: Examining linkages from selected coastal regions of the United States. Harmful Algae 2008, 8, 39–53. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Smil, V. Nitrogen and food production: Proteins for human diets. Ambio 2002, 31, 126–131. [Google Scholar] [CrossRef] [PubMed]
- Godfray, H.C.J.; Beddington, J.R.; Crute, I.R.; Haddad, L.; Lawrence, D.; Muir, J.F.; Pretty, J.; Robinson, S.; Thomas, S.M.; Toulmin, C. Food Security: The Challenge of Feeding 9 Billion People. Science 2017, 327, 812–818. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Giddey, S.; Badwal, S.P.S.; Kulkarni, A. Review of electrochemical ammonia production technologies and materials. Int. J. Hydrog. Energy 2013, 38, 14576–14594. [Google Scholar] [CrossRef]
- Philibert, C. Renewable energy for industry. In Proceedings of the IJISEA Annual Meeting @ NREL, Golden, CO, USA, 4 April 2018. [Google Scholar]
- Nancharaiah, Y.V.; Mohan, S.V.; Lens, P.N.L. Recent advances in nutrient removal and recovery in biological and bioelectrochemical systems. Bioresour. Technol. 2016, 215, 173–185. [Google Scholar] [CrossRef]
- Lan, R.; Tao, S. Direct ammonia alkaline anion-exchange membrane fuel cells. Electrochem. Solid-State Lett. 2010, 13, 8–11. [Google Scholar] [CrossRef]
- Katayama, Y.; Okanishi, T.; Muroyama, H.; Matsui, T.; Eguchi, K. Enhancement of ammonia oxidation activity over Y2O3-modified platinum surface: Promotion of NH2, ad dimerization process. J. Catal. 2016, 344, 496–506. [Google Scholar] [CrossRef] [Green Version]
- Aoki, Y.; Yamaguchi, T.; Kobayashi, S.; Kowalski, D.; Zhu, C.; Habazaki, H. High-Efficiency Direct Ammonia Fuel Cells Based on BaZr0.1Ce0.7Y0.2O3−δ/Pd Oxide-Metal Junctions. Glob. Chall. 2018, 2, 1700088. [Google Scholar] [CrossRef] [Green Version]
- Lipman, T.; Shah, N. Ammonia as an Alternative Energy Storage Medium for Hydrogen Fuel Cells; eScholarship Repository, University of California: Oakland, CA, USA, 2007. [Google Scholar]
- Mehta, C.M.; Khunjar, W.O.; Nguyen, V.; Tait, S.; Batstone, D.J. Technologies to Recover Nutrients from Waste Streams: A Critical Review. Crit. Rev. Environ. Sci. Technol. 2015, 45, 385–427. [Google Scholar] [CrossRef] [Green Version]
- Arredondo, M.R.; Kuntke, P.; Jeremiasse, A.W.; Sleutels, T.H.J.A.; Buisman, C.J.N.; Heijne, A.T. Bioelectrochemical systems for nitrogen removal and recovery from wastewater. Environ. Sci. Water Res. Technol. 2015, 1, 22–33. [Google Scholar] [CrossRef]
- Ward, A.J.; Arola, K.; Brewster, E.T.; Mehta, C.M.; Batstone, D.J. Nutrient recovery from wastewater through pilot scale electrodialysis. Water Res. 2018, 135, 57–65. [Google Scholar] [CrossRef] [PubMed]
- Melnikov, S.; Loza, S.; Sharafan, M.; Zabolotskiy, V. Electrodialysis treatment of secondary steam condensate obtained during production of ammonium nitrate. Technical and economic analysis. Sep. Purif. Technol. 2016, 157, 179–191. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, X.; Wang, Y.; Du, Y.; Feng, H.; Xu, T. Simultaneous recovery of ammonium and phosphorus via the integration of electrodialysis with struvite reactor. J. Memb. Sci. 2015, 490, 65–71. [Google Scholar] [CrossRef]
- Kozaderova, O.A.; Niftaliev, S.I.; Kim, K.B. Ionic Transport in Electrodialysis of Ammonium Nitrate. Russ. J. Electrochem. 2018, 54, 363–367. [Google Scholar] [CrossRef]
- Kozaderova, O.A.; Kim, K.B.; Gadzhiyeva, C.S.; Niftaliev, S.I. Electrochemical characteristics of thin heterogeneous ion exchange membranes. J. Memb. Sci. 2020, 604, 118081. [Google Scholar] [CrossRef]
- Aminov, O.M.; Shaposhnik, V.A.; Guba, A.A.; Kutsenko, A.E. Coupled transport of ammonium ions with hydrogen and hydroxide ions during electrodialysis in the region of overlimiting current densities. Sorpt. Chromatogr. Process 2013, 13, 816–822. [Google Scholar]
- Rybalkina, O.A.; Tsygurina, K.A.; Melnikova, E.D.; Pourcelly, G.; Nikonenko, V.V.; Pismenskaya, N.D. Catalytic effect of ammonia-containing species on water splitting during electrodialysis with ion-exchange membranes. Electrochim. Acta 2019, 299, 946–962. [Google Scholar] [CrossRef]
- Yan, H.; Wu, L.; Wang, Y.; Irfan, M.; Jiang, C.; Xu, T. Ammonia capture from wastewater with a high ammonia nitrogen concentration by water splitting and hollow fiber extraction. Chem. Eng. Sci. 2020, 227, 115934. [Google Scholar] [CrossRef]
- Franck-Lacaze, L.; Sistat, P.; Huguet, P. Determination of the pKa of poly (4-vinylpyridine)-based weak anion exchange membranes for the investigation of the side proton leakage. J. Memb. Sci. 2009, 326, 650–658. [Google Scholar] [CrossRef]
- Shi, L.; Xiao, L.; Hu, Z.; Zhan, X. Nutrient recovery from animal manure using bipolar membrane electrodialysis: Study on product purity and energy efficiency. Water Cycle 2020, 1, 54–62. [Google Scholar] [CrossRef]
- Saabas, D.; Lee, J. Recovery of ammonia from simulated membrane contactor effluent using bipolar membrane electrodialysis. J. Memb. Sci. 2022, 644, 120081. [Google Scholar] [CrossRef]
- van Linden, N.; Bandinu, G.L.; Vermaas, D.A.; Spanjers, H.; van Lier, J.B. Bipolar membrane electrodialysis for energetically competitive ammonium removal and dissolved ammonia production. J. Clean. Prod. 2020, 259, 120788. [Google Scholar] [CrossRef]
- Lide, D.R.; Baysinger, G.; Berger, L.I.; Kehiaian, H.V.; Roth, D.L.; Zwillinger, D.; Goldberg, R.N.; Haynes, W.M. CRC Handbook of Chemistry and Physics; CRC Press: New York, NY, USA, 1997. [Google Scholar]
- Howitt, S.M.; Udvardi, M.K. Structure function and regulation of ammonium transporters in plants. Biochim. Biophys. Acta-Biomembr. 2000, 1465, 152–170. [Google Scholar] [CrossRef] [Green Version]
- Verkman, A.S.; Mitra, A.K. Structure and function of aquaporin water channels. Am. J. Physiol.-Ren. Physiol. 2000, 278, F12–F28. [Google Scholar] [CrossRef]
- Agre, P. The aquaporin water channels. Proc. Am. Thorac. Soc. 2006, 3, 5–13. [Google Scholar] [CrossRef]
- Meuwly, M.; Bach, A.; Leutwyler, S. Grotthus-type and diffusive proton transfer in 7-hydroxyquinoline·(NH3)n clusters. J. Am. Chem. Soc. 2001, 123, 11446–11453. [Google Scholar] [CrossRef]
- Lim, D.W.; Sadakiyo, M.; Kitagawa, H. Proton transfer in hydrogen-bonded degenerate systems of water and ammonia in metal-organic frameworks. Chem. Sci. 2018, 10, 16–33. [Google Scholar] [CrossRef] [Green Version]
- Melnikova, E.D.; Tsygurina, K.A.; Pismenskaya, N.D.; Nikonenko, V.V. Influence of Protonation-Deprotonation Reactions on Diffusion of Ammonium Chloride through an Anion Exchange Membrane. Membr. Membr. Technol. 2021, 11, 360–370. [Google Scholar] [CrossRef]
- Vasil’eva, V.I.; Shaposhnik, V.A.; Zemlyanukhina, I.A.; Grigorchuk, O.V. Facilitated diffusion of amino acids in ion-exchange membranes. Russ. J. Phys. Chem. A 2003, 77, 1017–1019. [Google Scholar]
- Vasil’eva, V.; Goleva, E.; Pismenskaya, N.; Kozmai, A.; Nikonenko, V. Effect of surface profiling of a cation-exchange membrane on the phenylalanine and NaCl separation performances in diffusion dialysis. Sep. Purif. Technol. 2019, 210, 48–59. [Google Scholar] [CrossRef]
- Ueno, K.; Doi, T.; Nanzai, B.; Igawa, M. Selective transport of neutral amino acids across a double-membrane system comprising cation and anion exchange membranes. J. Memb. Sci. 2017, 537, 344–352. [Google Scholar] [CrossRef]
- Ouellette, R.J.; Rawn, J.D. 31—Lipids and Biological Membranes. In Organic Chemistry, 2nd ed.; Ouellette, R.J., Rawn, J.D., Eds.; Academic Press: Cambridge, MA, USA, 2018; pp. 1001–1032. [Google Scholar] [CrossRef]
- Liu, Y.; Qin, M.; Luo, S.; He, Z.; Qiao, R. Understanding Ammonium Transport in Bioelectrochemical Systems towards its Recovery. Sci. Rep. 2016, 6, 22547. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Helfferich, F.G. Ion Exchange; McGraw-Hill: New York, NY, USA, 1962. [Google Scholar]
- Ji, Y.; Luo, H.; Geise, G.M. Specific co-ion sorption and diffusion properties influence membrane permselectivity. J. Memb. Sci. 2018, 563, 492–504. [Google Scholar] [CrossRef]
- Filippov, A.N.; Kononenko, N.A.; Demina, O.A. Diffusion of electrolytes of different natures through the cation-exchange membrane. Colloid J. 2017, 79, 556–566. [Google Scholar] [CrossRef]
- Demina, O.A.; Kononenko, N.A.; Falina, I.V.; Demin, A.V. Theoretical Estimation of Differential Diffusion Permeability Coefficients of Ion Exchange Membranes. Colloid J. 2017, 79, 259–269. [Google Scholar] [CrossRef]
- Nikonenko, V.V.; Yaroslavtsev, A.B.; Pourcelly, G. Ion Transfer in and Through Charged Membranes: Structure, Properties, and Theory. In Ionic Interactions in Natural and Synthetic Macromolecules; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2012; pp. 267–335. [Google Scholar] [CrossRef]
- Mills, R.; Lobo, V.M.M. A critical examination of data compiled from the literature. In Self-Diffusion in Electrolyte Solutions; Elsevier Science Publishers B.V.: Amsterdam, The Netherlands, 1989. [Google Scholar]
- Hua, W.; Verreault, D.; Huang, Z.; Adams, E.M.; Allen, H.C. Cation Effects on Interfacial Water Organization of Aqueous Chloride Solutions. I. Monovalent Cations: Li+, Na+, K+, and NH4+. J. Phys. Chem. B 2014, 118, 8433–8440. [Google Scholar] [CrossRef]
- Fuocco, A.; Zwijnenberg, H.; Galier, S.; Balman, H.R.; de Luca, G. Structural properties of cation exchange membranes: Characterization, electrolyte effect and solute transfer. J. Memb. Sci. 2016, 520, 45–53. [Google Scholar] [CrossRef] [Green Version]
- Zabolotsky, V.I.; Nikonenko, V.V. Effect of structural membrane inhomogeneity on transport properties. J. Memb. Sci. 1993, 79, 181–198. [Google Scholar] [CrossRef]
- Bhown, A.; Cussler, E.L. Mechanism for Selective Ammonia Transport through Poly(vinylammonium thiocyanate) Membranes. J. Am. Chem. Soc. 1991, 113, 742–749. [Google Scholar] [CrossRef]
- Phillip, W.A.; Martono, E.; Chen, L.; Hillmyer, M.A.; Cussler, E.L. Seeking an ammonia selective membrane based on nanostructured sulfonated block copolymers. J. Memb. Sci. 2009, 337, 39–46. [Google Scholar] [CrossRef]
- Pez, G.P.; Laciak, D.V. Ammonia Separation Using Semipermeable Membranes. U.S. Patent No. 4,762,535, 9 August 1988. [Google Scholar]
- Simons, R. Electric field effects on proton transfer between ionizable groups and water in ion exchange membranes. Electrochim. Acta 1984, 29, 151–158. [Google Scholar] [CrossRef]
- Frank, M.J.W.; Kuipers, J.A.M.; van Swaaij, W.P.M. Diffusion coefficients and viscosities of CO2+H2O, CO2+CH3OH, NH3+H2O, and NH3+CH3OH liquid mixtures. J. Chem. Eng. Data 1996, 41, 297–302. [Google Scholar] [CrossRef] [Green Version]
- Kamcev, J.; Paul, D.R.; Freeman, B.D. Ion activity coefficients in ion exchange polymers: Applicability of Manning’s counterion condensation theory. Macromolecules 2015, 48, 8011–8024. [Google Scholar] [CrossRef]
- Sarapulova, V.; Shkorkina, I.; Mareev, S.; Pismenskaya, N.; Kononenko, N.; Larchet, C.; Dammak, L.; Nikonenko, V. Transport characteristics of fujifilm ion-exchange membranes as compared to homogeneous membranes AMX and CMX and to heterogeneous membranes MK-40 and MA-41. Membranes 2019, 9, 84. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Berezina, N.P.; Kononenko, N.A.; Dyomina, O.A.; Gnusin, N.P. Characterization of ion-exchange membrane materials: Properties vs structure. Adv. Colloid Interface Sci. 2008, 139, 3–28. [Google Scholar] [CrossRef]
- Kamcev, J.; Paul, D.R.; Freeman, B.D. Effect of fixed charge group concentration on equilibrium ion sorption in ion exchange membranes. J. Mater. Chem. A 2017, 5, 4638–4650. [Google Scholar] [CrossRef]
- van Linden, N.; Spanjers, H.; van Lier, J.B. Application of dynamic current density for increased concentration factors and reduced energy consumption for concentrating ammonium by electrodialysis. Water Res. 2019, 163, 114856. [Google Scholar] [CrossRef]
- Zabolotskii, V.I.; Shel’deshov, N.V.; Gnusin, N.P. Dissociation of Water Molecules in Systems with Ion-exchange Membranes. Russ. Chem. Rev. 1988, 57, 801–808. [Google Scholar] [CrossRef]
- Simons, R. Water splitting in ion exchange membranes. Electrochim. Acta 1985, 30, 275–282. [Google Scholar] [CrossRef]
- Tanaka, Y. Acceleration of water dissociation generated in an ion exchange membrane. J. Memb. Sci. 2007, 303, 234–243. [Google Scholar] [CrossRef]
- Brazier, B.W. Membrane Transport of Nutrients. Am. J. Food Nutr. 2001, 4, 135–137. [Google Scholar] [CrossRef]
- Barrett, K.; Brooks, H.; Boitano, S.; Barman, S. Ganong’s Review of Medical Physiology, 23rd ed.; McGraw Hill Medicals: New York, NY, USA, 2010. [Google Scholar]
- Silbernagl, S.; Scheller, D. Formation and Excretion of NH3− NH4+. New Aspects of an old problem. Klinsche Wochenschrift. 1986, 64, 862–870. [Google Scholar] [CrossRef] [PubMed]
- Mizutani, Y. Structure of ion exchange membranes. J. Memb. Sci. 1990, 49, 121–144. [Google Scholar] [CrossRef]
- Güler, E.; van Baak, W.; Saakes, M.; Nijmeijer, K. Monovalent-ion-selective membranes for reverse electrodialysis. J. Memb. Sci. 2014, 455, 254–270. [Google Scholar] [CrossRef]
- Berezina, N.P.; Timofeev, S.V.; Kononenko, N.A. Effect of conditioning techniques of perfluorinated sulphocationic membranes on their hydrophylic and electrotransport properties. J. Memb. Sci. 2002, 209, 509–518. [Google Scholar] [CrossRef]
- Pismenskaya, N.D.; Nevakshenova, E.E.; Nikonenko, V.V. Using a Single Set of Structural and Kinetic Parameters of the Microheterogeneous Model to Describe the Sorption and Kinetic Properties of Ion-Exchange Membranes. Pet. Chem. 2018, 58, 465–473. [Google Scholar] [CrossRef]
- Lteif, R.; Dammak, L.; Larchet, C.; Auclair, B. Conductivité électrique membranaire: Étude de l’effet de la concentration, de la nature de l’electrolyte et de la structure membranaire. Eur. Polym. J. 1999, 35, 1187–1195. [Google Scholar] [CrossRef]
- Karpenko, L.V.; Demina, O.A.; Dvorkina, G.A.; Parshikov, S.B.; Larchet, C.; Auclair, B.; Berezina, N.P. Comparative study of methods used for the determination of electroconductivity of ion-exchange membranes. Russ. J. Electrochem. 2001, 37, 287–293. [Google Scholar] [CrossRef]
- Sosa-Fernández, P.A.; Post, J.W.; Nabaala, H.L.; Bruning, H.; Rijnaarts, H. Experimental evaluation of anion exchange membranes for the desalination of (Waste) water produced after polymer-flooding. Membranes 2020, 10, 352. [Google Scholar] [CrossRef] [PubMed]
- Danielli, F.J.; Cadenhead, D.A.; Rosenberg, M.D. Progress in Surface and Membrane Science; Academic Press: Cambridge, MA, USA, 2016; Volume 7. [Google Scholar]
- Lévêque, A. Les Lois de La Transmission de Chaleur Par Convection. Ann. des Mines 1928, 13, 201–299. [Google Scholar]
| Parameter | Description | Value | Reference |
|---|---|---|---|
| d | Membrane thickness | AMX 127 ± 5 μm | * |
| CMX 172 ± 5 μm | * | ||
| δL = δR | Diffusion-layer thickness | 247 μm | Equation (S1) |
| KCl (NH4Cl) electrolyte-diffusion coefficient in solution | 1.99 × 10−9 m2/s | ||
| Ka | Acid-dissociation constant of NH3 | 5.62 × 10−7 mol/m3 | [28] |
| Kw | Water-dissociation constant | 10−8 mol2/m6 | [28] |
| k1 | Rate constant of forward reaction (3) | 1.78 × 105 s−1 | Equation (S2) |
| k−1 | Rate constant of backward reaction (3) | 107 m3/(s × mol) | k1 × Kb |
| k2 | Rate constant of forward reaction (4) | 5.63 s−1 | Equation (S2) |
| k−2 | Rate constant of backward reaction (4) | 107 m3/(s × mol) | k2 × Ka |
| kd | Rate constant of water dissociation | 2 × 10−5 s−1 | [52] |
| kr | Rate constant of water recombination | 1.18 × 108 m3/(s × mol) | kd/(Kw × cw) |
| cw | Concentration of water | 5.55 × 104 mol/m3 | |
| Diffusion coefficients of species in solutions | 1.64 × 10−9 m2/s | [53] | |
| 1.96 × 10−9 m2/s | [28] | ||
| 2.03 × 10−9 m2/s | [28] | ||
| 9.3 × 10−9 m2/s | [28] | ||
| 5.3 × 10−9 m2/s | [28] | ||
| 1.96 × 10−9 m2/s | [28] | ||
| Diffusion coefficient of species in the membrane | 4.4 × 10−10 m2/s | ||
| 2.7 × 10−11 m2/s | ** | ||
| 2.7 × 10−11 m2/s | ** | ||
| 2.8 × 10−9 m2/s | |||
| 1.6 × 10−9 m2/s | |||
| 2.7 × 10−11 m2/s | ** | ||
| Activity coefficients of species in membrane | 0.03 | ** | |
| 1 | |||
| 1 | |||
| 1 | ** | ||
| 0.03 | ** | ||
| 1 | |||
| εs | Relative permittivity in solution | 80 | [28] |
| εm | Relative permittivity in membrane | 30 | [54] |
| Q | Ion-exchange capacity | 7600 ± 1000 mol/m3 H2O | [55] |
| pH | pH value in both streams | 5.4 ± 0.2 | * |
| Chloride-ion concentration at x = d + δR | 0.1–1 ± 0.001 M | * | |
| p | Porosity | 0.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Skolotneva, E.; Tsygurina, K.; Mareev, S.; Melnikova, E.; Pismenskaya, N.; Nikonenko, V. High Diffusion Permeability of Anion-Exchange Membranes for Ammonium Chloride: Experiment and Modeling. Int. J. Mol. Sci. 2022, 23, 5782. https://doi.org/10.3390/ijms23105782
Skolotneva E, Tsygurina K, Mareev S, Melnikova E, Pismenskaya N, Nikonenko V. High Diffusion Permeability of Anion-Exchange Membranes for Ammonium Chloride: Experiment and Modeling. International Journal of Molecular Sciences. 2022; 23(10):5782. https://doi.org/10.3390/ijms23105782
Chicago/Turabian StyleSkolotneva, Ekaterina, Kseniia Tsygurina, Semyon Mareev, Ekaterina Melnikova, Natalia Pismenskaya, and Victor Nikonenko. 2022. "High Diffusion Permeability of Anion-Exchange Membranes for Ammonium Chloride: Experiment and Modeling" International Journal of Molecular Sciences 23, no. 10: 5782. https://doi.org/10.3390/ijms23105782
APA StyleSkolotneva, E., Tsygurina, K., Mareev, S., Melnikova, E., Pismenskaya, N., & Nikonenko, V. (2022). High Diffusion Permeability of Anion-Exchange Membranes for Ammonium Chloride: Experiment and Modeling. International Journal of Molecular Sciences, 23(10), 5782. https://doi.org/10.3390/ijms23105782