The Strong Enhancement of Electron-Impact Ionization Processes in Dense Plasma by Transient Spatial Localization
Abstract
1. Introduction
2. Results
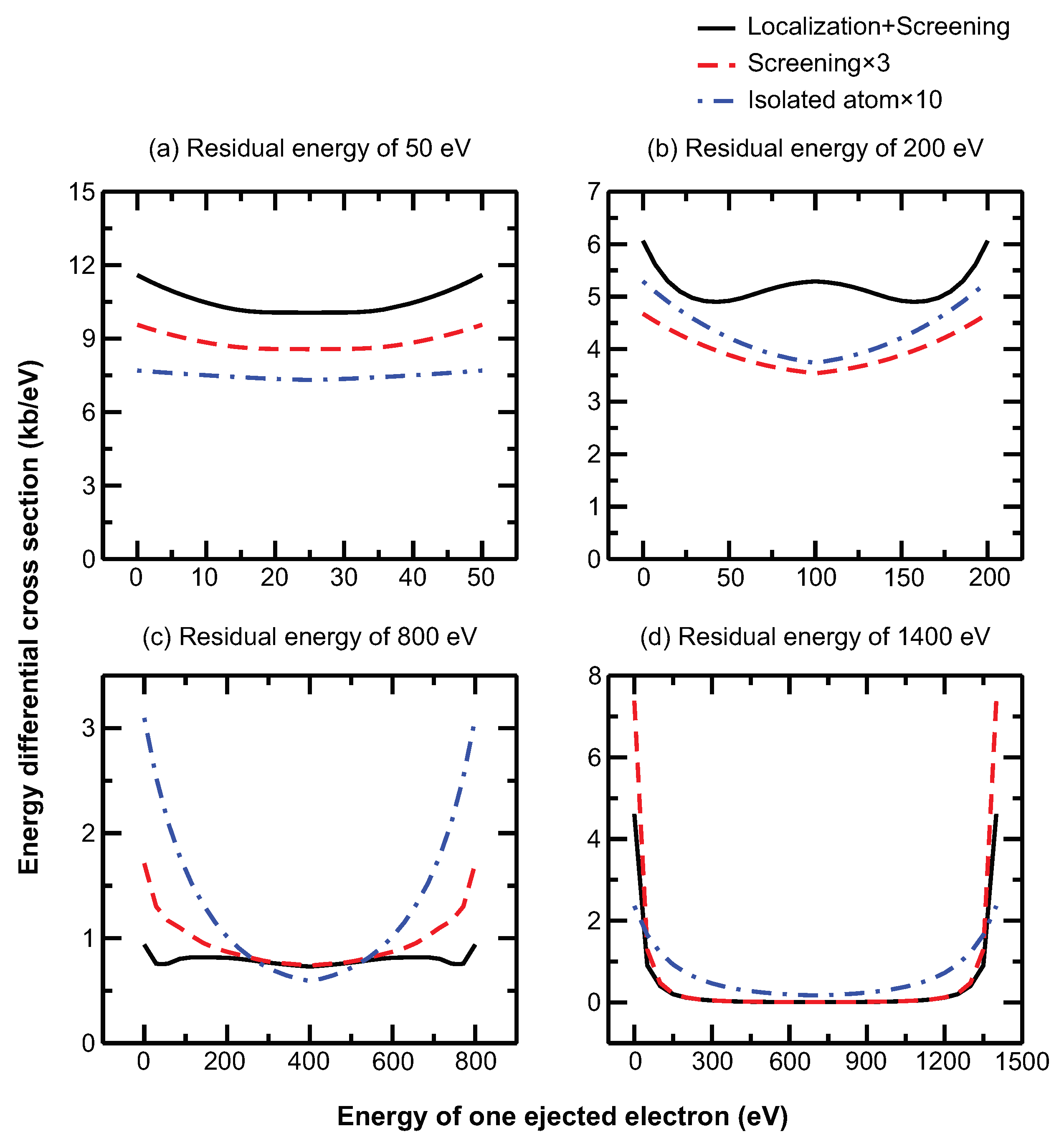
2.1. New Features of Energy Differential Cross Sections
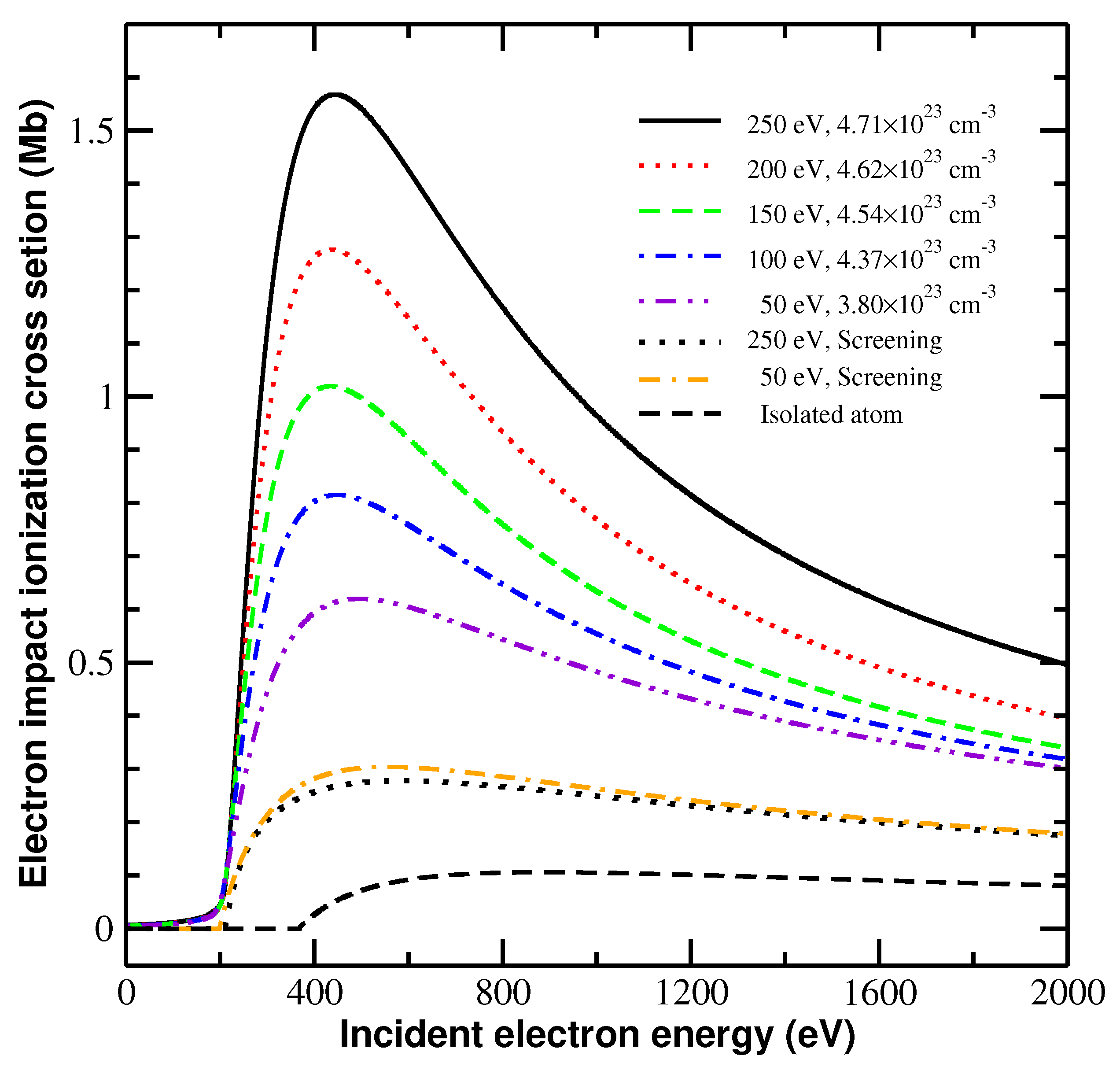
2.2. TSLCE-Induced Enhancement of Integral Cross Sections
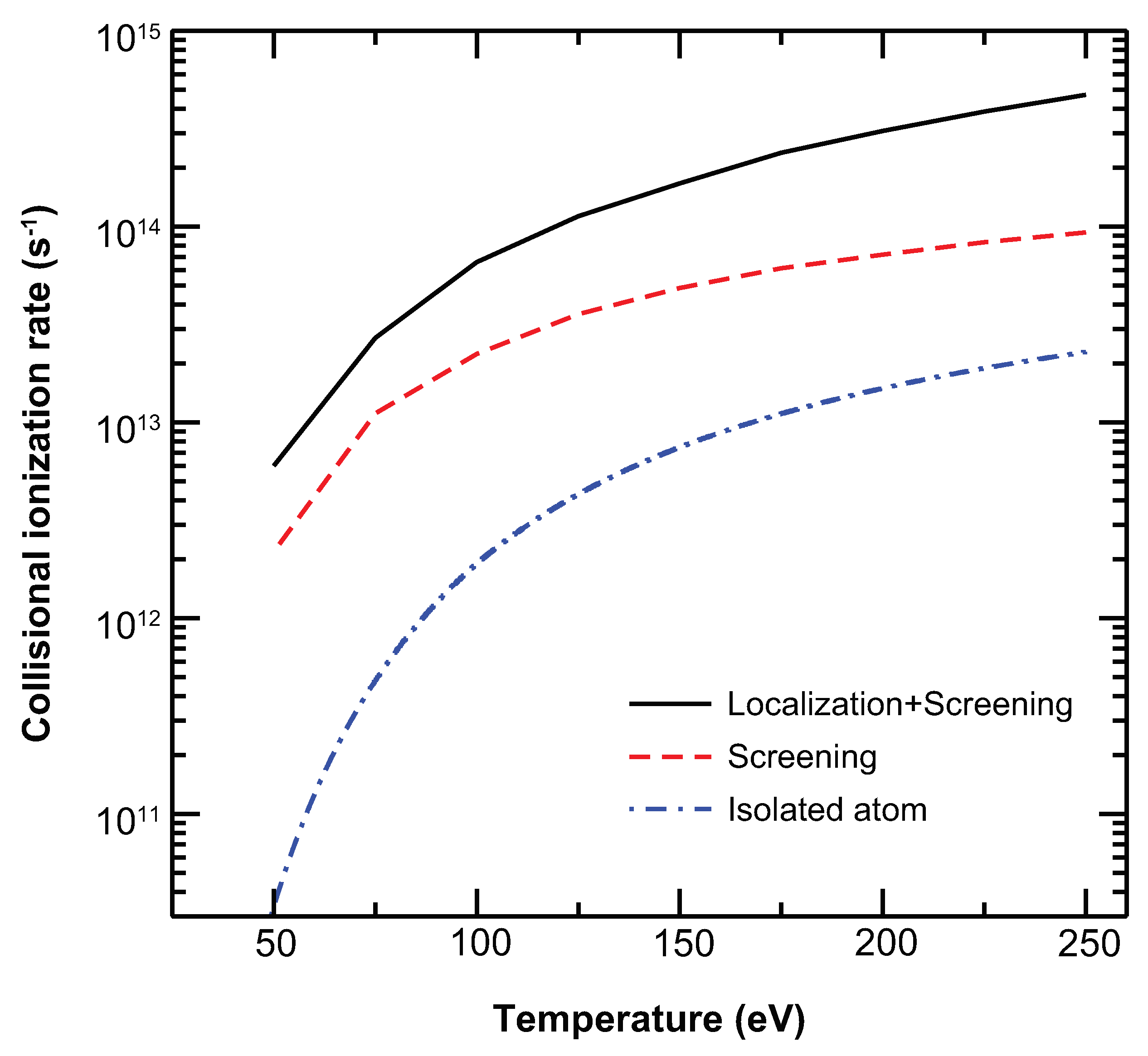
2.3. Greatly Increased Collisional Ionization Rates in Dense Plasmas
2.4. Comparison with Experiments and Other Theoretical Results
3. Discussion
4. Methods
4.1. Plasma Screening Potential
4.2. Localized Wave Functions of Continuum Electrons
4.3. Differential and Integral Cross Sections of Electron-Impact Ionization
4.4. Collisional Ionization Rates
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Booth, N.; Robinson, A.P.L.; Hakel, P.; Clarke, R.J.; Dance, R.J.; Doria, D.; Gizzi, L.A.; Gregori, G.; Koester, P.; Labate, L. Laboratory measurements of resistivity in warm dense plasmas relevant to the microphysics of brown dwarfs. Nat. Commun. 2015, 6, 8742. [Google Scholar] [CrossRef] [PubMed]
- Rose, S.J. New experimental possibilities for measuring radiative opacity under conditions in the Sun’s interior. Plasma Phys. Control. Fusion 2005, 47, B735. [Google Scholar] [CrossRef]
- Hu, S.X.; Militzer, B.; Goncharov, V.N.; Skupsky, S. Strong Coupling and Degeneracy Effects in Inertial Confinement Fusion Implosions. Phys. Rev. Lett. 2010, 104, 235003. [Google Scholar] [CrossRef]
- Caillabet, L.; Canaud, B.; Salin, G.; Mazevet, S.; Loubeyre, P. Change in Inertial Confinement Fusion Implosions upon Using an Ab Initio Multiphase DT Equation of State. Phys. Rev. Lett. 2011, 107, 115004. [Google Scholar] [CrossRef]
- Glenzer, S.H.; Redmer, R. X-ray Thomson scattering in high energy density plasmas. Rev. Mod. Phys. 2009, 81, 1625. [Google Scholar] [CrossRef]
- Drake, R.P. Focus on high energy density physics. Phys. Plasmas 2009, 16, 055501. [Google Scholar] [CrossRef]
- Müller, A. Electron-ion collisions: Fundamental processes in the focus of applied research. Adv. At. Mol. Opt. Phys. 2008, 55, 293. [Google Scholar]
- Landi, E.; Landini, M. Radiative losses of optically thin coronal plasmas. Astron. Astrophys. 1999, 347, 401. [Google Scholar]
- Bryans, P.; Landi, E.; Savin, D.W. A new approach to analyzing solar coronal spectra and updated collisional ionization equilibrium calculations. II. Additional ionization rate coefficients. Astrophys. J. 2009, 691, 1540. [Google Scholar] [CrossRef]
- Costa, F.; Traoré-Dubuis, A.; Álvarez, L.; Lozano, A.I.; Ren, X.; Dorn, A.; Limao-Vieira, P.; Blanco, F.; Oller, J.C.; Munoz, A.; et al. A Complete Cross Section Data Set for Electron Scattering by Pyridine: Modelling Electron Transport in the Energy Range 0–100 eV. Int. J. Mol. Sci. 2020, 21, 6947. [Google Scholar] [CrossRef]
- Lozano, A.I.; Costa, F.; Ren, X.G.; Dorn, A.; Álvarez, L.; Blanco, F.; Limao-Vieira, P.; Garca, G. Double and Triple Differential Cross Sections for Single Ionization of Benzene by Electron Impact. Int. J. Mol. Sci. 2021, 22, 4601. [Google Scholar] [CrossRef] [PubMed]
- Kallman, T.R.; Palmeri, P. Atomic Data for X-ray Astrophysics. Rev. Mod. Phys. 2007, 79, 79. [Google Scholar] [CrossRef]
- Lennon, M.A.; Bell, K.L.; Gilbody, H.B.; Hughes, J.G.; Kingston, A.E.; Murray, M.J.; Smith, F.J. Recommended Data on the Electron Impact Ionization of Atoms and Ions: Fluorine to Nickel. J. Phys. Chem. Ref. Data 1988, 17, 1285. [Google Scholar] [CrossRef]
- Kallne, E.; Jones, L.A. Measurements of the ionisation rates of lithium-like ions. J. Phys. B At. Mol. Opt. Phys. 1977, 10, 3637. [Google Scholar] [CrossRef][Green Version]
- Kwon, D.-H.; Savin, D.W. Electron-impact ionization of P-like ions forming Si-like ions. Astrophys. J. 2014, 784, 13. [Google Scholar] [CrossRef]
- Kwon, D.-H.; Savin, D.W. Theoretical electron-impact-ionization cross section for Fe11+ forming Fe12+. Phys. Rev. A 2012, 86, 022701. [Google Scholar] [CrossRef]
- Janev, R.K.; Zhang, S.B.; Wang, J.G. Review of quantum collision dynamics in Debye plasmas. Matter Radiat. Extrem. 2016, 1, 237. [Google Scholar] [CrossRef]
- Zammit, M.C.; Fursa, D.V.; Bray, I. Convergent-close-coupling calculations for excitation and ionization processes of electron-hydrogen collisions in Debye plasmas. Phys. Rev. A 2010, 82, 052705. [Google Scholar] [CrossRef]
- Debye, P.; Hückel, E. The theory of electrolytes I. The lowering of the freezing point and related occurrences. Phys. Z. 1923, 24, 185. [Google Scholar]
- Rozsnyai, B.F. Relativistic Hartree-Fock-Slater Calculations for Arbitrary Temperature and Matter Density. Phys. Rev. A 1972, 5, 1137. [Google Scholar] [CrossRef]
- Stewart, J.C.; Pyatt, K.D., Jr. Lowering of Ionization Potentials in Plasmas. Astrophys. J. 1966, 144, 1203. [Google Scholar] [CrossRef]
- Ecker, G.; Kröll, W. Lowering of the Ionization Energy for a Plasma in Thermodynamic Equilibrium. Phys. Fluids 1963, 6, 62. [Google Scholar] [CrossRef]
- Bransden, B.H. Atomic Collision Theory; The Benjamin/Cummings Publishing Company, Inc.: London, UK; Amsterdam, The Netherlands; Don Mills, ON, Canada; Sydney, Australia; Tokyo, Japan, 1983. [Google Scholar]
- Liu, P.F.; Gao, C.; Hou, Y.; Zeng, J.L.; Yuan, J.M. Transient space localization of electrons ejected from continuum atomic processes in hot dense plasma. Commun. Phys. 2018, 1, 95. [Google Scholar] [CrossRef]
- Bahcall, J.N.; Ulrich, R.K. Solar models, neutrino experiments, and helioseismology. Rev. Mod. Phys. 1988, 60, 297. [Google Scholar] [CrossRef]
- Bahcall, J.N.; Serenelli, A.M.; Pinsonneault, M. How Accurately Can We Calculate the Depth of the Solar Convective Zone? Astrophys. J. 2004, 614, 464. [Google Scholar] [CrossRef]
- Basu, S.; Antia, H.M. Helioseismology and Solar Abundances. Phys. Rep. 2008, 457, 217. [Google Scholar] [CrossRef]
- Christophorou, L.G.; Olthoff, J.K. Electron interactions with plasma processing gases: Present status and future needs. Appl. Surf. Sci. 2002, 192, 309. [Google Scholar] [CrossRef]
- Gamaly, E.G.; Rapp, L.; Roppo, V.; Juodkazis, S.; Rode, A.V. Generation of high energy density by fs-laser-induced confined microexplosion. New J. Phys. 2013, 15, 025018. [Google Scholar] [CrossRef]
- Vasenkov, A.V.; Kushner, M.J. Electron energy distributions and anomalous skin depth effects in high-plasma-density inductively coupled discharges. Phys. Rev. E 2002, 66, 066411. [Google Scholar] [CrossRef]
- Vinko, S.M.; Ciricosta, O.; Preston, T.R.; Rackstraw, D.S.; Wark, J.S. Investigation of femtosecond collisional ionization rates in a solid-density aluminium plasma. Nat. Commun. 2015, 6, 6397. [Google Scholar] [CrossRef]
- van den Berg, Q.Y.; Fernandez-Tello, E.V.; Burian, T.; Chalupsky, J.; Chung, H.-K.; Ciricosta, O.; Dakovski, G.L.; Hajkova, V.; Hollebon, P.; Juha, L.; et al. Clocking Femtosecond Collisional Dynamics via Resonant X-ray Spectroscopy. Phys. Rev. Lett. 2018, 120, 055002. [Google Scholar] [CrossRef] [PubMed]
- LCLS Website. 2014. Available online: http://lcls.slac.stanford.edu/ (accessed on 10 March 2022).
- Ehrhardt, H.; Jung, K.; Knoth, G.; Schlemmer, P. Differential cross sections of direct single electron impact ionization. Z. Phys. D-Atoms Mol. Clust. 1986, 1, 3. [Google Scholar] [CrossRef]
- Biswas, R.; Sinha, C. Double- and single-differential and total ionization cross sections for electron-impact ionization of a helium atom. Phys. Rev. A 1996, 54, 2944. [Google Scholar] [CrossRef] [PubMed]
- Kai, T. Single-differential and integral cross sections for electron-impact ionization for the damage of carbon clusters irradiated with X-ray free-electron lasers. Phys. Rev. A 2010, 81, 023201. [Google Scholar] [CrossRef]
- Bandyooadhyay, A.; Roy, K.; Mandal, P.; Sil, N.C. Single-differential and total ionization cross sections of a hydrogen atom by electron impact. Phys. Rev. A 1995, 51, 2151. [Google Scholar] [CrossRef] [PubMed]
- Guerra, M.; Amaro, P.; Machado, J.; Santos, J.P. Single differential electron impact ionization cross sections in the binary-encounter-Bethe approximation for the low binding energy regime. J. Phys. B At. Mol. Opt. Phys. 2015, 48, 185202. [Google Scholar] [CrossRef]
- Liu, P.F.; Zeng, J.L.; Yuan, J.M. A practical theoretical formalism for atomic multi-electron processes: Direct multiple ionization by a single auger decay or by impact of a single electron or photon. J. Phys. B At. Mol. Opt. Phys. 2018, 51, 075202. [Google Scholar] [CrossRef]
- Kramida, A.; Ralchenko, Y.; Reader, J.; NIST ASD Team. 2018. Available online: https://physics.nist.gov/asd (accessed on 19 March 2022).
- Lotz, W. Electron-impact ionization cross-sections and ionization rate coefficients for atoms and ions from hydrogen to calcium. Z. Phys. 1968, 216, 241. [Google Scholar] [CrossRef]
- Burgess, A.; Chidichimo, M.C. Electron impact ionization of complex ions. Mon. Not. R. Astron. Soc. 1983, 203, 1269. [Google Scholar] [CrossRef]
- Dere, K.P. Ionization rate coefficients for the elements hydrogen through zinc. Astronom. Astrophys. 2007, 466, 771. [Google Scholar] [CrossRef]
- Golden, L.B.; Sampson, D.H. Ionization of highly charged ions by electron impact. J. Phys. B At. Mol. Opt. Phys. 1977, 10, 2229. [Google Scholar] [CrossRef]
- Clark, R.E.H.; Abdallah, J.; Mann, J.B. Integral and differential cross sections for electron impact ionization. Astrophys. J. 1991, 381, 597. [Google Scholar] [CrossRef]
- Thomson, J. XLII. Ionization by moving electrified particles. Philos. Mag. Ser. 1912, 23, 449–457. [Google Scholar] [CrossRef]
- Stabler, R.C. Classical Impulse Approximation for Inelastic Electron-Atom Collisions. Phys. Rev. 1964, 133, A1268. [Google Scholar] [CrossRef]
- Cryziński, M. Classical Theory of Atomic Collisions. I. Theory of Inelastic Collisions. Phys. Rev. 1965, 138, A336. [Google Scholar] [CrossRef]
- Burgess, A.; Percival, I.C. Classical Theory of Atomic Scattering. Adv. At. Mol. Phys. 1968, 4, A109. [Google Scholar]
- Csanak, G.; Taylor, H.S.; Yaris, R. Many-Body Methods Applied to Electron Scattering from Atoms and Molecules. II. Inelastic Processes. Phys. Rev. A 1971, 3, 1322. [Google Scholar] [CrossRef]
- Younger, S.M. Electron-impact-ionization cross sections for highly ionized heliumlike atoms. Phys. Rev. A 1980, 22, 1425. [Google Scholar] [CrossRef]
- Mann, J.B. Excitation collision strengths for iron ions calculated with a distorted wave method. At. Data Nucl. Data Tables 1983, 29, 407. [Google Scholar] [CrossRef]
- Sampson, D.H.; Zhang, H.L.; Fontes, C.J. A fully relativistic approach for calculating atomic data for highly charged ions—ScienceDirect. Phys. Rep. 2009, 477, 111. [Google Scholar] [CrossRef]
- Urdampilleta, I.; Kaastra, J.S.; Mehdipour, M. X-ray emission from thin plasmas Collisional ionization for atoms and ions of H to Zn. Astronom. Astrophys. 2017, 601, A85. [Google Scholar] [CrossRef][Green Version]
- Holubová, L.; Kyzek, S.; Ďurovcová, I.; Fabová, J.; Horvthová, E.; Ševčovičová, A.; Gálová, G. Non-Thermal Plasma—A New Green Priming Agent for Plants? Int. J. Mol. Sci. 2020, 21, 9466. [Google Scholar] [CrossRef] [PubMed]
- Polčic, P.; Machala, Z. Effects of Non-Thermal Plasma on Yeast Saccharomyces cerevisiae. Int. J. Mol. Sci. 2021, 22, 2247. [Google Scholar] [CrossRef] [PubMed]
- Friedrich, H. Theoretical Atomic Physics; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Schnittman, J.D.; Krolik, J.H.; Noble, S.C. X-ray spectra from magnetohydrodynamic simulations of accreting black holes. Astrophys. J. 2013, 769, 156. [Google Scholar] [CrossRef]
- Deprince, J.; Bautista, M.; Fritzsche, S.; García, J.A.; Kallman, T.R.; Mendoza, C.; Palmeri, P.; Quinet, P. Plasma environment effects on K lines of astrophysical interest I. Atomic structure, radiative rates, and Auger widths of oxygen ions. Astronom. Astrophys. 2019, 624, A74. [Google Scholar] [CrossRef]
- Gu, M.F. The flexible atomic code. Can. J. Phys. 2008, 86, 675. [Google Scholar] [CrossRef]
- Jönsson, P.; He, X.; Fischerb, F.; Grantc, I.P. The grasp2K relativistic atomic structure package. Comput. Phys. Commun. 2007, 177, 597. [Google Scholar] [CrossRef]
- Son, S.K.; Thiele, R.; Jurek, Z.; Ziaja, B.; Santra, R. Quantum-Mechanical Calculation of Ionization-Potential Lowering in Dense Plasmas. Phys. Rev. X 2014, 4, 031004. [Google Scholar] [CrossRef]
- Hu, S.X. Continuum Lowering and Fermi-Surface Rising in Strongly Coupled and Degenerate Plasmas. Phys. Rev. Lett. 2017, 119, 065001. [Google Scholar] [CrossRef]
- Zeng, J.L.; Li, Y.J.; Gao, C.; Yuan, J.M. Screening potential and continuum lowering in a dense plasma under solar-interior conditions. Astronom. Astrophys. 2020, 634, A117. [Google Scholar] [CrossRef]
- Zeng, J.L.; Li, Y.J.; Hou, Y.; Yuan, J.M. Ionization potential depression and ionization balance in dense carbon plasma under solar and stellar interior conditions. Astronom. Astrophys. 2020, 644, A92. [Google Scholar] [CrossRef]
- Zeng, J.L.; Gao, C.; Liu, P.F.; Li, Y.J.; Meng, C.S.; Hou, Y.; Kang, D.D.; Yuan, J.M. Electron Localization Enhanced Photon Absorption for the Missing Opacity in Solar Interior. Sci. China Phys. Mech. Astron. 2022, 65, 233011. [Google Scholar] [CrossRef]
- Dharma-Wardana, M.W.C.; Taylor, R. Exchange and correlation potentials for finite temperature quantum calculations at intermediate degeneracies. J. Phys. C Solid State Phys. 1981, 14, 629. [Google Scholar] [CrossRef]
- Ichimaru, S.; Iyetomi, H.; Tanaka, S. Statistical physics of dense plasmas: Thermodynamics, transport coefficients and dynamic correlations. Phys. Rep. 1987, 149, 91. [Google Scholar] [CrossRef]
- Zeng, J.L.; Liu, P.F.; Gao, C.; Li, Y.J.; Yuan, J.M. Strong Enhancement of Electron-Impact-Ionization Processes in Hot Dense Plasma by Transient Spatial Localization. Available online: https://europepmc.org/article/ppr/ppr223922 (accessed on 20 December 2020).


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, J.; Ye, C.; Liu, P.; Gao, C.; Li, Y.; Yuan, J. The Strong Enhancement of Electron-Impact Ionization Processes in Dense Plasma by Transient Spatial Localization. Int. J. Mol. Sci. 2022, 23, 6033. https://doi.org/10.3390/ijms23116033
Zeng J, Ye C, Liu P, Gao C, Li Y, Yuan J. The Strong Enhancement of Electron-Impact Ionization Processes in Dense Plasma by Transient Spatial Localization. International Journal of Molecular Sciences. 2022; 23(11):6033. https://doi.org/10.3390/ijms23116033
Chicago/Turabian StyleZeng, Jiaolong, Chen Ye, Pengfei Liu, Cheng Gao, Yongjun Li, and Jianmin Yuan. 2022. "The Strong Enhancement of Electron-Impact Ionization Processes in Dense Plasma by Transient Spatial Localization" International Journal of Molecular Sciences 23, no. 11: 6033. https://doi.org/10.3390/ijms23116033
APA StyleZeng, J., Ye, C., Liu, P., Gao, C., Li, Y., & Yuan, J. (2022). The Strong Enhancement of Electron-Impact Ionization Processes in Dense Plasma by Transient Spatial Localization. International Journal of Molecular Sciences, 23(11), 6033. https://doi.org/10.3390/ijms23116033





