Impact of DNA Repair Kinetics and Dose Rate on RBE Predictions in the UNIVERSE
Abstract
:1. Introduction
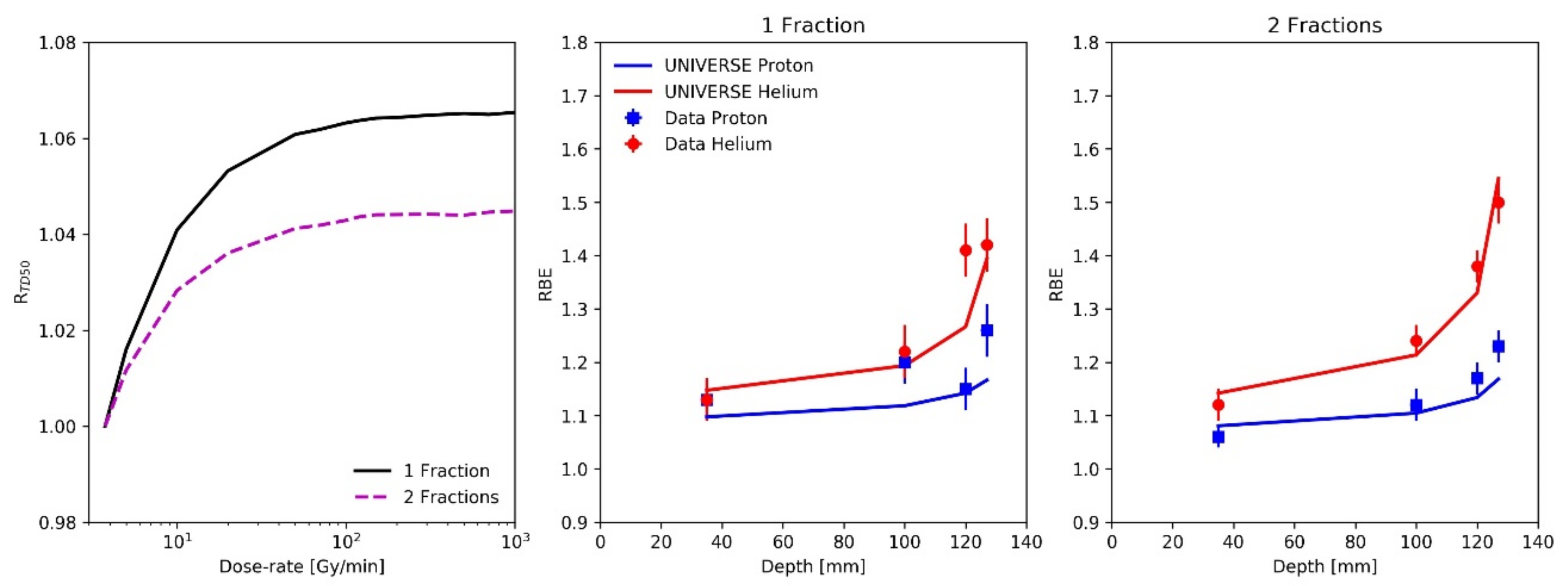
2. Results
| Endpoint | Reference | ||||
|---|---|---|---|---|---|
| DU145 | 5.9 × 10−3 | 0.17 | 4 | 100 | [25,26] |
| Rat Spinal Cord (considering repair during parameter fit) | 3.5 × 10−5 | 9.8 × 10−3 | 11.4 | 129.6 | [27,28,29] |
| Rat Spinal Cord (neglecting repair during parameter fit) | 6.5 × 10−3 | 8.5 × 10−3 | - | - | [27,28] |
3. Discussion
4. Conclusions
5. Materials and Methods
5.1. Experimental Data from Literature
5.2. Modeling Approach
5.3. RBE Definitions
5.4. Monte Carlo Simulation of Dose, Dose-Rate, and Rat Spinal Cord RBE in Spread-Out Bragg Peak
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Giovannini, G.; Böhlen, T.; Cabal, G.; Bauer, J.; Tessonnier, T.; Frey, K.; Debus, J.; Mairani, A.; Parodi, K. Variable RBE in proton therapy: Comparison of different model predictions and their influence on clinical-like scenarios. Radiat. Oncol. 2016, 11, 68. [Google Scholar] [CrossRef] [Green Version]
- Paganetti, H.; Blakely, E.; Carabe-Fernandez, A.; Carlson, D.J.; Das, I.J.; Dong, L.; Grosshans, D.; Held, K.D.; Mohan, R.; Moiseenko, V.; et al. Report of the AAPM TG-256 on the relative biological effectiveness of proton beams in radiation therapy. Med. Phys. 2019, 46, e53–e78. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Inaniwa, T.; Furukawa, T.; Kase, Y.; Matsufuji, N.; Toshito, T.; Matsumoto, Y.; Furusawa, Y.; Noda, K. Treatment planning for a scanned carbon beam with a modified microdosimetric kinetic model. Phys. Med. Biol. 2010, 55, 6721–6737. [Google Scholar] [CrossRef] [PubMed]
- Mairani, A.; Magro, G.; Tessonnier, T.; Böhlen, T.T.; Molinelli, S.; Ferrari, A.; Parodi, K.; Debus, J.; Haberer, T. Optimizing the modified microdosimetric kinetic model input parameters for proton and4He ion beam therapy application. Phys. Med. Biol. 2017, 62, N244–N256. [Google Scholar] [CrossRef]
- Mein, S.; Dokic, I.; Klein, C.; Tessonnier, T.; Böhlen, T.T.; Magro, G.; Bauer, J.; Ferrari, A.; Parodi, K.; Haberer, T.; et al. Biophysical modeling and experimental validation of relative biological effectiveness (RBE) for 4He ion beam therapy. Radiat. Oncol. 2019, 14, 123. [Google Scholar] [CrossRef] [Green Version]
- Liew, H.; Klein, C.; Zenke, F.T.; Abdollahi, A.; Debus, J.; Dokic, I.; Mairani, A. Modeling the Effect of Hypoxia and DNA Repair Inhibition on Cell Survival after Photon Irradiation. Int. J. Mol. Sci. 2019, 20, 6054. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liew, H.; Mein, S.; Debus, J.; Dokic, I.; Mairani, A. Modeling Direct and Indirect Action on Cell Survival after Photon Irradiation under Normoxia and Hypoxia. Int. J. Mol. Sci. 2020, 21, 3471. [Google Scholar] [CrossRef]
- Liew, H.; Mein, S.; Dokic, I.; Haberer, T.; Debus, J.; Abdollahi, A.; Mairani, A. Deciphering time-dependent DNA damage complexity, repair and oxygen tension: A mechanistic model for FLASH-dose-rate radiotherapy. Int. J. Radiat. Oncol. 2021, 110, 574–586. [Google Scholar] [CrossRef] [PubMed]
- Liew, H.; Meister, S.; Mein, S.; Tessonnier, T.; Kopp, B.; Held, T.; Haberer, T.; Abdollahi, A.; Debus, J.; Dokic, I.; et al. Combined DNA Damage Repair Interference and Ion Beam Therapy: Development, Benchmark, and Clinical Implications of a Mechanistic Biological Model. Int. J. Radiat. Oncol. 2021, 112, 802–817. [Google Scholar] [CrossRef] [PubMed]
- Liew, H.; Mein, S.; Tessonnier, T.; Abdollahi, A.; Debus, J.; Dokic, I.; Mairani, A. The Impact of Sub-Millisecond Damage Fixation Kinetics on the In Vitro Sparing Effect at Ultra-High Dose Rate in UNIVERSE. Int. J. Mol. Sci. 2022, 23, 2954. [Google Scholar] [CrossRef]
- Bennett, P.V.; Johnson, A.M.; Ackerman, S.E.; Chaudhary, P.; Keszenman, D.J.; Wilson, P.F. Dose-Rate Effects of Protons and Light Ions for DNA Damage Induction, Survival and Transformation in Apparently Normal Primary Human Fibroblasts. Radiat. Res. 2021, 197, 298–313. [Google Scholar] [CrossRef] [PubMed]
- Matsuura, T.; Egashira, Y.; Nishio, T.; Matsumoto, Y.; Wada, M.; Koike, S.; Furusawa, Y.; Kohno, R.; Nishioka, S.; Kameoka, S.; et al. Apparent absence of a proton beam dose rate effect and possible differences in RBE between Bragg peak and plateau. Med. Phys. 2010, 37, 5376–5381. [Google Scholar] [CrossRef] [PubMed]
- Schmid, T.E.; Dollinger, G.; Hauptner, A.; Hable, V.; Greubel, C.; Auer, S.; Friedl, A.A.; Molls, M.; Röper, B. No Evidence for a Different RBE between Pulsed and Continuous 20 MeV Protons. Rare 2009, 172, 567–574. [Google Scholar] [CrossRef] [PubMed]
- Schmid, T.E.; Dollinger, G.; Hable, V.; Greubel, C.; Zlobinskaya, O.; Michalski, D.; Molls, M.; Röper, B. Relative biological effectiveness of pulsed and continuous 20 MeV protons for micronucleus induction in 3D human reconstructed skin tissue. Radiother. Oncol. 2010, 95, 66–72. [Google Scholar] [CrossRef] [PubMed]
- Zlobinskaya, O.; Siebenwirth, C.; Greubel, C.; Hable, V.; Hertenberger, R.; Humble, N.; Reinhardt, S.; Michalski, D.; Röper, B.; Multhoff, G.; et al. The Effects of Ultra-High Dose Rate Proton Irradiation on Growth Delay in the Treatment of Human Tumor Xenografts in Nude Mice. Rare 2014, 181, 177–183. [Google Scholar] [CrossRef] [Green Version]
- Joiner, M.; van der Kogel, A. (Eds.) Basic Clinical Radiobiology, 5th ed.; CRC Press; Taylor & Francis Group: Boca Raton, FL, USA, 2018; ISBN 978-1-4441-7963-7. [Google Scholar]
- Inaniwa, T.; Suzuki, M.; Furukawa, T.; Kase, Y.; Kanematsu, N.; Shirai, T.; Hawkins, R.B. Effects of Dose-Delivery Time Structure on Biological Effectiveness for Therapeutic Carbon-Ion Beams Evaluated with Microdosimetric Kinetic Model. Radiat. Res. 2013, 180, 44–59. [Google Scholar] [CrossRef]
- Inaniwa, T.; Kanematsu, N.; Suzuki, M.; Hawkins, R.B. Effects of beam interruption time on tumor control probability in single-fractionated carbon-ion radiotherapy for non-small cell lung cancer. Phys. Med. Biol. 2015, 60, 4105–4121. [Google Scholar] [CrossRef]
- Takei, H.; Inaniwa, T. Effect of Irradiation Time on Biological Effectiveness and Tumor Control Probability in Proton Therapy. Int. J. Radiat. Oncol. Biol. Phys. 2019, 105, 222–229. [Google Scholar] [CrossRef]
- Manganaro, L.; Russo, G.; Cirio, R.; Dalmasso, F.; Giordanengo, S.; Monaco, V.; Muraro, S.; Sacchi, R.; Vignati, A.; Attili, A. A Monte Carlo approach to the microdosimetric kinetic model to account for dose rate time structure effects in ion beam therapy with application in treatment planning simulations. Med. Phys. 2017, 44, 1577–1589. [Google Scholar] [CrossRef] [Green Version]
- Herr, L. Modeling of Time-Dose-LET Effects in the Cellular Response to Radiation. Ph.D. Thesis, Technische Universität, Darmstadt, Germany, 2015. [Google Scholar]
- Kasamatsu, K.; Tanaka, S.; Miyazaki, K.; Takao, S.; Miyamoto, N.; Hirayama, S.; Nishioka, K.; Hashimoto, T.; Aoyama, H.; Umegaki, K.; et al. Impact of a spatially dependent dose delivery time structure on the biological effectiveness of scanning proton therapy. Med. Phys. 2022, 49, 702–713. [Google Scholar] [CrossRef]
- Saager, M.; Peschke, P.; Brons, S.; Debus, J.; Karger, C.P. Determination of the proton RBE in the rat spinal cord: Is there an increase towards the end of the spread-out Bragg peak? Radiother. Oncol. 2018, 128, 115–120. [Google Scholar] [CrossRef] [PubMed]
- Hintz, L.; Glowa, C.; Saager, M.; Euler-Lange, R.; Peschke, P.; Brons, S.; Grün, R.; Scholz, M.; Mein, S.; Mairani, A.; et al. Relative biological effectiveness of single and split helium ion doses in the rat spinal cord increases strongly with linear energy transfer. Radiother. Oncol. 2022, 170, 224–230. [Google Scholar] [CrossRef] [PubMed]
- Adrian, G.; Konradsson, E.; Lempart, M.; Bäck, S.; Ceberg, C.; Petersson, K. The FLASH effect depends on oxygen concentration. Br. J. Radiol. 2019, 93, 20190702. [Google Scholar] [CrossRef] [PubMed]
- El-Awady, R.A.; Dikomey, E.; Dahm-Daphi, J. Radiosensitivity of human tumour cells is correlated with the induction but not with the repair of DNA double-strand breaks. Br. J. Cancer 2003, 89, 593–601. [Google Scholar] [CrossRef] [Green Version]
- Debus, J.; Scholz, M.; Haberer, T.; Peschke, P.; Jäkel, O.; Karger, C.P.; Wannenmacher, M. Radiation Tolerance of the Rat Spinal Cord after Single and Split Doses of Photons and Carbon Ions. Radiat. Res. 2003, 160, 536–542. [Google Scholar] [CrossRef]
- Karger, C.P.; Peschke, P.; Sanchez-Brandelik, R.; Scholz, M.; Debus, J. Radiation tolerance of the rat spinal cord after 6 and 18 fractions of photons and carbon ions: Experimental results and clinical implications. Int. J. Radiat. Oncol. Biol. Phys. 2006, 66, 1488–1497. [Google Scholar] [CrossRef]
- Pop, L.A.; Millar, W.T.; van der Plas, M.; van der Kogel, A.J. Radiation tolerance of rat spinal cord to pulsed dose rate (PDR-) brachytherapy: The impact of differences in temporal dose distribution. Radiother. Oncol. 2000, 55, 301–315. [Google Scholar] [CrossRef]
- Herr, L.; Friedrich, T.; Durante, M.; Scholz, M. A Model of Photon Cell Killing Based on the Spatio-Temporal Clustering of DNA Damage in Higher Order Chromatin Structures. PLoS ONE 2014, 9, e83923. [Google Scholar] [CrossRef]
- Núñez, M.I.; Villalobos, M.; Olea, N.; Valenzuela, M.T.; Pedraza, V.; McMillan, T.J.; Ruiz de Almodóvar, J.M. Radiation-induced DNA double-strand break rejoining in human tumour cells. Br. J. Cancer 1995, 71, 311–316. [Google Scholar] [CrossRef] [Green Version]
- Tommasino, F.; Friedrich, T.; Scholz, U.; Taucher-Scholz, G.; Durante, M.; Scholz, M. A DNA Double-Strand Break Kinetic Rejoining Model Based on the Local Effect Model. Rare 2013, 180, 524–538. [Google Scholar] [CrossRef] [Green Version]
- McMahon, S.J. The linear quadratic model: Usage, interpretation and challenges. Phys. Med. Biol. 2018, 64, 01TR01. [Google Scholar] [CrossRef] [PubMed]
- Friedrich, T. Proton RBE dependence on dose in the setting of hypofractionation. Br. J. Radiol. 2020, 93, 20190291. [Google Scholar] [CrossRef] [PubMed]
- Hall, E.J. Radiation dose-rate: A factor of importance in radiobiology and radiotherapy. Br. J. Radiol. 1972, 45, 81–97. [Google Scholar] [CrossRef] [PubMed]
- Steel, G.G.; Down, J.D.; Peacock, J.H.; Stephens, T.C. Dose-rate effects and the repair of radiation damage. Radiother. Oncol. 1986, 5, 321–331. [Google Scholar] [CrossRef]
- Ruiz de Almodóvar, J.M.; Bush, C.; Peacock, J.H.; Steel, G.G.; Whitaker, S.J.; McMillan, T.J. Dose-rate effect for DNA damage induced by ionizing radiation in human tumor cells. Radiat. Res. 1994, 138, S93–S96. [Google Scholar] [CrossRef]
- Stephens, T.C.; Eady, J.J.; Peacock, J.H.; Steel, G.G. Split-dose and low dose-rate recovery in four experimental tumour systems. Int. J. Radiat. Biol. Relat. Stud. Phys. Chem. Med. 1987, 52, 157–170. [Google Scholar] [CrossRef]
- Scholz, M.; Friedrich, T.; Magrin, G.; Colautti, P.; Ristić-Fira, A.; Petrović, I. Characterizing Radiation Effectiveness in Ion Beam Therapy Part I: Introduction and Biophysical Modeling of RBE Using the LEMIV. Front. Phys. 2020, 8, 272. [Google Scholar] [CrossRef]
- Elsässer, T.; Krämer, M.; Scholz, M. Accuracy of the Local Effect Model for the Prediction of Biologic Effects of Carbon Ion Beams In Vitro and In Vivo. Int. J. Radiat. Oncol. 2008, 71, 866–872. [Google Scholar] [CrossRef]
- Grün, R.; Friedrich, T.; Elsässer, T.; Krämer, M.; Zink, K.; Karger, C.P.; Durante, M.; Engenhart-Cabillic, R.; Scholz, M. Impact of enhancements in the local effect model (LEM) on the predicted RBE-weighted target dose distribution in carbon ion therapy. Phys. Med. Biol. 2012, 57, 7261–7274. [Google Scholar] [CrossRef] [Green Version]
- Carante, M.P.; Aricò, G.; Ferrari, A.; Karger, C.P.; Kozlowska, W.; Mairani, A.; Sala, P.; Ballarini, F. In Vivo Validation of the BIANCA Biophysical Model: Benchmarking against Rat Spinal Cord RBE Data. Int. J. Mol. Sci. 2020, 21, 3973. [Google Scholar] [CrossRef]
- Friedrich, T.; Durante, M.; Scholz, M. Modeling cell survival after photon irradiation based on double-strand break clustering in megabase pair chromatin loops. Radiat. Res. 2012, 178, 385–394. [Google Scholar] [CrossRef] [PubMed]
- Mairani, A.; Böhlen, T.T.; Dokic, I.; Cabal, G.; Brons, S.; Haberer, T. Modelling of cell killing due to sparsely ionizing radiation in normoxic and hypoxic conditions and an extension to high LET radiation. Int. J. Radiat. Biol. 2013, 89, 782–793. [Google Scholar] [CrossRef] [PubMed]
- Grün, R.; Friedrich, T.; Krämer, M.; Scholz, M. Systematics of relative biological effectiveness measurements for proton radiation along the spread out Bragg peak: Experimental validation of the local effect model. Phys. Med. Biol. 2017, 62, 890–908. [Google Scholar] [CrossRef] [PubMed]
- Sachs, R.K.; van den Engh, G.; Trask, B.; Yokota, H.; Hearst, J.E. A random-walk/giant-loop model for interphase chromosomes. Proc. Natl. Acad. Sci. USA 1995, 92, 2710–2714. [Google Scholar] [CrossRef] [Green Version]
- Johnston, P.J.; Olive, P.L.; Bryant, P.E. Higher-Order Chromatin Structure-Dependent Repair of DNA Double-Strand Breaks: Modeling the Elution of DNA from Nucleoids. Radiat. Res. 1997, 148, 561–567. [Google Scholar] [CrossRef]
- Johnston, P.J.; MacPhail, S.H.; Banáth, J.P.; Olive, P.L. Higher-Order Chromatin Structure-Dependent Repair of DNA Double-Strand Breaks: Factors Affecting Elution of DNA from Nucleoids. Radiat. Res. 1998, 149, 533–542. [Google Scholar] [CrossRef]
- Yokota, H.; van den Engh, G.; Hearst, J.E.; Sachs, R.K.; Trask, B.J. Evidence for the organization of chromatin in megabase pair-sized loops arranged along a random walk path in the human G0/G1 interphase nucleus. J. Cell Biol. 1995, 130, 1239–1249. [Google Scholar] [CrossRef] [Green Version]
- Ostashevsky, J. A Polymer Model for the Structural Organization of Chromatin Loops and Minibands in Interphase Chromosomes. Mol. Biol. Cell 1998, 9, 3031–3040. [Google Scholar] [CrossRef] [Green Version]
- Elsässer, T.; Weyrather, W.K.; Friedrich, T.; Durante, M.; Iancu, G.; Krämer, M.; Kragl, G.; Brons, S.; Winter, M.; Weber, K.-J.; et al. Quantification of the relative biological effectiveness for ion beam radiotherapy: Direct experimental comparison of proton and carbon ion beams and a novel approach for treatment planning. Int. J. Radiat. Oncol. Biol. Phys. 2010, 78, 1177–1183. [Google Scholar] [CrossRef]
- Tommasino, F.; Friedrich, T.; Jakob, B.; Meyer, B.; Durante, M.; Scholz, M. Induction and Processing of the Radiation-Induced Gamma-H2AX Signal and Its Link to the Underlying Pattern of DSB: A Combined Experimental and Modelling Study. PLoS ONE 2015, 10, e0129416. [Google Scholar] [CrossRef] [Green Version]
- Liang, Y.; Fu, Q.; Wang, X.; Liu, F.; Yang, G.; Luo, C.; Ouyang, Q.; Wang, Y. Relative biological effectiveness for photons: Implication of complex DNA double-strand breaks as critical lesions. Phys. Med. Biol. 2017, 62, 2153–2175. [Google Scholar] [CrossRef] [PubMed]
- Stewart, R.D.; Yu, V.K.; Georgakilas, A.G.; Koumenis, C.; Park, J.H.; Carlson, D.J. Effects of radiation quality and oxygen on clustered DNA lesions and cell death. Radiat. Res. 2011, 176, 587–602. [Google Scholar] [CrossRef] [PubMed]
- Chatterjee, A.; Schaefer, H.J. Microdosimetric structure of heavy ion tracks in tissue. Radiat. Environ. Biophys. 1976, 13, 215–227. [Google Scholar] [CrossRef]
- Kiefer, J.; Straaten, H. A model of ion track structure based on classical collision dynamics. Phys. Med. Biol. 1986, 31, 1201–1209. [Google Scholar] [CrossRef] [PubMed]
- Kase, Y.; Kanai, T.; Matsufuji, N.; Furusawa, Y.; Elsässer, T.; Scholz, M. Biophysical calculation of cell survival probabilities using amorphous track structure models for heavy-ion irradiation. Phys. Med. Biol. 2008, 53, 37–59. [Google Scholar] [CrossRef] [PubMed]
- Elsässer, T.; Cunrath, R.; Krämer, M.; Scholz, M. Impact of track structure calculations on biological treatment planning in ion radiotherapy. New J. Phys. 2008, 10, 075005. [Google Scholar] [CrossRef]
- Barkas, W.H. Nuclear Research Emulsions: Techniques and Theory; Academic Press: Cambridge, MA, USA, 1963. [Google Scholar]
- Elsässer, T.; Scholz, M. Cluster effects within the local effect model. Radiat. Res. 2007, 167, 319–329. [Google Scholar] [CrossRef]
- Brons, S.; Taucher-Scholz, G.; Scholz, M.; Kraft, G. A track structure model for simulation of strand breaks in plasmid DNA after heavy ion irradiation. Radiat. Environ. Biophys. 2003, 42, 63–72. [Google Scholar] [CrossRef]
- Friedrich, T.; Durante, M.; Scholz, M. Simulation of DSB yield for high LET radiation. Radiat. Prot. Dosim. 2015, 166, 61–65. [Google Scholar] [CrossRef]
- Böhlen, T.T.; Cerutti, F.; Chin, M.P.W.; Fassò, A.; Ferrari, A.; Ortega, P.G.; Mairani, A.; Sala, P.R.; Smirnov, G.; Vlachoudis, V. The FLUKA Code: Developments and Challenges for High Energy and Medical Applications. Nucl. Data Sheets 2014, 120, 211–214. [Google Scholar] [CrossRef] [Green Version]
- Ferrari, A.; Sala, P.R.; Fassò, A.; Ranft, J. FLUKA: A Multi-Particle Transport Code (Program Version 2005); CERN Yellow Reports: Monographs; CERN: Geneva, Switzerland, 2005; ISBN 978-92-9083-260-7. [Google Scholar]
- Parodi, K.; Mairani, A.; Brons, S.; Hasch, B.G.; Sommerer, F.; Naumann, J.; Jäkel, O.; Haberer, T.; Debus, J. Monte Carlo simulations to support start-up and treatment planning of scanned proton and carbon ion therapy at a synchrotron-based facility. Phys. Med. Biol. 2012, 57, 3759–3784. [Google Scholar] [CrossRef] [PubMed]
- Mairani, A.; Brons, S.; Cerutti, F.; Fassò, A.; Ferrari, A.; Krämer, M.; Parodi, K.; Scholz, M.; Sommerer, F. The FLUKA Monte Carlo code coupled with the local effect model for biological calculations in carbon ion therapy. Phys. Med. Biol. 2010, 55, 4273–4289. [Google Scholar] [CrossRef] [PubMed]
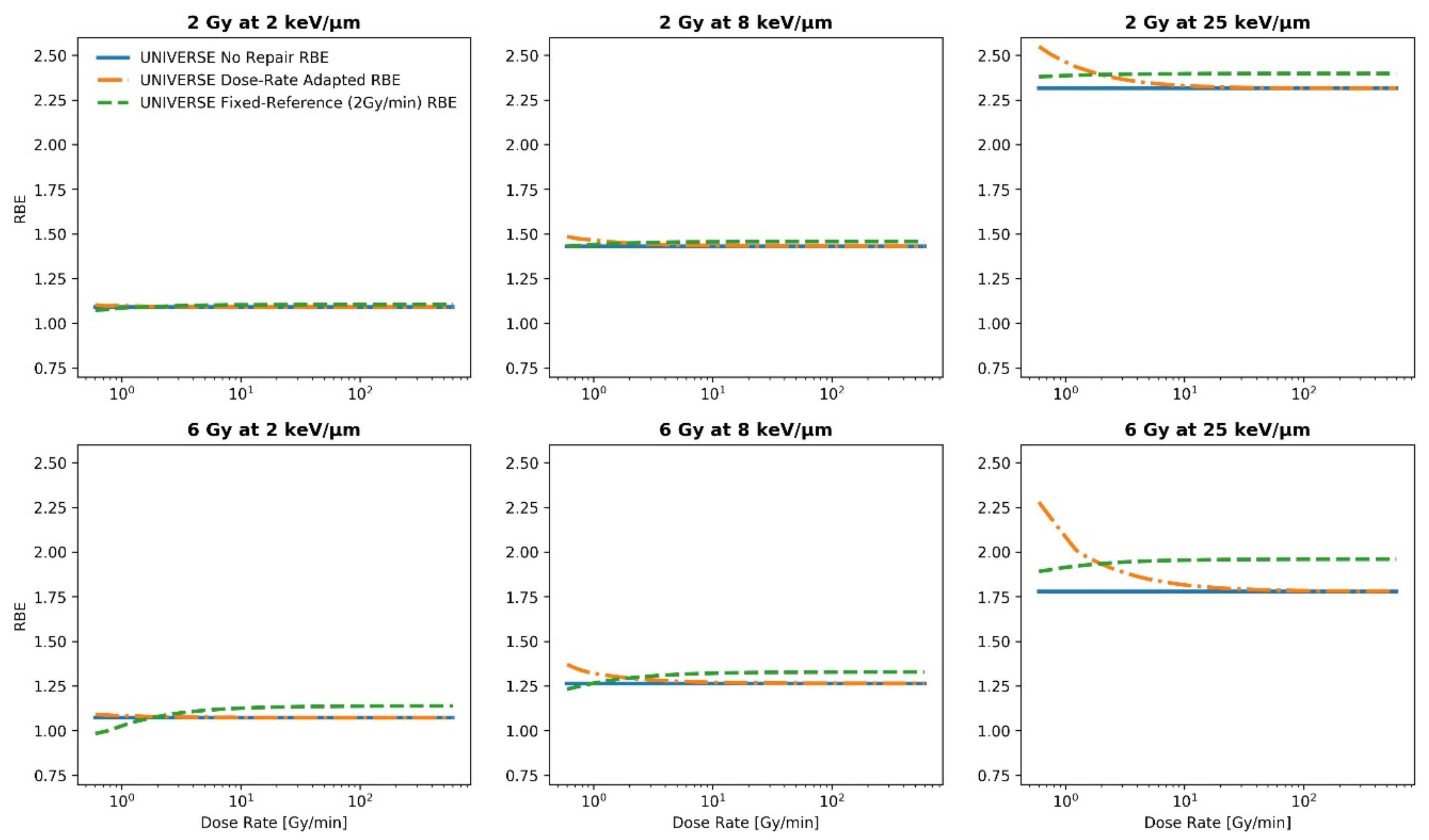
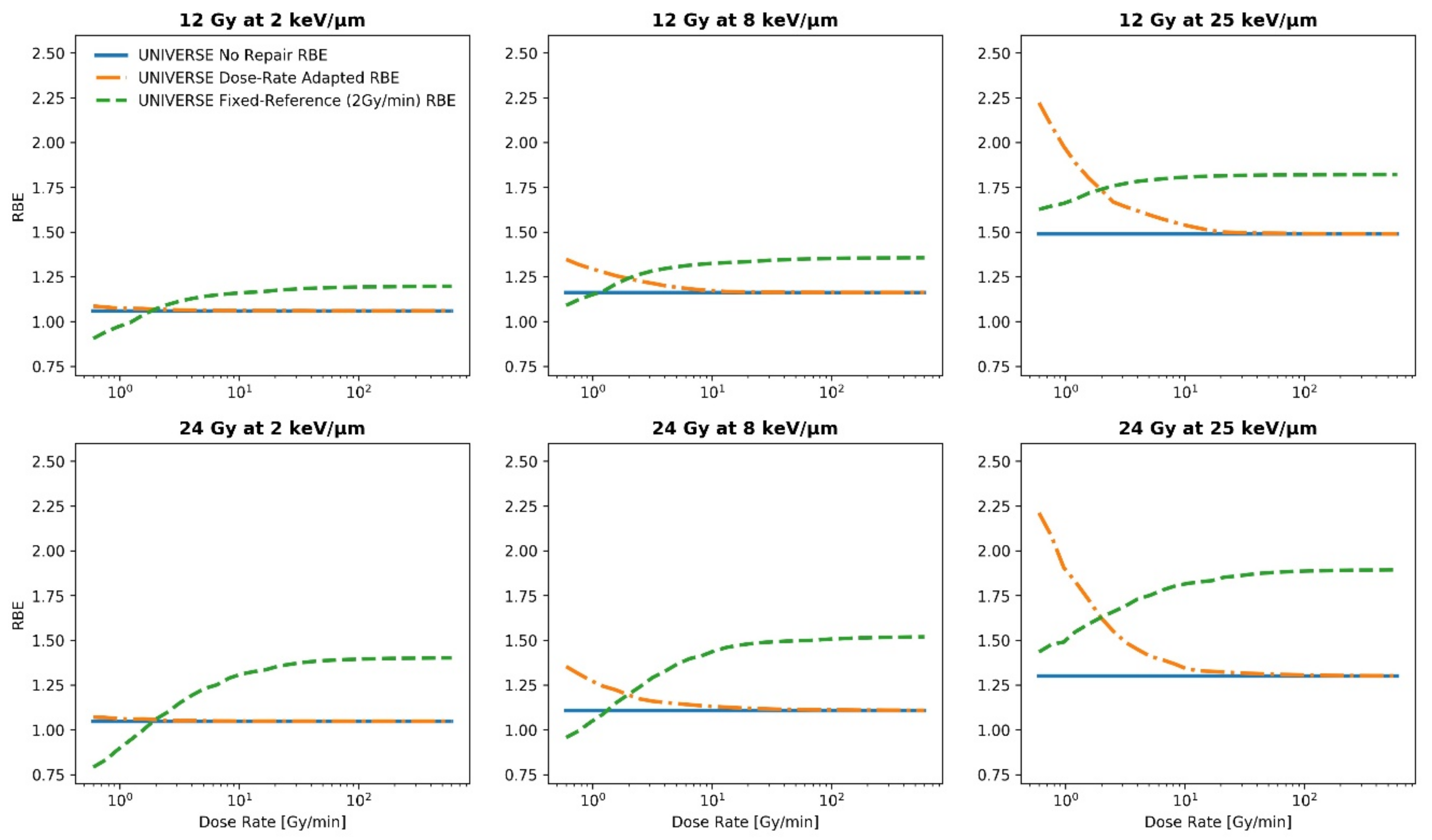
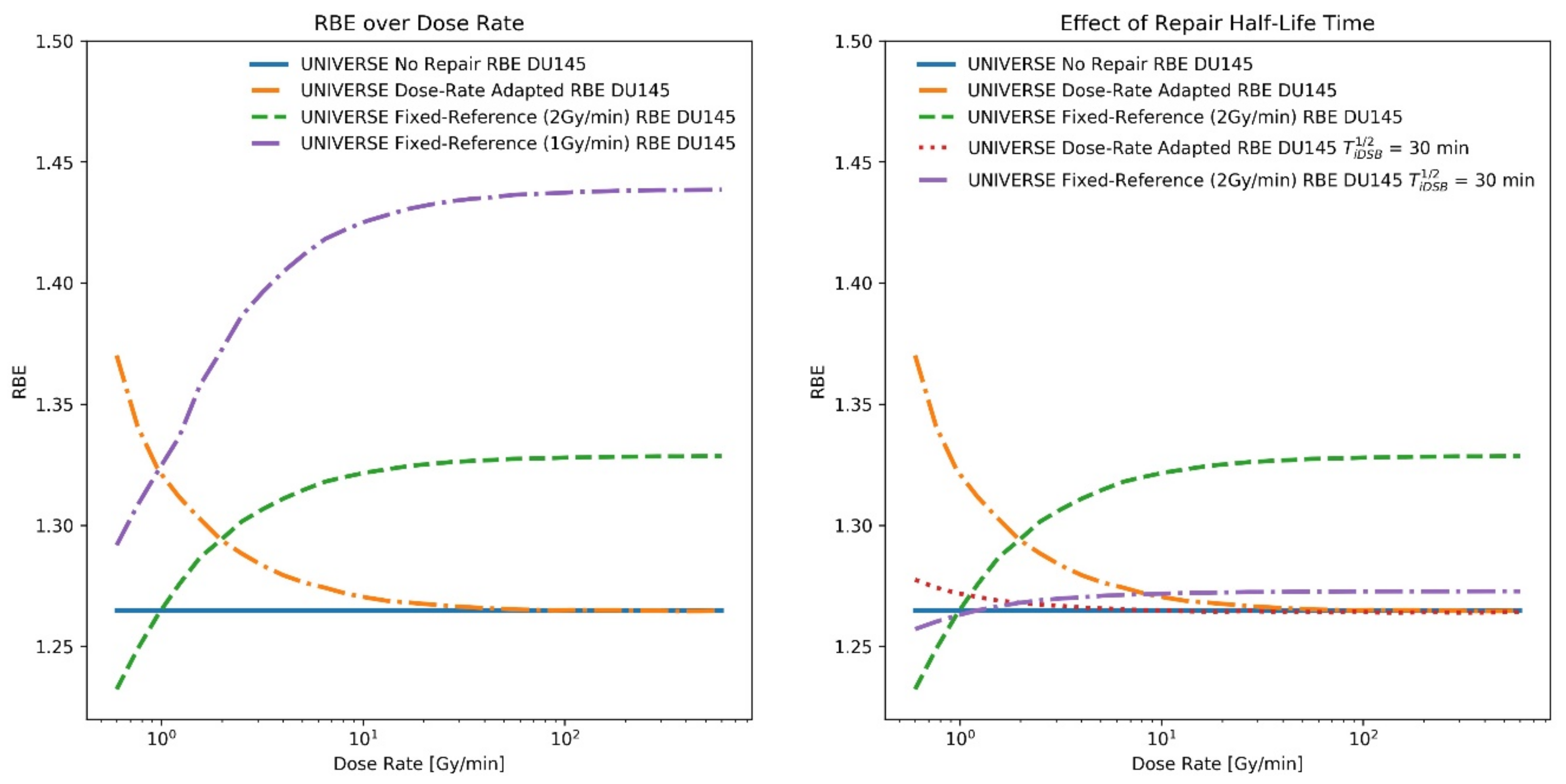
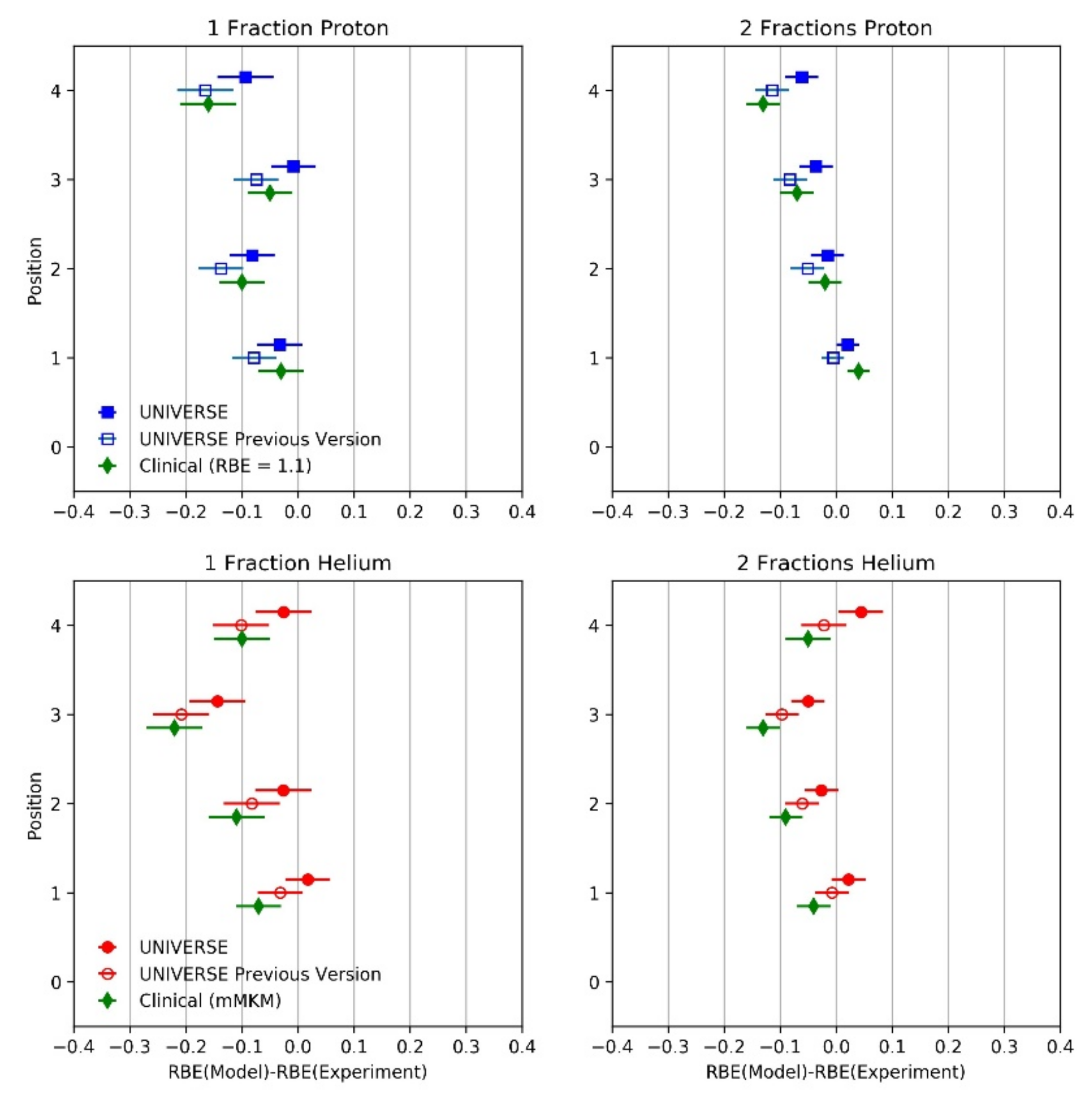
| Dose | |||
|---|---|---|---|
| 2 Gy | 1.3% | 1.8% | 3.5% |
| 6 Gy | 6.2% | 5.1% | 9.9% |
| 12 Gy | 12.9% | 16.6% | 22.2% |
| 24 Gy | 34.1% | 36.8% | 45.4% |
| Particle (No. of Fractions) | Depth [mm] | Dose-Rate [Gy/min] | RTD50 | LETd [keV/µm] |
|---|---|---|---|---|
| Proton (1 Fraction) | 35 | 11 | 1.042 | 2.0 |
| 100 | 18 | 1.051 | 3.0 | |
| 120 | 42 | 1.059 | 4.1 | |
| 127 | 53 | 1.061 | 5.3 | |
| Proton (2 Fractions) | 35 | 8 | 1.022 | 2.0 |
| 100 | 14 | 1.031 | 3.0 | |
| 120 | 31 | 1.038 | 4.1 | |
| 127 | 41 | 1.040 | 5.3 | |
| Helium (1 Fraction) | 35 | 11 | 1.042 | 4.2 |
| 100 | 11 | 1.042 | 9.3 | |
| 120 | 10 | 1.041 | 14.4 | |
| 127 | 9 | 1.036 | 22.0 | |
| Helium (2 Fractions) | 35 | 8 | 1.022 | 4.2 |
| 100 | 7 | 1.018 | 9.3 | |
| 120 | 7 | 1.018 | 14.4 | |
| 127 | 6 | 1.015 | 22.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liew, H.; Mein, S.; Tessonnier, T.; Karger, C.P.; Abdollahi, A.; Debus, J.; Dokic, I.; Mairani, A. Impact of DNA Repair Kinetics and Dose Rate on RBE Predictions in the UNIVERSE. Int. J. Mol. Sci. 2022, 23, 6268. https://doi.org/10.3390/ijms23116268
Liew H, Mein S, Tessonnier T, Karger CP, Abdollahi A, Debus J, Dokic I, Mairani A. Impact of DNA Repair Kinetics and Dose Rate on RBE Predictions in the UNIVERSE. International Journal of Molecular Sciences. 2022; 23(11):6268. https://doi.org/10.3390/ijms23116268
Chicago/Turabian StyleLiew, Hans, Stewart Mein, Thomas Tessonnier, Christian P. Karger, Amir Abdollahi, Jürgen Debus, Ivana Dokic, and Andrea Mairani. 2022. "Impact of DNA Repair Kinetics and Dose Rate on RBE Predictions in the UNIVERSE" International Journal of Molecular Sciences 23, no. 11: 6268. https://doi.org/10.3390/ijms23116268
APA StyleLiew, H., Mein, S., Tessonnier, T., Karger, C. P., Abdollahi, A., Debus, J., Dokic, I., & Mairani, A. (2022). Impact of DNA Repair Kinetics and Dose Rate on RBE Predictions in the UNIVERSE. International Journal of Molecular Sciences, 23(11), 6268. https://doi.org/10.3390/ijms23116268






