Twelve-Nitrogen-Atom Cyclic Structure Stabilized by 3d-Element Atoms: Quantum Chemical Modeling
1
Department of Analytical Chemistry, Certification and Quality Management, Kazan National Research Technological University, K. Marx Street 68, Kazan 420015, Russia
2
Kazan Department of Joint Supercomputer Center of Russian Academy of Sciences—Branch of Federal Scientific Center “Scientific Research Institute for System Analysis of the RAS”, Lobachevskii Street 2/31, Kazan 420111, Russia
*
Author to whom correspondence should be addressed.
Int. J. Mol. Sci. 2022, 23(12), 6560; https://doi.org/10.3390/ijms23126560
Submission received: 9 May 2022
/
Revised: 9 June 2022
/
Accepted: 10 June 2022
/
Published: 12 June 2022
(This article belongs to the Special Issue Simple Substances of Non-metals: Molecular Structures Modeling with Using DFT and More Advanced Methods of Quantum Chemistry)
Abstract
:Using various versions of density functional theory (DFT), DFT M06/TZVP, DFT B3PW91/TZVP, DFT OPBE/TZVP, and, partially, the MP2 method, the possibility of the existence of 3d-element (M) compounds with nitrogen having unusual M: nitrogen ratio 1:12, unknown for these elements at the present, was shown. Structural parameter data were presented. It was shown that all MN4 groupings have tetragonal-pyramidal structure. It was noted that the bond lengths formed by nitrogen atoms and an M atom were equal to each other only in the case of M = Ti, V, Cr and Co, whereas for other Ms, they were slightly different; moreover, the bond angles formed by nitrogen atoms and an M atom were equal to 90.0°, or practically did not differ from this value. Thermodynamic parameters, NBO analysis data and HOMO/LUMO images for this compound were also presented. Good agreement between the calculated data obtained using the above three quantum chemical methods was also noted.
1. Introduction
In our previous article [1], a quantum chemical calculation of the carbon-nitrogen compound molecular and electronic structures having a structural formula (1) with an unusual ratio between the number of carbon and nitrogen atoms (1:12) was performed, and the principal possibility of its existence was shown using quantum chemical methods DFT B3PW91/TZVP, MP2/TZVP and MP3/TZVP. Owing to the structural formation with the participation of the central carbon atom, the stabilization of the structural fragment of twelve nitrogen atoms (N12) took place. According to the data presented in [2,3,4,5,6,7,8,9,10], this grouping of atoms, if it is capable of existing by itself, is very unstable. It seemed interesting to find out whether the chemical compounds of the general formula (2) C(N12), similar to that described in [1], exist, but contain atoms of various 3d elements (M) instead of a carbon atom.
![Ijms 23 06560 i001]()
![Ijms 23 06560 i002]()
Additionally, in the case of a positive answer to this question, to what degree do the molecular and electronic structure parameters of such compounds, as well as their thermodynamic characteristics, depend on the nature of the M atom? There is no information in the literature about such compounds, although a number of publications were devoted to two-element chemical substances containing atoms of s-, p- or d-elements and nitrogen atoms (in particular, [11,12] and articles by [13,14,15,16,17,18,19,20] in the last 5 years). It should be noted that almost every one of these works mentioned the possible use of such compounds as potential high-energy materials. Consequently, this article will be dedicated to the consideration of chemical compounds having the above formula (2).
2. Method
In the given work, the density functional theory (DFT), which combines the standard extended split valence basis set TZVP and the most modern hybrid functional M06 described in [21], was used. For comparison, another version of the DFT method, DFT with the B3PW91 functional, was described extensively in [22,23,24] and used by us, in particular, in [25]. Application of the given version of the DFT method was due to the fact that, according to [22,23,24], it allows one to obtain, as a rule, the most exact (i.e., close to experimental) values of the molecular structures and geometric parameters, as well as much more accurate values for thermodynamic and other physical-chemical parameters in comparison to other DFT method variants. In addition, the molecular and electronic structures of the investigated compounds were calculated using the DFT OPBE/TZVP method, which combines the above-mentioned TZVP basis and the non-hybrid OPBE functional [26,27], that in the case of 3d-element complexes gives a fairly accurate ratio of the high-pin state energy stability in regard to the low-spin state and, at the same time, reliably characterizes the key geometric parameters of the metal complexes’ molecular structures [27,28,29,30,31]. As an alternative, the perturbation theory method [32], MP2 [33], in combination with the TZVP basis set was used. These calculations were performed using the Gaussian09 program package [34]. This calculation method was used in our previous article [25], and the correspondence with the found stationary points to the energy minima in all cases was proved by calculating the second derivatives of the energy to the coordinates of the atoms, wherein all equilibrium structures corresponding to the minimum points on the potential energy surfaces had only real (and, moreover, always positive) frequency values. From the optimized structures for further consideration, the one with the lowest total energy was selected. Unfortunately, at the moment we had to limit ourselves to calculations using different versions of the DFT method, because for the analyzed compounds, completing the calculation with any of the higher-level methods (QCISD, CCSD, and even MP3) led us to failure due to the complexity of these methods, as well as our limited time and energy costs. Natural bond orbital (NBO) analysis was performed using NBO version 3.1, integrated with Gaussian09 program package [34] according to the methodology described in [35]. NBO methods are well known for excellent numerical stability and convergence regarding basis set expansion, sensibly proportionate to convergence of energy and other calculated wavefunction properties (unlike Mulliken analysis and related overlap-dependent methods). The standard thermodynamic parameters of formation, H0f,298, S0f,298 and G0f,298 for the M(N12) compounds were calculated according to the methodology described in [36].
3. Results and Discussion
According to the data from each of the three above-mentioned methods of quantum chemical calculation, most of the M(N12) chemical compounds have molecular structures (2) where M–any of 3d-elements are capable of independent existence. Sc and Zn are the only exceptions. For the first of them, such a compound cannot arise due to its limited valence capabilities; for the second, although it is possible, it is unlikely (it was confirmed by our calculations). The most important geometric parameters of molecular structures of M(N12) compounds for various M (the lengths of chemical bonds between atoms and bond angles) revealed using the DFT M06/TZVP method are presented in Table 1. For comparison, this Table also presents the molecular structure parameters calculated by the same method, for the chemical compound that can be considered as a kind of “progenitor” of the studied metal complexes, namely H4(N12), as a result of the substitution of all four hydrogen atoms in which all compounds are of type (2). The similar data calculated by the DFT B3PW91/TZVP and DFT OPBE/TZVP methods are presented in Tables S1–S8 (see Supplementary Materials). From these data, all three methods gave very close values for the key parameters of these molecular structure. It seems appropriate to discuss the results produced by any one of them, and namely DFT M06/TZVP as the most advanced among DFT B3PW91/TZVP and DFT OPBE/TZVP methods.
As can be seen from Table 1, the MN4 atom grouping (chelate node) in each of the chemical compounds has a tetragonal-pyramidal structure with a very significant (more than 30°) deviation from the plane formed by four nitrogen atoms bonded to the M atom. Examples of such structures are shown in Figure 1. It should be noted that, in contrast to the grouping of MN4 atoms, the grouping of four nitrogen atoms included in the chelate node in all M(N12) discussed compounds was strictly flat (the sum of the angles N1N4N7, N4N7N10, N7N10N1 and N10N1N4 in each is 360.0°). Moreover, this grouping had the shape of either a square (in the case of M = Ti, V, Cr, Co) or an isosceles trapezoid (in the case of M = Mn, Fe, Ni, Cu). Accordingly, in the first four complexes, all M–N bond lengths were equal to each other, whereas in the rest, they were not equal (Table 1). It is interesting that the diagonals of these quadrangles (N1—N7) and (N4—N10) in seven of these eight compounds were the same in length and were 325.9 (Ti), 321.9 (V), 326.4 (Cr), 326.4 (Co), 333.4 (Ni) and 343.0 (Cu) pm. For M = Mn, there were small differences between them, 332.9 and 332.7 pm, respectively. Thus, in each of the M(N12) considered compounds, the M atom was to some extent elevated above the plane of four donor nitrogen atoms; the height of this rise strongly depended on the M nature and varied from 67.4 pm (in Ni(N12)) to 104.4 pm (in Ti(N12)) (Table 1), which correlated rather well with the sizes of M(II) and M(IV) of the analyzed 3d elements. In contrast to the N4 groups, the 12-membered macrocycles N12 formed by nitrogen atoms were non-coplanar, and very significant deviations from coplanarity took place for them (Table 1). Interestingly, as a result of the formation of any of these compounds, a decrease in the deviation degree from this macrocycle coplanarity compared to that for the H4(N12) ligand occurred. This deviation, as can be seen from Table 1, varied from 34.7° in the case of Cu(N12) to 63.7° in the case of Fe(N12) depending on the M nature. Based on this, the M(N12) considered compounds could be clearly divided into two equal groups. The first of them (A) included Ti(N12), V(N12), Cr(N12) and Co(N12), whose molecular structures have the C4v symmetry group. The second (B) included Mn(N12), Fe(N12), Ni(N12) and Cu(N12), whose molecular structures have the C1 symmetry group, i.e., devoid of any symmetry elements. The molecular structure of the H4(N12) ligand was also completely asymmetric. In this structure, two N–H bonds are directed inside the N12 macrocycle, while the other two are outside it (Figure 1). The dipole electric moment values for these compounds calculated using each of the DFT M06/TZVP, DFT B3PW91/TZVP, and DFT OPBE/TZVP methods were very different from zero (Table 2), which is understandable because of the lack of a center of symmetry in each of them. The μ values calculated by two other DFT methods (in Debye units), are given in Table S9 (see Supplementary Materials).
Key data of NBO analysis and, namely, the effective charge values on 3d-element atoms and nitrogen atoms for examined chemical compounds obtained by DFT M06/TZVP method, are presented in Table 3. Similar results calculated using the DFT B3PW91/TZVP and DFT OPBE/TZVP methods are presented in Table S10 (see Supplementary Materials). Obviously, numerical values of the squared operator of the angular moment of the total spin of the system <S**2> in the case of Ti(N12) and Ni(N12) correspond to total spin of system S = 0, in the case of V(N12) and Cu(N12) – S = 1/2, in the case of Cr(N12) and Fe(N12) − S = 1, and in the case of Mn(N12) and Co(N12) – S = 3/2. This allowed us to assume that in the analyzed compounds, in the case of M = Ti, the electronic configuration of the central ion 3d0 was formed in the cases of M = V – 3d1, M = Cr − 3d2, M = Mn – 3d3, M = Fe – 3d4, M = Co – 3d5, M = Ni – 3d6, and M = Cu – 3d7 that correspond to the oxidation state of the central M(IV) atom. Two additional points should be noted. Firstly, the effective charges on the M atoms in all cases differed very significantly from the value +4.000 ē that would apply if all chemical bonds between M and N atoms were ionic. Secondly, the charges on both M and nitrogen atoms strongly depended on the atomic nature of the 3d element. However, this fact indicates that in the all discussed compounds, a very high degree of delocalization of the electron density was found. The ground states of M(N12) are a spin singlet (MS = 1) (M = Ti, Ni), doublet (M = V, Cu), triplet (M = Cr, Fe) and quartet (M = Mn, Co). In this case, the next excited energy state with a different spin multiplicity MS (triplet for M = Ti, Ni, quartet for M = V, Cu, singlet for M = Cr, quintet for M = Fe, sextet for M = Mn and doublet for M = Co) was located above the ground state by 125.5; 2.5; 160.7; 63.4; 26.2; 12.5; 58.9; and 27.4 kJ/mol, so that a spin crossover could be expected only for Ni(N12).
The images of the highest occupied and lowest vacant (unoccupied) molecular orbitals (HOMO and LUMO, respectively) produced by the DFT M06/TZVP method are presented in Figure 2, Figure 3 and Figure 4. These images demonstrated that there was no similarity between the shapes of both HOMO and LUMO for different M(N12) values. Interestingly, there was a marked difference in the energies of these MOs, not only for different complexes, but even for electrons with different spins in each of these complexes (Figure 2 and Figure 3). Spin density distribution diagrams of the studied complexes are shown in Figure 5.
Comparing the calculation data for the parameters of the molecular structures of the M(N12) compounds with the analogous parameters of the C(N12) compound described in our previous article [1], it can be noted that the M–N bond lengths for any of the above M are much larger than the bond length of C–N to C(N12). This is a quite expected result, since the radius of any of these M atoms was much larger than the radius of the carbon atom. At the same time, the lengths of the N–N bonds in these compounds did not differ much from each other, as a result of which the size of the cell formed by four nitrogen atoms N1, N4, N7 and N10 was almost the same. In the case of a carbon atom, the size of this cell turns out to be sufficient for the center of the atom to be in the plane of the [N1N4N7N10] atoms, while in the case of any of the M atoms, this size is insufficient. It is precisely because of this that in M(N12), the deviation of the M atoms from this plane takes place, which, on the whole, is more significant the greater the radius of the M(IV) ion.
The standard thermodynamic parameters of formation (H0f,298, S0f,298, and G0f,298) for the chemical compounds are presented in Table 4. All of these parameters were positive, and, therefore, these compounds could not be obtained from the most thermodynamically stable, simple substances formed by the corresponding 3d-element and nitrogen (i.e., 3d-metal and molecular dinitrogen N2). It is noteworthy that in most cases, S0f,298 values for M(N12) are higher than for H4(N12) (the only exception is V(N12), while for G0f,298, half of the M(N12) complexes (M = Cr, Co, Ni, Cu) have higher values of this parameter compared to those for the H4(N12), while the other half (M = Ti, V, Mn, Fe) have lower values (Table 4). The dynamics of changes in the values H0f,298 and G0f,298 in the series Ti-Cu are the same—when moving from Ti to Cr, they increase, from Cr to Mn they decrease, and from Mn to Cu they increase again, ultimately exceeding the corresponding values for H4(N12). Thus, it can be argued that for at least four of the eight M, owing to the formation of the M(N12) investigated compounds, stabilization of the N12 cyclic carcass s happens. In this connection, it should be noted that for the compound C(N12) similar in structural formula and spatial (molecular) structure as described in [1], the values of the parameters H0f,298, S0f,298 and G0f,298, calculated by the method M06/TZVP, were 1793.1 kJ/mol, 377.7 J/mol∙K and 2020.7 kJ/mol respectively, i.e., quite close to those for M(N12) presented in Table 4.
In the end of this section of the article, it seems appropriate to compare the results of quantum chemical calculations of the molecular structures of these compounds obtained by the M06/TZVP method with the results of calculations of a higher level, in particular, by the DFT M062X/Def2TZVP method. Some of these data are presented in Table S14 (see Supplementary Materials). They are still incomplete (because the implementation of this method requires significantly more time and technological costs compared to those for the DFT M06/TZVP method), and so far, we have managed to obtain the corresponding data only for five compounds of the M(N12) type, namely for M = Cr, Mn, Fe, Co, Cu (which took about 2 months for us). As you can see when comparing them with similar data for the corresponding complexes of the above 3d elements obtained by the DFT M06/TZVP method, they are, on the whole, close to each other. Thus, it can be argued that the three versions of the DFT method we used, namely, those with the M06, B3PW91 OPBE functionals, and the TZVP basis set, are quite reliable for predicting the specifics of the molecular structures of the M(N12) compounds under consideration.
Unfortunately, at this point in time, we could not use the simplest version of the MP method, namely MP2, to calculate any of the M(N12) compounds (due to problems with the convergence of the results and many times longer calculation time compared to even the DFT M062X/Def2TZVP method, we were unable to complete the calculation even within 8 (!!) months).
4. Conclusions
In this way, the data obtained using the DFT M06/TZVP method, unambiguously predicted the possible existence of new, so far unknown in chemical science, coordination compounds of various 3d-elements with nitrogen having M(N12) composition (M = Ti, V, Cr, Mn, Fe, Co, Ni, Cu). So, we also obtained similar results and conclusions using two other versions of the density functional theory, the DFT B3PW91/TZVP and DFT OPBE/TZVP methods, and also using the MP2 method (see Supplementary Materials, Table S14). However, due to significant time costs, it was possible to implement them only for four of the eight considered compounds M(N12), namely, for M = Cr, Fe, Co, Cu.
Comparing the calculation data for the molecular structure parameters of the M(N12) compounds with the analogous parameters of the C(N12) compound described in our previous article [1], it can be noted that the M–N bond lengths for any of the above M were much larger than the bond length C–N to C(N12). This is a quite expected result, because the radius of any of these M atoms is much larger than the carbon atom radius. At the same time, the lengths of the N–N bonds in these compounds are not much different from each other, and as a result, the cell size formed by four nitrogen atoms N1, N4, N7 and N10 was almost the same. In the case of a carbon atom, the cell size that turns out to be sufficient for the atom center is in the plane of the [N1N4N7N10] atoms, while in the case of any M atoms, this size is insufficient. Because of this, in M(N12) there is an M atoms deviation from this plane, which, in general, is more significant the larger the ion M(IV) radius.
It is interesting and somewhat unexpected that, according to calculations, there is a division of M(N12) compounds into two categories, in the first of them (Ti(N12), V(N12), Cr(N12) and Co(N12)), all of the M–N bond lengths are the same; in the second (Mn(N12), Fe(N12), Ni(N12) and Cu(N12)), they are equal only in pairs. No correlation between the electronic configuration of the central atom 3d element M and the compound M(N12) belonging to the corresponding category was observed. The compound molecular structures in the first category have C4v symmetry, and those in the second are completely asymmetric. It may be expected that the electric dipole moments of the first category of compounds would be lower compared to those of the second category. In fact, there is an inverse relationship between these values. The deviation from the MN4 chelate node coplanarity is also more pronounced in the first category of complexes. Nevertheless, the grouping of four N4 nitrogen atoms bonded to the M atom in any of these compounds is strictly planar. In this regard, the discussed compounds differed only in that in first category of compounds, all non-bonding angles between nitrogen atoms in this group were equal to 90.0°, while in second category of compounds, only pairwise equality of these angles, as well as the M–N bond lengths, was found.
In our opinion, the results of quantum chemical calculations within the framework of each of these three methods provide a reason for more thorough study of all 3d-metal-nitrogen-containing macrocyclic compounds analyzed in this article. It should be noted in this connection that the use of DFT computational methods of a higher level compared to DFT M06/TZVP (i.e., DFT M062X/Def2TZVP) gives practically the same results as the DFT M06/TZVP method (both in qualitative and quantitative terms), but requires less time. First of all, it is necessary to confirm their existence in the experiment. Judging by the very high values of ∆H0f,298 and ∆G0f,298 (more than 1500 kJ/mol), all of these compounds are high-energy substances, and that is why, it seems to us, if the synthesis of these exotic compound is successful, they will undoubtedly find some practical application, at least in the above capability.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/ijms23126560/s1.
Author Contributions
Conceptualization, O.V.M.; Methodology, O.V.M. and D.V.C.; Software, D.V.C.; Validation, O.V.M. and D.V.C.; Formal Analysis, O.V.M. and D.V.C.; Investigation, O.V.M. and D.V.C.; Resources, D.V.C.; Data Curation, D.V.C.; Writing—Original Draft Preparation, O.V.M. and D.V.C.; Writing—Review and Editing, O.V.M.; Visualization, O.V.M. and D.V.C.; Supervision, O.V.M.; Project Administration, O.V.M.; Funding Acquisition, D.V.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
All quantum chemical calculations were performed at the Joint Supercomputer Center of Russian Academy of Sciences—Branch of Federal Scientific Center “Scientific Research Institute for System Analysis of the RAS”, which is acknowledged for technical support. The contribution by author Denis V. Chachkov was funded by the state assignment to the Federal Scientific Center “Scientific Research Institute for System Analysis of the RAS” for scientific research. Additionally, this study was carried out using the equipment of the Center for Collective Use “Nanomaterials and Nanotechnology” of the Kazan National Research Technological University with the financial support of the Ministry of Science and Higher Education of the Russian Federation under agreement No. 075-15-2021-699.
Conflicts of Interest
The authors declare that they have no conflict of interest, financial or otherwise.
References
- Chachkov, D.V.; Mikhailov, O.V. New Chemical Compound with Unusual Ratio of Number of Carbon and Nitrogen Atoms—C(N12): Quantum-Chemical Modelling. RSC Adv. 2021, 11, 35974–35981. [Google Scholar] [CrossRef]
- Klapötke, T.M.; Harcourt, R.D. The interconversion of N12 to N8 and two equivalents of N2. J. Mol. Struct. 2001, 541, 237–242. [Google Scholar] [CrossRef]
- Olah, G.A.; Prakash, G.K.S.; Rasul, G. N62+ and N42+ Dications and Their N12 and N10 Azido Derivatives: DFT/GIAO-MP2 Theoretical Studies. J. Am. Chem. Soc. 2001, 123, 3308–3310. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.S.; Zhao, J.F. Theoretical Study of Potential Energy Surfaces for N12 Clusters. J. Phys. Chem. A 2002, 106, 5367–5372. [Google Scholar] [CrossRef]
- Bruney, L.Y.; Bledson, T.M.; Strout, D.L. What Makes an N12 Cage Stable? Inorg. Chem. 2003, 42, 8117–8120. [Google Scholar] [CrossRef] [PubMed]
- Samartzis, P.C.; Woodtke, A.M. All-nitrogen chemistry: How far are we from N60? Int. Rev. Phys. Chem. 2006, 25, 1952–2005. [Google Scholar] [CrossRef]
- Greschner, M.J.; Zhang, M.; Majumdar, A.; Liu, H.; Peng, F.; Tse, J.S.; Yao, Y. A New Allotrope of Nitrogen as High-Energy Density Material. J. Phys. Chem. A 2016, 120, 2920–2925. [Google Scholar] [CrossRef]
- Mikhailov, O.V.; Chachkov, D.V. Molecular structures and thermodynamics of stable N4, N6 and N8 neutral polynitrogens according to data of QCISD(T)/TZVP method. Chem. Phys. Lett. 2020, 753, 137594. [Google Scholar] [CrossRef]
- Chachkov, D.V.; Mikhailov, O.V. Tetra-, hexa-, and octanitrogen molecules: A quantum chemical design and thermodynamic properties. Russ. Chem. Bull. 2020, 69, 2067–2072. [Google Scholar] [CrossRef]
- Mikhailov, O.V. Molecular and Electronic Structures of Neutral Polynitrogens: Review on the Theory and Experiment in 21st Century. Int. J. Mol. Sci. 2022, 23, 2841. [Google Scholar] [CrossRef]
- Straka, M. N6 ring as a planar hexagonal ligand in novel M(η6-N6) species. Chem. Phys. Lett. 2002, 358, 531–536. [Google Scholar] [CrossRef]
- Lee, E.P.F.; Dyke, J.M.; Claridge, R.P. Ab Initio Calculations on Al2N4 and AlNn (n = 4 to 7): Potential Precursors of High Energy Density Materials. J. Phys. Chem. A 2002, 106, 8680–8695. [Google Scholar] [CrossRef]
- Choi, C.; Yoo, H.-W.; Goh, E.M.; Cho, S.G.; Jung, Y.S. Ti(N5)4 as a Potential Nitrogen-Rich Stable High-Energy Density Material. J. Phys. Chem. A 2016, 120, 4249–4255. [Google Scholar] [CrossRef] [PubMed]
- Brathwaite, A.D.; Abbott-Lyon, H.L.; Duncan, M.A. Distinctive Coordination of CO vs N2 to Rhodium Cations: An Infrared and Computational Study. J. Phys. Chem. A 2016, 120, 7659–7670. [Google Scholar] [CrossRef]
- Ding, K.; Xu, H.; Yang, Y.; Li, T.; Chen, Z.; Ge, Z.; Zhu, W.; Zheng, W. Mass Spectrometry and Theoretical Investigation of VNn+ (n = 8, 9, and 10) Clusters. J. Phys. Chem. A 2018, 122, 4687–4695. [Google Scholar] [CrossRef]
- Bykov, M.; Bykova, E.; Koemets, E.; Fedotenko, T.; Aprilis, G.; Glazyrin, K.; Liermann, H.-P.; Ponomareva, A.V.; Tidholm, J.; Tasnadi, F.; et al. High-pressure synthesis of a nitrogen-rich inclusion compound ReN8 xN2 with conjugated polymeric nitrogen chains. Angew. Chem. Int. Ed. 2018, 57, 9048–9053. [Google Scholar] [CrossRef] [Green Version]
- Ge, Z.; Ding, K.; Li, Y.; Xu, H.; Chen, Z.; Ma, Y.; Li, T.; Zhu, W.; Zheng, W. Structural evolution of LiNn+ (n = 2, 4, 6, 8, and 10) clusters: Mass spectrometry and theoretical calculations. RSC Adv. 2019, 9, 6762–6769. [Google Scholar] [CrossRef] [Green Version]
- Ding, K.; Li, T.; Xu, H.; Li, Y.; Ge, Z.; Zhu, W.; Zheng, W. Mass spectrometry detection of LiN12+ cluster and theoretical investigation of its structures and stability. Chem. Phys. Lett. 2020, 747, 137310. [Google Scholar] [CrossRef]
- Ding, K.; Chen, H.; Xu, H.; Yang, B.; Ge, Z.; Lu, C.; Zheng, W. Identification of octahedral coordinated ZrN12+ cationic clusters by mass spectrometry and structure searches. Dalton Trans. 2021, 50, 10187–10192. [Google Scholar] [CrossRef]
- Yuan, J.N.; Xia, K.; Wu, J.F.; Sun, J. High-energy-density pentazolate salts: CaN10 and BaN10. Sci. China Phys. Mech. Astron. 2021, 64, 218211. [Google Scholar] [CrossRef]
- Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar] [CrossRef] [Green Version]
- Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Wang, Y. Generalized gradient approximation for the exchange-correlation hole of a many-electron system. Phys. Rev. B 1996, 54, 16533–16539. [Google Scholar] [CrossRef] [Green Version]
- Medvedev, M.G.; Bushmarinov, I.S.; Sun, J.; Perdew, J.P.; Lyssenko, K.A. Density functional theory is straying from the path toward the exact functional. Science 2017, 355, 49–52. [Google Scholar] [CrossRef] [PubMed]
- Mikhailov, O.V.; Chachkov, D.V. DFT Quantum-Chemical Modeling Molecular Structures of Cobalt Macrocyclic Complexes with Porphyrazine or Its Benzo-Derivatives and Two Oxygen Acido Ligands. Int. J. Mol. Sci. 2020, 21, 9085. [Google Scholar] [CrossRef]
- Hoe, W.M.; Cohen, A.; Handy, N.C. Assessment of a new local exchange functional OPTX. Chem. Phys. Lett. 2001, 341, 319–328. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [Green Version]
- Paulsen, H.; Duelund, L.; Winkler, H.; Toftlund, H.; Trautwein, A.X. Free Energy of Spin-Crossover Complexes Calculated with Density Functional Methods. Inorg. Chem. 2001, 40, 2201–2203. [Google Scholar] [CrossRef]
- Swart, M.; Groenhof, A.R.; Ehlers, A.W.; Lammertsma, K. Validation of Exchange−Correlation Functionals for Spin States of Iron Complexes. J. Phys. Chem. A 2004, 108, 5479–5483. [Google Scholar] [CrossRef]
- Swart, M.; Ehlers, A.W.; Lammertsma, K. Performance of the OPBE exchange-correlation functional. Mol. Phys. 2004, 102, 2467–2474. [Google Scholar] [CrossRef]
- Swart, M. Metal–ligand bonding in metallocenes: Differentiation between spin state, electrostatic and covalent bonding. Inorg. Chim. Acta 2007, 360, 179–189. [Google Scholar] [CrossRef]
- Møller, C.; Plesset, M.S. Note on an approximation treatment for many-electron systems. Phys. Rev. 1934, 46, 618–622. [Google Scholar] [CrossRef] [Green Version]
- Head-Gordon, M.; Pople, J.A.; Frisch, M.J. MP2 energy evaluation by direct methods. Chem. Phys. Lett. 1988, 153, 503–506. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. (Eds.) Gaussian 09, Revision A.01; Gaussian, Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Weinhold, F.; Landis, C.R.; Glendening, E.D. What is NBO analysis and how is it useful? Int. Rev. Phys. Chem. 2016, 35, 399–440. [Google Scholar] [CrossRef]
- Ochterski, J.W. Thermochemistry in Gaussian; Gaussian, Inc.: Wallingford, CT, USA, 2000. [Google Scholar]
Figure 1.
Molecular structures of the compounds H4(N12) (a,b), Fe(N12) (c,d) and Co(N12) (e,f) obtained as a result of DFT M06/TZVP quantum chemical calculation: front view (a,c,e), side view (b,d,f).
Figure 1.
Molecular structures of the compounds H4(N12) (a,b), Fe(N12) (c,d) and Co(N12) (e,f) obtained as a result of DFT M06/TZVP quantum chemical calculation: front view (a,c,e), side view (b,d,f).
Figure 2.
The images of highest occupied (HOMO) and lowest unoccupied (LUMO) molecular orbitals in the M(N12)] complexes of group A obtained by DFT M06/TZVP method. The values of energies of these molecular orbitals (in brackets) are given in eV. The symbol “alpha” corresponds to electron with spin (+1/2), “beta”, to electron with spin (−l/2).
Figure 2.
The images of highest occupied (HOMO) and lowest unoccupied (LUMO) molecular orbitals in the M(N12)] complexes of group A obtained by DFT M06/TZVP method. The values of energies of these molecular orbitals (in brackets) are given in eV. The symbol “alpha” corresponds to electron with spin (+1/2), “beta”, to electron with spin (−l/2).
Figure 3.
The images of highest occupied (HOMO) and lowest unoccupied (LUMO) molecular orbitals in the M(N12)] complex of group B obtained by DFT M06/TZVP method. The values of energies of these molecular orbitals (in brackets) are given in eV. The symbol “alpha” corresponds to electron with spin (+1/2), “beta”, to electron with spin (−l/2).
Figure 3.
The images of highest occupied (HOMO) and lowest unoccupied (LUMO) molecular orbitals in the M(N12)] complex of group B obtained by DFT M06/TZVP method. The values of energies of these molecular orbitals (in brackets) are given in eV. The symbol “alpha” corresponds to electron with spin (+1/2), “beta”, to electron with spin (−l/2).
Figure 4.
The images of highest occupied (HOMO) and lowest unoccupied (LUMO) molecular orbitals in the H4(N12) obtained by DFT M06/TZVP method. The values of energies of these molecular orbitals (in brackets) are given in eV.
Figure 4.
The images of highest occupied (HOMO) and lowest unoccupied (LUMO) molecular orbitals in the H4(N12) obtained by DFT M06/TZVP method. The values of energies of these molecular orbitals (in brackets) are given in eV.
Figure 5.
The images of spin density distribution in M(N12) complexes obtained by DFT M06/TZVP method: (a) V(N12), (b) Cr(N12), (c) Mn(N12), (d) Fe(N12), (e) Co(N12), (f) Ni(N12), (g) Cu(N12).
Figure 5.
The images of spin density distribution in M(N12) complexes obtained by DFT M06/TZVP method: (a) V(N12), (b) Cr(N12), (c) Mn(N12), (d) Fe(N12), (e) Co(N12), (f) Ni(N12), (g) Cu(N12).
Table 1.
Key parameters of molecular structures of M(N12) compounds calculated by DFT M06/TZVP method.
Table 1.
Key parameters of molecular structures of M(N12) compounds calculated by DFT M06/TZVP method.
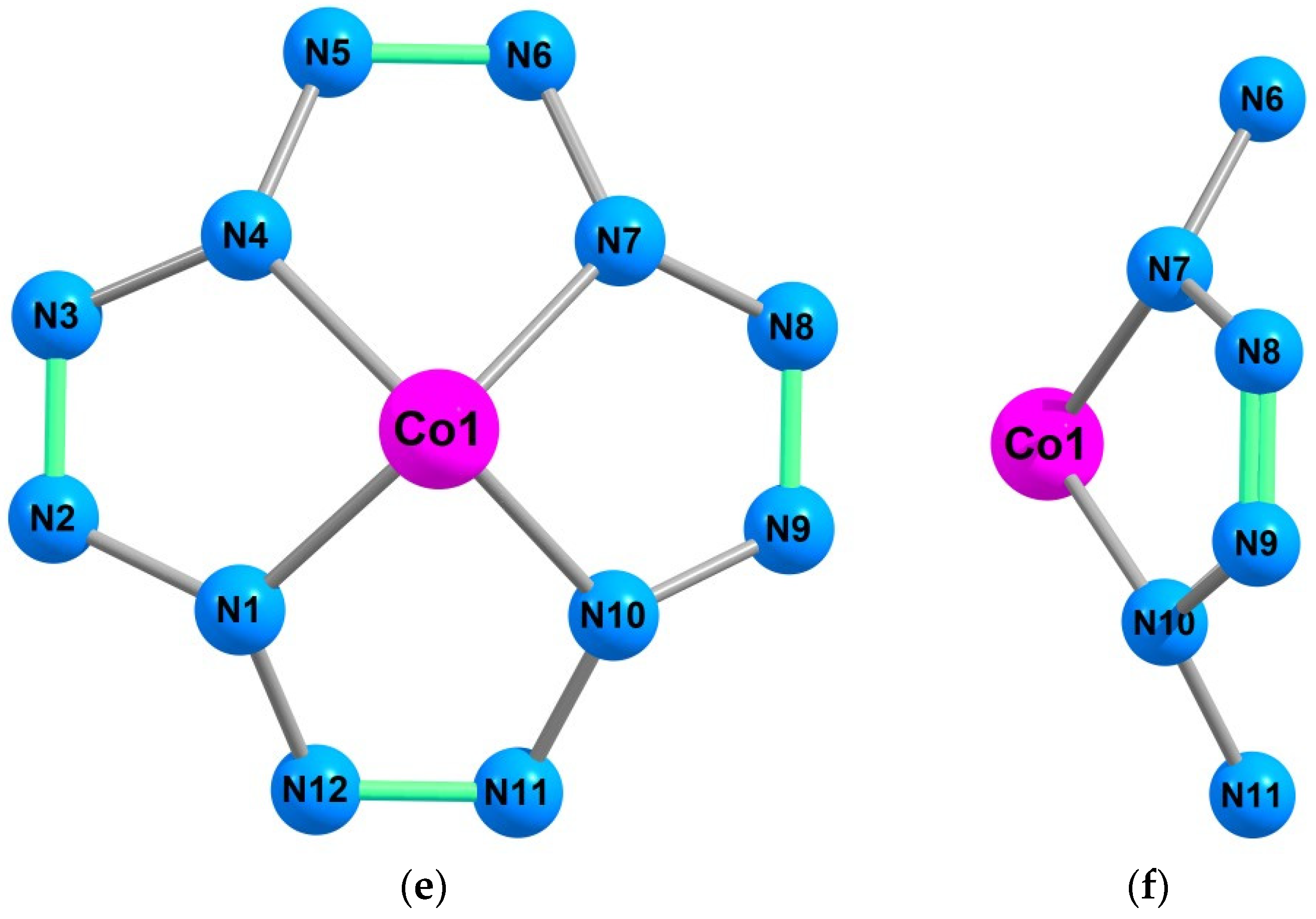
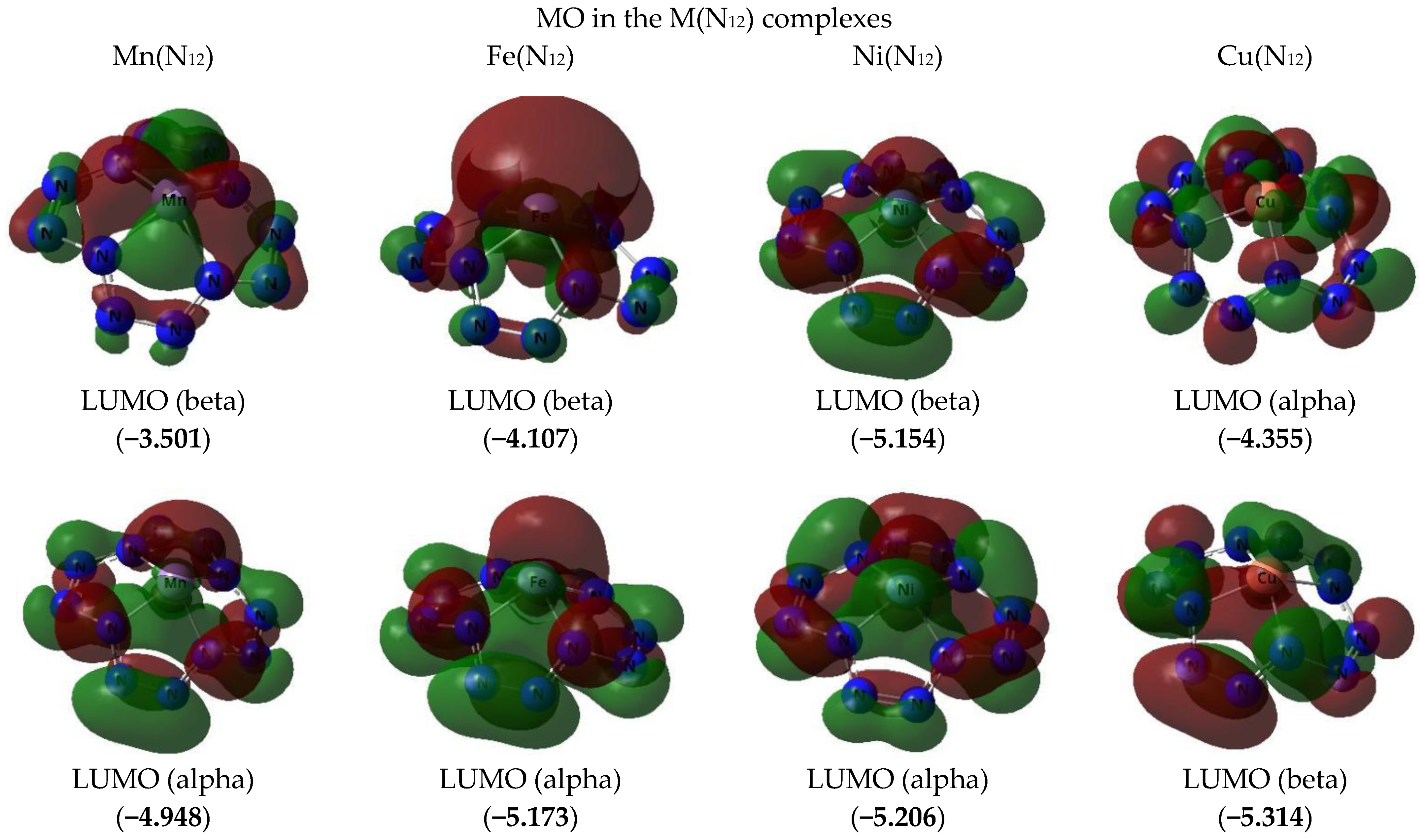
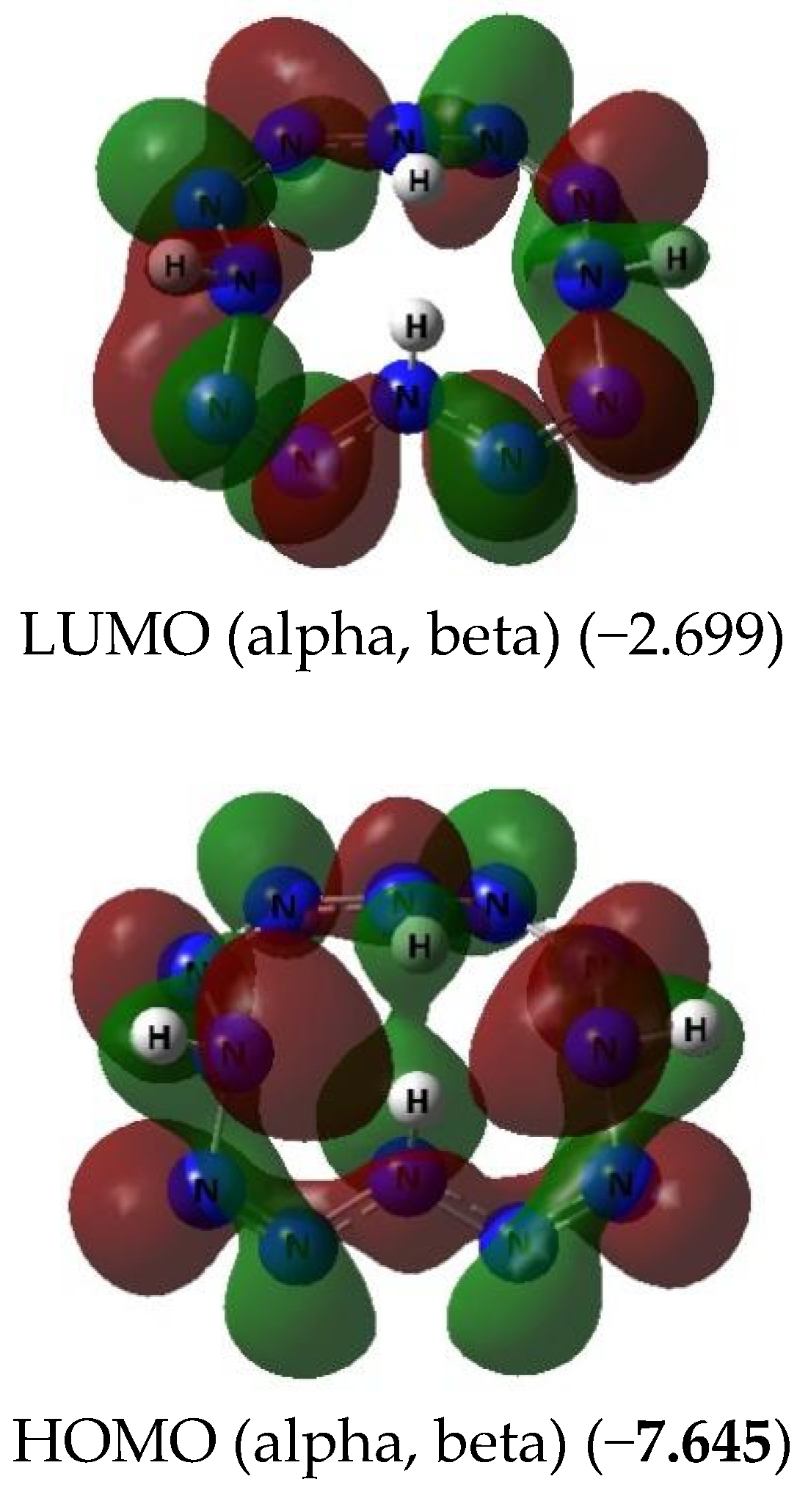
| 3d-Element (M) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Structural Parameter | Ti | V | Cr | Mn | Fe | Co | Ni | Cu | (H4N12) |
| M–N bond lengths in the MN4 chelate node, pm | |||||||||
| M1N1 | 193.5 | 188.2 | 186.3 | 191.1 | 183.7 | 181.2 | 179.6 | 186.0 | - |
| M1N4 | 193.5 | 188.2 | 186.3 | 191.1 | 182.6 | 181.2 | 179.9 | 184.2 | - |
| M1N7 | 193.5 | 188.2 | 186.3 | 190.0 | 182.6 | 181.2 | 179.6 | 184.2 | - |
| M1N10 | 193.5 | 188.2 | 186.3 | 190.0 | 183.7 | 181.2 | 179.5 | 186.0 | - |
| Nitrogen–nitrogen bond lengths in macrocycle, pm | |||||||||
| N1N2 | 138.0 | 137.9 | 139.1 | 131.7 | 145.3 | 137.4 | 140.6 | 146.3 | 148.1 |
| N2N3 | 125.2 | 125.0 | 123.8 | 129.6 | 123.4 | 124.8 | 121.3 | 123.2 | 123.4 |
| N3N4 | 138.0 | 137.9 | 139.1 | 131.7 | 137.2 | 137.4 | 151.2 | 134.5 | 135.1 |
| N4N5 | 138.0 | 137.9 | 139.1 | 145.3 | 138.5 | 137.4 | 130.2 | 139.9 | 135.1 |
| N5N6 | 125.2 | 125.0 | 123.8 | 123.7 | 124.3 | 124.8 | 131.4 | 122.5 | 123.4 |
| N6N7 | 138.0 | 137.9 | 139.1 | 136.0 | 138.5 | 137.4 | 130.2 | 139.9 | 148.1 |
| N7N8 | 138.0 | 137.9 | 139.1 | 138.8 | 137.2 | 137.4 | 151.2 | 134.5 | 149.5 |
| N8N9 | 125.2 | 125.0 | 123.8 | 124.2 | 123.4 | 124.8 | 121.3 | 123.2 | 122.8 |
| N9N10 | 138.0 | 137.9 | 139.1 | 138.7 | 145.3 | 137.4 | 140.6 | 146.3 | 136.1 |
| N10N11 | 138.0 | 137.9 | 139.1 | 136.1 | 131.5 | 137.4 | 136.1 | 131.1 | 136.0 |
| N11N12 | 125.2 | 125.0 | 123.8 | 123.7 | 130.0 | 124.8 | 125.6 | 129.8 | 122.8 |
| N12N1 | 138.0 | 137.9 | 139.1 | 145.2 | 131.5 | 137.4 | 136.1 | 131.1 | 149.5 |
| Distance from the center of the M atom to the plane formed by donor nitrogen atoms in the MN4 chelate node. pm | |||||||||
| 104.4 | 97.5 | 89.9 | 90.9 | 83.2 | 78.5 | 67.4 | 70.3 | - | |
| Bond angles in the MN4 chelate node, deg | |||||||||
| N1M1N4 | 73.1 | 74.4 | 76.6 | 77.9 | 77.8 | 79.2 | 81.9 | 81.8 | - |
| N4M1N7 | 73.1 | 74.4 | 76.6 | 75.9 | 77.6 | 79.2 | 82.3 | 81.0 | - |
| N7M1N10 | 73.1 | 74.4 | 76.6 | 75.5 | 77.8 | 79.2 | 81.9 | 81.8 | - |
| N10M1N1 | 73.1 | 74.4 | 76.6 | 75.9 | 79.3 | 79.2 | 81.6 | 82.7 | - |
| Bond angles sum (BAS), deg | 292.4 | 297.6 | 306.4 | 305.2 | 312.5 | 316.8 | 327.7 | 327.3 | - |
| Deviation from coplanarity, deg | 67.6 | 62.4 | 53.6 | 54.8 | 47.5 | 43.2 | 32.3 | 32.7 | - |
| Non-bond angles in the MN4 chelate node, deg | |||||||||
| N1N4N7 | 90.0 | 90.0 | 90.0 | 89.1 | 90.7 | 90.0 | 89.7 | 90.8 | 103.9 |
| N4N7N10 | 90.0 | 90.0 | 90.0 | 90.9 | 90.7 | 90.0 | 89.7 | 90.8 | 68.1 |
| N7N10N1 | 90.0 | 90.0 | 90.0 | 90.9 | 89.3 | 90.0 | 90.3 | 89.2 | 96.9 |
| N10N1N4 | 90.0 | 90.0 | 90.0 | 89.1 | 89.3 | 90.0 | 90.3 | 89.2 | 68.1 |
| Non-bond angles sum (NBAS), deg | 360.0 | 360.0 | 360.0 | 360.0 | 360.0 | 360.0 | 360.0 | 360.0 | 337.0 |
| Deviation from coplanarity, deg | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 23.0 |
| Bond angles in 5-membered cycles, deg | |||||||||
| M1N1N2 | 119.7 | 119.8 | 118.6 | 116.1 | 117.0 | 117.4 | 116.5 | 113.0 | - |
| N1N2N3 | 112.4 | 111.9 | 112.6 | 114.8 | 109.9 | 112.7 | 116.0 | 111.1 | 114.9 |
| N2N3N4 | 112.4 | 111.9 | 112.6 | 114.8 | 114.4 | 112.7 | 110.1 | 119.2 | 116.7 |
| N3N4M1 | 119.7 | 119.8 | 118.6 | 116.1 | 118.9 | 117.4 | 114.6 | 114.6 | - |
| M1N4N5 | 119.7 | 119.8 | 118.6 | 116.6 | 118.6 | 117.4 | 113.4 | 114.9 | - |
| N4N5N6 | 112.4 | 111.9 | 112.6 | 110.8 | 112.2 | 112.7 | 113.9 | 114.6 | 116.8 |
| N5N6N7 | 112.4 | 111.9 | 112.6 | 115.5 | 112.2 | 112.7 | 113.9 | 114.6 | 114.9 |
| N6N7M1 | 119.7 | 119.8 | 118.6 | 118.9 | 118.6 | 117.4 | 113.3 | 114.9 | - |
| M1N7N8 | 119.7 | 119.8 | 118.6 | 118.5 | 118.9 | 117.4 | 114.6 | 114.6 | - |
| N7N8N9 | 112.4 | 111.9 | 112.6 | 113.0 | 114.4 | 112.7 | 110.1 | 119.2 | 116.4 |
| N8N9N10 | 112.4 | 111.9 | 112.6 | 113.0 | 109.9 | 112.7 | 116.0 | 111.0 | 120.9 |
| N9N10M1 | 119.7 | 119.8 | 118.6 | 118.5 | 117.0 | 117.4 | 116.6 | 113.0 | - |
| M1N10N11 | 119.7 | 119.8 | 118.6 | 118.9 | 116.8 | 117.4 | 115.3 | 111.3 | - |
| N10N11N12 | 112.4 | 111.9 | 112.6 | 115.4 | 113.4 | 112.7 | 113.6 | 116.3 | 120.9 |
| N11N12N1 | 112.4 | 111.9 | 112.6 | 110.8 | 113.4 | 112.7 | 113.6 | 116.3 | 116.4 |
| N12N1M1 | 119.7 | 119.8 | 118.6 | 116.6 | 116.8 | 117.4 | 115.3 | 111.3 | - |
| Deviation of macrocycle (N12) from coplanarity, deg | 80.4 | 76.4 | 85.2 | 97.8 | 74.0 | 75.6 | 93.6 | 103.0 | 137.7 |
| The difference between macrocycle deviation (N12) in (H4N12) and in M(N12), deg | 57.3 | 61.3 | 52.5 | 39.9 | 63.7 | 52.1 | 44.1 | 34.7 | - |
Table 2.
Electric dipole moments (μ, Debye) of M(N12) compounds calculated by DFT M06/TZVP method.
| M | Ti | V | Cr | Mn | Fe | Co | Ni | Cu | (H4) |
|---|---|---|---|---|---|---|---|---|---|
| μ | 8.43 | 7.30 | 4.81 | 5.40 | 4.65 | 4.00 | 2.92 | 3.11 | 4.75 |
Table 3.
NBO analysis data for M(N12) and H4(N12) calculated by DFT M06/TZVP method.
| Effective Charge on Atom, in Units of Electron Charge (ē) | <S**2> | |||||||
|---|---|---|---|---|---|---|---|---|
| M | M1 | N1 (N4) | N2 (N6) | N3 (N5) | N7 (N10) | N8 (N12) | N9 (N11) | |
| Ti | 1.1781 | −0.3028 | 0.0042 | 0.0042 | −0.3028 | 0.0041 | 0.0042 | 0 |
| (−0.3028) | −0.0042 | −0.0042 | (−0.3028) | −0.0041 | −0.0042 | |||
| V | 0.7623 | −0.2071 | 0.0083 | 0.0083 | −0.2071 | 0.0083 | 0.0083 | 0.7532 |
| (−0.2071) | −0.0083 | −0.0083 | (−0.2071) | −0.0083 | −0.0083 | |||
| Cr | 0.7069 | −0.2275 | 0.0253 | 0.0254 | −0.2275 | 0.0255 | 0.0254 | 2.2481 |
| (−0.2275) | −0.0253 | −0.0254 | (−0.2275) | −0.0255 | −0.0254 | |||
| Mn | 0.8408 | −0.1900 | 0.0002 | 0.0002 | −0.2975 | 0.0118 | 0.0121 | 3.9244 |
| (−0.1899) | −0.0629 | (−0.0081) | (−0.2975) | (−0.0078) | −0.0629 | |||
| Fe | 0.5588 | −0.1263 | 0 | 0.0636 | −0.2315 | 0.0636 | 0 | 2.0654 |
| (−0.2316) | −0.0102 | −0.0101 | (−0.1263) | −0.0045 | −0.0045 | |||
| Co | 0.5406 | −0.1783 | 0.0216 | 0.0216 | −0.1783 | 0.0216 | 0.0217 | 3.7832 |
| (−0.1783) | −0.0216 | −0.0216 | (−0.1783) | −0.0216 | −0.0217 | |||
| Ni | 0.4074 | −0.1928 | 0.0748 | 0.0427 | −0.1190 | 0.0427 | 0.0748 | 0.0364 |
| (−0.1190) | (−0.0096) | (−0.0095) | (−0.1928) | −0.0002 | −0.0002 | |||
| Cu | 0.6256 | −0.1576 | −0.0131 | 0.0729 | −0.2579 | 0.073 | −0.0131 | 0.7751 |
| (−0.2581) | −0.0361 | −0.0361 | (−0.1577) | −0.0068 | −0.0729 | |||
| (H4) | - | −0.4932 | −0.0262 | 0.0543 | −0.4934 | −0.0316 | 0.058 | 0 |
| (−0.3478) | (−0.0263) | −0.0544 | (−0.3109) | (−0.0319) | −0.058 | |||
The symbol (**) in this case means raising to the power of 2 (i.e., squaring).
Table 4.
Standard thermodynamic parameters of formation (H0f,298, S0f,298 and G0f,298) for various M(N12) calculated by DFT M06/TZVP method.
Table 4.
Standard thermodynamic parameters of formation (H0f,298, S0f,298 and G0f,298) for various M(N12) calculated by DFT M06/TZVP method.
| M | Standard Thermodynamic Parameters of Formation | ||
|---|---|---|---|
| H0f,298, kJ/mol | S0f,298, J/mol∙K | G0f,298, kJ/mol | |
| Ti | 1562.3 | 398.3 | 1792.8 |
| V | 1662.2 | 399.1 | 1890.4 |
| Cr | 1833.8 | 403.2 | 2061.7 |
| Mn | 1571.7 | 404.1 | 1801.0 |
| Fe | 1744.8 | 403.4 | 1972.9 |
| Co | 1823.6 | 404.2 | 2052.2 |
| Ni | 1933.7 | 412.6 | 2159.7 |
| Cu | 2033.9 | 405.0 | 2263.3 |
| H4 | 1705.9 | 399.3 | 2004.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
MDPI and ACS Style
Mikhailov, O.V.; Chachkov, D.V. Twelve-Nitrogen-Atom Cyclic Structure Stabilized by 3d-Element Atoms: Quantum Chemical Modeling. Int. J. Mol. Sci. 2022, 23, 6560. https://doi.org/10.3390/ijms23126560
AMA Style
Mikhailov OV, Chachkov DV. Twelve-Nitrogen-Atom Cyclic Structure Stabilized by 3d-Element Atoms: Quantum Chemical Modeling. International Journal of Molecular Sciences. 2022; 23(12):6560. https://doi.org/10.3390/ijms23126560
Chicago/Turabian StyleMikhailov, Oleg V., and Denis V. Chachkov. 2022. "Twelve-Nitrogen-Atom Cyclic Structure Stabilized by 3d-Element Atoms: Quantum Chemical Modeling" International Journal of Molecular Sciences 23, no. 12: 6560. https://doi.org/10.3390/ijms23126560
APA StyleMikhailov, O. V., & Chachkov, D. V. (2022). Twelve-Nitrogen-Atom Cyclic Structure Stabilized by 3d-Element Atoms: Quantum Chemical Modeling. International Journal of Molecular Sciences, 23(12), 6560. https://doi.org/10.3390/ijms23126560
Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.
