Decoding the Effect of Hydrostatic Pressure on TRPV1 Lower-Gate Conformation by Molecular-Dynamics Simulation
Abstract
:1. Introduction
2. Materials and Methods
2.1. MD Simulation Setup
2.2. Root Mean Square Deviation (RMSD) Analysis
2.3. Radius of Gyration Analysis
2.4. Radius Analysis
2.5. Statistical Analysis
3. Results
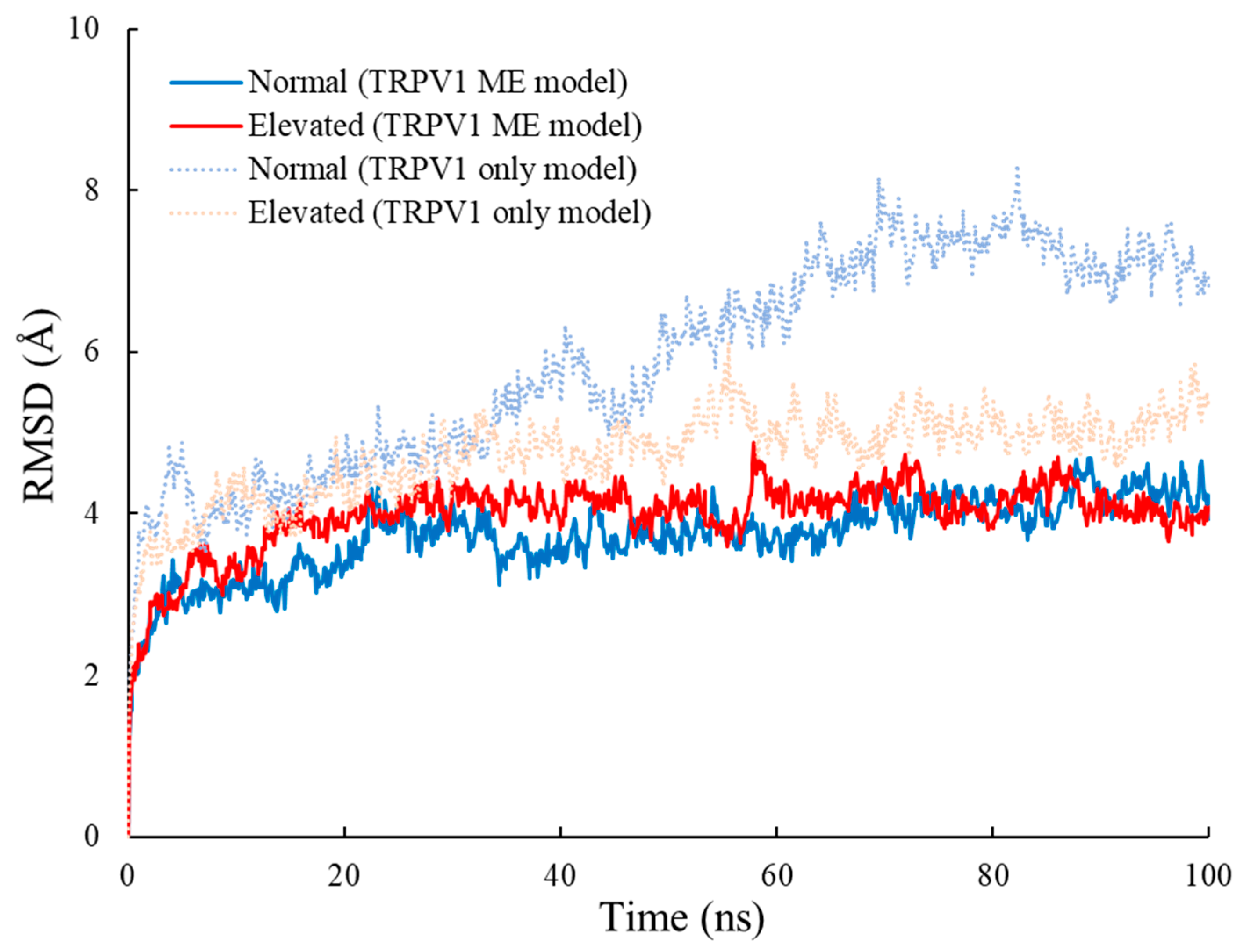
3.1. RMSD
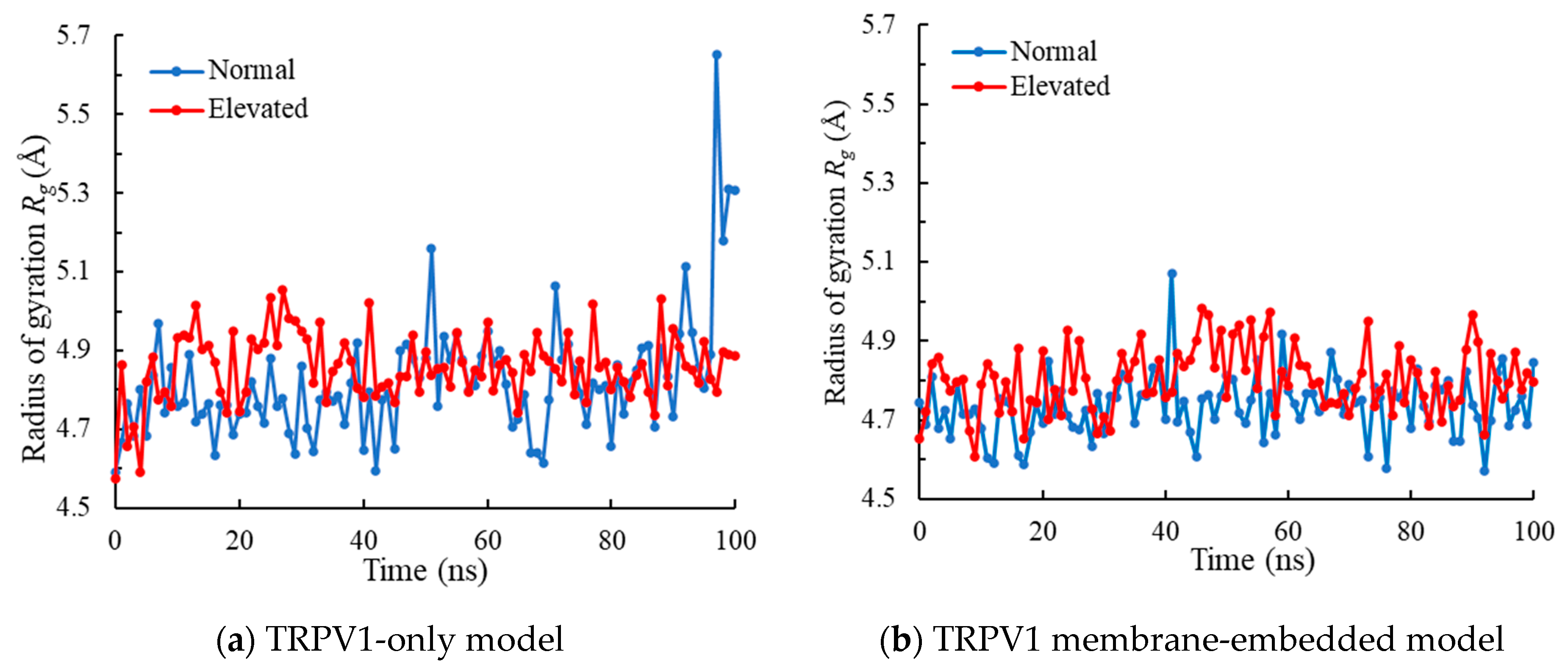
3.2. Radius of Gyration
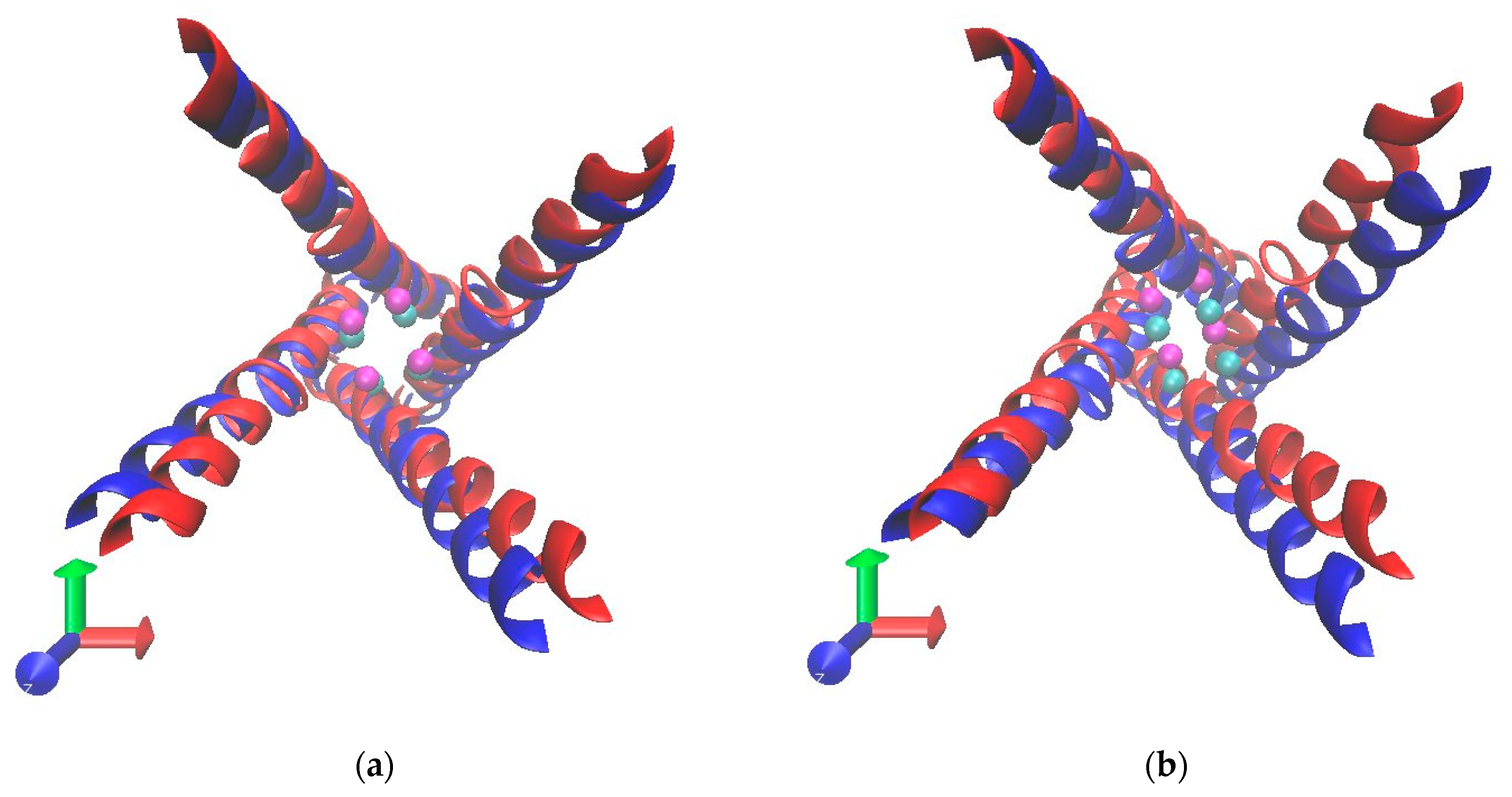
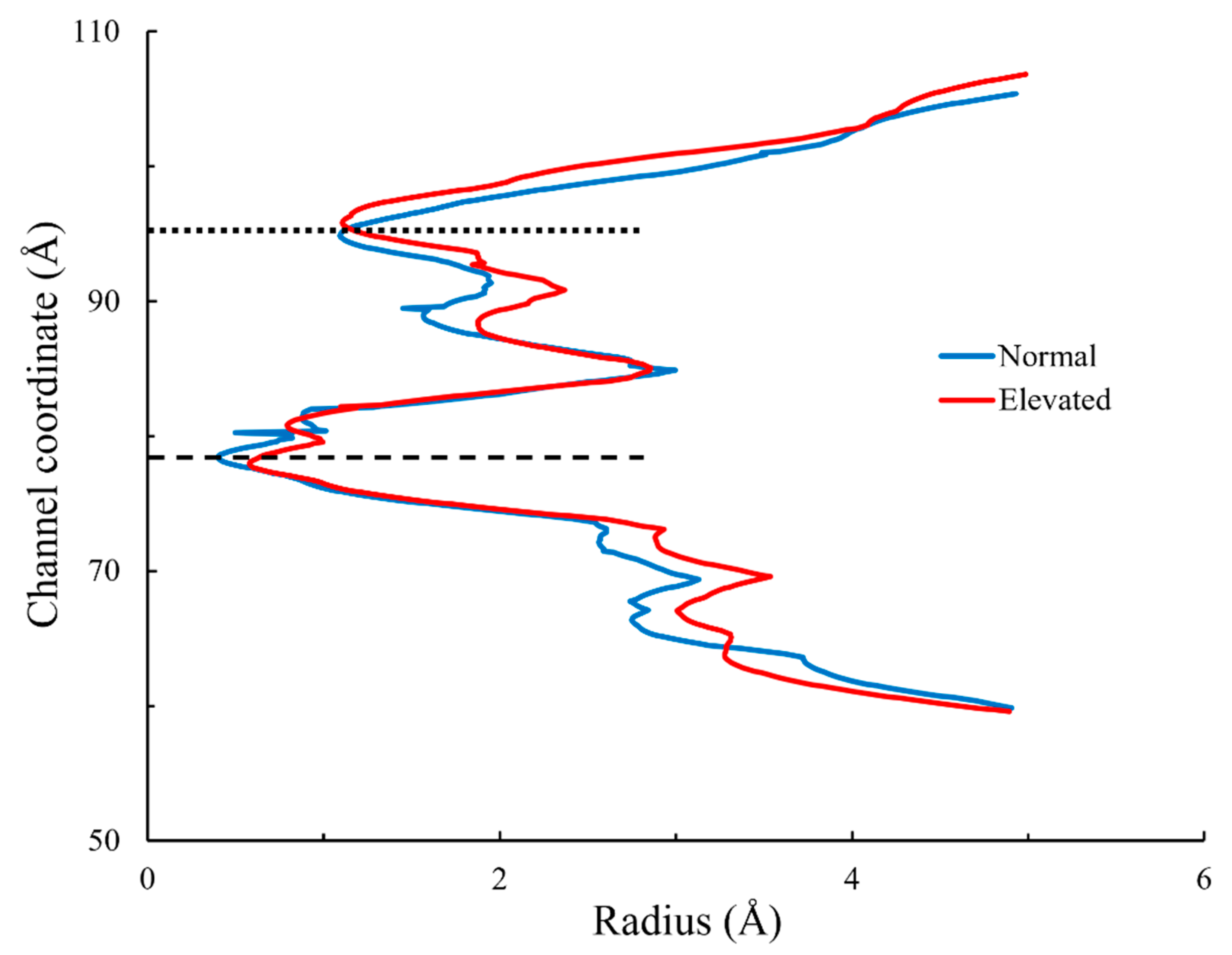
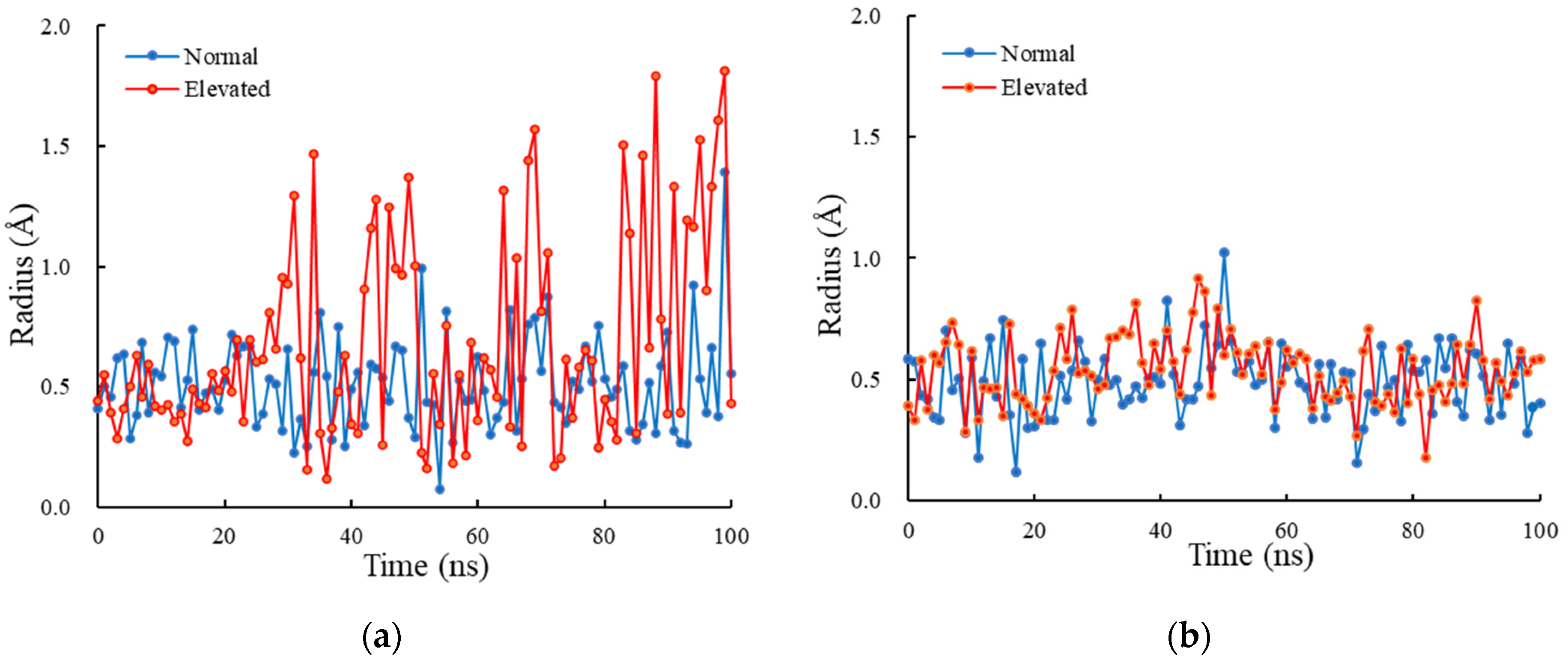
3.3. Radius of Lower Gate
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Machiele, R.; Motlagh, M.; Patel, B.C. Intraocular pressure. In StatPearls; StatPearls Publishing: Treasure Island, FL, USA, 2021. [Google Scholar]
- Tsai, J.C. Best of gleams. Gleams 2008. Available online: http://glaucoma.org/high-eye-pressure-and-glaucoma/ (accessed on 8 February 2022).
- Wang, Y.X.; Xu, L.; Wei, W.B.; Jonas, J.B. Intraocular pressure and its normal range adjusted for ocular and systemic parameters. The Beijing Eye Study 2011. PLoS ONE 2018, 13, e0196926. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Peichl, L. Retinal ganglion cells. In Encyclopedia of Neuroscience; Binder, M.D., Hirokawa, N., Windhorst, U., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 3507–3513. [Google Scholar]
- Chauhan, B.C.; Pan, J.; Archibald, M.L.; LeVatte, T.L.; Kelly, M.E.; Tremblay, F. Effect of intraocular pressure on optic disc topography, electroretinography, and axonal loss in a chronic pressure-induced rat model of optic nerve damage. Investig. Ophthalmol. Vis. Sci. 2002, 43, 2969–2976. [Google Scholar] [PubMed]
- Guo, L.; Moss, S.E.; Alexander, R.A.; Ali, R.R.; Fitzke, F.W.; Cordeiro, M.F. Retinal ganglion cell apoptosis in glaucoma is related to intraocular pressure and IOP-induced effects on extracellular matrix. Investig. Ophthalmol. Vis. Sci. 2005, 46, 175–182. [Google Scholar] [CrossRef]
- Agar, A.; Li, S.; Agarwal, N.; Coroneo, M.T.; Hill, M.A. Retinal ganglion cell line apoptosis induced by hydrostatic pressure. Brain Res. 2006, 1086, 191–200. [Google Scholar] [CrossRef]
- Sappington, R.M.; Sidorova, T.; Long, D.J.; Calkins, D.J. TRPV1: Contribution to retinal ganglion cell apoptosis and increased intracellular Ca2+ with exposure to hydrostatic pressure. Investig. Ophthalmol. Vis. Sci. 2009, 50, 717–728. [Google Scholar] [CrossRef] [Green Version]
- Yang, F.; Zheng, J. Understand spiciness: Mechanism of TRPV1 channel activation by capsaicin. Protein Cell 2017, 8, 169–177. [Google Scholar] [CrossRef] [Green Version]
- Csekő, K.; Beckers, B.; Keszthelyi, D.; Helyes, Z. Role of TRPV1 and TRPA1 ion channels in inflammatory bowel diseases: Potential therapeutic targets? Pharmaceuticals 2019, 12, 48. [Google Scholar] [CrossRef] [Green Version]
- Bujak, J.K.; Kosmala, D.; Szopa, I.M.; Majchrzak, K.; Bednarczyk, P. Inflammation, cancer and immunity-implication of TRPV1 channel. Front. Oncol. 2019, 9, 1087. [Google Scholar] [CrossRef]
- Liedtke, W. TRPV channels’ role in osmotransduction and mechanotransduction. Handb. Exp. Pharmacol. 2007, 179, 473–487. [Google Scholar]
- Jin, M.; Berrout, J.; O’Neil, R.G. Regulation of TRP channels by osmomechanical stress. In TRP Channels; Zhu, M.X., Ed.; CRC Press/Taylor & Francis: Boca Raton, FL, USA, 2011. [Google Scholar]
- Caterina, M.J.; Schumacher, M.A.; Tominaga, M.; Rosen, T.A.; Levine, J.D.; Julius, D. The capsaicin receptor: A heat-activated ion channel in the pain pathway. Nature 1997, 389, 816–824. [Google Scholar] [CrossRef] [PubMed]
- Owsianik, G.; Talavera, K.; Voets, T.; Nilius, B. Permeation and selectivity of TRP channels. Annu. Rev. Physiol. 2006, 68, 685–717. [Google Scholar] [CrossRef] [PubMed]
- Yin, J.; Kuebler, W.M. Mechanotransduction by TRP channels: General concepts and specific role in the vasculature. Cell Biochem. Biophys. 2010, 56, 1. [Google Scholar] [CrossRef] [PubMed]
- Pinton, P.; Giorgi, C.; Siviero, R.; Zecchini, E.; Rizzuto, R. Calcium and apoptosis: ER-mitochondria Ca2+ transfer in the control of apoptosis. Oncogene 2008, 27, 6407–6418. [Google Scholar] [CrossRef] [Green Version]
- Wegierski, T.; Steffl, D.; Kopp, C.; Tauber, R.; Buchholz, B.; Nitschke, R.; Kuehn, E.W.; Walz, G.; Köttgen, M. TRPP2 channels regulate apoptosis through the Ca2+ concentration in the endoplasmic reticulum. EMBO J. 2009, 28, 490–499. [Google Scholar] [CrossRef] [Green Version]
- Wen, H.; Qin, F.; Zheng, W. Toward elucidating the heat activation mechanism of the TRPV1 channel gating by molecular dynamics simulation. Proteins 2016, 84, 1938–1949. [Google Scholar] [CrossRef] [Green Version]
- Wen, H.; Zheng, W. Decrypting the heat activation mechanism of TRPV1 channel by molecular dynamics simulation. Biophys. J. 2018, 114, 40–52. [Google Scholar] [CrossRef] [Green Version]
- Van Der Spoel, D.; Lindahl, E.; Hess, B.; Groenhof, G.; Mark, A.E.; Berendsen, H.J.C. GROMACS: Fast, flexible, and free. J. Comput. Chem. 2005, 26, 1701–1718. [Google Scholar] [CrossRef]
- MacKerell, A.D., Jr.; Banavali, N.K. All-atom empirical force field for nucleic acids: II. Application to molecular dynamics simulations of DNA and RNA in solution. J. Comput. Chem. 2000, 21, 105–120. [Google Scholar] [CrossRef]
- Berman, H.M.; Westbrook, J.; Feng, Z.; Gilliland, G.; Bhat, T.N.; Weissig, H.; Shindyalov, I.N.; Bourne, P.E. The protein data bank. Nucleic Acids Res. 2000, 28, 235–242. [Google Scholar] [CrossRef] [Green Version]
- Guex, N.; Peitsch, M.C. SWISS-MODEL and the Swiss-PdbViewer: An environment for comparative protein modeling. Electrophoresis 1997, 18, 2714–2723. [Google Scholar] [CrossRef] [PubMed]
- Lomize, M.A.; Lomize, A.L.; Pogozheva, I.D.; Mosberg, H.I. OPM: Orientations of proteins in membranes database. Bioinfomatics 2006, 22, 623–625. [Google Scholar] [CrossRef] [PubMed]
- Jo, S.; Lim, J.B.; Klauda, J.B.; Im, W. CHARMM-GUI membrane builder for mixed bilayers and its application to yeast membranes. Biophys. J. 2009, 97, 50–58. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lee, J.; Cheng, X.; Swails, J.M.; Yeom, M.S.; Eastman, P.K.; Lemkul, J.A.; Wei, S.; Buckner, J.; Jeong, J.C.; Qi, Y.; et al. CHARMM-GUI input generator for NAMD, GROMACS, AMBER, OpenMM, and CHARMM/OpenMM simulations using the CHARMM36 additive force field. J. Chem. Theory Comput. 2016, 12, 405–413. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Andersen, H.C. Molecular dynamics simulations at constant pressure and/or temperature. J. Chem. Phys. 1980, 72, 2384–2393. [Google Scholar] [CrossRef] [Green Version]
- Martyna, G.J.; Hughes, A.; Tuckerman, M.E. Molecular dynamics algorithms for path integrals at constant pressure. J. Chem. Phys. 1999, 110, 3275–3290. [Google Scholar] [CrossRef]
- Parrinello, M.; Rahman, A. Polymorphic transitions in single crystals: A new molecular dynamics method. J. Appl. Phys. 1981, 52, 7182–7190. [Google Scholar] [CrossRef]
- Darden, T.; York, D.; Pedersen, L. Particle mesh Ewald: An N⋅log(N) method for Ewald sums in large systems. J. Chem. Phys. 1993, 98, 10089–10092. [Google Scholar] [CrossRef] [Green Version]
- Root Mean Square Deviations in Structure. Available online: https://manual.gromacs.org/current/reference-manual/analysis/rmsd.html#root-mean-square-deviations-in-structure (accessed on 27 December 2021).
- Smart, O.S.; Neduvelil, J.G.; Wang, X.; Wallace, B.A.; Sansom, M.S.P. HOLE: A program for the analysis of the pore dimensions of ion channel structural models. J. Mol. Graphics 1996, 14, 354–360. [Google Scholar] [CrossRef]
- Liao, M.; Cao, E.; Julius, D.; Cheng, Y. Structure of the TRPV1 ion channel determined by electron cryo-microscopy. Nature 2013, 504, 107–112. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.R.; Makhatadze, G.I. Molecular determinant of the effects of hydrostatic pressure on protein folding stability. Nat. Commun. 2017, 8, 14561. [Google Scholar] [CrossRef] [PubMed]
- Gross, M.; Jaenicke, R. Proteins under pressure. Eur. J. Biochem. 1994, 221, 617–630. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, M.C.; Crehuet, R.; Lindorff-Larsen, K. Computing, analyzing, and comparing the radius of gyration and hydrodynamic radius in conformational ensembles of intrinsically disordered proteins. Methods Mol. Biol. 2020, 2141, 429–445. [Google Scholar]
- Baig, M.H.; Sudhakar, D.R.; Kalaiarasan, P.; Subbarao, N.; Wadhawa, G.; Lohani, M.; Khan, M.K.A.; Khan, A.U. Insight into the effect of inhibitor resistant S130G mutant on physico-chemical properties of SHV type beta-lactamase: A molecular dynamics study. PLoS ONE 2014, 9, e112456. [Google Scholar] [CrossRef]
- Lobanov, M.; Bogatyreva, N.S.; Galzitskaia, O.V. Radius of gyration is indicator of compactness of protein structure. Mol. Biol. 2008, 42, 701–706. [Google Scholar] [CrossRef]
- Cao, E.; Liao, M.; Cheng, Y.; Julius, D. TRPV1 structures in distinct conformations reveal activation mechanisms. Nature 2013, 504, 113–118. [Google Scholar] [CrossRef]
- Zheng, W.; Qin, F. A combined coarse-grained and all-atom simulation of TRPV1 channel gating and heat activation. J. Gen. Physiol. 2015, 145, 443–456. [Google Scholar] [CrossRef] [Green Version]
- Huffer, K.E.; Aleksandrova, A.A.; Jara-Oseguera, A.; Forrest, L.R.; Swartz, K.J. Global alignment and assessment of TRP channel transmembrane domain structures to explore functional mechanisms. eLife 2020, 9, e58660. [Google Scholar] [CrossRef]
- Jara-Oseguera, A.; Bae, C.; Swartz, K.J. An external sodium ion binding site controls allosteric gating in TRPV1 channels. eLife 2016, 5, e13356. [Google Scholar] [CrossRef] [Green Version]
- Lengyel, M.; Enyedi, P.; Czirjak, G. Negative influence by the force: Mechanically induced hyperpolarization via K2P background potassium channels. Int. J. Mol. Sci. 2021, 22, 9062. [Google Scholar] [CrossRef] [PubMed]
- Jóhanna, Á.; Martin, C. Eukaryotic mechanosensitive channels. Annu. Rev. Biophys. 2010, 39, 111–137. [Google Scholar]
- Kumar, C.V.; Swetha, R.G.; Anbarasu, A.; Ramaiah, S. Computational analysis reveals the association of threonine 118 methionine mutation in PMP22 resulting in CMT-1A. Adv. Bioinform. 2014, 2014, 502618. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zamri, M.H.B.; Ujihara, Y.; Nakamura, M.; Mofrad, M.R.K.; Sugita, S. Decoding the Effect of Hydrostatic Pressure on TRPV1 Lower-Gate Conformation by Molecular-Dynamics Simulation. Int. J. Mol. Sci. 2022, 23, 7366. https://doi.org/10.3390/ijms23137366
Zamri MHB, Ujihara Y, Nakamura M, Mofrad MRK, Sugita S. Decoding the Effect of Hydrostatic Pressure on TRPV1 Lower-Gate Conformation by Molecular-Dynamics Simulation. International Journal of Molecular Sciences. 2022; 23(13):7366. https://doi.org/10.3390/ijms23137366
Chicago/Turabian StyleZamri, Muhammad Harith Bin, Yoshihiro Ujihara, Masanori Nakamura, Mohammad R. K. Mofrad, and Shukei Sugita. 2022. "Decoding the Effect of Hydrostatic Pressure on TRPV1 Lower-Gate Conformation by Molecular-Dynamics Simulation" International Journal of Molecular Sciences 23, no. 13: 7366. https://doi.org/10.3390/ijms23137366
APA StyleZamri, M. H. B., Ujihara, Y., Nakamura, M., Mofrad, M. R. K., & Sugita, S. (2022). Decoding the Effect of Hydrostatic Pressure on TRPV1 Lower-Gate Conformation by Molecular-Dynamics Simulation. International Journal of Molecular Sciences, 23(13), 7366. https://doi.org/10.3390/ijms23137366





