Orientation Polarization Spectroscopy—Toward an Atomistic Understanding of Dielectric Relaxation Processes
Abstract
:1. Introduction
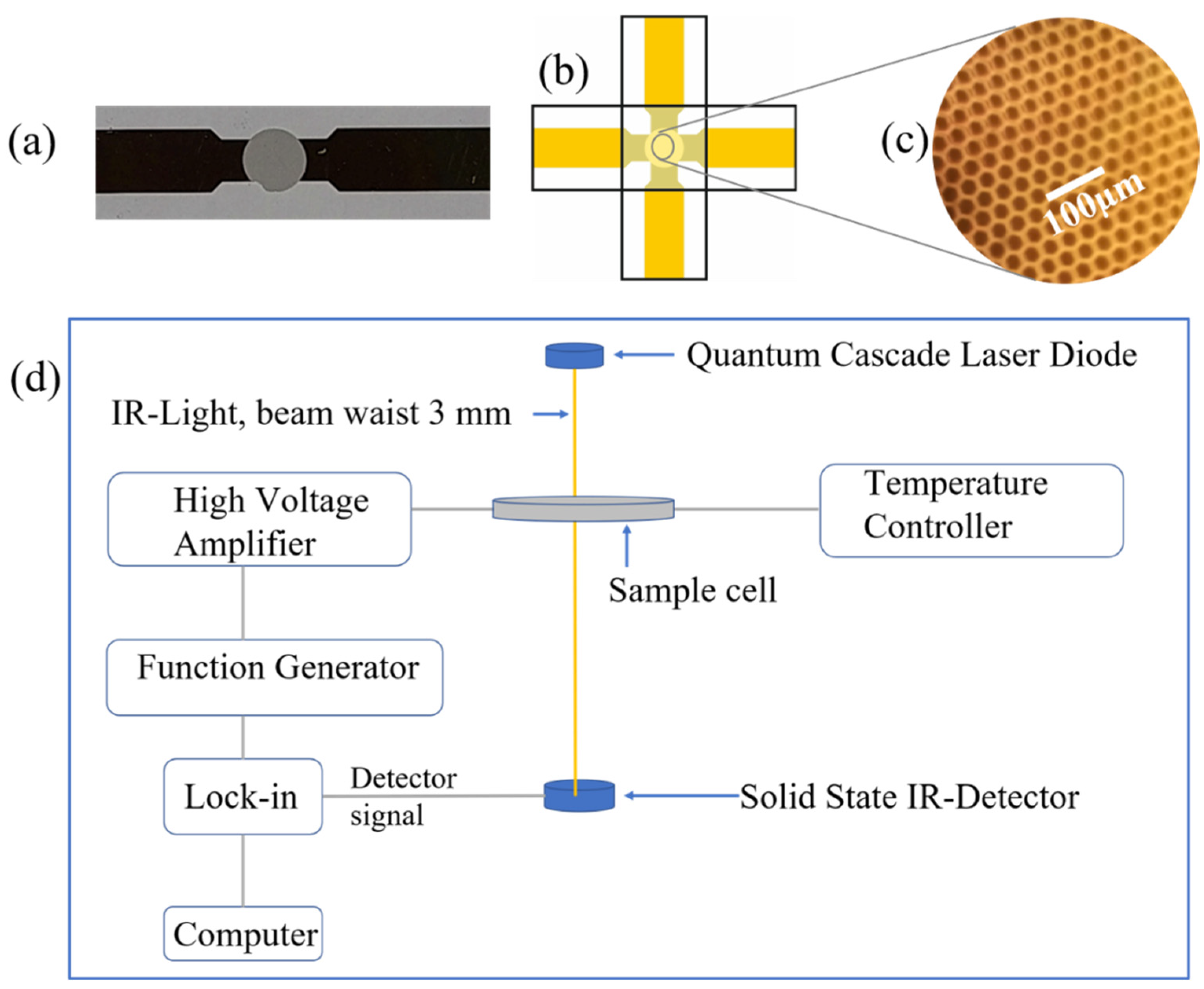
2. Theory of Operation for IR-Based Orientation Polarization Spectroscopy
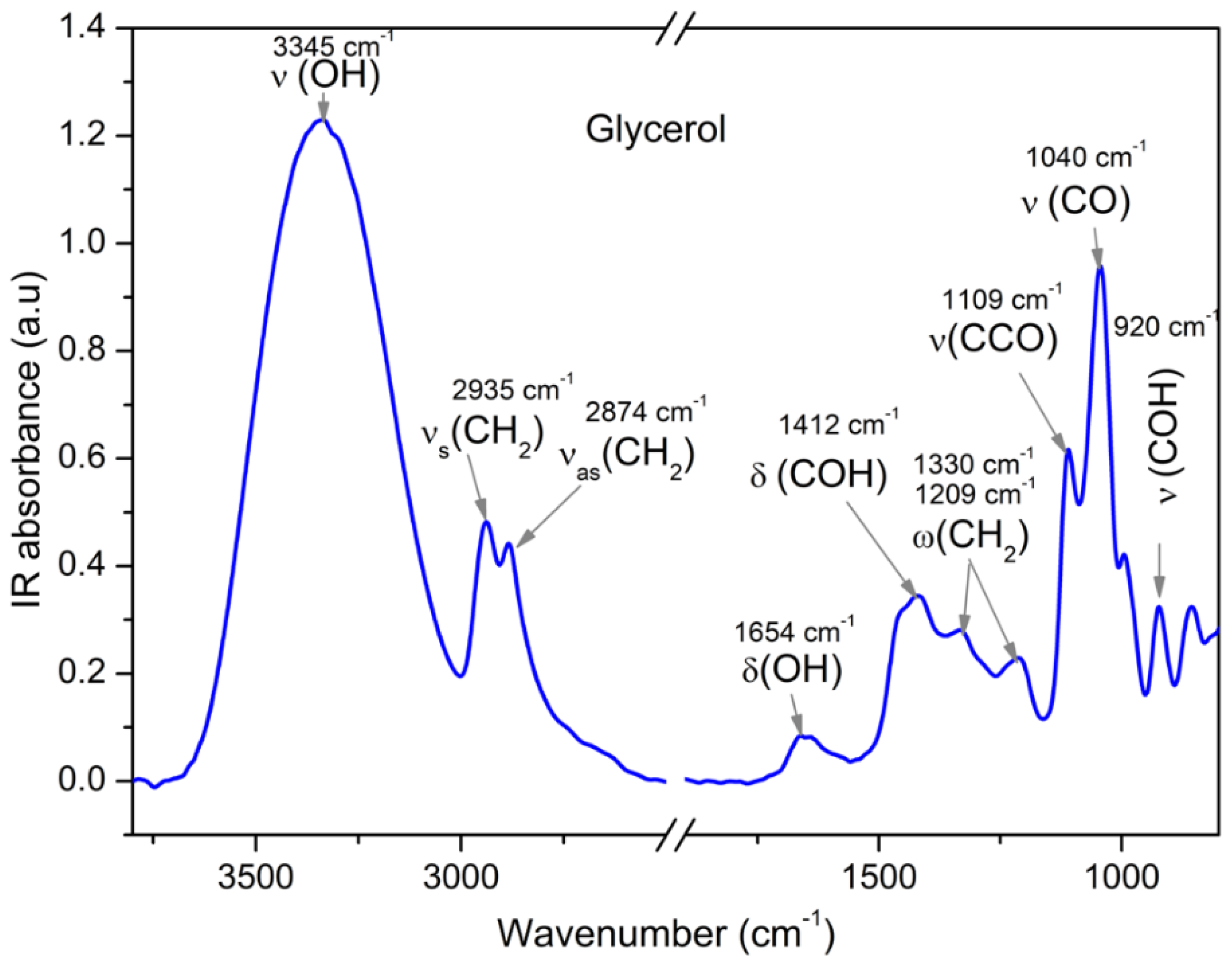
3. Experimental Section
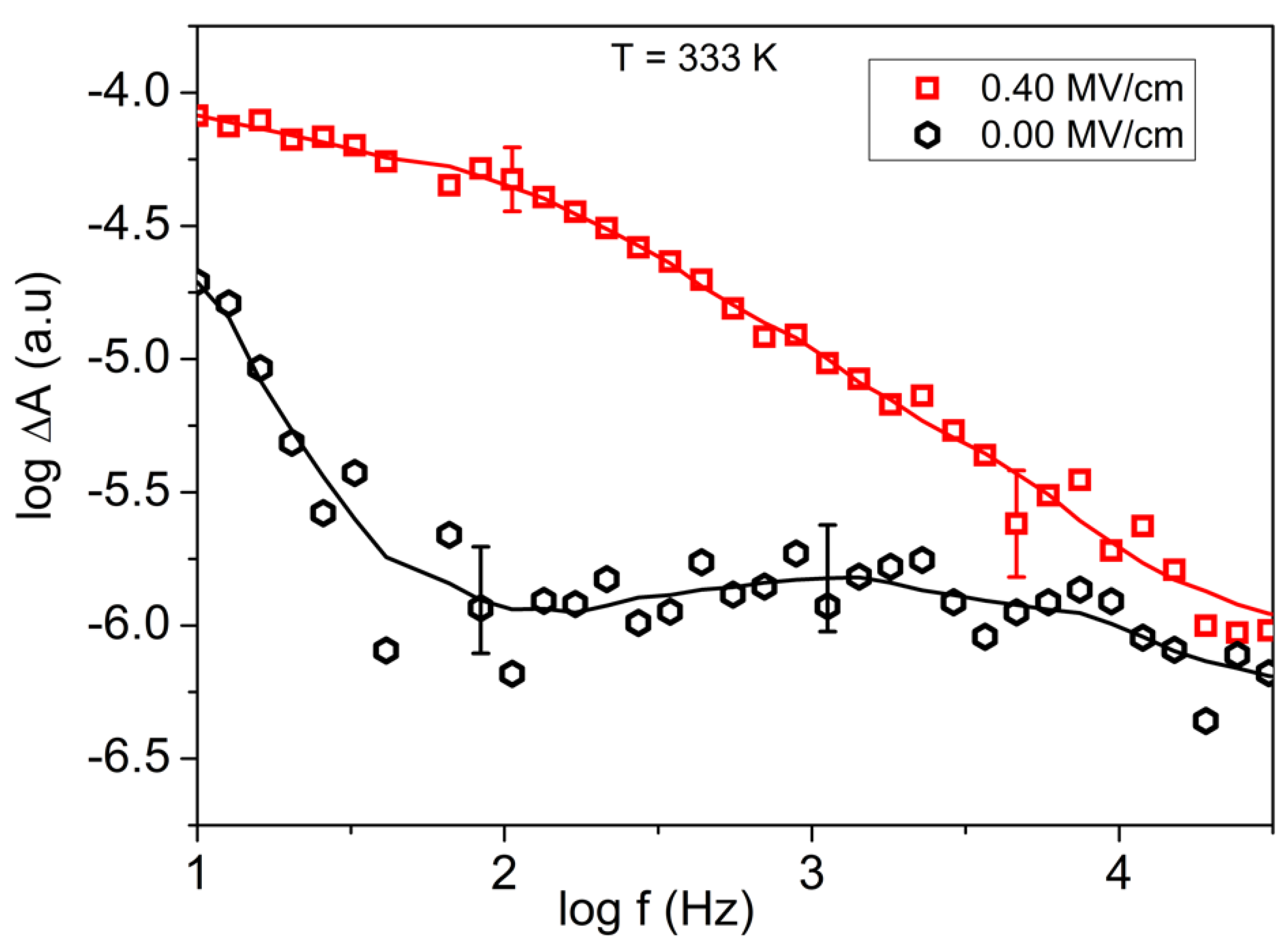
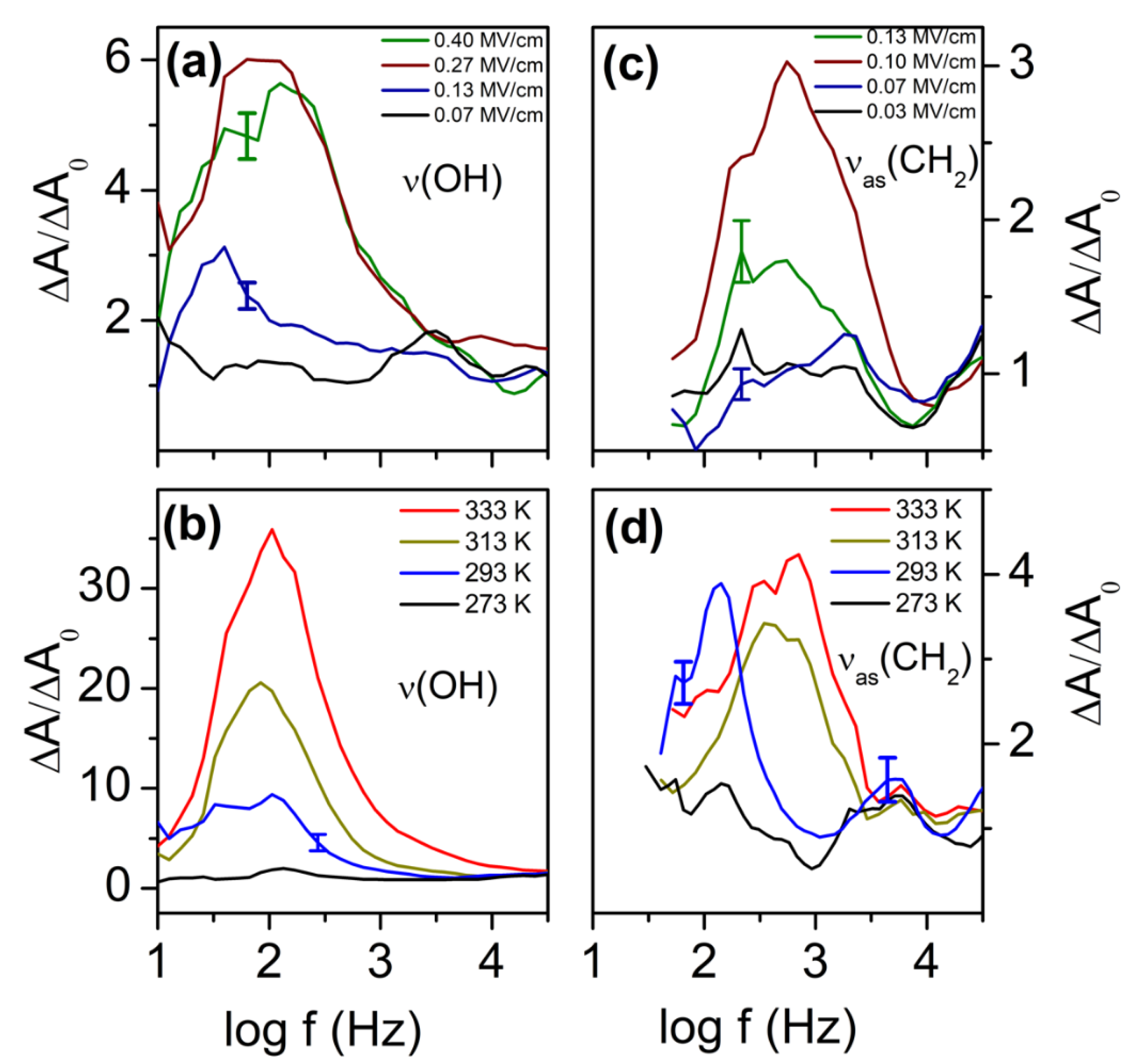
4. Results and Discussion
5. Perspectives
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Einstein, A. Zur Theorie Der Brownschen Bewegung. Ann. Der Phys. 1906, 324, 371–381. [Google Scholar] [CrossRef] [Green Version]
- Debye, P. Einige Resultate Einer Kinetischen Theorie Der Isolatoren. Phys. Z 1912, 13, 97. [Google Scholar]
- Debye, P. Zur Theorie Der Anomalen Dispersion im Gebiete der langwelligen elektrischen Strahlung. Verhandl. Deut. Phys. Ges. 1913, 15, 777. [Google Scholar]
- Debye, P.J.W. Polare Molekeln (Polar Molecules); Verlag von S. Hirzel: Leipzig, Germany, 1929. [Google Scholar]
- Chelli, R.; Procacci, P.; Cardini, G.; Valle, R.G.D.; Califano, S. Glycerol Condensed Phases Part I. A Molecular Dynamics Study. Phys. Chem. Chem. Phys. 1999, 1, 871–877. [Google Scholar] [CrossRef]
- Gabriel, J.P.; Tress, M.; Kossack, W.; Popp, L.; Kremer, F. Molecular Heterogeneities in the Thermal Expansivity of Polyalcohols. J. Chem. Phys. 2021, 154, 024503. [Google Scholar] [CrossRef] [PubMed]
- Schönhals, A.; Kremer, F. Broadband Dielectric Measurement Techniques (10−6 Hz to 1012 Hz). In Broadband Dielectric Spectroscopy; Kremer, F., Schönhals, A., Eds.; Springer: Heidelberg, Germany, 2003; pp. 35–57. ISBN 978-3-642-56120-7. [Google Scholar]
- Kremer, F.; Loidl, A. The Scaling of Relaxation Processes—Revisited. In The Scaling of Relaxation Processes; Kremer, F., Loidl, A., Eds.; Advances in Dielectrics; Springer International Publishing: Cham, Switzerland, 2018; pp. 1–21. ISBN 978-3-319-72706-6. [Google Scholar]
- Grzybowski, A.; Paluch, M. Universality of Density Scaling. In The Scaling of Relaxation Processes; Kremer, F., Loidl, A., Eds.; Advances in Dielectrics; Springer International Publishing: Cham, Switzerland, 2018; pp. 77–119. ISBN 978-3-319-72706-6. [Google Scholar]
- Win, K.Z.; Menon, N. Glass Transition of Glycerol in the Volume-Temperature Plane. Phys. Rev. E 2006, 73, 040501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Grzybowski, A.; Grzybowska, K.; Zioło, J.; Paluch, M. Correlations between Isobaric and Isochoric Fragilities and Thermodynamical Scaling Exponent for Glass-Forming Liquids. Phys. Rev. E 2006, 74, 041503. [Google Scholar] [CrossRef] [PubMed]
- Pawlus, S.; Grzybowski, A.; Kołodziej, S.; Wikarek, M.; Dzida, M.; Góralski, P.; Bair, S.; Paluch, M. Density Scaling Based Detection of Thermodynamic Regions of Complex Intermolecular Interactions Characterizing Supramolecular Structures. Sci. Rep. 2020, 10, 9316. [Google Scholar] [CrossRef] [PubMed]
- Salehpour, S.; Dubé, M.A. Reaction Monitoring of Glycerol Step-Growth Polymerization Using ATR-FTIR Spectroscopy. Macromol. React. Eng. 2012, 6, 85–92. [Google Scholar] [CrossRef]
- Schönhals, A.; Kremer, F. Theory of Dielectric Relaxation. In Broadband Dielectric Spectroscopy; Kremer, F., Schönhals, A., Eds.; Springer: Heidelberg, Germany, 2003; pp. 1–33. ISBN 978-3-642-56120-7. [Google Scholar]
- Haken, H.; Christoph Wolf, H. The Quantum-Mechanical Treatment of Rotational and Vibrational Spectra. In Molecular Physics and Elements of Quantum Chemistry: Introduction to Experiments and Theory; Haken, H., Christoph Wolf, H., Eds.; Advanced Texts in Physics; Springer: Heidelberg, Germany, 1995; pp. 171–197. ISBN 978-3-662-03075-2. [Google Scholar]
- Shigeto, S.; Hiramatsu, H.; Hamaguchi, H. Structure and Dipole Moments of the Two Distinct Solvated Forms of P-Nitroaniline in Acetonitrile/CCl4 As Studied by Infrared Electroabsorption Spectroscopy. J. Phys. Chem. A 2006, 110, 3738–3743. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.-C.; Shigeto, S. Infrared Electroabsorption Spectroscopy of N,N-Dimethyl-p-Nitroaniline in Acetonitrile/C2Cl4: Solvation of the Solute and Self-Association of Acetonitrile. J. Phys. Chem. A 2011, 115, 4448–4456. [Google Scholar] [CrossRef] [PubMed]
- Takashima, K.; Furukawa, Y. Vibrational Stark Effect of 9-Cyanoanthracene Dispersed in a Poly(Methyl Methacrylate) Film. Chem. Phys. Lett. 2015, 633, 252–255. [Google Scholar] [CrossRef]
- Schneider, S.H.; Boxer, S.G. Vibrational Stark Effects of Carbonyl Probes Applied to Reinterpret IR and Raman Data for Enzyme Inhibitors in Terms of Electric Fields at the Active Site. J. Phys. Chem. B 2016, 120, 9672–9684. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, H.H.; Loukianov, A.D.; Ogilvie, J.P.; Abramavicius, D. Two-Dimensional Electronic Stark Spectroscopy of a Photosynthetic Dimer. J. Chem. Phys. 2020, 153, 144203. [Google Scholar] [CrossRef] [PubMed]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kremer, F.; Kipnusu, W.K.; Fränzl, M. Orientation Polarization Spectroscopy—Toward an Atomistic Understanding of Dielectric Relaxation Processes. Int. J. Mol. Sci. 2022, 23, 8254. https://doi.org/10.3390/ijms23158254
Kremer F, Kipnusu WK, Fränzl M. Orientation Polarization Spectroscopy—Toward an Atomistic Understanding of Dielectric Relaxation Processes. International Journal of Molecular Sciences. 2022; 23(15):8254. https://doi.org/10.3390/ijms23158254
Chicago/Turabian StyleKremer, Friedrich, Wycliffe Kiprop Kipnusu, and Martin Fränzl. 2022. "Orientation Polarization Spectroscopy—Toward an Atomistic Understanding of Dielectric Relaxation Processes" International Journal of Molecular Sciences 23, no. 15: 8254. https://doi.org/10.3390/ijms23158254
APA StyleKremer, F., Kipnusu, W. K., & Fränzl, M. (2022). Orientation Polarization Spectroscopy—Toward an Atomistic Understanding of Dielectric Relaxation Processes. International Journal of Molecular Sciences, 23(15), 8254. https://doi.org/10.3390/ijms23158254






