Analysis of Integrin αIIb Subunit Dynamics Reveals Long-Range Effects of Missense Mutations on Calf Domains
Abstract
:1. Introduction
2. Results
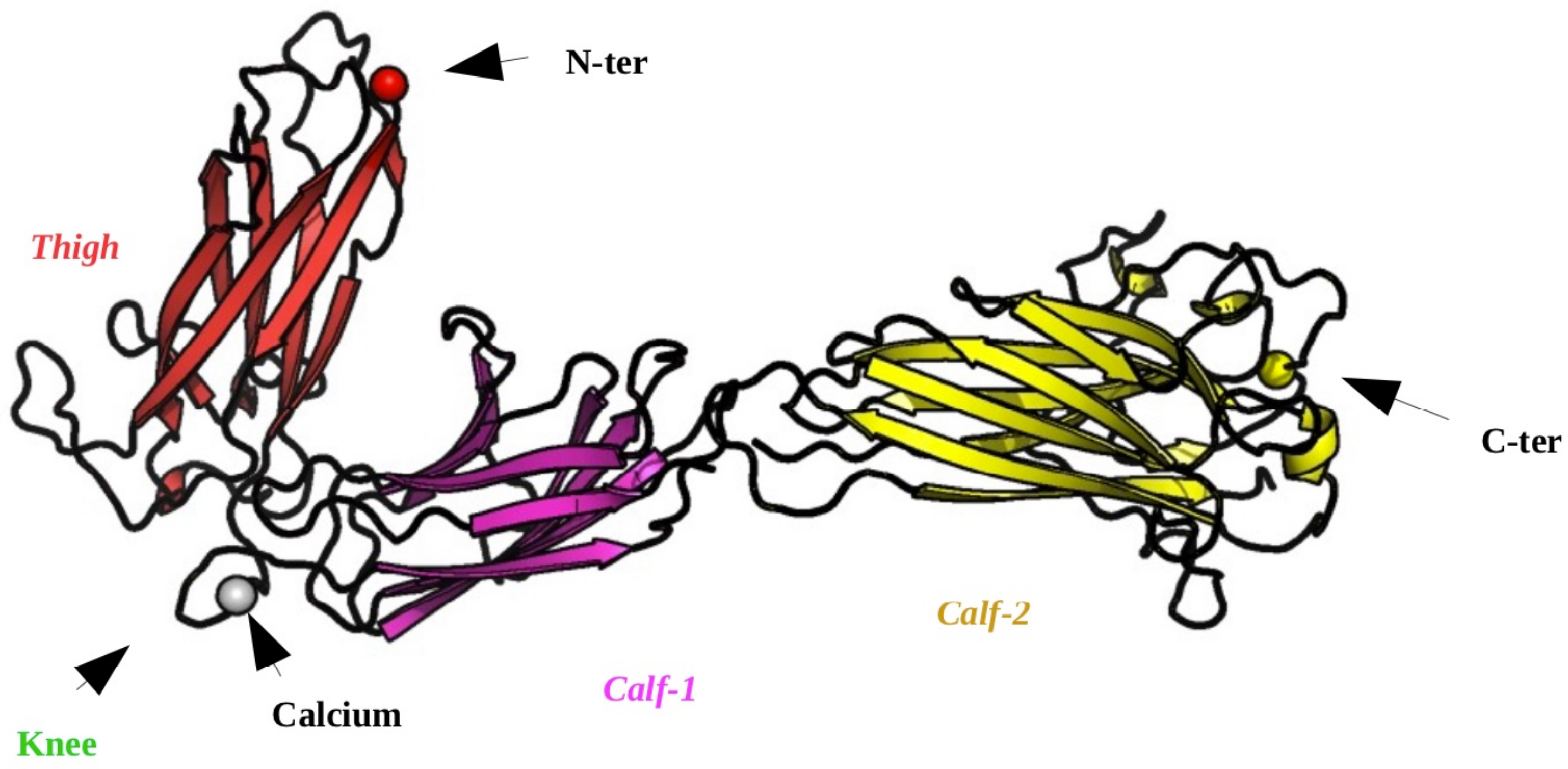
2.1. Structural Modeling of the Calf-2 Domain
2.2. Designing the Calf-1 + Calf-2 Simulation System
2.2.1. Molecular Dynamics
2.2.2. Assessing the Impact of the Adjunction of the Calf-2 Domain to Calf-1
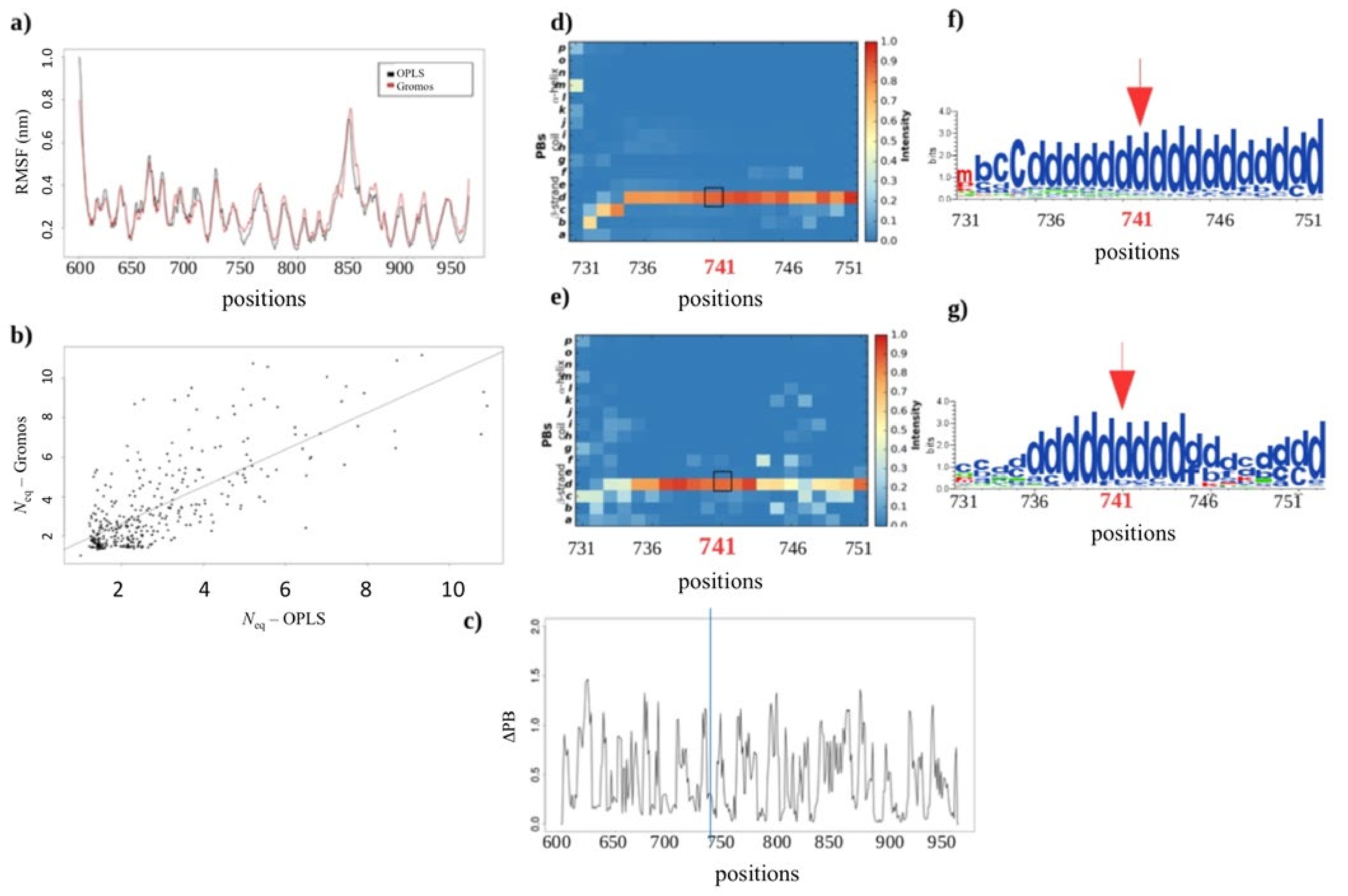
2.2.3. MD Simulations: Potential Impact of the Change in Forcefields
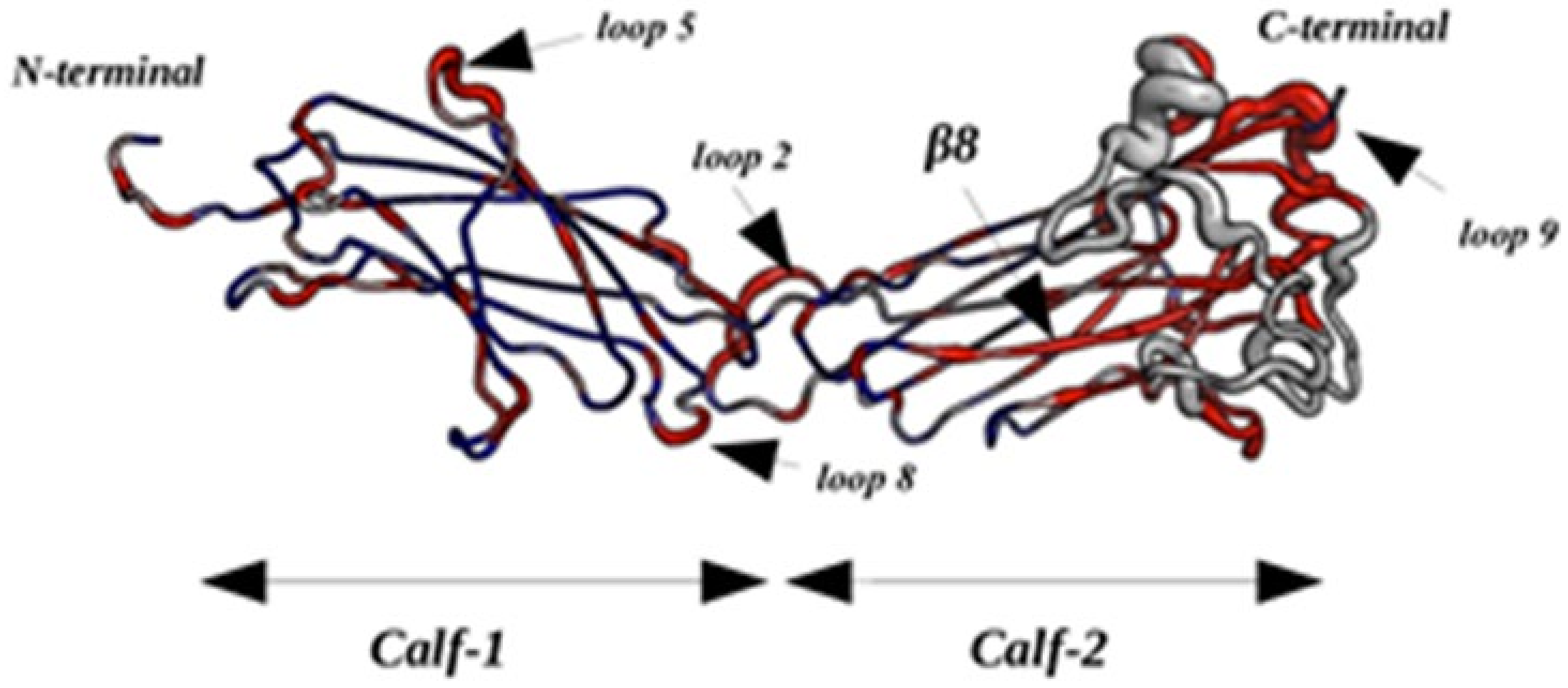
2.2.4. Dynamics of Expertly Modeled Loops of the Calf-2 Domain
2.3. Modeling Punctual Mutations to Generate Structural Variants of Interest
2.3.1. Analyses of the Variants
2.3.2. Assessing the Structural Impact of the GT Variant P741R
2.3.3. Analysis of the GT H798P and S926L Variants of the Calf-2 Domain
Local Structural Changes Due to H798P
Non-Local Impact of the Single Amino Acid Variation in the Calf-2 Domain
Local and Non-Local Structural Impacts Due to S926L
2.3.4. Dynamics of Thigh and Calf-1 Domains
3. Discussion
4. Materials and Methods
4.1. Structural Data
4.2. Studied Variants
4.3. Molecular Dynamics
4.4. Protein Block Analysis
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
References
- Hynes, R.O. Integrins: Bidirectional, allosteric signaling machines. Cell 2002, 110, 673–687. [Google Scholar] [CrossRef] [Green Version]
- Huang, J.; Li, X.; Shi, X.; Zhu, M.; Wang, J.; Huang, S.; Huang, X.; Wang, H.; Li, L.; Deng, H.; et al. Platelet integrin αiibβ3: Signal transduction, regulation, and its therapeutic targeting. J. Hematol. Oncol. 2019, 12, 26. [Google Scholar] [CrossRef] [Green Version]
- Xu, X.P.; Kim, E.; Swift, M.; Smith, J.W.; Volkmann, N.; Hanein, D. Three-dimensional structures of full-length, membrane-embedded human α(iib)β(3) integrin complexes. Biophys. J. 2016, 110, 798–809. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhu, J.; Luo, B.H.; Xiao, T.; Zhang, C.; Nishida, N.; Springer, T.A. Structure of a complete integrin ectodomain in a physiologic resting state and activation and deactivation by applied forces. Mol. Cell 2008, 32, 849–861. [Google Scholar] [CrossRef] [Green Version]
- Goguet, M.; Narwani, T.J.; Petermann, R.; Jallu, V.; de Brevern, A.G. In silico analysis of glanzmann variants of calf-1 domain of α(iib)β(3) integrin revealed dynamic allosteric effect. Sci. Rep. 2017, 7, 8001. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Zhu, J. Structural determinants of the integrin transmembrane domain required for bidirectional signal transmission across the cell membrane. J. Biol. Chem. 2021, 297, 101318. [Google Scholar] [CrossRef]
- Botero, J.P.; Lee, K.; Branchford, B.R.; Bray, P.F.; Freson, K.; Lambert, M.P.; Luo, M.; Mohan, S.; Ross, J.E.; Bergmeier, W.; et al. Glanzmann thrombasthenia: Genetic basis and clinical correlates. Haematologica 2020, 105, 888–894. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nurden, A.T. Glanzmann thrombasthenia. Orphanet J. Rare Dis. 2006, 1, 10. [Google Scholar] [CrossRef] [PubMed]
- Nurden, A.T.; Nurden, P. Inherited thrombocytopenias: History, advances and perspectives. Haematologica 2020, 105, 2004–2019. [Google Scholar] [CrossRef] [PubMed]
- Norton, T.; Newberry, D.; Jnah, A. Neonatal alloimmune thrombocytopenia: A concise review. Adv. Neonatal Care 2021, 21, 115–121. [Google Scholar] [CrossRef]
- Zdravic, D.; Yougbare, I.; Vadasz, B.; Li, C.; Marshall, A.H.; Chen, P.; Kjeldsen-Kragh, J.; Ni, H. Fetal and neonatal alloimmune thrombocytopenia. Semin. Fetal Neonatal Med. 2016, 21, 19–27. [Google Scholar] [CrossRef]
- Jallu, V.; Dusseaux, M.; Panzer, S.; Torchet, M.F.; Hezard, N.; Goudemand, J.; de Brevern, A.G.; Kaplan, C. Alphaiibbeta3 integrin: New allelic variants in glanzmann thrombasthenia, effects on itga2b and itgb3 mrna splicing, expression, and structure-function. Hum. Mutat. 2010, 31, 237–246. [Google Scholar] [CrossRef] [Green Version]
- Jallu, V.; Poulain, P.; Fuchs, P.F.; Kaplan, C.; de Brevern, A.G. Modeling and molecular dynamics of hpa-1a and -1b polymorphisms: Effects on the structure of the β3 subunit of the αiibβ3 integrin. PLoS ONE 2012, 7, e47304. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jallu, V.; Poulain, P.; Fuchs, P.F.; Kaplan, C.; de Brevern, A.G. Modeling and molecular dynamics simulations of the v33 variant of the integrin subunit β3: Structural comparison with the l33 (hpa-1a) and p33 (hpa-1b) variants. Biochimie 2014, 105, 84–90. [Google Scholar] [CrossRef] [PubMed]
- Pagani, G.; Pereira, J.P.V.; Stoldt, V.R.; Beck, A.; Scharf, R.E.; Gohlke, H. The human platelet antigen-1b (pro(33)) variant of α(iib)β(3) allosterically shifts the dynamic conformational equilibrium of this integrin toward the active state. J. Biol. Chem. 2018, 293, 4830–4844. [Google Scholar] [CrossRef] [Green Version]
- Mansour, W.; Hauschner, H.; Seligsohn, U.; Rosenberg, N.; Einav, Y. Natural and artificial mutations in αiib integrin lead to a structural deformation of a calcium-binding site. Protein J. 2014, 33, 474–483. [Google Scholar] [CrossRef]
- Laguerre, M.; Sabi, E.; Daly, M.; Stockley, J.; Nurden, P.; Pillois, X.; Nurden, A.T. Molecular dynamics analysis of a novel β3 pro189ser mutation in a patient with glanzmann thrombasthenia differentially affecting αiibβ3 and αvβ3 expression. PLoS ONE 2013, 8, e78683. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nurden, A.T.; Pillois, X.; Fiore, M.; Alessi, M.C.; Bonduel, M.; Dreyfus, M.; Goudemand, J.; Gruel, Y.; Benabdallah-Guerida, S.; Latger-Cannard, V.; et al. Expanding the mutation spectrum affecting αiibβ3 integrin in glanzmann thrombasthenia: Screening of the itga2b and itgb3 genes in a large international cohort. Hum. Mutat. 2015, 36, 548–561. [Google Scholar] [CrossRef]
- Koker, M.Y.; Sarper, N.; Albayrak, C.; Zulfikar, B.; Zengin, E.; Saraymen, B.; Albayrak, D.; Koc, B.; Avcilar, H.; Karakükcü, M.; et al. New αiibβ3 variants in 28 turkish glanzmann patients; structural hypothesis for complex activation by residues variations in i-egf domains. Platelets 2021, 1–11. [Google Scholar] [CrossRef]
- Delano, W.L. The Pymol Molecular Graphics System on World Wide Web. 2013. Available online: http://www.Pymol.Org (accessed on 1 November 2021).
- Lee, J.; Lee, D.; Park, H.; Coutsias, E.A.; Seok, C. Protein loop modeling by using fragment and analytical loop closure. Proteins 2010, 78, 3428–3436. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- McGuffin, L.J.; Bryson, K.; Jones, D.T. The psipred protein structure prediction server. Bioinformatics 2000, 16, 404–405. [Google Scholar] [CrossRef]
- Drozdetskiy, A.; Cole, C.; Procter, J.; Barton, G.J. Jpred4: A protein secondary structure prediction server. Nucleic Acids Res. 2015, 43, W389–W394. [Google Scholar] [CrossRef]
- Bornot, A.; Etchebest, C.; de Brevern, A.G. Predicting protein flexibility through the prediction of local structures. Proteins 2011, 79, 839–852. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- De Brevern, A.G.; Bornot, A.; Craveur, P.; Etchebest, C.; Gelly, J.C. Predyflexy: Flexibility and local structure prediction from sequence. Nucleic Acids Res. 2012, 40, W317–W322. [Google Scholar] [CrossRef] [Green Version]
- Narwani, T.J.; Etchebest, C.; Craveur, P.; Léonard, S.; Rebehmed, J.; Srinivasan, N.; Bornot, A.; Gelly, J.C.; de Brevern, A.G. In silico prediction of protein flexibility with local structure approach. Biochimie 2019, 165, 150–155. [Google Scholar] [CrossRef] [Green Version]
- Altschul, S.F.; Madden, T.L.; Schäffer, A.A.; Zhang, J.; Zhang, Z.; Miller, W.; Lipman, D.J. Gapped blast and psi-blast: A new generation of protein database search programs. Nucleic Acids Res. 1997, 25, 3389–3402. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ye, Y.; Godzik, A. Flexible structure alignment by chaining aligned fragment pairs allowing twists. Bioinformatics 2003, 19 (Suppl. 2), ii246–ii255. [Google Scholar] [CrossRef] [Green Version]
- Barnoud, J.; Santuz, H.; Craveur, P.; Joseph, A.P.; Jallu, V.; de Brevern, A.G.; Poulain, P. Pbxplore: A tool to analyze local protein structure and deformability with protein blocks. PeerJ 2017, 5, e4013. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Akhila, M.V.; Narwani, T.J.; Floch, A.; Maljković, M.; Bisoo, S.; Shinada, N.K.; Kranjc, A.; Gelly, J.C.; Srinivasan, N.; Mitić, N.; et al. A structural entropy index to analyse local conformations in intrinsically disordered proteins. J. Struct. Biol. 2020, 210, 107464. [Google Scholar] [CrossRef]
- De Brevern, A.G. Analysis of protein disorder predictions in the light of a protein structural alphabet. Biomolecules 2020, 10, 1080. [Google Scholar] [CrossRef] [PubMed]
- Craveur, P.; Joseph, A.P.; Esque, J.; Narwani, T.J.; Noël, F.; Shinada, N.; Goguet, M.; Leonard, S.; Poulain, P.; Bertrand, O.; et al. Protein flexibility in the light of structural alphabets. Front. Mol. Biosci. 2015, 2, 20. [Google Scholar] [CrossRef] [Green Version]
- Narwani, T.J.; Craveur, P.; Shinada, N.K.; Floch, A.; Santuz, H.; Vattekatte, A.M.; Srinivasan, N.; Rebehmed, J.; Gelly, J.C.; Etchebest, C.; et al. Discrete analyses of protein dynamics. J. Biomol. Struct. Dyn. 2020, 38, 2988–3002. [Google Scholar] [CrossRef]
- Adzhubei, I.A.; Schmidt, S.; Peshkin, L.; Ramensky, V.E.; Gerasimova, A.; Bork, P.; Kondrashov, A.S.; Sunyaev, S.R. A method and server for predicting damaging missense mutations. Nat. Methods 2010, 7, 248–249. [Google Scholar] [CrossRef] [Green Version]
- Nelson, E.J.; Nair, S.C.; Peretz, H.; Coller, B.S.; Seligsohn, U.; Chandy, M.; Srivastava, A. Diversity of glanzmann thrombasthenia in southern India: 10 novel mutations identified among 15 unrelated patients. J. Thromb. Haemost. JTH 2006, 4, 1730–1737. [Google Scholar] [CrossRef] [PubMed]
- Zheng, H.; Chordia, M.D.; Cooper, D.R.; Chruszcz, M.; Müller, P.; Sheldrick, G.M.; Minor, W. Validation of metal-binding sites in macromolecular structures with the checkmymetal web server. Nat. Protoc. 2014, 9, 156–170. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Scott, C.E.; Kucharski, A.N., Jr.; Kekenes-Huskey, P.M. Molecular dynamics study of divalent ion coordination in ef hand proteins. Biophys. J. 2016, 110, 209. [Google Scholar] [CrossRef] [Green Version]
- Scott, C.E.; Kekenes-Huskey, P.M. Molecular basis of s100a1 activation at saturating and subsaturating calcium concentrations. Biophys. J. 2016, 110, 1052–1063. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gelly, J.C.; de Brevern, A.G. Protein peeling 3d: New tools for analyzing protein structures. Bioinformatics 2011, 27, 132–133. [Google Scholar] [CrossRef] [Green Version]
- Gelly, J.C.; de Brevern, A.G.; Hazout, S. ‘Protein peeling’: An approach for splitting a 3d protein structure into compact fragments. Bioinformatics 2006, 22, 129–133. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gelly, J.C.; Etchebest, C.; Hazout, S.; de Brevern, A.G. Protein peeling 2: A web server to convert protein structures into series of protein units. Nucleic Acids Res. 2006, 34, W75–W78. [Google Scholar] [CrossRef] [Green Version]
- de Brevern, A.G.; Etchebest, C.; Hazout, S. Bayesian probabilistic approach for predicting backbone structures in terms of protein blocks. Proteins 2000, 41, 271–287. [Google Scholar] [CrossRef] [Green Version]
- Sali, A.; Blundell, T.L. Comparative protein modelling by satisfaction of spatial restraints. J. Mol. Biol. 1993, 234, 779–815. [Google Scholar] [CrossRef]
- Krivov, G.G.; Shapovalov, M.V.; Dunbrack, R.L., Jr. Improved prediction of protein side-chain conformations with scwrl4. Proteins 2009, 77, 778–795. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Van Der Spoel, D.; Lindahl, E.; Hess, B.; Groenhof, G.; Mark, A.E.; Berendsen, H.J. Gromacs: Fast, flexible, and free. J. Comput. Chem. 2005, 26, 1701–1718. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Tirado-Rives, J. The opls [optimized potentials for liquid simulations] potential functions for proteins, energy minimizations for crystals of cyclic peptides and crambin. J. Am. Chem. Soc. 1988, 110, 1657–1666. [Google Scholar] [CrossRef] [PubMed]
- Van Gunsteren, W.F.; Berendsen, H.J. Groningen Molecular Simulation (Gromos) Library Manual; Biomos: Groningen, The Netherlands, 1987. [Google Scholar]
- Tina, K.G.; Bhadra, R.; Srinivasan, N. Pic: Protein interactions calculator. Nucleic Acids Res. 2007, 35, W473–W476. [Google Scholar] [CrossRef] [Green Version]
- Joseph, A.P.; Agarwal, G.; Mahajan, S.; Gelly, J.C.; Swapna, L.S.; Offmann, B.; Cadet, F.; Bornot, A.; Tyagi, M.; Valadié, H. A short survey on protein blocks. Biophys Rev. 2010, 2, 137–145. [Google Scholar] [CrossRef] [PubMed]
- Joseph, A.P.; Srinivasan, N.; de Brevern, A.G. Progressive structure-based alignment of homologous proteins: Adopting sequence comparison strategies. Biochimie 2012, 94, 2025–2034. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dong, X.; Mi, L.Z.; Zhu, J.; Wang, W.; Hu, P.; Luo, B.H.; Springer, T.A. A(v)β(3) integrin crystal structures and their functional implications. Biochemistry 2012, 51, 8814–8828. [Google Scholar] [CrossRef] [Green Version]
- Xiong, J.P.; Mahalingham, B.; Alonso, J.L.; Borrelli, L.A.; Rui, X.; Anand, S.; Hyman, B.T.; Rysiok, T.; Müller-Pompalla, D.; Goodman, S.L.; et al. Crystal structure of the complete integrin alphavbeta3 ectodomain plus an alpha/beta transmembrane fragment. J. Cell Biol. 2009, 186, 589–600. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Skolnick, J. Tm-align: A protein structure alignment algorithm based on the tm-score. Nucleic Acids Res. 2005, 33, 2302–2309. [Google Scholar] [CrossRef] [PubMed]
- Shen, M.Y.; Sali, A. Statistical potential for assessment and prediction of protein structures. Protein Sci. 2006, 15, 2507–2524. [Google Scholar] [CrossRef] [Green Version]
- Faure, G.; Joseph, A.P.; Craveur, P.; Narwani, T.J.; Srinivasan, N.; Gelly, J.C.; Rebehmed, J.; de Brevern, A.G. Ipbavizu: A pymol plugin for an efficient 3d protein structure superimposition approach. Source Code Biol. Med. 2019, 14, 5. [Google Scholar] [CrossRef] [PubMed]
- Gelly, J.C.; Joseph, A.P.; Srinivasan, N.; de Brevern, A.G. Ipba: A tool for protein structure comparison using sequence alignment strategies. Nucleic Acids Res. 2011, 39, W18–W23. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Joseph, A.P.; Srinivasan, N.; de Brevern, A.G. Improvement of protein structure comparison using a structural alphabet. Biochimie 2011, 93, 1434–1445. [Google Scholar] [CrossRef] [Green Version]
- Sen, M.; Yuki, K.; Springer, T.A. An internal ligand-bound, metastable state of a leukocyte integrin, αxβ2. J. Cell Biol. 2013, 203, 629–642. [Google Scholar] [CrossRef]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anies, S.; Jallu, V.; Diharce, J.; Narwani, T.J.; de Brevern, A.G. Analysis of Integrin αIIb Subunit Dynamics Reveals Long-Range Effects of Missense Mutations on Calf Domains. Int. J. Mol. Sci. 2022, 23, 858. https://doi.org/10.3390/ijms23020858
Anies S, Jallu V, Diharce J, Narwani TJ, de Brevern AG. Analysis of Integrin αIIb Subunit Dynamics Reveals Long-Range Effects of Missense Mutations on Calf Domains. International Journal of Molecular Sciences. 2022; 23(2):858. https://doi.org/10.3390/ijms23020858
Chicago/Turabian StyleAnies, Sali, Vincent Jallu, Julien Diharce, Tarun J. Narwani, and Alexandre G. de Brevern. 2022. "Analysis of Integrin αIIb Subunit Dynamics Reveals Long-Range Effects of Missense Mutations on Calf Domains" International Journal of Molecular Sciences 23, no. 2: 858. https://doi.org/10.3390/ijms23020858
APA StyleAnies, S., Jallu, V., Diharce, J., Narwani, T. J., & de Brevern, A. G. (2022). Analysis of Integrin αIIb Subunit Dynamics Reveals Long-Range Effects of Missense Mutations on Calf Domains. International Journal of Molecular Sciences, 23(2), 858. https://doi.org/10.3390/ijms23020858






