A Multi-Scale Study on Deformation and Failure Process of Metallic Structures in Extreme Environment
Abstract
1. Introduction
2. Models and Methods
3. Results and Discussion
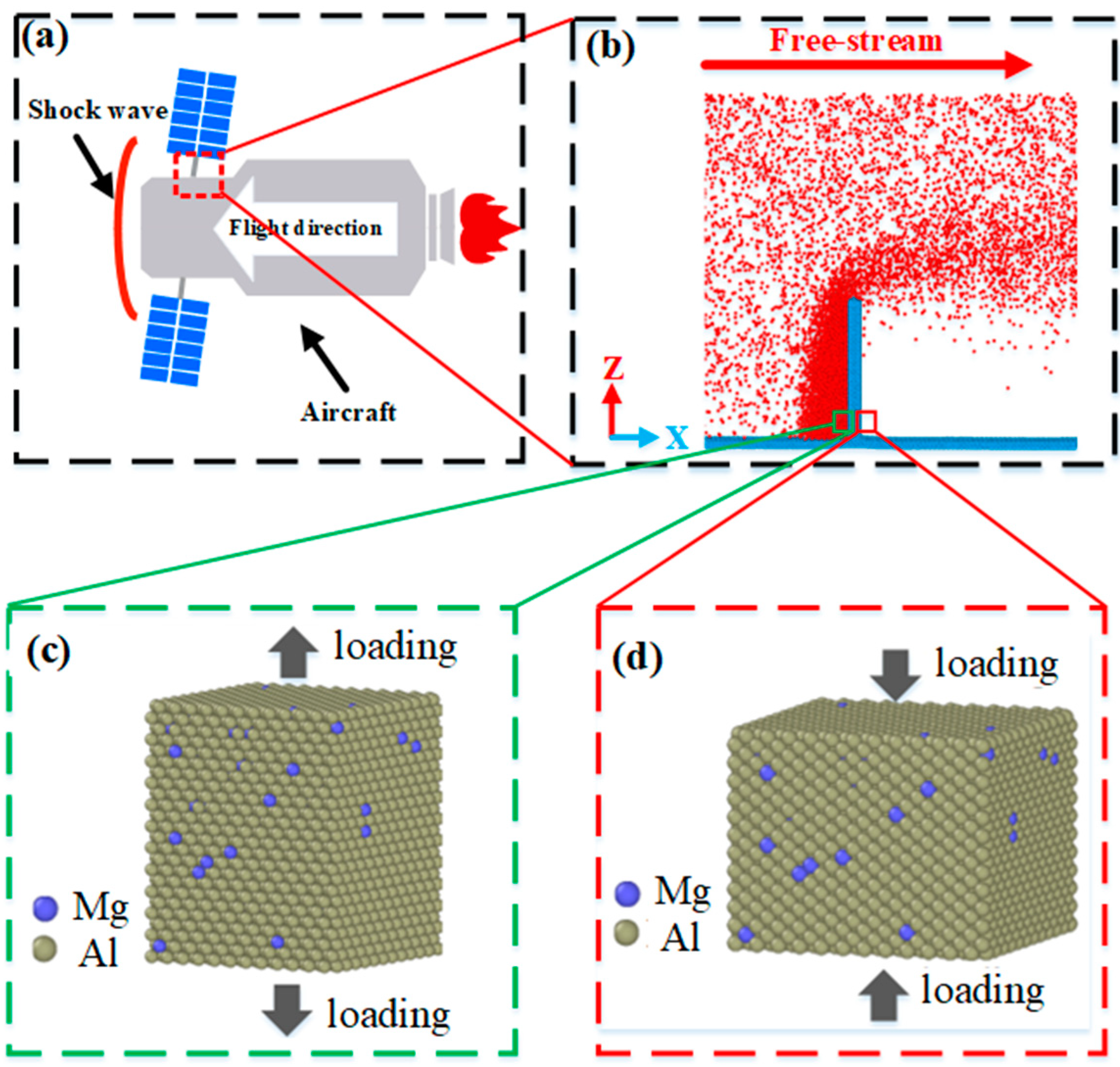
3.1. Aerodynamic Simulation
3.1.1. Details of the Aerodynamic Model
3.1.2. Outflow Field Analysis of a Plate in Hypersonic Reentry Flow
3.2. Deformation and Failure of Metal Model in Extreme Environment
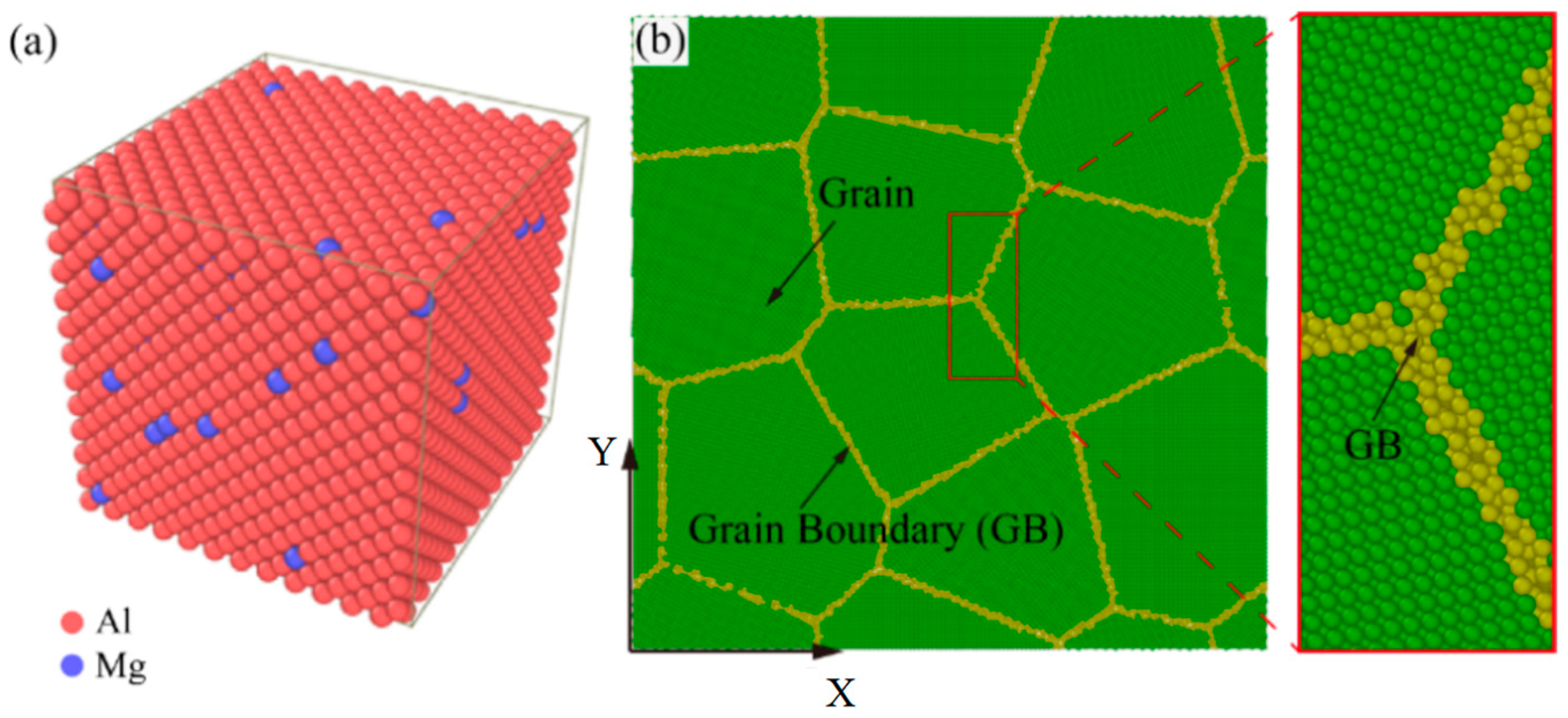
3.2.1. Model and Validation
3.2.2. The Model of Pure Al and Model with Central Crack
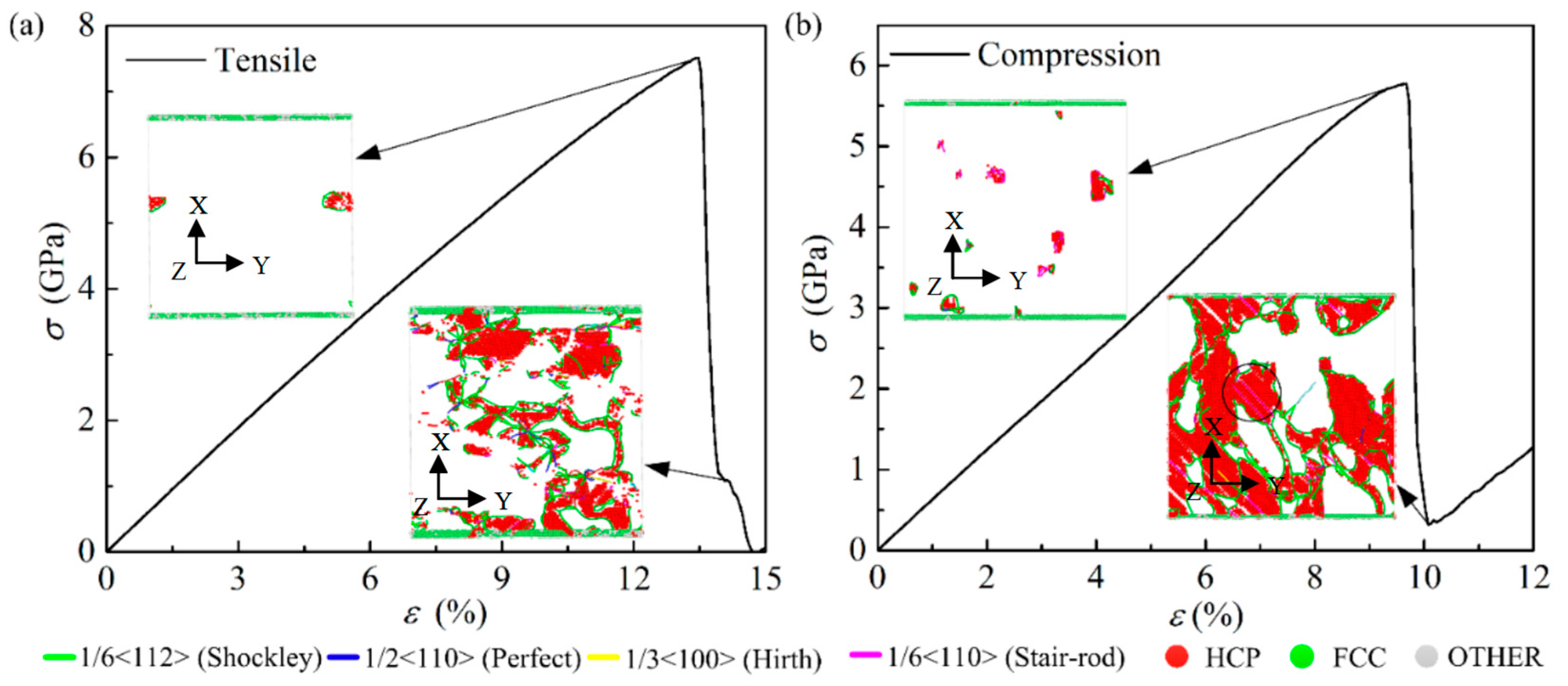
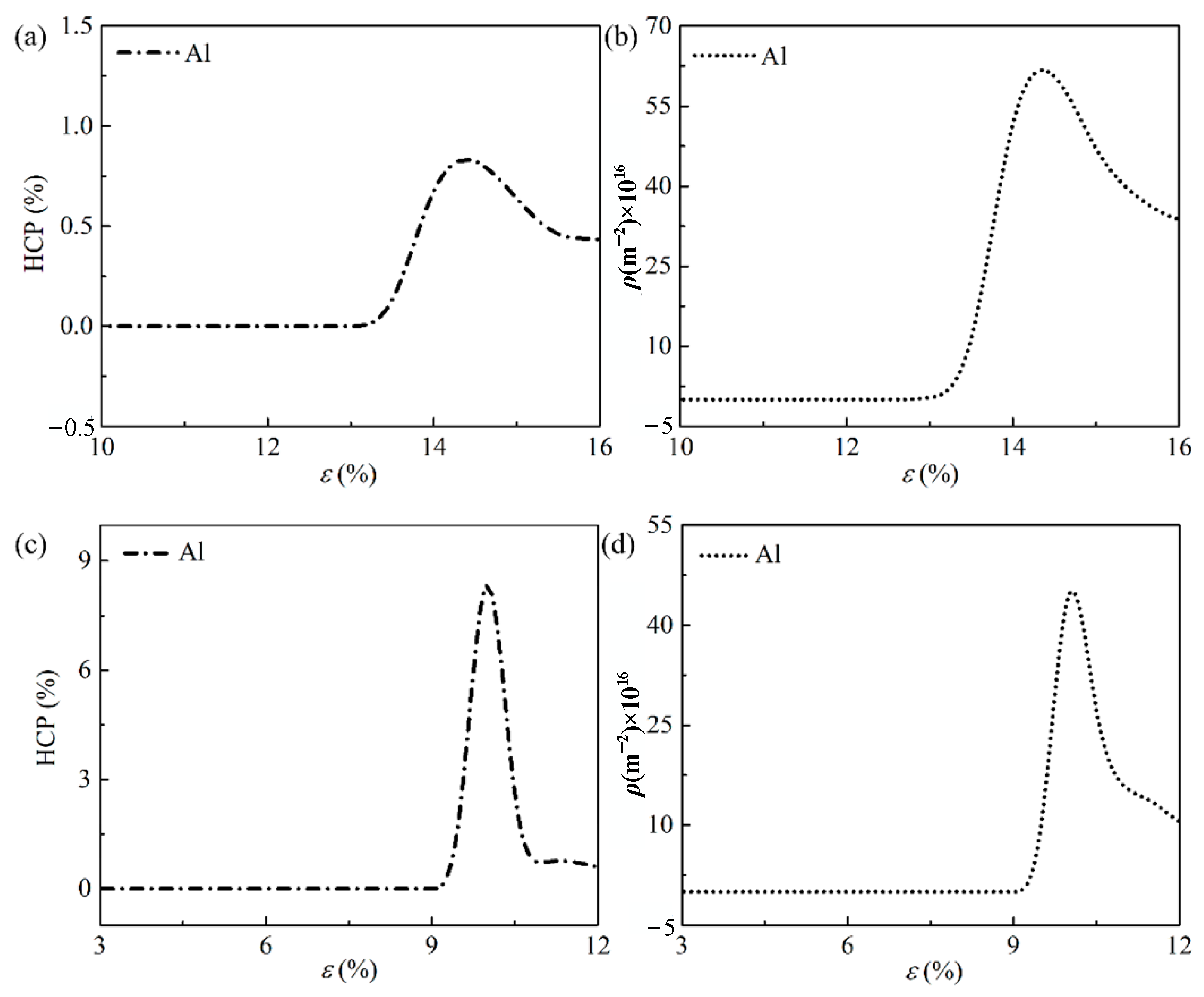
3.2.3. The Deformation Behaviors of Pure Al under Tension and Compression Loading
3.2.4. The Evolution of Atomic Defects in Al-2%Mg Single Crystal Alloy with Different Temperatures
3.3. The Mechanical Properties and Plastic Transformation Mechanism in Al-2%Mg Alloy
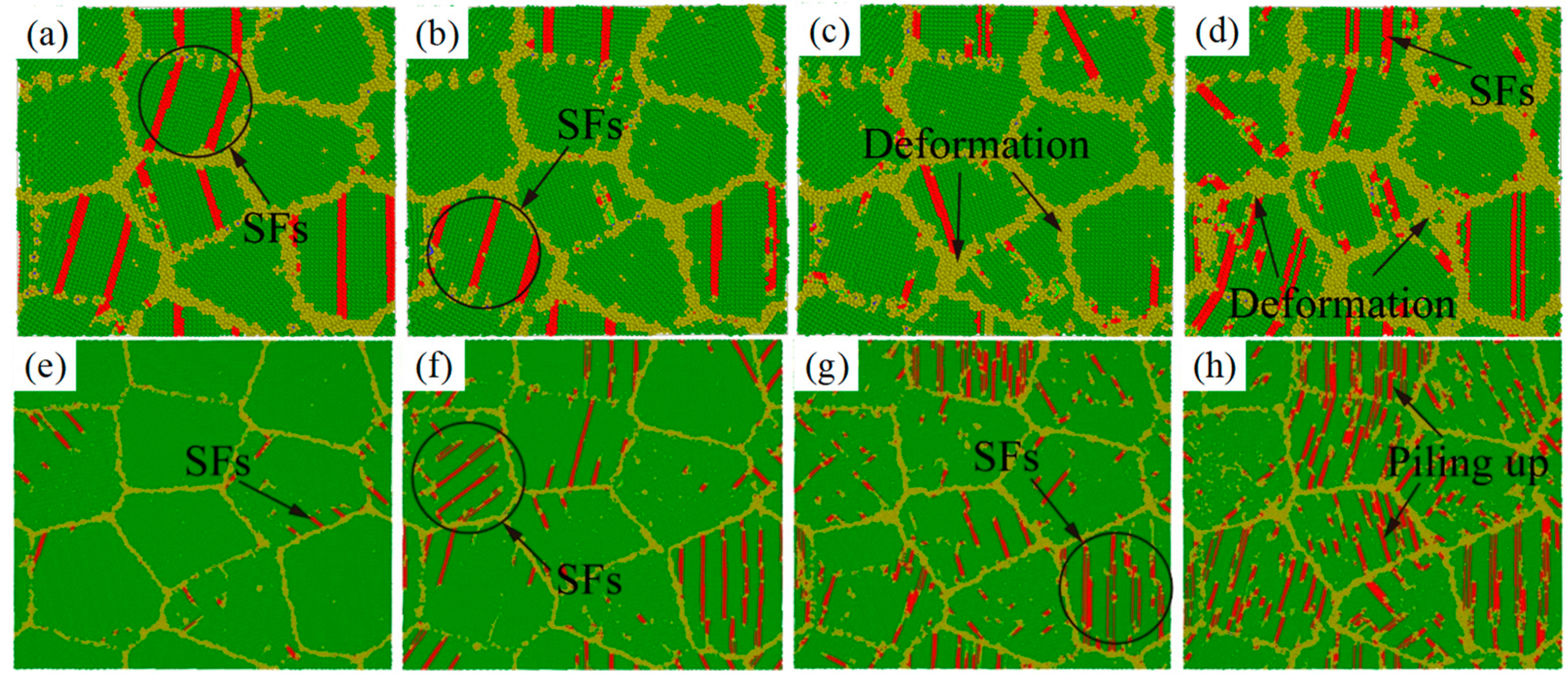
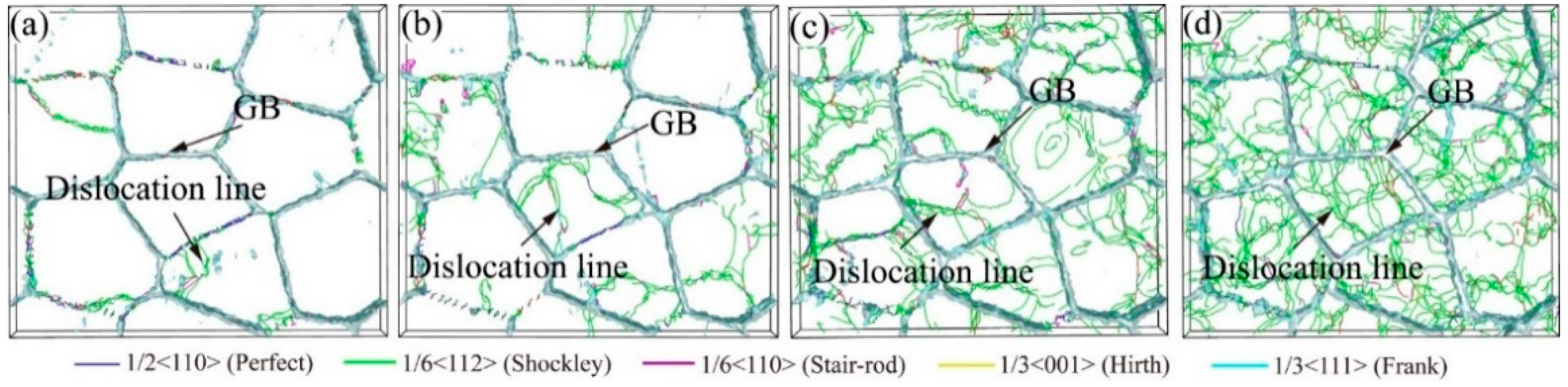
3.3.1. Effect of Grain Size on Mechanical Properties and Structural Evolution of Al-2%Mg
3.3.2. Effect of Strain Rates on Plastic Mechanism of Polycrystalline Al-2%Mg Alloy
4. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Reyhanoglu, M.; Alvarado, J. Estimation of debris dispersion due to a space vehicle breakup during reentry. Acta Astronaut. 2013, 86, 211–218. [Google Scholar] [CrossRef]
- Deependran, B.; Kurian, J. Material Thermal Degradation Under Reentry Aerodynamic Heating. J. Spacecr. Rocket. 2014, 51, 1319–1328. [Google Scholar]
- Wu, Z.; Hu, R.; Xi, Q.; Wang, X.; Zhe, W. Space Debris Reentry Analysis Methods and Tools. Chin. J. Aeronaut. 2011, 24, 9. [Google Scholar] [CrossRef]
- Caggiano, A.; Etse, G. Coupled thermo–mechanical interface model for concrete failure analysis under high temperature. Comput. Methods Appl. Mech. Eng. 2015, 289, 498–516. [Google Scholar] [CrossRef]
- Li, Z.; Ma, Q.; Cui, J. Finite Element Algorithm for Dynamic Thermoelasticity Coupling Problems and Application to Transient Response of Structure with Strong Aerothermodynamic Environment. Commun. Comput. Phys. 2016, 20, 773–810. [Google Scholar] [CrossRef]
- Li, Z.H.; Peng, A.P.; Ma, Q.; Dang, L.N.; Tang, X.W.; Sun, X.Z. Gas-kinetic unified algorithm for computable modeling of Boltzmann equation and application to aerothermodynamics for falling disintegration of uncontrolled Tiangong-No.1 spacecraft. Adv. Aerodyn. 2019, 1, 21. [Google Scholar] [CrossRef]
- Hashiguchi, K. General Description of Elastoplastic Deformation/Sliding Phenomena of Solids in High Accuracy and Numerical Efficiency: Subloading Surface Concept. Arch. Comput. Methods Eng. 2013, 20, 361–417. [Google Scholar] [CrossRef]
- Dastjerdi, S.; Malikan, M.; Eremeyev, V.A.; Akgz, B.; Civalek, M. Mechanical simulation of artificial gravity in torus-shaped and cylindrical spacecraft. Acta Astronaut. 2020, 179, 330–344. [Google Scholar] [CrossRef]
- Ji, H.; Li, D. A novel nonlinear finite element method for structural dynamic modeling of spacecraft under large deformation. Thin-Walled Struct. 2021, 165, 107926. [Google Scholar] [CrossRef]
- Li, Z.H.; Zhang, H.X. Gas-kinetic numerical studies of three-dimensional complex flows on spacecraft re-entry. J. Comput. Phys. 2009, 228, 1116–1138. [Google Scholar] [CrossRef]
- Li, Z.H.; Peng, A.P.; Fang, F.; Li, S.X.; Zhang, S.Y. Gas-kinetic unified algorithm for hypersonic aerothermodynamics covering various flow regimes solving Boltzmann model equation. Acta Phys. Sin. 2015, 64, 224703. [Google Scholar]
- Peng, A.P.; Li, Z.H.; Wu, J.L.; Jiang, X.Y. Implicit gas-kinetic unified algorithm based on multi-block docking grid for multi-body reentry flows covering all flow regimes. J. Comput. Phys. 2016, 327, 919–942. [Google Scholar] [CrossRef]
- Jie, L.; Li, Z.; Li, X.; Shi, W. Monte Carlo Simulation of Spacecraft Reentry Aerothermodynamics and Analysis for Ablating Disintegration. Commun. Comput. Phys. 2018, 23, 1037–1051. [Google Scholar]
- Zhonghua, L.I.; Dang, L.; Zhihui, L.I. Navier-Stokes/DSMC hybrid algorithm for hypersonic flows with chemical non-equilibrium. Acta Aeronaut. Astronaut. Sin. 2018, 39, 122229. [Google Scholar]
- Zhu, C.; Ji, J.; Zhang, Z.; Dong, S.; Wei, N.; Zhao, J. Huge stretchability and reversibility of helical graphenes using molecular dynamics simulations and simplified theoretical models. Mech. Mater. 2021, 153, 103683. [Google Scholar] [CrossRef]
- Hua, A.; Zhao, J.; Zhang, J.; Yu, P.; Wei, N.; Guo, W. Revealing the size effect mechanism of reversible grain boundary migration in nanocrystalline coppers: Molecular dynamics simulations and a refined disconnection model. J. Mech. Phys. Solids 2022, 161, 104832. [Google Scholar] [CrossRef]
- Ning, W.; Chen, Y.; Cai, K.; Zhang, Y.; Zhao, J. Unusual thermal properties of graphene origami crease: A molecular dynamics study. Green Energy Environ. 2020, 7, 86–94. [Google Scholar]
- Byon, S.M.; Kim, H.S.; Lee, Y. Investigation of the size effect on crack propagation using finite element method and strain gradient plasticity. J. Mater. Process. Technol. 2007, 191, 193–197. [Google Scholar] [CrossRef]
- Chen, W.; Zeng, X.; Chen, L.; Yang, X.; Wang, F. Competition between plasticity- and void-based dynamic damage behaviors of single crystal HCP-Zr by considering the high strain rate and temperature. Mech. Mater. 2019, 141, 103261. [Google Scholar] [CrossRef]
- Jing, P.; Yuan, L.; Shivpuri, R.; Xu, C.; Zhang, Y.; Shan, D.; Guo, B. Evolution of spherical nanovoids within copper polycrystals during plastic straining: Atomistic investigation. Int. J. Plast. 2018, 100, 122–141. [Google Scholar] [CrossRef]
- Lubarda, V.A.; Schneider, M.S.; Kalantar, D.H.; Remington, B.A.; Meyers, M.A. Void growth by dislocation emission. Acta Mater. 2004, 52, 1397–1408. [Google Scholar] [CrossRef]
- Krull, H.; Yuan, H. Suggestions to the cohesive traction–separation law from atomistic simulations. Eng. Fract. Mech. 2011, 78, 525–533. [Google Scholar] [CrossRef]
- Ma, Z.; Liu, J.; Wang, G.; Wang, H.; Wei, Y.; Gao, H. Strength gradient enhances fatigue resistance of steels. Sci. Rep. 2016, 6, 22156. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Yuan, L.; Zhang, S.; Sun, C.; Wang, W.; Yang, G.; Li, Q.; Wei, Y. The influence of combined gradient structure with residual stress on crack-growth behavior in medium carbon steel. Eng. Fract. Mech. 2019, 209, 369–381. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, F.; Zhang, X.; Zhang, J.; Zhong, Z. Crack propagation in gradient nano-grained metals with extremely small grain size based on molecular dynamic simulations. Int. J. Fract. 2022, 233, 71–83. [Google Scholar] [CrossRef]
- Li, X.; Wei, Y.; Lu, L.; Lu, K.; Gao, H. Dislocation nucleation governed softening and maximum strength in nano-twinned metals. Nature 2010, 464, 877–880. [Google Scholar] [CrossRef]
- Fan, Z.; Wei, C.; Ville, V.; Ari, H. Efficient molecular dynamics simulations with many-body potentials on graphics processing units. Comput. Phys. Commun. 2017, 218, 10–16. [Google Scholar] [CrossRef]
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Liu, X.Y.; Ohotnicky, P.P.; Adams, J.B.; Rohrer, C.L.; Hyland, R.W. Anisotropic surface segregation in Al-Mg alloys. Surf. Sci. 1997, 373, 357–370. [Google Scholar] [CrossRef]
- Hirel, P. Atomsk: A tool for manipulating and converting atomic data files. Comput. Phys. Commun. 2015, 197, 212–219. [Google Scholar] [CrossRef]
- Stukowski, A. Structure identification methods for atomistic simulations of crystalline materials. Model. Simul. Mater. Sci. Eng. 2012, 20, 045021. [Google Scholar] [CrossRef]
- Stukowski, A. Computational Analysis Methods in Atomistic Modeling of Crystals. JOM 2014, 66, 399–407. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and analysis of atomistic simulation data with OVITO–the Open Visualization Tool. Model. Simul. Mater. Sci. Eng 2010, 18, 2154–2162. [Google Scholar] [CrossRef]
- Ratner, M.A. Understanding molecular simulation: From algorithms to applications, by Daan Frenkel and Berend Smit. Phys. Today 1997, 50, 66. [Google Scholar]
- Jones, J.E. On the determination of molecular fields. II. From the equation of state of gas. Proc. Roy. Soc. A 1924, 106, 463–477. [Google Scholar]
- Rappe, A.K.; Casewit, C.J.; Colwell, K.S.; Goddard, W.A.I.; Skiff, W.M.J. UFF, A Full Periodic Table Force Field for Molecular Mechanics and Molecular Dynamics Simulations. J. Am. Chem. Soc. 1992, 114, 10024–10035. [Google Scholar] [CrossRef]
- Zhou, X.; Johnson, R.; Wadley, H. Misfit-energy-increasing dislocations in vapor-deposited CoFe/NiFe multilayers. Phys. Rev. B 2004, 69, 144113. [Google Scholar] [CrossRef]
- Nitol, M.S.; Adibi, S.; Barrett, C.D.; Wilkerson, J.W. Solid solution softening in dislocation-starved Mg–Al alloys. Mech. Mater. 2020, 150, 103588. [Google Scholar] [CrossRef]
- Zhang, L.; Lu, C.; Shibuta, Y. Shear response of grain boundaries with metastable structures by molecular dynamics simulations. Model. Simul. Mater. Sci. Eng. 2018, 26, 035008. [Google Scholar] [CrossRef]
- Zhu, J.Q.; Yang, Q.S.; Liu, X. Investigation on the Tensile Behavior of Graphene-Aluminum Nano-Laminated Composites by Molecular Dynamics Simulation. Key Eng. Mater. 2019, 804, 1–6. [Google Scholar] [CrossRef]
- Mishin, Y.; Farkas, D.; Mehl, M.J.; Papaconstantopoulos, D.A. Interatomic potentials for monoatomic metals from experimental data and ab initio calculations. CiteSeer 1999, 59, 3393. [Google Scholar]
- Pogorelko, V.V.; Mayer, A.E. Influence of copper inclusions on the strength of aluminum matrix at high-rate tension. Mater. Sci. Eng. A Struct. Mater. Prop. Misrostruct. Process. 2015, 642, 351–359. [Google Scholar] [CrossRef]
- Tong, W. Detection of plastic deformation patterns in a binary aluminum alloy. Exp. Mech. 1997, 37, 452–459. [Google Scholar] [CrossRef]
- Guder, V.; Sengul, S. Tensile strength and failure mechanism of hcp zirconium nanowires: Effect of diameter, temperature and strain rate. Comput. Mater. Sci. 2020, 177, 109551. [Google Scholar] [CrossRef]
- Wang, J.P.; Liang, J.W.; Wen, Z.X.; Yue, Z.F. Atomic simulation of void location effect on the void growth in nickel-based single crystal. Comput. Mater. Sci. 2019, 160, 245–255. [Google Scholar] [CrossRef]
- Liu, J.; Fan, X.; Gu, C.; Shi, Y.; Zheng, W. Effect of voids on nanocrystalline gold ultrathin film. Comput. Mater. Sci. 2021, 189, 110255. [Google Scholar] [CrossRef]



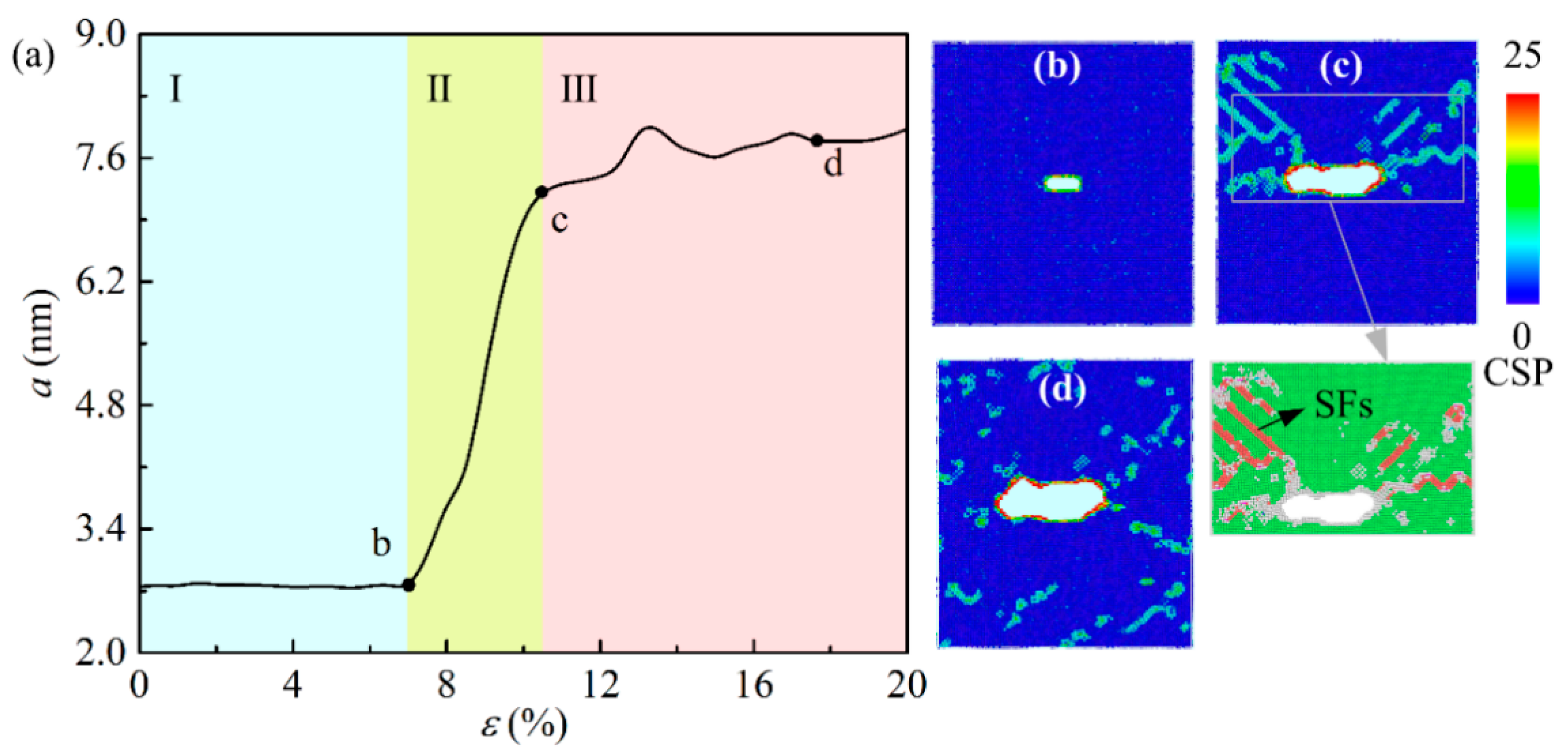
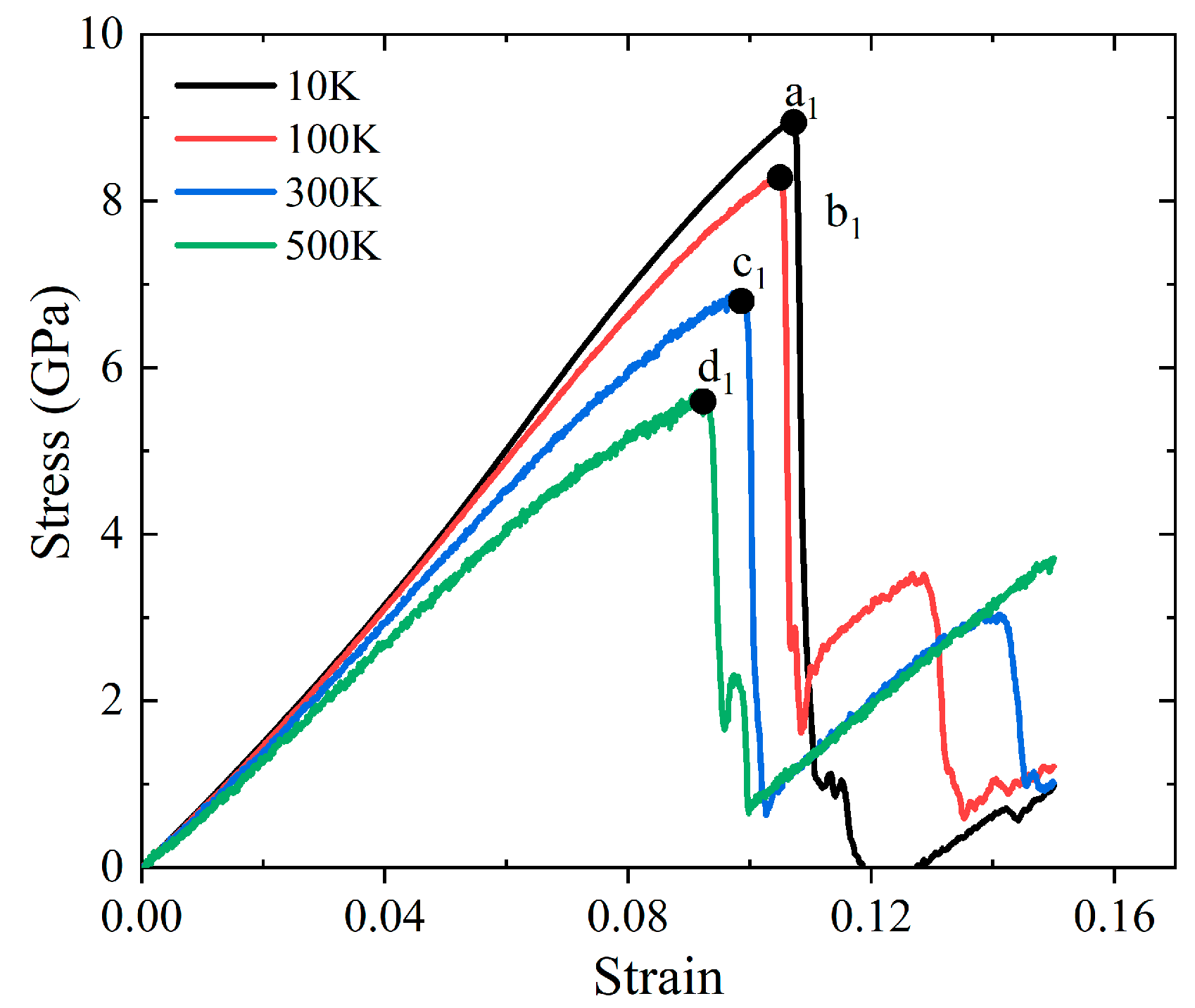

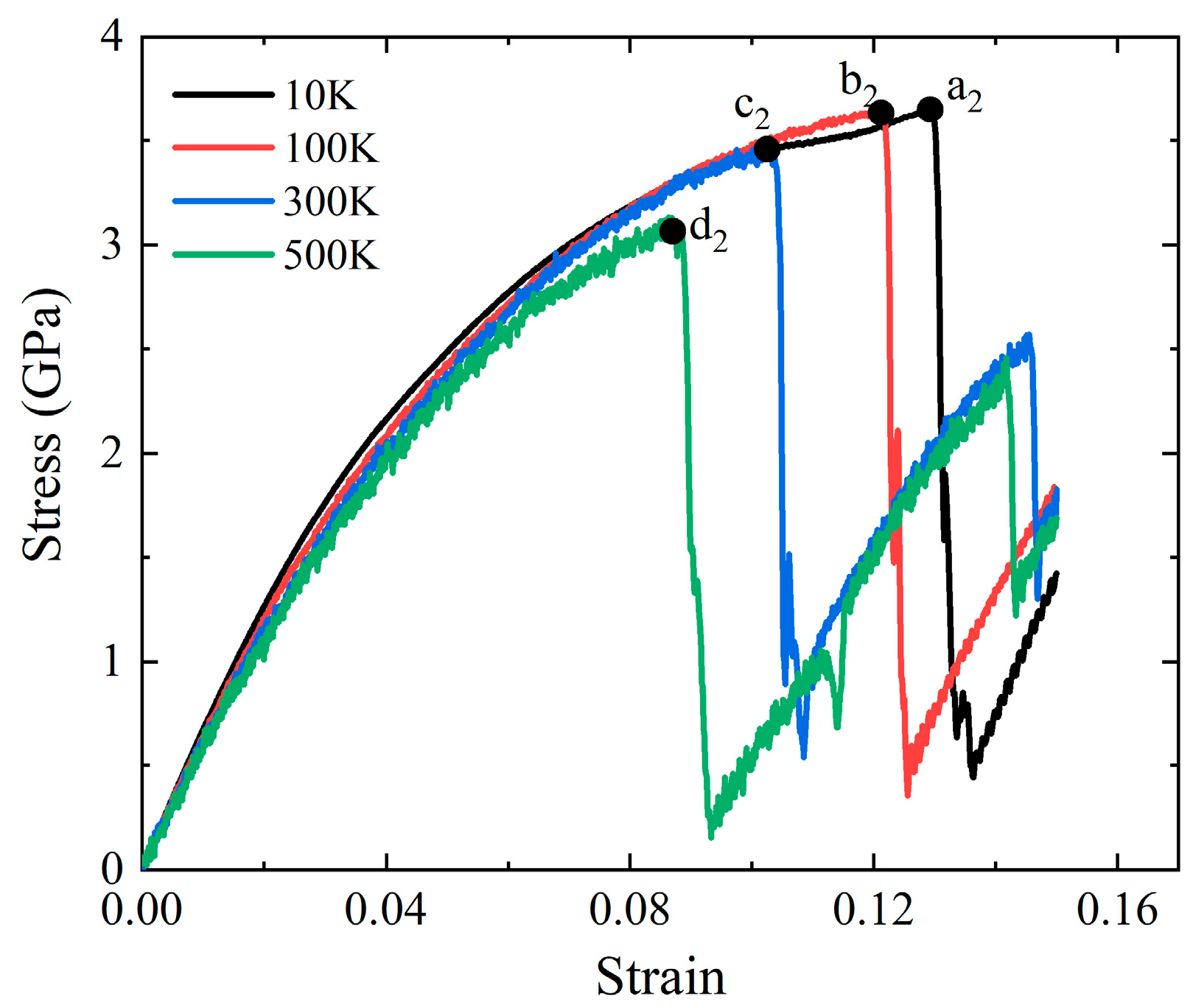
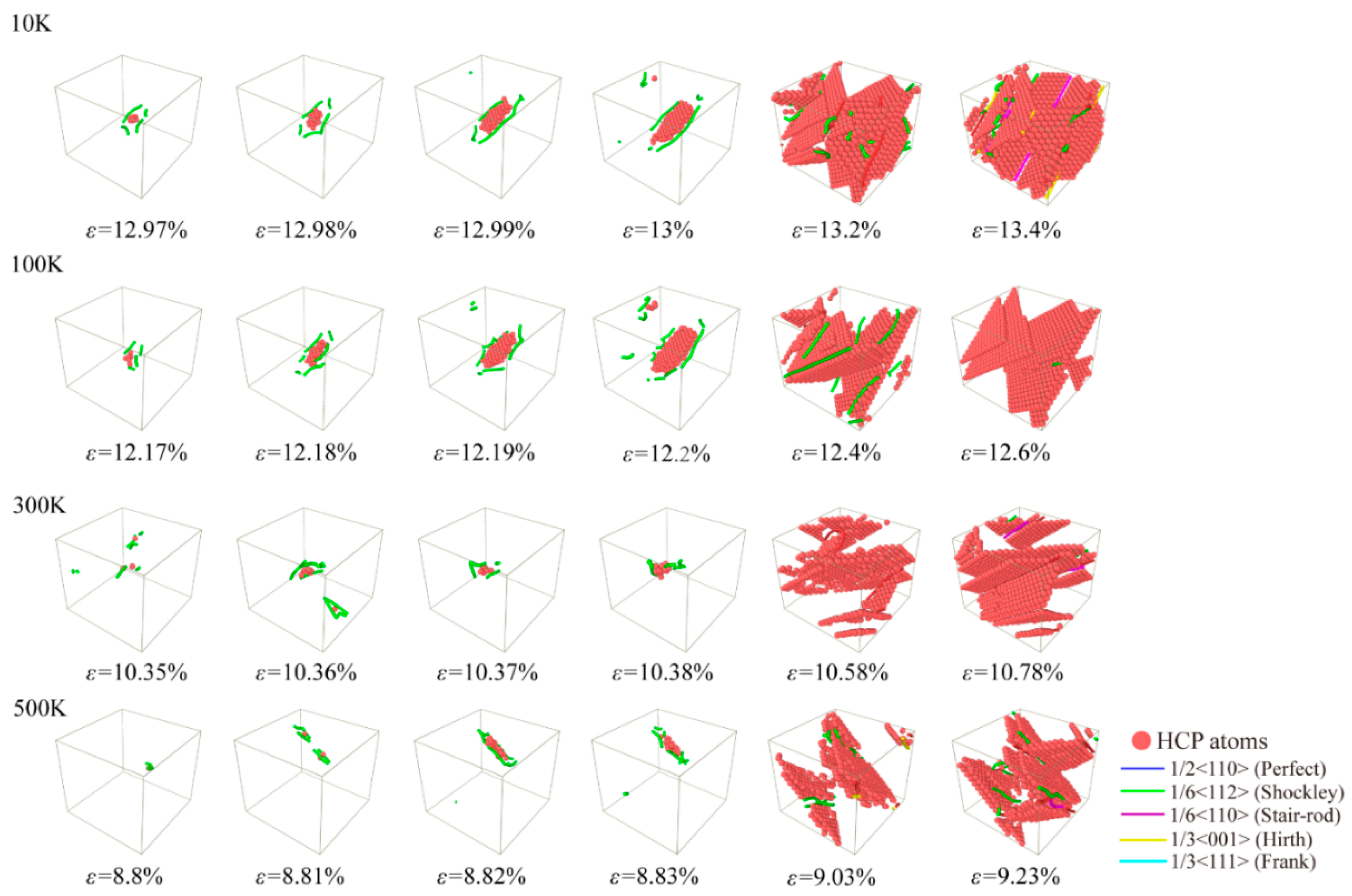
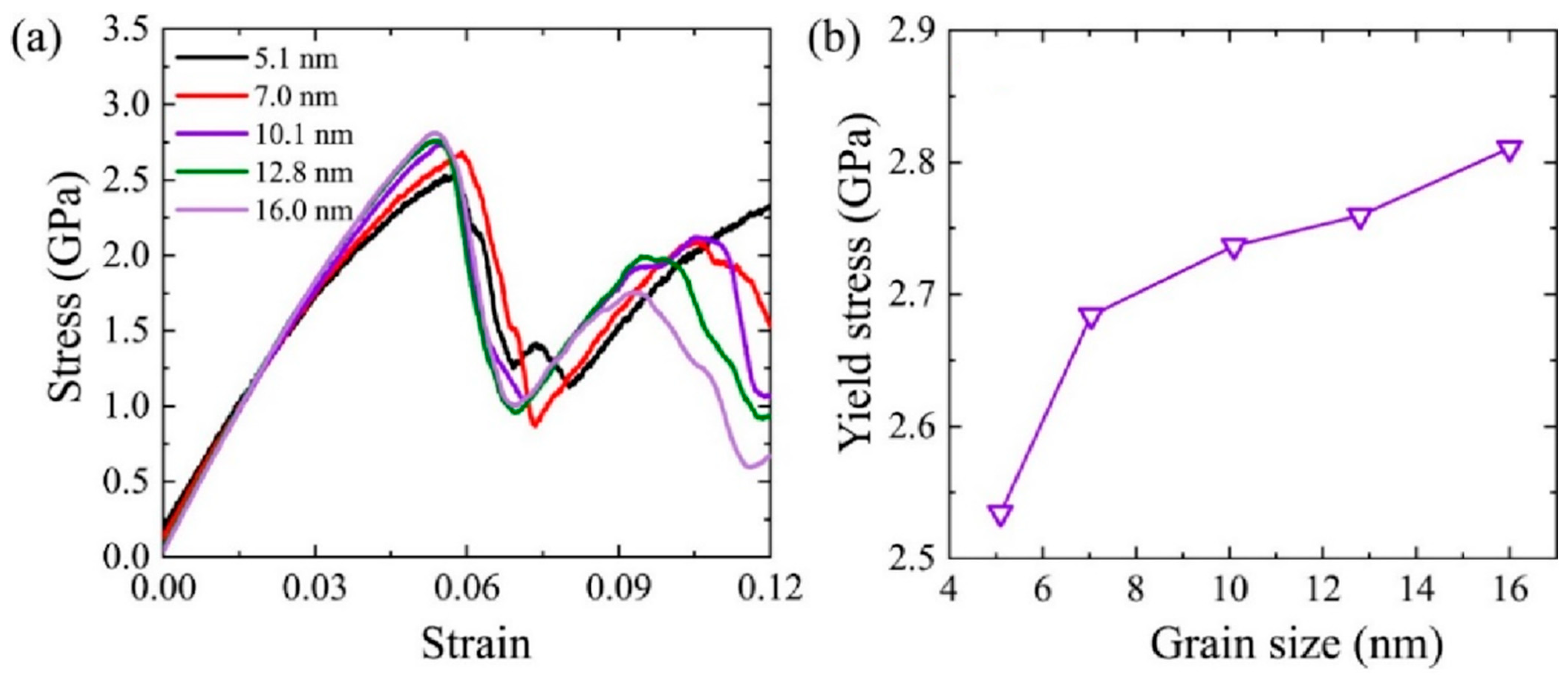
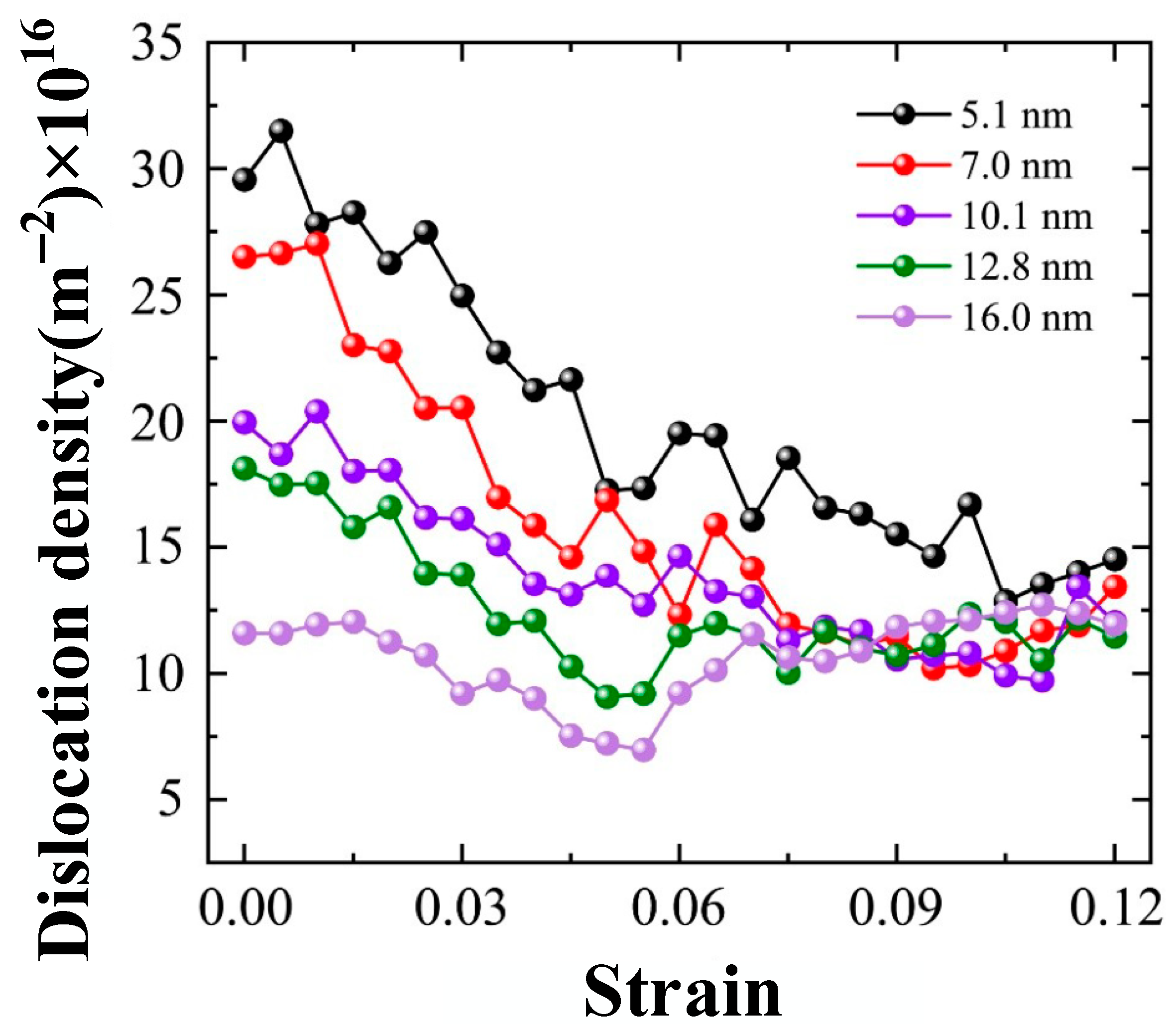

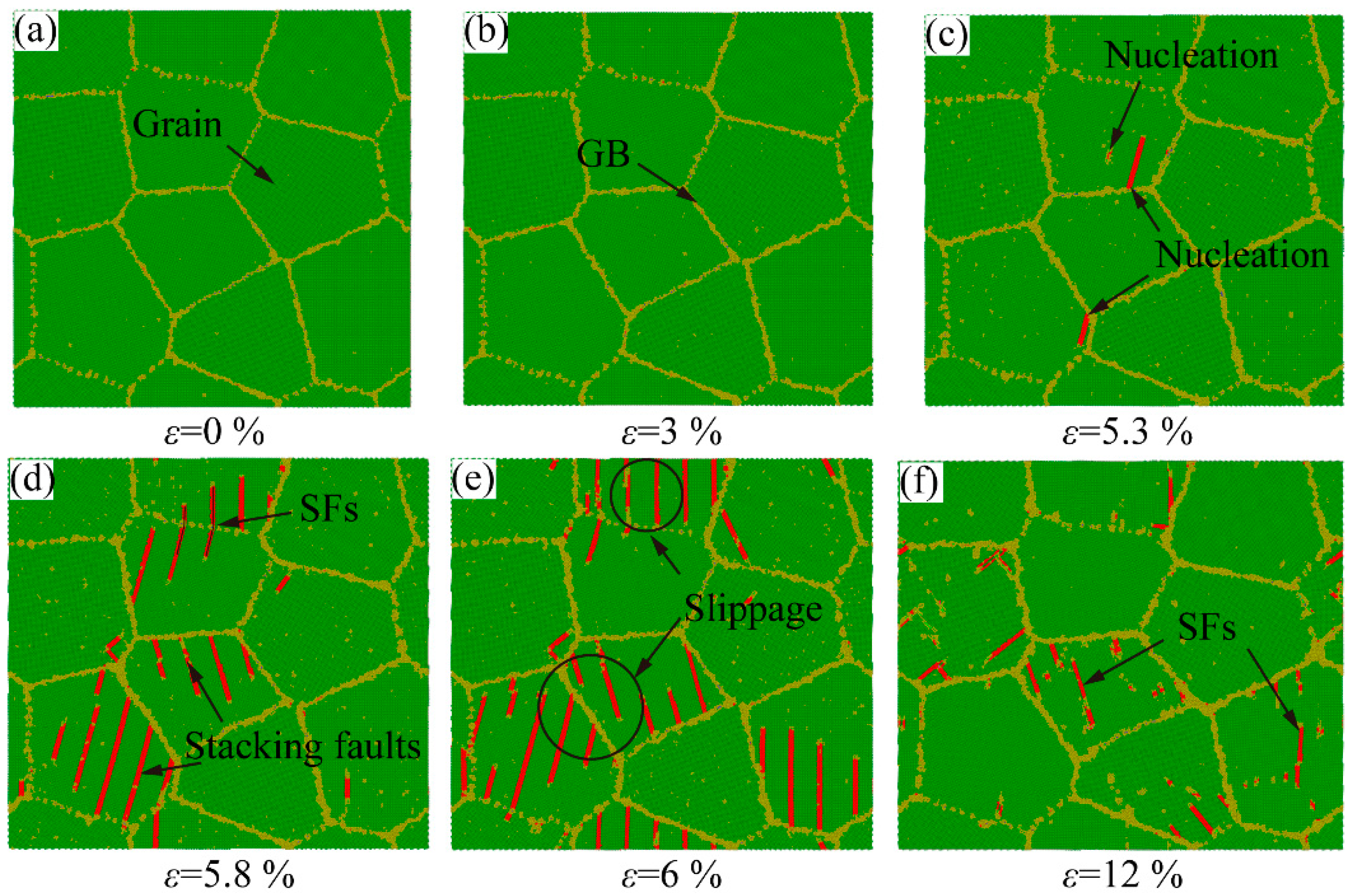
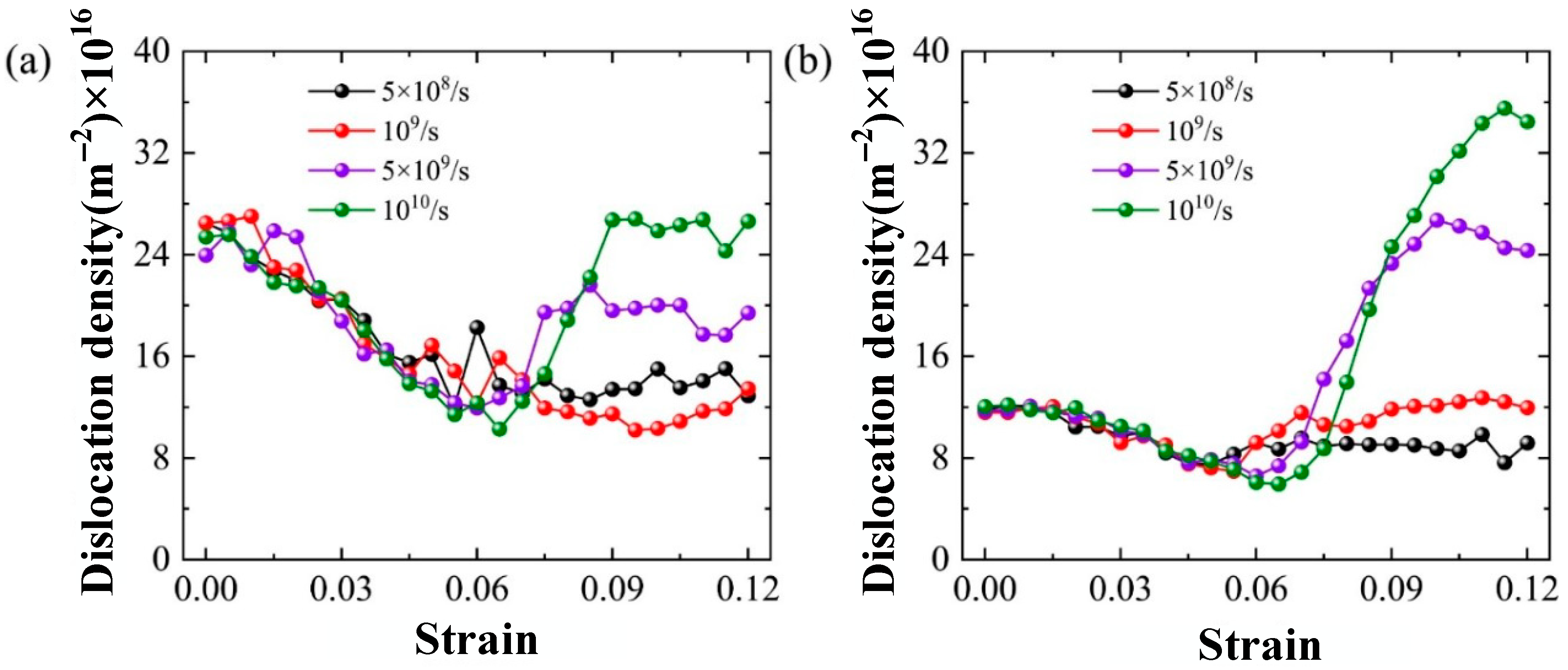
| Young’s Modulus (GPa) | Yield Stress (GPa) | Potential | |
|---|---|---|---|
| Zhu et al. [40] | 60 | 7.8 | Mishin [41] |
| This work1 | 59 | 7.8 | Mishin [41] |
| This work2 | 75 | 7.2 | Liu [29] |
| Model | Grain Size (nm) | x × y × z (nm3) | Number of Atoms |
|---|---|---|---|
| Model 1 | 5.1 | 16.2 × 16.2 × 4.9 | 74,796 |
| Model 2 | 7.0 | 22.3 × 22.3 × 4.9 | 142,512 |
| Model 3 | 10.1 | 32.0 × 32.0 × 4.9 | 295,944 |
| Model 4 | 12.8 | 40.5 × 40.5 × 4.9 | 475,224 |
| Model 5 | 16.0 | 50.6 × 50.6 × 4.9 | 744,096 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.-H.; Lu, C.; Shi, A.; Zhao, S.; Ou, B.; Wei, N. A Multi-Scale Study on Deformation and Failure Process of Metallic Structures in Extreme Environment. Int. J. Mol. Sci. 2022, 23, 14437. https://doi.org/10.3390/ijms232214437
Li Z-H, Lu C, Shi A, Zhao S, Ou B, Wei N. A Multi-Scale Study on Deformation and Failure Process of Metallic Structures in Extreme Environment. International Journal of Molecular Sciences. 2022; 23(22):14437. https://doi.org/10.3390/ijms232214437
Chicago/Turabian StyleLi, Zhi-Hui, Chenchen Lu, Aiqiang Shi, Sihan Zhao, Bingxian Ou, and Ning Wei. 2022. "A Multi-Scale Study on Deformation and Failure Process of Metallic Structures in Extreme Environment" International Journal of Molecular Sciences 23, no. 22: 14437. https://doi.org/10.3390/ijms232214437
APA StyleLi, Z.-H., Lu, C., Shi, A., Zhao, S., Ou, B., & Wei, N. (2022). A Multi-Scale Study on Deformation and Failure Process of Metallic Structures in Extreme Environment. International Journal of Molecular Sciences, 23(22), 14437. https://doi.org/10.3390/ijms232214437





