Multi-Trait Genomic Prediction Improves Accuracy of Selection among Doubled Haploid Lines in Maize
Abstract
:1. Introduction
2. Results
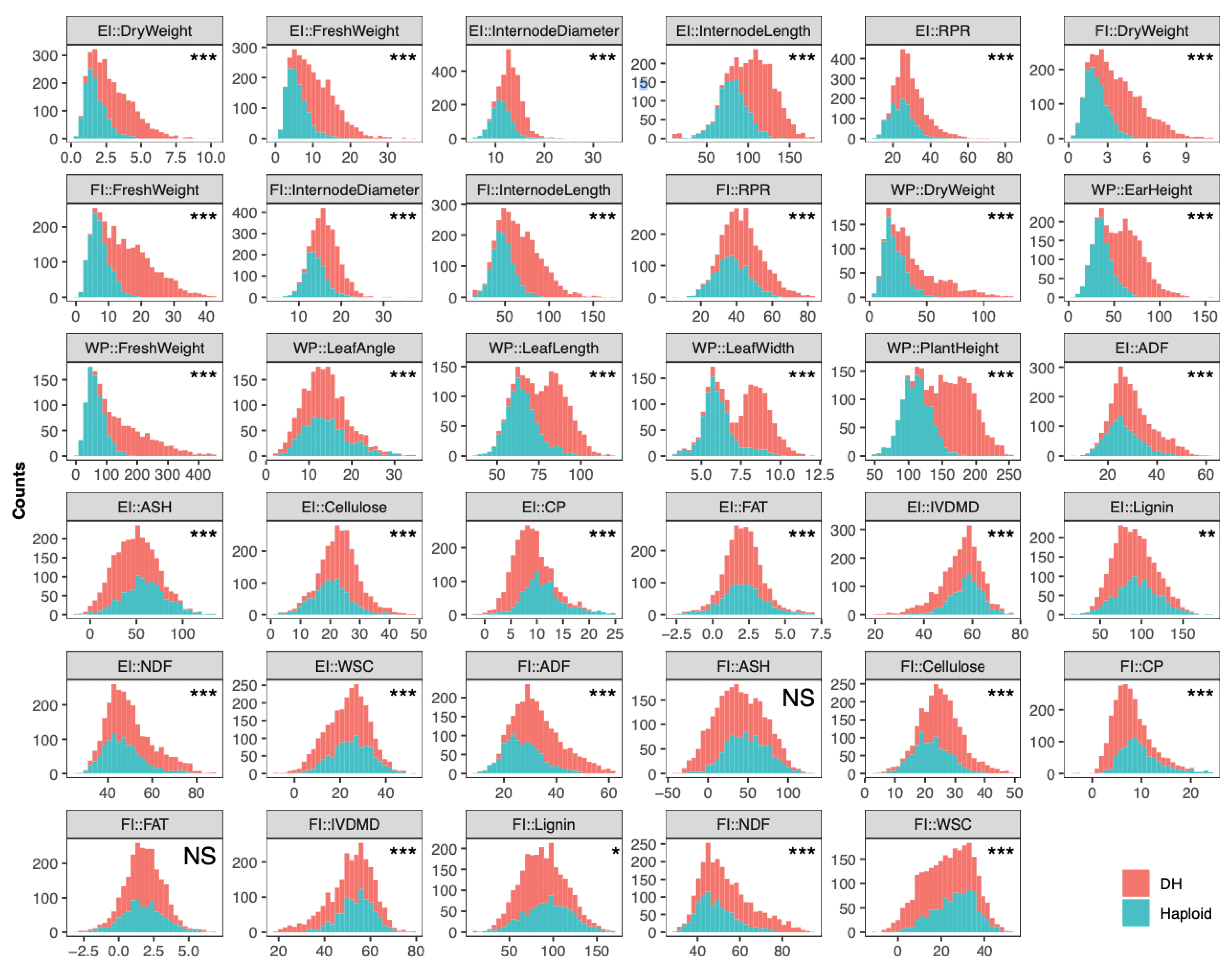
2.1. Characterizing Phenotypes of 35 Traits in DH and Corresponding Haploid Populations
2.2. Phenotypic and Genetic Correlations between DH and Haploid Lines
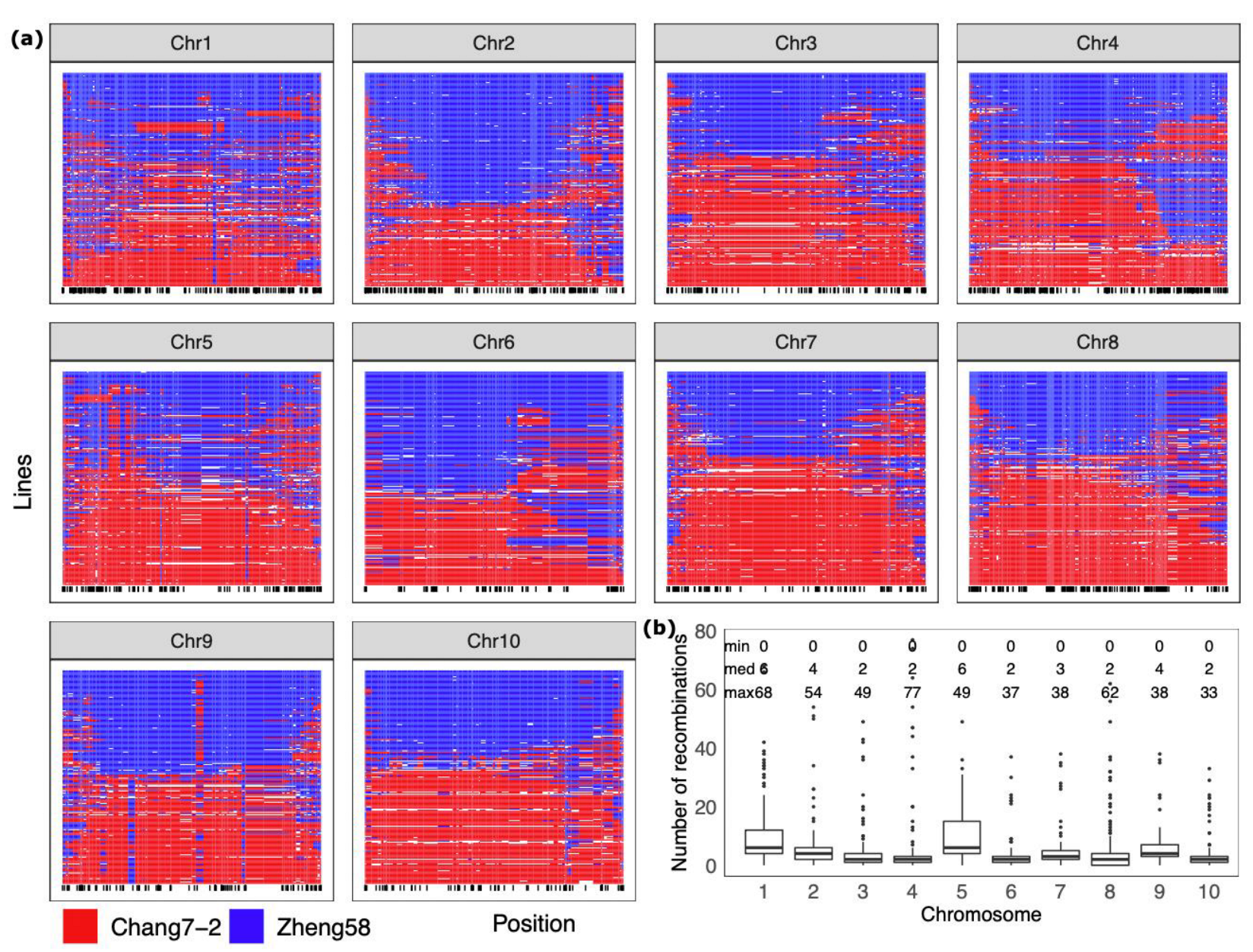
2.3. Characterization of Genomic Segment Composition of DH Lines
2.4. Genomic Prediction of Stalk Quality Traits Evaluated in the DH Population
2.4.1. Single-Environment Prediction in the DH Population
2.4.2. Multi-Environment Prediction in the DH Population
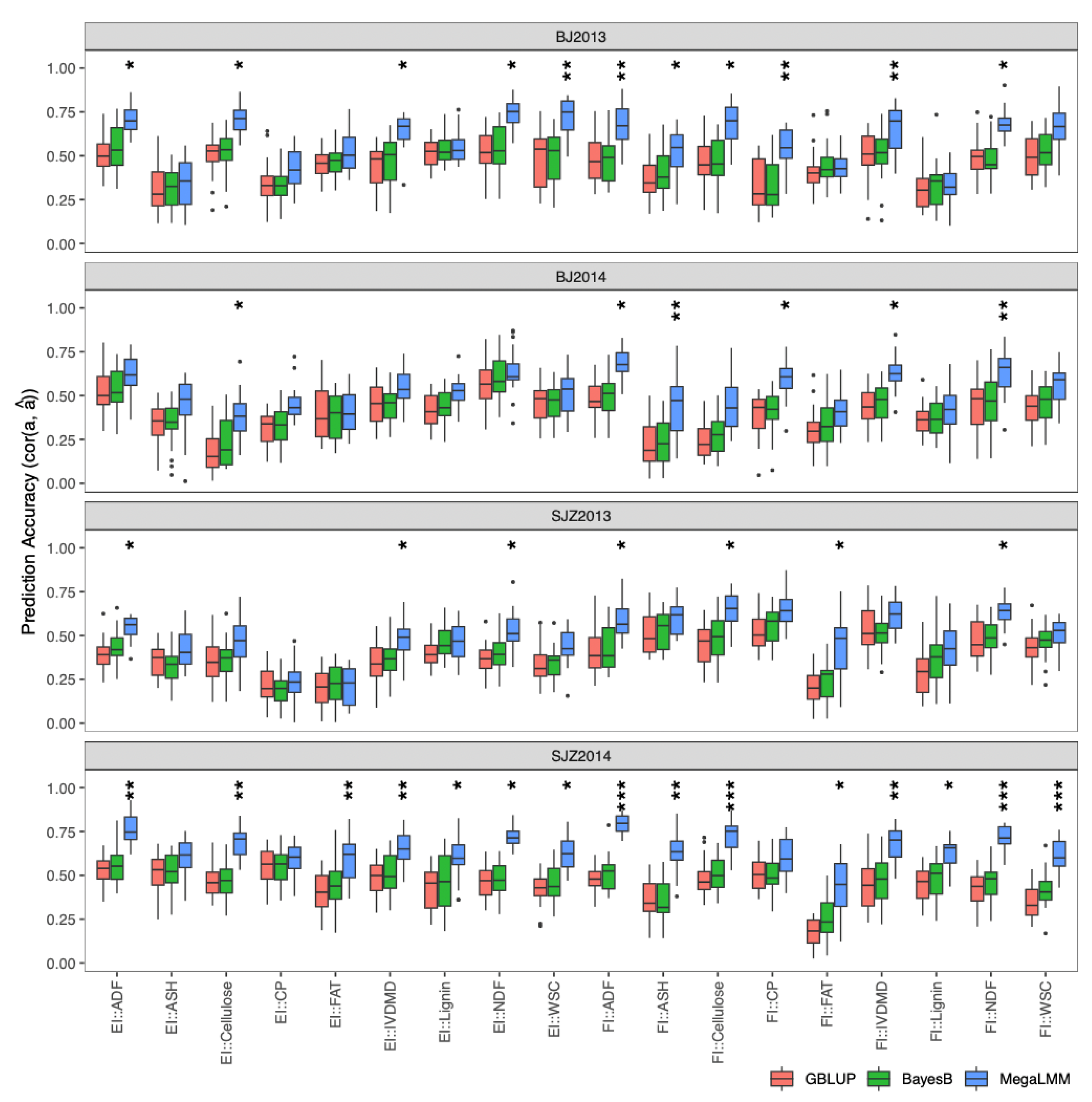
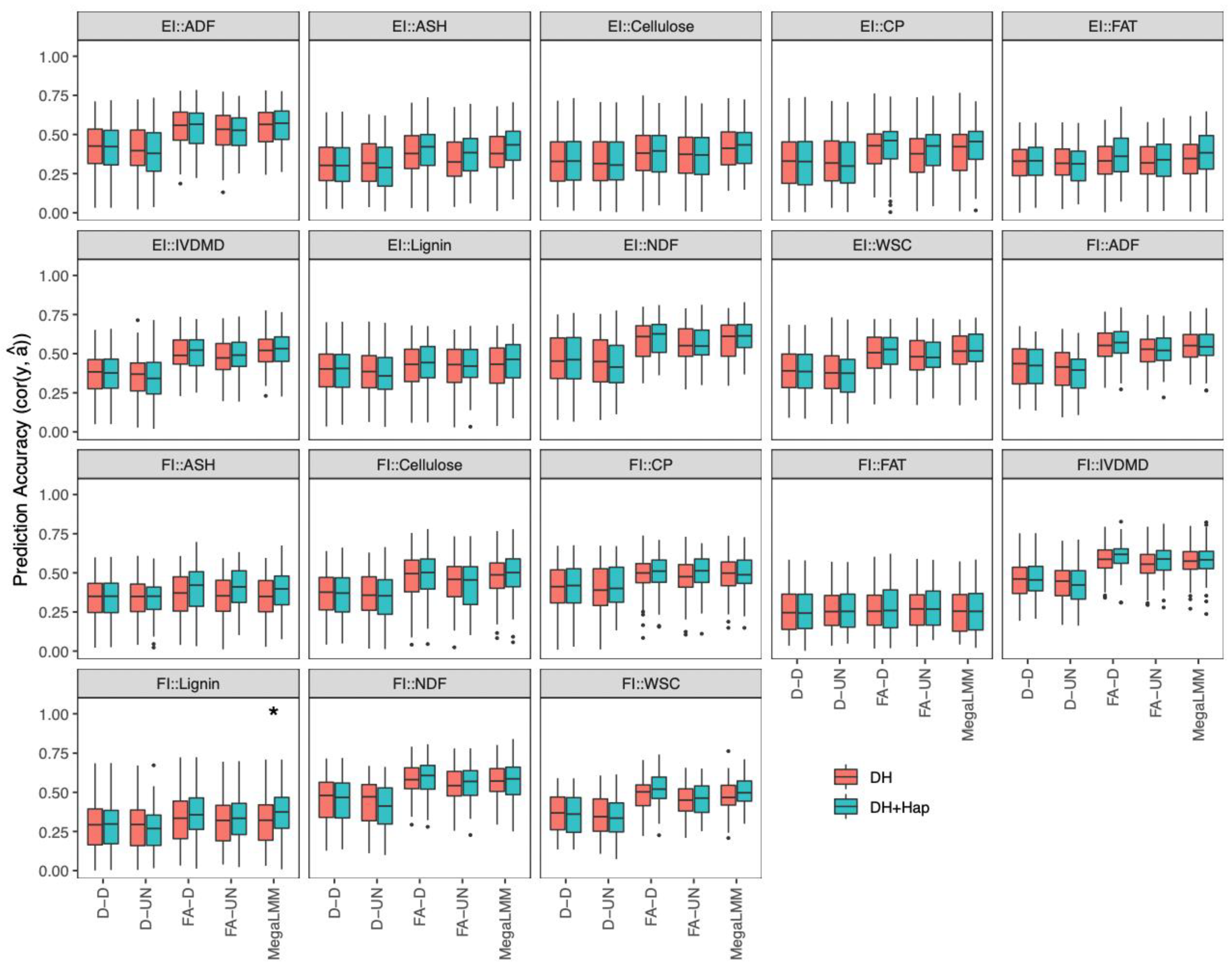
2.4.3. Prediction of DH Phenotypes with Both DHs and Haploids in a Single-Environment Trial
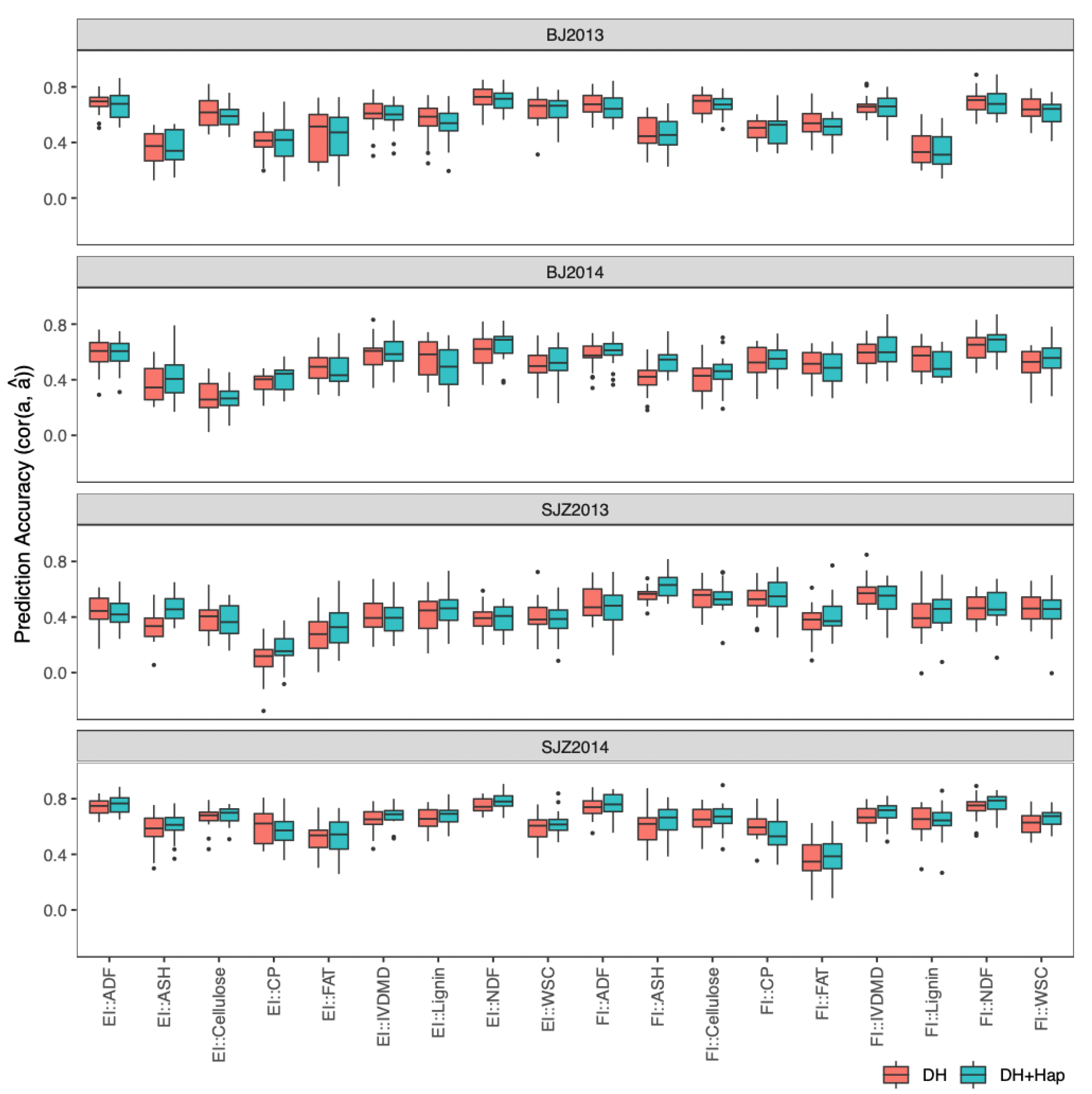
2.4.4. Prediction of DH Phenotypes with Both DHs and Haploids in Multi-Environment Trials
3. Discussion
4. Materials and Methods
4.1. Plant Materials and Field Experiments
4.2. Phenotype Evaluation and Analysis
4.3. Genotype Analysis
4.4. Estimation of Phenotypic and Genotypic Correlations between Haploid and Doubled Haploid (DH) Populations
4.5. Graphical Genotypes
4.6. Genomic Prediction
4.6.1. Single-Environment Prediction in the DH Population
4.6.2. Multi-Environment Prediction in the DH Population
4.6.3. Use Both DH and Haploid Lines to Predict DH Lines in a Single-Environment Trial
4.6.4. Use Both DH and Haploid Lines to Predict DH Lines in Multi-Environment Trials
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Melchinger, A.E.; Schipprack, W.; Würschum, T.; Chen, S.; Technow, F. Rapid and Accurate Identification of in Vivo-Induced Haploid Seeds Based on Oil Content in Maize. Sci. Rep. 2013, 3, 2129. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chaikam, V.; Nair, S.K.; Martinez, L.; Lopez, L.A.; Utz, H.F.; Melchinger, A.E.; Boddupalli, P.M. Marker-Assisted Breeding of Improved Maternal Haploid Inducers in Maize for the Tropical/Subtropical Regions. Front. Plant Sci. 2018, 871, 1–14. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chaikam, V.; Molenaar, W.; Melchinger, A.E.; Boddupalli, P.M. Doubled Haploid Technology for Line Development in Maize: Technical Advances and Prospects. Theor. Appl. Genet. 2019, 132, 3227–3243. [Google Scholar] [CrossRef] [Green Version]
- Geiger, H.H.; Gordillo, G.A.; Koch, S. Genetic Correlations among Haploids, Doubled Haploids, and Testcrosses in Maize. Crop Sci. 2013, 53, 2313–2320. [Google Scholar] [CrossRef]
- Valeriu, R. Selection and Breeding Experiments at the Haploid Level in Maize (Zea Mays L.). J. Plant Breed. Crop Sci. 2012, 4, 72–79. [Google Scholar] [CrossRef]
- Brauner, P.C.; Müller, D.; Schopp, P.; Böhm, J.; Bauer, E.; Schön, C.C.; Melchinger, A.E. Genomic Prediction within and among Doubled-Haploid Libraries from Maize Landraces. Genetics 2018, 210, 1185–1196. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, J.; Cheng, D.; Guo, S.; Yang, Z.; Chen, M.; Chen, C.; Jiao, Y.; Li, W.; Liu, C.; Zhong, Y.; et al. Genomic Selection to Optimize Doubled Haploid-Based Hybrid Breeding in Maize. bioRxiv 2020. [Google Scholar] [CrossRef]
- Wang, N.; Wang, H.; Zhang, A.; Liu, Y.; Yu, D.; Hao, Z.; Ilut, D.; Glaubitz, J.C.; Gao, Y.; Jones, E.; et al. Genomic Prediction across Years in a Maize Doubled Haploid Breeding Program to Accelerate Early-Stage Testcross Testing. Theor. Appl. Genet. 2020, 133, 2869–2879. [Google Scholar] [CrossRef] [PubMed]
- Beyene, Y.; Gowda, M.; Pérez-Rodríguez, P.; Olsen, M.; Robbins, K.R.; Burgueño, J.; Prasanna, B.M.; Crossa, J. Application of Genomic Selection at the Early Stage of Breeding Pipeline in Tropical Maize. Front. Plant Sci. 2021, 12, 685488. [Google Scholar] [CrossRef]
- Hill, W.G. Genetic correlation. In Brenner’s Encyclopedia of Genetics; Elsevier: Amsterdam, The Netherlands, 2013; pp. 237–239. [Google Scholar] [CrossRef]
- Ganal, M.W.; Durstewitz, G.; Polley, A.; Bérard, A.; Buckler, E.S.; Charcosset, A.; Clarke, J.D.; Graner, E.M.; Hansen, M.; Joets, J.; et al. A Large Maize (Zea Mays L.) SNP Genotyping Array: Development and Germplasm Genotyping, and Genetic Mapping to Compare with the B73 Reference Genome. PLoS ONE 2011, 6, e28334. [Google Scholar] [CrossRef] [Green Version]
- Burgueño, J.; de los Campos, G.; Weigel, K.; Crossa, J. Genomic Prediction of Breeding Values When Modeling Genotype × Environment Interaction Using Pedigree and Dense Molecular Markers. Crop Sci. 2012, 52, 707–719. [Google Scholar] [CrossRef] [Green Version]
- Runcie, D.; Cheng, H. Pitfalls and Remedies for Cross Validation with Multi-Trait Genomic Prediction Methods. G3 Genes Genomes Genet. 2019, 9, 3727–3741. [Google Scholar] [CrossRef] [Green Version]
- Bouckaert, R.R.; Frank, E. Evaluating the replicability of significance tests for comparing learning algorithms. In Advances in Knowledge Discovery and Data Mining. PAKDD 2004; Lecture Notes in Computer; Springer: Berlin/Heidelberg, Germany, 2004; Volume 3056, pp. 3–12. [Google Scholar] [CrossRef] [Green Version]
- Xu, S. Quantitative Genetics; Springer Nature Switzerland AG: Cham, Switzerland, 2022; ISBN 9783030839390. [Google Scholar]
- Mathew, B.; Léon, J.; Sillanpää, M.J. Impact of Residual Covariance Structures on Genomic Prediction Ability in Multienvironment Trials. PLoS ONE 2018, 13, e0201181. [Google Scholar] [CrossRef] [Green Version]
- Malosetti, M.; Bustos-Korts, D.; Boer, M.P.; Van Eeuwijk, F.A. Predicting Responses in Multiple Environments: Issues in Relation to Genotype × Environment Interactions. Crop Sci. 2016, 56, 2210–2222. [Google Scholar] [CrossRef]
- Montesinos-López, O.A.; Montesinos-López, A.; Crossa, J.; Toledo, F.H.; Pérez-Hernández, O.; Eskridge, K.M.; Rutkoski, J. A Genomic Bayesian Multi-Trait and Multi-Environment Model. G3 Genes Genomes Genet. 2016, 6, 2725–2774. [Google Scholar] [CrossRef] [Green Version]
- Hu, H.; Campbell, M.T.; Yeats, T.H.; Zheng, X.; Runcie, D.E.; Covarrubias-Pazaran, G.; Broeckling, C.; Yao, L.; Caffe-Treml, M.; Gutiérrez, L.; et al. Multi-Omics Prediction of Oat Agronomic and Seed Nutritional Traits across Environments and in Distantly Related Populations. Theor. Appl. Genet. 2021, 134, 4043–4054. [Google Scholar] [CrossRef] [PubMed]
- James Crow 90 Years Ago: The Beginning of Hybrid Maize. Genetics 1998, 148, 923–928. [CrossRef] [PubMed]
- Caballero, A. Quantitative Genetics; Cambridge University Press: Cambridge, UK, 2020; Volume 15, ISBN 2013206534. [Google Scholar]
- Xu, X.; Li, L.; Dong, X.; Jin, W.; Melchinger, A.E.; Chen, S. Gametophytic and Zygotic Selection Leads to Segregation Distortion through in Vivo Induction of a Maternal Haploid in Maize. J. Exp. Bot. 2013, 64, 1083–1096. [Google Scholar] [CrossRef]
- Hu, H.; Meng, Y.; Wang, H.; Liu, H.; Chen, S. Identifying Quantitative Trait Loci and Determining Closely Related Stalk Traits for Rind Penetrometer Resistance in a High-Oil Maize Population. Theor. Appl. Genet. 2012, 124, 1439–1447. [Google Scholar] [CrossRef]
- Meng, Y.; Li, J.; Liu, J.; Hu, H.; Li, W.; Liu, W.; Chen, S. Ploidy Effect and Genetic Architecture Exploration of Stalk Traits Using DH and Its Corresponding Haploid Populations in Maize. BMC Plant Biol. 2016, 16, 50. [Google Scholar] [CrossRef] [Green Version]
- Covarrubias-Pazaran, G. Genome-Assisted Prediction of Quantitative Traits Using the r Package Sommer. PLoS ONE 2016, 11, e0156744. [Google Scholar] [CrossRef] [Green Version]
- Pérez, P.; De Los Campos, G. Genome-Wide Regression and Prediction with the BGLR Statistical Package. Genetics 2014, 198, 483–495. [Google Scholar] [CrossRef] [PubMed]
- Isik, F.; Holland, J.; Maltecca, C. Genetic Data Analysis for Plant and Animal Breeding; Springer: Cham, Switzerland, 2017; ISBN 9783319551753. [Google Scholar]
- Wickham, H. Ggplot2: Elegant Graphics for Data Analysis; Springer Nature: Berlin, Germany, 2016; ISBN 978-0-387-98140-6. [Google Scholar]
- Endelman, J.B. Ridge Regression and Other Kernels for Genomic Selection with R Package rrBLUP. Plant Genome 2011, 4, 250–255. [Google Scholar] [CrossRef] [Green Version]
- Runcie, D.E.; Qu, J.; Cheng, H.; Crawford, L. MegaLMM: Mega-Scale Linear Mixed Models for Genomic Predictions with Thousands of Traits. Genome Biol. 2021, 22, 213. [Google Scholar] [CrossRef]

| BJ2014 | SJZ2014 | |||||||
|---|---|---|---|---|---|---|---|---|
| Trait | ||||||||
| Agronomic Traits | ||||||||
| EI::DryWeight | 0.37 | 0.32 | 0.35 | 0.72 | 0.39 | 0.28 | 0.42 | 0.72 |
| EI::FreshWeight | 0.45 | 0.38 | 0.40 | 0.77 | 0.53 | 0.39 | 0.48 | 0.82 |
| EI::InternodeDiameter | 0.26 | 0.26 | 0.31 | 0.62 | 0.46 | 0.37 | 0.42 | 0.80 |
| EI::InternodeLength | 0.37 | 0.37 | 0.38 | 0.77 | 0.48 | 0.47 | 0.48 | 0.79 |
| EI::mRPR | 0.21 | 0.20 | 0.09 | 0.21 | 0.56 | 0.53 | 0.51 | 0.88 |
| FI::DryWeight | 0.29 | 0.22 | 0.24 | 0.57 | 0.47 | 0.42 | 0.44 | 0.78 |
| FI::FreshWeight | 0.36 | 0.25 | 0.34 | 0.63 | 0.54 | 0.45 | 0.51 | 0.83 |
| FI::InternodeDiameter | 0.25 | 0.32 | 0.27 | 0.62 | 0.45 | 0.45 | 0.41 | 0.80 |
| FI::InternodeLength | 0.54 | 0.32 | 0.38 | 0.73 | 0.41 | 0.27 | 0.32 | 0.57 |
| FI::mRPR | 0.39 | 0.44 | 0.40 | 0.79 | 0.61 | 0.44 | 0.50 | 0.86 |
| WP::DryWeight | 0.36 | 0.44 | 0.44 | 0.78 | 0.54 | 0.51 | 0.59 | 0.88 |
| WP::EarHeight | 0.64 | 0.47 | 0.55 | 0.83 | 0.52 | 0.59 | 0.59 | 0.83 |
| WP::FreshWeight | 0.44 | 0.41 | 0.46 | 0.78 | 0.62 | 0.51 | 0.61 | 0.89 |
| WP::LeafAngle | 0.60 | 0.61 | 0.48 | 0.85 | 0.70 | 0.51 | 0.42 | 0.76 |
| WP::LeafLength | 0.66 | 0.56 | 0.63 | 0.89 | 0.58 | 0.64 | 0.64 | 0.91 |
| WP::LeafWidth | 0.36 | 0.36 | 0.46 | 0.79 | 0.30 | 0.41 | 0.34 | 0.66 |
| WP::PlantHeight | 0.53 | 0.43 | 0.52 | 0.82 | 0.49 | 0.57 | 0.54 | 0.80 |
| Stalk quality traits | ||||||||
| EI::ADF | 0.32 | 0.32 | 0.41 | 0.71 | 0.37 | 0.39 | 0.37 | 0.64 |
| EI::ASH | 0.22 | 0.25 | 0.22 | 0.53 | 0.33 | 0.26 | 0.33 | 0.59 |
| EI::Cellulose | 0.14 | 0.20 | 0.14 | 0.30 | 0.26 | 0.27 | 0.30 | 0.52 |
| EI::CP | 0.31 | 0.29 | 0.36 | 0.72 | 0.32 | 0.24 | 0.28 | 0.52 |
| EI::FAT | 0.21 | 0.20 | 0.19 | 0.43 | 0.24 | 0.16 | 0.15 | 0.32 |
| EI::IVDMD | 0.30 | 0.27 | 0.42 | 0.71 | 0.34 | 0.31 | 0.31 | 0.53 |
| EI::Lignin | 0.26 | 0.24 | 0.34 | 0.59 | 0.35 | 0.26 | 0.23 | 0.55 |
| EI::NDF | 0.41 | 0.36 | 0.53 | 0.79 | 0.37 | 0.29 | 0.34 | 0.62 |
| EI::WSC | 0.29 | 0.28 | 0.38 | 0.67 | 0.27 | 0.21 | 0.27 | 0.45 |
| FI::ADF | 0.39 | 0.40 | 0.49 | 0.81 | 0.36 | 0.31 | 0.29 | 0.59 |
| FI::ASH | 0.17 | 0.24 | 0.21 | 0.46 | 0.23 | 0.26 | 0.19 | 0.37 |
| FI::Cellulose | 0.22 | 0.30 | 0.30 | 0.64 | 0.29 | 0.30 | 0.30 | 0.53 |
| FI::CP | 0.28 | 0.28 | 0.27 | 0.56 | 0.32 | 0.28 | 0.23 | 0.49 |
| FI::FAT | 0.17 | 0.22 | 0.06 | 0.26 | 0.19 | 0.15 | 0.06 | 0.14 |
| FI::IVDMD | 0.39 | 0.34 | 0.50 | 0.80 | 0.40 | 0.34 | 0.29 | 0.60 |
| FI::Lignin | 0.20 | 0.20 | 0.25 | 0.47 | 0.38 | 0.29 | 0.22 | 0.47 |
| FI::NDF | 0.40 | 0.35 | 0.51 | 0.79 | 0.39 | 0.29 | 0.31 | 0.63 |
| FI::WSC | 0.24 | 0.27 | 0.34 | 0.65 | 0.32 | 0.28 | 0.32 | 0.62 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, H.; Meng, Y.; Liu, W.; Chen, S.; Runcie, D.E. Multi-Trait Genomic Prediction Improves Accuracy of Selection among Doubled Haploid Lines in Maize. Int. J. Mol. Sci. 2022, 23, 14558. https://doi.org/10.3390/ijms232314558
Hu H, Meng Y, Liu W, Chen S, Runcie DE. Multi-Trait Genomic Prediction Improves Accuracy of Selection among Doubled Haploid Lines in Maize. International Journal of Molecular Sciences. 2022; 23(23):14558. https://doi.org/10.3390/ijms232314558
Chicago/Turabian StyleHu, Haixiao, Yujie Meng, Wenxin Liu, Shaojiang Chen, and Daniel E. Runcie. 2022. "Multi-Trait Genomic Prediction Improves Accuracy of Selection among Doubled Haploid Lines in Maize" International Journal of Molecular Sciences 23, no. 23: 14558. https://doi.org/10.3390/ijms232314558
APA StyleHu, H., Meng, Y., Liu, W., Chen, S., & Runcie, D. E. (2022). Multi-Trait Genomic Prediction Improves Accuracy of Selection among Doubled Haploid Lines in Maize. International Journal of Molecular Sciences, 23(23), 14558. https://doi.org/10.3390/ijms232314558







