Theoretical Analysis of Polynuclear Zinc Complexes Isolobally Related to Hydrocarbons
Abstract
:1. Introduction
2. Results and Discussion
2.1. The Zn–Zn Bond: Experimental Data
2.2. The Isolobal Analogies of CpZn, PhZn and Zn(CO)2 Fragments
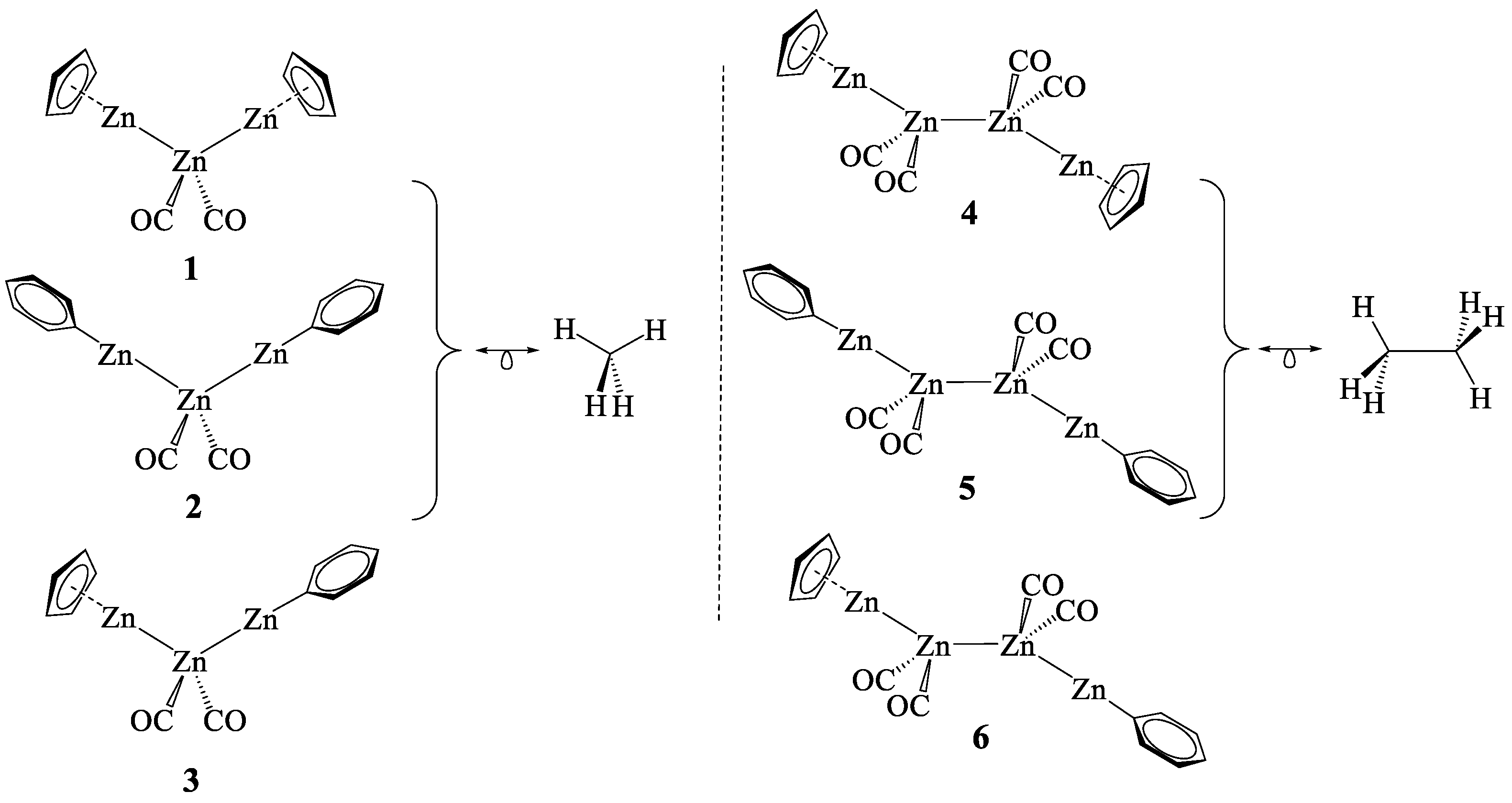
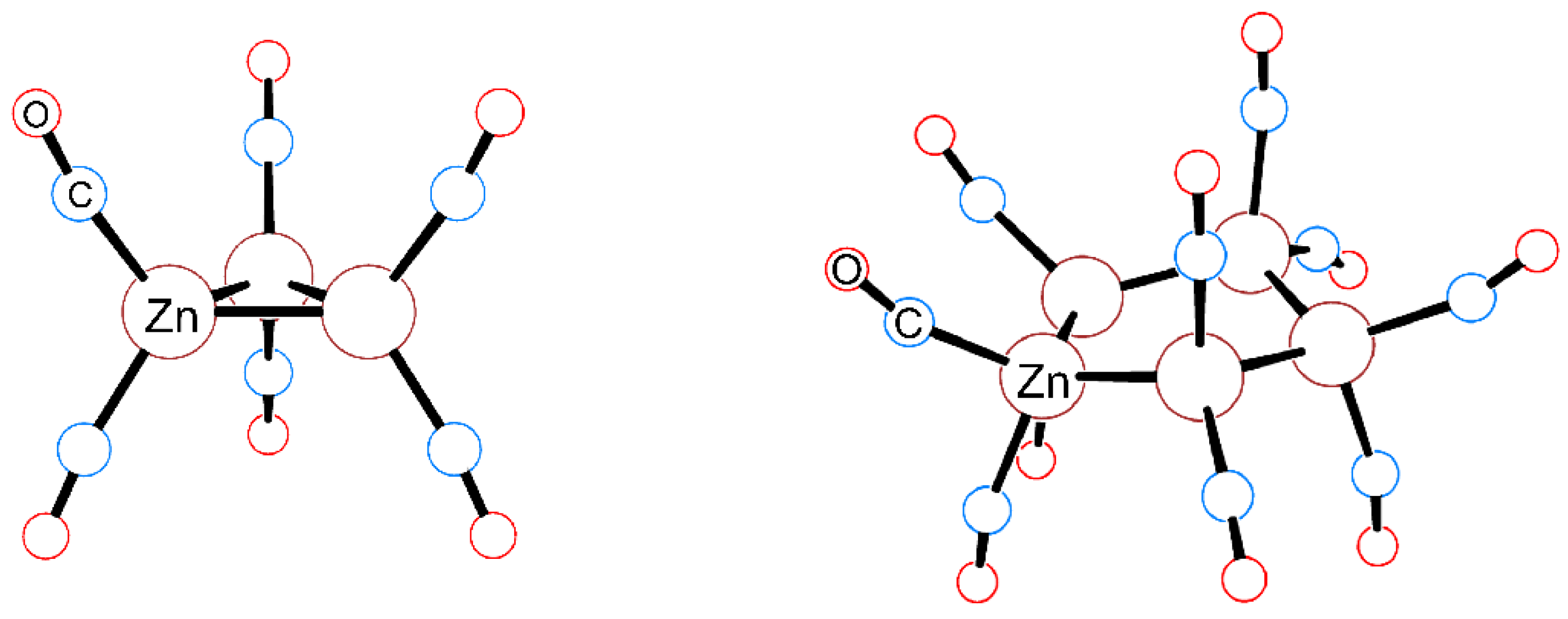
2.3. The Zn–Zn Bond in Complexes 1–6
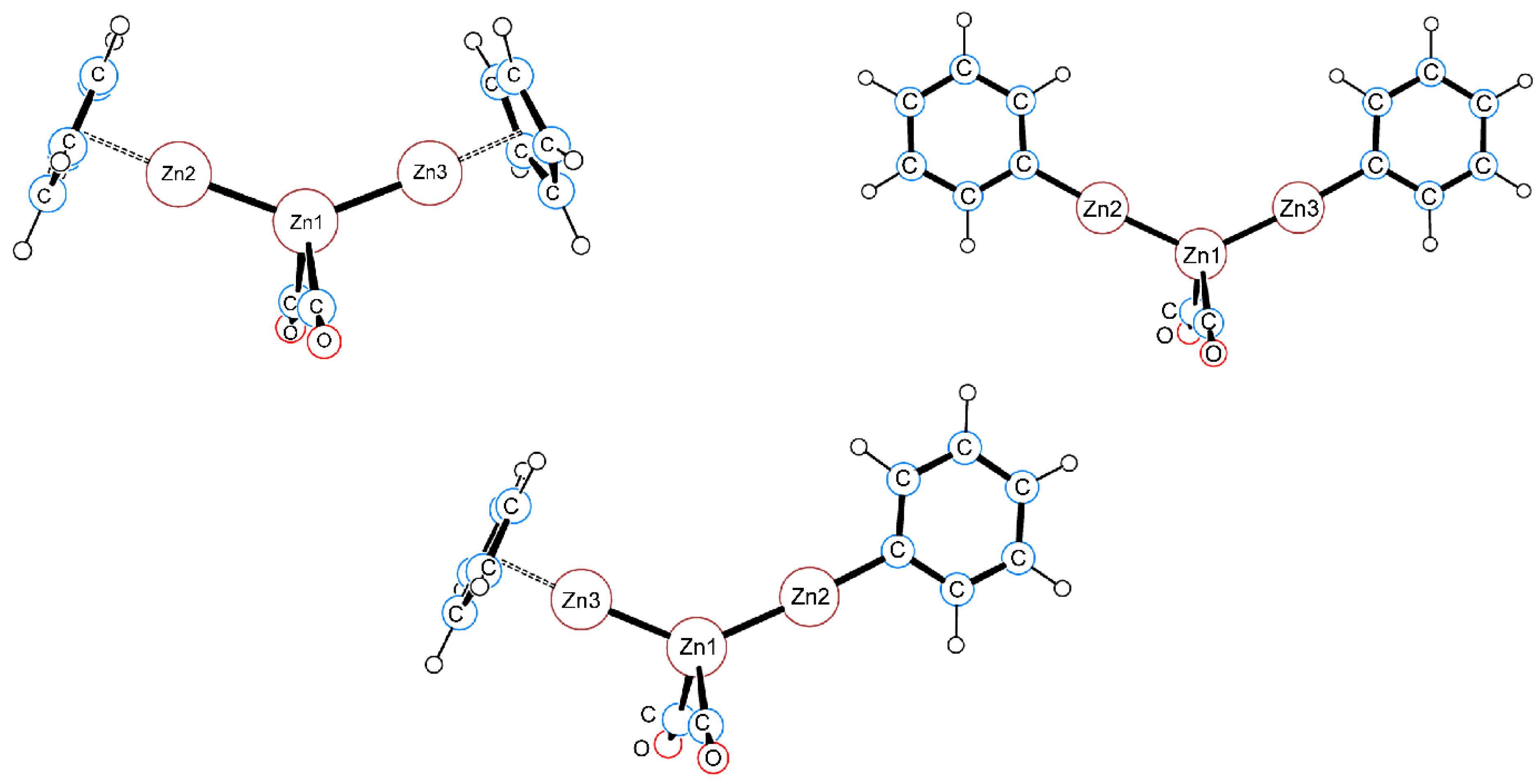
2.4. QTAIM Analysis of the Zn–Zn Bond in Complexes 1–6
2.5. The Zn–Zn Bond in Complexes 7 and 8
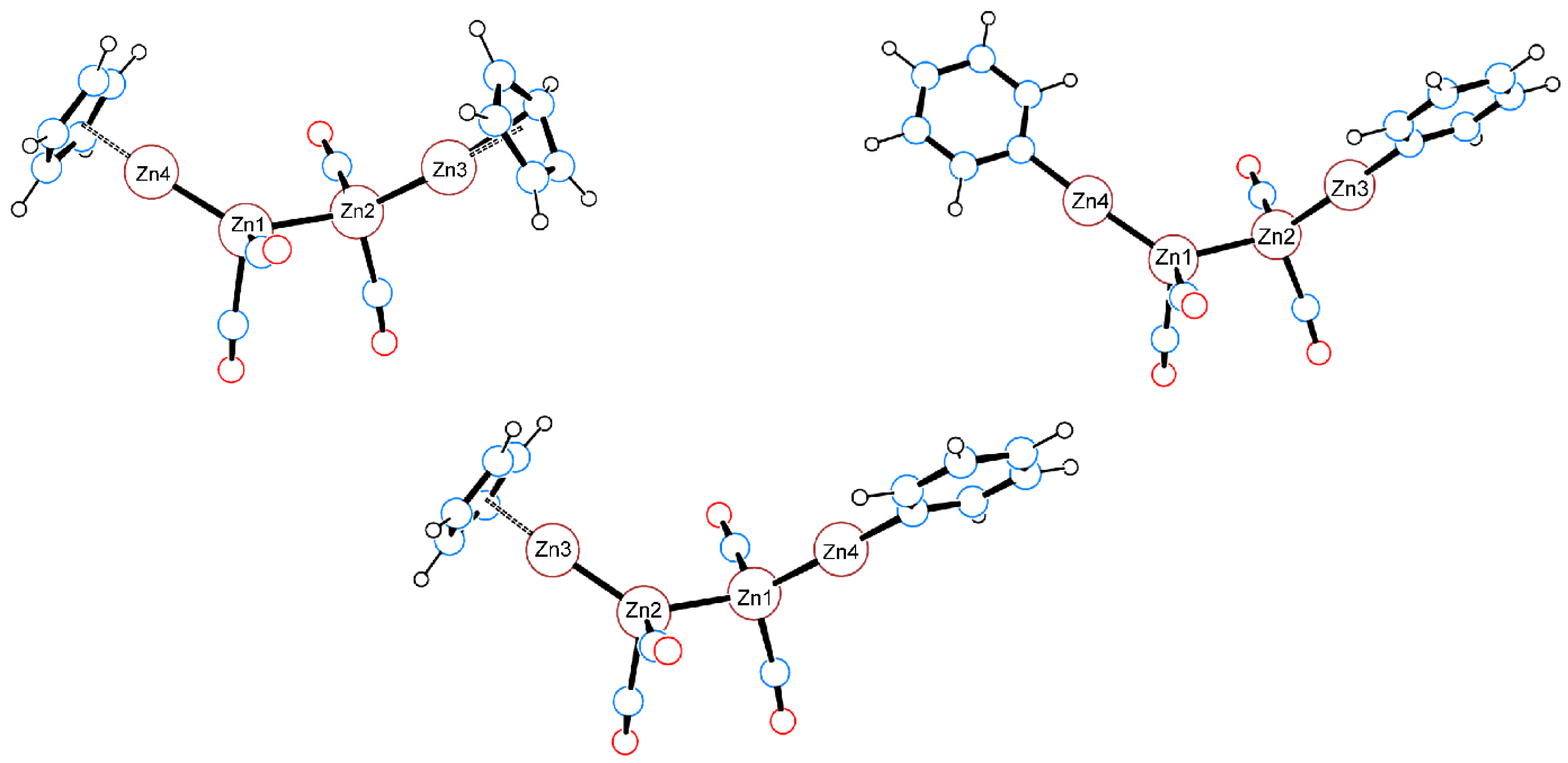
2.6. QTAIM Analysis of the Zn–Zn Bond in Complexes 7–8
2.7. The Source Function and Electron Localization Function in Complexes 1–8
3. Materials and Methods
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Resa, I.; Carmona, E.; Gutierrez-Puebla, E.; Monge, A. Decamethyldizincocene, a stable compound of Zn(I) with a Zn-Zn bond. Science 2004, 305, 1136–1138. [Google Scholar] [CrossRef] [PubMed]
- Grirrane, A.; Resa, I.; Rodriguez, A.; Carmona, E.; Alvarez, E.; Gutierrez-Puebla, E.; Monge, A.; Galindo, A.; del Río, D.; Andersen, R.A. Zinc-zinc bonded zincocene structures. Synthesis and characterization of Zn2(eta5-C5Me5)2 and Zn2(eta5-C5Me4Et)2. J. Am. Chem. Soc. 2007, 129, 693–703. [Google Scholar] [CrossRef] [PubMed]
- Del Río, D.; Galindo, A.; Resa, I.; Carmona, E. Theoretical and synthetic studies on [Zn2(η5- C5Me5)2]: Analysis of the Zn-Zn bonding interaction. Angew. Chem.—Int. Ed. 2005, 44, 1244–1247. [Google Scholar] [CrossRef]
- Van der Maelen, J.F.; Gutiérrez-Puebla, E.; Monge, A.; García-Granda, S.; Resa, I.; Carmona, E.; Fernández-Díaz, M.T.; McIntyre, G.J.; Pattison, P.; Weber, H.P. Experimental and theoretical characterization of the Zn-Zn bond in [Zn2(eta5-C5Me5)2]. Acta Crystallogr. B. 2007, 63, 862–868. [Google Scholar] [CrossRef] [Green Version]
- del Rio, D.; Resa, I.; Rodriguez, A.; Sánchez, L.; Köppe, R.; Downs, A.J.; Tang, C.Y.; Carmona, E. IR and Raman characterization of the zincocenes (eta(5)-C5Me5)2Zn2 and (eta(5)-C5Me5)(eta(1)-C5Me5)Zn. J. Phys. Chem. A 2008, 112, 10516–10525. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Z.; Wright, R.J.; Olmstead, M.M.; Rivard, E.; Brynda, M.; Power, P.P. A zinc-zinc-bonded compound and its derivatives bridged by one or two hydrogen atoms: A new type of Zn-Zn bonding. Angew. Chem.—Int. Ed. 2006, 45, 5807–5810. [Google Scholar] [CrossRef]
- Zhu, Z.; Brynda, M.; Wright, R.J.; Fischer, R.C.; Merrill, W.A.; Rivard, E.; Wolf, R.; Fettinger, J.C.; Olmstead, M.M.; Power, P.P. Synthesis and Characterization of the Homologous M—M Bonded Series Ar′MMAr′ (M) Zn, Cd, or Hg; Ar′) Hydride Species. J. Am. Chem. Soc. 2007, 129, 10847–10857. [Google Scholar] [CrossRef]
- Freitag, K.; Banh, H.; Ganesamoorthy, C.; Gemel, C.; Seidel, R.W.; Fischer, R.A. Cp* as a removable protecting group: Low valent Zn(i) compounds by reductive elimination, protolytic and oxidative cleavage of Zn–Cp*. Dalton Trans. 2013, 42, 10540–10544. [Google Scholar] [CrossRef]
- Fedushkin, I.L.; Skatova, A.A.; Ketkov, S.Y.; Eremenko, O.V.; Piskunov, A.V.; Fukin, G.K. [(dpp-bian)Zn-Zn(dpp-bian)]: A zinc-zinc-bonded compound supported by radical-anionic ligands. Angew. Chem.—Int. Ed. 2007, 46, 4302–4305. [Google Scholar] [CrossRef]
- Fedushkin, I.L.; Eremenko, O.V.; Skatova, A.A.; Piskunov, A.V.; Fukin, G.K.; Ketkov, S.Y.; Irran, E.; Schumann, H. Binuclear zinc complexes with radical-anionic diimine ligands. Organometallics 2009, 28, 3863–3868. [Google Scholar] [CrossRef]
- Schuchmann, D.; Westphal, U.; Schulz, S.; Flörke, U.; Bläser, D.; Boese, R. The reaction of dizincocene with preservation of the Zn-Zn bond. Angew. Chem.—Int. Ed. 2009, 48, 807–810. [Google Scholar] [CrossRef] [PubMed]
- Nayek, H.P.; Lühl, A.; Schulz, S.; Köppe, R.; Roesky, P.W. Aminotroponiminatozinc(I) complexes: Syntheses and spectroscopic analyses. Chem.—A Eur. J. 2011, 17, 1773–1777. [Google Scholar] [CrossRef] [PubMed]
- Tsai, Y.C.; Lu, D.Y.; Lin, Y.M.; Hwang, J.K.; Yu, J.S.K. Structural transformations in dinuclear zinc complexes involving Zn-Zn bonds. Chem. Commun. 2007, 4125–4127. [Google Scholar] [CrossRef] [Green Version]
- Yu, J.; Yang, X.J.; Liu, Y.; Pu, Z.; Li, Q.S.; Xie, Y.; Schaefer, H.F.; Wu, B. Dinuclear versus mononuclear zinc compounds from reduction of LZnCl2 (L = α-diimine ligands): Effects of the ligand substituent, reducing agent, and solvent. Organometallics 2008, 27, 5800–5805. [Google Scholar] [CrossRef]
- Grirrane, A.; Resa, I.; Rodriguez, A.; Carmona, E. Synthesis and structural characterization of dizincocenes Zn2(eta(5)-C5Me5)2 and Zn2(eta(5)-C5Me4Et)2. Coord. Chem. Rev. 2008, 252, 1532–1539. [Google Scholar] [CrossRef]
- Li, T.; Schulz, S.; Roesky, P.W. Synthesis, reactivity and applications of zinc-zinc bonded complexes. Chem. Soc. Rev. 2012, 41, 3759–3771. [Google Scholar] [CrossRef]
- Carmona, E.; Galindo, A. Direct bonds between metal atoms: Zn, Cd, and Hg compounds with metal-metal bonds. Angew. Chem.—Int. Ed. 2008, 47, 6526–6536. [Google Scholar] [CrossRef]
- Jin, L.; Fu, L.; Ding, Y.H. Zinc(0) chemistry: Does the missing 18-electron zinc tricarbonyl really exist? Phys. Chem. Chem. Phys. 2010, 12, 10956–10962. [Google Scholar] [CrossRef]
- Echeverría, J.; Falceto, A.; Alvarez, S. Zinc–Zinc Double Bonds: A Theoretical Study. Angew. Chem.—Int. Ed. 2017, 56, 10151–10155. [Google Scholar] [CrossRef]
- Saha, R.; Pan, S.; Chattaraj, P.K.; Merino, G. Filling the void: Controlled donor-acceptor interaction facilitates the formation of an M-M single bond in the zero oxidation state of M (M = Zn, Cd, Hg). Dalton Trans. 2020, 49, 1056–1064. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, M.; Wu, S.; Zhong, R.; Liu, Y.; Arif, A.M.; Geng, Y.; Su, Z. All-Metallic Zn=Zn Double-π Bonded Octahedral Zn2M4 (M=Li, Na) Clusters with Negative Oxidation State of Zinc. Chem. Phys. Chem. 2020, 21, 459–463. [Google Scholar] [CrossRef]
- Li, D.Z.; Zhang, L.J.; Pei, L. On the nature of bonding in a new boronyl species Zn2(BO)2: A linear four-center two-electron σ bond. Phys. Chem. Chem. Phys. 2022, 24, 287–294. [Google Scholar] [CrossRef]
- Kalita, A.J.; Sarmah, K.; Guha, A.K. Weak Zinc-Zinc slipped triple bond in Zn2Li6 cluster. Polyhedron 2022, 225, 116032. [Google Scholar] [CrossRef]
- Ayala, R.; Carmona, E.; Galindo, A. The dizinc bond as a ligand: A computational study of elongated dizinc bonds. Inorg. Chim. Acta 2018, 470, 197–205. [Google Scholar] [CrossRef] [Green Version]
- Ayala, R.; Galindo, A. A theoretical study of the bonding capabilities of the zinc-zinc double bond. Int. J. Quantum. Chem. 2019, 119, e25823. [Google Scholar] [CrossRef]
- Ayala, R.; Galindo, A. A QTAIM and DFT study of the dizinc bond in non-symmetric [CpZn2Ln] complexes. J. Organomet. Chem. 2019, 898, 120878. [Google Scholar] [CrossRef]
- Bader, R.F.W. Atoms in Molecules: A Quantum Theory; Clarendon Press: Oxford, UK, 1990; ISBN 9780198558651. [Google Scholar]
- Popelier, P.L.A. Atoms in Molecules. An Introduction; Prentice Hall: London, UK, 2000. [Google Scholar]
- Bader, R.F.W. The Quantum Mechanical Basis of Conceptual Chemistry. Mon. für Chem.—Chem. Mon. 2005, 136, 819–854. [Google Scholar] [CrossRef]
- Bader, R.F.W. A quantum theory of molecular structure and its applications. Chem. Rev. 1991, 91, 893–928. [Google Scholar] [CrossRef]
- Cortés-Guzmán, F.; Bader, R.F.W. Complementarity of QTAIM and MO theory in the study of bonding in donor–acceptor complexes. Coord. Chem. Rev. 2005, 249, 633–662. [Google Scholar] [CrossRef]
- Groom, C.R.; Bruno, I.J.; Lightfoot, M.P.; Ward, S.C. The Cambridge structural database. Acta Crystallogr. Sect. B Struct. Sci. Cryst. Eng. Mater. 2016, 72, 171–179. [Google Scholar] [CrossRef]
- Cordero, B.; Gómez, V.; Platero-Prats, A.E.; Revés, M.; Echeverría, J.; Cremades, E.; Barragán, F.; Alvarez, S. Covalent radii revisited. J. Chem. Soc. Dalton Trans. 2008, 21, 2832–2838. [Google Scholar] [CrossRef] [PubMed]
- Jiang, S.; Chen, M.; Xu, X. Formation of Zn-Zn and Zn-Pd Bonded Complexes by Reactions of Terminal Zinc Hydrides with Pd(II) Species. Inorg. Chem. 2019, 58, 13213–13220. [Google Scholar] [CrossRef]
- Chen, M.; Jiang, S.; Maron, L.; Xu, X. Transition metal-induced dehydrogenative coupling of zinc hydrides. Dalton Trans. 2019, 48, 1931–1935. [Google Scholar] [CrossRef] [PubMed]
- Bollermann, T.; Gemel, C.; Fischer, R.A. Organozinc ligands in transition metal chemistry. Coord. Chem. Rev. 2012, 256, 537–555. [Google Scholar] [CrossRef]
- Banh, H.; Dilchert, K.; Schulz, C.; Gemel, C.; Seidel, R.W.; Gautier, R.; Kahlal, S.; Saillard, J.-Y.; Fischer, R.A. Atom-Precise Organometallic Zinc Clusters. Angew. Chem. Int. Ed. 2016, 55, 3285–3289. [Google Scholar] [CrossRef] [PubMed]
- Banh, H.; Hornung, J.; Kratz, T.; Gemel, C.; Pöthig, A.; Gam, F.; Kahlal, S.; Saillard, J.Y.; Fischer, R.A. Embryonic brass: Pseudo two electron Cu/Zn clusters. Chem. Sci. 2018, 9, 8906–8913. [Google Scholar] [CrossRef] [PubMed]
- Molon, M.; Gemel, C.; Fischer, R.A. From AlCp*- and GaCp*-ligated ruthenium hydrides to zinc-rich heterometallic complexes. Eur. J. Inorg. Chem. 2013, 2013, 3616–3622. [Google Scholar] [CrossRef]
- Bollermann, T.; Freitag, K.; Gemel, C.; Seidel, R.W.; Fischer, R.A. Reactivity of [Zn2Cp*2] toward transition-metal complexes: Synthesis and characterization of [Cp*M(ZnCp*)3] (M = Ni, Pd, Pt). Organometallics 2011, 30, 4123–4127. [Google Scholar] [CrossRef]
- Freitag, K.; Molon, M.; Jerabek, P.; Dilchert, K.; Rösler, C.; Seidel, R.W.; Gemel, C.; Frenking, G.; Fischer, R.A. Zn⋯Zn interactions at nickel and palladium centers. Chem. Sci. 2016, 7, 6413–6421. [Google Scholar] [CrossRef] [Green Version]
- Freitag, K.; Gemel, C.; Jerabek, P.; Oppel, I.M.; Seidel, R.W.; Frenking, G.; Banh, H.; Dilchert, K.; Fischer, R.A. The σ-aromatic clusters [Zn3]+ and [Zn2Cu]: Embryonic brass. Angew. Chem.—Int. Ed. 2015, 54, 4370–4374. [Google Scholar] [CrossRef]
- Hicks, J.; Underhill, E.J.; Kefalidis, C.E.; Maron, L.; Jones, C. A Mixed-Valence Tri-Zinc Complex, [LZnZnZnL] (L=Bulky Amide), Bearing a Linear Chain of Two-Coordinate Zinc Atoms. Angew. Chem.—Int. Ed. 2015, 54, 10000–10004. [Google Scholar] [CrossRef]
- Gervasio, G.; Bianchi, R.; Marabello, D. About the topological classification of the metal-metal bond. Chem. Phys. Lett. 2004, 387, 481–484. [Google Scholar] [CrossRef]
- Cremer, D.; Kraka, E. A Description of the Chemical Bond in Terms of Local Properties of Electron Density and Energy, in Conceptual Approaches in Quantum Chemistry—Models and Applications. Croat. Chem. Acta 1984, 57, 1259–1281. [Google Scholar]
- Macchi, P.; Proserpio, D.M.; Sironi, A. Experimental electron density in a transition metal dimer: Metal-metal and metal-ligand bonds. J. Am. Chem. Soc. 1998, 120, 13429–13435. [Google Scholar] [CrossRef]
- Macchi, P.; Sironi, A. Chemical bonding in transition metal carbonyl clusters: Complementary analysis of theoretical and experimental electron densities. Coord. Chem. Rev. 2003, 238–239, 383–412. [Google Scholar] [CrossRef]
- Espinosa, E.; Alkorta, I.; Elguero, J.; Molins, E. From weak to strong interactions: A comprehensive analysis of the topological and energetic properties of the electron density distribution involving X-H⋯F-Y systems. J. Chem. Phys. 2002, 117, 5529–5542. [Google Scholar] [CrossRef]
- Chu, T.; Belding, L.; Poddutoori, P.K.; Van Der Est, A.; Dudding, T.; Korobkov, I.; Nikonov, G.I. Unique molecular geometries of reduced 4- and 5-coordinate zinc complexes stabilised by diiminopyridine ligand. Dalton Trans. 2016, 45, 13440–13448. [Google Scholar] [CrossRef]
- Cadenbach, T.; Gemel, C.; Fischer, R.A. Molecular cut-outs of Mo/Zn hume-rothery phases: Synthesis and structure of [{Mo(CO)4}4(Zn)6(μ-ZnCp*)4]. Angew. Chem.—Int. Ed. 2008, 47, 9146–9149. [Google Scholar] [CrossRef]
- Czajkowski, M.A.; Koperski, J. The Cd2 and Zn2 van der Waals dimers revisited. Correction for some molecular potential parameters. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 1999, 55, 2221–2229. [Google Scholar] [CrossRef]
- Van der Maelen, J.F.; Cabeza, J.A. A topological analysis of the bonding in [M2(CO)10] and [M3(μ-H)3(CO)12] complexes (M = Mn, Tc, Re). Theor. Chem. Acc. 2016, 135, 64. [Google Scholar] [CrossRef]
- Becke, A.D.; Edgecombe, K.E. A simple measure of electron localization in atomic and molecular systems. J. Chem. Phys. 1990, 92, 5397–5403. [Google Scholar] [CrossRef]
- Silvi, B.; Savin, A. Classification of chemical bonds based on topological analysis of electron localization functions. Nature 1994, 371, 683–686. [Google Scholar] [CrossRef]
- Staroverov, V.N.; Scuseria, G.E.; Tao, J.; Perdew, J.P. Comparative assessment of a new nonempirical density functional: Molecules and hydrogen-bonded complexes. J. Chem. Phys. 2003, 119, 12129–12137. [Google Scholar] [CrossRef]
- Tao, J.; Perdew, J.P.; Staroverov, V.N.; Scuseria, G.E. Climbing the density functional ladder: Nonempirical meta–generalized gradient approximation designed for molecules and solids. Phys. Rev. Lett. 2003, 91, 146401. [Google Scholar] [CrossRef] [Green Version]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision C.01; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Glendening, E.D.; Reed, A.E.; Carpenter, J.E.; Weinhold, F. NBO Version 3.1.; Gaussian Inc.: Pittsburgh, PA, USA, 2003. [Google Scholar]
- Keith, T.A. AIMALL; Version 16.05.18; TK Gristmill Software: Overland Park, KS, USA, 2016. [Google Scholar]
- Lu, T.; Chen, F. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef]
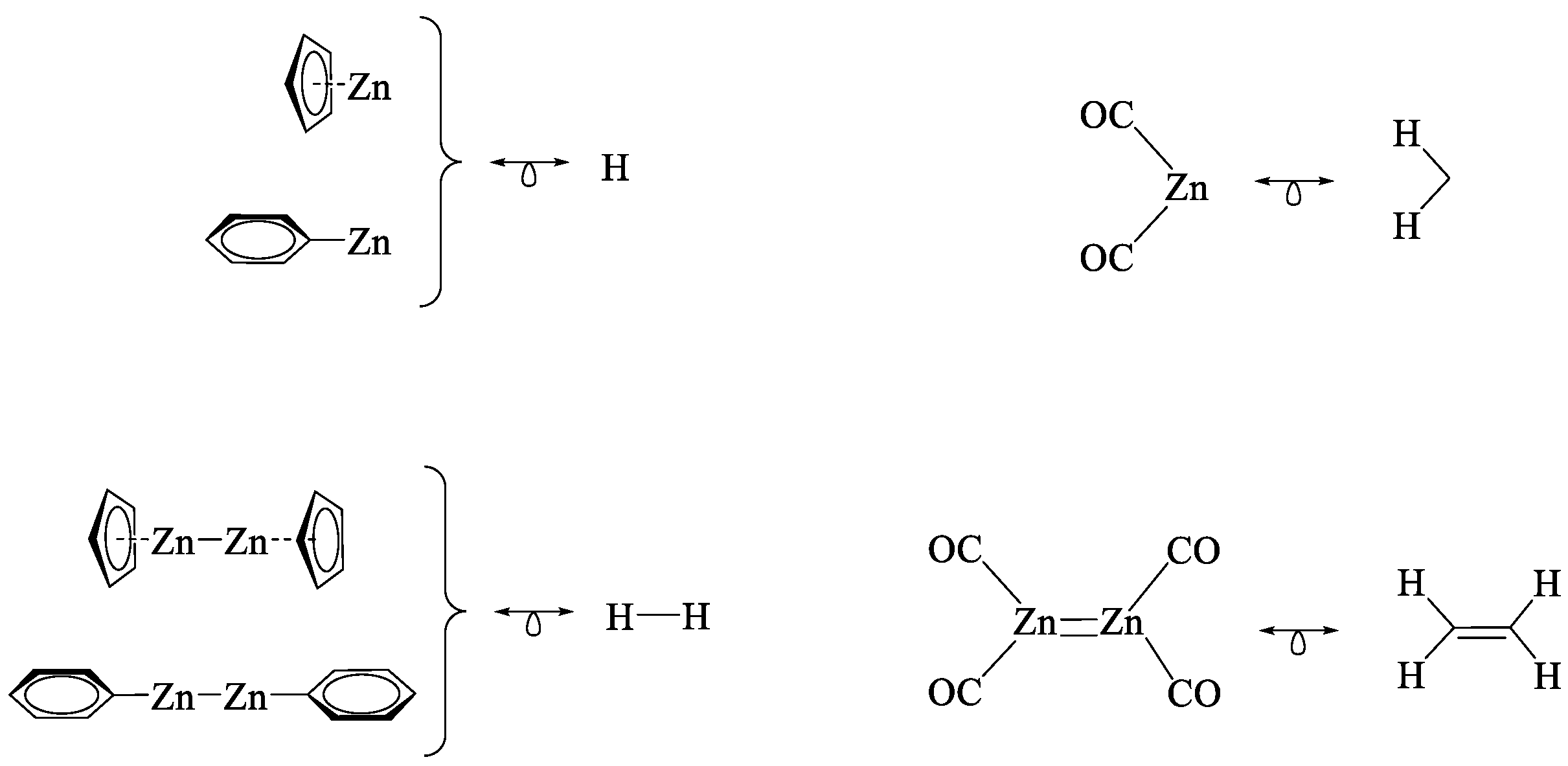
| 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| Zn–Zn | 2.386 | 2.416 | 2.392, 2.413 a | 2.375, 2.491 a | 2.403, 2.498 a | 2.375, 2.402 b, 2.495 a |
| Zn–CCO | 2.118 | 2.060 | 2.088 | 2.088, 2.100 | 2.065, 2.079 | 2.067, 2.090, 2.076, 2.099 |
| Zn–Cpcentroid | 1.960 | - | 1.959 | 1.960 | - | 1.958 |
| Zn–CPh | - | 1.973 | 1.974 | - | 1.972 | 1.973 |
| C–O | 1.134 | 1.137 | 1.135 | 1.135, 1.138 | 1.137, 1.139 | 1.136, 1.137, 1.139 |
| Zn–Zn–Zn | 138.5 | 129.4 | 133.9 | 134.0 | 129.9 | 130.7, 133.1 |
| CCO–Zn–CCO | 91.9 | 94.0 | 92.9 | 92.5 | 92.9 | 92.4, 93.0 |
| Zn–Zn–Cpcentroid | 177.3 | - | 177.1 | 176.4 | - | 176.6 |
| Zn–Zn–CPh | - | 176.4 | 176.8 | - | 176.8 | 176.7 |
| Complex | Zn–Zn | ρBCP | ▽2ρBCP | |VBCP|/GBCP | GBCP/ρBCP | HBCP/ρBCP | εBCP | δ(Zn,Zn) | WBI | ∫Zn∩Znρ |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2.386 | 0.058 | 0.041 | 1.633 | 0.483 | −0.306 | 0.013 | 0.746 | 0.84 | 0.678 |
| 2 | 2.416 | 0.057 | 0.027 | 1.724 | 0.432 | −0.313 | 0.032 | 0.733 | 0.69 | 0.661 |
| 3 | 2.392 2.413 | 0.057 0.058 | 0.041 0.027 | 1.625 1.737 | 0.484 0.428 | −0.303 −0.315 | 0.019 0.024 | 0.729 0.749 | 0.84 0.70 | 0.679 0.659 |
| 4 | 2.375 2.491 | 0.059 0.048 | 0.044 0.023 | 1.618 1.719 | 0.492 0.424 | −0.304 −0.305 | 0.017 0.001 | 0.781 0.750 | 0.86 0.59 | 0.682 0.674 |
| 5 | 2.403 2.498 | 0.058 0.047 | 0.028 0.024 | 1.720 1.701 | 0.436 0.429 | −0.314 −0.301 | 0.026 0.004 | 0.770 0.496 | 0.72 0.60 | 0.664 0.667 |
| 6 | 2.375 2.402 2.495 | 0.058 0.059 0.048 | 0.043 0.029 0.023 | 1.618 1.718 1.709 | 0.491 0.436 0.427 | −0.304 −0.314 −0.303 | 0.017 0.027 0.006 | 0.778 0.774 0.498 | 0.86 0.72 0.59 | 0.682 0.666 0.672 |
| 7 | 8 | |
|---|---|---|
| Zn–Zn | 2.430 | 2.445, 2.459, 2.495 |
| Zn–CCO | 1.973 | 2.050–2.062 |
| C–O | 1.141 | 1.138–1.140 |
| Zn–Zn–Zn | 60.0 | 104.6, 106.6, 107.2 |
| CCO–Zn–CCO | 105.7 | 95.8, 95.9, 96.7 |
| Complex | Zn–Zn | ρBCP | ▽2ρBCP | |VBCP|/GBCP | GBCP/ρBCP | HBCP/ρBCP | εBCP | δ(Zn,Zn) | WBI | ∫Zn∩Znρ |
|---|---|---|---|---|---|---|---|---|---|---|
| 7 | 2.430 | 0.052 | 0.045 | 1.567 | 0.500 | −0.283 | 0.641 | 0.552 | 0.59 | 0.556 |
| 8 | 2.445 2.459 2.495 | 0.051 0.050 0.047 | 0.032 0.031 0.025 | 1.659 1.658 1.687 | 0.451 0.450 0.431 | −0.297 −0.296 −0.296 | 0.036 0.033 0.051 | 0.593 0.552 0.497 | 0.65 0.62 0.55 | 0.634 0.633 0.634 |
| [Zn2(CO)4] | 2.278 | 0.067 | 0.084 | 1.481 | 0.609 | −0.316 | 0.050 | 0.996 | 1.09 | 0.784 |
| Complex | %SFba | %SFZn | %SFO |
|---|---|---|---|
| 1 | 42.19–36.39 ZnCp-ZnCO | 1.73 | 6.45 |
| 2 | 43.89–36.40 ZnPh-ZnCO | 2.31 | 6.56 |
| 3 | 41.87–35.61 ZnCp-ZnCO 44.04–37.22 ZnPh-ZnCO | 2.33 1.68 | 6.77 6.28 |
| 4 | 42.27–37.16 ZnCp-ZnCO 33.29–33.29 ZnPh-ZnCO | 0.73/0.16 2.06 | 6.13 7.77 |
| 5 | 44.06–37.88 ZnPh-ZnCO 32.53–32.53 ZnPh-ZnCO | 0.62/0.35 2.77 | 6.06 8.09 |
| 6 | 42.17–37.19 ZnCp-ZnCO 44.07–37.94 ZnPh-ZnCO 32.70–33.06 ZnPh-ZnCO | 0.72/0.36 0.69/0.14 2.07/2.074 | 6.14 6.04 7.93 |
| 7 | 31.10–31.10 * 22.40 | 7.86 | 6.53 4.03 |
| 8 | 34.09–34.09 (aver) * −9.78 (aver) | [−0.15–1.08] | 7.02 (aver) 2.01 (aver) |
| Complex | V(ZnCp-ZnCO) | V(ZnPh-ZnCO) | V(ZnCO-ZnCO) |
| 1 | 2.38 | ||
| 2 | 2.23 | ||
| 3 | 2.33 | 2.28 | |
| 4 | 2.45 | 1.61 | |
| 5 | 2.35 | 1.50 | |
| 6 | 2.45 | 2.36 | 1.55 |
| 7 | 1.23 | ||
| 8 | 1.56 1.71 (×2) 1.84 (×2) | ||
| [Zn2(CO)4] | 3.05 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ayala, R.; Galindo, A. Theoretical Analysis of Polynuclear Zinc Complexes Isolobally Related to Hydrocarbons. Int. J. Mol. Sci. 2022, 23, 14858. https://doi.org/10.3390/ijms232314858
Ayala R, Galindo A. Theoretical Analysis of Polynuclear Zinc Complexes Isolobally Related to Hydrocarbons. International Journal of Molecular Sciences. 2022; 23(23):14858. https://doi.org/10.3390/ijms232314858
Chicago/Turabian StyleAyala, Regla, and Agustín Galindo. 2022. "Theoretical Analysis of Polynuclear Zinc Complexes Isolobally Related to Hydrocarbons" International Journal of Molecular Sciences 23, no. 23: 14858. https://doi.org/10.3390/ijms232314858
APA StyleAyala, R., & Galindo, A. (2022). Theoretical Analysis of Polynuclear Zinc Complexes Isolobally Related to Hydrocarbons. International Journal of Molecular Sciences, 23(23), 14858. https://doi.org/10.3390/ijms232314858







