A Cost Effective Scheme for the Highly Accurate Description of Intermolecular Binding in Large Complexes
Abstract
1. Introduction
2. Results
2.1. The Reference Interaction Energies
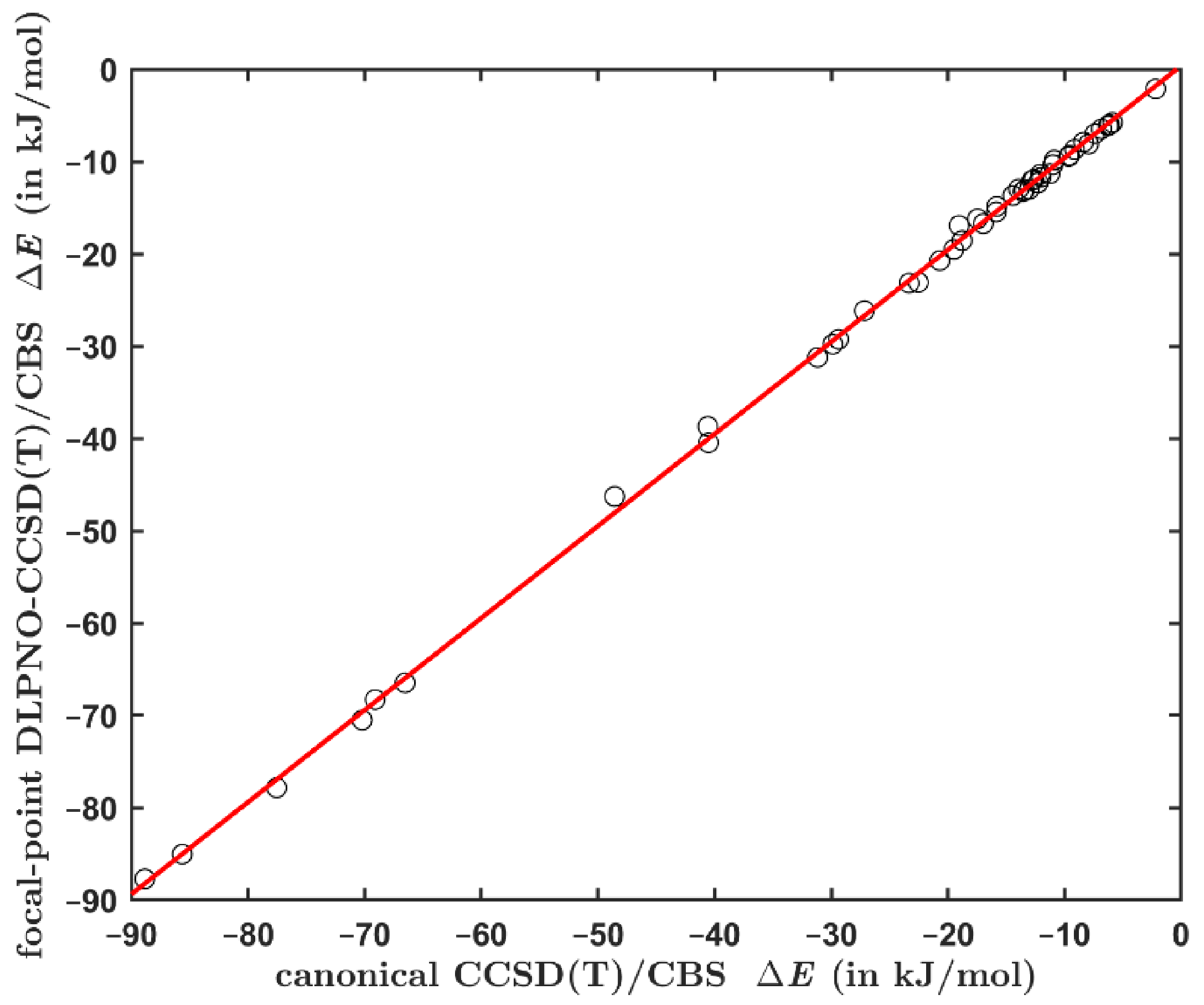
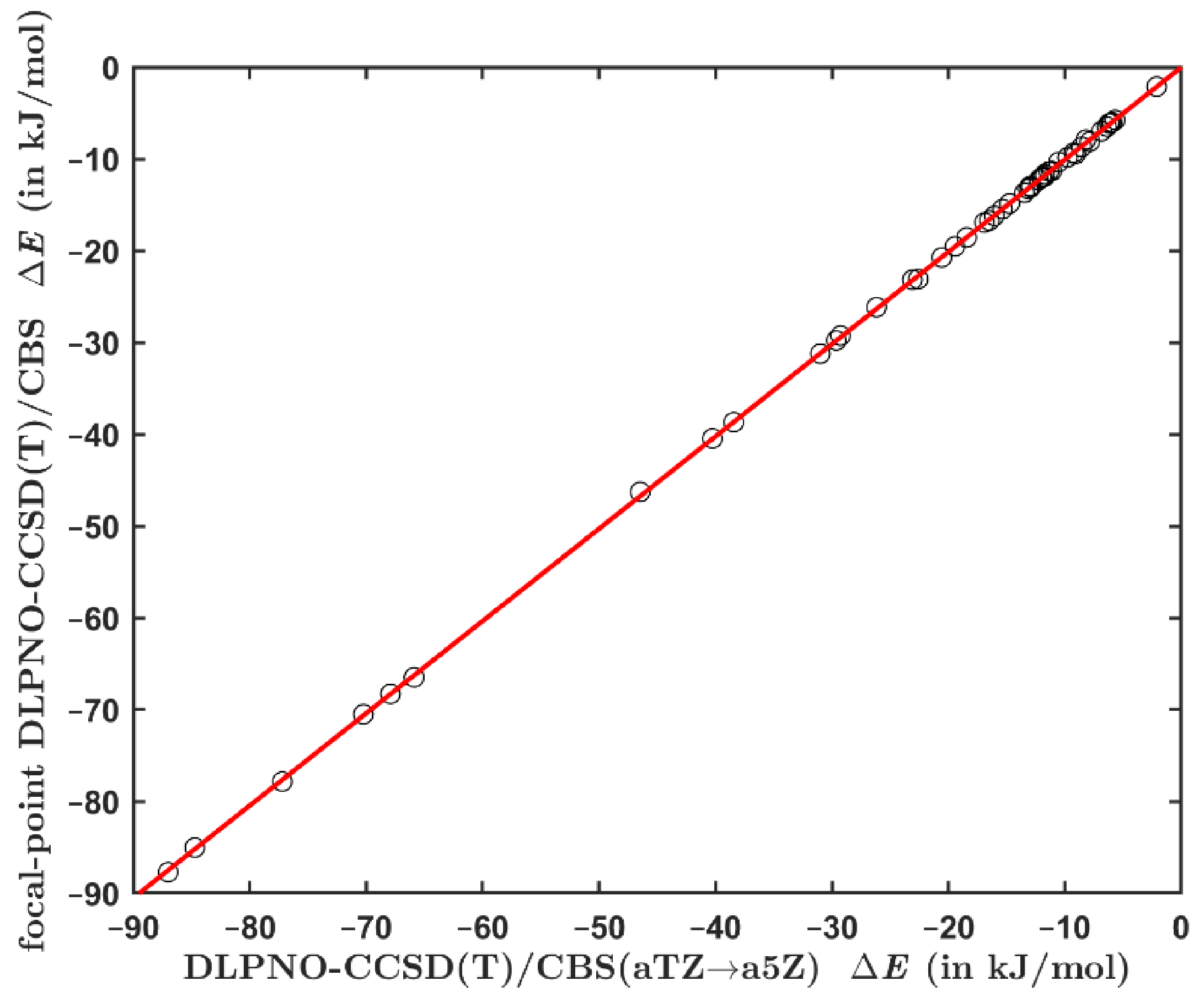
2.2. Comparing the Canonical and DLPNO-Based CCSD(T) Data
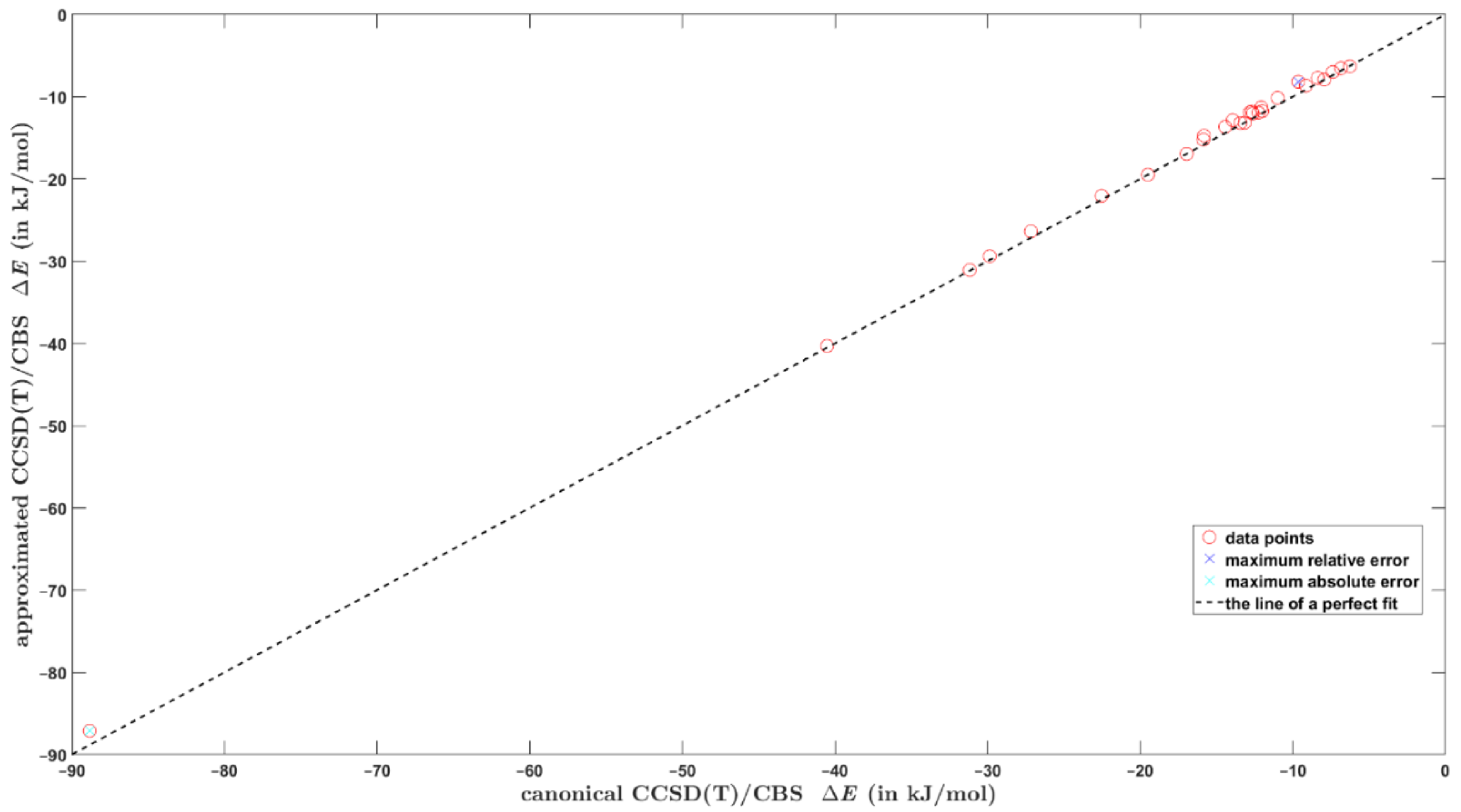
2.3. The Fittings Scheme for Smaller Basis Sets
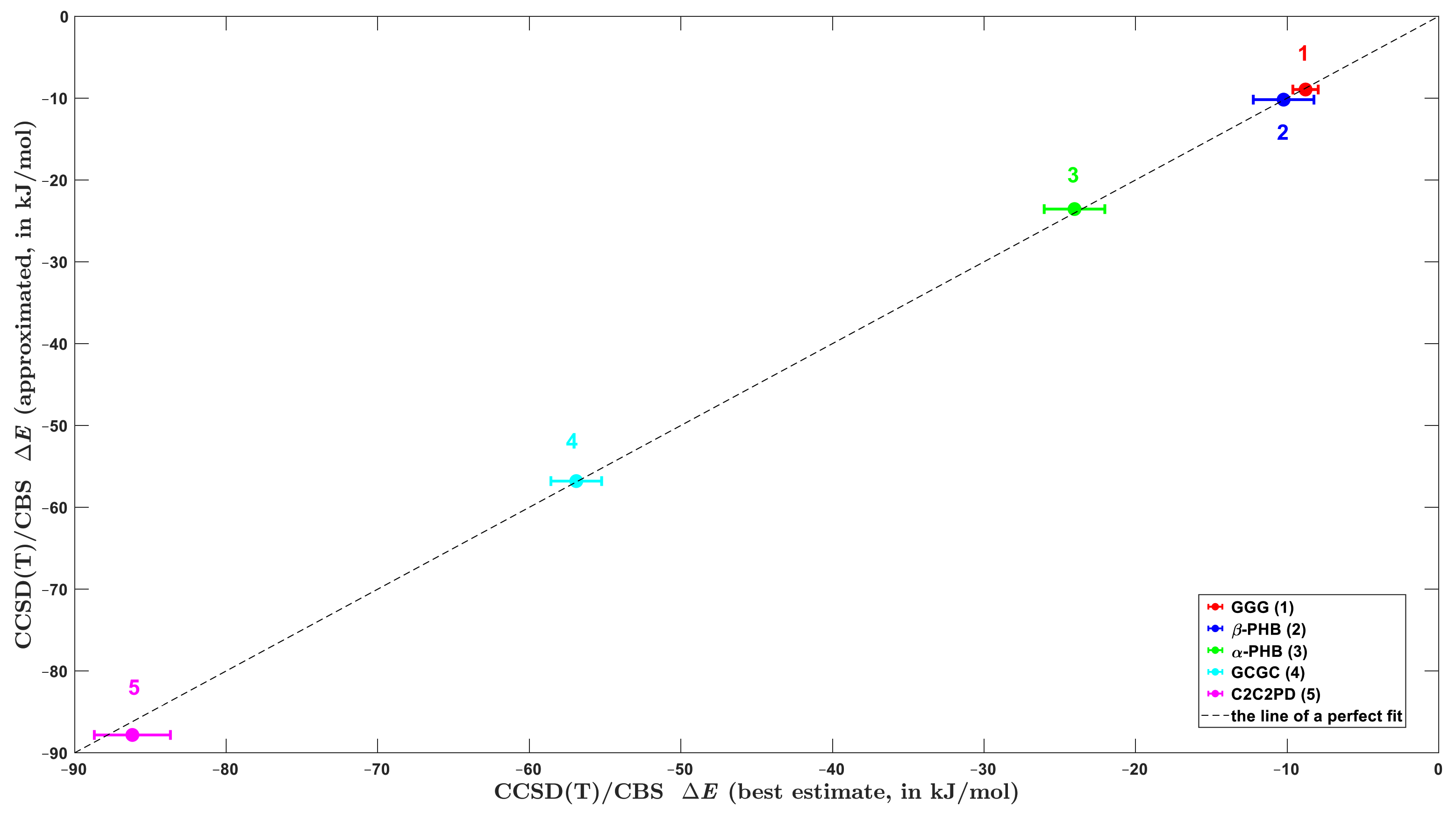
2.4. Testing Large Systems
3. Discussion
4. Materials and Methods
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bernstein, E. Intra- and Intermolecular Interactions between Non-covalently Bonded Species, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2020. [Google Scholar]
- Jin, M.Y.; Zhen, Q.; Xiao, D.; Tao, G.; Xing, X.; Yu, P.; Xu, C. Engineered non-covalent π interactions as key elements for chiral recognition. Nat. Commun. 2022, 13, 3276. [Google Scholar] [CrossRef] [PubMed]
- Jiao, Y.; Chen, X.-Y.; Stoddard, J.F. Weak bonding strategies for achieving regio- and site-selective transformations. Chem 2022, 8, 414–438. [Google Scholar] [CrossRef]
- Jena, S.; Dutta, J.; Tulsiyan, K.D.; Sahu, A.K.; Choudhury, S.S.; Biswal, H.S. Noncovalent interactions in proteins and nucleic acids: Beyond hydrogen bonding and π-stacking. Chem. Soc. Rev. 2022, 51, 4261–4286. [Google Scholar] [CrossRef] [PubMed]
- Puzzarini, C.; Spada, L.; Alessandrini, S.; Barone, V. The challenge of non-covalent interactions: Theory meets experiment for reconciling accuracy and interpretation. J. Phys. Condens. Matter. 2020, 32, 343002. [Google Scholar] [CrossRef] [PubMed]
- Patkowski, K. Recent developments in symmetry-adapted perturbation theory. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2020, 10, e1452. [Google Scholar] [CrossRef]
- Shahbaz, M.; Szalewicz, K. Evaluation of methods for obtaining dispersion energies used in density functional calculations of intermolecular interactions. Theor. Chem. Acc. 2019, 138, 25. [Google Scholar] [CrossRef]
- Carter-Fenk, C.; Lao, K.U.; Herbert, J.M. Predicting and Understanding Non-Covalent Interactions Using Novel Forms of Symmetry-Adapted Perturbation Theory. Acc. Chem. Res. 2021, 54, 3679–3690. [Google Scholar] [CrossRef]
- Sharapa, D.I.; Margraf, J.T.; Hesselmann, A.; Clark, T. Accurate Intermolecular Potential for the C60 Dimer: The Performance of Different Levels of Quantum Theory. J. Chem. Theory Comput. 2017, 13, 274–285. [Google Scholar] [CrossRef]
- Szalewicz, K.; Jeziorski, J. Physical mechanisms of intermolecular interactions from symmetry-adapted perturbation theory. J. Molec. Model. 2022, 28, 273. [Google Scholar] [CrossRef]
- Calvin, J.A.; Peng, C.; Rishi, V.; Kumar, A.; Valeev, E.F. Many-Body Quantum Chemistry on Massively Parallel Computers. Chem. Rev. 2021, 121, 1203–1231. [Google Scholar] [CrossRef]
- Burns, L.A.; Faver, J.C.; Zheng, Z.; Marshall, M.S.; Smith, D.G.A.; Vanommeslaeghe, K.; MacKerrel, A.D.; Merz, K.M.; Sherrill, C.D. The BioFragment Database (BFDb): An open-data platform for computational chemistry analysis of noncovalent interactions. J. Chem. Phys. 2017, 147, 161727. [Google Scholar] [CrossRef]
- Zhang, I.Y.; Grüneis, A. Coupled Cluster Theory in Materials Science. Front. Mater. 2019, 6, 123. [Google Scholar] [CrossRef]
- Kříž, K.; Nováček, M.; Řezáč, J. Non-Covalent Interactions Atlas Benchmark Data Sets 3: Repulsive Contacts. J. Chem. Theory Comput. 2021, 17, 1548–1561. [Google Scholar] [CrossRef]
- Kříž, K.; Řezáč, J. Non-covalent interactions atlas benchmark data sets 4: σ-hole interactions. Phys. Chem. Chem. Phys. 2022, 24, 14794–14804. [Google Scholar] [CrossRef]
- Spicher, S.; Caldeweyher, E.; Hansen, A.; Grimme, S. Benchmarking London dispersion corrected density functional theory for noncovalent ion–π interactions. Phys. Chem. Chem. Phys. 2021, 23, 11635–11648. [Google Scholar] [CrossRef]
- Huang, H.-H.; Wang, Y.-S.; Chao, S.D. A Minimum Quantum Chemistry CCSD(T)/CBS Data Set of Dimeric Interaction Energies for Small Organic Functional Groups: Heterodimers. ACS Omega 2022, 7, 20059–20080. [Google Scholar] [CrossRef]
- Czernek, J.; Brus, J. Parametrizing the Spatial Dependence of 1H NMR Chemical Shifts in π-Stacked Molecular Fragments. Int. J. Mol. Sci. 2020, 21, 7908. [Google Scholar] [CrossRef]
- Gyevi-Nagy, L.; Kállay, M.; Nagy, P.R. Integral-direct and parallel implementation of the CCSD(T) method: Algorithmic developments and large-scale applications. J. Chem. Theory Comput. 2020, 16, 366–384. [Google Scholar] [CrossRef]
- Nagy, P.R.; Gyevi-Nagy, L.; Lőrincz, B.D.; Kállay, M. Pursuing the bases set limit of CCSD(T) non-covalent interaction energies for medium-sized complexes: Case study on the S66 compilation. Mol. Phys. 2022, e2109526. [Google Scholar] [CrossRef]
- Riplinger, C.; Neese, F. An efficient and near linear scaling pair natural orbital based local coupled cluster method. J. Chem. Phys. 2013, 138, 034106. [Google Scholar] [CrossRef]
- Riplinger, C.; Sandhoefer, B.; Hansen, A.; Neese, F. Natural triple excitations in local coupled cluster calculations with pair natural orbitals. J. Chem. Phys. 2013, 139, 134101. [Google Scholar] [CrossRef] [PubMed]
- Riplinger, C.; Pinski, P.; Becker, U.; Valeev, E.F.; Neese, F. Sparse maps–A systematic infrastructure for reduced-scaling electronic structure methods. II. Linear scaling domain based pair natural orbital coupled cluster theory. J. Chem. Phys. 2016, 144, 024109. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.; Riplinger, C.; Becker, U.; Liakos, D.G.; Minenkov, Y.; Cavallo, L.; Neese, F. Communication: An improved linear scaling perturbative triples correction for the domain based local pair-natural orbital based singles and doubles coupled cluster method [DLPNO-CCSD(T)]. J. Chem. Phys. 2018, 148, 011101. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.; Riplinger, C.; Liakos, D.G.; Becker, U.; Saitow, M.; Neese, F. Linear scaling perturbative triples correction approximations for open-shell domain-based local pair natural orbital coupled cluster singles and doubles theory [DLPNO-CCSD(T0/T)]. J. Chem. Phys. 2020, 152, 024116. [Google Scholar] [CrossRef]
- Liakos, D.G.; Sparta, M.; Kesharwani, M.K.; Martin, J.M.L.; Neese, F. Exploring the Accuracy Limits of Local Pair Natural Orbital Coupled-Cluster Theory. J. Chem. Theory Comput. 2015, 11, 1525–1539. [Google Scholar] [CrossRef]
- Liakos, D.G.; Guo, Y.; Neese, F. Comprehensive Benchmark Results for the Domain Based Local Pair Natural Orbital Coupled Cluster Method (DLPNO-CCSD(T)) for Closed- and Open-Shell Systems. J. Phys. Chem. A 2020, 124, 90–100. [Google Scholar] [CrossRef]
- Chen, J.-L.; Sun, T.; Wang, Y.-B.; Wang, W. Toward a less costly but accurate calculation of the CCSD(T)/CBS noncovalent interaction energy. J. Comput. Chem. 2020, 41, 1252–1260. [Google Scholar] [CrossRef]
- Beck, M.E.; Riplinger, C.; Neese, F. Unraveling individual host–guest interactions in molecular recognition from first principles quantum mechanics: Insights into the nature of nicotinic acetylcholine receptor agonist binding. J. Comput. Chem. 2021, 42, 293–302. [Google Scholar] [CrossRef]
- Villot, C.; Ballesteros, F.; Wang, D.; Lao, K.U. Coupled Cluster Benchmarking of Large Noncovalent Complexes in L7 and S12L as Well as the C60 Dimer, DNA–Ellipticine, and HIV–Indinavir. J. Phys. Chem. A 2022, 126, 4326–4341. [Google Scholar] [CrossRef]
- Sandler, I.; Chen, J.; Taylor, M.; Sharma, S.; Ho, J. Accuracy of DLPNO-CCSD(T): Effect of Basis Set and System Size. J. Phys. Chem. A 2021, 125, 1553–1563. [Google Scholar] [CrossRef]
- Kruse, H.; Mladek, A.; Gkionis, K.; Hansen, A.; Grimme, S.; Sponer, J. Quantum Chemical Benchmark Study on 46 RNA Backbone Families Using a Dinucleotide Unit. J. Chem. Theory Comput. 2015, 11, 4972–4991. [Google Scholar] [CrossRef]
- Altun, A.; Neese, F.; Bistoni, G. Extrapolation to the Limit of a Complete Pair Natural Orbital Space in Local Coupled-Cluster Calculations. J. Chem. Theory Comput. 2020, 16, 6142–6149. [Google Scholar] [CrossRef]
- East, A.L.L.; Allen, D.L. The heat of formation of NCO. J. Chem. Phys. 1993, 99, 4638–4650. [Google Scholar] [CrossRef]
- Jurečka, P.; Šponer, J.; Černý, J.; Hobza, P. Benchmark database of accurate (MP2 and CCSD(T) complete basis set limit) interaction energies of small model complexes, DNA base pairs, and amino acid pairs. Phys. Chem. Chem. Phys. 2006, 8, 1985–1993. [Google Scholar] [CrossRef]
- Wang, H.; Tashiro, K. Reinvestigation of Crystal Structure and Intermolecular Interactions of Biodegradable Poly(3-Hydroxybutyrate) α-Form and the Prediction of Its Mechanical Property. Macromolecules 2016, 49, 581–594. [Google Scholar] [CrossRef]
- Phongtamrug, S.; Tashiro, K. X-ray Crystal Structure Analysis of Poly(3-hydroxybutyrate) β-Form and the Proposition of a Mechanism of the Stress-Induced α-to-β Phase Transition. Macromolecules 2019, 52, 2995–3009. [Google Scholar] [CrossRef]
- Sedlak, R.; Janowski, T.; Pitoňák, M.; Řezáč, J.; Pulay, P.; Hobza, P. Accuracy of Quantum Chemical Methods for Large Noncovalent Complexes. J. Chem. Theory Comput. 2013, 9, 3364–3374. [Google Scholar] [CrossRef]
- Kent, P.R.C.; Annaberdiyev, A.; Benali, A.; Bennett, M.C.; Landinez Borda, E.J.; Doak, P.; Hao, H.; Jordan, K.D.; Krogel, J.T.; Kylänpää, I.; et al. QMCPACK: Advances in the development, efficiency, and application of auxiliary field and real-space variational and diffusion quantum Monte Carlo. J. Chem. Phys. 2020, 152, 174105. [Google Scholar] [CrossRef]
- Benali, A.; Shin, H.; Heinonen, O. Quantum Monte Carlo benchmarking of large noncovalent complexes in the L7 benchmark set. J. Chem. Phys. 2020, 153, 194113. [Google Scholar] [CrossRef]
- Morales-Silva, M.A.; Jordan, K.D.; Shulenburger, L.; Wagner, L.K. Frontiers of stochastic electronic structure calculations. J. Chem. Phys. 2021, 154, 170401. [Google Scholar] [CrossRef]
- Ballesteros, F.; Dunivan, S.; Lao, K.U. Coupled cluster benchmarks of large noncovalent complexes: The L7 dataset as well as DNA–ellipticine and buckycatcher–fullerene. J. Chem. Phys. 2021, 154, 154104. [Google Scholar] [CrossRef] [PubMed]
- Al-Hamdani, Y.S.; Nagy, P.R.; Zen, A.; Barton, D.; Kállay, M.; Bradenburg, J.G.; Tchatkenko, A. Interactions between large molecules pose a puzzle for reference quantum mechanical methods. Nat. Commun. 2021, 12, 3927. [Google Scholar] [CrossRef] [PubMed]
- Boys, S.F.; Bernardi, F. The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors. Mol. Phys. 1970, 19, 553–566. [Google Scholar] [CrossRef]
- Riley, K.E.; Pitoňák, M.; Jurečka, P.; Hobza, P. Stabilization and Structure Calculations for Noncovalent Interactions in Extended Molecular Systems Based on Wave Function and Density Functional Theories. Chem. Rev. 2010, 110, 5023–5063. [Google Scholar] [CrossRef]
- Marshall, M.S.; Burns, L.A.; Sherrill, C.D. Basis set convergence of the coupled-cluster correction: Best practices for benchmarking non-covalent interactions and the attendant revision of the S22, NBC10, HBC6, and HSG databases. J. Chem. Phys. 2011, 135, 194102. [Google Scholar] [CrossRef] [PubMed]
- Řezáč, J.; Riley, K.E.; Hobza, P. S66: A Well-balanced Database of Benchmark Interaction Energies Relevant to Biomolecular Structures. J. Chem. Theory Comput. 2011, 7, 2427–2438. [Google Scholar] [CrossRef]
- Bootsma, A.N.; Doney, A.C.; Wheeler, S.E. Predicting the Strength of Stacking Interactions between Heterocycles and Aromatic Amino Acid Side Chains. J. Am. Chem. Soc. 2019, 141, 11027–11035. [Google Scholar] [CrossRef]
- Liu, Y.; Li, J.; Felker, P.M.; Bačić, Z. HCl–H2O dimer: An accurate full-dimensional potential energy surface and fully coupled quantum calculations of intra- and intermolecular vibrational states and frequency shifts. Phys. Chem. Chem. Phys. 2021, 23, 7101–7114. [Google Scholar] [CrossRef]
- Sexton, T.M.; Van Benschoten, W.Z.; Tschumper, G.S. Dissociation energy of the HCN⋯HF dimer. Chem. Phys. Lett. 2020, 748, 137382. [Google Scholar] [CrossRef]
- Hoobler, P.R.; Turney, J.M.; Agarwal, J.; Schaefer III, J.F. Fundamental Vibrational Analyses of the HCN Monomer, Dimer and Associated Isotopologues. ChemPhysChem 2018, 19, 3257–3265. [Google Scholar] [CrossRef]
- Carter-Fenk, K.; Lao, K.U.; Liu, K.-Y.; Herbert, J.M. Accurate and Efficient ab Initio Calculations for Supramolecular Complexes: Symmetry-Adapted Perturbation Theory with Many-Body Dispersion. J. Phys. Chem. Lett. 2019, 10, 2706–2714. [Google Scholar] [CrossRef]
- Halkier, A.; Helgaker, T.; Jørgensen, P.; Klopper, W.; Koch, H.; Olsen, J.; Wilson, A.K. Basis-set convergence in correlated calculations on Ne, N2, and H2O. Chem. Phys. Lett. 1998, 286, 243–252. [Google Scholar] [CrossRef]
- Pinski, P.; Riplinger, C.; Valeev, E.F.; Neese, F. Sparse maps–A systematic infrastructure for reduced-scaling electronic structure methods. I. An efficient and simple linear scaling local MP2 method that uses an intermediate basis of pair natural orbitals. J. Chem. Phys. 2015, 143, 034108. [Google Scholar] [CrossRef]
- Vogiatzis, K.D.; Klopper, W. Accurate non-covalent interactions with basis-set corrections from interference-corrected perturbation theory: Comparison with the S22B database. Mol. Phys. 2013, 111, 2299–2305. [Google Scholar] [CrossRef]
- Peterson, K.A.; Woon, D.E.; Dunnig, T.J., Jr. Benchmark calculations with correlated wave functions. J. Chem. Phys. 1994, 100, 7410–7415. [Google Scholar] [CrossRef]
- Takatani, T.; Hohenstein, E.G.; Malagoli, M.; Marshall, M.C.; Sherrill, C.D. Basis set consistent revision of the S22 test set of noncovalent interaction energies. J. Chem. Phys. 2010, 132, 144104. [Google Scholar] [CrossRef]
- Ye, H.-Z.; Berkelbach, T.C. Correlation-Consistent Gaussian Basis Sets for Solids Made Simple. J. Chem. Theory Comput. 2022, 18, 1595–1606. [Google Scholar] [CrossRef]
- Neese, F.; Valeev, E.F. Revisiting the Atomic Natural Orbital Approach for Basis Sets: Robust Systematic Basis Sets for Explicitly Correlated and Conventional Correlated ab initio Methods? J. Chem. Theory Comput. 2011, 7, 33–43. [Google Scholar] [CrossRef]
- Altun, A.; Ghosh, S.; Riplinger, C.; Neese, F.; Bastoni, G. Addressing the System-Size Dependence of the Local Approximation Error in Coupled-Cluster Calculations. J. Phys. Chem. A 2021, 125, 9932–9939. [Google Scholar] [CrossRef]
- Kesharwani, M.K.; Karton, M.; Sylvetsky, N.; Martin, J.M.L. The S66 Non-Covalent Interactions Benchmark Reconsidered Using Explicitly Correlated Methods Near the Basis Set Limit. Austr. J. Chem. 2018, 71, 238–248. [Google Scholar] [CrossRef]
- Ehlers, S.; Grimme, S.; Hansen, A. Conformational Energy Benchmark for Longer n-Alkane Chains. J. Phys. Chem. A 2022, 126, 3521–3535. [Google Scholar] [CrossRef]
- Li, X.; Spada, L.; Alessandrini, S.; Zheng, Y.; Lengsfeld, K.G.; Grabow, J.-U.; Feng, G.; Puzzarini, C.; Barone, V. Stacked but not Stuck: Unveiling the Role of π→π* Interactions with the Help of the Benzofuran–Formaldehyde Complex. Angew. Chem. Int. Ed. 2022, 61, 264–270. [Google Scholar] [CrossRef] [PubMed]
- Goerigk, L.; Hansen, A.; Bauer, C.; Ehrlich, S.; Najibi, A.; Grimme, S. A look at the density functional theory zoo with the advanced GMTKN55 database for general main group thermochemistry, kinetics and noncovalent interactions. Phys. Chem. Chem. Phys. 2017, 19, 32184–32215. [Google Scholar] [CrossRef] [PubMed]
- Al-Hamdani, Y.S.; Tkatchenko, A. Understanding non-covalent interactions in larger molecular complexes from first principles. J. Chem. Phys. 2019, 150, 010901. [Google Scholar] [CrossRef]
- Czernek, J.; Brus, J.; Czerneková, V. A computational inspection of the dissociation energy of mid-sized organic dimers. J. Chem. Phys. 2022, 156, 204303. [Google Scholar] [CrossRef] [PubMed]
- Becucci, M.; Mazzoni, F.; Pietraperzia, G.; Řezáč, J.; Nachtigallová, D.; Hobza, P. Non-covalent interactions in anisole–(CO2)n (n = 1, 2) complexes. Phys. Chem. Chem. Phys. 2017, 19, 22749–22758. [Google Scholar] [CrossRef]
- Leforestier, C.; Tekin, A.; Jansen, G.; Herman, M. First principles potential for the acetylene dimer and refinement by fitting to experiments. J. Chem. Phys. 2011, 135, 234306. [Google Scholar] [CrossRef]
- Frish, M.J.; Trucks, J.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16; Revision C.01; Gaussian, Inc.: Wallingford, CT, USA, 2019. [Google Scholar]
- The Benchmark Energy & Geometry Database (BEGDB). Available online: http://www.begdb.org/ (accessed on 5 October 2022).
- Werner, H.J.; Knowles, P.J.; Manby, F.R.; Black, J.A.; Doll, K.; Hesselmann, A.; Kats, D.; Kohn, A.; Korona, T.; Kreplin, D.A.; et al. The Molpro quantum chemistry package. J. Chem. Phys. 2020, 152, 144107. [Google Scholar] [CrossRef]
- Vahtras, O.; Almlöf, J.; Feyereisen, M.W. Integral approximations for LCAO-SCF calculations. Chem. Phys. Lett. 1993, 213, 514–518. [Google Scholar] [CrossRef]
- Weigend, F.; Häser, M. RI-MP2: First derivatives and global consistency. Theor. Chem. Acc. 1997, 97, 331–340. [Google Scholar] [CrossRef]
- Weigend, F.; Häser, M.; Patzelt, H.; Ahlrichs, R. RI-MP2: Optimized auxiliary basis sets and demonstration of efficiency. Chem. Phys. Lett. 1998, 294, 143–152. [Google Scholar] [CrossRef]
- Balasubramani, S.G.; Chen, G.P.; Coriani, S.; Diedenhofen, M.; Frank, M.S.; Franzke, Y.J.; Furche, F.; Grotjahn, R.; Harding, M.E.; Hättig, C.; et al. TURBOMOLE: Modular program suite for ab initio quantum-chemical and condensed-matter simulations. J. Chem. Phys. 2020, 152, 184107. [Google Scholar] [CrossRef]
- Neese, F. Software update: The ORCA program system–Version 5.0. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2022, 12, e1606. [Google Scholar] [CrossRef]

| Type of System | Description | Components of the DFT-SAPT Energy | Best Estimate of | ||||
|---|---|---|---|---|---|---|---|
| dispersion-dominated complex from Set3x6 | aniline:methane | –6.5 | 18.9 | –1.9 | –17.3 | –6.8 | –6.84 a |
| anisole:methane | –7.1 | 19.9 | –1.6 | –18.5 | –7.3 | –7.39 a | |
| 1-Nap:methane | –9.0 | 25.3 | –1.8 | –23.4 | –8.9 | –9.14 a | |
| 1-Nap:CO | –9.4 | 24.0 | –3.4 | –20.2 | –9.0 | –8.37 a | |
| 1-Nap:CO2 | –13.1 | 28.6 | –3.2 | –24.6 | –12.3 | –12.68 a | |
| anisole:anisole | –32.8 | 72.8 | –8.6 | –57.6 | –26.1 | –27.16 a | |
| mixed-interactions complex from Set3x6 | anisole:ammonia | –16.1 | 24.3 | –3.7 | –15.7 | –11.2 | –12.00 a |
| 1-Nap:ethyne | –25.1 | 35.0 | –10.1 | –17.4 | –17.5 | –16.96 a | |
| HCl:HCl | –11.3 | 17.6 | –6.3 | –9.2 | –9.2 | –7.94 a | |
| benzene:water | –13.5 | 19.2 | –5.1 | –14.7 | –14.0 | –13.43 a | |
| anisole:CO2 | –20.5 | 28.6 | –3.5 | –18.8 | –14.1 | –15.86 a | |
| ethyne:ethyne | –9.0 | 11.6 | –2.9 | –6.9 | –7.3 | –6.26 a | |
| electrostatics-dominated complex from Set3x6 | 1-Nap:ammonia | –70.0 | 80.6 | –28.7 | –22.8 | –40.9 | –40.52 a |
| HCl:water | –41.5 | 50.7 | –17.6 | –14.3 | –22.8 | –22.47 b | |
| HCN:HF | –42.6 | 42.9 | –18.5 | –11.8 | –30.1 | –31.09 c | |
| NCH:FH | –15.4 | 11.5 | –3.4 | –5.2 | –12.4 | –12.34 c | |
| HCN:HCN | –25.2 | 20.3 | –6.8 | –7.8 | –19.5 | –19.83 d | |
| 1-Nap:water | –46.2 | 50.0 | –15.8 | –16.6 | –28.6 | –29.86 a | |
| furan:toluene stacked complex from reference [48] | configuration #1 | –9.0 | 26.5 | –2.9 | –29.2 | –14.5 | –14.43 |
| configuration #2 | –8.9 | 27.6 | –3.1 | –29.8 | –14.2 | –13.94 | |
| configuration #3 | –7.3 | 26.5 | –2.8 | –29.3 | –12.9 | –12.62 | |
| configuration #4 | –7.7 | 25.9 | –3.1 | –28.3 | –13.2 | –12.82 | |
| configuration #5 | –7.6 | 25.6 | –2.8 | –27.8 | –12.5 | –12.06 | |
| configuration #6 | –6.7 | 23.7 | –2.6 | –25.9 | –11.5 | –11.00 | |
| configuration #7 | –5.3 | 20.8 | –2.2 | –23.5 | –10.1 | –9.65 | |
| miscellaneous | anthracene: cyclopropenium | –58.5 | 81.8 | –60.3 | –48.3 | –85.3 | (–89.96 ±0.84) e |
| pyridine:pyridine | –12.0 | 28.2 | –3.3 | –29.8 | –16.8 | –15.82 a | |
| large | α-PHB model | –14.7 | 17.5 | –3.8 | –25.1 | –26.1 | –24.03 f |
| β-PHB model | –8.1 | 29.1 | –4.0 | –28.4 | –11.4 | –10.23 f | |
| C2C2PD | –37.1 –30.8 h | 114.3 107.2 h | –12.8 –10.7 h | –147.1 –154.3 h | –82.7 –88.6 h | (–87.82 ±2.51) g | |
| GCGC | –37.4 –34.6 h | 104.1 97.5 h | –9.5 –8.6 h | –111.9 –115.1 h | –54.7 –60.9 h | (–56.90 ±1.67) g | |
| GGG | 11.3 12.0 h | 27.8 25.7 h | –6.2 –5.6 h | –39.9 –41.0 h | –6.9 –8.9 h | (–8.79 ±0.84) g | |
| Method | α-PHB | β-PHB | GGG | GCGC | C2C2PD |
|---|---|---|---|---|---|
| extrapolations using Equations (3)–(5) | 23.56 | 10.18 | 8.95 | 56.79 | 87.81 |
| the focal point analysis using Equation (2) | 24.03 | 10.23 | 8.87 | 56.44 | 86.19 |
| SAPT-DFT | 26.14 | 11.43 | 6.88 | 54.69 | 82.68 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Czernek, J.; Brus, J.; Czerneková, V. A Cost Effective Scheme for the Highly Accurate Description of Intermolecular Binding in Large Complexes. Int. J. Mol. Sci. 2022, 23, 15773. https://doi.org/10.3390/ijms232415773
Czernek J, Brus J, Czerneková V. A Cost Effective Scheme for the Highly Accurate Description of Intermolecular Binding in Large Complexes. International Journal of Molecular Sciences. 2022; 23(24):15773. https://doi.org/10.3390/ijms232415773
Chicago/Turabian StyleCzernek, Jiří, Jiří Brus, and Vladimíra Czerneková. 2022. "A Cost Effective Scheme for the Highly Accurate Description of Intermolecular Binding in Large Complexes" International Journal of Molecular Sciences 23, no. 24: 15773. https://doi.org/10.3390/ijms232415773
APA StyleCzernek, J., Brus, J., & Czerneková, V. (2022). A Cost Effective Scheme for the Highly Accurate Description of Intermolecular Binding in Large Complexes. International Journal of Molecular Sciences, 23(24), 15773. https://doi.org/10.3390/ijms232415773






